45 PENYELESAIAN INTEGRAL RANGKAP DUA DENGAN METODE SIMPSON DAN KUADRAATUR GAUSS
IRWAN
Jurusan Matematika,
Fakultas Sains dan Teknologi, UINAM e-mail:[email protected]
Info:
Jurnal MSA Vol. 2 No. 1 Edisi: Januari – Juni 2014 Artikel No.: 7
Halaman: 45 - 50 ISSN Print: 2355-083X Prodi Matematika UINAM
ABSTRAK
Penyelesaian integral rangkap dua suatu fungsi yang kompleks dengan cara analitik memerlukan waktu yang banyak dan ketelitian yang tinggi bahwa terkadang sulit untuk mendapatkan solusinya. Namun demikian, hal tersebut tidak jadi kendala karena dapat digunakan pendekatan lain untuk lebih cepat menemukan solusinya dengan pendekatan numerik diantarnya metode Simpson dan Kuadratur Gauss. Penyelesaian numerik integral rangkap dua dengan metode Simpson dan Kuadratur Gauss yang menggunakan program Matlab, mampu memberikan nilai integrasi dalam waktu yang lebih cepat. Kasus pertama dengan persamaan 𝑓(𝑥, 𝑦) = 2𝑥√𝑥2+ 𝑦 hasil integrasi yang diperoleh metode Simpson adalah 4,1053
dalam waktu 1,632 detik dan Kuadratur Gauss memperoleh nilai 4,1241 dalam waktu 0,0164 detik, kemudian dengan persamaan 𝑓(𝑥, 𝑦) = 𝑒𝑦cos(𝑥) diperoleh hasil dengan metode Simpson adalah 5,3781 dalam waktu 1,52 detik dan Kuadratur Gauss hasil integralnya 5,3573 dalam
waktu 0,0119 detik. Ketiga dengan persamaan 𝑓(𝑥, 𝑦) =3𝑥𝑦2√𝑥3+1
√2𝑦2+2 hasil
yang diperoleh metode Simpson adalah 6,6058 dalam waktu 1,9005 detik dan Kuadratur Gauss memperoleh hasil integralnya 6,6052 dalam waktu 0,0126 detik. Hasil perhitungan integrasi Simpson memberikan nilai yang mendekati nilai sebenarnya dengan mengambil 𝑛 genap. Secara komputasi integrasi Kuadratur Gauss memiliki kecepatan yang tinggi dalam penyelesaiannya. Hal ini dikarenakan tidak menggunakan pembagi area yang banyak seperti pada metode Simpson.
Kata kunci: Metode numerik, Integral rangkap dua, metode Simpson, metode Kuadratur Gauss
1. PENDAHULUAN
Penggunaan matematika dalam memecahkan suatu persoalan dalam kehidupan nyata yaitu dengan mengubah atau menyajikan masalah yang ada ke dalam suatu model atau konsep yang tepat. Pengubahan ini berarti menerjemahkan bahasa kehidupan nyata dan komponen-komponen yang ada pada suatu masalah ke dalam bahasa matematik yang dinyatakan dalam bentuk simbol-simbol. Hal tersebut merujuk pada ciri khas matematika yang bersifat abstrak dan menggunakan bahasa simbol. Salah satu penyelesaian matematika yang dipilih penulis dalam penulisan karya ini adalah integral. Jika
fungsi yang diintegrasikan mempunyai satu variabel, proses disebut Quadrature Mechanic, dan bila fungsi mempunyai dua variabel bebas, proses disebut Cubature Mechanic (Nasution dan Zakaria, 2001:140).
Penerapan integral rangkap dua banyak ditemui dalam bidang sains dan rekayasa, seperti menghitung persamaan volume, luas, massa, pusat massa, dan momen inersia. Contoh-contoh tersebut umumnya memiliki fungsi yang bentuknya rumit sehingga tidak dapat diselesaikan secara analitik. Yang dimaksud dengan metode analitik adalah metode penyelesaian matematika dengan rumus-rumus
46
aljabar yang sudah baku. Nilai yang diperoleh adalah nilai yang sebenarnya. Namun metode analitik, tidak selalu mudah memperoleh solusi bahkan ada yang tidak dapat diperoleh solusi, maka solusi persoalan sebenarnya masih dapat dicari dengan menggunakan metode numerik. Metode numerik merupakan teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat dipecahkan dengan operasi perhitungan atau aritmatika biasa (tambah, kurang, kali dan bagi). Pendekatan numerik yang digunakan untuk menyelesaikan integral rangkap dua adalah integrasi Simpson dan integrasi Kuadratur Gauss. Hal tersebut didasarkan pada perolehan nilai integrasi yang semakin mendekati nilai yang sebenarnya bila dibandingkan dengan metode lainnya.
Metode integrasi Simpson merupakan pengembangan integrasi trapezoida(Basuki dan Ramadijanti, 2005:83). Pendekatan metode Simpson akan memberikan hasil yang paling akurat. Sifat inilah yang menyebabkan metode ini dipakai secara luas (Sutanta, 2004:121).
2. Integral Rangkap Dua
Persamaan integral rangkap dua termasuk integral Qubature mechanic, dengan fungsi integran mempunyai dua variabel bebas. Integrasi dinyatakan sebagai:
𝐼 = ∫ ∫ 𝑓(𝑥, 𝑦)𝑐𝑑 𝑎𝑏 𝑑𝑥𝑑𝑦 = ∫ [∫ 𝑓(𝑥, 𝑦)𝑑𝑦𝑎𝑏 𝑐𝑑 ] 𝑑𝑥.
Metode Simpson
Thomas Simpson mengembangkan metode yang lebih baik lagi, yang disebut aturan Simpson.
Aturan Simpson 1/3
𝐼 ≅ℎ
3(𝑓0+ 4𝑓1+ 𝑓2)
Aturan Simpson 1/3 Gabungan
𝐼𝑡𝑜𝑡 ≅ℎ 3(𝑓0 + 4 ∑ 𝑓𝑖 𝑛−1 𝑖=1,3,5 + 2 ∑ 𝑓𝑖 + 𝑓𝑛 𝑛−2 𝑖=2,4,6 )
Metode Kuadratur Gauss
Pendekatan integrasi yang berbeda dengan metode Simpson dikembangkan oleh Gauss dan dinamakan metode kuadratur Gauss. Dengan metode Kuadratur Gauss, batasan-batasan yang terdapat metode Simpson dihilangkan. Di sini kita tidak perlu lagi menentukan titik diskrit berjarak sama, tetapi nilai integrasi numerik cukup diperoleh dengan menghitung nilai 𝑓(𝑥) pada beberapa titik tertentu. Integrasi Gauss dengan pendekatan 2 titik
∫ 𝑓(𝑥)𝑑𝑥𝑎𝑏 =(𝑏−𝑎) 2 ∫ 𝑓 [ (𝑎+𝑏)+(𝑏−𝑎)𝑡 2 ] 1 −1 𝑑𝑡. 3. METODE PENELITIAN
Langkah-langkah yang dilakukan dalam rangka untuk mencapai tujuan penelitian adalah sebagai berikut:
1. Menyelesaikan integral rangkap dua dengan metode Simpson 1/3
a. Penurunan rumus integral rangkap dua dengan metode Simpson 1/3
b. Algoritma integral rangkap dua dengan metode Simpson 1/3
c. Diagram alur (flowchart) integral rangkap dua dengan metode Simpson 1/3
2. Menyelesaikan integral rangkap dua dengan metode Kuadratur Gauss 2 titik
a. Penurunan rumus integral rangkap dua dengan metode Kuadratur Gauss 2 titik b. Algoritma integral rangkap dua dengan
metode Kuadratur Gauss 2 titik
c. Diagram alur (flowchart) integral rangkap dua dengan metode Kuadratur Gauss 2 titik.
47
4. PEMBAHASAN
Rumus Umum intergral rangkap dua metode Simpson 𝐼 = (ℎ𝑥 3) ( ℎ𝑦 3) [𝑓(𝑥𝑖,𝑦𝑖,0) + 4𝑓(𝑥𝑖,𝑦𝑖,1) + 2𝑓(𝑥𝑖,𝑦𝑖,2) + 4𝑓(𝑥𝑖,𝑦𝑖,3) + ⋯ + 2𝑓(𝑥𝑖,𝑦𝑖,𝑛−2) + 4𝑓(𝑥𝑖,𝑦𝑖,𝑛−1) + 𝑓(𝑥𝑖,𝑦𝑖,𝑛)]
Dari rumusan intergral rangkap dua metode Simpson tersebut selanjutnya untuk memudahkan dalam membuatan atau penyusunan program untuk mencari selosinya, maka diberikan algoritma integral rangkap dua dengan metode Simpson 1/3 sebagai berikut;
a. Mendefinisikan fungsi integran
b. Menentukan batas dua variabel integrasi [𝑎, 𝑏] dan [𝑐, 𝑑]
c. Menentukan banyaknya interval/segmen (𝑛) dengan syarat 𝑛 genap
d. Pilih batas integran yang akan diselesaikan terlebih dahulu.
Jika batas yang dipilih 𝑥, maka hitung ℎ𝑥 = 𝑏 − 𝑎
𝑛
Jika batas yang dipilih 𝑦, maka hitung ℎ𝑦 =𝑑 − 𝑐
𝑛
e. Integrasi pertama;
Jika batas yang dipilih 𝑥, maka hitung 𝑥 =ℎ𝑥
3 [𝑓(𝑥0, 𝑦) + 4 ∑ 𝑓(𝑥𝑖, 𝑦) + 𝑛−1
𝑖ganjil 2 ∑𝑛−2𝑖genap𝑓(𝑥𝑖, 𝑦)+ 𝑓(𝑥𝑛, 𝑦)]
Jika batas yang dipilih 𝑦, maka hitung 𝑦 =ℎ𝑦
3 [𝑓(𝑥, 𝑦0) + 4 ∑ 𝑓(𝑥, 𝑦𝑖) + 𝑛−1
𝑖ganjil 2 ∑𝑛−2𝑖genap𝑓(𝑥, 𝑦𝑖)+ 𝑓(𝑥, 𝑦𝑛)] f. Selanjutnya hasil yang diperoleh dari
langkah (e) dijadikan fungsi integran untuk mencari batas berikutnya.
g. Integrasi kedua;
Jika batas yang dipilih 𝑥, maka hitung 𝐼 =ℎ𝑦
3 [𝑓(𝑥, 𝑦0) + 4 ∑ 𝑓(𝑥, 𝑦𝑖) + 𝑛−1
𝑖ganjil 2 ∑𝑛−2𝑖genap𝑓(𝑥, 𝑦𝑖)+ 𝑓(𝑥, 𝑦𝑛)] Jika batas yang dipilih 𝑦, maka hitung 𝐼 =ℎ𝑥
3 [𝑓(𝑥0, 𝑦) + 4 ∑ 𝑓(𝑥𝑖, 𝑦) + 𝑛−1
𝑖ganjil 2 ∑𝑛−2𝑖genap𝑓(𝑥𝑖, 𝑦)+ 𝑓(𝑥𝑛, 𝑦)] h.Tulis hasil integral.
Masukkan fungsi integran f(x,y) dan
batas-batasnya Masukkan banyaknya interval (n) Batas integran bernilai x mulai Hitung ℎ𝑥= (𝑏 − 𝑎)/𝑛 𝑥 =ℎ𝑥 3 [𝑓(𝑥0, 𝑦) + 4 ∑𝑛−1𝑖ganjil𝑓(𝑥𝑖, 𝑦) + 2 ∑𝑛−2𝑖genap𝑓(𝑥𝑖, 𝑦)+ 𝑓(𝑥𝑛, 𝑦)] Hitung ℎ𝑦= (𝑑 − 𝑐)/𝑛 𝑦 =ℎ𝑦 3 [𝑓(𝑥, 𝑦0) + 4 ∑𝑛−1𝑖ganjil𝑓(𝑥, 𝑦𝑖) + 2 ∑𝑛−2𝑖genap𝑓(𝑥, 𝑦𝑖)+ 𝑓(𝑥, 𝑦𝑛)] Hitung: 𝐼 =ℎ𝑦 3 [𝑓(𝑥, 𝑦0) + 4 ∑𝑛−1𝑖ganjil𝑓(𝑥, 𝑦𝑖) + 2 ∑𝑛−2𝑖genap𝑓(𝑥, 𝑦𝑖)+ 𝑓(𝑥, 𝑦𝑛)] Hitung: 𝐼 =ℎ𝑥 3 [𝑓(𝑥0, 𝑦) + 4 ∑𝑛−1𝑖ganjil𝑓(𝑥𝑖, 𝑦) + 2 ∑𝑛−2𝑖genap𝑓(𝑥𝑖, 𝑦)+ 𝑓(𝑥𝑛, 𝑦)] Tulis hasil selesai
48
Rumus Integral Rangkap Dua dengan metode Kuadratur Gauss 2 Titik
Dengan menggunakan Gauss di dapatkan solusi integral rangkap dua:
𝐼 = ∫ ∫ 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 𝑏 𝑎 𝑑 𝑐 = (𝑏 − 𝑎 2 ) ( 𝑑 − 𝑐 2 ) ∑ 𝑐𝑖𝑐𝑗𝑓(𝑥𝑖, 𝑦𝑖) 𝑛 𝑖=1 𝑗=1 Dari rumusan intergral rangkap dua metode Kuadratur Gauss 2 titik tersebut selanjutnya untuk memudahkan dalam membuatan atau penyusunan program untuk mencari selosinya, maka diberikan algoritma integral rangkap dua dengan metode Kuadratur Gauss sebagai berikut; a. Inisialisasi koefisien Gauss
𝑐1 = 𝑐2 = 1 𝑡1 = 1
√3, 𝑡2 = − 1 √3
b. Definisikan fungsi integran
c. Tentukan batas dua variabel integrasi [𝑎, 𝑏] dan [𝑐, 𝑑] d. Hitung 𝑥𝑖 = 𝑏−𝑎 2 𝑡 + 𝑎+𝑏 2 Hitung 𝑦𝑖 = 𝑑−𝑐 2 𝑡 + 𝑑+𝑐 2 e. Hitung: sum = ∑𝑛𝑖=1𝑐𝑖 ∗ 𝑐𝑗∗ 𝑓(𝑥𝑖, 𝑦𝑖) 𝑗=1 𝑖dan𝑗 = 1 sampai 𝑛. f. Hitung : 𝐼 = (𝑏−𝑎 2 ) ∗ ( 𝑑−𝑐 2 ) ∗ sum g. Tulis hasil integral.
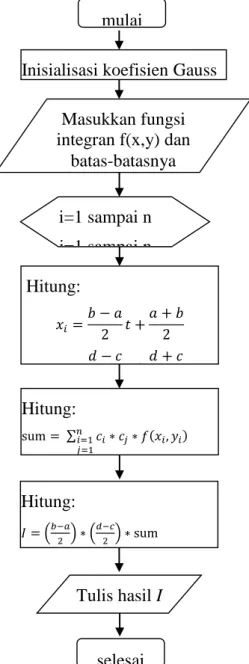
Berdasarkan algoritma tersebut di atas, maka berikut digambarkan penyelesaian integral rangkap dua dengan metode Kuadratur Gauss melalui diagram Alur (flowchart)
dengan metode Kuadratur Gauss 2 Titik
Dengan kedua Flowchart tersebut, dibuatlah program penyelesaian melalui MATLAB dengan tiga persamaan yang diambil adalah untuk persamaan pertama∫ ∫ 2𝑥√𝑥1 2 + 𝑦
0 𝑑𝑥𝑑𝑦
3 0
metode Simpson memberikan hasil dengan mengambil interval sebanyak empat kali diperoleh hasil integral sebesar 4,1053 dan Kuadratur Gauss 4,1241. Waktu penghitungan komputasi metode Simpson 1,632 detik dan Kuadratur Gauss 0,0164 detik. Persamaan kedua ∫ ∫ 𝑒01 02 𝑦cos(𝑥) 𝑑𝑥𝑑𝑦 diperoleh hasil integral dengan metode Simpson 5,3781 dan Kuadratur Gauss 5,3573. Waktu
Gambar 2. Flowchart Integral Rangkap Dua penghitungan komputasi metode simpson 1,52 detik dan Kuadratur Gauss 0,0119 detik.
mulai
Inisialisasi koefisien Gauss
Masukkan fungsi integran f(x,y) dan
batas-batasnya Hitung: 𝑥𝑖= 𝑏 − 𝑎 2 𝑡 + 𝑎 + 𝑏 2 𝑦𝑖= 𝑑 − 𝑐 2 𝑡 + 𝑑 + 𝑐 2 Hitung: sum = ∑𝑛𝑖=1𝑐𝑖∗ 𝑐𝑗∗ 𝑓(𝑥𝑖, 𝑦𝑖) 𝑗=1 Hitung: 𝐼 = (𝑏−𝑎 2 ) ∗ ( 𝑑−𝑐 2 ) ∗ sum selesai i=1 sampai n j=1 sampai n Tulis hasil I
49 Persamaan terakhir ∫ ∫ 3𝑥𝑦2√𝑥3+1 𝑑𝑦𝑑𝑥√2𝑦2+2 2.2 0.5 1.5 0.1
diperoleh hasil integral dengan metode Simpson 6,6058 dan Kuadratur Gauss 6,6052. Waktu penghitungan komputasi metode Simpson 1,9005 detik dan Kuadratur Gauss 0,0126 detik.
5. KESIMPULAN
Hasil perhitungan integrasi Simpson memberikan nilai yang mendekati nilai sebenarnya dengan mengambil 𝑛 genap. Secara komputasi integrasi Kuadratur Gauss memiliki kecepatan yang tinggi dalam penyelesaiannya. Hal ini dikarenakan tidak menggunakan pembagi area yang banyak seperti pada metode Simpson
6. DAFTAR PUSTAKA
Basuki, Achmad, dan Nana Ramadijanti. 2005.
Metode Numerik dan Algoritma Komputasi. Yogyakarta: Penerbit Andi. Kosasih, P. Buyung. 2006. Komputasi Numerik
Teori dan Aplikasi. Yogyakarta: Penerbit Andi.
Munir, Rinaldi. 2003. Metode Numerik . Revisi Kedua. Bandung: Informatika.
Nasution, Amrinsyah, dan Hasballah Zakaria.
2001. Metode Numerik dalam Ilmu Rekayasa Sipil. Bandung:penerbit ITB. Penny dan Lindfield. 1995. Numerical Methods
Using Matlab. Ellis Hoorwood: Great Britain.
Purcell, Edwin J, Dale Varbeg, Steven E. Rigdon. 2004. Edisi Kedelapan Kalkulus Jilid 2. Jakarta: Penerbit Erlangga.
Sahid, M.Sc. 2005. Pengantar Komputasi
Numerik dengan Matlab.
Yogyakarta:Penerbit Andi.
Setiawan, Agus. 2006. Pengantar Metode Numerik. Yogyakarta: Penerbit Andi. Sumartojo, Noeniek. 1987. Kalkulus Lanjutan
Universitas Indonesia. Jakarta.
Sutanta, Edhy. 2004. Algoritma Teknik Penyelesaian Permasalahan untuk Komputasi.Yogyakarta: Penerbit Graha Ilmu.
Triatmodjo, Bambang. 2002. Metode Numerik Dilengkapi Dengan Program Komputer. Yogyakarta : Beta Offset.
Weber, Jean E. 1999. Analisis Matematik Penerapan Bisnis dan Ekonomi.Edisi Keempat-jilid 2. Jakarta: Penerbit Erlangga.
Yulikuspartono.2004. Pengantar Logika dan Algoritma.ANDI: Yogyakarta-http/google.com/