Pemrograman Linier Model Transportasi.

(1)

i

PEMROGRAMAN LINIER:

MODEL TRANSPORTASI

Oleh:

Ni Ketut Tari Tastrawati, S.Si, M.Si

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS UDAYANA

(2)

ii

KATA PENGANTAR

Kebutuhan akan sumber belajar bagi mahasiswa di Jurusan Matematika yang mengambil mata kuliah Pemrograman Linear, maupun yang akan dan sedang mengerjakan Tugas Akhir mengenai Pemrograman Linear, khususnya kajian model transportasi, merupakan pertimbangan disusunnya karya tulis ini. Pemanfaatan karya tulis ini sebagai sumber belajar diharapkan dapat mengoptimalkan pembelajaran di kelas, maupun memperlancar proses penyelesaian Tugas Akhir mahasiswa di Jurusan Matematika, FMIPA Universitas Udayana.

Materi-materi yang disajikan dalam tulisan ini disusun dalam tiga bab, meliputi: Kajian Transportasi, Pemecahan Masalah Transportasi, dan Kasus-kasus Masalah Transportasi. Bab Kajian Transportasi membahas mengenai Definisi & Aplikasi Model Transportasi dan Keseimbangan Model Transportasi. Bagian Pemecahan Masalah Transportasi membahas tentang Langkah-langkah Dasar dari Teknik Transportasi yang meliputi Penyelesaian Fisibel Awal dan Proses Menuju Solusi Optimal. Bagian ketiga menyajikan Kasus-kasus Masalah Transportasi, meliputi: Masalah Transportasi Tidak Seimbang; Ada jalan Rusak; Penalti Terhadap Permintaan yang Tidak Terpenuhi; dan Soal Memaksimumkan. Tulisan ini disusun secara runtun bagian demi bagian, dengan harapan dapat memudahkan pembaca untuk memahami isi materi.

Akhir kata, tiada gading yang tak retak , keterbatasan dari isi tulisan ini memerlukan penyempuraan lebih lanjut di masa mendatang. Walaupun demikian, diharapkan tulisan ini dapat memberikan manfaat yang sebesar-besarnya bagi pengguna.

Bukit Jimbaran, 11 Desember 2015

(3)

iii

DAFTAR ISI

PENGANTAR………..………... ii

DAFTAR ISI ………...……….………. iii

BAB I. MODEL TRANSPORTASI……….………..………..…... 1 1.1 Definisi dan Aplikasi Model Transportasi ….………..…..….. 1.2 Keseimbangan Model Transportasi …..………...

1 3

BAB II. PEMECAHAN MASALAH TRANSPORTASI ……… 6

2.1 Langkah-langkah Dasar dari Teknik Transportasi ……….….…..…

2.1.1 Penyelesaian Fisibel Awal ……….………

2.1.2 Proses Menuju Solusi Optimal ……….………..

6 6 15

(4)

1

BAB I

MODEL TRANSPORTASI

Model transportasi merupakan salah satu kasus khusus dari persoalan pemrograman linier. Model transportasi pada dasarnya merupakan sebuah program linear yang dapat dipecahkan oleh metode simpleks yang biasa. Tetapi, strukturnya yang khusus memungkinkan pengembangan sebuah prosedur pemecahan, yang disebut teknik transportasi, yang lebih efisien dalam hal perhitungan.

1.1 Model Transportasi dan Aplikasinya

Hal-hal yang dibahas dalam persoalan transportasi mencakup masalah pendistribusian suatu komuditas dari sejumlah sumber (supply) ke sejumlah tujuan (demand), yang ditujukan untuk meminimalkan terjadinya ongkos pengangkutan.

Data yang digunakan dalam model meliputi data berikut: (1) Tingkat penawaran di setiap sumber; (2) Jumlah permintaan di setiap tujuan; dan (3) Biaya transportasi untuk setiap unit barang dari setiap sumber ke setiap tujuan.

Sebuah tujuan dapat menerima permintaan dari 1 sumber atau lebih dari satu sumber (karena terdapat hanya satu barang). Model yang dibentuk bertujuan untuk menentukan jumlah yang harus dikirimkan dari setiap sumber ke setiap tujuan yang ditujukan untuk meminimalkan biaya transportasi total.

Model transportasi memiliki beberapa kegunaan untuk memecahkan beberapa permasalahan, diantaranya: permasalahan distribusi (alokasi), permasalahan bisnis lainnya (alokasi dana untuk investasi, analisis lokasi, keseimbangan lini perakitan, perencanaan produksi, pengiklanan, dan pembelanjaan modal).

Ciri- ciri khusus persoalan transportasi menurut Dimyati, et al (2003) adalah: 1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.

2. Kuantitas komoditas atau barang yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan, besarnya tertentu.

3. Komoditas yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai dengan permintaan dan atau kapasitas sumber.

4. Ongkos pengangkutan kapasitas dari suatu sumber ke suatu tujuan, besarnya tertentu.

Model transportasi dari sebuah jaringan dengan m sumber dan n tujuan disajikan pada gambar di bawah. Node mewakili sebuah sumber dan tujuan. Busur

(5)

2

tujuan dan mewakili jumlah barang yang dikirimkan dari sumber i ke tujuan j.

Model LP yang mewakili masalah transportasi, secara umum sebagai berikut: ai = Jumlah supply pada sumber i

bj = Jumlah permintaan pada tujuan j

cij = Harga satuan transportasi antara sumber i dan tujuan j

Dengan demikian, maka formulasi program linearnya adalah sebagai berikut: Minimumkan ∑ ∑ Dengan batasan ∑ ∑

(6)

3

Dalam bentuk tabel dapat disajikan seperti berikut ini: Tujuan

1 2 n Persediaan

Sumber 1 ... 2 … … … … … m Permintaan …

1.2 Keseimbangan Model Transportasi

Apabila total supply sama dengan total demand, maka suatu model transportasi dikatakan seimbang, diwakili oleh persamaan berikut :

∑ ∑

Jika kondisi batasan ini tidak terpenuhi, atau mungkin jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah yang diminta, dikatakan bahwa model persoalan disebut sebagai model yang tidak seimbang. Untuk kondisi model yang tidak seimbang diatasi dengan membuat seimbang dengan cara memasukkan variabel dummy.

Contoh 1 (Model Transportasi Standar)

(7)

4

Denver Miami

Los Angeles 1000 2690

Detroit 1250 1350

New Orleans 1275 850

Bagan jarak di atas diidentifikasi menjadi biaya per mobil dengan tarif 8 sen per mil, menghasilkan biaya yang mewakili dalam model umum:

Denver (1)

Miami (2) Los Angeles

(1)

80 215

Detroit (2)

100 108

New Orleans (3)

102 68

Dari table diatas,karena penawaran total (=1000+1500+1200=3700) sama dengan permintaan total (=2300+1400=3700), maka model transportasi yang dihasilkan berimbang. Sehingga model LP masalah ini memiliki batasan yang semuanya berbentuk persamaan:

Minumumkan Dengan batasan

(8)

5

mewakili tujuan. Unsur biaya diringkaskan dalam sudut timur laut sel matriks . Model MG dapat diringkas seperti diperlihatkan pada tabel.

Tujuan

Denver Miami

(1) ( 2)

Penawaran

Los Angeles (1) 1000

Sumber Detroit (2) 1500

New Orleans (3) 1200

Permintaan 2300 1400 x11 x12

x21 x22

x31 x32

80 215

100 108

(9)

6

BAB II

PEMECAHAN MASALAH TRANSPORTASI

2.1 Langkah-langkah Dasar dari Teknik Transportasi

Dalam bagian ini kami perkenalkan perincian untuk pemecahan model transportasi. Metode ini menggunakan langkah-langkah metode simpleks secara langsung dan hanya berbeda dalam perincian penerapan kondisi optimalitas dan kelayakan.

Langkah-langkah dasar dari teknik transportasi adalah dengan 1. Langkah 1: Menentukan penyelesaian fisibel awal.

2. Langkah 2: Menentukan variabel masuk dari di antara variabel non dasar. Untuk metode simplek, jika semua variabel masuk memenuhi kondisi optimalitas, berhenti; jika tidak maka lanjutkan ke langkah 3

3. Langkah 3: Tentukan variabel keluar (menggunakan kondisi kelayakan) dari di antara variabel-variabel dalam pemecahan dasar saat ini; lalu temukan pemecahan dasar baru. Selanjutnya kembali ke langkah 2.

1.1.1 Penyelesaian Fisibel Awal

Untuk menentukan penyelesaian awal masalah transportasi dengan penyelesaian fisibel awal. Beberapa metode yang biasa digunakan, dintaranya: metode sudut barat laut, metode biaya terendah, dan metode pendekatan Vogel. Masing-masing metode memiliki keuntungan yang berbeda. Metode sudut barat laut merupakan metode yang paling mudah, akan tetapi biasanya dibutuhkan lebih banyak iterasi untuk mencapai penyelesaian optimal dibandingkan dengan metode biaya terendah atau metode pendekatan Vogel. Tidak ada teori yang akan menjamin bahwa penyelesaian awal merupakan penyelesaian optimal.

Jika tabel transportasi terdiri dari m baris dan n kolom, maka penyelesaian awal harus menghasilkan m + n – 1 buah variabel basis (sel yang terisi). Jika penyelesain awal berisi kurang dari m + n – 1 buah variabel basis maka harus ditambahkan variabel dummy agar proses pengecakan keoptimalan dan iterasi dapat dilakukan.

 Metode Sudut Barat Laut ( northwest-corner rule)

Contoh :

(10)

7

Biaya pengiriman (ribuan) dari dari pabrik ke kota disajikan dalam tabel berikut.

Pabrik Kota

A B C

1 20 5 8

2 15 20 10

3 25 10 19

Tentukan penyelesaian fisibel awal dengan metode sudut barat laut.

Penyelesaian :

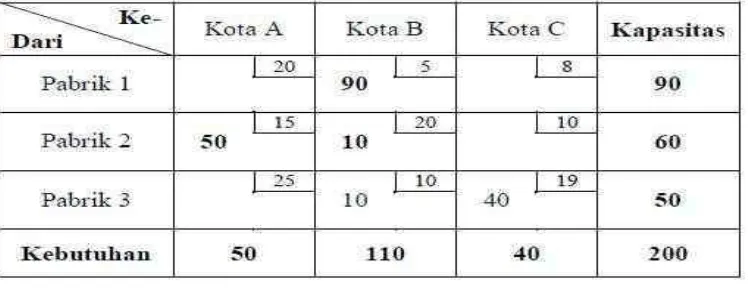
Jumlah kapasitas yang dimiliki pabrik 1,2, dan 3 adalah 90 + 60 + 50 = 200 ton, sedangkan jumlah permintaan di setiap kota A,B, dan C adalah 50 + 110 + 40 = 200 ton. Karena jumlah permintaan dan penawaran sama, proses iterasi dapat dimulai. Biaya pengiriman perunit barang ditunjukkan pada ujung kanan atas tiap sel. Disisi kanan merupakan jumlah persediaan barang dari tiap pabrik, sedangkan sisi bawah tabel adalah jumlah permintaan tiap kota.

Ujung barat laut dari tabel adalah sel c11 = 20. Sel ini diisi sebanyak

mungkin. Pabrik 1 mempunyai 90 ton barang sedangkan kota A memerlukan 50 ton. Sehingga x11 diisi sebanyak mungkin, yaitu 50 ton.

Dengan mengisi x11 = 50 maka otomatis permintaan kota A sudah terpenuhi

(11)

8

Selanjutnya sel c12 = 5 akan diisi dengan barang sebanyak mungkin. Pabrik

1 hanya mempunyai 90 ton dan sudah dikirimkan ke kota A sebanyak 50 ton sehingga tersisa 40 ton. Di sisi lain, kota B membutuhkan sebanyak 110 ton. Maka x12 = 40. Sehingga pabrik 1 sudah kehabisan barang sehingga x13

(12)

9

Karena barang pabrik 1 sudah habis, selanjutnya ujung barat lautanya adalah sel c22 = 20. Pabrik 2 memiliki 60 ton barang sedangkan kota B

tinggal membutuhkan 70 ton barang lagi. Maka x22 = 60 dan x23 tidak boleh

diisi lagi. Sehingga semua barang sudah tersalurkan.

Penyelesaian fisibel awal dengan metode sudut barat laut adalah sebagai berikut:

Biaya total pendistribusian sebesar 50(20) + 40(5) + 60(20) + 10(10) + 40(19) = 3.260 (ribuan).

Jumlah sel basis (sel terisi) = 5 sel, yaitu sama dengan jumlah baris + jumlah kolom – 1 = 3 + 3 - 1 = 5. Sehingga jumlah basisnya mencukupi dan tidak perlu variabel basis dummy.

 Metode Biaya Terendah

Metode Biaya Terendah menggunakan cara yang hampir sama dengan metode sudut barat laut, namun pengisian sel tidak dilakukan dari sisi barat laut, tetapi dari sel yang biaya pengirimannya terendah. Sel dengan biaya terendah diisi dengan barang semaksimal mungkin. Sel-sel yang biaya terendahnya sama, dapat dipilih dengan cara sembarang.

Contoh :

Pertimbangkan soal sebelumnya yang menggunakan metode biaya terendah.

Penyelesaian :

Biaya terkecil adalah pengiriman dari pabrik 1 ke kota B dengan c12 = 5

(13)

10

sini pabrik 1 sudah kehabisan barang sehingga x11 dan x13 tidak bisa

terisi lagi.

Dari sisa sel yang masih bisa diisi pengiriman dengan biaya terendah adalah dari pabrik 3 ke kota B dengan biaya c32 = 10. x32 diisi sebanyak 20 untuk

memenuhi permintaan kota b yaitu 110 ton.

(14)

11

Kota

A B C Persediaan

1 90

Pabrik

2 60

3 50

Permintaan 50 110 40 90

20 40

30 20

20 8

15 20 10

25 10 19

5

 Metode Pendekatan Vogel

Metode Pendekatan Vogel menggunakan cara yang lebih kompleks dibandingkan dengan metode-metode sebelumnya. Tetapi umumnya lebih mendekati solusi optimalnya.

Langkah-langkah mendapatkan solusi awal dengan Metode Pendekatan Vogel adalah sebagai berikut :

1. hitunglah selisih dua sel dengan biaya terkecil pada setiap baris dan kolom

2. Tetukan baris/kolom berdasarkan (1) yang selisihnya terbesar. Jika ada lebih dari 1, pilihlah secara sembarang.

3. Dari hasil langkah (2), sel dengan biaya terkecil diisi sebanyak banyaknya. Kemudian hilangkan baris/kolom yang dihabiskan karena pengisian tersebut pada perhitungan berikutnya. Jika baris dan kolom

terhapus secara bersamaan, maka ditambahkan variabel

buatan/dummy.

(15)

12 Contoh :

Selesaikan contoh sebelumnya dengan metode Pendekatan Vogel. Penyelesaian :

Perhatikan baris 1, sel yang biayanya terkecil berturut-turut adalah c12

= 5 dan c13 = 8. Selisihnya = 8 – 5 = 3.

Dengan cara yang sama dihitung selisih 2 sel dengan biaya terkecil pada tiap baris dan kolom. Hasilnya sebagai berikut.

Baris atau Kolom 2 Sel dengan Biaya Terkecil

Selisih

Baris-1 c12 = 5 dan c13 = 8 8 – 5 = 3

Baris-2 c21 = 15 dan c23 = 10 15 – 10 = 5

Baris-3 c32 = 10 dan c33 = 19 19 – 10 = 9*

Kolom-1 c11 = 20 dan c21 = 15 20 – 15 = 5

Kolom-2 c12 = 5 dan c32 = 10 10 – 5 = 5

Kolom-3 c13 = 8 dan c23 = 10 10 – 8 = 2

Dari table terlihat bahwa selisih terbesar yaitu 9 terletak pada baris ke 3. Dengan biaya terkecil pada baris ke 3 yaitu c32 = 10. Pada sel ini

dimasukan barang semaksimal mungkin yaitu sebesar 50 ton. Sehingga x32

(16)

13

karena sudah kehabisan barang. Dengan cara yang sama diperoleh (tentu saja tanpa melibatkan baris 3) :

Baris atau Kolom 2 Sel dengan Biaya Terkecil

Selisih

Baris-1 c12 = 5 , c13 = 8 8 – 5 = 3

Baris-2 c21 = 15 , c23 = 10 15 – 10 = 5

Kolom-1 c11 = 20 , c21 = 15 20 – 15 = 5

Kolom-2 c12 = 5 , c22 = 20 20 – 5 = 15*

Kolom-3 C13 = 8 , c23 = 10 10 – 8 = 2

Selisih terbesar ada pada kolom 2 yaitu 15, dengan biaya terkecilnya terletak pada baris 1 yaitu c21 = 5. sel ini diisi barang sebanyak mungkin,

sebesar 110 ton, tetapi karena kolom 2 sudah terpenuhi 50 ton pada iterasi sebelumnya maka x12 = 60, sel lain pada kolom 2 tidak dapat diisi lagi,

karena sudah terpenuhi

Begitu seterusnya, selisih 2 sel dengan biaya terkecil pada baris 1 dan 2 berturut-turut adalah 12 dan 5. Selisih pada kolom 1 dan 3 adalah 5 dan 2. Nilai maksimum terjadi pada baris 1, maka x13 = 30 dan baris 1 tidak boleh

(17)

14

Kota

A B C

selisih

1 90 3 3 12*

Pabrik

2 60 5 5 5

3 50 9* - -

50 110 40

Selisih 5 5 2

5 15* 2

5 - 2

60 30

50

20 8

15 20 10

25 10 19

5

sisanya tinggal sel pada baris yang sama sehingga diisi mulai dari sel yang biayanya terkecil, yaitu x23 = 10 dan x21 = 50.

(18)

15

Kota

A B C

selisih

1 90 3 3 12*

Pabrik

2 60 5 5 5

3 50 9* - -

50 110 40

Selisih 5 5 2

5 15* 2

5 - 2

60 30

50 10

50

20 8

15 20 10

25 10 19

5

1.1.2 Proses Menuju Solusi Optimal

Solusi Optimal akan diperoleh setelah penentuan solusi awal tadi, dan langkah berikutnya adalah mengecek apakah solusi tersebut sudah optimal. Menentukan entering dan leaving variable adalah tahap berikutnya dari pemecahan persoalan transportasi, setelah solusi fisible awal diperoleh. Cara menentukan entering dan leaving variable yaitu dengan menggunakan metode stepping stone dan metode Modified Distribution Method (MODI).

1. Metode Stepping Stone

Syarat : Jumlah rute atau sel yang mendapat alokasi harus sebanyak Jumlah Kolom + Jumlah Baris – 1

Langkah – langkahnya :

(19)

16

ii. Mulai dari sel ini, kita membuat jalur tertutup melalui sel-sel yang mendapatkan alokasi menuju sel kosong terpilih kembali. Jalur tertutup ini bergerak secara horizontal dan vertikal saja.

iii. Mulai dengan tanda (+) pada sel kosong terpilih, kita menempatkan tanda (-) dan (+) secara bergantian pada setiap sudut jalur tertutup. iv. Menghitung indeks perbaikan dengan cara menjumlahkan biaya

transportasi pada sel bertanda (+) dan mengurangkan biaya transportasi pada sel bertanda (-).

v. Mengulangi tahap 1 sampai 4 hingga indeks perbaikan untuk semua sel kosong telah terhitung. Jika indeks perbaikan dari sel-sel kosong lebih besar atau sama dengan nol, solusi optimal telah tercapai.

Contoh :

1) Tiga pabrik barang dengan kapasitas 90 ton, 60 ton dan 50 ton hendak mengirim barang ke tiga kota dengan kebutuhan masing – masing kota adalah 50 ton, 110 ton dan 40 ton.

Biaya pengiriman (ribuan) dari dari pabrik ke kota disajikan dalam tabel berikut.

Pabrik Kota

A B C

1 20 5 8

2 15 20 10

3 25 10 19

Berapakan total biaya optimal yang harus dikeluarkan perusahaan dalam memenuhi kebutuhan ketiga kota tersebut ?

Penyelesaian :

 Tabel Transportasi

(20)

17

 Dengan metode sudut barat laut diperoleh table fisible awal sebagai berikut :

 Tabel Alokasi Pertama dengan metode Stepping Stone

Biaya pengiriman untuk alokasi tahap pertama : 50(20) + 40(5) + 60(20) + 10(10) + 40(19) = 3260

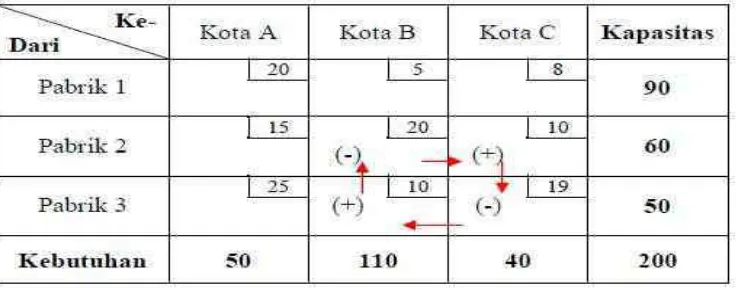
 Menguji sel–sel yang masih kosong, apakah masih bisa memiliki nilai negatif atau tidak, artinya masih bisa menurunkan biaya transportasi atau tidak. Sel yang diuji adalah : Sel . Pengujian dilakukan pada setiap sel kosong tersebut dengan menggunakan metode Stepping Stone. Pada metode ini, pengujian dilakukan mulai dari sel

1

2

(21)

18

kosong tersebut, selanjutnya bergerak (boleh searah jarum jam dan boleh berlawanan) secara lurus/tidak boleh diagonal, ke arah sel yang telah terisi dengan alokasi, begitu seterusnya sampai kembali ke sel kosong tersebut. Setiap pergerakan ini akan mengurangi dan menambah secara bergantian biaya pada sel kosong tersebut. Perhatikan tanda panah dan tanda (+) atau (-) nya.

Pengujian

Sel = 8 – 19 + 10 – 5 = - 6 Sel = 15 – 20 + 5 -20 = - 20 Sel = 10 – 19 + 10 – 20 = - 19 Sel = 25 – 20 + 5 – 10 = 0

 Merubah alokasi pengiriman ke sel , yang pengujian sebelumnya memiliki pergerakan :

[image:21.595.147.521.623.772.2]

(22)

19 Sel menjadi 0 karena 50 – 50 = 0 Sel menjadi 90 karena 40 + 50 = 90 Sel menjadi 10 karena 60 – 50 = 10 Sel menjadi 50 karena 0 + 50 = 50

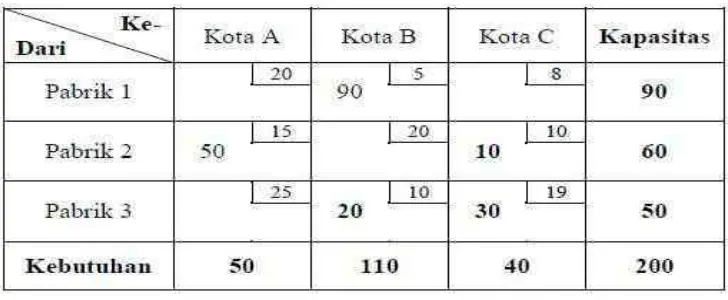
 Pengujian :

Sel = 20 – 5 + 20 – 15 = 20 (menjadi lebih mahal 20/ton) Sel = 8 – 19 + 10 – 5 = - 6

Sel = 10 – 19 + 10 – 20 = -19

Sel = 25 – 15 + 20 – 10 = 20 (menjadi lebih mahal 20/ton)

Dari hasil pengujian tersebut, ternyata sel masih dapat memberikan penurunan biaya sebesar RP 19/ton. Dengan demikian memang perlu

dilakukan perubahan alokasi pengiriman, dengan mencoba

mengalokasikan pengiriman ke sel dengan langkah :

[image:22.595.149.517.297.442.2]

(23)

20 Sel menjadi 0 karena 10 – 10 = 0 Sel menjadi 10 karena 0 + 10 = 10 Sel menjadi 20 karena 10 + 10 = 20 Sel menjadi 50 karena 40 - 10 = 30

 Pengujian

Sel = 20 – 5 + 10 – 19 + 10 - 15 = 1 (menjadi lebih mahal 1/ton) Sel = 8 – 19 + 10 – 5 = - 6

Sel = 20 – 10 + 19 – 10 = 19 (lebih mahal 19/ton) Sel = 25 – 15 + 10 – 19 = 1 (menjadi lebih mahal 1/ton)

Dari hasil pengujian tersebut, ternyata sel masih dapat memberikan penurunan biaya sebesar 6/ton. Dengan demikian memang perlu

dilakukan perubahan alokasi pengiriman, dengan mencoba

mengalokasikan pengiriman ke sel dengan langkah :

[image:23.595.143.507.74.224.2]

(24)

21 Sel menjadi 60 karena 90 – 30 = 60 Sel menjadi 30 karena 0 + 30 = 30 Sel menjadi 50 karena 20 + 30 = 50 Sel menjadi 0 karena 30 - 30 = 0

Nilai alokasi pada sel dan tidak mengalami perubahan karena tidak termasuk dalam pergerakan pengujian sel tersebut.

 Pengujian

Sel = 20 – 8 + 10 – 15 = 7 → menjadi lebih mahal 7/ton Sel = 20 – 5 + 8 – 10 = 13 → menjadi lebih mahal 13/ton Sel = 25 – 15 + 10 – 8 + 5 - 10 = 7 → lebih mahal 7/ton Sel = 19 – 10 + 5 – 8 = 6 → menjadi lebih mahal 6/ton)

Dari hasil pengujian tersebut, ternyata semua sel sudah tidak ada yang bernilai negatif lagi, atau dengan kata lain semua sel sudah tidak dapat memberikan penurunan biaya lagi, sehingga dengan demikian dapat dikatakan kasus telah optimal, dengan total biaya :

Biaya mengirim 60 ton dari P1 ke kota B = 60 x 5 = 300 Biaya mengirim 30 ton dari P1 ke kota C = 30 x 8 = 240 Biaya mengirim 50 ton dari P2 ke kota A = 50 x 15 = 750 Biaya mengirim 10 ton dari P2 ke kota C = 10 x 10 = 100 Biaya mengirim 50 ton dari P3 ke kota B = 50 x 10 = 500 ---+

Total biaya pengirimannya = 1890 Kesimpulan :

Jadi, total biaya optimal yang harus dikeluarkan perusahaan dalam memenuhi kebutuhan ketiga kota tersebut adalah Rp. 1.890.000,00.

2. Modified Distribution Method (MetodeMODI)

(25)

22

Ri = nilai yang ditetapkan untuk baris i Kj = nilai yang ditetapkan untuk kolom j

cij = biaya transportasi dari sumber i ke tujuan j Ada lima langkah dalam aplikasi metode MODI, yaitu :

1) Menghitung nilai setiap baris dan kolom, dengan menetapkan Ri +Kj = cij

Formula tersebut berlaku untuk sel yang mendapat alokasi saja. 2) Setelah semua persamaan telah tertulis, tetapkan R1 = 0

3) Mencari solusi untuk semua R dan K.

4) Menghitung indeks perbaikan dengan menggunakan formula cij - Ri - Kj

5) Mengaplikasikan kriteria optimalitas sebagaimana pada metode stepping stone.

Contoh :

Dengan kasus yang sama seperti contoh pada metode stepping stone. Berapakan total biaya optimal yang harus dikeluarkan perusahaan dalam memenuhi kebutuhan ketiga kota tersebut?

Penyelesaian : Langkah-langkah:

 Tabel awal yang digunakan adalah tabel NWC

 Perubahan Alokasi 1

a) Buat variabel Ri dan Kj untuk masing-masing baris dan kolom.

b) Hitung sel yang berisi (nilai tiap kolom dan tiap baris) dengan rumus:

Nilai baris 1 = R1 = 0

Mencari nilai kolom A :

0 + KA = 20, nilai kolom A = 20

(26)

23

; R2 + 5 = 20 ; R2 = 15

; R3 + 5 = 10 ; R3 = 5

; 5 + KC = 19 ; KC = 14

Nilai–nilai ini kemudian diletakkan pada baris/kolom yang bersangkutan, seperti terlihat pada tabel berikut :

c) Menghitung index perbaikan setiap sel yang kosong dengan rumus: Index perbaikan =

Sel Indeks Perbaikan

2 – A 15 – 15 – 20 -20

3 – A 25 – 5 – 20 0

1 – C 8 – 0 – 14 -6

2 – C 10 – 15 – 14 -19

d) Memilih titik tolak perubahan

Sel yang mempunyai indeks perbaikan negatif berarti bila diberi alokasi akan dapat mengurangi jumlah biaya pengangkutan. Bila nilainya positif berarti pengisian akan menyebabkan kenaikan biaya pengangkutan.

Sel yang merupakan titik tolak perubahan adalah sel yang indeksnya bertanda negatif , dan angkanya terbesar . Dalam tabel diatas ternyata yang memenuhi syarat adalah sel 2 – A. Oleh karena itu sel ini dipilih sebagai sel yang akan diisi.

e) Memperbaiki alokasi Buat jalur tertutup.

Biaya transportasi = 90 (5) + 50 (15) + 10 (20) + 10 (10) + 40 (19) = 2260

f) Ulangi langkah – langkah tersebut sampai diperoleh biaya terendah.

 Perubahan Alokasi ke-2

(27)

24

b) Hitung sel yang berisi (nilai tiap kolom dan tiap baris) dengan rumus :

Mencari nilai kolom B :

0 + KB = 5, nilai kolom B = 5

Mencari nilai kolom dan baris yang lain : ; R2 + 5 = 20 ; R2 = 15

; 15 + KA = 15 ; KA = 0

; R3 + 5 = 10 ; R3 = 5

; 5 + KC = 19 ; KC = 14

Nilai–nilai ini kemudian diletakkan pada baris/kolom yang bersangkutan, seperti terlihat pada tabel berikut :

c)Menghitung index perbaikan setiap sel yang kosong dengan rumus:

Index perbaikan =

1 – A 20 – 0 – 0 20

1 – C 8 – 0 – 14 -6

2 – C 10 – 15 – 14 -19

3 – A 25 – 5 – 0 20

(28)

25

 Perubahan Alokasi ke-3

a) Buat variabel Ri dan Kj untuk masing-masing baris dan kolom.

b) Hitung sel yang berisi (nilai tiap kolom dan tiap baris) dengan rumus:

Mencari nilai kolom dan baris yang lain : ; R3 + 5 = 10 ; R3 = 5

; 5 + KC = 19 ; KC = 14

; R2 + 14 = 10 ; R2 = -4

; -4 + KA = 15 ; KC = 19

(29)

26

1 – A 20 – 0 – 19 1

1 – C 8 – 0 – 14 -6

2 – B 20 + 4 – 5 19

3 – A 25 – 5 – 19 1

Sel yang merupakan titik tolak perubahan adalah sel 1 – C. e) Memperbaiki alokasi

Buat jalur tertutup.

 Perubahan Alokasi ke -4

a) Buat variabel Ri dan Kj untuk masing-masing baris dan kolom. b) Hitung sel yang berisi (nilai tiap kolom dan tiap baris) dengan

rumus :

Mencari nilai kolom dan baris yang lain : ; 0 + KC = 8 ; KC = 8

; R2 + 8 = 10 ; R2 = 2

; 2 + KA = 15 ; KA = 13

(30)

27

Nilai – nilai ini kemudian diletakkan pada baris/kolom yang bersangkutan, seperti terlihat pada tabel berikut :

1– A 20 – 0 – 13 7

2 – B 20 – 2 – 5 13

3 – A 25 – 5 – 5 15

3 – C 19 – 5 – 8 6

Karena indeks perbaikan pada setiap sel sudah tidak ada yang negatif, maka tabel pada perubahan alokasi ke-3 sudah optimal.

 Kesimpulan

(31)

28

DAFTAR PUSTAKA

Taha, Hamdy A. 1982. Riset Operasi Jilid 1. Tanggerang : Binarupa Aksara.

Siang, Jong Jek. 2011. Riset Operasi dalam Pendekatan Algoritma. Yogyakarta: ANDI. Dimyati, Tjutju Tarliah dan Akhmad Dimyati. 2003. Operations Research Model–

model Pengambilan Keputusan. Bandung: Sinar Baru Algensindo. Subagyo, Pangestu dkk. 2000. Dasar – dasar Operations Research. Yogyakarta :

(32)

PEMROGRAMAN LINIER:

MODEL TRANSPORTASI

by

Ni Ketut Tari Tastrawati

FILE

TIME SUBMITTED 07-FEB-2016 07:09PM

SUBMISSION ID 628713855

WORD COUNT 4377

CHARACTER COUNT 23667

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

16

%

SIMILARITY INDEX

16

%

INTERNET SOURCES

0

%

PUBLICATIONS

0

%

STUDENT PAPERS

1

8

%

2

5

%

3

2

%

4

1

%

5

<

1

%

6

<

1

%

7

<

1

%

EXCLUDE QUOTES OFF

EXCLUDE

BIBLIOGRAPHY OFF

EXCLUDE MATCHES OFF