KAJIAN RUANG WAKTU KERR-NEWMAN DALAM GRAVITASI EINSTEIN - ITS Repository

KAJIAN RUANG WAKTU KERR-NEWMAN DALAM GRAVITASI

EINSTEIN

ANDIKA IRAWAN NRP 1112100070 Dosen Pembimbing

Dr.rer.nat Bintoro Anang Subagyo

JURUSAN FISIKA

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember

KAJIAN RUANG WAKTU KERR-NEWMAN DALAM GRAVITASI

EINSTEIN

ANDIKA IRAWAN NRP 1112100070 Dosen Pembimbing

Dr.rer.nat Bintoro Anang Subagyo

JURUSAN FISIKA

Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember

STUDY OF KERR-NEWMAN SPACETIME

IN EINSTEIN GRAVITY

ANDIKA IRAWAN NRP 1112100070 Supervisor

Dr.rer.nat Bintoro Anang Subagyo

Department of PHYSICS

KAJIAN RUANG WAKTU KERR-NEWMAN DALAM GRAVITASI EINSTEIN

Nama : ANDIKA IRAWAN

NRP : 1112100070

Jurusan : Fisika FMIPA

Pembimbing : Dr.rer.nat Bintoro Anang Subagyo, M.Si

ABSTRAK

Dalam laporan tugas akhir ini telah dikaji solusi dari persamaan Einstein-Maxwell. Metrik dari solusi ini disebut sebagai metrik Kerr-Newman yang berotasi dan bermuatan tidak sama dengan nol. Pada awalnya dibahas so-lusi statis dan simetri bola, yaitu Schwarzschild dan Reissner-Nordstrom yang masing-masing merupakan solusi yang tidak bermuatan dan bermu-atan. Kemudian untuk mendapatkan solusi berotasi, ruang-waktu diputar menggunakan algoritma Newman-Janis sehingga didapatkan solusi Kerr dan Kerr-Newman. Di sini juga dikaji sifat-sifat disekitarevent horizon

metrik Kerr-Newman.

STUDY OF KERR-NEWMAN SPACETIME IN EINSTEIN GRAVITY

Name : ANDIKA IRAWAN

NRP : 1112100070

Department : Physics

Supervisor : Dr.rer.nat Bintoro Anang Subagyo, M.Si

ABSTRACT

In this report we studied the solution of Einstein-Maxwell equations. The metric of solutions known as Kerr-Newman metric which are rota-ting and having non zero charge. In the beginning we discussed static and spherically symmetric solution,i.e.Schwarzhild and Reisnerr-Nordstrom

that are charged and non-charged solution respectively. In order to obtain spinning solution,we rotate spacetime following Newman-Janis algorithm for Kerr and Newman. We discussed also the main feture of Kerr-Newman near event horizon.

Alhamdulillaahirabbil’alamiin

Puji syukur penulis panjatkan kehadirat ALLAH SWT karena atas karunia-Nya penulis dapat menyelesaikan Tugas Akhir dengan judul

”KAJIAN RUANG-WAKTU KERR-NEWMAN DALAM GRAVITASI EINSTEIN”

Tugas akhir ini diharapkan dapat membantu rekan-rekan mahasiswa S1 yang ingin belajar lebih mendalam tentang Fisika terutama di sekitar to-pik solusi persamaan medan Einstein.

Terselesaikannya tugas akhir ini tidak luput dari bantuan berbagai pi-hak. Penulis mengucapkan terima kasih dengan setulus hati kepada:

1. Emak dan Bapak tercinta atas semua yang telah diberikan kepada penulis. Penulis tidak akan pernah mampu membalasnya.

2. Bapak Dr.rer.nat Bintoro Anang Subagyo, yang tak hanya membim-bing penulis dalam penyelesaian Tugas Akhir. Penulis mohon maaf atas segala kesalahan yang telah penulis lakukan.

3. Bapak Agus Purwanto, D.Sc selaku dosen penguji. Terima kasih atas semua kritik yang membangun dan saran yang telah diberikan kepada penulis.

4. Bapak Heru Sukamto, M.Si selaku dosen penguji. Terimakasih atas segala bimbingannya selama menjadi mahasiswa terutama pada ke-giatan olimpiade.

5. Bapak Dr. Yono Hadi Pramono, M.Eng selaku Ketua Jurusan Fisika atas kepercayaannya kepada penulis

6. Bapak Dr. Mashuri selaku dosen wali penulis selama mahasiswa. 7. Bapak Achmad Zainuri, S.Pd, guru penulis yang telah ”meracuni”

dan ”men-comblangkan” penulis dengan ilmu Fisika di saat-saat pe-nulis sangat membenci Fisika. Bu Tri atas semua buku-buku Fisika Lanjut yang mengarahkan penulis untuk memilih Jurusan Fisika. 8. Kawan-kawan di LaFTiFA, Mas Nur, Mas Yo, Mas Fadlol, Mas

Fi-qi, Mas Usykur, Mbak Philin, Bayu, Afif, Ira, Anom, Afidah dan Adam. Penulis mengucapkan terima kasih secara khusus kepada Mas Nur atas bantuan referensinya serta Afif atas bantuan dalam pengetikan lampiran.

9. FBI 2012, teman-teman sepanjang masa penulis penulis. Terima kasih telah menjadi teman terbaik penulis dan telah mewarnai

dupan penulis. Physics ON! Physics ON! Fisika, FBI Fisika Buat Indonesia.

10. Saudara-saudara UKM PSHT ITS. Terima kasih telah atas keken-talan persaudaraannya. Suro Diro Joyo Diningrat Lebur Dening Pa-ngastuti, Ngluruk Tanpo Bolo, Menang Tanpo Ngasorake.

11. PSDM Himasika ITS, PSDM BEM ITS serta Divisi Kaderisasi Fosif sebagai wadah penulis untuk belajar berorganisasi.

12. Adik-adik Gamma 2013 yang sering bertempur dan adu batin de-ngan Antares 2014 demi adik-adiknya, Fisika 2015.

13. Serta semua pihak yang tidak dapat penulis tuliskan satu per satu.

Semoga Laporan tugas akhir ini bermanfaat bagi pihak-pihak yang berkepentingan serta menjadi sumbangan yang berguna bagi almamater.

Surabaya, 31 Januari 2016

ABSTRAK ix

ABSTRACT xi

Kata Pengantar xiii

DAFTAR ISI xv

DAFTAR TABEL xvii

DAFTAR GAMBAR xix

1 PENDAHULUAN 1

1.1 Latar Belakang . . . 1

1.2 Perumusan Masalah . . . 2

1.3 Tujuan . . . 2

1.4 Metode Penelitian . . . 3

1.5 Sistematika Penulisan . . . 3

2 PERSAMAAN MEDAN EINSTEIN 5 2.1 Persamaan Geodesik . . . 5

2.2 Tensor kurvatur . . . 9

2.3 Tensor Energi-Momentum . . . 10

2.4 Persamaan Medan Einstein . . . 14

2.5 Algoritma Newman-Janis . . . 16

3 SOLUSI STATIK PERSAMAAN MEDAN EINSTEIN 19 3.1 Solusi Schwarzchild . . . 19

3.2 Solusi Reissner-Nordstrom . . . 24

4 SOLUSI BEROTASI PERSAMAAN MEDAN EINSTEIN 27 4.1 Solusi Kerr . . . 27

4.2 Solusi Kerr-Newman . . . 32

5 DISKUSI 37

6 PENUTUP 45

6.1 Kesimpulan . . . 45

6.2 Saran . . . 45

DAFTAR PUSTAKA 47 A 49 A.1 Persamaan Geodesik . . . 49

A.2 Tensor Kurvatur . . . 55

A.3 Tensor Energi-Momentum . . . 57

A.4 Persamaan Medan Einstein . . . 62

A.5 Solusi Schwarzschild . . . 69

A.6 Solusi Reissner-Nordstrom . . . 88

A.7 Solusi Kerr . . . 97

A.8 Solusi Kerr-Newman . . . 124

2.1 Geodesik pada ruang datar 2 dimensi . . . 5

2.2 Geodesik pada ruang lengkung 2 dimensi . . . 6

2.3 2 titik yang dihubungkan dengan 3 lintasan . . . 7

2.4 Translasi vektor pada ruang lengkung . . . 9

5.1 Ergosphere dan SIR pada lubang hitam Kerr-Newman . . . 41

5.1 Kedudukan lubang hitam bermuatan dan berotasi . . . 37

PENDAHULUAN

1.1 Latar Belakang

Gravitasi antar berbagai partikel telah diterangkan dengan sangat baik oleh Newton dengan Hukum Gravitasi Universal-nya yaitu partikel-partikel di alam semesta saling tarik menarik dengan gaya yang berban-ding lurus dengan hasil kali dari massa masing-maisng partikel dan ber-banding terbalik dengan kuadrat dari jarak diantara mereka. Hukum ini sangat berhasil dalam menerangkan sifat-sifat pergerakan benda langit de-ngan ketelitian yang cukup tinggi.

Pada tahun 1905, Albert Einstein mencetuskan teorinya yang diberi nama Teori Relativitas Khusus. Teori ini merumuskan ulang bagaimana formasi ruang-waktu. Teori ini didasarkan pada 2 postulat yaitu semua hukum fisika harus berbentuk sama (invarian) pada semua kerangka acu-an dacu-an kecepatacu-an cahaya adalah kecepatacu-an mutlak. Koreksi dari hukum gravitasi universal Newton terhadap teori ini adalah jika misal terdapat partikel-partikel yang salah satunya digerakkan dan yang lain diam (rela-tif terhadap partikel yang lain), maka gaya gravitasi antar partikel tersebut akan berubah secara spontan tak peduli berapapun besarnya. Kata ”spont-an” dipakai karena perubahan jarak antara partikel 1 dengan partikel lain-nya akan berubah saat itu juga. Hal ini berarti komunikasi antar berbagai partikel tersebut terjadi sangat cepat (spontan) yang melebihi kecepatan cahaya tak bergantung berapapun besar jaraknya, sehingga hal ini telah melanggar postulat ke-2 Teori Relativitas Khusus.

Teori Relativitas Khusus dapat menjelaskan dengan sangat baik untuk kerangka acuan yang satu yang bergerak relatif dengan kerangka acuan yang lain dengan kecepatan konstan yang sangat tinggi (mendekati kece-patan cahaya). Untuk kerangka acuan yang bergerak relatif dengan perce-patan konstan, maka pada tahun 1916 Albert Einstein men-generalisasi Teori Relativitas Khusus dengan mencetuskan Teori Relativitas Umum yaitu teori yang menjelaskan kerangka acuan yang saling bergerak rela-tif dengan suatu percepatan. Dalam teori ini gravitasi bukan dipandang sebagai gaya, tetapi lebih sebagai manifestasi dari kelengkungan ruang-waktu. Efek kelengkungan ruang-waktu terjadi jika ada benda bermassa. Semakin besar massa suatu benda, maka semakin besar pula efek keleng-kungan ruang-waktunya. Formulasi dari kelengkeleng-kungan ruang-waktu ini

dirumuskan dalam persamaannya yang terkenal yaitu Persamaan Medan Einstein.

Solusi dari persamaan medan Einstein pertama kali dikerjakan oleh Karl Schwarzschild pada tahun yang sama sejak Teori Relativitas Umum dipublikasikan. Schwarzschild memberikan solusi statik dan simetri bola untuk persamaan medan Einstein. Hasil yang didapatkan adalah lubang hitam (black hole) statik. Lubang hitam adalah suatu benda dengan ke-rapatan massa sangat tinggi sehingga kelengkungan ruang-waktu di seki-tarnya sangat kuat. Kekuatan dari kelengkungan ruang-waktu ini mampu menarik benda-benda di sekitarnya hingga cahaya pun tidak bisa keluar setelah masuk ke dalamnya.

Secara astrofisika, benda langit umumnya berputar (berotasi). Karena solusi Schwarzschild hanya untuk lubang hitam yang tidak berotasi, maka seharusnya terdapat solusi lain untuk sumber massa yang berotasi. Pada tahun 1963, Roy Patrick Kerr menemukan solusi bagi persamaan medan Einstein untuk sumber massa yang berotasi.

Jika persamaan medan Einstein digabungkan dengan persamaan Ma-xwell, maka akan didapat persamaan medan Einstein-Maxwell. Solusi statik untuk persamaan ini dikerjakan oleh Hans Jacob Reissner dan Gun-nar Nordstrom yang diberi nama solusi Reissner-Nordstrom yaitu solusi untuk lubang hitam yang statik, bermuatan dan simetri bola. Kemudian ji-ka lubang hitam yang bermuatan ini juga berotasi, maji-ka aji-kan didapatji-kan solusi Kerr-Newman.

1.2 Perumusan Masalah

Rumusan masalah pada Tugas Akhir ini adalah bagaimana mendapatk-an solusi Kerr dmendapatk-an Kerr-Newmmendapatk-an dengmendapatk-an menerapkmendapatk-an Algoritma Newmmendapatk-an- Newman-Janis pada metrik Schwarzschild dan Reissner-Nordstrom yang diungkapk-an dalam koordinat null.

1.3 Tujuan

diungkapkan dalam koordinat null. Kemudian dicari sifat-sifat didekat horison peristiwa dari metrik Kerr-Newman

1.4 Metode Penelitian

Metode yang digunakan dalam penyusunan Tugas Akhir ini adalah metode analitis dari studi literatur.

1.5 Sistematika Penulisan

Dalam penulisan Tugas Akhir ini , terdiri dari 6 bab. Pada bab I diura-ikan mengenai motivasi dan sejarah singkat munculnya Teori Relativitas Umum. Pada bab II akan diuraikan beberapa Persamaan Medan Einstein yang dipakai yaitu bagaimana mendapat Persamaan Medan Einstein serta Algoritma Newman-Janis yaitu metode untuk mendapatkan solusi lubang hitam berotasi dari lubang hitam statik. Pada bab III akan diturunkan so-lusi statik dari Persamaan Medan Einstein yaitu soso-lusi Schwarzschild dan solusi Reissner-Nordstrom. Pada bab IV akan diturunkan solusi berota-si Persamaan Medan Einstein yaitu soluberota-si Kerr dan Soluberota-si Kerr-Newman dengan menggunakan Algoritma Newman-Janis. Bab V adalah diskusi yang berisi penjelasan mengenasi sifat-sifat di sekitar horison peristiwa lubang hitam Kerr-Newman. Bab 6 adalah kesimpulan dan saran. Lam-piran berisi penurunan rumus secara detail. Pada tugas akhir ini, indeks yang digunakan untuk huruf yunani (misalµ) berjalan dari (0,1,2,3) dan

untuk indeks huruf latin (misali) untuk indeks yang berjalan dari (1,2,3),

PERSAMAAN MEDAN EINSTEIN

Persamaan medan Einstein adalah persamaan yang menggambarkan kelengkungan ruang waktu yang diakibatkan oleh distribusi materi di se-kitarnya. Penjelasan mengenai persamaan medan Einstein beserta deriva-sinya ditunjukan pada subbab-subbab berikut.

2.1 Persamaan Geodesik

Geodesik adalah jarak terpendek antara 2 titik. Pada ruang koordinat kartesian, geodesiknya adalah garis lurus, sedangkan pada koordinat bola geodesiknya adalah panjang busur terpendek yang menghubungkan 2 titik tersebut pada lingkaran bola dengan jari-jari terbesar. Perhatikan gambar berikut,

Gambar 2.1: Geodesik pada ruang datar 2 dimensi

Dari Gambar 2.1 diatas, terlihat bahwa jarak terdekat antara titik pe-nalti bola ke titik tengah lapangan adalah garis lurus PQ. Sedangkan dari Gambar 2.2 di bawah ini, terlihat bahwa jarak terdekat antara 2 titik pada ruang lengkung 2 dimensi adalah kurva lengkung PQ.

Misal terdapat 2 titik A dan B yang dihubungkan oleh 3 buah lintasan seperti Gambar 2.3 di bawah ini. Koordinatnya diberikan oleh persamaan

xµ _=xµ_(sA)dan_xµ _=xµ_(sB), dengan_sadalah suatu parameter. Dari

Gambar 2.2:Geodesik pada ruang lengkung 2 dimensi

gambar di atas,C′ danC′′bukanlah panjang stasioner tetapi merupakan

suatu deviasi/simpangan dariC. Untuk memperoleh panjang stasioner ini,

maka variasiδxµ_{pada 2 titikAdanBharus bernilai nol.}

δxµ(sA) =δxµ(sB) = 0 (2.1)

Kemudian didefinisikan Lagrangian adalah fungsi darixµdan

turuna-nannya terhadap parameters

L=L (

xµ,dx µ

ds , s

)

(2.2)

sehingga integral aksi adalah

I=

∫ sB

sA

L (

xµ,dx µ

ds , s

)

Agar didapatkan panjang kurva stasioner, maka variasi dari integral di atas harus bernilai nol

δI=

∫ sB

sA

δL (

xµ,dx µ

ds , s

)

ds= 0 (2.4)

dengan definisi variasi adalahδL(xµ_,dxµ

ds , s

)

δL=L (

xµ+δxµ,dx µ

ds +δ dxµ

ds , s

) − L

(

xµ,dx µ

ds , s

)

(2.5)

Suku pertama pada pers.(2.5) diekspansikan dalam deret Taylor (lihat Lam-piran A.1) kemudian disubstitusikan ke pers.(2.4) sehingga

δI=

∫ sB

sA

[

d ds

(

∂_L d(∂x_∂sµ)

)

− ∂L

∂xµ

]

δxµds= 0 (2.6)

sehingga didapatkan persamaan Lagrange

d ds

(

∂_L d(∂x_∂sµ)

)

− ∂L

∂xµ = 0 (2.7)

Panjang stasioner untuk suatu kurva adalah

dengansadalah suatu parameter. Bentuk integral tersebut didapatkan dari

persamaan metrik berikut:

dl2 = gµνdxµdxν (2.9)

sehingga Lagrangian yang bersesuaian dengan bentuk bentuk integral (2.8) diatas adalah

L =

Suku pertama pers.(2.7) di atas dapat diperoleh dari pers.(2.10) yaitu

d

dan suku ke-2 pers.(2.7)

∂_L

kemudian disubstitusikan pada pers.(2.7) di atas. Hasil yang diperoleh adalah persamaan geodesik sebagai berikut.

d2xρ

Pada suku ke-2 pers.(2.13) di atas, terdapat koefisienΓρ

µν yang disebut

sehingga dari pers.(2.13) di atas, akan diperoleh geodesik berupa garis lurus.

2.2 Tensor kurvatur

Jika terdapat suatu vektorAµ pada ruang Minkowski dan ditranslasi

ditranslasikan secara paralel pada dua titik sepanjang lintasan tertutup C, maka posisi vektor tersebut akan berimpit dengan vektor awal sebelum di-translasi. Tetapi pada ruang Riemann, jika suatu vektor ditranslasikan se-cara paralel pada dua titik sepanjang lintasan tertutup C, maka operasinya akan bergantung pada lintasannya seperti pada Gambar fig:2.4 dibawah ini.

Gambar 2.4: Translasi vektor pada ruang lengkung

Jika perubahan vektor itu adalah∆Aµ, maka:

∆Aµ=

I

C δAµ=

I

C

ΓνµρAνdxρ (2.14)

Dari teorema Stokes, integral kontur tertutupC dapat ditransformasi ke

integral luasanSsehingga

∆Aµ=1 2

I

C

[

Dγ(Γρ µνAρ

)

−Dν(Γρ µγAρ

)]

denganDγ adalah operator turunan kovarian. Operator ini dapat

disim-plifikasi menjadi operator turunan biasa non-tensorDγ → ∂γ. Integral

(2.15) akan menjadi

∆Aµ =

µγν adalah tensor kurvatur Riemann

Rρ_µγν =∂γΓρ

Tensor kurvatur Riemann menggambarkan bagaimana bentuk dari keleng-kungan ruang-waktu. Kemudian didefinisikan tensor Ricci yang merupak-an tensor rmerupak-ank-2 sebagai berikut

Rµγ≡Rρ_µγρ=∂γΓρ

serta scalar Ricci adalah

R_≡Rµ_µ=gµγRµγ (2.19)

2.3 Tensor Energi-Momentum

Tensor Energi-Momentum adalah kuantitas tensor yang mendekripsik-an kerapatmendekripsik-an dmendekripsik-an fluks dari energi dmendekripsik-an momentum. Ditinjau aksi ymendekripsik-ang berbentuk

denganLadalah fungsi dari kuantitas qyang mendeskripsikan keadaan

sistem dan turunan pertamanya. Karena∫

maka ∫

Ladalah rapat Lagrangian. Penulisan ∂x∂qµ bisa ditulis sebagai

∂µq=q,µ. Persamaan gerak bisa didapatkan dengan memberikan variasi

pada pers.(2.20) di atas sehingga

δI = 1

Suku ke-2 persamaan di atas dapat dijabarkan menjadi

∂_L

sehingga pers.(2.21) menjadi

δI= 1

Dari teorema Gauss∫

Ω∂µF µ₌∫

SF µ_n

µdS= 0denganFµadalah suatu

medan tensor, maka suku ke-2 persamaan di atas lenyap (lihat lampiran A.3) sehingga:

δI = 1

Sehingga didapatkan

yang disebut sebagai persamaan Euler-Lagrange. Karena rapat lagrangian merupakan fungsi dari kuantitasqdan turunan pertamanyaq,µyaituL=

L(q, q,µ), maka

Kemudian substitusikan nilai dari∂L

∂q dari pers.(2.25) ke dalam pers.(2.26)

di atas sehingga:

∂L

∂xµ bisa dituliskan sebagai

∂L

∂xµ = δνµ∂ L

∂xν, sehingga pers.(2.27)

menjadi

dan didapatkan

∂

µ adalah definisi untuk tensor campuran energi-momentum.

Untuk medan elektromagnetik, Lagrangian medan elektromagnetik be-bas diberikan oleh:

LF(Fµν) =−

1 4µ0

FµνFµν (2.30)

dengan asumsi bahwa tidak ada sumber arus (Jν= 0) sehinga persamaan

Maxwell menjadi

∂µFµν = 0 (2.31)

denganFµν merupakan tensor kuat medan. Tensor kuat medan_Fµν ini

Fµν =∂µAν₋∂νAµ (2.32)

dengan bentuk kovariannya adalah

Fµν =∂µAν−∂νAµ (2.33)

Untuk mendefinisikan tensor energi momentum pada medan Elektro-magnetik, maka dihitung dulu turunan dari rapat lagrangian sebagai beri-kut:

∂νL= ∂L

∂Aγ

∂µAγ+ ∂L

∂(∂µAγ)

∂ν(∂µAγ) (2.34)

dengan

∂L

∂Aγ∂µAγ=∂µ

[

∂L

∂(∂µAγ)

]

∂µAγ (2.35)

serta dari definisi

∂νL=δ_νµ∂µL (2.36)

maka didapatkan

∂µ

[

∂L

∂(∂µAγ)

∂µAγ−δνµL

]

≡∂µTνµ= 0 (2.37)

denganTµ

ν adalah tensor energi-momentum campuran. Dengan

mensubs-titusikan pers.(2.30) ke dalam persamaan di atas, maka didapatkan

T_νµ =− 1

µ0

FµγFνγ+ 1 4µ0

δµ_νFγλFγλ (2.38)

dengan bentuk kontravarian dan kovariannya masing-masing adalah:

Tµν =−_µ1

0

FνγFµγ+ 1 4µ0

Tµν =−1

µ0

F_νγFµγ+ 1 4µ0

gµνFγλFγλ (2.40)

Tensor energi momentum pers.(2.40) menggambarkan distribusi energi dan momentum yang disebabkan oleh medan elektromagnetik

2.4 Persamaan Medan Einstein

Persamaan medan Einstein adalah persamaan yang menggambarkan kelengkungan ruang waktu yang diakibatkan oleh distribusi materi di se-kitarnya. Bentuk kelengkungan ruang-waktu digambarkan oleh bentuk tensor metrik dan bentuk tensor metrik dipengaruhi oleh bagaiamana dis-tribusi massa sebagai sumber dari gravitasi. Integral aksi total yang dise-babkan aksi massa sumber dan aksi oleh gravitasi adalah:

I=IG+IM (2.41)

denganIGmerupakan aksi oleh medan gravitasi pada ruang vakum

(dima-na tidak ada sumber medan) danIM merupakan aksi oleh massa sumber.

Kemudian diambil variasi dari pers.(2.41) di atas agar diperoleh aksi mi-nimum yaitu

δI = δIG+δIM

0 = δIG+δIM

−δIM = δIG (2.42)

dengan nilai dari masing-masingδIGdanδIMdapat dilihat pada lampiran

A.4. Jika kedua nilai ini disubstitusikan pada pers.(2.42), maka didapatkan

−δIM = δIG

−₂1

c

∫

Ω

Tµνδgµν√−gdΩ = − c3

16πG

∫

Ω

(

Rµν−

1 2gµνR

) √

−gδgµνdΩ

dari pers.(2.43) di atas, maka akan di dapatkan:

Rµν−1₂gµνR = 8πG

c4 Tµν

(2.44)

Pers.(2.44) merupakan Persamaan Medan Einstein. Ruas kiri persamaan medan Einstein menggambarkan kelengkungan ruang-waktu dan ruas ka-nannya menggambarkan distribusi materi. Interpretasi dari persamaan ini adalah materi menyebabkan ruang waktu melengkung atau kelengkungan ruang waktu memerintahkan materi untuk bergerak.

Jika pers.(2.44) dibentuk dalam tensor campuranRµ_νdanT_νµmaka

ak-an didapatkak-an:

Rµν−

1 2δ

µ νR =

8πG c4 T

µ ν

(2.45)

Kemudian dilakukan kontraksi indeksν _→µpada persamaan di atas

se-hingga

Rµ_µ−1

2δ

µ µR =

8πG c4 T

µ µ

(2.46)

Karena

δ_µµ=δ0₀+δ₁1+δ₂2+δ₃3= 4 (2.47)

maka

R₋2R = 8πG

c4 T R = −8πG

c4 T (2.48)

sehingga pers.(2.44) dapat diungkapkan dengan bentuk yang lain menjadi:

Rµν =

8πG c4

(

Tµν−

1 2gµνT

)

2.5 Algoritma Newman-Janis

Schwarzschild telah memecahkan solusi untuk Persamaan Medan Ein-stein di atas yaitu solusi untuk medan statik dan simetri bola. Penjelasan tentang solusi Schwarzschild ini disajikan dalam bab 3. Karena umumnya benda langit berotasi, maka dari solusi Schwarzschild ini kemudian di-kembangkan solusi untuk yang non-statik yakni berotasi yaitu solusi Kerr. Setelah ditemukannya solusi Kerr yang masih murni, Newman dan Janis dapat menunjukkan bahwa solusi Kerr dapat diturunkan dengan cara lain yang selanjutnya disebut sebagai Algoritma Newman-Janis. Algoritma ini diterapkan pada metrik Schwarzschild yang kemudian menghasilkan solu-si Kerr dan jika Algoritma ini diterapkan pada metrik Reissner-Nordstrom (solusi statik dan simetri bola dari persamaan medan Einstein-Maxwell), maka akan didapatkan solusi Kerr-Newman. Algoritma Newman-Janis adalah sebagai berikut:

1. Menuliskan bentuk metrik ke dalam koordinat null dengan transfor-masi sebagai berikut:

u=t−r∗dengan r∗ merupakan tortoise koordinat

2. Menuliskan tensor metrik kontravarian dari metrik pada metode per-tama dalam suku-suku vektor-4 null yaitu:

gµν =−lµnν−lνnµ+mµm¯ν+ ¯mµmν

dengan

lµlµ=nµnµ=mµmµ= 0

−lµnµ=mµm¯µ= 1

lµmµ=nµmµ= 0

3. Mentransformasikan koordinatxµmenjadi koordinat kompleks_x˜µ

xµ→x˜µ (2.50)

4. Dilakukan transformasi sebagai berikut

˜

Metrik yang dihasilkan dari algoritma ini adalah metrik Kerr dan me-trik Kerr-Newman yang dinyatakan dalam koordinat null. Kemudian un-tuk menganalisa sifat-sifat seperti singularitas dan event horizon, metrik ini ditransformasikan dalam koordinatBoyer-Lidquistyaitu dengan cara:

dt=du+r

2_+a2

∆ dr, dψ =dϕ+

a

SOLUSI STATIK PERSAMAAN MEDAN EINSTEIN

3.1 Solusi Schwarzchild

Solusi Schwazschild adalah solusi untuk Persamaan Medan Einstein untuk kasus statik dan simetri bola dari massaM. Statik berarti tensor

me-trikgµνtidak bergantung waktu atau∂γgµν = 0, sertads2harus invarian

terhadap transformasix0 _{→ −x}0(pembalikan waktu). Konsekuensinya

adalahds2tidak boleh mengandung suku_dxi_dx0yang menjadikannya

ti-dak invarian terhadap transformasi pembalikan waktu ataugi0=g0i= 0.

Karena tensor metrik tidak bergantung waktu serta elemen garisnya tidak boleh terdapat suku silang antaratdengan(r, θ, ϕ), maka tensor metrik

gµν hanya memiliki elemen diagonal yang koefisiennya merupakan

fung-si dari parameterrsaja untuk mempertahankan bentuk simetri bola.

ds2=−U(r)dt2+V(r)dr2+W(r)r2(dθ2+sin2θdϕ2) (3.1)

Dari kondisi khusus yang didapatkan di sini, maka 10 komponen bebas tensor metrik yang secara umum bergantung padaxµ menjadi tereduksi

hanya menjadi 4 komponen bebas yang merupakan fungsirsaja.

Kare-na persamaan medan merupakan turuKare-nan ke-2 dari tensor metrik, maka 3 fungsiU(r), V(r)danW(r)di atas bisa direduksi hanya menjadi 2 fungsi

saja. Karenarmerupakan parameter radial, maka bisa digantikan dengan

sembarang fungsir. Misal kan diambilW r2= ˆr2, makarˆ=√W r, serta

drˆ

dr =

√

W

(

1 + r 2W

dW dr

)

(3.2)

maka

V dr2= V

W

(

1 + r 2W

dW dr

)−2

dˆr2_≡V dˆ rˆ2 (3.3)

denganV ≡Vˆ. Dengan cara yang sama maka bisa didapatkanU ≡Uˆ.

Dengan menggantirmenjadirˆ, maka elemen garis diatas akan menjadi

ds2=−Vˆ(ˆr)dt2+ ˆU(ˆr)dr2+ ˆr2(dθ2+sin2θdϕ2) (3.4)

Kemudian dengan menghilangkan tanda topi pada persamaan di atas serta dipilih fungsi dariUdanV adalah

U(r) =e2ν(r),danV(r) =e2λ(r) (3.5)

maka elemen garisnya akan menjadi

ds2=−e2νc2dt2+e2λdr2+ (r2dθ2+r2sin2θdϕ2) (3.6)

Dari elemen garis pers.(3.6) di atas, maka didapatkan tensor metrik

gµν sebagai berikut

gµν =



  

−e2ν 0 0 0 0 e2λ 0 0 0 0 r2 0 0 0 0 r2sin2

θ



 

 (3.7)

dengan bentuk kontravarian dari tensor metrik diatas adalah

gµν =



  

−e−2ν _{0 0 0}

0 e−2λ 0 0 0 0 r−2 0 0 0 0 r−2_sin−2_θ



 

 (3.8)

Nilai dari simbol Christoffel jenis ke-2 dari tensor metrik pers.(3.7) di atas adalah

Γρ

µν =gρσΓσ,µν =

1 2g

ρσ_{(∂νgµσ+∂µgνσ−∂σgµν)}

Γ001 = Γ010=ν ′

Γ1

00 = ν

′

e(2ν−2λ)

Γ111 = λ ′

Γ122 = −re −2λ

Γ133 = −rsin 2

θ e−2λ (3.9)

Γ212 = Γ221=

1

r

Γ233 = −sinθcosθ

Γ313 = Γ331=

1

r

Γ323 = Γ332=cotθ

Tensor Ricci dapat dihitung dengan menggunakan persamaan

Rµν=∂νΓσµσ−∂σΓσµν+ ΓρµνΓσρν−ΓρµνΓσρσ (3.10)

Karena Tensor Ricci bersifat simetri(Rµν =Rνµ), maka hanya memiliki

10 komponen bebas. Untuk komponen Ri0,(i= 1,2,3) :

Ri0=∂0Γiσσ −∂σΓσi0+ Γ ρ iσΓ

σ ρ0−Γ

ρ

i0Γσρσ (3.11)

dengan kondisi statik mensyaratkan bahwa∂0gµν = 0sehingga∂0Γσiσ =

0. Tensor Ricci menjadi

Ri0=−∂jΓji0+ Γ ρ ijΓ

j ρ0−Γ

ρ i0Γ

j

ρj (3.12)

Dengan menggunakan nilaiΓi

j0 = 0,Γ ρ

0ρ = 0danΓ0ij = 0, maka

dida-patkan

Ri0=R0i= 0 (3.13)

arah diagonal (Rµµ). Nilai dariRµµini adalah

Rµµ = ∂µΓσµσ−∂σΓσµµ+ ΓσρµΓρµσ−ΓρµµΓσρσ

Untukµ= 0

R00 = ∂0Γσ0σ−∂σΓσ00+ Γ ρ

0σΓσρ0−Γ ρ 00Γσρσ

=

{

−ν′′+ν′λ′₋ν′2₋2ν ′

r

}

e(2ν−2λ) (3.14)

Untukµ= 1

R11 = ∂1Γσ1σ−∂σΓσ11+ Γρ1σΓσρ1−Γρ11Γσρσ

= ν′′+ (ν′)2−λ′ν′−2λ

′

r (3.15)

Untukµ= 2

R22 = ∂2Γσ2σ−∂σΓσ22+ Γρ2σΓσρ2−Γρ22Γσρσ

= (1 +rν′

−rλ′

)e(−2λ)

−1 (3.16)

Untukµ= 3

R33 = ∂3Γσ3σ−∂σΓσ33+ Γ ρ

3σΓσρ3−Γ ρ 33Γσρσ

= sin2θ[(1 +rν′₋rλ′)e(−2λ)₋1]

= sin2θ R22 (3.17)

−ν′′+ν′λ′−ν′2−2

rν ′

= 0 (3.18)

ν′′−ν′λ′+ν′2−2

rλ ′

= 0 (3.19)

(1 +rν′−rλ′)e(−2λ)= 1 (3.20)

Kemudian pers.(3.18) dan pers.(3.19) dijumlahkan sehingga

−2

r (ν ′

+λ′) = 0

atau

(ν′+λ′) = 0

ν+λ = konstan (3.21)

Padar→ ∞, metrik harus kembali pada bentuk Minkowskiηµνsehingga νdanλ→0.

maka

ν+λ= 0→ν=−λ (3.22)

dengan memasukkan pers.(3.22) ke pers.(3.20), maka

(1 + 2rν′)e(2ν)= d

dr

[

re(2ν)]= 1 (3.23)

Kemudian pers.(3.23) diintegralkan sehingga

∫

d[re(2ν)]=

∫

dr re(2ν)=r+C (3.24)

denganCmerupakan konstanta integrasi yang mempunyai nilai (lihat

lam-piran A.5)

sehingga metriknya akan menjadi

ds2 = − (

1−2m

r

)

c2(dt)2+

(

1−2m

r

)−1

(dr)2+r2dΩ2

(3.26) metrik pada pers.(3.26) tersebut merupakan metrik Schwarzschild.

3.2 Solusi Reissner-Nordstrom

Solusi Schwazschild adalah solusi untuk Persamaan Medan Einste-in untuk kasus statik dan simetri bola dari massaM. Konsekuensi dari

asumsi ini adalah tensor energi momentumTµν bernilai0. Jika massaM

tersebut bermuatan totalq, maka nilai tensor energi momentumTµνtidak

sama dengan nol tetapi merupakan tensor energi momentum untuk med-an elektromagnetik ymed-ang disebabkmed-an oleh muatmed-an totalq. Dari pers.(2.44)

yaitu persamaan medan Einstein

Rµν =

8πG c4

(

Tµν−

1 2gµνT

)

(3.27)

dengan tensor energi-momentum yaitu pers.(2.40)

Tµν =−F_νγFµγ+1 4gµνF

γλ_{Fγλ (3.28)}

sertaFµνmerupakan tensor kuat medan yaitu

Fµν =∂µAν−∂νAµ (3.29)

NilaiTdari pers.(3.27) di atas adalah nol sehingga pers.(3.27) menjadi

Rµν = 8πG

c4 Tµν (3.30)

momentum adalah (lihat lampiran A.6)

T00 = −

1 2f

2_(e−2λ₎

T11 =

1 2f

2_e−2ν

(3.31)

T22 = −

1 2r

2

f2e−2λ−2ν

T33 = −

1 2r

2

f2e−2λ−2νsin2θ

Dengan menggunakan cara yang sama pada solusi Schwarzschild, akan didapatkan metrik Reissner-Nordstrom sebagai berikut:

ds2 = − (

1−2m

r + Q2

r2

)

du2+

(

1−2m

r + Q2

r2

)−1

dr2+r2dΩ2

(3.32)

dengan

Q2_{≡ −} q 2_G

8πϵ2 0c4

(3.33)

Metrik di atas merupakan generalisasi dari metrik Schwarzschild. Jika diambilQ = 0pada metrik di atas yang berarti massaM menjadi tidak

SOLUSI BEROTASI PERSAMAAN MEDAN EINSTEIN

Solusi Schwarzschild dan solusi Reissner Nordstrom adalah solusi un-tuk persamaan medan Einstein yang statik dan simetri bola yang masing-masing bersesuaian dengan massaMyang tidak bermuatan dan massaM

yang bermuatan q. Karena pada umumnya benda langit berotasi, maka

diperlukan adanya solusi untuk massaM bermuatanqyang berotasi

gu-na men-generalisasi solusi Schwarzschild dan solusi Reissner Nordstrom. Pada subbab berikut akan dibahas bagaimana solusi persamaan medan Einstein untuk kasus berotasi dengan menggunakan Algoritma Newman-Janis. Jika algoritma Newman-Janis diterapkan pada metrik Scwarzschi-ld, maka akan didapatkan solusi Kerr sedangkan jika algoritma Newman-Janis diterapkan pada metrik Reissner-Nordstrom, maka akan didapatkan solusi Kerr-Newman.

4.1 Solusi Kerr

Untuk memperoleh solusi Kerr dengan Algoritma Newman-Janis, ma-ka langma-kah yang dilakuma-kan yaitu membentuk metrik Schwarzschild dalam koordinat null yaitu dengan menerapkan transformasiu=t₋r∗_dengan r∗adalah koordinat_tortoiseyang diberikan oleh

dr=

(

1−2m

r

)

dr∗ (4.1)

sehingga bentuk metrik Schwarzschild dalam ungkapan koordinat null men-jadi:

ds2 = − (

1−2m

r

)

du2−2du dr+r2dΩ2 _(4.2)

Tensor metrik dari elemen garis di atas adalah:

gµν =

dengan bentuk kontravariannya adalah:

gµν =

Komponen-komponen vektor-4 null yang bersesuaian dengan tensor me-trik di atas adalah:

Kemudian nilair ditransformasikan menjadi bentuk kompleks

yai-tur _→ r˜. Dengan menghilangkan tanda ̃, maka bentuk vektor-4 null

pers.(4.5) di atas menjadi

lµ = (0,₋1,0,0)

Kemudian dilakukan transformasi

xρ→x′ρ=xρ+iacosθ(δ₀ρ−δρ₁) (4.9)

sehingga diperoleh

u→u′ = u+iacosθ r_→r′ = r₋iacosθ θ→θ′ = θ

atau

u = u′

−iacosθ=u′

−iacosθ′ r = r′+iacosθ=r′+iacosθ′

(4.11)

denganv′ , r′

, θ′

, ϕ′adalah kuantitas riil. Vektor-vektor basis

bertransfor-masi dengan menggunakan aturan rantai:

∂ ∂xµ →

∂ ∂x′µ =

∂xν ∂x′µ

∂ ∂xν

atau dapat dituliskan :

∂µ→∂µ′ = ∂xν

∂x′µ∂ν (4.12)

Setelah ditransformasi dengan menghilangkan tanda ’, hasil transformasi-nya adalah:

lµ∂µ = −∂r nµ∂µ = −∂u+1

2

(

1− 2mr

r2_+a2cos2_θ

)

∂r

mµ∂µ = √ 1

2(r−iacosθ)

(

iasinθ∂v−iasinθ∂r+∂θ+ i

sinθ∂ϕ

)

¯

mµ∂µ = √ 1

2(r+iacosθ)

(

−iasinθ∂v+iasinθ∂r+∂θ−_sini

θ∂ϕ

)

atau

Selanjutnya komponen-komponen tensor metrik kontravariangµν

da-pat dibentuk yaitu:

gµν =−lµnν−lµnν+mµm¯ν+mνm¯µ (4.15)

Maka tensor metrik Kontravariannya adalah:

gµν =

sehingga elemen garisnya menjadi:

ρ2 = r2+a2cos2θ (4.17)

∆ = r2+a2−2mr (4.18)

Pers.(4.16) merupakan metrik kerr yang menggambarkan massa M

yang berotasi. Parameter rotasi ditunjukkan dengan adanya sukuayang

sebanding dengan momentum sudut.

4.2 Solusi Kerr-Newman

Solusi Reissner-Nordstrom adalah solusi untuk lubang hitam yang sta-tik, simetri bola dan bermuatan. Sama seperti analogi dari generalisasi so-lusi Schwarzschild ke soso-lusi Kerr, soso-lusi Reissner-Nordstrom juga dapat digeneralisasi ke solusi Kerr-Newman menggunakan Algoritma Newman-Janis. Metrik Reissner Nordstrom ditransformasi dengan menggunakan

u=t−r∗, dengan

r∗adalah tortoise koordinat yang memenuhi

dr=

(

1−2m

r + Q2

r2

)

dr∗ (4.19)

sehingga bentuk metrik Reissner-Nordstrom menjadi:

ds2 = − (

1−2m

r + Q2

r2

)

du2−2du dr+r2dΩ2 (4.20)

Tensor metrik dari elemen garis di atas adalah:

gµν =



   

−(1−2m r +

Q2

r2

)

−1 0 0

−1 0 0 0

0 0 r2 0

0 0 0 r2sin2θ



   

(4.21)

gµν =

Komponen-komponen vektor-4 null yang bersesuaian dengan tensor metrik di atas adalah:

lµ _{= (0,−1,0,0)}

Kemudian nilair ditransformasikan menjadi bentuk kompleks yaitu r → r˜ = r+iy. Dengan menghilangkan tanda aksen, maka bentuk

lµ = (0,₋1,0,0)

nµ =

( −1,1

2

(

1−m

r − m

¯

r + Q2

rr¯

)

,0,0

)

mµ = 1

¯

r√2

(

0,0,1, i

sinθ

)

¯

mµ = 1

r√2

(

0,0,1, i

sinθ

)

(4.25)

atau

lµ_∂

µ = −∂r nµ∂µ = −∂u+1

2

(

1−m_r −m_r¯ +Q

2

rr¯

)

∂r

mµ∂µ = 1 ¯

r√2

(

∂θ+ i

sinθ∂ϕ

)

¯

mµ∂µ = 1

r√2

(

∂θ−_sini

θ∂ϕ

)

(4.26)

setelah itu dilakukan transformasi

xρ→x′ρ=xρ+iacosθ(δ₀ρ−δ₁ρ) (4.27)

sehingga diperoleh

u→u′ = u+iacosθ r_→r′ = r₋iacosθ θ→θ′ = θ

atau

u = u′

−iacosθ=u′

−iacosθ′ r = r′+iacosθ=r′+iacosθ′

(4.29)

denganv′ , r′

, θ′

, ϕ′adalah kuantitas riil. Vektor-vektor basis

bertransfor-masi dengan menggunakan aturan rantai:

∂ ∂xµ →

∂ ∂x′µ =

∂xν ∂x′µ

∂ ∂xν

atau dapat dituliskan :

∂µ→∂µ′ = ∂xν

∂x′µ∂ν (4.30)

Setelah ditransformasi dengan menghilangkan tanda ’, hasil transformasi-nya adalah:

lµ∂µ = −∂r nµ∂µ = −∂u+1

2

(

1− 2mr−Q

2

r2_+a2_cos2_θ

)

∂r

mµ∂µ = √ 1

2(r−ia cosθ)

(

iasinθ∂v−iasinθ∂r+∂θ+ i

sinθ∂ϕ

)

¯

mµ∂µ = √ 1

2(r+iacosθ)

(

−iasinθ∂v+iasinθ∂r+∂θ−_sini

θ∂ϕ

)

atau

Selanjutnya komponen-komponen tensor metrik kontravariangµν _dapat

dibentuk yaitu:

gµν=−lµnν₋lµnν+mµm¯ν+mνm¯µ (4.33)

dengan tensor metrik Kontravariannya adalah:

gµν =

sehingga elemen garisnya menjadi:

ds2 = −

DISKUSI

Persamaan Medan Einstein memiliki banyak solusi tetapi dalam tugas akhir ini hanya dirumuskan ulang solusi untuk 4 macam lubang hitam. Jika solusinya adalah solusi statik (tidak ada momentum angular), maka solusi-nya adalah metrik Schwarzschild dan Reissner-Nordstrom yang masing-masing mencirikan lubang hitam bermassam tanpa muatan listrik, dan

lubang hitam bermassamdengan muatanq. Jika solusinya adalah solusi

yang berotasi, maka solusinya adalah metrik Kerr dan Kerr-Newman yang masing-masing mencirikan lubang hitam bermassamdengan momentum

angularJtanpa muatan listrik, dan lubang hitam bermassamdengan

de-ngan momentum angularJdan bermuatanq. Keempat metrik ini adalah

solusi lubang hitam dari relativitas umum. Hubungan 4 metrik ini adalah seperti pada tabel berikut

Tabel 5.1:Kedudukan lubang hitam bermuatan dan berotasi

Tidak berotasi (J=0) Berotasi (J̸= 0)

Tidak bermuatan (Q=0) Schwarzschild Kerr

Bermuatan (Q̸= 0) Reissner-Nordstrom Kerr-Newman

Bentuk metrik dari koordinat null pers.(4.34) dapat ditransformasi ke bentukBoyer-Lindquistdengan menerapkan transformasi berikut:

dt=du+r

2_+a2

∆ dr, dψ =dϕ+

a

∆dr (5.1)

maka diperoleh metrik Kerr-Newman dalam koordinat Boyer-Lindquist:

ds2 = −∆

ρ2

(

asin2θdψ₋dt)2+sin

2 θ ρ2

(

(r2+a2)dψ₋a dt)2

+ρ

2

∆2dr 2₊

ρ2dθ2 (5.2)

Dalam bab diskusi ini akan dikaji mengenai sifat-sifat di sekitar ruang

waktu Kerr-Newman. Sifat yang akan dikaji antara lain tentang horison peristiwa Event Horizon (EH) dan pergeseran merah permukaan (Surface of Infinite Red-shift (SIR)). EH dapat dicari dari permukaanhypernull. Persamaan permukaanhypernull adalah

f(x0, x1, x2, x3) = 0 (5.3)

dengan vektor normal yang merupakan vektor kovarian

nµ= ∂f

∂xµ (5.4)

Koordinat Boyer-Lindquist mempunyai singularitas di∆ = 0sehingga

r2₋2mr+a2+Q2 = 0

r=r± = m_±√m2_−a2_−Q2 (5.5)

denganr+ merupakan solusi untuk daerah di luar sumber massa danr−

untuk daerah di dalam sumber massa. Pada diskusi ini hanya dibahas un-tukr+saja (diluar sumber massa)

r=r+ = m+

√

m2_−a2_−Q2 (5.6)

sehingga persamaan permukaanhyperadalah

f = r−r+

= r₋m₋√m2_−a2_−Q2 (5.7)

dengan nilainµadalah

nµ = ∂f

Permukaanhyperakan null jikanµnµ= 0, tetapi

nµnµ = gµνnνnµ

= g11n1n1

= g11

= ∆

ρ2 (5.9)

sehingganµ_n

µakan sama dengan nol jika∆ = 0ataur =r+. Karena nµ_n

µ = 0 padar = r+, maka r = r+adalah permukaan hypernull.

Cahaya yang merambat melewati batas ini setelah melalui permukaan ini tidak akan pernah keluar melalui permukaan ini. permukaan ini disebut sebbagai event horizon sehingga event horizon untuk solusi Kerr-Newman adalah :

r=r+=m+

√

m2_−a2_−Q2 (5.10)

Cahaya yang bergerak menjauh di sekitar permukaanhypernull akan meng-alami pergeseran merah gravitasional, artinya panjang gelombang cahaya akan semakin memanjang menjadi lebih besar. Besar fraksi perubahan panjang gelombang ini dinyatakan dengan konstantazyang tidak

berdi-mensi yaitu

z=λ0−λe

λe = λ0

λe−1 (5.11)

denganc=λv, maka

z =

c v0

c ve

−1

= ve

v0−

1 (5.12)

denganνeadalah besarnya frekuensi yang dipancarkan danνoadalah

cahaya dipancarkan dir2dan diterima pengamat dir1, maka

z = v2

v1 −

1 =

√

g00(r1) g00(r2)−

1

(5.13)

dengan nilaig00(r)untuk ruang-waktu Kerr-Newman adalah

g00(r) = −

(

1−2mr−Q

2

ρ2

)

(5.14)

r1diasumsikan sangat jauh dari sumber(r→ ∞)sehingga tensor metrik

akan kembali ke ruang-waktu datar (Minkowskian):

g00(r1) = −1 (5.15)

sehingga

z = √ 1

−g00(r2)

−1

=

√

1 1−2mrρ−2Q2

−1

=

√

ρ2

ρ2_−2mr−Q2 −1

(5.16)

Saatρ2_→2mr+Q2, maka_{z→ ∞}dan nilai_g

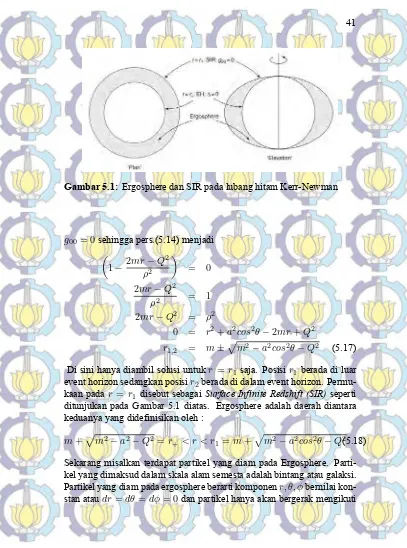
Gambar 5.1: Ergosphere dan SIR pada lubang hitam Kerr-Newman

g00= 0sehingga pers.(5.14) menjadi

(

1−2mr−Q

2

ρ2

)

= 0

2mr₋Q2

ρ2 = 1

2mr−Q2 = ρ2

0 = r2+a2cos2θ−2mr+Q2 r1,2 = m±

√

m2_−a2_cos2_θ−Q2 (5.17)

Di sini hanya diambil solusi untukr=r1saja. Posisir1berada di luar

event horizon sedangkan posisir2berada di dalam event horizon.

Permu-kaan padar =r1disebut sebagaiSurface Infinite Redshift (SIR)seperti

ditunjukan pada Gambar 5.1 diatas. Ergosphere adalah daerah diantara keduanya yang didefinisikan oleh :

m+√m2_−a2_−Q2_=r

+< r < r1=m+

√

m2_−a2_cos2_θ−Q2(5.18)

Sekarang misalkan terdapat partikel yang diam pada Ergosphere. Parti-kel yang dimaksud dalam skala alam semesta adalah bintang atau galaksi. Partikel yang diam pada ergosphere berarti komponenr, θ, ϕbernilai

lintasan geodesik timelikenya, yaitu

ds2=− (

1−2mr−Q

2

ρ2

)

c2dt2 (5.19)

di dalam Ergosphere denganr < r1, maka

r < r1

r < m+√m2_−a2_cos2_θ−Q2 r₋m < √m2_−a2_cos2_θ−Q2 r2−2mr+m2 < m2−a2cos2θ−Q2 r2+a2cos2θ+Q2 < 2mr

(5.20)

atau

ρ2+Q2 < 2mr

ρ2 < 2mr−Q2 (5.21)

sehingga

ds2 = − (

1−2mr−Q

2

ρ2

)

c2dt2

ds2 > 0 (5.22)

Ada yang kurang dari hasil ini karena untuk partikel realds2 _{<0, maka}

diasumsikan terdapat setidaknya 1 koordinat yang tidak nol antarar, θdan ϕ. Diasumsikan partikel berada dirdanθyang tertentu, tetapi bergerak

kearahϕpositif, maka kecepatan 4-partikel adalah

uµ= dx

µ

dτ =

(

u0, u1, u2, u3)

= (u0,0,0, u3)

= u0

(

1,0,0,u 3

u0

)

= u0

(

1,0,0,Ω c

)

denganΩ = dϕ_dt = dϕ_dτdτ dt =c

u3

u0 kondisi untukuµtimelike adalah

ds2 = gµνuµuν<0 (5.24)

solusi untukg00

g33 + 2

Misalkan diambil

−g_g03

33

= ω

c (5.28)

sehingga terdapat 2 solusi yaitu

Ωmin = ω−

maka agar pertidaksamaan (5.26) terpenuhi, nilaiΩharus berada pada

ren-tang

denganΩadalah kecepatan angular partikel pada Ergosphere Kerr-Newman

yang nilainya bergantung padarkarena tensor metriknya bergantung

pa-dar. Karenag00 < 0, makaΩmin < 0sehingga partikel bisa bergerak

berputar melawan arah rotasi lubang hitam. Ketikarmendekati SIR,

ma-kag00 →0danΩmin = 0danΩmax= 2ωsehingga partikel tidak bisa

lagi untuk bergerak melawan arah rotasi dari lubang hitam, tetapi partikel masih bisa diam (menurut pengamat yang jauh dari massa sumber). Ke-mudian jika partikel telah masuk ke dalam ergosfer, makaΩ = 0sehingga

PENUTUP

6.1 Kesimpulan

Dalam tugas akhir ini, telah diturunkan solusi lubang hitam untuk per-samaan medan Einstein yaitu untuk solusi statik adalah solusi Schwa-rzschild dan solusi Reissner-Nordstrom. Kemudian setelah diterapkan me-tode Newman-Janis pada kedua metrik tersebut, dihasilkan solusi Reissner-Nordstrom dan solusi Kerr-Newman. Disekitar lubang hitam Kerr-Newman terdapat ergosphere yang membedakannya dengan lubang hitam Schwa-rzschild dan Reissner-Nordstrom. Partikel berada di dekat horizon dapat bergerak berlawanan arah rotasi lubang hitam, sedangkan partikel yang berada tepat pada SIR partikel tersebut tidak bisa lagi bergerak melawan arah rotasi lubang hitam, dan setelah masuk pada ergosfer, partikel akan bergerak melingkar searah gerakan sumber massa. Dengan kata lain, SIR adalah batas dari partikel untuk dapat mempertahankan keadaan diamnya. Partikel yang dimaksud dalam skala ini adalah bintang atau galaksi. Parti-kel yang bergerak ke arah massaMdan melewati event horizon tidak bisa

lagi bergerak ke arah luar sekalipun itu cahaya. Selanjutnya massaMini

disebut sebagaiblackhole.

6.2 Saran

Saran untuk penelitian selanjutnya yaitu dengan mengkaji sifat-sifat ruang-waktu Kerr-Newman pada daerah di bagian dalam event horizon serta dengan menambahkan partikel uji yang bermuatan.

Jika ditambahkan 1 dimensi ekstra pada ruang-waktu Kerr-Newman, maka salah satu solusi yang didapatkan adanyaBlack Stringyang bermu-atan dan berotasi. Untuk kasus Black String yang tidak bermubermu-atan telah dikerjakan pada arXiv:1205.1656 [gr-qc].

[1] S. Chandrasekar, The Mathematical Theory of Blackhole, Oxford University Press, 1983

[2] S. P. Drake and P. Szekeres, Gen. Rel. Grav. 32, 445 (2000) doi:10.1023/A:1001920232180 [gr-qc/9807001].

[3] D. L. Wiltshire, M. Visser dan S. M. Scott,The Kerr spacetime: Ro-tating black holes in general relativity, Cambridge University Press, 2009

[4] E. Poisson,A Relativist’s Toolkit: The Mathematics of Black-holes Mechanics, Cambridge University Press, 2004

[5] L. D. Landau, E.M. LifshitzThe Classical Theory of Fields, Butter-worth Heinemann, 1975

[6] D. McMahon,Relativity Demystified, McGraw-Hill, 2006

[7] M. Dalarsson, N. Dalarsson,Tensor Calculus, Relativity, and Cos-mology: A First Course, Elsevier.Inc, 2005

[8] R. d’Inverno, Introducing Einstein’s Relativity, Clarendon Press, 1992

[9] R. Adler, M. Bazin dan M. Schiffer,Introduction to General Relati-vity, McGraw-Hill Kogakusha Ltd, 1965

[10] L. Ryder,Introduction to General Relativity, Cambridge University Press, 2009

[11] S. Carroll,Spacetime and Geometry: An Introduction to General Relativity, Addison Wesley, 2004

[12] A. Purwanto,Pengantar Kosmologi, ITS Press, 2009

[13] A. F. Arrosyidi,Solusi Schwarzschild dan Kerr Untuk Medan Gra-vitasi Einstein, Skripsi Universitas Airlangga, 2012

[14] http://mathworld.wolfram.com/Hypersurface.html

A.1 Persamaan Geodesik

Lagrangian didefinisikan sebagai fungsi dari koordinatxµdan turunan

pertamanya:

L=L (

xµ,dx µ

ds , s

)

(A.1)

sehingga integral aksi adalah

I=

∫ sB

sA

L (

xµ,dx µ

ds , s

)

ds (A.2)

dengan variasi integral aksi

δI=

∫ sB

sA

δ_L

(

xµ,dx µ

ds , s

)

ds= 0 (A.3)

serta

δL=L (

xµ+δxµ,dx µ

ds +δ dxµ

ds , s

) − L

(

xµ,dx µ

ds , s

)

(A.4)

Suku pertama pada pers.(A.4) diekspansikan dalam deret Taylor

ngan mengambil suku ke-0 dan ke-1

pers.(A.5) disubstitusikan ke pers.(A.3)

δI =

suku ke-3 pers.(A.6) lenyap karena

karena

maka didapatkan

∂L

pers.(A.9) disebut persamaanEuler-Lagrange. Dari persamaan metrik

dl2 = gµνdxµdxν

panjang kurva stasioner adalah

I=l(s) =

pers.(A.11) jika dibandingkan dengan pers.(A.2) akan didapatkan Lagra-ngian yaitu

L =

maka

Dari pers.(A.13) dan pers.(A.15) jika disubstitusikan ke pers.(A.9) sehing-ga

A.2 Tensor Kurvatur

Perubahan vektor kovarianAµ

∆Aµ=

I

C δAµ =

I

C

Γρ

µνAρdxν (A.17)

Dari teorema Stokes, integral kontur tertutupC dapat ditransformasi ke

integral luasanSsehingga

∆Aµ=

1 2

I

C

[

Dγ

(

ΓρµνAρ

) −Dν

(

ΓρµγAρ

)]

dSγν (A.18)

denganDγadalah operator turunan kovarian. Operator ini dapat

disimpli-fikasi menjadi operator turunan biasa non-tensorDγ →∂γseperti berikut:

Dγ

(

ΓρµνAρ

)

≡ DγCµν

= ∂γCµν−Γσ

µγCσν−ΓσγνCµσ (A.19)

Dν(Γρ µγAρ

)

≡ DνCµγ

= ∂νCµγ−ΓσµνCσγ−ΓσνγCµσ (A.20)

Dari pers.(A.19) dan pers.(A.20), maka

Dγ(Γρ µνAρ

)

−Dν(Γρ µγAρ

)

= DγCµν−DνCµγ

= ∂γCµν−Γµγσ Cσν−ΓσγνCµσ

−(∂νCµγ−Γσ

µνCσγ−ΓσνγCµσ

)

= ∂γCµν₋ΓσµγCσν−∂νCµγ+ ΓσµνCσγ

karena tensor permukaan merupakan tensor simetrik (dSγν _=dSνγ_),

ma-Dari pers.(A.22), maka simplifikasiDγ →∂γ bisa digunakan, sehingga

pers.(A.18) menjadi:

∆Aµ =

µγνadalah tensor kurvatur Riemann

Rρ_µγν =∂γΓρ

Tensor Ricci didefinisikan dari tensor kurvatur Riemann

Rµγ≡Rρ_µγρ =∂γΓρ

serta scalar Ricci adalah

R_≡Rµ

µ =gµγRµγ (A.28)

A.3 Tensor Energi-Momentum

q,µyaitu

=0(teoremaGauss)

−

sehingga didapatkan persamaanEuler-Lagrange:

∂L

∂q −∂µ ∂L

∂(∂µq)

Turunan pertama terhadap Lagrangian

Pers.(A.32) adalah tensor energi-momentum.

Untuk Medan Elektromagnetik, rapat Lagrangian adalah

L=−1

4FµνF

karenaF =F(∂µAµ)−→ L=L(Aµ, ∂µAµ), maka pers.(A.30)

menja-di

∂_L ∂Aν −∂µ

∂_L

∂(∂µAν) = 0 (A.34)

Substitusi pers.(A.33) ke dalam pers.(A.34). Suku pertama pers.(A.34) adalah

∂L

∂Aν

= −∂AµJ

µ

∂Aν

= −δ_µνJµ

= −Jν (A.35)

untuk suku ke-2:

∂_L

∂(∂µAν) = − 1 4

∂ ∂(∂µAν)

{

FαβFαβ}

= −1₄gραgσβ ∂

∂(∂µAν){FαβFρσ} = −1₄gραgσβ

{

∂(∂αAβ−∂βAα)

∂(∂µAν) Fρσ+Fαβ

∂(∂ρAσ−∂σAρ)

∂(∂µAν)

}

= −1

4g

ρα_gσβ{(_δµ αδβν−δ

µ βδ

ν α

)

Fρσ+Fαβ(δ_ρµδ_σν−δ_σµδν_ρ)}

= −1

4

{

(gρµgσν−gρνgσµ)Fρσ+Fαβ(gµαgνβ−gναgµβ)}

= −1

4{F

µν_−Fνµ_+Fµν_−Fνµ_}

= −1

4{F

µν_+Fµν_+Fµν_+Fµν_}

= −1

44F

µν

= −Fµν (A.36)

Substitusi pers.(A.35) dan pers.(A.36) ke dalam pers.(A.34) sehingga di-dapatkan

Pers.(A.37) adalah persamaan Maxwell. Untuk keadaan tidak ada arus

Jν _{= 0, maka}

∂µFµν = 0 (A.38)

Parameterquntuk medan elektromagnetik adalahAµ, sehingga tensor

energi-momentum pers.(A.32) untuk medan elektromagnetik adalah

Tν

µ = ∂µAλ ∂_L ∂(∂νAλ)−δ

ν µL

= −Fνλ∂µAλ+

1 4δ

ν µFλγFλγ

= −Fνλ(∂µAλ−∂λAµ)−Fνλ∂λAµ+

1 4δ

ν

µFλγFλγ

= −FνλFµλ−Fνλ∂λAµ+

1 4δ

ν µFλγFλγ

= −FνλFµλ−∂λ(FνλAµ) +Aµ∂λFνλ

| {z }

=0

+1 4δ

ν µFλγFλγ

= −FνλFµλ−∂λ(FνλAµ) +1 4δ

ν

µFλγFλγ (A.39)

Karena∂νT_µν = 0, maka suku ke-2:

∂ν∂λ(FνλAµ) = 1 2





∂ν∂λ(FνλAµ) +∂ν∂λ(FνλAµ)

| {z }

ν↔λ



 

= 1 2

{

∂ν∂λ(FνλAµ) +∂λ∂ν(FλνAµ)

}

= 1 2

{

∂ν∂λ(FνλAµ)−∂ν∂λ(FνλAµ)

}

= 0 (A.40)

Sehingga pers.(A.39) menjadi

T_µν = −FνλFµλ+

1 4δ

ν

A.4 Persamaan Medan Einstein

Aksi medan gravitasi pada ruang vakum

IG=

1

c

∫

ΩL

G(gµν, ∂σgµν)√−gdΩ (A.42)

dengan bentuk dariLGadalah

LG=− c4

16πGR (A.43)

Pers.(A.43)disubstitusikan ke pers.(A.42)

IG=− c

3

16πG

∫

Ω

R√−gdΩ (A.44)

jika dilakukan variasi terhadapIGdi atas, maka

δIG=− c3

16πG

∫

Ω

δ√₋gR dΩ (A.45)

dengan

δ(√₋gR) = δ(√₋ggµνRµν

)

= (δ√₋g)gµνRµν+√−g(δgµν)Rµν

+√−ggµν(δRµν) (A.46)

karena

maka

δ√−g = ∂

√ −g ∂g δg

= − 1

2√−gδg

= −₂√1

−g(−ggµνδg µν₎

= − √

−g

2 gµνδg

µν _(A.48)

Substitusi pers.(A.48) ke pers.(A.46)

δ(√−gR) = − √

−g

2 gµνδg

µν_gµν_Rµν+√_−g(δgµν_)Rµν

+√−ggµν(δRµν) = −

√ −g

2 gµνδg

µν_R+√_−g(δgµν_)Rµν

+√−ggµν(δRµν)

= √−g

(

Rµν−

1 2gµνR

)

δgµν+√−ggµν(δRµν)

dengan suku ke-3 adalah

Karena turunan kovarian tensor metrik adalah nol

Dλgµν = ∂λgµν+ Γµρλg ρν_{+ Γ}ν

ρλgµρ= 0 ∂λgµν = −Γµ_ρλgρν−Γν

ρλgµρ (A.51)

Dνgµν = ∂νgµν+ Γµρνgρν+ Γνρνgµρ= 0 ∂νgµν = −Γµ

ρνgρν−Γνρνgµρ (A.52)

serta dengan menubstitusikan pers.(A.51) dan pers.(A.52) ke dalam pers.(A.50), maka didapatkan

gµνδRµν = gµνδ(∂νΓλ µλ

)

−gµνδ(∂λΓλ µν

)

−∂λgµνδΓλ

µν+∂νgµνδΓλµλ

+gµν(Γγ

νγδΓλµλ−Γ γ λγδΓλµν

)

= gµν∂ν(δΓλ µλ

)

−gµν∂λ(δΓλ µν

)

−∂λgµνδΓλ

µν+∂νgµνδΓλµλ

+gµν(Γγ

νγδΓλµλ−Γ γ λγδΓλµν

)

= ∂ν(gµνδΓλ µλ

)

| {z }

λ↔ν

−∂λ(gµνδΓλ µν

)

+ Γγνγ

(

gµνδΓλµλ

)

| {z }

λ↔ν

−Γγ_λγ(gµνδΓλµν

)

= ∂λ

(

gµλδΓνµν−gµνδΓλµλ

)

+Γγ_λγ(gµλδΓνµν−gµνδΓλµν

) _(A.53)

Didefinisikan vektor-4

ωλ=gµλδΓµνν −gµνδΓλµν (A.54)

Nilai simbol Christoffel

Kemudian dari definisi vektor-4 dan nilai simbol Christoffel di atas, pers.(A.54) dan pers.(A.55) disubstitusikan ke dalam pers.(A.53) sehingga didapatkan

gµνδRµν = ∂λωλ+ Γγλγω

substitusi pers.(A.56) ke dalam pers.(A.49)

δ(√−gR) = √−g

pers.(A.57) disubstitusikan pers.(A.45) sehingga

δIG = −

=0(teoremaGauss)



Sedangkan aksi oleh massa sumber adalah

δIM =1

c

∫

Ω

maka

Pers.(A.62) disubstitusikan ke pers.(A.58) sehingga didapatkan

δIM =

Aksi total adalah

I = IG+IM δI = δIG+δIM = 0

δIG=−δIM (A.64)

dari pers.(A.58) dan pers.(A.63), didapatkan

Pers.(A.65) adalah persamaan medan Einstein. Dalam ungkapan tensor campuran, pers.(A.65) menjadi

Rµ

Jika dilakukanν→µpada semua suku pers.(A.66) di atas, maka

Rµ

Pers.(A.67) disubstitusikan ke dalam pers.(A.98) sehingga didapatkan ung-kapan lain dari persamaan medan Einstein

Rµν =

A.5 Solusi Schwarzschild

Metrik dengan adanya sumber massaM pada koordinat bola:

sehinggaV ≡Vˆ. Dengan cara yang sama maka bisa didapatkanU ≡

ˆ

U. Dengan menggantirmenjadirˆ, maka elemen garis diatas akan menjadi

ds2=−Vˆ(ˆr)dt2+ ˆU(ˆr)dr2+ ˆr2(dθ2+sin2θdϕ2) (A.72)

Dengan menghilangkan tanda topi pada persamaan di atas, maka

ds2=−V(r)dt2+U(r)dr2+r2(dθ2+sin2θdϕ2) (A.73)

serta dipilih fungsi dariU danV adalah

U(r) =e2ν(r),danV(r) =e2λ(r) (A.74)

maka elemen garisnya akan menjadi

ds2=−e2νc2dt2+e2λdr2+ (r2dθ2+r2sin2θdϕ2) (A.75)

Maka tensor metriknya

gµν =



  

−e2ν _{0 0 0}

0 e2λ _{0 0}

0 0 r2 ₀

0 0 0 r2sin2 θ



 

 (A.76)

karena

gµν = (gµν)

−1 _(A.77)

Maka bentuk kontravarian dari tensor metrik diatas adalah

gµν =



  

−e−2ν _{0 0 0}

0 e−2_{λ 0 0}

0 0 r−2 ₀

0 0 0 r−2_sin−2 θ



 

Persamaan untuk mencari simbol Christoffel adalah

Γµ,υρ=

1 2

(

∂gµυ ∂xρ +

∂gρµ ∂xυ −

∂gυρ ∂xµ

)

(A.79)

Maka untuk tensor metrik diatas, komponen-komponennya adalah

Γ0,00 = 1

2(∂0g00+∂0g00−∂0g00) = 0

Γ0,01= Γ0,10 =

1

2(∂1g00+∂0g00−∂0g00) = 1

2

(

∂(₋e2ν) ∂r

)

= −ν′e2ν

Γ0,02 = Γ0,20=

1

2(∂2g00+∂0g00−∂0g00) = 0

Γ0,03= Γ0,30 =

1

2(∂3g00+∂0g00−∂0g00) = 0

Γ0,11 =

1

2(∂1g01+∂1g10−∂0g11) = 1

2(0 + 0−0) = 0

Γ0,12= Γ0,21 =

1

2(∂2g01+∂1g20−∂0g12) = 1

2(0 + 0−0) = 0

Γ0,13= Γ0,31 =

1

2(∂3g01+∂1g30−∂0g13) = 1

Γ0,22 = 1

2(∂2g02+∂2g20−∂0g22) = 0

Γ0,23= Γ0,32 =

1

2(∂3g02+∂2g03−∂0g23) = 0

Γ0,33 =

1

2(∂3g03+∂3g30−∂0g33) = 0

Γ1,00 =

1

2(∂0g10+∂0g01−∂1g00) = 1

2

(

0 + 0−∂ (

−e2ν) ∂r

)

= ν′ e2ν

Γ1,01= Γ1,10 = 1

2(∂1g10+∂0g11−∂1g01) = 0

Γ1,02= Γ1,20 =

1

2(∂2g10+∂0g21−∂1g02) = 0

Γ1,03= Γ1,30 = 1

2(∂3g10+∂0g31−∂1g03) = 0

Γ1,11 = 1

2(∂1g11+∂1g11−∂1g11) = 1

2

(

2λ′e2λ)

= λ′e2λ

Γ1,12= Γ1,21 =

1

2(∂2g11+∂1g21−∂1g12) = 0

Γ1,13= Γ1,31 = 1

Γ1,22 = 1

2(∂2g12+∂2g21−∂1g22) = 1

2(0 + 0−(2r)) = −r

Γ1,23= Γ1,32 = 1

2(∂3g12+∂2g31−∂1g23) = 0

Γ1,33 =

1

2(∂3g13+∂3g31−∂1g33) = 1

2

(

0 + 0−(2rsin2θ))

= −rsin2θ

Γ2,00 = 1

2(∂0g20+∂0g02−∂2g00) = 1

2(0 + 0−0) = 0

Γ2,01= Γ2,10 = 1

2(∂1g20+∂0g12−∂2g01) = 0

Γ2,02= Γ2,20 =

1

2(∂2g20+∂0g22−∂2g02) = 1

2(0 + 0−0) = 0

Γ2,12= Γ2,21 =

1

2(∂2g21+∂1g22−∂2g12) = 1

2(0 + (2r)−0) = r

Γ2,13= Γ2,31 =

1

Γ2,22= Γ2,21 = 1

2(∂2g22+∂2g22−∂2g22) = 1

2(0) = 0

Γ2,23= Γ2,32 =

1

2(∂3g22+∂2g32−∂2g23) = 0

Γ2,33 =

1

2(∂3g23+∂3g32−∂2g33) = 1

2

(

0 + 0−(r2.sinθ.cosθ))

= −r2.sinθ.cosθ

Γ3,00 =

1

2(∂0g30+∂0g03−∂3g00) = 0

Γ3,01= Γ3,10 =

1

2(∂1g30+∂0g13−∂3g01) = 0

Γ3,02= Γ3,20 =

1

2(∂2g30+∂0g23−∂3g02) = 0

Γ3,03= Γ3,30 =

1

2(∂3g30+∂0g33−∂3g03) = 0

Γ3,11 =

1

2(∂1g31+∂1g13−∂3g11) = 0

Γ3,12= Γ3,21 = 1

2(∂2g31+∂1g23−∂3g12) = 0

Γ3,13= Γ3,31 =

1

2(∂3g31+∂1g33−∂3g13) = 1

2

(

Γ3,22 = 1

2(∂2g32+∂2g23−∂3g22) = 0

Γ3,23= Γ3,32 =

1

2(∂3g32+∂2g33−∂3g23) = 1

2

(

0 +(r2.sinθcosθ)−0) = r2sinθcosθ

Γ3,33 =

1

2(∂3g33+∂3g33−∂3g33) = 0

Nilai simbol Christoffel Jenis ke-2 dapat dicari dengan menggunakan persamaan berikut:

Γµ

υρ =gµτΓτ,υρ (A.80)

Nilai-nilai tersebut adalah

Γ000 = g00Γ0,00

= 0 Γ001= Γ010 = g0τΓτ,01

= g00Γ0,01=−e(−2ν).

(

−ν′e(2ν))=ν′

= g01Γ1,01= 0

= g02Γ2,01= 0

= g03Γ3,01= 0

Γ002= Γ020 = g0τΓτ,20

= g00Γ0,20

= 0 Γ003= Γ030 = g0τΓτ,30

= g00Γ0,30

Γ011 = g0τΓτ,11

= g00Γ0,11

= 0 Γ012= Γ021 = g0τΓτ,12

= g00Γ0,12

= 0 Γ013= Γ031 = g0τΓτ,13

= g00Γ0,13

= 0 Γ022 = g0τΓτ,22

= g00Γ0,22

= 0 Γ023= Γ032 = g0τΓτ,23

= g00Γ0,23

= 0 Γ033 = g0τΓτ,33

= g00Γ0,33

= 0

Γ100 = g1τΓτ,00

= g11Γ1,00

= e(−2λ).(ν′e(2ν))

= ν′e(2ν−2λ)

Γ101= Γ110 = g1τΓτ,01

= g11Γ1,01

Γ102= Γ120 = g1τΓτ,02

= g11Γ1,02

= 0 Γ103= Γ130 = g1τΓτ,03

= g11Γ1,03

= 0 Γ111 = g1τΓτ,11

= g11Γ1,11

= e(−2λ).(λ′e(2λ))

= λ′

Γ1

12= Γ121 = g1τΓτ,12

= g11Γ1,12

= 0 Γ113= Γ131 = g1τΓτ,13

= g11Γ1,13

= 0

Γ1

22 = g1τΓτ,22

= g11Γ1,22

= e(−2λ).(−r) = −re(−2λ)

Γ123= Γ132 = g1τΓτ,23

= g11Γ1,23

= 0 Γ133 = g1τΓτ,33

= g11Γ1,33

= e(−2λ).(₋rsin2θ)

Γ200 = g1τΓτ,00

= g22Γ2,00

= 0 Γ201= Γ210 = g2τΓτ,01

= g22Γ2,01

= 0 Γ202= Γ220 = g2τΓτ,02

= g22Γ2,02

= 0 Γ203= Γ230 = g2τΓτ,03

= g22Γ2,03

= 0 Γ211 = g22Γ2,11

= 0 Γ212= Γ221 = g2τΓτ,12

= g22Γ2,12

= (r)−2.(r) = 1

r

Γ2

13= Γ231 = g22Γ2,13

= 0 Γ222= Γ222 = g22Γ2,22

= 0 Γ223= Γ232 = g22Γ2,23

= 0 Γ233= Γ233 = g22Γ2,33

= (r)−2.(−r2sinθcosθ)