ABSTRAK
Cindy, 2016. Sifat-sifat Segitiga Siku-siku pada Geometri Bola. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Segitiga siku-siku pada geometri bola didefinisikan sebagai segitiga yang memiliki paling tidak satu sudut siku-siku. Skripsi ini membahas ketidakmiripan antara sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid. Fakta ini menginspirasi definisi baru untuk segitiga siku-siku pada geometri bola yang disebut dengan Spherical Half-sum Triangle. Spherical Half-sum Triangle adalah segitiga yang salah satu besar sudutnya merupakan jumlah kedua sudut lainnya. Kemudian dengan definisi ini akan ditunjukkan bahwa sifat-sifat segitiga siku-siku pada geometri bola memiliki kemiripan dengan sifat-sifat segitiga siku-siku pada geometri Euclid. Kemiripan tersebut antara lain: sudut keliling yang menghadap diameter lingkaran besarnya lebih dari , terdapat bentuk kuadrat dalam rumus Pythagoras, dan diagonal persegi panjang selalu membentuk dua buah segitiga siku-siku.
ABSTRACT
Cindy, 2016. The Characteristics of Spherical Half-sum Triangle. Thesis. Mathematics Education Study Program, Mathematics and Science Education Department, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Right triangle in spherical geometry defines as a triangle which is have at least one right angle. This thesis defines about dissimilarities that arise between the characteristics of right triangle in spherical geometry and in Euclidean geometry. This fact inspired a new definition for spherical right triangle that called Spherical Half-sum Triangle. Spherical Half-sum Triangle defined as a triangle which is one angle equals the sum of the other two. Further, with this new definition will be shown that the characteristics of Spherical Half-sum Triangle more similar like the Euclidean one. The characteristics of Spherical Half-sum Triangle are: measure of an angle which is opposite a diameter of a circle more than there are squared terms in the spherical Pythagorean theorem, and a diagonal of spherical rectangle create two traditional right triangles.
SIFAT-SIFAT SEGITIGA SIKU-SIKU PADA GEOMETRI BOLA Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Oleh: CINDY NIM: 121414079
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
SIFAT-SIFAT SEGITIGA SIKU-SIKU PADA GEOMETRI BOLA Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika
Oleh: CINDY NIM: 121414079
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
iv
HALAMAN PERSEMBAHAN
On a dark gloomy day,
remember that every little drop of rain prepares you to be even stronger
to flourish on a sunny day. (HJ Story)
vii ABSTRAK
Cindy, 2016. Sifat-sifat Segitiga Siku-siku pada Geometri Bola. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Segitiga siku-siku pada geometri bola didefinisikan sebagai segitiga yang memiliki paling tidak satu sudut siku-siku. Skripsi ini membahas ketidakmiripan antara sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid. Fakta ini menginspirasi definisi baru untuk segitiga siku-siku pada geometri bola yang disebut dengan Spherical Half-sum Triangle. Spherical Half-sum Triangle adalah segitiga yang salah satu besar sudutnya merupakan jumlah kedua sudut lainnya. Kemudian dengan definisi ini akan ditunjukkan bahwa sifat-sifat segitiga siku-siku pada geometri bola memiliki kemiripan dengan sifat-sifat segitiga siku-siku pada geometri Euclid. Kemiripan tersebut antara lain: sudut keliling yang menghadap diameter lingkaran besarnya lebih dari , terdapat bentuk kuadrat dalam rumus Pythagoras, dan diagonal persegi panjang selalu membentuk dua buah segitiga siku-siku.
viii ABSTRACT
Cindy, 2016. The Characteristics of Spherical Half-sum Triangle. Thesis. Mathematics Education Study Program, Mathematics and Science Education Department, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Right triangle in spherical geometry defines as a triangle which is have at least one right angle. This thesis defines about dissimilarities that arise between the characteristics of right triangle in spherical geometry and in Euclidean geometry. This fact inspired a new definition for spherical right triangle that called Spherical Half-sum Triangle. Spherical Half-sum Triangle defined as a triangle which is one angle equals the sum of the other two. Further, with this new definition will be shown that the characteristics of Spherical Half-sum Triangle more similar like the Euclidean one. The characteristics of Spherical Half-sum Triangle are: measure of an angle which is opposite a diameter of a circle more than there are squared terms in the spherical Pythagorean theorem, and a diagonal of spherical rectangle create two traditional right triangles.
ix
KATA PENGANTAR
Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa karena atas berkat dan karunia-Nya penulis dapat menyelesaikan skripsi
dengan judul “Sifat-sifat Segitiga Siku-siku pada Geometri Bola”. Skripsi
ini disusun untuk melengkapi salah satu syarat memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.
Banyak hambatan dan rintangan yang penulis alami selama penyusunan skripsi ini. Namun penulis tetap semangat dan dapat menyelesaikan skripsi karena tidak terlepas dari doa, bantuan, dan dukungan berbagai pihak. Oleh karena itu, pada kesempatan kali ini penulis ingin mengucapkan terima kasih kepada beberapa pihak, diantaranya:
1. Bapak Rohandi, Ph.D. selaku dekan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.
2. Bapak Dr. Marcellinus Andy Rudhito, S.Pd. selaku ketua Jurusan Pendidikan Matematika dan Ilmu Pengetahhuan Alam.
3. Bapak Dr. Hongki Julie, M.Si. selaku ketua Program Studi Pendidikan Matematika, Universitas Sanata Dharma.
4. Bapak Prof. Dr. St. Suwarsono selaku Dosen Pembimbing Akademik. 5. Bapak Antonius Yudhi Anggoro, M.Si. selaku dosen pembimbing
skripsi yang telah menyediakan waktu, tenaga, dan pikiran untuk membimbing penulis dengan sabar. Terima kasih atas segala masukan dan motivasi selama penyusunan skripsi ini.
6. Bapak Hartono, Ph.D. dan Ibu Veronika Fitri Rianasari, M.Sc. atas berbagai saran untuk proses pencarian informasi dalam skripsi ini. 7. Ibu Dra. Haniek Sri Pratini, M.Pd. dan Ibu C. Novella Krisnamurti,
x
8. Bapak dan Ibu dosen Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah mendidik penulis selama menuntut ilmu di Universitas Sanata Dharma.
9. Staf sekretariat JPMIPA yang telah memberikan pelayanan kesekretariatan.
10.Staf Perpustakaan Universitas Sanata Dharma yang telah memberikan pelayanan dan fasilitas selama pengerjaan skripsi ini.
11.Kedua orang tua penulis yang tiada henti memberi semangat, kepercayaan, dan doa dalam studi ini.
12.Teman-teman perantau dan pejuang gelar sarjana, Andita Prastiti, Maria Mater Dei Ayu, Elizabeth Nada, Adhi Kristian, Yunita Maria Ndoi, Bernadette Andika, Namiera Yushendea, Stacia Elvaretta, Nanda Ayu, Stepani Elsa, Fransisca Putri, dan Malvin Choco yang senantiasa berbagi suka duka selama pengerjaan skripsi ini.
13.Teman-teman Pendidikan Matematika angkatan 2012 khususnya kelas B, terlebih Trisona Agustina, Natalia Ika, Yohana Kristin, Scolastika Lintang, Dita Anggraini, Gregoria Yanu, Agustina Galuh, Rara Maharani, Maria Sri Dian, dan Richardus Adelbertus yang telah menyemangati, menemani, berbagi informasi, dan berjuang bersama selama proses pembelajaran di Universitas Sanata Dharma.
14.Teman-teman satu bimbingan skripsi yang saling menyemangati, berbagi informasi, dan berkeluh kesah bersama selama penulisan skripsi ini.
15.Semua pihak yang telah membantu dan tidak dapat disebutkan satu persatu.
Semoga tulisan ini dapat memberikan manfaat dan wawasan yang lebih kepada setiap pembacanya.
Yogyakarta, 22 September 2016
xi DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR SIMBOL ... xiii
DAFTAR GAMBAR ... xiv
DAFTAR LAMPIRAN ... xvi
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Batasan Masalah... 4
C. Rumusan Masalah ... 4
D. Tujuan Penelitian ... 5
E. Manfaat Penelitian ... 5
F. Metode Penelitian... 6
G. Sistematika Penulisan ... 6
xii
A. Sejarah Munculnya Geometri Bola ... 8
B. Konsep Dasar Dalam Geometri Bola ... 11
BAB III SEGITIGA SIKU-SIKU PADA GEOMETRI BOLA ... 23
A. Spherical Half-sum Triangle ... 23
B. Sifat-sifat Segitiga Siku-siku ... 37
BAB IV PENUTUP ... 51
A. Kesimpulan ... 51
B. Saran ... 52
xiii
DAFTAR SIMBOL
: titik
: titik berlawanan
: garis
: segmen garis dengan titik akhir dan
: panjang / jarak ke
: sudut
: besar sudut
: segitiga
: Persegi panjang
xiv
DAFTAR GAMBAR
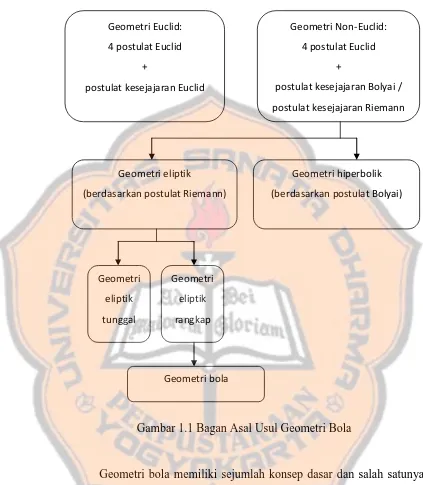
Gambar 1.1 Bagan Asal Mula Geometri Bola ... 3
Gambar 2.1 Ilustrasi Pusat Bola ... 11
Gambar 2.2 Ilustrasi Radius Bola ... 12
Gambar 2.3 Ilustrasi Diameter Bola ... 12
Gambar 2.4 Ilustrasi Lingkaran... 13
Gambar 2.5 Ilustrasi Lingkaran Besar ... 14
Gambar 2.6 Ilustrasi garis dari Dua Titik... 14
Gambar 2.7 Ilustrasi Segmen Garis ... 16
Gambar 2.8 Ilustrasi I Keantaraan ... 17
Gambar 2.9 Ilustrasi II Keantaraan ... 17
Gambar 2.10 Ilustrasi III Keantaraan ... 18
Gambar 2.11 Ilustrasi Sudut ... 19
Gambar 2.12 Ilustrasi Segitiga ... 19
Gambar 2.13 Ilustrasi Segitiga Siku-siku ... 20
Gambar 2.14 Ilustrasi Lingkaran Luar Segitiga ... 21
Gambar 3.1 Ilustrasi I Teorema 3.1 ... 24
Gambar 3.2 Ilustrasi II Teorema 3.1 ... 25
Gambar 3.3 Ilustrasi III Teorema 3.1 ... 26
Gambar 3.4 Ilustrasi Rumus Pythagoras ... 27
Gambar 3.5 Ilustrasi Persegi Panjang ... 29
xv
Gambar 3.7 Ilustrasi Teorema 3.3 ... 31
Gambar 3.8 Ilustrasi Lune ... 39
Gambar 3.9 Ilustrasi Lema 3.1 ... 39
Gambar 3.10 Ilustrasi Lema 3.2 ... 40
Gambar 3.11 Ilustrasi I Teorema 3.5 ... 43
Gambar 3.12 Ilustrasi II Teorema 3.5 ... 43
Gambar 3.13 Ilustrasi III Teorema 3.5 ... 44
Gambar 3.14 Ilustrasi IV Teorema 3.5... 45
Gambar 3.15 Ilustrasi V Teorema 3.5 ... 46
Gambar 3.16 Ilustrasi Teorema 3.6 ... 48
xvi
DAFTAR LAMPIRAN
Lampiran A.1. Segitiga Kutub Lampiran A.2. Segitiga Kongruen
1 BAB I PENDAHULUAN
A. Latar Belakang
Geometri berasal dari dua kata Yunani geo dan metrein. Geo berarti bumi, dan metrein berarti ukuran. Dengan demikian, secara etimologis geometri dapat diartikan sebagai ilmu pengukuran bumi. Meskipun berasal dari kata Yunani, orang-orang Yunani bukanlah yang memulai penggunaan geometri dalam kehidupan sehari-hari. Orang-orang Mesirlah yang pertama kali menggunakan geometri dalam kehidupan sehari-hari. Mereka menggunakan geometri untuk mengatasi masalah banjir tahunan yang terjadi di sungai Nil.
Geometri dipandang sebagai sistem deduktif, yaitu suatu sistem yang memiliki pengertian-pengertian pangkal atau unsur-unsur yang tidak memiliki definisi. Sekitar 300 tahun sebelum masehi, muncul seorang matematikawan bernama Euclid yang menulis buku mengenai geometri. Buku yang ditulis oleh Euclid berjudul ‘Elements’ di mana isinya menjelaskan mengenai definisi, postulat, dan teorema.
Pada geometri Euclid terdapat lima buah postulat, di mana postulat kelima yang ditulis oleh Euclid disebut sebagai postulat kesejajaran Euclid. Postulat tersebut berbunyi “Pada sebuah bidang, jika sebuah garis
Beberapa matematikawan mengatakan bahwa postulat kesejajaran Euclid dianggap terlalu rumit untuk disebut sebagai postulat. Mereka mengatakan bahwa postulat kesejajaran Euclid dapat dibuktikan dengan empat postulat sebelumnya.
Playfair merupakan salah satu matematikawan yang mencoba untuk membuktikan postulat kesejajaran Euclid. Playfair menemukan postulat yang berbunyi “jika diberikan sebuah garis dan sebuah titik di luar , maka dapat dibuat sebuah garis yang sejajar dengan garis dan melalui .” Namun postulat Playfair dianggap masih memiliki makna yang sama dengan postulat kesejajaran Euclid. Hingga akhirnya Bolyai-Lobachevsky menemukan postulat kesejajarannya yang berbunyi “jika diberikan sebuah garis dan sebuah titik di luar garis tersebut, maka dapat dibuat lebih dari satu garis yang sejajar dengan garis dan melalui .” dan Riemann menemukan postulat kesejajarannya yang berbunyi “jika diberikan sebuah garis l dan sebuah titik P di luar garis tersebut,
Geometri bola memiliki sejumlah konsep dasar dan salah satunya membahas mengenai segitiga siku-siku. Segitiga siku-siku didefinisikan sebagai segitiga yang memiliki setidaknya satu sudut siku-siku. Namun dengan definisi tersebut terdapat ketidakmiripan antara sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid. Fakta tersebut menginspirasi definisi baru untuk segitiga
Geometri Euclid:
4 postulat Euclid
+
postulat kesejajaran Euclid
Geometri Non-Euclid:
4 postulat Euclid
+
postulat kesejajaran Bolyai /
postulat kesejajaran Riemann
Geometri eliptik
(berdasarkan postulat Riemann)
Geometri hiperbolik
(berdasarkan postulat Bolyai)
Geometri eliptik tunggal Geometri eliptik rangkap Geometri bola
siku-siku yang disebut dengan Spherical Half-sum Triangle. Spherical Half-sum Triangle merupakan segitiga yang salah satu besar sudutnya merupakan jumlah kedua sudut lainnya. Dengan definisi baru ini akan ditunjukkan bahwa sifat segitiga siku-siku pada geometri bola memiliki kemiripan dengan sifat segitiga siku-siku pada geometri Euclid. Kemiripan sifat tersebut antara lain: besar sudut keliling yang menghadap diameter lingkaran lebih dari , terdapat bentuk kuadrat dalam rumus Pythagoras, dan diagonal persegi panjang membentuk dua buah segitiga siku-siku. B. Batasan Masalah
Dalam skripsi ini, bola diasumsikan sebagai bola satuan. Bola satuan yang dimaksud adalah bola yang memiliki radius satu satuan. C. Rumusan Masalah
Berdasarkan latar belakang yang ada, rumusan masalah dalam penelitian ini yaitu:
1. Bagaimana ketidakmiripan sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid, berdasarkan definisi awal segitiga siku-siku?
2. Bagaimana definisi baru segitiga siku-siku pada geometri bola?
D. Tujuan Penelitian
Penelitian ini bertujuan untuk:
1. Untuk mendeskripsikan ketidakmiripan sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid berdasarkan definisi awal segitiga siku-siku.
2. Untuk mendeskripsikan definisi baru segitiga siku-siku pada geometri bola.
3. Untuk mendeskripsikan sifat-sifat segitiga siku-siku pada geometri bola yang sebelumnya tidak mirip dengan sifat-sifat segitiga siku-siku pada geometri Euclid berdasarkan definisi yang baru.
E. Manfaat Penelitian
Manfaat yang dapat diambil dari penelitian ini adalah: 1. Bagi Pembaca
Pembaca dapat mengetahui bagaimana konsep dasar geometri bola, definisi segitiga siku-siku, ketidakmiripan sifat-sifat segitiga siku-siku pada geometri bola dan geometri Euclid, definisi baru untuk segitiga siku-siku pada geometri bola, dan sifat-sifat segitiga siku-siku berdasarkan definisi baru.
2. Bagi Penulis
sifat-sifat segitiga siku-siku pada geometri bola berdasarkan dengan definisi yang telah ada maupun definisi yang baru.
3. Bagi Universitas
Universitas dapat menambah koleksi skripsi dalam bidang geometri khususnya mengenai geometri bola. Selain itu, skripsi ini dapat menjadi referensi pembelajaran matematika mengenai geometri non-Euclid.
F. Metode Penelitian
Metode yang digunakan penulis dalam menyusun skripsi ini adalah metode studi pustaka. Metode ini dilakukan dengan mengkaji berbagai referensi berupa jurnal dan buku yang berkaitan dengan geometri bola sehingga penulis tidak menemukan suatu hal baru.
Langkah-langkah yang dilakukan dalam penelitian ini adalah: 1. Mempelajari berbagai referensi yang diperlukan, khususnya mengenai
geometri bola.
2. Menyajikan kembali definisi-definisi serta teorema-teorema yang menjadi dasar dalam geometri bola.
3. Menyusun materi-materi yang telah dikumpulkan secara sistematis untuk memudahkan pembaca dalam memahaminya.
G. Sistematika Penulisan
batasan masalah, tujuan penelitian, manfaat penelitian, metode penelitian, dan sistematika penulisan dalam skripsi ini.
Bab kedua membahas sejarah munculnya geometri bola serta konsep dasar dalam geometri bola yang akan digunakan pada pembahasan bab berikutnya.
8 BAB II
SEJARAH DAN KONSEP DASAR GEOMETRI BOLA
Bab ini membahas sejarah munculnya geometri bola dan konsep dasar yang akan digunakan sebagai landasan pembahasan pada bab berikutnya. Konsep dasar yang akan dibahas antara lain titik, garis, sudut, lingkaran, keantaraan, segitiga, dan kongruensi segitiga pada geometri bola. Berikut merupakan penjelasan mengenai sejarah munculnya geometri bola. A. Sejarah Munculnya Geometri Bola
Euclid menyebutkan lima buah postulat dalam geometri, kelima postulat tersebut antara lain (Own Byer, 2010):
1. Dari dua titik sembarang dapat dibentuk sebuah garis. 2. Sebuah garis dapat diperpanjang sampai tak hingga.
3. Jika diberikan sebuah titik dan jari-jari, maka dapat dibentuk sebuah lingkaran dengan titik tersebut sebagai pusatnya.
4. Semua sudut siku-siku sama besar.
5. Pada sebuah bidang, jika sebuah garis dipotongkan dengan dua garis lainnya dan dua garis tersebut diperpanjang hingga bertemu pada satu titik, maka jumlah sudut dalam sepihak pada pihak yang bertemu disatu titik adalah lebih dari .
matematikawan menganggap bahwa postulat kesejajaran yang ditulis oleh Euclid terlalu rumit untuk disebut sebagai postulat. Beberapa matematikawan menganggap bahwa postulat kesejajaran tersebut dapat dibuktikan dengan menggunakan empat postulat sebelumnya. Beberapa matematikawan tersebut antara lain Proclus dari Aleksandria (410-485), John Wallis (1616-1703), dan Girolamo Saccheri dari Italia (1667-1733). Mereka mencoba untuk membuktikan kebenaran dugaan tersebut, namun usaha yang dilakukan gagal hingga akhirnya matematikawan asal Skotlandia yaitu John Playfair (1748-1819) menemukan postulat yang ekuivalen dengan postulat kesejajaran Euclid. Postulat tersebut berbunyi: “jika diberikan sebuah garis dan sebuah titik di luar , maka dapat
dibuat sebuah garis yang sejajar dengan garis dan melalui .”
Postulat tersebut dinamakan postulat Playfair, dan postulat ini dianggap lebih sederhana jika dibandingkan dengan postulat kesejajaran Euclid. Postulat Playfair dan postulat kesejajaran Euclid dianggap masih memiliki makna yang sama.
Euclid yang digabung dengan postulat Bolyai-Lobachevsky sebagai postulat hiperbolik, dan lima postulat ini menjadi dasar dari geometri hiperbolik.
Munculnya geometri hiperbolik dirasa masih belum mampu menjawab sejumlah pertanyaan geometri dalam bidang astronomi. Bernhard Riemann (1826-1866) menawarkan postulat baru untuk menggantikan postulat kesejajaran Euclid guna mengatasi masalah dalam bidang astronomi. Pada postulat yang ditawarkan Riemann, diasumsikan bahwa tidak ada garis yang sejajar. Postulat tersebut berbunyi “jika diberikan sebuah garis l dan sebuah titik P di luar garis tersebut, maka tidak dapat dibuat garis lain yang sejajar dengan garis l dan melalui P.” Postulat ini menjadi dasar munculnya geometri eliptik guna mengatasi masalah pada bidang astronomi. Geometri eliptik sendiri terbagi menjadi geometri eliptik tunggal dan geometri eliptik rangkap. Geometri eliptik tunggal direpresentasikan dalam setengah bola, sedangkan geometri eliptik rangkap direpresentasikan dalam bola utuh. Geometri bola merupakan bagian dari geometri eliptik rangkap (David Gans, 1973).
B. Konsep Dasar Dalam Geometri Bola
Dalam pembahasan geometri bola di bawah ini, akan diasumsikan bahwa bola memiliki radius ukuran satu satuan.
Definisi 2.1 (Wentworth, 1899: 381)
Bola merupakan permukaan di mana setiap titik pada permukaan tersebut berjarak sama dari sebuah titik yang disebut pusat.
Titik yang dimaksud pada definisi di atas merupakan titik pusat bola. Pada gambar 2.1, titik merupakan pusat bola .
Definisi 2.2 (Wentworth, 1899: 381)
Segmen garis lurus yang menghubungkan titik pada permukaan bola dengan titik pusat bola disebut sebagai radius.
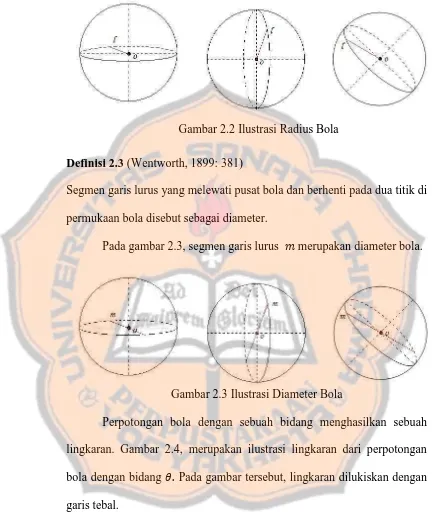
[image:30.595.85.514.245.622.2]Radius pada bola diilustrasikan pada gambar 2.2, di mana pada gambar tersebut radius dinamai .
Definisi 2.3 (Wentworth, 1899: 381)
Segmen garis lurus yang melewati pusat bola dan berhenti pada dua titik di permukaan bola disebut sebagai diameter.
Pada gambar 2.3, segmen garis lurus merupakan diameter bola.
[image:31.595.83.518.121.653.2]Perpotongan bola dengan sebuah bidang menghasilkan sebuah lingkaran. Gambar 2.4, merupakan ilustrasi lingkaran dari perpotongan bola dengan bidang Pada gambar tersebut, lingkaran dilukiskan dengan garis tebal.
Gambar 2.2 Ilustrasi Radius Bola
Jika bidang yang memotong bola melalui pusat bola, maka lingkaran yang terbentuk disebut lingkaran besar. Sedangkan jika bidang tersebut tidak melalui pusat bola maka lingkaran yang terbentuk disebut lingkaran kecil. Nampak pada gambar 2.5, lingkaran besar yang terbentuk dari perpotongan bola dengan bidang .
[image:32.595.86.511.100.626.2]Setiap lingkaran besar memiliki dua buah titik pusat, dan dua titik pusat tersebut berjarak sama terhadap setiap titik pada lingkaran besar. Dua titik pusat dari sebuah lingkaran besar disebut sebagai titik berlawanan. Sehingga setiap titik pada bola menentukan titik lainnya yang disebut sebagai titik lawan. Pada gambar 2.5, titik dan merupakan pusat lingkaran besar dan juga merupakan titik berlawanan. Contoh nyata dari lingkaran besar adalah garis bujur dan garis khatulistiwa. Sedangkan contoh nyata dari dua titik berlawanan adalah kutub utara dan kutub selatan.
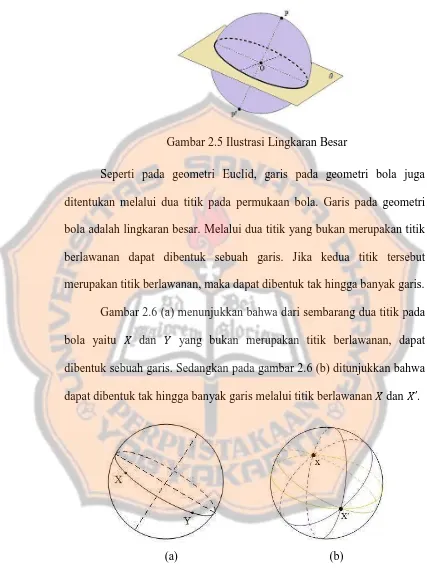
Seperti pada geometri Euclid, garis pada geometri bola juga ditentukan melalui dua titik pada permukaan bola. Garis pada geometri bola adalah lingkaran besar. Melalui dua titik yang bukan merupakan titik berlawanan dapat dibentuk sebuah garis. Jika kedua titik tersebut merupakan titik berlawanan, maka dapat dibentuk tak hingga banyak garis.
Gambar 2.6 (a) menunjukkan bahwa dari sembarang dua titik pada bola yaitu dan yang bukan merupakan titik berlawanan, dapat dibentuk sebuah garis. Sedangkan pada gambar 2.6 (b) ditunjukkan bahwa dapat dibentuk tak hingga banyak garis melalui titik berlawanan dan .
[image:33.595.85.512.108.679.2]Pada geometri Euclid, sebuah garis dapat diperpanjang sampai tak hingga panjangnya. Hal tersebut berbeda dengan garis pada geometri bola, karena garis pada geometri bola memiliki batas. Misalkan titik merupakan sebuah titik pada garis, jika lingkaran besar tersebut ditelusuri mulai dari titik , maka penelusuran tersebut akan berakhir pada titik juga. Jika pada geometri Euclid terdapat konsep kesejajaran garis, maka pada geometri bola tidak ada konsep kesejajaran garis sebagai akibat dari postulat kesejajaran Riemann.
Dua titik pada garis membagi garis menjadi dua buah busur. Jika kedua titik tersebut bukan merupakan titik berlawanan maka garis terbagi menjadi busur panjang dan busur pendek. Dalam geometri bola, busur terpendek dipandang sebagai segmen garis. Suatu segmen garis yang
dibatasi oleh titik dan dinotasikan dengan , lalu panjang busur terpendek tersebut didefinisikan sebagai jarak antara dua titik. Jadi jarak antara kedua titik tersebut disebut juga sebagai panjang segmen garis pada
geometri bola. Panjang dinotasikan dengan .
Sebagai ilustrasi perhatikan gambar 2.7 (a). Pada gambar tersebut terdapat dua busur yang terbentuk dari dua titik dan titik yang dilukiskan sebagai garis putus-putus dan garis yang tidak putus-putus.
Berikut merupakan tabel perbandingan konsep jarak pada geometri Euclid dan geometri bola:
No Pada geometri Euclid Pada geometri bola 1. Jarak dua titik diukur
sepanjang garis yang menghubungkan kedua titik tersebut. Hanya ada sebuah jarak yang dapat diukur.
Jarak pada lingkaran besar diukur dari dua titik yang menghubungkannya. Terdapat dua jarak yang dapat diukur. Jarak yang digunakan adalah jarak terpendek. 2. Tidak ada jarak terpanjang
atau terpendek dari dua titik yang diberikan.
Jarak terpanjang dari dua titik adalah 180˚.
3. Dari dua titik yang diberikan hanya dapat dilukis sebuah segmen garis.
Dari dua titik yang bukan merupakan titik berlawanan, terdapat sebuah segmen garis.
Jika kedua titik tersebut merupakan titik berlawanan, terdapat tak hingga banyak segmen garis yang terbentuk, dan memiliki panjang yang sama yaitu 180˚.
[image:35.595.84.518.102.713.2](a) (b) Gambar 2.7 Ilustrasi Segmen Garis
Definisi 2.4 (Moise, 1990: 60)
Pada geometri Euclid, titik dikatakan berada diantara titik dan jika:
[image:36.595.84.513.193.631.2](i) , , dan kolinier (ii)
Gambar 2.8 menunjukkan konsep di atas.
Konsep keantaraan pada geometri bola didefinisikan seperti pada konsep keantaraan pada geometri Euclid, dengan menggunakan segmen
garis. Pada gambar 2.9 tampak bahwa berada diantara .
Namun terdapat sebuah perbedaan sifat antara konsep keantaraan pada geometri Euclid, dengan konsep keantaraan pada geometri bola. Perbedaan tersebut timbul karena memungkinkannya untuk tidak terdapat keantaraan pada geometri bola. Jika diberikan tiga titik , , pada garis
Gambar 2.8 Ilustrasi I Keantaraan
dengan jarak setiap titik adalah 120˚ seperti pada gambar 2.10, maka tidak
ada satupun titik yang berada diantara kedua titik lainnya. Hal ini dikarenakan tidak terbuktinya syarat (ii) pada konsep keantaraan. Seharusnya tetapi pada kasus ini , yang menyebabkan tidak berada diantara dan , yang menyebabkan tidak berada diantara dan , serta yang menyebabkan tidak berada diantara dan .
Definisi 2.5 (Wentworth, 1899: 389)
Sudut pada geometri bola merupakan perpotongan dua buah segmen garis.
Pada gambar 2.11, sudut yang terbentuk dari dan dinotasikan dengan , sedangkan besar dinotasikan dengan . Besar sudut dalam geometri bola didefinisikan sebagai besar
[image:37.595.85.513.201.600.2]Definisi 2.6 (Wentworth, 1899: 392)
Segitiga pada geometri bola merupakan gabungan tiga segmen garis yang menghubungkan tiga titik non kolinear.
Misalkan terdapat tiga titik non kolinear , , dan . Selanjutnya
dibentuk , , dan sehingga terbentuk sebuah segitiga yang dinotasikan dengan . Gambar 2.12 ini merupakan contoh segitiga dalam geometri bola, yaitu dan .
Berbeda dengan geometri Euclid, jumlah besar sudut dalam sebuah segitiga pada geometri bola tidak sama dengan melainkan lebih dari
[image:38.595.84.512.85.635.2]Gambar 2.11 Ilustrasi Sudut
dan kurang dari (Wentworth, 1899: 393), selain itu jumlah dari
ketiga sisinya kurang dari (Wentworth, 1899: 397) . Definisi 2.7 (Dickinson, 2008: 24)
Segitiga siku-siku pada geometri bola merupakan segitiga yang memiliki paling tidak satu sudut siku-siku.
Gambar 2.13 merupakan contoh segitiga siku-siku pada geometri bola. Pada gambar tersebut, memiliki satu sudut yang besarnya yaitu , dan memiliki dua sudut siku-siku yaitu dan .
Definisi 2.8 (Dickinson, 2008: 26)
Lingkaran luar segitiga merupakan lingkaran yang memuat semua titik sudut segitiga.
[image:39.595.84.515.236.626.2]Untuk setiap segitiga pada geometri bola, dapat dibuat lingkaran luar segitiga yang memuat ketiga titik sudut segitiga tersebut. Pada gambar 2.14, memiliki lingkaran luar segitiga dengan pusat dan mamiliki lingkaran luar segitiga dengan pusat .
Seperti pada geometri Euclid, pada geometri bola juga terdapat aturan kongruensi pada segitiga. Jika kongruen dengan , maka dinotasikan dengan . Pada geometri bola jika dua buah segitiga terletak pada bola berukuran sama memenuhi satu dari empat syarat di bawah ini, maka kedua segitiga tersebut dikatakan kongruen. Empat syarat tersebut antara lain:
1. Dua buah sisi yang bersesuaian sama panjang dan sebuah sudut yang diapit oleh kedua sisi tersebut sama besar.
2. Dua buah sudut yang bersesuaian sama besar dan sisi di antara kedua sudut tersebut sama panjang.
3. Setiap sisi yang bersesuaian sama panjang. 4. Setiap sudut yang bersesuaian sama besar.
[image:40.595.87.510.107.618.2]Selain aturan kongruensi, aturan segitiga sama kaki pada geometri bola juga serupa dengan aturan segitiga sama kaki pada geometri Euclid. Pada segitiga sama kaki, sudut-sudut yang berhadapan dengan sisi-sisi yang sama panjang akan memiliki besar sudut yang sama. Sebaliknya, sisi-sisi yang berhadapan dengan sudut yang sama besar akan memiliki
23 BAB III
SEGITIGA SIKU-SIKU PADA GEOMETRI BOLA
A. Spherical Half-sum Triangle
Pada bab sebelumnya telah disebutkan definisi dari segitiga siku-siku pada geometri bola, yaitu segitiga yang memiliki paling tidak satu sudut siku-siku. Bab ini membahas definisi baru segitiga siku-siku yang disebut dengan Spherical Half-sum Triangle sebagai akibat dari adanya ketidakmiripan sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid berdasarkan definisi awal segitiga siku-siku. Selanjutnya, akan ditunjukkan bahwa Spherical Half-sum Triangle memiliki kemiripan sifat dengan segitiga siku-siku pada geometri Euclid.
Segitiga siku-siku pada geometri bola dan geometri Euclid memiliki sejumlah kesamaan sifat, misalnya aturan kongruensi dan aturan segitiga sama kaki. Namun nampak juga tiga ketidakmiripan sifat berdasarkan fakta-fakta berikut:
1. Sudut keliling yang menghadap diameter lingkaran besarnya selalu lebih dari .
Teorema 3.1 (Dickinson, 2008: 24)
Bukti:
Pada gambar 3.1, perhatikan bahwa dan segmen garis yang
membentuk yaitu dan membentuk sebuah segitiga, yaitu dengan sebagai titik pusat lingkaran luar . Titik
merupakan pusat lingkaran dan merupakan diameter lingkaran,
sehingga berada pada dan membagi dua sama panjang. Karena merupakan titik pada lingkaran dan merupakan pusat lingkaran, mengakibatkan . Karena maka dan merupakan segitiga sama kaki, hal ini menyebabkan dan . Selain
itu, karena berada pada , menyebabkan dan
. Karena jumlah sudut dalam segitiga lebih dari
, maka sehingga:
Sekarang perhatikan gambar 3.2, gambar tersebut mengilustrasikan sudut keliling yang menghadap sebuah diameter lingkaran pada geometri Euclid. Pada geometri Euclid, besar sudut keliling yang menghadap diameter lingkaran adalah , sehingga
. Sehingga segitiga yang terbentuk dari segmen garis
lurus , , dan selalu segitiga siku-siku karena salah satu sudutnya merupakan sudut siku-siku. Kemudian jika kita perhatikan kembali gambar 3.1, sudut yang menghadap diameter lingkaran yaitu besarnya lebih dari . Sehingga segitiga yang terbentuk dari
, , dan belum tentu merupakan segitiga siku-siku. Jika atau besarnya tidak sama dengan , maka
[image:44.595.86.514.125.633.2]bukan merupakan segitiga siku-siku. Dari sini nampak ketidakmiripan antara sifat segitiga siku-siku pada geometri Euclid dan geometri bola. Gambar 3.3 berikut merupakan contoh bahwa segitiga yang terbentuk belum tentu merupakan segitiga siku-siku. Contoh berikut telah diuji kebenarannya dan tidak perlu diragukan lagi.
Perhatikan gambar 3.3, merupakan sudut yang
menghadap diameter lingkaran yaitu . Selain itu, dan membentuk sebuah segitiga yaitu di mana ,
, dan . Tidak terbentuk satupun
sudut siku-siku pada sehingga bukan merupakan segitiga siku-siku.
2. Pada geometri Euclid dan geometri bola terdapat teorema Pythagoras, namun ada perbedaan diantara keduanya. Perbedaan tersebut timbul karena tidak terdapat bentuk kuadrat pada rumus Pythagoras geometri bola. Diberikan di mana , dan Jika
, maka rumus Pythagoras pada geometri Euclid adalah
. Sedangkan pada geometri bola rumusnya adalah
.
Teorema 3.2 (Brink, 1942)
Pada di mana , dan . Jika , maka .
[image:45.595.82.519.97.684.2]Bukti:
merupakan segitiga siku-siku pada geometri bola dan
Pada gambar 3.4 (a), diandaikan sebagai segmen
garis yang melalui garis khatulistiwa dan merupakan segmen garis yang melalui garis lintang. Pada gambar 3.4 (b) diberikan bidang yang
memotong tegak lurus segmen garis lurus pada dan segmen
garis lurus pada . Bidang tersebut juga memotong segmen garis
lurus pada .
siku-siku pada siku-siku pada siku-siku pada siku-siku pada
Dari didapatkan bahwa:
Dari persamaan (1) dan (2) :
3. Diagonal persegi panjang tidak selalu membentuk dua buah segitiga siku-siku pada geometri bola.
Persegi panjang pada geometri bola didefinisikan sebagai segi empat yang keempat sudutnya kongruen. Suatu persegi panjang yang titik sudutnya , , , dan dinotasikan dengan . Diagonal persegi panjang tidak selalu membentuk segitiga siku-siku pada geometri bola. Gambar 3.5 merupakan .
[image:48.595.90.514.228.638.2]
Berikut merupakan contoh persegi panjang pada geometri bola yang diagonalnya tidak membentuk dua buah segitiga siku-siku, dan semua ukuran pada contoh berikut telah diuji kebenarannya, sehingga tidak perlu diragukan lagi.
Perhatikan gambar 3.6, terbentuk di mana
dan ini sesuai dengan
definisi persegi panjang yang telah disebutkan sebelumnya. Jika
dilukis sebuah diagonal yaitu , maka terbentuk dan . Pada kedua segitiga tersebut, dan
Pada dan tidak terdapat
satupun sudut yang besarnya , berarti segitiga yang terbentuk dari
diagonal bukan merupakan segitiga siku-siku.
[image:49.595.87.513.104.610.2]Karena terdapat beberapa perbedaan ini, timbul inspirasi untuk definisi baru segitiga siku-siku. Definisi baru tersebut didapatkan melalui pembuktikan teorema di bawah ini. Teorema ini berhubungan dengan lokasi dari pusat lingkaran luar segitiga, berikut pembuktiannya:
Teorema 3.3 (Dickinson, 2008: 26)
Jika diberikan dengan pusat lingkaran luar segitiga , maka:
a. dan berada pada sisi yang sama terhadap jika dan hanya jika
.
b. berada pada jika dan hanya jika
.
c. dan berada pada sisi yang berlawanan dengan jika dan hanya jika .
Bukti (a) :
Misalkan dan berada pada sisi yang sama terhadap
seperti pada gambar 3.7 (a). Jika merupakan jari-jari lingkaran luar segitiga, maka . Jika
dan , maka dan merupakan segitiga sama
kaki. Karena hal tersebut, menyebabkan dan
. Di lain pihak, dan
[image:50.595.85.514.189.631.2]sehingga:
Jadi,
Misalkan . Andaikan tidak
benar bahwa dan berada pada sisi yang sama terhadap .
Maka berada pada atau dan berada pada sisi yang
berbeda terhadap . Kasus 1
Jika berada pada , maka dan
. Karena merupakan jari-jari
lingkaran luar segitiga, maka . Jika dan
, maka dan merupakan segitiga sama kaki.
Karena dan merupakan segitiga sama kaki, maka
dan , sehingga:
Telah didapatkan bahwa
,
hal ini kontradiksi dengan permisalan di atas bahwa
.
Kasus 2
Jika dan berada pada sisi yang berbeda terhadap , maka dan . Karena
merupakan jari-jari lingkaran luar segitiga, maka
. Karena dan maka dan
merupakan segitiga sama kaki. Karena dan
merupakan segitiga sama kaki, maka dan
, sehingga:
Jadi, . Telah didapatkan bahwa
,
hal ini kontradiksi dengan permisalan di atas bahwa
.
Bukti (b):
Misalkan berada pada seperti pada gambar 3.7 (b).
Karena merupakan jari-jari lingkaran luar segitiga, maka . Karena dan maka dan merupakan segitiga sama kaki. Hal ini menyebabkan dan . Di lain pihak, dan sehingga:
Jadi, .
Misalkan dan andaikan tidak benar
bahwa berada pada , maka dan berada pada sisi yang
sama terhadap atau dan berada pada sisi yang berbeda
terhadap .
Menurut teorema 3.3 (a) didapatkan
,
hal ini kontradiksi dengan permisalan di atas bahwa
.
Pada pembuktian kasus 2 teorema 3.3 (a) didapatkan
hal ini kontradiksi dengan permisalan di atas bahwa
.
Dari kedua kasus tersebut ternyata muncul kontardiksi, hal ini menunjukkan bahwa asumsi salah.
Bukti (c) :
Misalkan dan berada pada sisi yang berbeda terhadap seperti pada gambar 3.7 (c). Karena
merupakan jari-jari lingkaran luar segitiga, maka . Karena dan , maka dan merupakan segitiga sama kaki. Hal tersebut menyebabkan
dan . Dilain pihak,
dan , sehingga:
Jadi, .
Misalkan . Andaikan tidak
benar bahwa dan berada pada sisi yang berbeda terhadap
maka dan berada pada sisi yang sama terhadap atau
berada pada .
,
hal ini kontradiksi dengan permisalan di atas bahwa
.
Selain itu, pada teorema 3.3 (a) kasus 1 didapatkan
,
hal ini kontradiksi dengan permisalan di atas bahwa
.
Dari kedua kasus tersebut ternyata muncul kontardiksi, hal ini menunjukkan bahwa asumsi salah.
Teorema 3.3 juga berlaku pada geometri Euclid, di mana pusat lingkaran lu r segitig ber ‘ i l m’ segitig jik h y jik semua sudut pada segitiga merupakan sudut lancip, pusat lingkaran luar segitiga berada pada segitiga jika dan hanya jika salah satu sudut pada segitiga merupakan sudut siku-siku, pusat lingkaran luar segitiga berada ‘ i lu r’ segitig jik h y jik s l h s tu su ut p segitig
merup k su ut tumpul. Ko sep ‘ i l m’ ‘ i lu r’ p t ip h mi
dengan mudah dalam geometri Euclid karena bidang terbagi dalam daerah e g lu s berhi gg ti k berhi gg . Su tu titik ber ‘ i l m’
segitiga jika titik berada pada luasan daerah berhingga. Sedangkan suatu titik ber ‘ i lu r’ segitig jik titik ber p lu s er h t k
l m’ ‘ i lu r’ segitig ti k p t i pt si sec r l gsu g. Oleh
karena itu, pada geometri bola, konsep ini digantikan dengan konsep ‘ber p sisi y g s m ’ ‘ber p sisi y g berbe ’ e g
hipotenusa, seperti nampak dalam teorema 3.3 di atas.
Salah satu sifat segitiga siku-siku pada geometri Euclid adalah pusat lingkar luarnya berada pada hipotenusa. Melihat hal tersebut, timbul inspirasi dalam membuat definisi baru untuk segitiga siku-siku pada geometri bola. Karena diinginkan adanya kemiripan antara sifat-sifat segitiga siku-siku pada geometri bola dengan sifat-sifat segitiga siku-siku pada geometri Euclid, maka dinyatakan bahwa pusat lingkaran luar segitiga siku-siku pada geometri bola juga terletak pada hipotenusanya. Menurut teorema 3.3 (b) hal ini berarti salah satu besar sudut pada segitiga tersebut merupakan jumlah kedua sudut lainnya. Oleh karena itu, segitiga siku-siku didefinisikan sebagai berikut:
Definisi 3.1 (Dickinson 2008: 28)
Segitiga siku-siku adalah segitiga yang salah satu besar sudutnya merupakan jumlah kedua sudut lainnya.
Istilah lain untuk segitiga siku-siku baru tersebut adalah Spherical Half-sum Triangle. Dalam skripsi ini Spherical Half-sum Triangle akan tetap disebut sebagai segitiga siku-siku.
B. Sifat-sifat Segitiga Siku-siku
definisi baru segitiga siku-siku. Penjelasan sifat-sifat segitiga siku-siku tersebut akan dibahas melalui teorema dan lema.
Pada awal bab ini, melalui teorema 3.1 telah dibuktikan bahwa besar sudut keliling yang menghadap diameter lingkaran lebih dari . Pada teorema tersebut telah ditunjukkan bahwa gabungan diameter lingkaran dan segmen garis yang membentuk sudut keliling yang menghadap diameter membentuk sebuah segitiga. Di mana sudut yang menghadap diameter lingkaran, besarnya merupakan jumlah kedua sudut lainnya. Oleh karena itu, melalui definisi baru segitiga siku-siku, segitiga yang terbentuk merupakan segitiga siku-siku. Dari sini muncul kemiripan dengan sifat segitiga siku-siku yang ada pada geometri Euclid.
Berikutnya akan ditunjukkan bahwa besar sudut yang menghadap diameter Berikut pembuktiannya melalui sebuah teorema:
Teorema 3.4 (Dickinson, 2008: 27)
Jika merupakan segitiga siku-siku yang memenuhi aturan
,
maka
.
Untuk membuktikan teorema ini dibutuhkan istilah lune dan dua buah lema. Definisi lune akan dibahas beserta dengan pembuktian lema mengenai rumus luas lune dan rumus luas segitiga sebagai berikut:
Lune merupakan bagian pada permukaan bola yang dibatasi oleh dua buah setengah lingkaran besar.
Seperti pada gambar 3.8, merupakan lune yang memiliki dua buah sudut yaitu dan . Besar kedua sudut tersebut sama yaitu
, kemudian dan disebut sebagai sudut pada lune. Lema 3.1 (Todhunter, 1886: 72)
Jika diberikan lune dengan besar sudut pada lune adalah , maka luas lune
Bukti:
[image:58.595.86.512.166.724.2]Gambar 3.8 Ilustrasi Lune
Bentuk lune yang besar sudutnya sama yaitu dan terletak pada
titik dan . Titik dan membagi dua sama panjang . Lukis lingkaran besar yang melalui titik dan seperti pada gambar 3.9
sehingga . Untuk mendapatkan luas lune, dibentuk
persamaan sebagai berikut: lu s lu e
lu s permuk bol
lu s lu e lu s permuk bol
lu s lu e
lu s lu e
Lema 3.2 (Todhunter, 1886: 73)
Jika merupakan segitiga pada geometri bola dan merupakan besar sudut pada segitiga, maka berlaku luas
.
[image:59.595.86.514.195.704.2]Bukti:
Perhatikan pada gambar 3.10 di atas. Bentuklah tiga buah lingkaran besar yang memuat sisi-sisi pada seperti nampak pada gambar. Titik berturut-turut merupakan titik lawan dari
sehingga lu s lu s . Ketiga lingkaran besar
saling berpotongan dan membentuk enam buah lune, di mana masing-masing lune memuat atau . Sehingga luas permukaan bola (selanjutnya ditulis ) menjadi:
lu s bu h lu e
Pada geometri bola, lema 3.2 di atas disebut sebagai teorema Girard. Melalui teorema tersebut dapat dibuktikan bahwa jumlah besar sudut pada segitiga lebih dari . Sebelumnya, karena luas selalu bernilai positif maka:
[image:60.595.84.516.238.702.2]
Selanjutnya, dengan menggunakan kedua lema di atas, akan dibuktikan teorema 3.4.
Bukti:
Menurut lema 3.2, luas , dengan demikian:
lu s
lu s
lu s
lu s
lu s
Berikutnya akan dibahas mengenai teorema Pythagoras dengan menggunakan definisi baru segitiga siku-siku. Dari definisi ini diharapkan teorema Pythagoras pada geometri bola juga memiliki bentuk kuadrat seperti teorema Pythagoras pada geometri Euclid. Berikut pembuktiannya: Teorema 3.5 (Dickinson, 2008: 27)
Jika merupakan segitiga siku-siku yang memenuhi aturan bahwa
di mana berturut-turut merupakan
dan , maka berlaku .
Perhatikan gambar 3.11, merupakan pusat bola, merupakan panjang segmen garis yang menghubungkan dan , dan merupakan panjang segmen garis lurus yang menghubungkan dan . Lukis segmen garis lurus melalui yang membagi menjadi dua bagian sama panjang, sehingga:
Perhatikan gambar 3.12, merupakan pusat bola, merupakan panjang segmen garis yang menghubungkan dan , dan merupakan
Gambar 3.11 Ilustrasi I Teorema 3.5
panjang segmen garis lurus yang menghubungkan dan . Lukis segmen garis lurus melalui yang membagi menjadi dua bagian sama panjang, sehingga:
Perhatikan gambar 3.13, merupakan pusat bola, merupakan panjang segmen garis yang menghubungkan dan , dan merupakan panjang segmen garis lurus yang menghubungkan dan . Lukis segmen garis lurus melalui yang membagi menjadi dua bagian sama panjang, sehingga:
[image:63.595.86.514.185.647.2]
Bentuk lingkaran luar , di mana merupakan pusat lingkaran luar . Karena menurut teorema 3.3 ,
maka berada pada . Karena merupakan pusat lingkaran luar
segitiga , maka membagi sama panjang sehingga . Selanjutnya dibentuk bidang datar yang melalui , , dan kemudian proyeksikan pada bidang seperti pada gambar 3.14. Notasikan
proyeksi pada bidang dengan . Karena berada pada , maka
terletak pada segmen garis lurus . Titik merupakan pusat bola, sehingga .
Perhatikan , karena , maka berlaku
. Selanjutnya, karena , , dan
, maka . Berikutnya, , y, dan
[image:64.595.84.512.108.678.2]berturut-turut merupakan panjang segmen garis lurus yang menghubungkan ke , ke , dan ke . Karena maka .
Selanjutnya perhatikan dan . Telah diketehui ,
, dan segme g ris lurus , ini mengakibatkan
dan memenuhi teorema Pythagoras, sehingga:
Sekarang perhatikan dan pada gambar 3.15, karena pusat lingkaran luar , maka . Karena panjang segmen garis
, maka . Lalu karena , ,
dan , maka . Selanjutnya merupakan
panjang segmen garis lurus yang menghubungkan ke . Karena
, maka .
Selanjutnya perhatikan dan , karena bi g t r pada , maka semua garis yang melalui pada bidang
akan tegak lurus dengan sehingga segme g ris lurus .
Berikutnya karena , , segme g ris lurus , dan
segme g ris lurus menyebabkan dan memenuhi
teorema Pythagoras, sehingga:
Karena telah didapatkan bahwa , maka merupakan pusat lingkaran luar pada bidang . Karena berada
pada segmen garis lurus , maka merupakan segitiga siku-siku
dengan segmen garis lurus sebagai hipotenusa. Hal ini menyebabkan berlakunya
Setelah didapat bahwa , subtitusi dengan
sehingga menjadi:
Rumus inilah yang kemudian diyakini sebagai teorema Pythagoras pada geometri bola. Hal ini disebabkan karena teorema Pythagoras ini lebih memiliki kemiripan dengan teorema Pythagoras pada geometri Euclid, sebab pada keduanya terdapat bentuk kuadrat.
Selanjutnya akan dibahas mengenai sifat diagonal pada persegi panjang. Pada pembahasan di bawah ini, akan dibuktikan bahwa diagonal pada persegi panjang akan membagi persegi panjang menjadi dua buah segitiga siku-siku yang kongruen. Untuk menunjukkan hal tersebut, akan dibuktikan terlebih dahulu teorema berikut:
Teorema 3.6 (M’Clelland, 1893: 32)
Jika diberikan sebuah dengan , maka panjang sisi-sisi yang bersebrangan sama panjang.
Bukti:
[image:67.595.85.512.240.633.2]Perpanjang dan hingga keduanya berpotongan pada dua titik yaitu dan yang merupakan titik berlawanan seperti nampak pada gambar 3.16. Karena maka merupakan segitiga sama kaki, sehingga . Selanjutnya, karena diketahui
bahwa maka sehingga merupakan segitiga sama kaki dan mengakibatkan . Dengan demikian:
Dengan cara yang serupa, dapat dibuktikan bahwa .
Selanjutnya akan dibuktikan bahwa diagonal persegi panjang membentuk dua buah segitiga siku-siku.
Teorema 3.7 (Dickinson, 2008: 31)
Jika merupakan diagonal , maka membagi menjadi dua buah segitiga siku-siku yang kongruen.
Bukti:
Diberikan dengan diagonal seperti pada gambar 3.17. Menurut teorema 3.6, dan , telah diketahui juga bahwa
. Karena ketiga hal tersebut, maka .
Selanjutnya, karena , maka . Sehingga:
Ini berarti bahwa merupakan segitiga siku-siku.
51 BAB IV PENUTUP A. Kesimpulan
Berdasarkan hasil pembahasan, dapat diambil kesimpulan bahwa: 1. Berdasarkan definisi segitiga siku-siku sebagai segitiga yang memiliki
setidaknya satu sudut siku-siku, terdapat tiga ketidakmiripan sifat segitiga siku-siku pada geometri bola dengan sifat segitiga siku-siku pada geometri Euclid. Ketidakmiripan tersebut antara lain: Sudut keliling yang menghadap diameter lingkaran besarnya selalu lebih dari , tidak terdapatnya bentuk kuadrat dalam rumus Pythagoras
geometri bola, dan diagonal persegi panjang tidak selalu membentuk dua buah segitiga siku-siku pada geometri bola.
2. Definisi baru segitiga siku-siku yang dinamai Spherical Half-sum Triangle adalah segitiga yang salah satu besar sudutnya merupakan jumlah kedua sudut lainnya. Definisi ini terinspirasi dari salah satu sifat segitiga siku-siku pada geometri Euclid dimana pusat lingkaran luar segitiga siku-siku harus berada pada hipotenusa.
52 kuadrat dalam rumus Pythagoras geometri bola, dan diagonal pada persegi panjang terbukti membentuk dua buah segitiga siku-siku.
B. Saran
Untuk penelitian selanjutnya, dapat dibahas mengenai sifat-sifat segitiga lancip pada geometri bola dengan sifat-sifat segitiga lancip pada geometri Euclid maupun sifat-sifat segitiga tumpul pada geometri bola dengan sifat-sifat segitiga tumpul pada geometri Euclid.
53 DAFTAR PUSTAKA
Brenke, W. (1943). Plane and Spherical Trigonometry. New York: The Dryden Press.
Brink, R.W. (1942). Spherical Trigonometry. New York: Appleton Century Crofts.
Byer, Owen, dkk. (2010). Methods of Euclidean geometry. United States of America: The Mathematical Association of America.
Dickinson, W. & Salmassi, M. (2008). The Right Right Triangle on the Sphere. The College Mathematics Journal, Vol. 39, 24-33.
Gans, D. (1973). An Introduction to Non-Euclidean Geometry. New York and London: Academic Press
M’Clelland, W.J. & Preston, T. (1893). A Treatise on Spherical Trigonometry
With Applications Spherical Geometry and Numerous Examples Part.I (ed.4). London: Macmillan.
M’Clelland, W.J. & Preston, T. (1886). A Treatise on Spherical Trigonometry
With Applications Spherical Geometry and Numerous Examples Part.II. London: Macmillan.
Moise, E.E. (1990). Elementary Geometry from an Advanced Standpoint (ed. 3). USA: Addison-Wesley.
Todhunter, I. (1886). Spherical Trigonometry for the use of colleges and Schools with Numerous Examples (ed.5). London: Macmillan.
SEGITIGA KUTUB
Definisi 1 (M’Clellan,1893 :26)
Segitiga kutub merupakan segitiga yang setiap titik sudut nya merupakan pusat lingkaran besar dari setiap segmen garis segitiga lainnya.
Pada ilustrasi segitiga kutub merupakan segitiga kutub dari karena merupakan pusat lingkaran besar yang memuat ,
merupakan pusat lingkaran besar yang memuat , merupakan pusat
lingkaran besar yang memuat . Sebaliknya, karena merupakan pusat
lingkaran besar yang memuat , merupakan pusat lingkaran besar
yang memuat , dan merupakan pusat lingkaran besar yang memuat maka merupakan segitiga kutub dari
SEGITIGA KONGRUEN
Teorema 1 (Wentworth, 1899 : 399)
Jika melalui pusat bola dilukiskan tiga buah diameter yaitu segmen garis lurus , dan melalui titik dibentuk lingkaran besar, maka dan merupakan segitiga yang kongruen.
Bukti:
Titik berturut-turut merupakan titik lawan dari titik , , hal ini menyebabkan , , ,
. Karena ukuran pada kedua segitiga
tersebut sama, maka .
Teorema 2 (Wentworth, 1899: 401)
Jika dua buah segitiga berada pada bola berukuran sama, di mana dua buah sisi yang bersesuaian sama panjang dan sudut yang diapit oleh kedua sisi sama besar, maka kedua segitiga tersebut kongruen.
Bukti:
Pada Ilustrasi Teorema 2.1, terdapat
di mana , , , dan . Karena dan
maka . Selanjutnya karena dan
maka
Dengan cara serupa dapat pula dibuktikan bahwa jika dua buah segitiga, di mana dua buah sudut yang bersesuaian sama besar dan sisi diantara kedua sudut tersebut sama panjang, maka kedua segitiga tersebut kongruen.
Teorema 3 (Wentworth, 1899: 382)
Jika dua buah segitiga terletak pada bola yang berukuran sama dan meliliki besar sudut yang sama pada sudut-sudut yang bersesuaian, maka keduanya memiliki panjang sisi yang sama pada sisi-sisi yang bersesuaian dan kedua segitiga tersebut kongruen.
Bukti:
Diberikan merupakan segitiga kutub dari dan merupakan segitiga kutub dari seperti pada Ilustrasi Teorema 3. Diketahui bahwa sudut-sudut yang bersesuaian pada dan sama besar. Karena hal tersebut, dan maupun merupakan segitiga kutub, maka sisi-sisi yang bersesuaian pada dan sama panjang. Karena sisi-sisi yang bersesuaian pada dan sama panjang, maka sudut-sudut yang bersesuaian pada dan sama besar. Karena dan berturut-turut merupakan segitiga kutub dari dan maka sisi-sisi yang bersesuaian pada dan sama panjang. Hal tersebut menyebabkan .
ATURAN SEGITIGA SAMA KAKI
Teorema 4 (Wentworth, 1899: 405)
Pada segitiga sama kaki, sudut-sudut yang berhadapan dengan sisi yang sama panjang akan memiliki sudut yang sama besar.
Bukti:
Pada Ilustrasi teorema 4, merupakan segitiga sama kaki di
mana . Lukis di mana merupakan titik yang membagi sama panjang. Perhatikan bahwa sisi-sisi yang bersesuaian pada
sama panjang. Karena sisi-sisi yang bersesuaian sama
panjang, maka sudut yang bersesuaian sama besar. Karena sudut-sudut yang bersesuaian sama besar maka
Teorema 5 (Wentworth, 1899: 406)
Jika pada sebuah segitiga terdapat dua buah sudut yang sama besar, maka sisi-sisi di hadapan kedua sudut tersebut sama panjang dan segitiga tersebut merupakan segitiga sama kaki.
Bukti:
Diberikan merupakan segitiga kutub dari
seperti nampak pada Ilustrasi teorema 5. Kemudian
karena , maka . Karena , maka
dan hal ini menyebabkan dan merupakan
segitiga sama kaki.