AN APPLICATION OF CLASSICAL POLYNOMIAL THEORY
IN OPTIMAL LADDER RECLINING PROBLEM(An Example of Problem Solving in Teaching Mathematics)
*Asep K. Supriatna
1and Stanley P. Dewanto
Dept. Mathematics, Faculty of Mathematics & Natural Sciences, Universitas Padjadjaran Km 21 Jatinangor Sumedang, Fax: 022-7794696
Abstract
The paper has twofold purposes. First, the paper demonstrates a stage-by-stage problem solving which is an important process that should be experienced by all mathematics students. It can be regarded as a model in teaching mathematics in the context of meaningful learning and constructivism. Second, in this paper we consider an application of classical polynomial theory in determining the existence of a ladder reclining problem. A ladder with 5 meters length is supposed to be placed so that the upper edge of the ladder reclines to a vertical wall while its lower edge touch the horizontal floor. It is also required that a part of the ladder touches a corner of certain geometric object (in this case a cube that has edges 1-meter length). We address the question on how many ways the ladder can be placed to satisfy such condition. Surprisingly, it was found that there are only two ways to place the ladder. Furthermore, in this paper we also give a necessary and sufficient condition in order a ladder with length l can be placed in the intended way so that a part of the ladder touches a part of a cube with edge k.
1. Introduction
Problem solving capability is regarded as one among the most important competences that should be mastered by all mathematics graduates. It is related to the capability of applying mathematical concept in everyday and real life problems. Other factors such as the ability of problem identification, choosing relevant factors, formulating mathematics description and its analysis, and interpreting back the results of the mathematical analysis into the real world are included in the problem solving capability. This kind of competence can be developed through an appropriate experience in the classroom activities on a regularly basis.
Many mathematics educators believe that the development of this competence can be achieved by students who well experienced both in hands and minds on problems. Knowing the real problems well, from where the mathematics problems come, will give a meaningful learning for the students who did the mathematical exercises. This will help them in understanding the mathematics and we believe that this will lead to increase their curiousness in extending the problems at hand. We also believe this scientific curiousness eventually will contribute to the development of a good transferable skill, namely inovation.
Meaningful learning and constructivism -- through problem solving -- are among the pedagogical jargons that increasingly popular to mathematics educators. However, the
* Presented in the-XI I National Conference of Mathematics, Bali 23-27 July 2004
1 Corresponding e-mail address: [email protected] and
models on how applying this approaches in the classrooms still limited to most mathematics educators. This paper is intended to fill this gap by demonstrating the development “simple” mathematics theorems from a simple riddle-like problem, as a result of a problem solving activity.
2. Understanding Problem Solving
The term problem solving occurs in many different professions and disciplines and has different meanings. Problem solving in mathematics has a more specific meaning, but it still open to different interpretations. So, problem solving is an all-encompassing term that means different things to different people at the same time, and different things to the same person at different times. In this paper, problem solving is defined as the process of applying previously acquired knowledge to new and unfamiliar non-routine situation [4].
Polya writes in How to Solve It that in studying modern heuristic, one “endeavors to understand the process of solving problems, especially the mental operations typically useful in this process” [5, p.129]. Under appropriate circumstances, one can learn to use heuristic, with the result being a demonstrable improvement in their problem solving performance.
Heuristic means a general strategy or suggestion, independent of any particular topic or subject matter, that helps problem solver approach and understand a problem and efficiently marshall their resources to solve it [6]. Following Polya, some important heuristic in problem solving are [6]:
1. Analysing and Understanding a Problem: a. Draw a diagram if at all possible. b. Examine special cases.
c. Try to simplify it by using symmetry or “without loss of generality”. 2. Designing and Planning a Solution:
a. Plan solutions hierarchically.
b. Be able to explain at any point of solution what you are doing and why, what you will do with the result of this operation.
3. Exploring Solutions to Difficult Problems: a. Consider a variety of equivalent problems.
b. Consider slight modifications of the original problem. c. Consider broad modifications of the original problem. 4. Verifying a Solution:
a. Use this specific test: does it use all the data? Conform to reasonable estimates?
b. Use the general test: can it be obtained differently? Reduced to known results? Can it be generate something?
3. The Ladder Reclining Problem
3.1. Problem statement:
Suppose we have a ladder with 5 meters length and a cube with has edges 1-meter length. It is supposed to be placed so that the upper edge of the ladder reclines to a vertical wall while its lower edge touches the horizontal floor. It is also required that a part of the ladder touches the corner of the cube (see Figure 1). To be specific, we want to know the answers to the following questions:
1. How many possible ways to lean the ladder satisfying such condition?
2. What is the maximum height of the wall (1+a in the figure) that can be touched by the ladder to satisfy such condition?
Figure 1
3.2. The Existence of Solutions
To answer the first question we will use some classical polynomial theorem. To set up the relationship between a and b we use Phytagorean theorem as follows:
25(1+ )2+(1+ )2= b
a . 1
On the other hand, we also have the following proportionality,
b
Now, the problem of determining the number of possible ways to lean the ladder satisfying such condition is equivalent to the problem of finding the number of positive real roots (zeros) of the polynomial
1
The Fundamental Theorem of Algebra guarantees that this polynomial has at least one root and at most four roots in the complex field. In general, the number of positive real roots can be determined by the Descartes’ rule of signs.
Consider the signs of the coefficients of the polynomial
0 following theorem is due to Descartes.
Theorem 1 (Descartes): The number of positive zeros of a polynomial f(x) is equal to the number of its sign changes, or differs from it by a positive even number. The number of negative zeros is obtained similarly from the number of sign changes in the sequence of coefficients of the polynomial f(-x).
f is also two. It implies that the possible number of the positive zeros (and also the negative zeros) is two and zero. Hence so far we can only conclude that the number of possible ways to recline the ladder is two or none. However, by trial and error, physically there is always one way to place the ladder. This means that we know for sure that there will be two ways and only two ways to place the ladder. In fact this can be shown analytically using the Sturm’s theorem by counting the number of sign changes in the Sturm chain. Next we will define the Sturm chain.
Sturm Chain
We begin with the following fundamental theorem of algebra.
Theorem 2: Every polynomial (5) can be written as a product of its irreducible factors in the form
Next, we consider a polynomial that has roots exactly the same to the roots of f(x), but with the simplest multiplicity,
) term one of the irreducible factors in (6) is differentiated according to the product rule of differentiation. This means that ϕ(x) and ϕ' x( ) does not have a common divisor except a constant c. So that if we divide ϕ(x) by ϕ' x( )then we will have a polynomial q1(x) with a remainder −ϕ2(x), which is a polynomial of a lower degree than ϕ' x( ). Divide ϕ' x( ) by )ϕ2(x to obtain a new remainder and do the procedure repeatedly to obtain Sturm chain
)
Theorem 3 (Sturm): Suppose that W(x)denotes the number of sign changes in the Sturm chain. If ϕ(x)is a polynomial with only simple zeros, and if a<b, ϕ(a)≠0 andϕ(b)≠0, then W(a)−W(b)is equal to the number of the zeros of the polynomial )ϕ(x in the closed interval [a,b].
To determine the end points of the closed interval [a,b] we use the following theorem [see Gellert et al. (1977, p. 123) for the proof].
Theorem 4: If αiis the zeros of the polynomial (5) then
(
1, 2, ,)
1 1 2 1 0maxα α ! αk < +an− +an− +!+a +a .
Using the Sturm chain we can determine the number of the positive zeros of the polynomial (4), which is the solution of our original reclining problem. The resulting closed interval is [-M,M] with M=1+1+2+−23+2+1=30. Hence, all the zeros are in the closed interval [-30,30]. However, in our problem, the meaningful zeros must be contained in the closed interval [0,5] or even smaller, e.g. [0,4] (see Figure 1). The resulting Sturm chain with the signs of the values of the function ϕ(x) is given in the following table.
Table 1: Sturm Chain
Sturm Chain The sign of ϕ(x)
x=0 x=3 x=4 x=5
1 2 23 2 )
( = 4+ 3− 2+ + x x x x x
ϕ ϕ(0)=+ ϕ(3)=- ϕ(3)=+ ϕ(5)=+
2 46 6 4 ) (
' = 3+ 2− + x x x x
ϕ ϕ'(0)=+ ϕ'(3)=+ ϕ'(3)=+ ϕ'(5)=+
4 / 3 4 / 29 4 / 49 )
( 2
2 x = x − x−
ϕ ϕ2(0)=- ϕ2(3)=+ ϕ2(3)=+ ϕ2(5)=+ 2401
/ 6032 2401 / 97968 ) (
3 x = x−
ϕ ϕ3(0)=- ϕ3(3)=+ ϕ3(3)=+ ϕ3(5)=+
887364 / 1020425 )
( 4 x =
ϕ ϕ4(0)=+ ϕ4(3)=+ ϕ4(3)=+ ϕ4(5)=+
The number of sign changes 2 1 0 0
We see from the Table that W(0)=2 and W(5)=0. Hence there are 2-0=2 real zeros in the closed interval [0,5]. Since W(3)=1 and W(4)=0, then we can also conclude that one of the real zeros is in [0,3]. The other zero is in [3,4] and there is no zero in [4,5]. Finally, we conclude that there are two different ways to recline the ladder in our problem. The maximum height that can be achieved by the ladder is somewhere between 1+3 meters and 1+4 meters.
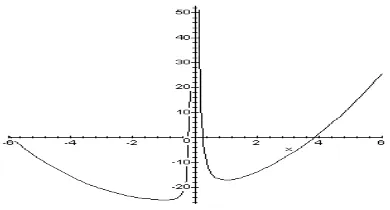
For comparison, to find the exact value of the zeros, we use Maple V and found that the first zero is 3.838501161 and the second zero is 0.260518353. This confirms that the maximum height of the vertical part of the ladder is in the interval [4,5] (4.838501161 meters to be exact). Maple V also found all the negative zeros, i.e. –0.168622783 and – 5.930396731. As predicted by the Sturm chain, all the four zeros are in the interval [-30,30]. Figure 2 show all positive zeros found by Maple V. Analytically, the formula of the
zeros for the quartic equation is found by L. Ferrari in the middle of the 16 century (http://mathworld.wolfram/QuarticEquation.html).
Figure 2: The graph of the equation ( )= 4+2 3−23 2+2 +1 x x x x x
f and its positive zeros
3.3. Extension of the Ladder Reclining Problem
We can extend the problem by doing the following simple experiment. By writing a simple computer program we can construct the following table showing the relationship among the length of the ladder (l), the length of the cube (q) and the number of ways in which the ladder can be placed on (n).
Table 2: The relationship among l, q and n.
Length of the ladder (l) Length of the cube (q)
Number of ways (n)
6 1 2
5 1 2
4 1 2
3 (minimum l ) 1 2
2 1 0
6 (minimum l) 2 2
5 2 0
9 (minimum l) 3 2
12 (minimum l) 4 2
15 (minimum l) 5 2
3*k (minimum l: conjecture) k 2 (conjecture)
We see from the table that there is a minimum bound for the length of the ladder in order the problem has a non-trivial solution. We may make a conjecture that if the length of the cube supporting the ladder, in order it can be placed in such a way as in our reclining problem, then the minimum length of the ladder is 3k. This observation leads to the following theorem.
Theorem 5 (Sufficient condition for positive solutions): If l≥3qthen there are exactly two positive solutions to the ladder reclining problem.
Proof:
General equation for the height of the vertical part of the ladder with the length of the ladder l and the length of the cube q is given by
According to Ferrari [2,3], the solution to this quartic equation is
2
Hence the third term of x is positive. The sum of the first two terms in x is also positive, i.e.
0 This shows that x is positive.
Since all of the coefficients of F(x) are positive except 2 2− 2≤2 2−9 2<0 q q l
q , then the number of sign changes in the coefficient of F(x) is two. This implies that the number of positive zeros of F(x) either two or zero. Considering that we have found one of the zeros then they must two zeros altogether. •
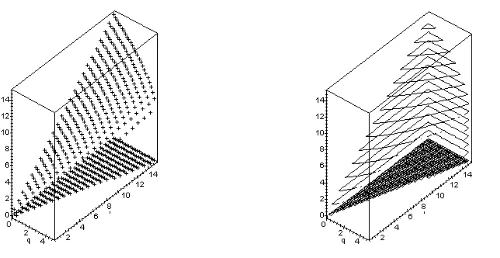
Figure 4: The point-plot and contour-plot of the positive zeros as a function q and l.
The condition l≥3qis not a necessary condition in order the reclining problem has two positive solutions. This can be seen by observing that the pair q=1 and l=2,85 produces a positive solution while l<3q. Figure 4 shows the point-plot and contour-plot of the positive zeros as a function q and l. There are some positive zeros if l>2qroughly.
In fact, 2q 2 is the lowest bound of l in order the problem to have a positive solution. This fact is summarised in the following theorem.
Theorem 5 (Necessary and sufficient condition for positive solutions): There are exactly two positive solutions to the ladder reclining problem if and only if
2 2q
l≥ .
Proof: ⇒
• Suppose that there is a positive solution, say x with x is real. This means
0
To show that x is positive, it is enough to show that the sum of the first two terms of x is positive as follows.
0 As in the poof of the previous theorem there exist another positive solution.
4. Concluding Remarks
1. In this paper we have applied some principles of classical theory in polynomial to solve a real world problem of a ladder reclining problem. Two simple theorems are constructed. There are some possible venues to proceed for future exercises. For example, by observing Figure 4, there are many pairs of (q.l) produce the same solutions. It is worth, theoretically, to explore these pairs and to find the possible mathematical structure describing the relationship of the pairs.
2. Problem solving strategies are both complex and subtle, as we saw in section 3. However, most of solutions may be obtained “based on principles that can be learned and practiced” [7, p. ix]. Referring to important heuristics in problem solving described by Polya (section 2), in terms of problem clarity, the example in this paper is self-understood, since it has been already simple by only presenting a special case (the length of the ladder is 5 meters) and it has provided a diagram representing the ladder as a line (section 3.1). Hence, one may proceed to next step, designing and planning a solution. Using the known relevant factors and conditions in section 3.1, one may find a polynomial describing the relationship between the factors. In this stage presumed previously acquired knowledge is applied to solve the polynomial problem (section 3.2). A solution is found and then it is verified by comparing to the numerical result by the help of mathematical software. The use of mathematical software also enables one to explore solution to a more difficult problem (section 3.3). [In fact, the use of technology (e.g. mathematical software) is encouraged by many institution [9] “to foster teaching and learning, increase student’ understanding of mathematical concepts, and prepare students for the use technology in their (future) careers or their graduate study [8, p. 10]].
References:
[1]. Gellert, W et al. (1977). The VNR Concise Encyclopedia of Mathematics. Van Nostrand Reinhold. New York.
[2] (http://mathworld.wolfram/CubicEquation.html).
[3] (http://mathworld.wolfram/QuarticEquation.html).
[4] National Council of Supervisors of Mathematics (1977). Position Paper on Basic Mathematical Skills. National Institute of Education. Washington, D.C.
[5] Polya, G. (1957). How to Solve It. Princeton University Press. Princeton, N.J.
[6] Schoenfeld, A.H. (1980). Heuristics in the Classroom. In Problem Solving in School Mathematics. The National Council of Teachers Mathematics, Inc. Virginia.
[7] Erickson, M.J. and J. Flowers (1999). Principles of Mathematics Problem Solving. Prentice Hall. London.
[8] The Mathematical Association of America (2003). Guidelines for Programs and Departments in Undergraduate Mathematical Sciences (Revised Edition).