PENENTUAN HARGA OPSI TIPE EROPA MENGGUNAKAN TRANSFORMASI FOURIER PADA MODEL PERSAMAAN DIFERENSIAL PARSIAL BLACK SCHOLES SKRIPSI

DIFERENSIAL PARSIAL BLACK SCHOLES

SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Rochi Ifahyani Siagian NIM : 063114009

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

DIFFERENTIAL EQUATION MODEL

THESIS

Presented As a Partial Fulfillment of The Requirements to Obtain The Sarjana Sains Degree

In Mathematics

by :

Rochi Ifahyani Siagian Student Number : 063114009

MATHEMATICS STUDY PROGRAM DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v “

!" #

vii

Puji dan syukur kepada Tuhan Yesus Kristus atas penyertaan dan kemurahanNya kepada penulis, sehingga penulis dapat menyelesaikan skripsi yang berjudul ”Penentuan Harga Opsi Tipe Eropa Menggunakan Transformasi Fourier Pada Model Persamaan Diferensial Parsial Black Scholes.” sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains di Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta.

Kesuksesan penyusunan ini tidak lepas dari dukungan dan bantuan dari banyak pihak, baik berupa materiil, moral, tenaga, maupun doa. Penulis mengucapkan terima kasih kepada :

1. Ibu Ch. Enny Murwaningtyas, S.Si., M.Si. selaku dosen pembimbing yang telah menyediakan waktu dan tenaga untuk memberikan bimbingan, masukan, dan perhatiannya yang besar serta saran dalam penyusunan skripsi ini.

2. Bapak Yosef Agung Cahyanta, S.T., M.T. selaku Dekan Fakultas Sains dan Teknologi.

3. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si. selaku Ketua Program Studi Matematika yang telah banyak membantu.

4. Bapak Ir. Ign. Aris Dwiatmoko, M.Sc. selaku penguji skripsi yang telah menyediakan waktu untuk memberikan saran dan masukan demi kesempurnaan skripsi ini.

5. Ibu M. V. Any Herawati, S.Si., M.Si. selaku dosen pembimbing akademik. 6. Bapak dan Ibu dosen Program Studi Matematika yang telah memberikan bekal

viii selama penulis menjalankan kuliah.

8. Perpustakaan Universitas Sanata Dharma yang memberikan fasilitas dan kemudahan kepada penulis.

9. Kedua orang tuaku yaitu Bapak Haden Siagian dan Ibu Murniati Sitorus yang telah memberikan kasih sayang yang besar dan memberikan dukungan dalam doa dan perhatian sehingga skripsi ini dapat terselesaikan.

10.Saudara-saudaraku yaitu Jeannie Setiyanti Siagian, Denny Irjanto Siagian, Putri Yunita Siagian, Rocha Ifahyana Siagian, dan Aditya Indra Wijaya, serta seluruh keluarga besarku atas semua perhatian, dukungan, serta doa yang tiada hentinya selama penelitian dan penyusunan skripsi ini.

11.Keluarga besar Rantetana yang juga turut serta memberikan dukungan dan doa selama penulis menjalankan kuliah dan menyelesaikan skripsi ini.

12.Kakak Mitra Samadara yang senantiasa memberikan semangat dan dukungan setiap hari melalui alat komunikasi sehingga penulis dapat menyelesaikan skripsi ini.

13.Sahabat-sahabat terkasih Ribka Anggarani Mandak, Diyah Sayekti, Titik Murwani, Metta, Victor, Tito, Liong, John Gobai, dan Demeninggus Pekei atas bantuannya kepada penulis baik dalam bentuk dukungan semangat dan membantu penulis dalam menyelesaikan persoalan-persoalan dalam penyusunan skripsi ini.

ix

Walaupun skripsi ini telah dibuat sebaik-baiknya oleh penulis, namun penulis menyadari masih banyak kekurangan dalam penuyusunan skripsi ini. Oleh kerana itu, penulis mengharapkan kritik dan saran demi penyempurnaan skripsi ini.

Akhirnya, semoga skripsi ini dapat memberikan wawasan dan pengetahuan bagi pembaca demi perkemabngan ilmu pengetahuan, khusunya dalam ilmu matematika.

Yogyakarta, 26 Maret 2010

xi

Saham merupakan objek finansial yang nilainya pada setiap waktu berubah-ubah sehingga pergerakannya berfluktuasi secara random. Untuk mengestimasi harga saham tersebut, maka dibuat suatu model matematika yang digambarkan dalam persamaan diferensial sebagai berikut

= _{+ 2} +

dimana S(t) merupakan harga saham pada waktu t dan t merupakan waktu kontinu, dan masing-masing merupakan mean dan standar deviasi dari return harga saham, dan merupakan variabel random berdistribusi normal. Model di atas sering disebut sebagai model harga saham gerak Brown yang merupakan model probabilistik karena terdapat unsur probabilistik yaitu . Dalam skripsi ini saham dibahas sebagai aset dasar dari suatu opsi tipe Eropa.

Opsi saham tipe Eropa merupakan suatu kontrak antara dua pihak dimana salah satu pihak (pembeli) memiliki hak dan bukan kewajiban, untuk membeli atau menjual saham sebagai aset dasarnya dari pihak lain (penjual) dengan harga yang telah ditentukan/ disepakati dan hanya dapat dilaksanakan pada masa jatuh tempo opsi tersebut. Opsi saham tipe Eropa dibedakan menjadi dua yaitu opsi beli dan opsi jual. Untuk menentukan harga opsi beli digunakan suatu model matematika yang disebut model persamaan diferensial parsial Black Scholes.

Model persamaan diferensial parsial Black Scholes merupakan model deterministik yang diperoleh dengan menurunkan model harga saham menggunakan Lemma Ito dan dinyatakan dalam persamaan di bawah ini

+1₂ + − = 0

dimana F merupakan fungsi pembayaran untuk harga opsi dan r merupakan tingkat suku bunga.

Walaupun masih terdapat S yang merupakan variabel random pada model Black Scholes, namun unsur probabilitas d yang terdapat dalam model tersebut dieliminasi dengan asumsi adanya proses hedging sehingga resiko yang disebabkan oleh kerandoman dari dW(t) tidak ada. Kemudian, model Black Scholes tersebut diselesaikan dengan menggunakan transformasi Fourier.

Prinsip penggunaan transformasi Fourier adalah dengan mengubah persamaan diferensial parsial Black Scholes menjadi persamaan panas dimana persamaan panas merupakan persamaan diferensial parsial yang sederhana. Dengan demikian diperoleh suatu penyelesaian yang merupakan formula harga opsi beli. Sementara itu, untuk mendapatkan formula harga opsi jual digunakan hubungan kesamaan opsi beli dan opsi jual.

xii

Stock is a financial object which its value changes every time so that its movement fluctuates randomly. In order to estimate the price stock, it need a mathematical model described in the following differential equation

= _{+ 2} +

where S(t) is the stock price on t, and t is a continuous time, each of and is a mean and standard deviation of the stock price return, and dW(t) is normally distributed random variable. The model above is often named as Brownian motion stock price model which is a probabilistic model since there is probabilistic element, dW(t). In this thesis, the stock is discussed as a basic asset of a Europe type option.

The European type stock option is a contract between two parties, where one of the parties (buyer) owns right and it is not an obligation to buy or to sell the stock as the basic asset from another party (seller) with an agreed price and it is only able to be conducted at the time period of the option. There are two type of European stock option, that are call and put option. To determine the call option price, it is used a mathematical model called Black Scholes partial differential equation model.

The Black Scholes partial differential equation model is a deterministic model acquired by decreasing the stock price model using Lemma Ito and it is expressed into the following equation

+1₂ + − = 0

where F is a payment function of the option price and r is an interest rate.

Although S still appears as a random variable in the Black Scholes model, but the probability element of dW(t) existing in the model is eliminated by an assumption that there is a hedging process, so that the risk caused by the randomness of dW(t) does not exist. Furthermore, the Black Scholes model is determined by using Fourier Transformation.

The principle of using the Fourier transformation is by changing the Black Scholes partial differential equation into hot equation, which is a simple partial differential equation. Thereby, we have a solution for call option price formula. Meanwhile, to achieve a put option price formula, the put-call parity is used.

xiii

HALAMAN JUDUL... i

HALAMAN JUDUL (INGGRIS)... ii

HALAMAN PERSETUJUAN PEMBIMBING... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERSEMBAHAN... v

PERNYATAAN PERSETUJUAN PUBLIKASI... vi

PRAKATA... vii

PERNYATAAN KEASLIAN KARYA... x

ABSTRAK... xi

ABSTRACT... xii

DAFTAR ISI... xiii

DAFTAR GAMBAR... xvii

BAB I PENDAHULUAN A. Latar Belakang ... 1

B. Perumusan Masalah... 4

C. Pembatasan Masalah... 4

D. Tujuan Penulisan... 5

E. Manfaat Penulisan... 5

F. Metode Penulisan... 5

xiv LOGNORMAL

A. Fungsi Kontinu... 8

B. Bilangan Kompleks dan Persamaan Euler... 14

C. Derivatif dan Antiderivatif... 16

D. Konvergensi Barisan dan Deret... 20

E. Deret Taylor... 28

F. Pengertian Deret Fourier... 31

G. Kekonvergenan Deret Fourier... 44

1. Sifat Koefisien Deret Fourier... 44

2. Teorema Riemann-Lebesgue dan Akibatnya... 47

3. Kernel Dirichlet... 49

H. Integral Fourier... 59

I. Deret Fourier Kompleks... 61

J. Integral Fourier Kompleks... 64

K. Persamaan Diferensial Biasa dan Parsial... 67

L. Keluarga Penyelesaian... 70

M. Masalah Syarat Batas... 71

N. Pemisahan Variabel... 73

O. Probabilitas... 74

P. Variabel Random dan Distribusinya... 76

Q. Distribusi Probabilitas Bersama/ Gabungan... 79

xv

T. Metode Fungsi Distribusi... 95

U. Distribusi Normal dan Lognormal... 95

V. Nilai Waktu Uang... 109

BAB III OPSI TIPE EROPA DAN PERSAMAAN DIFERENSIAL PARSIAL BLACK SCHOLES A. Opsi Tipe Eropa... 115

1. Pengertian Saham... 115

2. Gerak Brown... 117

3. Lemma Ito... 122

4. Model Gerak Brown... 126

5. Pengertian Opsi Eropa... 128

6. Arbitrase... 134

7. Hubungan kesamaan opsi beli dan jual... 136

B. Persamaan Diferensial Parsial Black Scholes... 140

1. Asumsi-Asumsi Dasar Persamaan Diferensial Parsial Black Scholes... 141

2. Model Persamaan Diferensial Parsial Black Scholes... 142

3. Syarat Nilai Batas dan Nilai Akhir untuk Opsi Eropa... 145

BAB IV FORMULA HARGA OPSI TIPE EROPA A. Transformasi Fourier ... 148

1. Konvolusi Fourier... 153

xvi

menjadi Persamaan Panas... 159 C. Penyelesaian Persamaan Diferensial Parsial Black Scholes

pada Opsi Beli dan Opsi Jual Tipe Eropa

1. Penyelesaian persamaan diferensial parsial Black Scholes

pada opsi beli tipe Eropa... 170 2. Penyelesaian persamaan diferensial parsial Black Scholes

pada opsi jual tipe Eropa... 183 BAB V PENUTUP

xvii

Gambar 2.1 Fungsi ganjil dan fungsi genap... 10

Gambar 2.2 Fungsi periodik kontinu g(x) dengan periode T... 11

Gambar 2.3 Kurva normal dengan mean dan variansi ... 97

PENDAHULUAN

A. Latar Belakang

Setiap orang dihadapkan pada berbagai pilihan dalam menentukan proporsi dana atau sumber daya yang mereka miliki untuk konsumsi saat ini dan di masa datang. Investasi merupakan komitmen untuk menanamkan sejumlah dana atau sumber daya lainnya pada saat ini dengan tujuan memperoleh sejumlah keuntungan di masa datang. Perkembangan dunia investasi tidak saja ditunjukkan oleh semakin meningkatnya jumlah dana yang diinvestasikan ataupun semakin banyaknya jumlah investor yang berinvestasi, tetapi juga ditunjukkan oleh semakin banyaknya alternatif instrumen investasi yang biasa dijadikan sebagai pilihan investor dalam berinvestasi.

Salah satu instrumen investasi yang telah banyak dikenal dan diperdagangkan oleh masyarakat adalah opsi. Opsi merupakan suatu kontrak antara dua pihak dimana salah satu pihak (pembeli) memiliki hak, bukan kewajiban, untuk membeli atau menjual dari pihak lain (penjual), suatu sekuritas (jaminan) atau aset tertentu seperti halnya saham, dengan harga yang telah ditentukan/ disepakati (strike price) dalam periode waktu yang juga telah ditentukan (exercise time).

memperdagangkan opsi di bursa resmi yang terorganisir. Di Indonesia, perda-gangan opsi baru disimulasikan di Bursa Efek Jakarta pada paro kedua tahun 2003 dan dilakukan pertama kali pada tanggal 6 Oktober 2004. Perdagangan opsi di Indonesia yang dikenal adalah opsi saham. Berdasarkan definisi opsi, maka opsi saham adalah opsi untuk membeli atau menjual saham. Selain itu, opsi yang diperdagangkan tidak hanya opsi saham, tetapi juga opsi indeks saham, opsi kurs valas, opsi obligasi, dan lain-lain. Dalam pasar opsi, yang diperjualbelikan bukanlah saham atau instrumen investasi finansial lainnya, melainkan hanyalah hak, baik hak untuk menjual maupun hak untuk membeli suatu aset dasar (un-derlying asset).

Berdasarkan jenisnya, opsi dibedakan menjadi dua, yaitu opsi beli (call option) dan opsi jual (put option). Opsi beli merupakan hak untuk membeli suatu sekuritas/ aset, sedangkan opsi jual merupakan hak untuk menjual suatu sekuritas/ aset. Opsi juga dibedakan atas waktu pembayaran (waktu dimana opsi tersebut dijalankan), yaitu opsi tipe Amerika dan opsi tipe Eropa. Opsi tipe Amerika adalah opsi yang dapat dilaksanakan kapan saja antara tanggal kesepakatan sampai masa jatuh temponya, sedangkan opsi tipe Eropa adalah opsi yang hanya dapat dilaksanakan pada masa jatuh tempo opsi tersebut. Dalam tulisan skripsi ini, penulis hanya akan membahas mengenai opsi tipe Eropa dengan aset dasar (seku-ritasnya) adalah saham.

karena pergerakan harga saham yang tidak menentu yang mempengaruhi harga opsi. Oleh karena itu, investor tersebut perlu mengetahui estimasi harga opsi yang rasional sebelum membeli opsi agar tidak mengalami kerugian dalam kegiatan menginvestasinya. Mengetahui estimasi harga opsi tipe Eropa yang rasional sama halnya dengan bagaimana menentukan harga opsi tersebut.

Persamaan diferensial parsial Black Scholes merupakan persamaan paling terkenal yang berani menerobos pasar dunia dalam penentuan harga opsi. Persamaan ini pertama kali diperkenalkan oleh Fischer Black, seorang kontraktor keuangan swasta di Cambridge, Massachutsetts, dan Myron Scholes, seorang asisten profesor keuangan di MIT (Massachusetts Institute of Technology) pada tahun 1973 dalam karya ilmiah mereka yang berjudul “The Pricing of Options and Corporate Liabilities”, yang secara garis besar berisi tentang model analitik yang digunakan untuk menentukan harga pasar yang rasional untuk opsi beli tipe Eropa.

transformasi Fourier digunakan untuk menyelesaikan persamaan diferensial parsial Black Scholes sehingga menghasilkan formula harga opsi tipe Eropa.

B. Perumusan Masalah

Bagaimana menentukan harga opsi tipe Eropa dengan formula yang diperoleh dari penyelesaian persamaan diferensial parsial Black Scholes menggunakan transformasi Fourier?

C. Pembatasan Masalah

Ada beberapa hal yang dibatasi dalam penulisan skripsi ini, antara lain: 1. Penulis hanya akan membahas opsi tipe Eropa dengan aset dasarnya adalah

saham.

2. Deret Taylor dalam penurunan Lemma Ito tidak dibahas secara mendalam. 3. Teorema 2.1.2 tentang kesamaan hasil kali trigonometri tidak dibuktikan. 4. Persamaan panas tidak dibahas secara mendalam.

Tujuan yang ingin dicapai penulis dalam penulisan ini adalah mempelajari dan mengetahui persamaan diferensial parsial Black Scholes terhadap opsi tipe Eropa dan menentukan harga opsi tipe Eropa dengan formula yang diperoleh dari penyelesaian persamaan diferensial parsial Black Scholes menggunakan transformasi Fourier.

E. Manfaat Penulisan

Manfaat yang akan diperoleh setelah mempelajari topik ini adalah dapat menentukan harga opsi tipe Eropa Black Scholes dengan formula yang diperoleh dari penyelesaian persamaan diferensial parsial Black Scholes menggunakan transformasi Fourier.

F. Metode Penulisan

BAB I: PENDAHULUAN

Dalam bab I dibahas tentang latar belakang, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika penulisan.

BAB II: DERET FOURIER, MASALAH SYARAT BATAS,

DAN DISTRIBUSI LOGNORMAL

DIFERENSIAL PARSIAL BLACK SCHOLES

Dalam bab III akan dibahas opsi tipe Eropa dan persamaan diferensial parsial Black Scoles.

BAB IV: FORMULA HARGA OPSI TIPE EROPA

Dalam bab IV akan dibahas transformasi Fourier, persamaan diferensial parsial Black Scholes menjadi persamaan panas, penyelesaian persamaan diferensial parsial Black Scholes pada opsi beli dan opsi jual tipe Eropa

BAB V: KESIMPULAN

BAB II

DERET FOURIER, MASALAH NILAI BATAS, DAN DISTIBUSI

LOGNORMAL

A. Fungsi Kontinu

Definisi 2.1.1

Suatu fungsi f adalah suatu aturan padanan yang menghubungkan setiap objek x

dalam suatu himpunan, yang disebut daerah asal, dengan sebuah nilai tunggal f(x)

dari himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah

hasil fungsi tersebut.

Definisi 2.1.2

Suatu fungsi f(x) yang terdefinisi pada interval − ≤ ≤ dikatakan fungsi genap

dalam interval tersebut jika

− = (2.1)

dan dikatakan fungsi ganjil dalam interval tersebut jika

− = − . (2.2)

Teorema 2.1.1

Hasil kali dua fungsi genap dan hasil kali dua fungsi ganjil adalah fungsi genap,

Bukti

a. Misalkan f(x) adalah hasil kali antara fungsi genap g(x) dan fungsi genap h(x),

maka f(x) = g(x)h(x). Akan ditunjukkan bahwa f(-x) = f(x).

f(-x) = g(-x)h(-x).

Karena g dan h adalah fungsi genap, maka

f(-x) = g(x)h(x)

= f(x).

Jadi, hasil kali dua fungsi genap adalah fungsi genap.

b. Misalkan f(x) adalah hasil kali antara fungsi ganjil g(x) dan fungsi ganjil h(x),

maka f(x) = g(x)h(x). Akan ditunjukkan bahwa f(-x) = f(x).

f(-x) = g(-x)h(-x).

Karena g dan h adalah fungsi ganjil, maka

f(-x) = (-g(x))(-h(x))

= g(x)h(x)

= f(x).

Jadi, hasil kali dua fungsi ganjil adalah fungsi genap.

c. Misalkan f(x) adalah hasil kali antara fungsi genap g(x) dan fungsi ganjil h(x),

maka f(x) = g(x)h(x). Akan ditunjukkan bahwa f(-x) = -f(x).

f(-x) = g(-x)h(-x).

Karena g adalah fungsi genap dan h adalah fungsi ganjil, maka

= -g(x)h(x)

f(-x) = -f(x).

Jadi, hasil kali antara fungsi genap dan fungsi ganjil adalah fungsi ganjil. ∎

Adapun, suatu fungsi f disebut simetri di x = 0 jika f adalah fungsi genap seperti

pada gambar (a) dalam Gambar 2.1 dan suatu fungsi f disebut antisimetri di x = 0 jika

f adalah fungsi ganjil seperti pada gambar (b) dalam Gambar 2.1.

Gambar 2.1: Fungsi ganjil dan fungsi genap

Definisi 2.1.3

Suatu fungsi g(x) dikatakan periodik dengan periode T jika

+ = (2.3)

untuk semua x, dan T merupakan konstanta positif. Nilai terkecil dari T disebut

sebagai periode terkecil atau periode dari g(x).

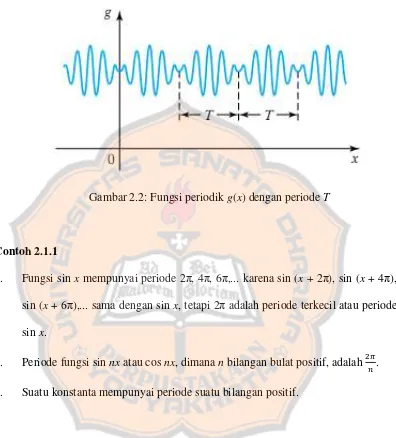
Gambar 2.2: Fungsi periodik g(x) dengan periode T

Contoh 2.1.1

1. Fungsi sin x mempunyai periode 2 , 4 , 6 ,... karena sin (x + 2 ), sin (x + 4 ),

sin (x + 6 ),... sama dengan sin x, tetapi 2 adalah periode terkecil atau periode

sin x.

2. Periode fungsi sin nx atau cos nx, dimana n bilangan bulat positif, adalah .

3. Suatu konstanta mempunyai periode suatu bilangan positif.

Dalam Contoh 2.1.1 di atas, kita dapat menemukan fungsi-fungsi trigonometri

seperti fungsi sinus dan kosinus. Masih banyak fungsi trigonometri lainnya, namun

Teorema 2.1.2

Andaikan diketahui fungsi-fungsi trigonometri yaitu sin , sin , cos , cos

dimana = 1, 2, 3, … dan = 1, 2, 3, … , maka berlaku kesamaan hasil kali

trigonometri sebagai berikut

1. sin sin = cos − − cos + , ≠ . (2.4)

2. sin cos = sin − + sin + , ≠ . (2.5)

3. cos cos = cos − + cos + , ≠ . (2.6)

4. sin + cos = 1, = . (2.7)

Teorema 2.1.2 di atas merupakan teorema dasar kalkulus trigonometri yang sangat

mudah untuk dibuktikan sehingga bukti teorema tersebut tidak diberikan dalam

skripsi ini.

Definisi 2.1.4 (Limit)

lim!→# = berarti bahwa untuk setiap $ > 0 yang diberikan, terdapat ' > 0

sedemikian sehingga untuk setiap x, 0 < ) − *) < ' maka berlaku ) − ) < $.

Definisi 2.1.5 (Limit kanan dan limit kiri)

Limit kanan yang dinyatakan dengan lim_!→#+ = berarti bahwa untuk setiap

$ > 0 yang diberikan, terdapat ' > 0 sedemikian sehingga untuk setiap x, 0 < −

lim!→#, = berarti bahwa untuk setiap $ > 0 yang diberikan, terdapat ' > 0

sedemikian sehingga untuk setiap x, 0 < − − * < ' maka berlaku ) − ) <

$.

Definisi 2.1.6 (Kekontinuan fungsi di suatu titik)

Suatu fungsi, f, dikatakan kontinu di c jika untuk setiap $ > 0 yang diberikan,

terdapat ' > 0 sedemikian sehingga untuk setiap x, ) − *) < ' maka berlaku

) − * ) < $.

Definisi 2.1.7

Fungsi f(x) disebut fungsi kontinu bagian demi bagian pada interval [a, b] bila

dipenuhi syarat-syarat berikut:

1. Interval [a, b] dapat dibagi menjadi sebanyak berhingga sub interval sehingga

f(x) kontinu pada setiap sub interval tersebut.

2. Limit dari f(x) jika x mendekati ujung-ujung dari sub interval ada dan berhingga.

Dengan kata lain, f(x) disebut fungsi kontinu bagian demi bagian bila dan hanya bila

B. Bilangan Kompleks dan Persamaan Euler

Definisi 2.2.1

Bilangan kompleks adalah bilangan yang berbentuk x + yi atau x + iy dengan x dan y

adalah bilangan real dan i2 = -1.

Biasanya z dipakai untuk menyatakan bilangan kompleks yang bentuknya

sesuai dengan definisi di atas dan ditulis z = x + yi, dimana x dapat dinyatakan juga

sebagai bagian real dari z dan y bagian imajiner dari z. Bagian real dan bagian

imajiner dari bilangan kompleks z biasanya dinyatakan dengan Re(z) dan Im(z),

sehingga jika x dan y adalah real dan z = x + iy, maka x = Re(z) dan y = Im(z).

Himpunan semua bilangan kompleks biasanya diberi notasi ℂ, sehingga dapat

ditulis ℂ = {z: z = x + iy, x∈ℝ dan y∈ℝ}. Jika Im(z) = 0, maka bilangan kompleks z

menjadi bilangan real x, sehingga bilangan real adalah keadaan khusus dari bilangan

kompleks. Oleh karena itu, kita dapat mengatakan bahwa himpunan bilangan real

merupakan himpunan bagian dari himpunan bilangan kompleks atau ℝ ⊂ ℂ. Jika

Re(z) = x = 0, dan Im(z) 0, maka z menjadi iy dan dinamakan bilangan imajiner

murni.

Definisi 2.2.2

Untuk setiap bilangan kompleks z = x + iy, maka bilangan kompleks

dinamakan konjugat bilangan z.

Diberikan suatu daerah asal 5 yang merupakan subhimpunan bidang kompleks

ℂ dan f suatu fungsi dari 5 ke dalam ℂ. Jika z menyatakan sembarang titik di dalam

5, dan z menyatakan bilangan kompleks dalam 5, maka z dinamakan suatu variabel

kompleks. Untuk z∈5 maka nilai fungsi f(z) adalah bilangan kompleks. Fungsi yang

bernilaikan bilangan kompleks disebut fungsi bernilai kompleks atau disingkat fungsi

kompleks. Jadi, fungsi f ini adalah fungsi kompleks dari variabel kompleks dengan

daerah definisi (daerah asal) 5. Nilai fungsi kerap dinyatakan dengan huruf w

sehingga fungsi f dengan domain definisi 5 ditulis w = f(z) dengan z∈5. Jika suatu

fungsi bernilai kompleks dari variabel kompleks f(z), maka f(z) = u(x,y) + iv(x,y)

dengan u dan v adalah fungsi bernilai real dari variabel real x dan y. Fungsi u(x,y) dan

v(x,y) berturut-turut dinamakan bagian real dan bagian imajiner dari fungsi f(z).

Dalam fungsi kompleks, ada beberapa fungsi elementer yang dikenal. Namun

dalam skripsi ini, penulis hanya akan membahas fungsi Euler yang merupakan fungsi

eksponensial.

Definisi 2.2.3

Untuk bilangan kompleks z didefinisikan

67_{= 6}! _{cos 4 + 3 sin 4 (2.8)}

Dalam Definisi 2.2.3, kita dapat melihat bahwa jika diambil z real, yaitu z = x +

i0, maka ruas kiri dari Persamaan (2.8) menjadi ex, sedangkan ruas kanan menjadi

6! _{cos 0 + 3 sin 0 = 6}!_{. Oleh karena itu, kita dapat mengatakan bahwa Persamaan}

(2.8) merupakan perluasan fungsi eksponensial real yang sudah kita kenal dalam

kalkulus. Jika diambil z = iy dengan y real, kita memperoleh hubungan yang

dijabarkan di atas. Dengan melihat Definisi 2.2.3 dengan z = ± iy, maka kita dapat

memperoleh rumus sebagai berikut

6±9: _{= cos 4 ± 3 sin 4. (2.9)}

Persamaan (2.9) di atas disebut sebagai persamaan Euler.

C. Derivatif dan Antiderivatif

Definisi 2.3.1

Turunan atau derivatif f yang dinyatakan dengan ′ (dibaca “f aksen”) untuk sebarang

nilai c adalah

< _{* = lim} =→>

* + ℎ − * ℎ

jika limitnya ada.

Teorema 2.3.1

Jika < * ada, maka f kontinu di c.

Bukti

= * +@ ! A@ #

!A# − * , dimana ≠ *.

lim!→# = lim!→#B * +@ ! A@ #_!A# − * C

= lim_!→# * + lim_!→#B@ ! A@ #_!A# − * C

= lim_!→# * + lim_!→#B@ ! A@ #_!A# C ∙ lim_!→# − * .

Berdasarkan Definisi 2.3.1 dan Definisi 2.1.4, maka

lim!→# = * + < * ∙ 0

= * .

Berdasarkan Definisi 2.1.5, maka f kontinu di c. ∎

Definisi 2.3.2

Suatu fungsi F disebut antiderivatif (anti turunan) dari fungsi f bila turunan dari F

adalah f.

Definisi 2.3.3 (Integral tentu)

Andaikan f suatu fungsi yang didefinisikan pada selang tertutup EF, GH. Jika

lim →IJ9L 9 ∆ 9

ada, maka f dikatakan terintegralkan pada EF, GH. Lebih lanjut, M_PO N disebut

integral tentu (atau integral Riemann) f dari a ke b yang didefinisikan oleh

M_PO N = lim →IJ9L 9∗ ∆ 9

Bilangan a dan b dalam M_PO N disebut berturut-turut sebagai batas bawah dan

batas atas integral, serta f(x) disebut integran.

Berikut ini akan diberikan penggunaan simetri dalam penghitungan integral

tentu.

Teorema 2.3.2 (Teorema simetri)

Jika f adalah fungsi genap, maka

M_ARR N = 2 M_>R N (2.10)

dan jika f adalah fungsi ganjil, maka

M_ARR N = 0. (2.11)

Bukti

a. Karena f adalah fungsi genap, maka

M_ARR N = M_AR> N + M_>R N

= M_R> − N − + M_>R N

= − M − −_>R N + M_>R N

= M_>R − N + M_>R N

= M_>R N + M_>R N

= 2 M_>R N .

b. Karena f adalah fungsi ganjil, maka

M_ARR N = M_AR> N + M_>R N

= M_R> − N − + M_>R N

= − M − −_>R N + M_>R N

= M_>R − N + M_>R N

= − M_>R N + M_>R N

= 0. ∎

Teorema 2.3.3 (Teorema periodik)

Jika f periodik dengan periode T, maka

MPSTOST N = MPO N . (2.12)

Bukti

Andaikan U = − sehingga = U + dan NU = N , sehingga

M_PSTOST N = M_PO U + NU.

Berdasarkan Definisi 2.1.3, maka

M_PSTOST N = M_PO U NU

D. Konvergensi Barisan dan Deret

Definisi 2.4.1 (Barisan)

Suatu barisan adalah himpunan dari bilangan-bilangan W , W , W_X, … dengan urutan

penyusunan yang pasti (atau dengan kata lain korespondensi dengan

bilangan-bilangan asli) dan tersusun menurut suatu aturan yang pasti.

Dari definisi di atas, kita juga dapat mengatakan bahwa suatu barisan (atau

barisan tak hingga) adalah suatu fungsi yang daerahnya hasilnya adalah himpunan

bilangan bulat positif.

Definisi 2.4.2 (Konvergensi barisan)

Suatu barisan YW ZS_L disebut mempunyai limit L(x) bila untuk sebarang $ > 0

ada bilangan bulat positif N sedemikian rupa sehingga )W − ) < $ bila

≤ [. Bila barisan YW ZS_L mempunyai limit L(x), maka barisan konvergen ke

L(x) dan ditulis

lim → W = .

Definisi 2.4.3 (Deret tak hingga)

Suatu deret tak hingga adalah suatu ungkapan bentuk

U + U + UX+ ⋯ + U + ⋯

Definisi 2.4.4 (Konvergensi deret tak hingga)

Andaikan Y^ Z adalah barisan jumlah bagian deret J_]L W_] . Jika barisan

Y^ Z konvergen ke limit S(x), maka deret itu konvergen dan S(x) disebut jumlah

deret, ditulis

^ = J]L W] .

Untuk sebuah deret tak terhingga J_]L W_] , didefinisikan jumlah parsial ke-n

dari deret tersebut sebagai jumlah n suku yang pertama dari deret tersebut, yaitu

^ = J]L W] .

Berdasarkan Definisi 2.4.4, suatu deret tak terhingga dapat dikatakan

konvergen ke f(x) pada suatu interval jika diberikan sebarang bilangan positif $,

sedemikian sehingga untuk setiap x di dalam interval tersebut terdapat suatu bilangan

bulat positif N, sehingga )^ − ) < $ untuk semua ≥ [.

Teorema 2.4.1 (Uji banding)

Andaikan J F_] dan J G_] adalah deret dengan suku-suku positif dan andaikan

F ≤ G , F ≤ G , FX ≤ GX, … , F]≤ G], …, maka

i. Jika J G_] (deret yang lebih besar) konvergen, maka J F_] (deret yang lebih kecil)

juga konvergen.

ii. Jika J F_] (deret yang lebih kecil) divergen, maka J G_] (deret yang lebih besar)

Bukti

i. Andaikan J G_] konvergen dan konvergen ke B, maka untuk semua n berlaku

G + G + GX+ ⋯ + G < J]L G] = `.

Karena hipotesis kita yaitu F ≤ G , F ≤ G , F_X ≤ G_X, … , F_] ≤ G_], … , maka

berlaku

F + F + FX+ ⋯ + F ≤ G + G + GX+ ⋯ + G

sehingga F + F + F_X+ ⋯ + F ≤ `.

Karena F + F + F_X+ ⋯ + F bersifat naik dan terbatas ke atas dengan batas

atas B, maka dapat dikatakan bahwa setiap jumlah parsial dari J F_] kurang dari B

dan akibatnya J F_] konvergen.

ii. Bagian ini merupakan ungkapan lain dari bagian (i) dengan memandang (ii)

merupakan kontraposisi dari (i). Jika J F_] divergen maka J G_] juga harus

divergen, karena konvergensi deret J G_] mengakibatkan J F_] juga konvergen. ∎

Definisi 2.4.5 (Deret konvergen mutlak)

Jika J )W_{]L ]} ) konvergen maka J_]L W_] disebut konvergen mutlak.

Definisi 2.4.6 (Konvergensi seragam)

Deret J_]L W_] disebut konvergen secara seragam ke S(x) dalam suatu interval jika

untuk setiap $ > 0 terdapat sebuah bilangan positif N sehingga untuk semua ≥ [

)^ − ^ ) < $, untuk semua x dalam interval.

Hal yang sangat mendasar dari definisi di atas adalah bahwa N hanya tergantung pada

$ dan tidak tergantung pada nilai x di dalam interval tersebut.

Selain dengan menentukan jumlah ^ dan kemudian menggunakan Definisi

2.4.6, Weierstrass M test dapat juga digunakan untuk membuktikan konvergensi

seragam dari suatu deret.

Teorema 2.4.2 (Uji Weierstrass M)

Andaikan deret J_]L W_] adalah deret yang semua sukunya terdefinisi pada suatu

interval. Jika terdapat deret konstan J_]L a_] yang konvergen, sehingga )W_] ) ≤

a] untuk semua x dalam interval tersebut, maka deret J]L W] konvergen mutlak

dan konvergen seragam pada interval tersebut.

Bukti

i. Pertama, akan dibuktikan J_]L W_] konvergen mutlak.

Bukti

Untuk setiap x dalam suatu interval, tiap suku deret J )W_{]L ]} ) kurang dari

atau sama dengan suku ke-n dari deret J_]L a_] yang konvergen, dan ditulis

)W] ) ≤ a] . Menurut Uji banding dalam Teorema 2.4.1, maka deret

J )W]L ] ) adalah deret yang konvergen. Dengan demikian berdasarkan

ii. Kedua, akan dibuktikan J_]L W_] konvergen seragam pada suatu interval

dimana semua suku dari deret tersebut terdefinisi pada interval tersebut.

Bukti

Jika pendekatan suatu fungsi f oleh jumlah parsial ke-n dari J_]L W_] yaitu

^ , maka besar kesalahan pada suatu titik x adalah selisih − ^ .

Selisih ini biasanya disebut sisa ke-n dari J_]L W_] dan ditulis b =

− ^ . Nilai mutlak dari sisa ke-n tersebut adalah

)b ) = ) − ^ )

= )W _S + W _S + W _SX + ⋯ )

≤)W S ) + )W S )+)W SX ) + ⋯

≤a S + a S + a SX+ ⋯

Jika = a _S + a _S + a _SX+ ⋯ merupakan sisa ke-n dari deret JI_]L a_]

yang konvergen, maka )b ) ≤ .

Karena JI_]L a_] adalah deret konstan yang konvergen, maka untuk setiap $ > 0

yang diberikan, terdapat bilangan bulat positif N sedemikian sehingga < $

untuk ≤ [.

Untuk nilai N yang sama, diperoleh

)b ) ≤ < $ untuk ≤ [.

Karena N tidak tergantung pada x, tetapi hanya bergantung pada nilai $, maka

Jadi terbukti bahwa JI_]L W_] konvergen mutlak dan konvergen seragam pada

interval tersebut. ∎

Teorema 2.4.3

Jika masing-masing suku dari deret tak hingga JI_]L W_] kontinu pada interval (a,

b) dan deret tersebut konvergen secara seragam ke jumlah f(x) pada interval ini, maka

i. f(x) juga kontinu pada interval tersebut,

ii. deret tersebut dapat diintegralkan suku demi suku, yaitu

M YJPO I]L W] ZN = J]LI M WPO ] N

atau dapat ditulis

M_PO N = M W_PO N + M W_PO N + ⋯ + M W_PO N + ⋯

Bukti

i. Andaikan diberikan x0, F < _> < G, dan andaikan diberikan $ > 0, maka harus

dicari ' sedemikian sehingga untuk 0 < ) − _>) < ' ⇒ ) − _> ) < $,

dan F < < G.

Karena deret JI_]L W_] konvergen secara seragam ke f(x), maka terdapat suatu

bilangan positif ' sedemikian sehingga

0 < ) − >) < ' ⇒ )^ − > ) <_X$, ≤ [. (2.13)

Fungsi ^_d sebagai jumlah bagian dari fungsi kontinu adalah juga kontinu.

0 < ) − >) < ' ⇒ )^d − ^d > ) <_X$.

Berdasarkan Persamaan (2.13), diperoleh

)^d − ) <_X$, )^d − > ) <_X$.

Dengan memilih ' = minY' , ' Z, maka 0 < ) − _>) < ' menunjukkan

) − > ) = ) − ^d + ^d − ^d > + ^d > − > )

≤) − ^d ) + )^d − ^d > ) + )^d > − > )

<_X$ +_X$ +_X$ = $ untuk 0 < ) − _>) < '.

Dengan demikian telah diperlihatkan bahwa

0 < ) − >) < ' ⇒ ) − > ) < $, F < < G.

Jadi f(x) juga kontinu pada interval (a, b).

ii. Seperti pembuktian sebelumnya, andaikan ^ adalah jumlah n bagian dari

deret JI_]L W_] , maka

M ^PO N = M WPO N + M WPO N + ⋯ + M WPO N .

Untuk membuktikan teorema di atas, harus ditunjukkan bahwa M ^_PO N

konvergen ke M_PO N , sehingga untuk setiap $ > 0 terdapat N sehingga

eM ^_PO N − M_PO N e < $, ≤ [. Untuk membuktikan ini, dipilih N yang

sangat besar sehingga

) − ^ ) <_OAPf , ≤ [, F < < G,

Oleh karena itu,

eM ^_PO N − M_PO N e = eM E_PO − ^ HN e

<_OAPf G − F = $, ≤ [.

Dengan demikian, deret tersebut dapat diintegralkan suku demi suku, yaitu

M YJPO I]L W] ZN = JI]L M WPO ] N . ∎

Teorema 2.4.4

Deret yang konvergen dapat didiferensialkan suku demi suku jika diketahui bahwa

suku-suku dari deret tersebut mempunyai turunan yang kontinu dan deret dari turunan

itu konvergen secara seragam, yakni jika W_]< =gh_g!i adalah kontinu pada interval

F, G , JI_]L W_] konvergen ke f(x) pada interval F, G , dan JI_]L W_]<

konvergen secara seragam pada interval F, G , maka < = JI_]L W_]< .

Bukti

Andaikan g(x) adalah jumlah dari deret turunan tersebut, dan ditulis

= JI W_]<

]L , F < < G.

Menurut Teorema 2.4.3, fungsi g(x) adalah fungsi kontinu, dimana

M!j

P N = J M WI]L P!j ]< N , F < < G,

sehingga

M!j

P N = J EWI]L ] − W] F H= J W]LI ] − J WI]L ] F .

M!j

P N = − F .

Jika kedua ruas diturunkan terhadap , maka = , F < < G.

Dengan kata lain, < = = JI_]L W_]< , F < < G.

Jadi terbukti bahwa deret tersebut dapat didiferensialkan suku demi suku. ∎

E. Deret Taylor

Definisi 2.5.1

Jika f berturunan pada semua tingkat pada = _>, maka definisika deret Taylor yang

bersesuaian dengan f di sekitar = _> adalah

= > + < > − > +@ kk_!l

! − > + ⋯ +

@n !l

! − > + ⋯

Dari Definisi 2.5.1 di atas, kita juga dapat mengatakan bahwa ekspansi deret

Taylor untuk sebuah fungsi f(x) yang berturunan (n + 1) kali pada suatu interval

terbuka yang memuat titik x0 dapat ditulis sebagai berikut.

= > + < > − > +@ kk_!l

! − > + ⋯ +

@n _!l

! − > +

@n+j _o

S ! − > S (2.14)

Suku terakhir dari rumus di atas adalah bentuk dari deret Taylor dengan suku

sisa dan dinyatakan dengan Rn+1. Mengingat bahwa f merupakan fungsi dengan satu

variabel maka dengan mengambil x0 = 0, deret Taylor pada Persamaan (2.14) di atas

= 0 + < _{0 +} << _{0 + b}

X. (2.15)

Selanjutnya ekspansi dari deret Taylor dengan satu variabel ini akan digunakan

untuk fungsi dengan dua variabel.

Misalkan bahwa fungsi F(y, z) mempunyai turunan parsial sampai suku ketiga

pada interval terbuka yang memuat titik dengan koordinat (y0, z0). Didefinisikan

sebuah fungsi f(x) = F(y + xh, z + xk), dimana h dan k merupakan bilangan-bilangan

yang cukup kecil sehingga f(x) berada di sekitar (y0, z0). Misalkan u = y + xh dan v = z

+ xk sehingga fungsi f(x) dapat ditulis f(x) = F(u, v). Dengan menggunakan aturan

rantai untuk fungsi dua variabel maka diperoleh turunan pertama dari fungsi f(x)

sebagai berikut.

= p U, q

′ = rs_rtrt_r!+rs_ruru_r!.

Karena U = 4 + ℎ dan q = 1 + v maka rt_r!= ℎ dan ru_r!= v , sehingga

diperoleh

′ = ℎrs_rt+ vrs_ru (2.16)

= ℎrs :S!=,7S!]

r :S!= + v

rs :S!=,7S!]

r 7S!] .

Untuk x = 0 maka

′ 0 = ℎrs :,7

r: + v

rs :,7 r7

′ 0 = ℎp_: 4, 1 + vp₇ 4, 1 ,

< _{0 = ℎp}

: 4>, 1> + vp7 4>, 1> . (2.17)

Dari Persamaan (2.16), maka kita dapat memperoleh turunan kedua dari f(x)

sebagai berikut

<_{′ = ℎ B}rws

rtwrt_r!+ r w_s rtru

ru r!C + v B

rw_s rurt

rt r!+

rw_s ruwru_r!C.

Karena U = 4 + ℎ dan q = 1 + v maka rt

r!= ℎ dan ru

r!= v , sehingga

diperoleh

<_{′ = ℎ B}rws rtwℎ + r

w_s

rtruvC + v B rw_s rurtℎ +

rw_s ruwvC

= ℎ rws

rtw+ ℎv r w_s

rtru+ vℎ

rws rurt+

rws ruwv .

Karena rws rtru =

rw_s

rurt, maka

<_{′ = ℎ} rws

rtw+ 2vℎ r w_s rtru+

rws

ruwv (2.18)

= ℎ rws :S!=,7S!]

r :S!=w + 2vℎr

w_{s :S!=,7S!]} r :S!= r 7S!] +

rw_{s :S!=,7S!]}

r 7S!] w v

Untuk x = 0 maka

<_{′ 0 = ℎ} rws :,7

r:w + 2vℎr w_{s :,7}

r:r7 + v

rw_{s :,7} r7w

= ℎ p_:: 4, 1 + 2vℎp_:7 4, 1 + v p₇₇ 4, 1 ,

dan karena f(x) berada di sekitar (y0, z0) maka diperoleh

<< _{0 = ℎ p}

:: 4>, 1> + 2ℎvp:7 4>, 1> + v p77 4>, 1> (2.19)

Kemudian Persamaan (2.15) dapat ditulis menjadi

− 0 = < _{0 +} << _{0 + b}

X (2.20)

Apabila Persamaan (2.17) dan (2.19), serta x = 1 disubstitusikan pada

Persamaan (2.20), maka diperoleh

∆p = 1 − 0

= ℎp: 4, 1 + vp7 4, 1 + ℎ p:: 4, 1 + ℎvp:7 4, 1 + v p77 4, 1 .

(2.21)

F. Pengertian Deret Fourier

Deret Fourier merupakan istilah yang diciptakan oleh penemunya yaitu Jean

Baptiste Joseph (Baron) Fourier (1768 – 1830), seorang fisikawan Prancis dan

matematikawan tekenal. Berdasarkan penelitiannya terhadap konduksi panas dalam

suatu benda padat, Fourier menciptakan suatu hukum atas hal tersebut yang dikenal

dengan nama Hukum Fourier (law of heat conduction atau Fourier’s law). Kemudian

Fourier mempublikasikan teori yang sangat penting dalam perkembangan dunia

matematika dan aplikasi, yaitu “Theorie Analytique de la Chaleur”. Teori tersebut

membicarakan perwakilan suatu fungsi sebarang terhadap deret trigonometri dalam

suatu interval, yang sekarang dikenal dengan nama Deret Fourier (Jeffrey, 2002).

Deret trigonometri yang didefinisikan oleh

F>+ F cos + G sin + F cos 2 + G sin 2 + ⋯

mempunyai periode 2x dengan F_>, F , … , G , G , … adalah bilangan real. Dengan

F>+ JIL F cos + G sin

dengan F dan G disebut koefisien-koefisien deret trigonometri. Berikut ini

merupakan definisi dari deret Fourier.

Definisi 2.6.1

Misalkan f(x) merupakan perwakilan dari deret Fourier yang terdefinisi pada interval

−x ≤ ≤ x dan f(x) kontinu bagian demi bagian pada interval tersebut, maka deret

Fourier yang bersesuaian dengan f(x) ditentukan oleh

= F_>+ JI_L F cos + G sin

= F_>+ F cos + G sin + F cos 2 + G sin 2 + ⋯ (2.22)

dimana koefisien F_>, F , … , G , G , … ditentukan oleh fungsi f(x).

Dari Definisi 2.6.1 di atas diperhatikan bahwa f(x) memuat dua jumlahan fungsi

yang tidak berhingga, yaitu fungsi kosinus dan fungsi sinus. Berdasarkan Persamaan

(2.1) maka fungsi kosinus dapat disebut sebagai fungsi genap dan berdasarkan

Persamaan (2.2) maka fungsi sinus dapat disebut sebagai fungsi ganjil.

Teorema 2.6.1

Andaikan fungsi cos nx, sin nx, cos mx, dan sin mx terdefinisi dalam interval −x ≤

≤ x, dimana n = 1, 2, 3, ... dan m = 1, 2, 3, ..., sedemikian sehingga berlaku

1. M sin_A sin N = 0, ≠ .

2. M sin_A cos N = 0, ≠ .

3. M cos_A cos N = 0, ≠ .

4. M sin_A N = 0.

5. M cos_A N = 0.

Bukti

1. Karena sin dan sin keduanya merupakan fungsi ganjil, maka dengan

menggunakan Persamaan (2.4) diperoleh

M sin_A sin N = M cos_A − − cos + N

= B

yA sin − − yS sin + C_A

= B z

yA sin − x − yS sin + x{ −

z_yA sinE − −x H − _yS sinE + −x H{C.

= B z_yA sin − x − _yS sin + x{ −

z−_yA sin − x + _yS sin + x{C.

Berdasarkan kenyataan bahwa sin − x = sin x = 0, maka diperoleh

M sin_A sin N = ∙ 0

2. Karena sin adalah fungsi ganjil dan cos adalah fungsi genap sehingga

berdasarkan Teorema 2.1.1 diketahui bahwa hasil kali fungsi ganjil dan fungsi

genap adalah fungsi ganjil, maka berdasarkan Persamaan (2.11) diperoleh

M sin_A cos N = 0.

3. Karena cos dan cos keduanya merupakan fungsi genap, maka dengan

menggunakan Persamaan (2.6) diperoleh

M cos_A cos N = M cos_A − + cos + N

= B _yA sin − + _yS sin + C

A

= B z

yA sin − x +yS sin + x{ −

z_yA sin − −x +_yS sin + −x {C

= B z

yA sin − x − yS sin + x{ −

z−_yA sin − x − _yS sin + x{C.

Berdasarkan kenyataan bahwa sin − x = sin x = 0, maka diperoleh

M cos_A cos N = ∙ 0

= 0.

4. Karena sin adalah fungsi ganjil, maka berdasarkan Persamaan (2.11) diperoleh

M sin_A N = 0.

5. M cos_A N =

yEsin HA

=

Karena fungsi sinus merupakan fungsi ganjil, maka

M cos_A N =

yEsin x + sin xH

= y∙ 0

= 0. ∎

Sifat-sifat di atas biasa disebut sebagai sifat-sifat ortogonalitas dari fungsi kosinus

dan sinus.

Kemudian dari Persamaan (2.22), kita dapat merumuskan formula untuk an dan

bn dalam persamaan tersebut yang bersesuaian dengan fungsi f(x) yang diberikan

dengan mengalikan f(x) dengan cos nx dan sin nx dimana n = 1, 2, 3,.. . Pertama-tama

akan dicari formula an dengan mengalikan cos nx pada Persamaan (2.22). Untuk itu,

diperoleh

cos = F>cos + F cos cos + F cos 2 cos + FXcos 3 cos

+ ⋯ + F A cos − 1 cos + F cos

+ F S cos + 1 cos + ⋯ + G sin cos + G cos 2 cos

+ ⋯

Dengan mengintegrasikan persamaan di atas dari – x hingga x , maka kita

M_A cos N = F_>M cos N_A}} + F M cos cos_A}} N

+ F M cos 2 cos N_A + F_XM cos 3 cos_A N + ⋯

+F _A M cos − 1 cos_A N + F M cos_A N +

+ F S M cos + 1 cos N_A + ⋯ + G M sin cos_A

+ G M cos 2 cos N_A + ⋯

Berdasarkan sifat-sifat ortogonalitas dari fungsi sinus dan kosinus yang dibuktikan

dalam Teorema 2.6.1, maka

M_A cos N = F M cos_A N .

Berdasarkan Persamaan (2.7) dan sedikit modifikasi yaitu cos = S~•€ S !,

maka

M cos_A N = M z_A S~•€ S !{N

= z +

S sin + 1 {_A

= zBx + _S sin + 1 xC − B −x + _S sin + 1 −x C{

= 2x

= x

dengan n 0, dan M 1 N_A = _{−x = 2x}x , maka diperoleh F_> = M_A N dan

Dengan cara yang sama dalam memperoleh formula an, maka kita dapat memperoleh

formula bn dengan mengalikan sin nx pada Persamaan (2.22) sedemikian sehingga

diperoleh

sin = F>sin + F cos sin + F cos 2 sin + ⋯

+ F A cos − 1 sin + F cos sin

+ F S cos + 1 sin + ⋯ + G sin sin + G cos 2 sin

+ ⋯ + G A sin − 1 sin + G sin

+ G S sin + 1 sin + ⋯

Dengan mengintegrasikan persamaan di atas dari – x hingga x , maka kita

memperoleh

M_A sin N = F_>M sin N_A}} + F M cos sin_A}} N +

F M cos 2 sin N_A + F_XM cos 3 sin N_A + ⋯ +

F A M cos − 1 sin_A N + F M cos sin_A N +

F S M cos + 1 sin N_A + ⋯ + G M sin sin_A +

G M sin 2 sin N_A + GXM sin 3 sin N_A + ⋯ +

G A M sin − 1 sin_A N + G M sin_A N +

G S M sin + 1 sin N_A .

Berdasarkan sifat-sifat ortogonalitas dari fungsi sinus dan kosinus yang dibuktikan

dalam Teorema 2.6.1, maka

Berdasarkan Persamaan (2.7) dan sedikit modifikasi yaitu sin = A~•€ S !,

maka

M sin_A N = M z_A A~•€ S !{N

= z −

S sin + 1 {_A

= zBx −

S sin + 1 xC − B −x − S sin + 1 −x C{

= 2x

= x

untuk n 0, maka G = M_A sin N untuk = 1,2, … .

Hasil-hasil tersebut merupakan formula Euler untuk koefisien an dan bn dalam

Persamaan (2.22). Oleh karena itu, kita dapat mendefinisikan deret Fourier yang

bersesuaian dengan f(x) sebagai berikut.

Definisi 2.6.2

Misalkan f(x) adalah fungsi yang terdefinisi pada interval −x ≤ ≤ x dan f(x)

kontinu bagian demi bagian pada interval tersebut, maka f(x) sebagai perwakilan dari

deret Fourier didefinisikan sebagai

= F_>+ JI_L F cos + G sin (2.23)

dengan koefisien-koefisien Fourier yang diberikan oleh formula Euler di bawah ini

untuk n = 1, 2, 3, ... .

Dengan memperhatikan Definisi 2.6.1 dan 2.6.2, maka deret Fourier memiliki

sifat yang mencerminkan periodiksitas dari fungsi sinus dan kosinusnya. Oleh karena

itu, interval −x ≤ ≤ x merupakan interval dasar dari ekspansi deret Fourier. Kita

juga dapat mendefinisikan perwakilan deret Fourier dari fungsi f(x) secara umum

pada interval − ≤ ≤ .

Definisi 2.6.3

Misalkan f(x) adalah fungsi yang terdefinisi pada interval − ≤ ≤ dan f kontinu

bagian demi bagian. Jadi, f(x) sebagai perwakilan dari deret Fourier didefinisikan

sebagai berikut

= F_>+ J zF cos !

„ + G sin !

„ {

I

L (2.24)

dimana a0, an, dan bn merupakan koefisien-koefisien yang diberikan dengan formula

Euler seperti berikut

F> = _„M_A„„ N , F =_„M_A„„ cos _„!N , G =_„M_A„„ sin _„!N

(2.25)

untuk n = 1, 2, 3, ... .

Dapat diperhatikan bahwa fungsi f(x) yang merupakan perwakilan dari deret

Contoh 2.6.1

Tentukan perwakilan deret Fourier dari f(x) = x + 1 untuk −1 ≤ ≤ 1.

Penyelesaian:

Pada contoh ini, L = 1.

Berdasarkan Definisi 2.6.3, maka kita dapat menentukan a0, an, dan bn.

F> = M_A + 1 N

= z + {

A

= zB + 1C − B − 1C{

= 1.

F = M_A + 1 cos x N

= M_A cos x + cos x N

= M_A cos x N + M cos x N_A

= ! €…† !− M_A €…† !N + ~•€ !

= B! €…† !+~•€_{w w}!+ ~•€ !C A

= B€…† +~•€_{w w} + ~•€ C − B€…† +~•€_{w w} + ~•€ C

= 0.

G = M_A + 1 cos x N

G = M_A cos x N + M cos x_A N

= −! ~•€ !− M_A ~•€ !N − ~•€ !

= B−! ~•€ !+€…†_{w w}!− ~•€ !C A

= B−~•€ +€…†_{w w} − ~•€ C − B~•€ −€…†_{w w} − ~•€ C

= − ~•€ + €…†_{w w}

= z−cos x +€…† {

= z€…† −cos x{.

Karena sin x = 0, dan cos x = −1 , maka

G = 0 + −1 −1

= A n+j

untuk n = 1, 2, 3, ... dengan n adalah bilangan bulat.

Kemudian langkah selanjutnya adalah mensubstitusikan koefisien-koefisien yang

sudah dicari ke dalam Persamaan (2.24), sehingga kita dapat memperoleh deret

Fourier yang diwakilkan dengan

= 1 + JI_L z0 + A n+jsin x {

= 1 + JI_L zA n+jsin x { untuk −1 ≤ ≤ 1.

Dengan melihat Definisi 2.6.3, maka Persamaan (2.24) dapat diekspansikan

= F_>+ J F cos ! „ I

L + JIL G sin _„!. (2.26)

Karena F_> dan JI_L F cos _„! keduanya adalah fungsi genap sehingga F_>+

JI F cos _„!

L adalah juga fungsi genap, andaikan ℎ = F>+ JIL F cos _„!

maka ℎ disebut sebagai deret kosinus Fourier. Sementara itu, karena

JI G sin _„!

L adalah fungsi ganjil, dan andaikan = JIL G sin _„!, maka

disebut sebagai deret sinus Fourier.

Berikut akan dicari koefisien-koefisien dari deret kosinus dan sinus Fourier.

1. Koefisien untuk deret kosinus Fourier

F> = _„M ℎ_A„„ N

Karena h(x) merupakan fungsi genap, maka dengan menggunakan Persamaan

(2.10) diperoleh

F> = _„z2 M ℎ N_>„ {

=

„M ℎ N

„

> .

F = _„M ℎ_A„„ cos _„!N .

Karena h(x) dan fungsi kosinus merupakan fungsi genap sehingga berdasarkan

Teorema 2.1.2 diketahui bahwa hail kali dua fungsi genap adalah fungsi genap,

maka berdasarkan Persamaan (2.10) diperoleh

F = _„z2 M ℎ_>„ cos _„!N {

=

„M cos

!

„ N

„

2. Koefisien untuk deret sinus Fourier

G = _„M_A„„ sin _„!N

Karena g(x) dan fungsi sinus merupakan fungsi ganjil sehingga berdasarkan

Teorema 2.1.2 diketahui bahwa hasil kali dua fungsi ganjil adalah fungsi genap,

maka berdasarkan Persamaan (2.10) diperoleh

G = _„z2 M_>„ sin _„!N {

= _„M_>„ sin _„!N .

Dengan demikian, kita dapat meringkas penjelasan mengenai deret kosinus dan sinus

Fourier di atas dalam Definisi 2.6.4.

Definisi 2.6.4 (Deret kosinus dan sinus Fourier)

Jika f(x) terdefinisi pada interval − ≤ ≤ dan f kontinu bagian demi bagian,

maka deret sinus yang bersesuaian dengan f(x) adalah

= JI zG sin _„!{

L , untuk − ≤ ≤ (2.27)

dimana

G =_„M_>„ sin _„!N , untuk = 1,2, … , (2.28)

dan deret kosinus yang bersesuaian dengan f(x) adalah

= F>+ JIL zF cos _„!{, untuk − ≤ ≤ (2.29)

dimana

G. Kekonvegrenan Deret Fourier

Dalam pembahasan sebelumnya mengenai pengertian deret Fourier, telah

diuraikan bentuk deret Fourier yang bersesuaian dengan suatu fungsi f(x) dimana f(x)

merupakan fungsi periodik dengan periode 2x dan kontinu bagian demi bagian dalam

interval −x < < x. Akan menjadi sangat baik jika deret Fourier yang diperoleh

konvergen ke f(x) sehingga dapat menjamin integral Fourier mempunyai suatu nilai

dan berhingga.

Untuk menjelaskan konvergensi deret Fourier, ada beberapa konsep yang perlu

sifat koefisien deret Fourier, Teorema Riemann-Lebesgue, dan Kernel Dirichlet.

1. Sifat Koefisien Deret Fourier

Sifat koefisien deret Fourier merupakan hal penting yang harus dibahas

sebelum membahas konvergensi deret Fourier. Sifat koefisien deret Fourier

tersebut yaitu

lim →IF = lim →IG = 0.

Sebelum kita membuktikan sifat koefisien deret Fourier di atas, akan dibuktikan

kesamaan parseval berikut ini yang digunakan dalam penurunan sifat koefisien

Teorema 2.7.1.1 (Kesamaan Parseval)

Andaikan deret Fourier yang bersesuaian dengan f(x) konvergen seragam ke f(x)

pada selang ‡– x, xˆ, maka berlaku kesamaam parseval di bawah ini, yaitu

M_A N = 2F> + J ‡F + G ˆdL ,

dimana nilai integralnya diandaikan ada dan berhingga.

Bukti

Deret Fourier yang bersesuaian dengan f(x) adalah

= F>+ JdL F cos + G sin .

= F_> + Jd_L F cos + G sin .

Dengan melakukan pengintegralan bagian demi bagian, maka

M_A N

= M F_{A >} N + M_A Jd_L F cos + G sin N

= F_>M_A N + Jd_L M_A F cos + G sin N

= F_>M_A N + J ‰M Fd_{L A} cos N + M G_A sin N Š

= F_>M_A N + J ‰F Md_{L A} cos N + G M_A sin N Š

Berdasarkan definisi koefisien-koefisien Fourier yang diberikan dalam Definisi

2.6.2, maka diperoleh

M_A N = 2xF_> F_>+ J EF F x + G G x Hd_L

= 2xF_> + x J ‰F + G Šd_L

Teorema 2.7.1.2

Andaikan f kontinu bagian demi bagian yang mempunyai bentuk deret Fourier

F>+ ‹ F cos + G sin I

L

dan f terdefinisi pada interval −x ≤ ≤ x dengan periode 2x, maka koefisien

deret Fourier F dan G memenuhi sifat

lim →IF = lim →IG = 0. (2.31)

Bukti

Andaikan ^_d adalah barisan jumlah parsial deret Fourier yang bersesuaian

dengan f(x) dan terdefinisi pada interval −x ≤ ≤ x, dan ditulis

^d = F>+ ‹ F cos + G sin d

L

dimana = 1,2,3, … .

Dengan melakukan pengintegralan bagian demi bagian, maka seperti pada

penurunan M_A N dalam Teorema 2.7.1.1, diperoleh

M_A ^d N = 2xF> + x J ‰F + G ŠdL dan

M E^_A d H N = 2xF> + x J ‰F + G ŠdL ,

sehingga

M E_A − ^d H N = M_A N − 2 M_A ^d N +

M E_A − ^d H N =M_A N − 4xF> − 2x J ‰F + G ŠdL +

2xF> + x J ‰F + G ŠdL

=M_A N − 2xF_> − x J ‰F + G Šd_L

=M_A N − x‡2F_> + J ‰F + G Šd_L ˆ.

Karena nilai M E_A − ^_d H N adalah tidak negatif, maka

M_A N − x‡2F> + J ‰F + G ŠdL ˆ≥ 0,

sehingga

M_A N ≥ ‡2F> + J ‰F + G ŠdL ˆ,

untuk semua N.

Untuk [ → ∞, maka

2F> + J ‰F + G ŠIL ≤ M_A N .

Pertidaksamaan di atas dikenal dengan pertidaksamaan Bessel untuk deret

Fourier. Karena M_A N nilainya ada dan berhingga, maka J ‰F +I_L

G H menjadi terbatas sehingga J ‰F + G ŠI_L konvergen. Oleh karena itu,

kita juga dapat mengatakan bahwa lim _→I‡F + G ˆ = 0 atau lim _→IF =

lim →IG = 0. ∎

2. Teorema Riemann-Lebesgue dan Akibatnya

Teorema 2.7.2.1 (Teorema Riemann-Lebesgue)

lim →IM_A cos N = lim →IM_A sin N = 0. (2.32)

Bukti

Telah diketahui bahwa M_A cos N merupakan koefisien F dalam deret

kosinus Fourier untuk fungsi f kontinu bagian demi bagian pada selang 0 ≤ ≤

x, dengan mengabaikan nilai pada Persamaan (2.30) jika deret Fourier

terdefinisi pada interval 0 ≤ ≤ dengan = x. Demikian pula

M_A sin N merupakan koefisien G dalam deret sinus Fourier untuk

fungsi f kontinu bagian demi bagian pada selang 0 ≤ ≤ x , dengan

mengabaikan nilai pada Persamaan (2.28) jika deret Fourier terdefinisi pada

interval 0 ≤ ≤ dengan = x. Menurut sifat koefisien deret Fourier, jika

→ ∞, maka lim _→IF = lim _→IG = 0 atau lim _→IM_A cos N =

lim →IM_A sin N = 0. ∎

Teorema 2.7.2.2 (Teorema akibat)

Jika f kontinu bagian demi bagian pada interval 0 ≤ ≤ x, maka

limd→IM_A sin dS !N = 0, (2.33)

Bukti

Karena sin Ž + ` = sin Ž cos ` + cos Ž sin `, maka M_A sin dS !N

atau M_A sin z[ +!{ N dapat ditulis menjadi M_A sin z[ +!{ N =

M_A sin [ cos!N + M_A cos [ sin!N . Karena fungsi cos!

dan sin! adalah fungsi kontinu bagian demi bagian pada interval 0 ≤ ≤

x, maka menurut Teorema 2.7.2.1 dapat ditulis menjadi

M_A sin dS !N

= M z_A cos!{ sin [ N + M z_A sin!{ cos [ N

= 0 + 0

= 0.

Jadi terbukti bahwa lim_d→IM_A sin dS !N = 0. ∎

3. Kernel Dirichlet

Kernel Dirichlet adalah suatu fungsi dengan bentuk •_d = +

Jd cos

Teorema 2.7.3.1

Andaikan fungsi •_d bersifat kontinu, dan merupakan fungsi genap dan

periodik dengan periode 2x, maka fungsi •_d memenuhi sifat-sifat di bawah

ini, yaitu

i. M •_{> d} N =

ii. •_d =€…†B dS

• wC

€…†•_w , ≠ 0, ±2, ±4, … .

Bukti

i. M •_{> d} N = M B + J_> d_L cos C N

= M N_> + M J_> d_L cos N

= B C

> + J B sin C> d

L

= B x − 0 C + Jd_L B sin x − sin 0 C

= .

ii. Akan dibuktikan bahwa •_d =€…†B dS

• wC

€…†•_w , ≠ 0, ±2, ±4, …. Untuk

membuktikannya, kita akan memperhatikan persamaan berikut.

Untuk = 1,2,3, … , [,

Jd zsin Bz + { C − sin Bz − { C{

L = sin!JdL 2 cos

⇔sin Bz[ + { C − sin z { = sin!Jd_L 2 cos

⇔ sin Bz[ + { C = sin!Jd_L 2 cos + sin z {

⇔ sin Bz[ + { C = 2sin!zJd_L cos + {

⇔ •_d = €…†BzdS j w{!C

€…†•_w . ∎

Teorema 2.7.3.2

Andaikan f(x) kontinu bagian demi bagian pada interval 0 ≤ ≤ x, dan turunan

kanan ‡ <_’ 0 ˆ ada, maka

limd→IM_> •d N = 0S (2.34)

dimana •_d adalah Kernel Dirichlet.

Bukti

Andaikan

limd→IM_> •d N = “d + ”d ,

dimana

“d = M E_> − 0S H•d N dan ”d = M_> 0S •d N .

Dengan menggunakan sifat bagian (ii) Kernel Dirichlet yang telah dibahas dalam

“d = M E − 0S H€…†B dS • wC €…†•_w N >

= M E@ ! A@ >+ H

€…†•_w sin B 2[ + 1 !_{C N}

> (2.35)

Andaikan p =E@ ! A@ >+ H

€…†•_w . Kita akan memperlihatkan bahwa F<