YUSEP MAULANA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2009
Problem. Supervised by FARIDA HANUM and PRAPTO TRI SUPRIYO.
Integer programming problem (IP) can be finalized with Lagrangian relaxation method. The idea of Lagrangian relaxation problem came from penalty method which is applied to look for solution of approximation from constrained programming problem. The formulation of Lagrangian relaxation related with Lagrangian multiplier. The Lagrangian multiplier from Lagrangian relaxation problem can be obtained by applying subgradient method or branch and bound method. In this paper, the value of Lagrangian multiplier from Lagrangian relaxation problem applies subgradient method. This paper also compares the solution between solving IP with Lagrangian relaxation and solving IP with linear programming relaxation. This paper utilized LINDO 6.1 software for obtaining the solution of linear programming relaxation problem and Lagrangian relaxation problem.
Lagrange. Dibimbing oleh FARIDA HANUM dan PRAPTO TRI SUPRIYO.
Masalah integer programming (IP) dapat diselesaikan dengan menggunakan metode relaksasi Lagrange. Ide dari permasalahan relaksasi Lagrange berawal dari metode penalti yang merupakan suatu metode yang digunakan untuk mencari solusi hampiran dari masalah pemrograman berkendala. Dalam formulasi masalah relaksasi Lagrange terkait dengan pengali Lagrange. Nilai pengali Lagrange pada masalah relaksasi Lagrange dapat ditentukan dengan menggunakan metode subgradien atau metode branch and bound. Pada karya ilmiah ini, nilai pengali Lagrange diperoleh dengan menggunakan metode subgradien. Pada karya ilmiah ini juga dilakukan pembandingan antara penyelesaian IP dengan relaksasi Lagrange dan penyelesaian IP dengan pemrograman linear relaksasi. Dalam karya ilmiah ini digunakan software LINDO 6.1 untuk memperoleh solusi dari masalah pemrograman linear relaksasi dan masalah relaksasi Lagrange.
YUSEP MAULANA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPERTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2009
NIM
: G54052834
Disetujui
Pembimbing I
Pembimbing II
Dra. Farida Hanum, M.Si. Drs. Prapto Tri Supriyo, M.Kom.
NIP. 19651019 199103 2 002 NIP. 19630715 199002 1 002
Diketahui
Dr. Drh. Hasim, DEA
NIP 19610328 198601 1 002
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
ilmiah ini berhasil diselesaikan. Judul dari karya ilmiah ini adalah Penyelesaian Masalah Integer
Programming dengan Metode Relaksasi Lagrange.
Terima kasih penulis ucapkan kepada:
1. ibu Dra. Farida Hanum, M.Si. selaku dosen pembimbing I atas segala kesabaran dalam
membimbing, ilmu dan nasihat selama bimbingan menjadi semangat bagi penulis;
2. bapak Drs. Prapto Tri Supriyo, M.Kom. selaku dosen pembimbing II atas segala kesabaran
dalam membimbing, ilmu dan nasihat selama bimbingan menjadi semangat bagi penulis; 3. bapak Donny Citra Lesmana, S.Si, M.Fin.Math. selaku dosen penguji atas segala waktu
luangnya, ilmu, saran dan nasihatnya;
4. semua dosen Departemen Matematika yang telah memberi ilmu pengetahuan bagi penulis;
5. keluagaku tersayang: ibu dan bapak kandungku (Uat Rasmanawati dan Mulyana) yang telah
memberi kasih sayang, doa, pendidikan, dan kerja kerasnya untuk menyekolahkan putramu ini. Tak lupa adikku Yudi Lesmana terima kasih atas doa dan nasihatnya;
6. nenekku Ratmini dan saudara-saudaraku Nia Damayanti, Yati Nurhayati, Adang Sugandi,
Diding Supriatna, Endang, Herman, Yuli Yanti, Karin M, M Idzhar, Ridwan A, Cica K, Oce, Toto, Hindun, Jenab atas semua doa, perhatiannya, dan nasihat yang telah diberikan;
7. staf tata usaha Departemen Matematika, ibu Ade, bapak Yono, bapak Bono, bapak Heri, dan
bapak Deni terima kasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di departemen Matematika;
8. ibu Susi terima kasih atas doa, dukungan, dan nasihatnya;
9. teman-teman satu bimbingan: Dwi Putri E, Bima Saputra, Rian Wahyu Utami, Makinun
Amin, dan Nurwahyuni, terima kasih atas doa, bantuan, dukungan semangat, dan nasihatnya; 10. Deden Ridwan atas doa, bantuan, dukungan semangat, dan nasihatnya;
11. Iwan Hermawan atas doa, bantuan, dan nasihatnya;
12. Muhammad Ilyas dan Verawati atas doa, bantuan, dan kesabarannya yang telah memberikan
waktu luang kepada penulis untuk belajar bersama.
13. Eko Budi atas doa, nasihat, dan kesabarannya dalam mengatur mahasiswa Matematika
angkatan 42;
14. teman-teman mahasiswa matematika angkatan 42: Dian Lestari, Dwi Lara Nolavia, Hesti
Lestari, Haryo G, Novita H, Titi N, Putranto H, Febrianti R, Ridwan Idham, Ritawati, Octavina, Gita A, Nyoman R, Megawati, Mirani, Suwarno, Hapsari, Ratna Galuh, Rafidha, Nur Dwi Privita, Hikmah R, Luri W, Ricken R, M Fachri, Ardy Kresna, Agnes, Dendy S, Handanu, Dendy, R Fitri, Arif I, M Sapto, Dewi, Rohmatul F, dan lainnya atas segala doa dan nasihatnya;
15. kakak kelas dan adik kelas mahasiswa Matematika atas doa dan dukungannya;
16. teman-teman kos “Pondok Sahabat”: Janji, Apid, Nasrul, Dolly, Rajib, Fahmi, Alfa, Iwan,
Ade, Eldy, Joger, Daud, Ardy, Bambang, Trisna dan lainnya atas doa dan kesetiakawanannya selama tinggal di kosan “Pondok Sahabat”.
Penulis menyadari tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.
Semoga karya ilmiah ini bermanfaat.
Bogor, September 2009
Yusep Maulana
Rasmanawati. Penulis merupakan putra pertama dari dua bersaudara.
Tahun 2005 penulis lulus dari SMA Negeri 2 Purwakarta dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB. Penulis memilih Program Studi Matematika, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis sering mengikuti beberapa kegiatan kepanitiaan yang diselenggarakan oleh Gugus Mahasiswa Matematika (GUMATIKA) IPB pada rentang waktu 2006-2008.
Halaman
DAFTAR TABEL ... viii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
II LANDASAN TEORI 2.1 Pemrograman Linear ... 1
2.2 Fungsi Konveks dan Fungsi Konkaf ... 3
2.3 Dualitas Pemrograman Linear ... 7
2.4 Integer Programming ... 7
2.5 Pemrograman Linear Relaksasi ... 7
2.6 Metode Penalti ... 8
2.7 Metode Gradien ... 8
2.8 Subgradien dan Subdiferensial ... 9
III RELAKSASI LAGRANGE 3.1 Metode subgradien ... 13
3.2 Perbandingan Masalah Relaksasi Lagrange dengan Pemrograman Linear Relaksasi Berdasarkan Nilai Batasnya ... 16
3.3 Perbaikan Relaksasi ... 17
IV SIMPULAN DAN SARAN 4.1 Simpulan ... 18
4.2 Saran ... 18
DAFTAR PUSTAKA ... 19
viii
1 Hubungan antara variabel keputusan dan kendala pada masalah primal
dan masalah dual ... 7
2 Solusi Lagrange yang mungkin dan nilai variabel dualnya ... 12
3 Fungsi linear dari ... 13
4 Metode subgradien dengan nilai untuk semua ... 14
5 Metode subgradien dengan nilai ... 14
6 Metode subgradien dengan nilai ... 15
7 Aplikasi metode subgradien untuk perbaikan relaksasi ... 17
DAFTAR GAMBAR
Halaman
1 Ilustrasi himpunan konveks dan bukan himpunan konveks ... 3
2 Ilustrasi fungsi konveks ... 3
3 Ilustrasi fungsi konkaf ... 4
4 Ilustrasi fungsi konkaf pada Teorema 4 ... 5
5 Fungsi linear sesepenggal ... 6
6 Fungsi konkaf linear sesepenggal ... 6
7 Fungsi konveks linear sesepenggal ... 6
8 Daerah fisibel untuk PL-relaksasi dari IP (2.8) ... 8
9 Ilustrasi subgradien pada fungsi konkaf ... 9
10 Fungsi linear sesepenggal pada Contoh 15 ... 10
11 Fungsi konveks linear sesepenggal ... 13
12 Ilustrasi hasil iterasi pada metode subgradien dengan , ... 14
13 Ilustrasi hasil iterasi pada metode subgradien dengan setengah dari nilai sebelumnya ... 15
14 Ilustrasi hasil iterasi pada metode subgradien dengan sepertiga dari nilai sebelumnya ... 15
DAFTAR LAMPIRAN
Halaman 1 Syntax Program LINDO 6.1 untuk Menyelesaikan PL-Relaksasi Masalah IP (2.8) Beserta Hasil yang Diperoleh ... 212 Syntax Program Lindo 6.1 untuk Menyelesaikan Masalah Relaksasi Lagrange pada Tabel 2 Beserta Hasil yang Diperoleh ... 21
3 Penjelasan Fungsi Objektif Masalah Relaksasi Lagrange dari Masalah IP (3.1) ... 25
4 Rincian Nilai-Nilai dengan Variasi Nilai ... 26
5 Syntax Program Lindo 6.1 untuk Menyelesaikan Masalah Relaksasi Lagrange dari Masalah IP (3.1) pada Tabel 5 & 6 ... 29
6 Kekonvergenan Barisan dan Deret dari Nilai-Nilai dan ... 32
7 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah PL-Relaksasi dan Masalah Dual Beserta Hasil yang Diperoleh ... 33
8 Penyelesaian Masalah Relaksasi Lagrange (3.6) dengan Menggunakan Persamaan (3.3) dan ... 34
9 Penyelesaian Masalah Relaksasi Lagrange (3.6) dengan Menggunakan Persamaan (3.3) dan ... 37
10 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Relaksasi Lagrange (3.6) Beserta Hasil yang Diperoleh ... 39
Salah satu observasi yang berguna dalam bidang komputasi di tahun 1970 adalah observasi terhadap permasalahan relaksasi Lagrange. Josep Louis Lagrange merupakan tokoh ahli ilmu sains dan astronomi dari Italia yang menemukan masalah relaksasi Lagrange. Josep Louis Lagrange lahir pada tahun 1736 di kota Turin, Italia. Kontribusi yang telah diberikan oleh Josep Louis Lagrange pada bidang ilmu matematik, di antaranya analisis teori bilangan dan mekanika celestial.
Relaksasi Lagrange merupakan suatu metode yang banyak digunakan dalam aplikasi pemrograman matematik. Fisher (2004) mengemukakan, bahwa pada tahun 1955 metode Lagrange digunakan pada permasalahan optimisasi diskret yaitu capital
budgeting oleh Lorie Savage. Pendekatan
relaksasi Lagrange oleh Held dan Karp di tahun 1970 berlandaskan pada masalah minimum spanning tree untuk menyelesaikan kasus traveling salesman problem. Selain itu, Fisher dan Shapiro di tahun 1973 menyelesaikan permasalahan penjadwalan dan masalah integer programming (IP) dengan metode relaksasi Lagrange. Sejak itu, daftar pengaplikasian relaksasi Lagrange terus
lokasi, penugasan, pemartisian, knapsack, pendistribusian produk dalam skala besar, rute kendaraan dan perancangan sistem perakitan (lihat Fisher 2004).
Pada karya ilmiah ini akan dibahas penyelesaian integer programming dengan metode relaksasi Lagrange, dengan rujukan utama adalah Fisher ML (1985). Ada beberapa metode yang telah dikembangkan untuk mencari solusi pengali Lagrange dari permasalahan relaksasi Lagrange pada model
integer programming, di antaranya metode
subgradien dan metode branch and bound (Fisher 1985). Pada pembahasan ini, solusi pengali Lagrange dari permasalahan relaksasi Lagrange ditentukan dengan menggunakan pendekatan metode subgradien.
1.2 Tujuan
Tujuan dari karya ilmiah ini meliputi: 1. memformulasikan relaksasi Lagrange dari
suatu integer programming (IP);
2. menyelesaikan masalah relaksasi Lagrange
dengan metode subgradien;
3. membandingkan penyelesaian IP dengan
relaksasi Lagrange dan penyelesaian IP dengan pemrograman linear relaksasi.
II LANDASAN TEORI
Untuk memahami masalah relaksasi Lagrange dalam karya ilmiah ini diperlukan beberapa pengertian / konsep berikut ini.
2.1 Pemrograman Linear
Salah satu konsep dasar yang harus
dipahami terkait konsep pemrograman linear di antaranya adalah fungsi linear dan pertidaksamaan linear.
Definisi 1 (Fungsi Linear)
Misalkan menyatakan
suatu fungsi dalam variabel-variabel . Fungsi
dikatakan linear jika dan hanya jika untuk
suatu himpunan konstanta ,
.
(Winston 2004) Sebagai contoh,merupakan fungsi linear, sedangkan bukan fungsi linear. Jika fungsi linear dan ! sembarang bilangan, maka
! merupakan persamaan
linear.
Definisi 2 (Pertidaksamaan Linear)
Untuk sembarang fungsi linear dan sembarang bilangan !,
pertidaksamaan " ! dan
# ! adalah pertidaksamaan
linear.
(Winston 2004)
Pemrograman linear (PL) atau linear
programming adalah suatu masalah optimisasi
yang memenuhi ketentuan-ketentuan sebagai berikut.
a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.
b) Nilai variabel-variabel keputusannya harus
kendala harus berupa persamaan linear atau pertidaksamaan linear.
c) Ada pembatasan tanda untuk setiap
variabel dalam masalah ini. Untuk sembarang variabel $ pembatasan tanda menentukan $ harus taknegatif %# &
atau tidak dibatasi tandanya (unrestricted
in sign).
(Winston 2004) Solusi PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.
Definisi 3 (Bentuk Standar PL)
Pemrograman linear min ' ()*
terhadap +* , (2.1)
* # -
dikatakan PL dalam bentuk standar, dengan *
dan ( vektor-vektor berukuran , vektor ,
berukuran . dan + matriks berukuran . /
yang disebut sebagai matriks kendala, dengan
. " .
(Nash & Sofer 1996) Sebagai catatan, yang dimaksud dengan vektor berukuran adalah vektor yang memiliki dimensi (ukuran) / .
Solusi Pemrograman Linear
Suatu masalah PL dapat diselesaikan
dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan satu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam pengembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.
Pada masalah PL (2.1), vektor * yang
memenuhi kendala +* , disebut solusi PL
(2.1). Misalkan matriks + dapat dinyatakan
sebagai + 0 1 , dengan 0 adalah matriks taksingular berukuran . / . yang
elemennya berupa koefisien variabel basis dan
1 merupakan matriks berukuran . / 2 .
yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks 0 disebut matriks basis
PL (2.1).
Misalkan * dapat dinyatakan sebagai
vektor * 3*1*04, dengan *0 adalah vektor basis dan *1 adalah vektor variabel nonbasis, maka +* , dapat dinyatakan sebagai
+* 0 1 36754
0*0 1*1 ,. (2.2)
Karena matriks 0 adalah matriks taksingular, maka0 memiliki invers, sehingga dari (2.2) *0 dapat dinyatakan sebagai
*0 028, 2 0281*1
.
(2.3)Definisi 4 (Solusi Basis)
Solusi dari suatu PL disebut solusi basis
jika memenuhi syarat berikut:
i. solusi tersebut memenuhi kendala pada
PL;
ii. kolom-kolom dari matriks kendala yang
berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.
(Nash & Sofer 1996)
Menurut Garfinkel & Nemhauser (1972), solusi dari suatu PL disebut solusi basis jika memenuhi *0 028,, *1 -.
Definisi 5 (Solusi Basis Fisibel)
Vektor * disebut solusi basis fisibel jika *
merupakan solusi basis dan * # -.
(Nash & Sofer 1996) Ilustrasi solusi basis dan solusi basis fisibel diberikan pada Contoh 1.
Contoh 1
Misalkan diberikan PL (2.4) berikut: min 9 2 2
terhadap 2 :
2 (2.4)
; <
: <# &,
maka dari PL (2.4) diperoleh
+ =22 & & & & & & &> dan , =: <>
.
Misalkan dipilih *0 : < ? dan *1 ?,maka matriks basisnya adalah
0 =& & && & & >
@
Nilai vektor variabel nonbasis ditentukan dengan vektor nol sehingga *1 & &A. Dengan menggunakan matriks basis di atas, maka diperoleh
*0 0B8, : < A (2.5)
Solusi (2.5) merupakan solusi basis, karena memenuhi kendala pada PL (2.4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.5) yaitu 0,
bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (2.5) juga merupakan solusi basis fisibel, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.
PL (2.1) dapat dinyatakan dalam bentuk
*0 dan *1 sebagai berikut:
min ' (0)*0 (1)*1
terhadap 0*0 1*1 , (2.6)
* # -,
dengan (0 vektor koefisien variabel basis
pada fungsi objektif dan (1 vektor koefisien
variabel nonbasis pada fungsi objektif. Jika persamaan (2.3) disubstitusikan pada fungsi objektif PL (2.6), maka diperoleh
9 (0) 0B8, 2 0B81*1 (1)*1
(0)0B8, C(1)2 (0)0B81D*1.
Hal yang juga penting dalam konsep pemrograman linear adalah daerah fisibel dan solusi optimum yang didefinisikan sebagai berikut.
Definisi 6 (Daerah Fisibel)
Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.
(Winston 2004)
Definisi 7 (Solusi Optimum)
Pada masalah maksimisasi, solusi optimum
suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Pada masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil. (Winston 2004)
2.2 Fungsi Konveks dan Fungsi Konkaf
Sebelum membahas fungsi konveks dan fungsi konkaf, terlebih dahulu akan dibahas himpunan konveks yang didefinisikan sebagai berikut.
Definisi 8 (Himpunan Konveks)
Misalkan S menyatakan himpunan titik.
Himpunan S adalah himpunan konveks jika segmen garis yang menghubungkan sembarang titik-titik dalam S seluruhnya termuat dalam S, atau dengan perkataan lain
himpunan E F G dikatakan himpunan
konveks jika untuk setiap *8 *H I E berlaku *8 2 *HI E,
dengan I J& K@
(Winston 2004) Ilustrasi himpunan konveks dan bukan himpunan konveks diberikan pada gambar di bawah ini.
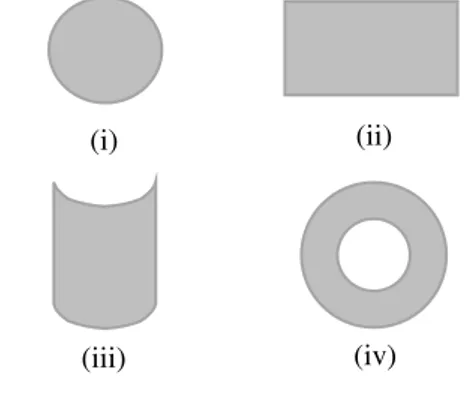
Gambar 1 Ilustrasi himpunan konveks dan bukan himpunan konveks.
Pada Gambar 1, lingkaran (i) dan persegi panjang (ii) merupakan himpunan konveks, sedangkan bidang (iii) dan cincin (iv) bukan himpunan konveks.
Konsep fungsi konveks dan fungsi konkaf yang digunakan pada karya ilmiah ini meliputi definisi-definisi berikut ini.
Definisi 9 (Fungsi Konveks)
Misalkan L E M G, dengan E himpunan
konveks yang takkosong di G . Fungsi
dikatakan konveks di E jika
*8 2 *H " *8 2 *H
untuk setiap *8 *HI E dan untuk setiap I J& K@
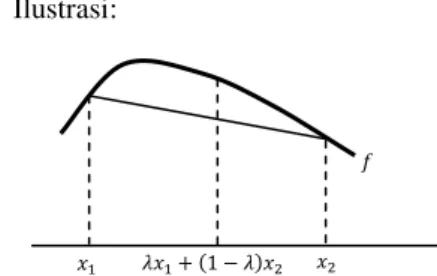
(Peressini et al. 1988) Ilustrasi:
Gambar 2 Ilustrasi fungsi konveks.
Definisi 10 (Fungsi Konkaf )
Misalkan L E M G, dengan E himpunan
konveks yang takkosong di G . Fungsi
dikatakan konkaf di E jika
(i) (ii)
(iii) (iv)
*8 2 *H # *8 2 *H untuk setiap *8 *HI E dan untuk setiap
I J& K@
(Peressini et al. 1988) Ilustrasi:
Gambar 3 Ilustrasi fungsi konkaf.
Berikut ini disampaikan cara memeriksa kekonkafan dan kekonveksan suatu fungsi dengan menggunakan fungsi turunan keduanya.
Teorema 1
Jika terdiferensialkan dua kali pada N,
maka fungsi konkaf pada N jika dan
hanya jika OO " & untuk setiap I N. Jika OO P & untuk setiap I N, maka
dikatakan fungsi konkaf sempurna (strictly
concave).
(Peressini et al. 1988) Sebagai catatan, teorema ini juga berlaku untuk fungsi konveks dengan mengganti tanda pertaksamaan ”"” pada fungsi turunan
keduanya dengan ”#”, sedangkan untuk
konveks sempurna dengan mengganti tanda pertaksamaan ”P” dengan ”Q”.
Ilustrasi dari Teorema 1 diberikan pada Contoh 2 & 3 berikut ini.
Contoh 2
Misalkan diberikan fungsi
2 ,
maka OO 2 P & untuk setiap bilangan
real . Jadi, fungsi ini konkaf sempurna (strictly concave).
Contoh 3
Misalkan diberikan fungsi , maka OO # & untuk setiap
bilangan real . Jadi, merupakan fungsi konveks.
Berikut ini disampaikan cara memeriksa kekonkafan dan kekonveksan suatu fungsi banyak variabel dengan menggunakan matriks Hesse. Teorema 2 digunakan untuk memeriksa kedefinitan matriks Hesse,
sedangkan Teorema 3 untuk memeriksa kekonkafan atau kekonveksan suatu fungsi. Sebelum membahas Teorema 2 & 3, terlebih dahulu akan disampaikan mengenai matriks simetrik dan minor utama yang didefinisikan sebagai berikut.
Definisi 11 (Matriks Simetrik)
Suatu matriks + berorde / disebut
simetrik jika +A +.
(Leon 1998) Keterangan:
+A menyatakan transpos dari matriks +.
Definisi 12 (Minor Utama)
Misalkan + matriks simetrik berukuran / . Minor utama (principal minor) ke-k
dari +, dilambangkan dengan R , adalah
determinan dari anak matriks + yang
diperoleh dengan menghilangkan 2
baris dan 2 kolom terakhir dari matriks +.
(Peressini et al. 1988)
Teorema 2
Misalkan + matriks simetrik berukuran / dan misalkan R adalah minor utama
ke- dari matriks + untuk " " , maka
1. + definit positif jika dan hanya jika
R Q & untuk @
2. + definit negatif jika dan hanya jika
2 R Q & untuk @
3. jika R Q &, R Q & ..., R B Q &, R &
maka + semidefinit positif.
4. jika 2 R Q & untuk 2 , dan R & maka + semidefinit negatif. (Peressini et al. 1988) Berikut ini diberikan contoh memeriksa kedefinitan matriks Hesse dari fungsi . Misalkan adalah fungsi dari variabel
(dituliskan dengan *
) dan mempunyai turunan parsial pertama dan kedua yang kontinu, maka gradien fungsi adalah
S * T U U U U V W * W W * W X W * W Y Z Z Z Z [
dan matriks Hesse dari fungsi adalah
\] * T U U U V ^_] * ^`a_ ^ _] * ^`a^`_ ^_] * ^`a^`b ^_] * ^`_^`a X ^_] * ^`b^`a ^_] * ^`__ X ^_] * ^`b^`_ c ^_] * ^`_^`b X ^_] * ^`b_ Y Z Z Z [ @ Contoh 4
Misalkan diberikan fungsi yang didefinisikan sebagai berikut:
* 2 ,
dengan * I G .
Gradien dan matriks Hesse fungsi adalah
S * d22 e dan
\] 322 22 4.
Dengan menggunakan minor utama dari \]
yaitu
R 2 P &
R f22 22 f &,
maka 2 R Q & dan R &. Menurut
Teorema 2, maka \] semidefinit negatif.
Teorema 3
Misalkan * mempunyai turunan parsial
kedua yang kontinu pada suatu himpunan konveks buka g di G @ Jika
1. matriks Hesse \] * dari adalah
semidefinit negatif pada g, maka *
adalah fungsi konkaf pada g,
2. matriks Hesse \] * dari adalah definit
negatif pada g, maka * adalah fungsi
konkaf sempurna pada g@
(Peressini et al. 1988) Catatan:
1. Definisi Himpunan Buka
Himpunan h F G dikatakan terbuka
di G jika * I h, terdapat bilangan i Q & sehingga j I G yang memenuhi k* 2 jk P i adalah juga anggota h.
(Bartle 1976) Sebagai catatan:
Di G , k k didefinisikan
sebagai l .
2. Teorema ini juga berlaku untuk fungsi
konveks dengan mengganti ”negatif” pada kedefinitan matriks \] dengan ”positif”.
Contoh 5
Misalkan diberikan fungsi yang didefinisikan sebagai berikut
* 2 ,
dengan * I G .
Dari Contoh 4 diketahui bahwa matriks \]
semidefinit negatif, dan menurut Teorema 3 maka merupakan fungsi konkaf.
Berikut ini diberikan hubungan kekonkafan fungsi dan turunannya untuk fungsi satu variabel.
Teorema 4
(Hubungan Kekonkafan dan Turunan) Jika fungsi terdiferensialkan pada selang
N, maka merupakan fungsi konkaf pada N
jika dan hanya jika garis singgung grafik fungsi selalu terletak di bawah atau pada grafik fungsi , dengan perkataan lain
" O 2 @
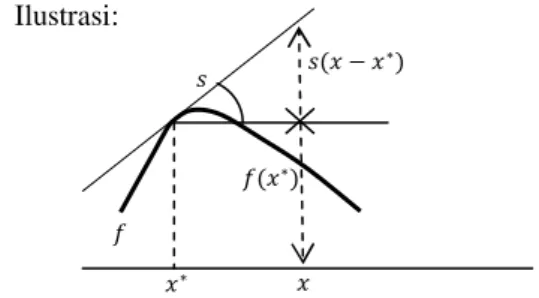
(Peressini et al. 1988) Ilustrasi:
Gambar 4 Ilustrasi fungsi konkaf pada Teorema 4.
Berikut ini diberikan hubungan antara fungsi linear sesepenggal dengan fungsi konkaf / konveks.
Definisi 13 (Fungsi Linear Sesepenggal) Fungsi linear sesepenggal (piecewise linear) merupakan fungsi yang terdiri atas
sepenggal-sepenggal fungsi linear.
(Wikipedia 2009)
Contoh 6 (Fungsi Linear Sesepenggal) Misalkan diberikan fungsi dengan
m : n " " n P 2 : n Q @o
Fungsi merupakan fungsi linear sesepenggal. Grafik fungsi diberikan pada gambar berikut ini.
p
p O 2
q
r
Gambar 5 Fungsi linear sesepenggal.
Teorema 5
Misalkan L G M G, dengan * s tuvw xy
z
v* 2 {v|, maka adalah fungsi konkaf. Bukti: Misalkan *8 *HI G , *} *8 2 *H, dan C*~D zv ~ *~2 {v ~ untuk • , maka *} zv *}2 {v zv *8 2 *H 2 {v Czv *82 {v D 2 Czv *H2 {v D@ Karena * s tu%w xyzv* 2 {v|, maka zv *82 {v # zv *82 {v dan zv *H2 {v # zv *H2 {v , sehingga *} Czv *82 {v D 2 zv *H2 {v # Czv *82 {v D 2 zv *H2 {v *8 2 *H . Ini berarti *8 2 *H # *8 2 *H .Jadi, * s tu%w xy
z
v* 2 {v| adalah fungsi konkaf.(Nemhauser & Wolsey 1999)
Contoh 7
(Fungsi Konkaf Linear Sesepenggal)
Misalkan diberikan fungsi dengan min€ 2; & •.
Menurut Teorema 5, merupakan fungsi konkaf. Fungsi juga merupakan fungsi linear sesepenggal. Jadi merupakan fungsi konkaf linear sesepenggal dengan
‚
n P n " " 2; & n Q @o
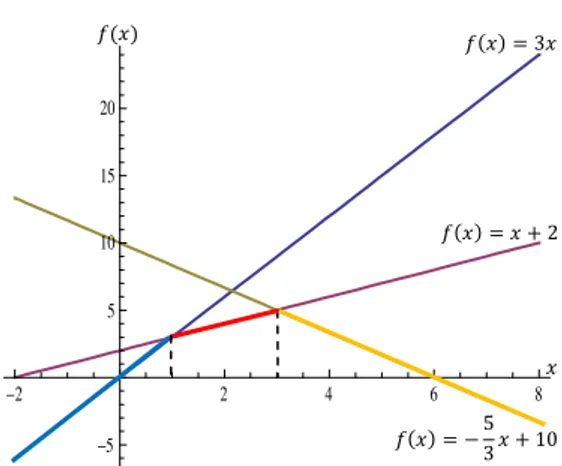
Grafik fungsi diberikan pada Gambar 6 yang ditandai dengan garis tebal.
Gambar 6 Fungsi konkaf linear sesepenggal.
Teorema 6
Misalkan L G M G, dengan *
s ƒ6%w xyzv* 2 {v|, maka adalah fungsi
konveks.
(Nemhauser & Wolsey 1999) Pembuktian Teorema 6 serupa dengan Teorema 5 dengan mengganti tanda pertaksamaan.
Contoh 8
(Fungsi Konveks Linear Sesepenggal)
Misalkan diberikan fungsi dengan maxy & & „ : : …
& 2 | untuk suatu # &.
Menurut Teorema 6, merupakan fungsi konveks. Fungsi juga merupakan fungsi linear sesepenggal. Jadi, merupakan fungsi konveks linear sesepenggal dengan
m
& 2& „ n & " Pn " " < & n Q <@o
Grafik fungsi diberikan pada Gambar 7 yang ditandai dengan garis tebal.
Gambar 7 Fungsi konveks linear sesepenggal.
2 2 4 6 8 10 20 30 2 2 4 6 8 5 5 10 15 20 1 2 3 4 5 6 7 10 20 30 40 50 60 70 2< & : 2 : & & „ : : … & 2
2.3 Dualitas Pemrograman Linear
Menurut Nemhauser & Wolsey (1999), dualitas pemrograman linear berkaitan dengan sepasang masalah PL. Salah satu dari sepasang masalah PL ini disebut masalah primal dan lainnya masalah dual.
Masalah dual dan primal berkaitan erat sedemikian sehingga solusi optimum dari salah satu masalah akan secara otomatis menghasilkan solusi optimum bagi masalah lainnya. Masalah dual adalah sebuah masalah PL yang diturunkan dari masalah PL primal dengan mengikuti kaidah-kaidah berikut: 1. untuk setiap kendala pada masalah primal
terdapat suatu variabel masalah dual; 2. untuk setiap variabel masalah primal
terdapat suatu kendala masalah dual; 3. koefisien dari sebuah variabel pada
kendala masalah primal membentuk koefisien yang terdapat pada ruas kiri kendala masalah dual yang bersesuaian dan koefisien fungsi objektif dari variabel terkait menjadi ruas kanan kendala masalah dual.
(Taha 1996)
Secara ringkas, hubungan antara variabel keputusan dan kendala pada masalah primal dan masalah dual diberikan dalam tabel berikut.
Tabel 1 Hubungan antara variabel keputusan dan kendala pada masalah primal dan masalah dual PRIMAL DUAL Minimisasi Maksimisasi Kendala # !% # & Variabel " !% " & !% tandanya tidak dibatasi Variabel # & " % Kendala " & # $ tandanya tidak dibatasi $
Keterangan: !$ dan $ menyatakan suatu bilangan
Misalkan suatu masalah PL primal dinyatakan sebagai berikut:
min 9 ()*
terhadap +* # , (P)
* # -,
maka dual dari masalah (P) adalah max † ,)‡
terhadap +)‡ " ( (D)
‡ # -,
dengan ( dan * vektor-vektor berukuran ,
dan ‡ vektor-vektor berukuran ., dan +
matriks berukuran . / .
Contoh dualitas pemrograman linear diberikan sebagai berikut.
Contoh 9 (Dualitas Pemrograman Linear)
Misalkan diberikan masalah primal sebagai berikut:
min 9 <
terhadap 2 #
2 " … (2.7)
: 2 ˆ # &, takterbatas, dan " &,
maka dual dari masalah (2.7) adalah max † p …p ˆp
terhadap p p p " <
2p p :p
p 2 p 2 p #
p # &, p " &, p takterbatas.
2.4 Integer Programming
Integer programming (IP) atau pemrograman integer adalah suatu pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Model integer programming biasanya dipilih untuk permasalahan yang variabel-variabelnya tidak dimungkinkan bertipe bilangan tidak bulat, misalnya variabel yang menyatakan banyaknya orang. Solusi integer programming dapat diselesaikan dengan banyak cara, di antaranya dengan menggunakan grafik, metode eliminasi dan substitusi. Salah satu cara yang cukup efektif untuk menyelesaikan
integer programming adalah dengan mengaplikasikan algoritme branch and bound. Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure
integer programming, dan jika hanya sebagian
yang harus berupa integer disebut mixed
integer programming. Jika IP dengan semua
variabelnya harus bernilai 0 atau 1, maka disebut 0-1 IP.
(Garfinkel & Nemhauser 1972)
2.5 Pemrograman Linear Relaksasi
Konsep pemrograman linear relaksasi atau PL-relaksasi diberikan dalam definisi berikut ini.
Definisi 14
(Pemrograman Linear Relaksasi)
Pemrograman linear relaksasi atau sering
disebut PL-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu IP dengan menghilangkan kendala integer pada setiap variabelnya.
Pada masalah maksimisasi, nilai optimum fungsi objektif PL-relaksasi lebih besar atau sama dengan nilai objektif IP, sedangkan untuk masalah minimisasi, nilai optimum fungsi objektif PL-relaksasi lebih kecil atau sama dengan nilai optimum fungsi objektif IP. (Winston 1995)
Contoh 10 (Pemrograman PL-Relaksasi)
Misalkan diberikan pemrograman integer sebagai berikut: max 9 … : terhadap " < & … " < (2.8) # & integer.
Jika kendala integer dihilangkan, maka PL-relaksasi dari masalah IP (2.8) yaitu
max 9 … :
terhadap " <
& … " <
# &.
Solusi optimum PL-relaksasi adalah
@ <, @ˆ<, dan 9 @< yang
diperoleh dengan menggunakan software LINDO 6.1 (lihat Lampiran 1). Jadi batas atas nilai objektif IP (2.8) adalah 9 @<. Daerah
yang diarsir pada Gambar 8 merupakan daerah fisibel PL-relaksasi masalah IP (2.8).
Gambar 8 Daerah fisibel untuk PL-relaksasi dari IP (2.8).
Keterangan:
= solusi optimum PL-relaksasi IP (2.8) = titik-titik fisibel bagi IP (2.8)
2.6 Metode Penalti
Metode penalti merupakan suatu metode untuk menemukan solusi hampiran dari masalah pemrograman berkendala.
Misalkan diberikan masalah minimisasi berkendala pertaksamaan
q m’%‰ tuts Šs ‹ƒu * Œ•Ž•ƒ•ƒ‘* " & ••u“ƒu$ . •ƒu* I ”
@
oSolusi masalah q dapat dihampiri dari
solusi masalah takberkendala qO yaitu
meminimumkan • * untuk * I ” , dengan • * diperoleh dari * dan kendala yang
ada dengan cara sebagai berikut:
1. • * mengandung suku “penalti” yang
akan menaikkan nilai • bila • melanggar
kendala ’$ * " &.
2. minimizer dari • * (yaitu *–—) di dekat
daerah kefisibelan dan *•— mendekati
minimizer dari masalah q .
(Peressini et al. 1988)
Fungsi objektif dari qO untuk
menghampiri masalah q adalah
• * * ˜ ’%™
x %w
*
dengan ’%™ * dinamakan fungsi penalti nilai
mutlak dan disebut parameter penalti, atau
q * * ˜J’%™ * K
x %w
dengan J’%™ * K dinamakan fungsi penalti
Courant-Beltrami asalkan dan ’ mempunyai
turunan parsial pertama yang kontinu.
2.7 Metode Gradien
Metode gradien merupakan suatu metode
untuk menemukan solusi hampiran dari masalah pemrograman takberkendala. Metode gradien ini terdiri dari beberapa metode di antaranya metode steepest descent dan metode
conjugate gradient. Pada pembahasan ini,
metode gradien yang digunakan adalah metode steepest descent. Konsep dari metode
steepest descent diberikan berikut ini.
Misalkan * adalah fungsi di G dengan turunan parsial pertama yang kontinu dan misalkan *š I G . Maka barisan steepest
descent ›* œ dengan titik awal *š untuk
meminimumkan fungsi * didefinisikan
sebagai
* ™ * 2 S C* D,
dengan adalah # & yang meminimumkan
fungsi
• 3* 2 S C* D4.
2.8 Subgradien dan Subdiferensial
Berikut ini diberikan konsep subgradien dan subdiferensial yang didefinisikan sebagai berikut.
Definisi 15 (Subgradien)
Misalkan E himpunan konveks yang
takkosong di G dan L G M G merupakan fungsi konkaf, maka vektor ž I G disebut
subgradien dari di *— I G jika untuk
semua * I G
* " *— ž * 2 *— .
(Nemhauser & Wolsey 1999) Sebagai catatan, definisi ini juga berlaku untuk fungsi konveks dengan mengganti tanda pertaksamaan ”"” dengan ”#”.
Ilustrasi:
Gambar 9 Ilustrasi subgradien pada fungsi konkaf
Definisi 16 (Subdiferensial)
Subdiferensial dari di *— adalah
himpunan semua subgradien dari di *— yang
dinyatakan dengan W *—
y
žL * " *— ž * 2 *— * I G|
.Jika W *— Ÿ , maka disebut
tersubdiferensialkan di *—.
(Nemhauser & Wolsey 1999) Berikut ini diberikan contoh subgradien dari fungsi di G .
Contoh 11
Misalkan diberikan fungsi dengan
2 .
Akan ditentukan subgradien dari fungsi di titik — . Untuk setiap I G: 2 # & ¡ 2 # & ¡ 2 2 " & ¡ 2 " 2 ¡ 2 " 2 2 ¡ " 2 2 .
Jadi, ¢ 2 adalah subgradien dari 2 di — . Ini berarti 2 I W .
Berikut ini diberikan contoh subgradien dari fungsi di G .
Contoh 12
Misalkan diberikan fungsi sebagai berikut:
* 2
dengan* I G
@
Akan ditentukan subgradien dari di titik
— 3 4. Untuk setiap I G : 2J 2 K " & ¡ 2J 2 K " & ¡ 2J2 2 2 2 2 K " & ¡ 2 2 2 " & ¡ 2 " 2 2 2 2 2 ¡ 2 " 2 2 … 2 2 … 2 ¡ 2 " 2 32…2…4Ad 22 e.
Jadi, ž 2… 2…A adalah subgradien dari * 2 di — 3 4. Ini berarti 2… 2… A I W £3 4¤.
Berikut ini diberikan cara lain untuk menentukan subgradien dari fungsi konveks atau konkaf yang terturunkan.
Teorema 7
Jika L G M G adalah fungsi konkaf dan
terturunkan di *—, maka W *— S *—
adalah gradien yang merupakan satu-satunya
subgradien. Sebaliknya, jika adalah fungsi konkaf dan W *— yž|, maka terturunkan
di *— dan ž S *— @
(Boyd & Vandenberghe 2007) Sebagai catatan, teorema tersebut juga berlaku untuk fungsi konveks.
¢ 2 —
¢
—
Berikut ini diberikan contoh subgradien
dari fungsi di G dengan fungsi
terturunkan.
Contoh 13
Misalkan diberikan fungsi dengan
2 seperti pada Contoh 11. Dari Contoh 2 telah ditunjukkan bahwa adalah fungsi konkaf. Karena O 2 selalu
ada untuk setiap I G, maka terturunkan di
setiap I G. Menurut Teorema 7, ¢ O 2 adalah subgradien dari di — , dan merupakan satu-satunya
subgradien dari di — .
Berikut ini diberikan contoh subgradien dari fungsi di G dengan fungsi yang terturunkan.
Contoh 14
Misalkan diberikan fungsi sebagai berikut:
* 2
dengan* I G seperti pada Contoh
12. Dari Contoh 5 telah ditunjukkan bahwa adalah fungsi konkaf. Karena
S * d22 e
selalu ada untuk setiap I G , maka
terturunkan di setiap I G
.
Menurut Teorema 7,ž S ¥3 4¦ d22 e 32…2…4
adalah satu-satunya subgradien dari di
— 3 4.
Pada bagian ini akan dibahas subgradien untuk salah satu jenis fungsi linear sesepenggal.
Teorema 8
Jika diberikan fungsi L G M G dengan * s tu%w xy
z
v* 2 {v| dan N *— y$L *—z
v*—2 {v|, maka zvadalah subgradien dari di *—, $ I N *— @
Bukti: Jika $ I N *— , maka *— zv*—2 {v. Akan ditunjukkan *— zv * 2 *— # * untuk $ I N *—
.
*— zv * 2 *— zv*—2 {v zv* 2 zv*— zv* 2 {v# * C‹ƒŽ•uƒ * ƒ•ƒ§ƒ•s tu%w xyz
v* 2 {v|D. Jadi — zv * 2 *— # * , * I G .Ini berarti zvI G merupakan subgradien
dari di *—, $ I N *— . Karena zvI G
merupakan subgradien dari di *—, maka
zvI W *— .
(Nemhauser & Wolsey 1999)
Sebagai catatan, teorema ini juga berlaku untuk kasus * s ƒ6%w xy
z
v* 2 {v|, dan bukti pernyataan tersebut dilakukan dengan cara serupa dengan mengganti tanda pertaksamaan ”#” dengan ”"”.Berikut ini diberikan contoh subgradien
dari fungsi linear sesepenggal.
Contoh 15
Misalkan diberikan fungsi dengan min€ 2; & •.
Akan ditentukan subgradien dan subdiferensial dari fungsi di titik — ,
— , dan — :.
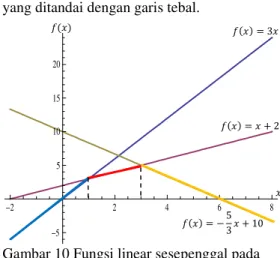
Grafik fungsi diberikan pada Gambar 10 yang ditandai dengan garis tebal.
Gambar 10 Fungsi linear sesepenggal pada Contoh 15.
Pada fungsi ini, ¨ , ! &, ¨ ,
! , dan ¨ 2;, ! &. Jika — ,
maka N — N y |. Menurut
Teorema 8, ¨ dan ¨ adalah subgradien dari di — sehingga subdiferensial dari di — adalah
W y |.
Jika — , maka N — N y |.
Menurut Teorema 8, ¨ dan ¨ 2;
adalah subgradien dari di — sehingga
subdiferensial dari di — adalah W € 2;•.
Jika — :, maka N — N : y |.
Menurut Teorema 8, ¨ 2; adalah subgradien dari di — : sehingga
subdiferensial dari di — : adalah W : €2;•. Perhatikan bahwa 2; adalah satu-satunya subgradien dari di — :.
2 2 4 6 8 5 5 10 15 20 2< &
metode yang terus dikembangkan dalam aplikasi pemrograman matematik. Sebagian besar konsep teoretis dari banyak aplikasi menggunakan metode ini, salah satunya adalah integer programming dengan melibatkan kendala yang ada. Ide dari permasalahan relaksasi Lagrange berawal dari metode penalti. Metode penalti ini merupakan suatu metode yang digunakan untuk mencari solusi hampiran dari masalah pemrograman berkendala.
Pada permasalahan relaksasi Lagrange, kendala yang direlaksasi digantikan dengan suku penalti pada fungsi objektifnya dengan melibatkan kendala yang direlaksasi dan variabel masalah dual.
Berikut ini akan disampaikan rumusan secara umum konsep dari relaksasi Lagrange, kemudian aplikasinya pada suatu contoh kuantitatif (numerik) masalah integer programming.
Misalkan diberikan masalah maksimisasi
integer programming sebagai berikut:
max (* (P)
terhadap +* " ,
©* " ª
* # - dan integer,
dengan * adalah vektor berukuran / , ,
adalah vektor berukuran . / , ª adalah
vektor berukuran « / , + merupakan matriks
berukuran . / , dan © merupakan matriks
berukuran « / . Matriks + dan matriks © merupakan matriks kendala, dengan . "
dan « " @
Untuk memformulasikan masalah relaksasi Lagrange, misalkan kendala yang akan direlaksasi (dilonggarkan) adalah +* " ,, dan
didefinisikan ¬ sebagai pengali Lagrange
yang merupakan vektor taknegatif berukuran
. / . Dengan memasukkan ¬ , 2 +* ke
dalam fungsi objektif (P) dan kendala +* " ,
dihilangkan, maka diperoleh permasalahan relaksasi Lagrange dari masalah (P) yaitu:
max ¬ (* ¬ , 2 +* -”®
terhadap ©* " ª
* # - dan integer,
dengan ¬ # -. Karena +* " , dan ¬ # -,
maka ¬ , 2 +* # -, sehingga jika kendala +* " , dilanggar (berarti +* Q ,) maka
. Suku ¬ , 2 +* merupakan suku penalti.
Selain itu, karena ¬ , 2 +* # - maka solusi
optimum dari masalah ini untuk suatu nilai
¬ # -, misalkan *—, merupakan batas atas dari
atau
¬ # (*— ¬ , 2 +*— #
(Fisher 1985). Dengan demikian, ¬ merupakan batas
atas dari .
Ada beberapa metode yang telah dikembangkan untuk mencari solusi pengali Lagrange dari permasalahan relaksasi Lagrange pada model integer programming, di antaranya metode subgradien dan metode
branch and bound (Fisher 1985).
Masalah relaksasi Lagrange memiliki keterkaitan dengan variabel masalah dual. Jika kendala +* " , pada masalah (P) direlaksasi,
maka terdapat suatu variabel dual ¬ yang
berpadanan dengan kendala tersebut. Karena
¬ , 2 +* # -, maka nilai ¬ yang baik untuk
menentukan solusi optimum dari (P) adalah ¬
yang meminimumkan ¬ . Jadi, ¬
merupakan solusi dari masalah min ¬
terhadap ¬ # -.
Berikut ini diberikan contoh numerik untuk memahami konsep relaksasi Lagrange.
Contoh 16
Misalkan diberikan permasalahan IP sebagai berikut: max … & : (1) terhadap „ : " & (2) " (3) " (4) (3.1) & " ¯" • : (5) ¯ integer, • : (6)
Jika kendala (2) direlaksasi, maka formulasi masalah relaksasi Lagrangenya menjadi
max … & : C & 2 „ : D … 2 „ & 2 & 2 : 2 : & terhadap " (3) " (4)
& " ¯" , • : (5) ¯ integer, • : (6)
dengan # &.
Sebelum menyelesaikan masalah IP (3.1) dengan menggunakan relaksasi Lagrange, maka berikut ini diberikan ilustrasi beberapa nilai pengali Lagrange yang meminimumkan fungsi objektif yang diperoleh dari hasil coba-coba, dengan solusi optimum ¯ pada Tabel 2 diperoleh dengan menggunakan
software LINDO 6.1 (lihat Lampiran 2).
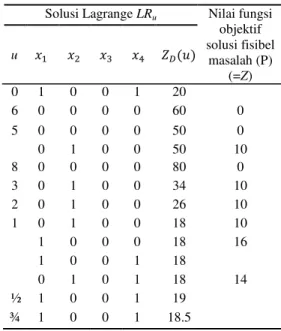
Tabel 2 Solusi Lagrange yang mungkin dan nilai variabel dualnya
Solusi Lagrange LRu Nilai fungsi
objektif solusi fisibel masalah (P) (=Z) u 0 1 0 0 1 20 6 0 0 0 0 60 0 5 0 0 0 0 50 0 0 1 0 0 50 10 8 0 0 0 0 80 0 3 0 1 0 0 34 10 2 0 1 0 0 26 10 1 0 1 0 0 18 10 1 0 0 0 18 16 1 0 0 1 18 0 1 0 1 18 14 ½ 1 0 0 1 19 ¾ 1 0 0 1 18.5
Nilai pada Tabel 2 diperoleh dari hasil substitusi nilai ¯ pada fungsi objektif (persamaan (1)).
Jika &, diperoleh solusi optimum yaitu &, dengan nilai
fungsi objektif & &. Solusi
& bukan merupakan solusi
fisibel dari masalah IP (3.1), karena nilai-nilai
¯ tersebut tidak memenuhi kendala IP (3.1)
yaitu kendala (2). Begitupun untuk , dan , solusi relaksasi Lagrange bukan solusi fisibel untuk IP (3.1).
Jika …, diperoleh solusi optimum
relaksasi Lagrange yaitu
&, dengan nilai fungsi objektif … …&, dan nilai fungsi objektif solusi fisibel
&. Hal yang sama jika „, diperoleh
solusi optimum relaksasi Lagrange yaitu
&. Dengan demikian,
dipilih yang meminimimumkan .
Dengan cara yang serupa, diperoleh nilai-nilai dan solusi fisibel untuk yang lain dengan hasilnya pada Tabel 2.
Pada Tabel 2, jika pengali Lagrange <
maka terdapat dua solusi Lagrange alternatif dengan nilai fungsi objektif < <&.
Solusi Lagrange pertama diperoleh dari output
software LINDO 6.1 (lihat Lampiran 2),
dengan solusi optimum relaksasi Lagrange
yaitu & sehingga nilai
fungsi objektif solusi fisibel &. Untuk
solusi Lagrange alternatif kedua diperoleh dari hasil coba-coba yaitu dengan menyubstitusikan semua kemungkinan nilai ¯ pada fungsi objektif yang memenuhi semua kendala. Solusi Lagrange alternatif
kedua diperoleh , &
sehingga nilai fungsi objektif solusi fisibel
&.
Pada Tabel 2, jika pengali Lagrange maka terdapat empat solusi Lagrange alternatif dengan nilai fungsi objektif
„. Solusi Lagrange pertama diperoleh dari
output software LINDO 6.1 (lihat Lampiran 2), dengan solusi optimum relaksasi Lagrange
yaitu , & sehingga
nilai fungsi objektif solusi fisibel &.
Solusi Lagrange alternatif lainnya diperoleh dari proses coba-coba juga yaitu dengan menyubstitusikan semua kemungkinan nilai ¯
pada fungsi objektif yang memenuhi semua kendala (lihat Tabel 2) dengan nilai
„. Solusi Lagrange alternatif ketiga
(lihat Tabel 2) bukan solusi fisibel untuk IP (3.1) karena nilai-nilai ¯ tersebut tidak memenuhi kendala IP (3.1).
Dari hasil coba-coba tersebut diperoleh batas nilai 18 yang merupakan nilai minimum fungsi objektif yang diperoleh dengan . Untuk meyakinkan hal tersebut, maka perlu ditunjukkan bahwa 18 adalah nilai optimum fungsi objektif dengan mengamati grafik fungsi nya. Jika semua kemungkinan solusi ¯ pada
Tabel 2 disubstitusikan pada fungsi objektif masalah relaksasi Lagrange, maka diperoleh beberapa fungsi linear dari yang diberikan pada Tabel 3.
Tabel 3 Fungsi linear dari Solusi masalah relaksasi
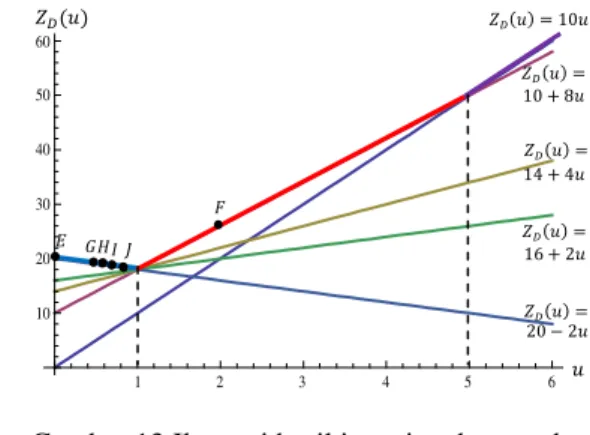
Lagrange LRu ZD(u) x1 = x2 = x3 = x4 = 0 10u x2 = 1, x1 = x3 = x4= 0 10+8u x2 = x4 = 1, x1 = x3 = 0 14+4u x1 = 1, x2 = x3 = x4 = 0 16+2u x1 = x4 = 1, x2 = x3 = 0 20-2u
Karena permasalahan ini adalah memaksimumkan fungsi objektif masalah relaksasi Lagrange, maka fungsi
merupakan maksimum dari sekumpulan fungsi linear tersebut, atau
maxy & & „ : : … & 2 |@
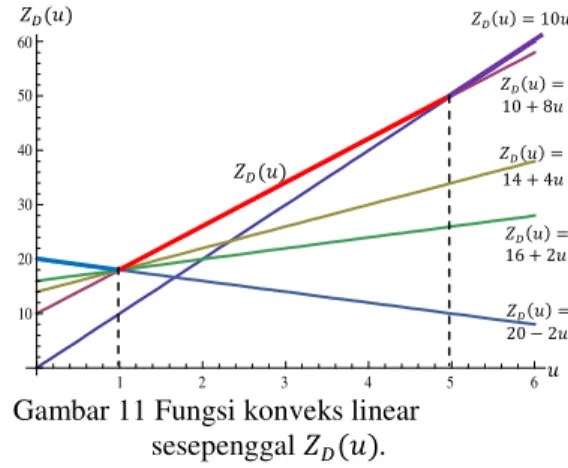
Grafik fungsi diberikan pada gambar berikut ini.
Gambar 11 Fungsi konveks linear sesepenggal .
Pada Gambar 11, Fungsi ditandai dengan garis tebal. Menurut Teorema 6, merupakan fungsi konveks. Fungsi juga terdiri atas sepenggal-sepenggal beberapa fungsi linear, sehingga fungsi merupakan fungsi linear sesepenggal. Jadi, fungsi adalah fungsi konveks linear sesepenggal dengan
m & 2& „ n & " Pn " " < & n Q <@ o
Dari Gambar 11 dapat dengan mudah terlihat bahwa fungsi minimum saat , sehingga benar bahwa nilai 18 adalah nilai minimum fungsi objektif .
Dapat ditunjukkan bahwa fungsi terturunkan pada setiap titik I G ° y <|
(lihat Lampiran 3). Nilai O untuk
I G ° y <| dapat diperoleh dari & 2
„ : , dengan ¯
merupakan solusi optimum masalah relaksasi Lagrange (-”± . Sebagai catatan, & 2
„ : diperoleh dari
kendala (2) yang direlaksasi.
Jika & P P , maka O & 2 C„ & & : D 2 . Jika
P P <, maka O & 2 C„ & & : & D „, dan jika
Q < maka O & 2 C„ & & & : & D &. Sebagai catatan, solusi
nilai-nilai ¯ tersebut dapat dilihat pada Tabel 2. Secara umum, gradien fungsi pada titik-titik terturunkan diberikan oleh +* 2 ,
(Fisher 1985).
Pengamatan ini menyarankan untuk mengaplikasikan metode gradien untuk
meminimumkan fungsi dengan
beberapa penyesuaian di titik-titik tempat fungsi takterturunkan. Di titik-titik tersebut digunakan subgradien sebagai pengganti gradien.
Konsep dari metode subgradien disampaikan berikut ini.
3.1 Metode Subgradien
Metode subgradien pada permasalahan ini digunakan untuk mencari nilai pengali Lagrange. Pada metode subgradien digunakan vektor +* 2 , yang merupakan gradien dari
fungsi , dengan * adalah solusi
optimum masalah relaksasi Lagrange LRu.
Prosedur untuk menentukan nilai pengali Lagrange dimulai dengan inisialisasi titik awal
š & dan digunakan rumus sebagai berikut:
¬ ™ s ƒ6 y& ¬ 2 , 2 +* |, (3.2)
dengan adalah step size bernilai skalar positif dan * adalah solusi optimum masalah
relaksasi Lagrange (L”± pada iterasi ke- .
Berikut ini adalah langkah-langkah penyelesaian masalah maksimisasi relaksasi Lagrange dengan metode subgradien (Freund, 2004)
• Langkah 0 (Inisialisasi)
Diawali dengan š &, dan dipilih step
size positif y |²wš.
• Langkah 1 (Penentuan subgradien)
Gradien +* 2 , ditentukan untuk setiap
iterasinya, dengan mencari solusi ¯ terlebih dahulu dari masalah relaksasi Lagrange. Jika +* 2 , &, maka iterasi
dihentikan. 1 2 3 4 5 6 10 20 30 40 50 60 & & „ : : … & 2
• Langkah 2 (Penentuan nilai )
Di setiap iterasi, digunakan persamaan (3.2) untuk memperoleh nilai . Kembali ke Langkah 1.
Pada bagian ini akan dibahas penentuan solusi nilai pengali Lagrange untuk masalah maksimisasi relaksasi Lagrange dari masalah IP (3.1) dengan menggunakan metode subgradien. Nilai-nilai tersebut ditentukan dari beberapa kasus barisan nilai . Berikut ini diberikan nilai-nilai yang diperoleh dari beberapa variasi nilai . Nilai-nilai untuk , diperlihatkan pada Tabel 4, dan rinciannya dapat dilihat di Lampiran 4 bagian 1.
Misalkan , dan misalkan š &,
maka dengan menggunakan persamaan
¬ ™ s ƒ6 y& ¬ 2 , 2 +* |
diperoleh
s ƒ6y& š2 š , 2 +*š | s ƒ6y& & 2 & 2 J„ &
& : K | s ƒ6y& |
Catatan:
, 2 +*š diberikan dari kendala yang
direlaksasi (kendala (2)) yaitu & 2
„ : , dengan solusi *
merupakan solusi optimum masalah relaksasi Lagrange yang diperoleh saat & (lihat
Lampiran 2 atau Tabel 2).
Tabel 4 Metode subgradien dengan nilai untuk semua k uk t k x1 x2 x3x4 ZD(uk) (ukTitik ,Z D(uk)) 0 0 1 1 0 0 1 20 C 1 2 1 0 1 0 0 26 D 2 0 1 1 0 0 1 20 C 3 2 1 0 1 0 0 26 D 4 0 1 1 0 0 1 20 C 5 2 1 0 1 0 0 26 D 6 0 1 0 0 1 20 C
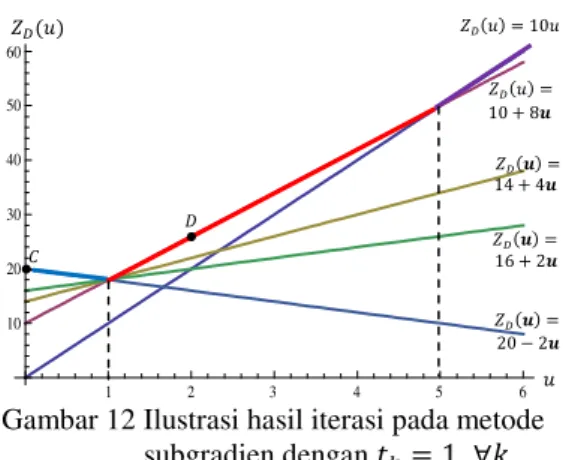
Untuk kasus pertama ini, metode subgradien menghasilkan & dan . Berikut ini diberikan ilustrasi dari hasil iterasi pada metode subgradien dengan , .
Gambar 12 Ilustrasi hasil iterasi pada metode subgradien dengan , . Karena iterasi tersebut menghasilkan nilai pengali Lagrange yang berulang-ulang, maka nilai step sizenya perlu diperbaiki.
Misalkan nilai step size yang digunakan Dengan cara serupa, dihasilkan nilai yang ditunjukkan pada Tabel 5. Rinciannya dapat dilihat pada Lampiran 4 bagian 2.
Tabel 5 Metode subgradien dengan nilai
k uk t k x1 x2 x3 x4 ZD(uk) Titik (uk, Z D(uk)) 0 0 1 1 0 0 1 20 E 1 2 ³ 0 1 0 0 26 F 2 0 ³ 1 0 0 1 20 : E 3 ³ ³„ 1 0 0 1 19 G 4 :³ ³ … 1 0 0 1 18.5 H 5 ˆ „³ ³ 1 0 0 1 18.25 I 6 < …³ 1 0 0 1 18.125 J
Solusi ¯ pada Tabel 5 dapat dilihat pada
Lampiran 2 & 5. Untuk kasus kedua ini, nilai konvergen ke 0 (lihat Lampiran 6 bagian 1) dengan nilai berurutan setengah dari nilai sebelumnya. Pada iterasi ini, iterasi pada metode subgradien cukup bagus karena nilai pengali Lagrangenya konvergen ke nilai optimum (lihat Lampiran 6 bagian 2). Berikut ini diberikan ilustrasi dari hasil iterasi pada metode subgradien dengan yang digunakan setengah dari nilai sebelumnya. 1 2 3 4 5 6 10 20 30 40 50 60 g ´ & „µ : :µ … µ & 2 µ µ µ µ &
Gambar 13 Ilustrasi hasil iterasi pada metode subgradien dengan setengah dari nilai sebelumnya.
Sekarang, akan dibahas kasus lain dari barisan nilai , yaitu sepertiga dari nilai sebelumnya, atau
.
Dengan cara serupa dihasilkan nilai-nilai yang ditunjukkan pada Tabel 6 berikut ini. Rinciannya dapat dilihat pada Lampiran 4 bagian 3.
Tabel 6 Metode subgradien dengan nilai
k uk t k x1 x2 x3 x4 ZD(uk) (uk, ZTitik D(uk) ) 0 0 1 1 0 0 1 20 K 1 2 ³ 0 1 0 0 26 L 2 0 ³¶ 1 0 0 1 20 K 3 2/9 ³ ˆ 1 0 0 1 19.55 M 4 8/27 ³„ 1 0 0 1 19.41 N 5 26/81 ³ : 1 0 0 1 19.35 O 6 80/243 ³ˆ ¶ 1 0 0 1 19.34 P 7 242/729 1 0 0 1 19.33 Q
Solusi ¯ pada Tabel 6 dapat dilihat pada Lampiran 2 & 5. Untuk kasus ketiga ini, nilai konvergen ke 0 (lihat Lampiran 6 bagian 3), akan tetapi laju kekonvergen lebih cepat dibandingkan dengan kasus kedua, karena nilai yang digunakan adalah sepertiga dari nilai sebelumnya. Pada iterasi ini, nilai pengali Lagrangenya konvergen ke (lihat Lampiran 6 bagian 4). Akan tetapi, jika
maka diperoleh solusi optimum
relaksasi Lagrange yaitu ,
& (lihat Lampiran 5) yang bukan
merupakan solusi fisibel dari masalah IP (3.1), karena solusi tersebut tidak memenuhi
kendala (2) pada IP (3.1). Dengan demikian, untuk kasus ketiga ini nilai pengali Lagrange konvergen ke titik yang bukan solusi optimumnya. Berikut ini diberikan ilustrasi dari hasil iterasi pada metode subgradien dengan yang digunakan sepertiga dari nilai sebelumnya.
Gambar 14 Ilustrasi hasil iterasi pada metode subgradien dengan dengan
sepertiga dari nilai sebelumnya. Dengan demikian, pengali Lagrange yang diperoleh dengan menggunakan metode subgradien adalah yang diperoleh bila
menggunakan kasus kedua.
Menurut Held, Wolfe, dan Crowder (1974), untuk M dan jika kedua kondisi
berikut ini dipenuhi, yaitu (i) M & dan
(ii) ·%wš %M ¸,
maka konvergen ke nilai optimal . Dengan uji deret kekonvergenan pada Tabel 5, diperoleh · %M (lihat Lampiran 6
bagian 5) yang sebenarnya melanggar kondisi kedua. Ini memperlihatkan bahwa kondisi kedua yaitu ·%wš %M ¸ merupakan syarat
cukup bagi konvergen ke nilai optimal (Fisher 1985). Terbukti dengan tidak terpenuhi kondisi kedua, iterasi pada metode subgradien diperoleh nilai pengali Lagrange yang konvergen ke nilai optimum . Nilai pada Tabel 4, 5, dan 6 diperoleh dari hasil coba-coba. Pada bagian ini diberikan rumus (Fisher 1985) yang dapat digunakan yaitu:
¬ 2 —
· ,%x% 2 · z%¯¯w *¯ @
dengan — adalah nilai fungsi objektif dari solusi fisibel (P) dan ¬ adalah nilai
fungsi objektif masalah relaksasi Lagrange dengan nilai ¬ pada iterasi ke- .
1 2 3 4 5 6 10 20 30 40 50 60 1 2 3 4 5 6 10 20 30 40 50 60 ¹ • h\N º & „ : : … & 2 & » -¼ ½¾ q & „ : : … & 2 & r
Untuk menggunakan persamaan (3.3), nilai
— diperbarui pada setiap iterasinya yaitu
dengan menyubstitusikan solusi ¯ yang
diperoleh dari masalah relaksasi Lagrange pada fungsi objektif masalah asli (P), sehingga diperoleh nilai — yang baru. Nilai skalar yang dapat digunakan adalah & P "
(Fisher 1985). Sering kali, ditentukan dengan permulaan š . Jika tidak ada peningkatan nilai pada dari iterasi ke- , maka dilakukan reduksi terhadap menjadi
¿À@ Aturan dipilih & P " telah dibuat secara empiris dengan baik, meskipun hal ini tidak menjamin bahwa persamaan (3.3) dapat memberikan kekonvergenan nilai pengali Lagrange yang optimum (Fisher 2004). Jika nilai ¬ —, maka metode yang biasa
dilakukan untuk memecahkan masalah ini adalah dengan membatasi jangkauan iterasi yang berulang-ulang (Fisher 1985). Sebagai contoh dapat dilihat pada Contoh 18.
3.2 Perbandingan Masalah Relaksasi Lagrange dengan Pemrograman Linear Relaksasi Berdasarkan Nilai Batasnya
Pada bagian ini akan dibandingkan antara solusi penyelesaian IP dengan relaksasi Lagrange dan solusi penyelesaian IP dengan PL-relaksasi dari permasalahan IP (3.1) berdasarkan nilai batasnya.
Contoh 17
Misalkan ÁÂ dinotasikan sebagai nilai optimum dari (P) dengan merelaksasi kendala
integernya atau disebut PL-relaksasi. Berikut
ini diberikan PL-relaksasi yang diperoleh dari masalah IP (3.1) dengan merelaksasi kendala
integernya yaitu: max ÁÂ … & : (1) terhadap „ : " & (2) " (3) (3.4) " (4) & " ¯" , • : (5) Solusi optimum PL-relaksasi (3.4) adalah
& & &@<, dengan nilai
fungsi objektif ÁÂ „ yang diperoleh
dengan menggunakan software LINDO 6.1 (lihat Lampiran 7). Untuk melakukan perbandingan, tuliskan terlebih dahulu bentuk standar PL dual dari masalah PL-relaksasi (3.4) tersebut.
Misalkan à •ƒuà dinotasikan sebagai
variabel dual yang berpadanan dengan
kendala (2), (3) dan (4) dan †¯ merupakan
variabel dual dari kendala ¯" , sehingga
bentuk PL dual dari masalah PL-relaksasi (3.4) adalah min & Ã Ã † † † † terhadap „ Ã † # … Ã † # & Ã † # & (3.5) : Ã † # : Ã Ã † † † † # &. Solusi optimum PL dual (3.5) adalah
à „ à † † † † &,
dengan nilai fungsi objektif 18 yang diperoleh dengan menggunakan software LINDO 6.1 (lihat Lampiran 7).
Pada permasalahan ini terdapat dua fakta. Pertama, nilai ÁÂ „ sama dengan nilai
batas atas yang diperoleh dari masalah relaksasi Lagrange (maksimisasi IP (3.1) dengan kendala (2) direlaksasi) yaitu
„@ Kedua, nilai variabel PL dual dengan
pada kendala (2) yaitu † & sama
dengan nilai variabel yang meminimumkan batas atas 18 pada masalah relaksasi Lagrange yaitu &.
Berikut ini diperlihatkan hubungan dengan Á untuk masalah maksimisasi relaksasi Lagrange. s tu›s ƒ6C(* ¬ , 2 +* Dœ, ¬ # - terhadap ©* " ª * # - dan integer; " s tu›s ƒ6C(* ¬ , 2 +* Dœ, ¬ # - terhadap ©* " ª * # -;
(PL dual) s tuys tu¬, Ī|, ¬ Ä # -
terhadap Ä© # ( 2 ¬+; s tu¬, Ī, ¬ Ä # - terhadap ¬+ Ä© # (. (PL dual) s ƒ6 (* terhadap +* " , ©* " ª * # -. ÁÂ.
Dari uraian di atas, bahwa " ÁÂ.
Dengan demikian, ketaksamaan tersebut merupakan relasi antara masalah relaksasi Lagrange dan PL-relaksasi dengan merelaksasi kendala integer. Secara logik, kondisi bisa saja ÁÂ atau P ÁÂ
(Fisher 1985). Apabila nilai lebih kecil dari nilai ÁÂ maka disebut strictly.
Nilai akan sama dengan ÁÂ jika solusi masalah relaksasi Lagrange tersebut nilainya tidak berubah meskipun dihilangkan kendala
integernya (Fisher, 1985). Terbukti pada
Contoh 17, nilai optimum ÁÂ „ sama
dengan batas atas masalah relaksasi Lagrange dengan nilai optimum „ sehingga
ÁÂ.
Relaksasi Lagrange yang baik adalah relaksasi yang dapat menyelesaikan masalah awal (P), dalam hal ini masalah IP (3.1) (Fisher 1985). Ini berarti, bahwa relaksasi Lagrange yang baik adalah relaksasi yang memberikan solusi batas atas masalah relaksasi Lagrange sama dengan batas nilai fungsi objektif masalah awal (P).
Pada pembahasan sebelumnya telah ditunjukkan bahwa batas atas masalah relaksasi Lagrange yang diperoleh dari merelaksasi kendala (2) dari masalah IP (3.1) adalah „. Batas atas masalah relaksasi
Lagrange tersebut dapat diperbaiki dengan menggunakan relaksasi Lagrange yang variabel-variabelnya bernilai integer.
3.3 Perbaikan Relaksasi
Kelebihan merelaksasi lebih dari satu kendala yaitu batas atas masalah relaksasi Lagrange yang diperoleh akan lebih mendekati atau sama dengan nilai batas solusi masalah awal (P). Berikut ini diberikan alternatif relaksasi dari masalah IP (3.1) dengan kendala yang direlaksasi lebih dari satu kendala. Sebagai ilustrasi, berikut ini diberikan contohnya.
Contoh 18
Dari permasalahan IP (3.1), jika kendala (3) dan (4) direlaksasi maka formulasi masalah relaksasi Lagrangenya menjadi:
max … & : C 2 D C 2 D … 2 & 2 & 2 : 2 terhadap „ : " & (2) & " ¯" , • : (5) (3.6) ¯ integer, • : (6) # &, dengan merupakan pengali Lagrange taknegatif. Solusi dari masalah relaksasi Lagrange (3.6) mensyaratkan bahwa semua variabel bernilai bilangan bulat nol atau satu. Sebagai catatan, jika digunakan maka akan diperoleh hasil yang berulang-ulang ke nilai &, & dan tidak
diperoleh peningkatan nilai pada dari iterasi ke- (lihat Lampiran 8), maka langkah selanjutnya adalah dilakukan reduksi terhadap menjadi . Secara empirik pada Tabel 7 ditunjukkan aplikasi metode subgradien untuk mencari nilai pengali Lagrange dengan menggunakan persamaan (3.2) dan nilai . Rincian iterasinya dapat dilihat pada Lampiran 9. Sebagai catatan, solusi optimum relaksasi Lagrange yaitu ¯ diperoleh dengan menggunakan
software LINDO 6.1 (lihat Lampiran 10).
Tabel 7 Aplikasi metode subgradien untuk perbaikan relaksasi
k u1 u2 Åk x1 x2 x3 x4 ZD(u1,u2) Z* 0 0 0 1 1 1 0 0 26 0 1 13 0 1 0 0 0 1 17 4 (fisibel untuk : k u1 u2 Åk x1 x2 x3 x4 ZD(u1,u2) Z* 2 0 0 1 1 1 0 0 26 4 3 11 0 1 1 0 1 0 16 16 (fisibel untuk …