UJI CHI SQUARE. (Uji data kategorik)

(1)

1

UJI CHI SQUARE

(Uji data kategorik)

A. Pendahuluan

Uji statistik nonparametrik ialah suatu uji statistik yang tidak memerlukan adanya

asumsi-asumsi mengenai sebaran data populasinya (belum diketahui sebaran datanya dan

tidak perlu berdistribusi normal). Oleh karenanya statistik ini juga dikemukakan sebagai

statistik bebas sebaran (tdk mensyaratkan bentuk sebaran parameter populasi, baik

normal atau tidak). Statistika non-parametrik dapat digunakan untuk menganalisis data

yang berskala Nominal atau Ordinal. Data berjenis Nominal dan Ordinal tidak menyebar

normal. Selain itu statistik ini dapat digunakan pada data yang berjumlah kecil, yakni kurang

dari 30 data.

Banyak alternatif uji statistik nonparametrik seperti yang ditunjukkan pada Lampiran.

Berbagai literatur memberikan pengelompokan kategori statistik nonparametrik dengan

berbagai cara yang berbeda. Namun demikian, secara sederhana dan berdasarkan

prosedur yang sering digunakan, uji-uji tersebut dapat dikelompokkan atas kategori

berikut:



Prosedur untuk data dari sampel tunggal



Prosedur untuk data dari dua kelompok atau lebih sampel bebas (independent)



Prosedur untuk data dari dua kelompok atau lebih sampel berhubungan

(dependent)



Korelasi peringkat dan ukuran-ukuran asosiasi lainnya

Distribusi Chi kuadrat digunakan untuk menguji homogenitas varians beberapa

populasi. Masih ada beberapa persoalan lain yang dapat diselesaikan dengan mengambil

manfaat distribusi chi-kuadrat ini, diantaranya :

1. Menguji proporsi untuk data multinom

2. Menguji kesamaan rata-rata data poisson

(2)

2

4. Menguji kesesuaian antara data hasil pengamatan dengan model distribusi dari mana

data itu diduga diambil, dan

5. Menguji model distribusi berdasarkan data hasil pengamatan.

B. Prosedur untuk Data dari Sampel Tunggal dengan Chi-Kuadrat

Akan diuji distribusi frekuensi kategori variabel motivasi hasil amatan dengan

distribusi frekuensi kategori variabel sama yang diharapkan. Hipotesis nol uji tersebut

adalah: tidak terdapat perbedaan distribusi variabel motivasi hasil amatan dengan

distribusi harapan. Prosedur ini banyak digunakan pada uji normalitas variabel.

Misalkan sebuah eksperimen menghasilkan peristiwa-peristiwa atau

kategori-kategori 𝐴

1

, 𝐴

2

, … , 𝐴

𝑘

yang saling terpisah masing-masing dengan peluang 𝑝

1

=

𝑃(𝐴

1

), 𝑝

2

= 𝑃(𝐴

2

), … . , 𝑝

𝑘

= 𝑃(𝐴

𝑘

).

Akan diuji pasangan hipotesis :

𝐻

₀

: 𝑝

_𝑖

= 𝑝

_𝑖𝑜

, 𝑖 = 1,2, … , 𝑘 dengan 𝑝

𝑖𝑜

sebuah harga yang diketahui

𝐻

𝑎

∶ 𝑝

𝑖

≠ 𝑝

𝑖𝑜

Disini, tentu saja ∑ 𝑝

𝑖

= ∑ 𝑝

𝑖𝑜

= 1

Agar mudah diingat, adanya kategori 𝐴

𝑖

, hasil pengamatan 𝑂

𝑖

dan hasil yang

diharapkan 𝐸

𝑖

, sebaiknya disusun dalam daftar sebagai berikut :

Kategori

𝐴

1

𝐴

2

...

𝐴

𝑘

Pengamatan

𝑂

₁

𝑂

₂

...

𝑂

_𝑘

Diharapkan

𝐸

1

𝐸

2

...

𝐸

𝑘

Rumus yang digunakan dalam uji tersebut adalah:



   k i i i i E E O 1 2 2 ( )



dengan keterangan:

(3)

3 i

O

= banyaknya kasus yang diamati dalam kategori i.

i

E

= banyaknya kasus yang diharapkan





k

i 1

= penjumlahan semua kategori k.

Contoh :

Dalam suatu eksperimen genetika menurut Mendell telah diketemukan bahwa semacam karakteristik diturunkan meurut perbandingan 1 : 3 : 3 : 9 untuk kategori-kategori A, B, C, dan D. Akhir-akhir ini dilakukan 160 kali pengamatan dan terdapat 5 kategori A, 23 kategori B, 32 kategori C dan 100 kategori D. Dengan menggunakan ∝= 0,05, apakah data di atas menguatkan teori genetika tersebut?

Penyelesaian :

Berdasarkan teori, diharapkan terdapat 1/16 X 160 = 10 kategori A, masing-masing 30 kategori B dan C, dan 90 kategori D. Data hasil pengamatan dan yang diharapkan adalah sebagai berikut.

Kategori A B C D

Pengamatan ( 𝑂𝑖) 5 23 32 100

Diharapkan (𝐸𝑖) 10 30 30 90

Dari rumus didapat :

𝑋2= ∑(𝑂𝑖− 𝐸𝑖) 2 𝐸𝑖 4 𝑖=4 =(5 − 10) 2 10 + (23 − 30)2 30 + (32 − 30)2 30 + (100 − 90)2 90 = 5,38

Dari tabel distribusi Chi kuadrat diperoleh 𝑋_{1−0,05;(4−1)}2 = 7,81. Sehingga pengujian memperlihatkan 𝐻0 diterima yang artinya teori menurut Mendell benar.

(4)

4 kategori O E (𝑂 − 𝐸) 2 𝐸 A 5 10 2,5 B 23 30 1,633333 C 32 30 0,133333 D 100 90 1,111111 TOTAL 160 160 5,377778

Dengan cara tersebut, maka diperoleh 2



_{= 5,377 atau 5, 38. Derajad kebebasan (db) uji}

tersebut adalah jumlah kategori (k) dikurangi 1 = 4 – 1 = 3. Pada taraf signifikasi () = 5% harga 2



tabel = 7,81. Karena

2



_{hitung <}



2

tabel, maka hipotesis nol diterima. Latihan :

Diduga bahwa 50% dari semacam kacang bentuknya keriput dan 50% lagi halus. Pengamatan dilakukan terhadap sebuah sampel acak terdiri atas 80 butir kacang dan terdapat 56 keriput sedangkan sisanya halus. Dalam taraf 0,05, dapatkah kita menyokong dugaan tersebut?

PENYELESAIAN

kategori Pengamatan Harapan (𝑂 − 𝐸)2

𝐸 Keriput 56 40 6,4 Halus 24 40 6,4 χ_ℎ𝑖𝑡2 12,8 𝜒_𝑡𝑎𝑏2 = 𝜒_0,05;12 = 3,841 Karena

𝜒ℎ𝑖𝑡2 = 12,8 > 3,84 = 𝜒𝑡𝑎𝑏2 maka H0 ditolak artinya dugaan bahwa 50% kacang keriput dan 50%

kacang halus tidak benar

(5)

5

Hollingshead (1949) meneliti pilihan kurikulum oleh pelajar di kota Elmtown ditinjau dari kelas sosialnya. Kurikulum yang ada mencakup persiapan ke PT, umum, dan perdagangan. Sedangkan kelas sosial yang ada dikelompokkan menjadi 4. Hipotesis nol yang diajukan Hollingshead adalah: proporsi siswa yang tercatat dalam ketiga kemungkinan kurikulum adalah sama untuk semua kelas sosial. Dengan

2



_{untuk k sampel independen, rumus yang digunakan} adalah sebagai berikut:



 





r i k j ij ij ij

E

O

1 1 2 2

(

)



dengan keterangan: ij O

= jumlah kasus yang diobservasi dalam baris ke i pada kolom ke j

ij E

= jumlah kasus yang diharapkan dalam baris ke i pada kolom ke j



  r i k j

1 1 _{= jumlah semua sel}

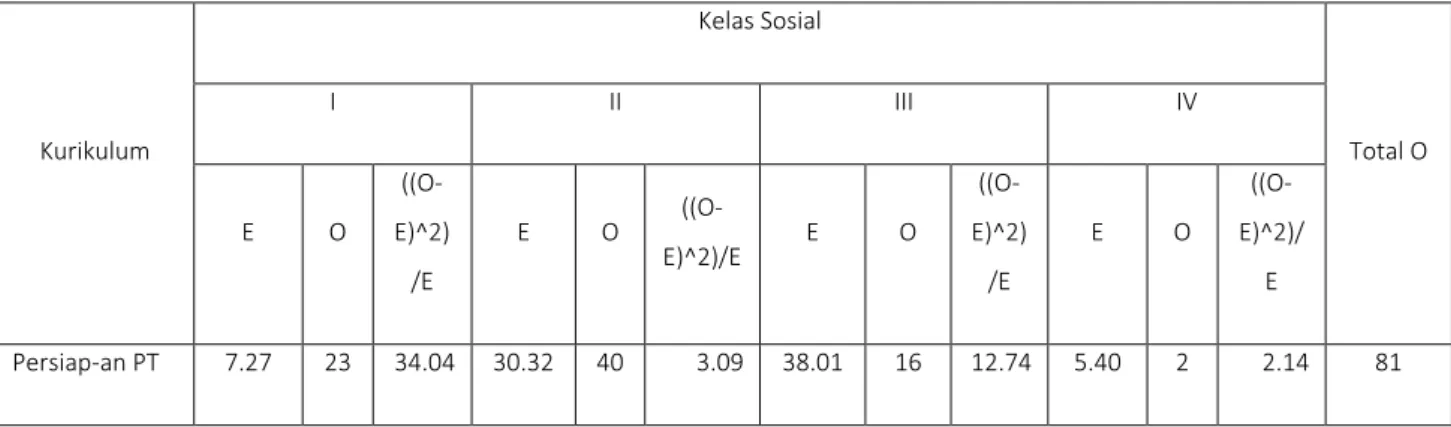
Dalam penelitian Hollingshead diperoleh data hasil observasi (O) dan data yang

diharapkan (O) seperti Tabel 2. Untuk menghitung i i i E E O 2 ) ( 

perlu dibuat kolom ((O-E)^2)/E.

Tabel 2. Uji Statistik Nonparametrik Data dari k Sampel Independen dengan Chi-Kuadrat Kurikulum Kelas Sosial Total O I II III IV E O ((O-E)^2) /E E O ((O-E)^2)/E E O ((O-E)^2) /E E O ((O-E)^2)/ E Persiap-an PT 7.27 23 34.04 30.32 40 3.09 38.01 16 12.74 5.40 2 2.14 81

(6)

6 Umum 18.58 11 3.09 77.49 75 0.08 97.13 107 1.00 13.80 14 0.00 207 Perdagangan 9.15 1 7.26 38.18 31 1.35 47.86 60 3.08 6.80 10 1.51 102 Total 35 44.40 14 6 4.52 183 16.82 26 3.65 390 2



_{= 44.40+4.52+16.82+3.65 = 69.39. Derajad kebebasan dalam uji tersebut, db = (4 - 1) * (3 -}

1) = 6. Dengan α= 5% dan db = 6 diperoleh 2



_{tabel = 12.59. Karena}



2 hitung > 2



_{tabel, maka Ho} tidak diterima.

D. Prosedur untuk Sampel Dependen

Uji McNemar dua sampel dependen dapat diperluas untuk dipakai dalam penelitian yang mempunyai lebih dari dua kelompok sampel. Perluasan ini, yakni uji Q Cochran k sampel berhubungan memberi suatu metode untuk menguji apakah tiga himpunan atau lebih mempunyai frekuensi atau proporsi saling berbeda atau tidak.

Rumus yang digunakan dalam uji Q Cochran adalah:



   



















_N i i N i i k j k j j j

L

k

G

k

Q

1 2 1 2 1 1 2

)

(

)

1 (

dengan keterangan: j

G

= jumlah keseluruhan “sukses” dalam kolom ke j

i

L

= jumlah keseluruhan “sukses” dalam barir ke i.

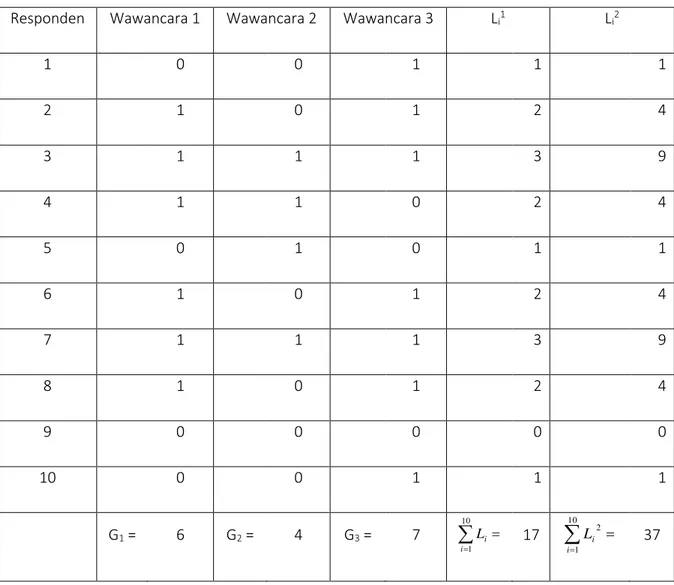
Misalkan diteliti pengaruh 3 cara wawancara terhadap kemungkinan jawaban dari 10 responden. Jika jawaban pertanyaan “ya” dikode 1 dan jawaban “tidak” dikode 0. Hipotesis nol penelitian ini berbunyi: kemungkinan jawaban “ya” adalah sama untuk ketiga jenis wawancara. Data penelitian ini ditunjukkan pada Tabel 3.

(7)

7

Tabel 3. Uji Statistik Nonparametrik Data dari k Sampel Dependen

dengan Uji Q Cochran

Responden Wawancara 1 Wawancara 2 Wawancara 3 Li1 Li2

1 0 0 1 1 1 2 1 0 1 2 4 3 1 1 1 3 9 4 1 1 0 2 4 5 0 1 0 1 1 6 1 0 1 2 4 7 1 1 1 3 9 8 1 0 1 2 4 9 0 0 0 0 0 10 0 0 1 1 1 G1 = 6 G2 = 4 G3 = 7



  10 1 i i L ₁₇



  10 1 2 i i L ₃₇

Berdasarkan tabel tersebut, maka Qdapat dihitung sbb:

37 ) 17 )( 3 ( } ) 17 ( ] ) 7 ( 3 ) 4 ( 3 ) 6 ( 3 ){[ 1 3 ( 2 2 2 2       Q Q_{= 0.180} db = k – 1 = 2

(8)

8

 = 0.05

Q_{tabel (}



2_{tabel) = 5.99.}

Q_{hitung <}Q_{tabel -> Ho diterima.}

E. Korelasi Peringkat dan Ukuran-Ukuran Asosiasi Lainnya

Koefisien kontingensi C adalah suatu ukuran kadar asosiasi atau relasi antara dua himpunan variabel. Ukuran ini berguna khususnya kalau kita hanya mempunyai data variabel dalam skala nominal. Koefisien kontingensi yang dihitung berdasarkan suatu tabel kontingensi akan mempunyai harga yang sama bagaimanapun katogori yang ada disusun dalam baris-baris dan kolom-kolomnya.

Rumus yang digunakan untuk menghitung koefisien kontingensi adalah sebagai berikut:

2 2







N

C

dimana



 





r i k j ij ij ij

E

O

1 1 2 2

(

)



Misalkan digunakan data hasil observasi pilihan kurikulum oleh pelajar di kota Elmtown ditinjau dari kelas sosialnya seperti Tabel 2. Dengan mengetahui harga

2



_{= 69.39; maka dapat} dihitung: 39 . 69 390 39 . 69   C = 0.39.

Dengan demikian berdasarkan pada data Tabel 2 diperoleh relasi atau asosiasi antara kelas sosial dan pilihan kurikulum adalah 0.39.

F. Chi square (uji independensi)

Untuk menlakukan analisis chi square kita memerlukan tabel bantu untuk mempermudah perhitungan dengan mengunakan uji chi square. Tabel yang biasa seperti pada format berikut: Sebuah contoh ilustrasi:

(9)

9 Variabel Variable dependen X2 Ya Tidak Variable independen Ya a b Tidak c d Rumus







a

b



a

c



b

d



c

d



n

bc

ad

n

X







2 2

1 /

2

Keterangan

Sel A adalah faktor yang terpapar (tidak patuh ) dan terjadi infeksi. Sel B adalah faktor yang terpapar dan tidak terjadi infeksi

Sel C adalah faktor yang tidak terpapar dan kejadian infeksi Sel D adalah faktor yang tidak terpapar dan tidak terjadi infeksi. Kasus 1.

Seorang manajer rumah sakit ingin mengetahui apakah terdapat perbedaan antara laki-laki dan perempuan dalam kedisiplinan bekerja. Kedisiplinan bekerja dalam kasus ini diukur dengan kelengkapan absensi kehadiran kerja setiap hari selama 1 bulan. Jika asumsi kedisiplinan kerja dihitung dengan jumlah tidak pernah absen dalam satu bulan dimana dalam satu bulan terdapat 26 hari kerja efektif.

Berdasarkan hasil pengamatan diperoleh data sebagai berikut:

ID Jenis kelamin Kedisiplinan ID Jenis kelamin Kedisiplinan

1 Laki-laki 24 16 Perempuan 23

(10)

10 3 Laki-laki 25 18 Perempuan 23 4 Laki-laki 26 19 Perempuan 23 5 Laki-laki 26 20 Perempuan 23 6 Laki-laki 26 21 Perempuan 23 7 Laki-laki 26 22 Perempuan 26 8 Perempuan 24 23 Perempuan 26 9 Perempuan 22 24 Laki-laki 25 10 Perempuan 23 25 Laki-laki 25 11 Perempuan 24 26 Laki-laki 26 12 Perempuan 23 27 Laki-laki 26 13 Perempuan 23 28 Laki-laki 26 14 Perempuan 23 29 Laki-laki 26 15 Perempuan 23 30 Laki-laki 26 Hint :

𝐻0: ada perbedaan antara jenis kelamin dengan kedisiplinan kerja

(11)

11

PRAKTEK UJI CHI SQUARE

Pengantar

Analisis kategorik disyaratkan skala data dalam bentuk kategorik. Sebelum masuk ke analisis lebih lanjut kita harus memahami apa dan bagaimana yang dimaksud dengan skala data. Skala data yang dikenal selama ini antara lain skala rasio, skala interval, skala ordinal dan skala nominal. Sifat yang prinsip dari sekala data adalah skala rasio dapat intervalkan, skala interval dapat di ordinalkan, skala ordinal dapat di nominalkan.

Skala rasio lebih menekankan pada hasil pengukuran dengan salah satu sifat adalah jarak antara satu pengamatan dengan pengamatan lain mempunyai jarak yang sama dan tidak memiliki nilai nol absolut. Skala interval hampir sama dengan skala rasio tetapi mempunyai nilai nol absolut. Skala ordinal memiliki sifat jarak antara satu pengamatan dengan pengamatan satunnya tidak mengharuskan memiliki jarak yang sama dan skala nominal lebih menekankan pada kaitannya mutually eksklusif (satu meniadakan yang lainnya).

Studi kasus

Seorang manajer rumah sakit ingin mengetahui apakah terdapat perbedaan antara laki-laki dan perempuan dalam kedisiplinan bekerja. Kedisiplinan bekerja dalam kasus ini diukur dengan kelengkapan absensi kehadiran kerja setiap hari selama 1 bulan. Jika asumsi kedisiplinan kerja dihitung dengan jumlah tidak pernah absen dalam satu bulan dimana dalam satu bulan terdapat 26 hari kerja efektif. Berdasarkan hasil pengamatan diperoleh data sebagai berikut:

(12)

12

ID Jenis kelamin Kedisiplinan ID Jenis kelamin Kedisiplinan

1 Laki-laki 24 16 Perempuan 23 2 Laki-laki 25 17 Perempuan 24 3 Laki-laki 25 18 Perempuan 23 4 Laki-laki 26 19 Perempuan 23 5 Laki-laki 26 20 Perempuan 23 6 Laki-laki 26 21 Perempuan 23 7 Laki-laki 26 22 Perempuan 26 8 Perempuan 24 23 Perempuan 26 9 Perempuan 22 24 Laki-laki 25 10 Perempuan 23 25 Laki-laki 25 11 Perempuan 24 26 Laki-laki 26 12 Perempuan 23 27 Laki-laki 26 13 Perempuan 23 28 Laki-laki 26 14 Perempuan 23 29 Laki-laki 26 15 Perempuan 23 30 Laki-laki 26

Pada kasus di atas didapatkan bahwa jenis skala data untuk variabel jenis kelamin adalah kategorik sedangkan pada variabel kedisiplinan skala data adala rasio.

Langkah penyelesaian

Merubah skala data dari rasio ke kategorik Langkah-langkah

1. Buka program spss, kemudian buat variabel jenis kelamin dan kedisiplinan.

2. Isikan data pada tabel tersebut ke dalam program spss. Sebelum data diisi ke dalam spss kita rubah dulu cara pemasukan data kedalam spss dimana yang jenis kelamin laki-laki kita beri kode

(13)

13

1 sedangkan perempuan kita beri kode 2. jadi yang dimasukan kedalam program spss adalah kodenya.

3. Setelah data terisi akan tampak seperti gambar berikut:

4. Setelah data dimasukan kedalam program spss. Kemudian langkah selanjutnya memberi label pada jenis kelamin yaitu dengan memberi label 1 adalah laki-laki dan 2 adalah perempuan dan merubah skala data variabel kedisiplinan menjadi 2 kategori yaitu disiplin dan tidak disiplin. Untuk merubah variabel kedisiplinan pada menu utama spss pilih Transform kemudian pilih Recode in to different variabel. Seperti terlihat pada gambar berikut:

(14)

14

Kemudian rubah kode kedisiplinan dengan 1 adalah disiplin dan 2 tidak disiplin. Seperti pada gambar berikut:

Pada variabel jenis kelamin beri label untuk 1 adalah laki-laki dan 2 adalah perempuan dan variabel kategori kedisiplinan diberi label 1 adalah disiplin dan 2 adalah tidak disiplin. Seperti pada gambar berikut:

(15)

15

5. Setelah data dikategorikan. Akan terlihat seperti gambar berikut:

6. Kemudian lakukan analisis data. Dari menu utama spss pilih Analize kemudian sub menu Deskriptif statistik, kemudian Crosstabs. Seperti pada gambar berikut:

(16)

16

7. Setelah itu masukan variabel jenis kelami kedalam kotak rows dan kategori kedisiplinan kedalam Coloums. Seperti tampak pada gambar berikut:

8. Pilih menu statistik untuk melakukan analisis atau menu yang lain sesuai dengan keinginan. Pada menu statistik pilih chi square dan risk.

(17)

17 9. Hasil analisis akan tampak pada gambar berikut: CROSSTABS

/TABLES=jeniskelamin BY kategorikedisiplinan /FORMAT= AVALUE TABLES

/STATISTIC=CHISQ RISK /CELLS= COUNT /COUNT ROUND CELL .

Crosstabs

[DataSet1]

Case Processing Summary

30 100,0% 0 ,0% 30 100,0%

jeniskelamin * kategori kedisiplinan

N Perc ent N Perc ent N Perc ent

Valid Mis sing Total

(18)

18

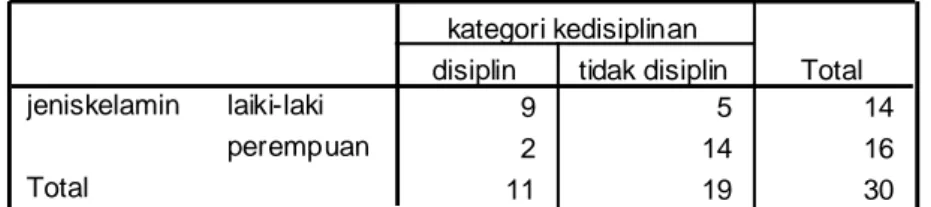
Tabel ini menujukan bahwa jumlah sampel yang dianalisis sebanyak 30 subjek dengan kategori missing variable tidak ada.

Berdasarkan analisis tabulasi silang diperoleh hasil bahwa laki-laki sebanyak 14 subjek perempuan 16 subjek sedang pada kedisiplinan 11 subjek yang tidak disiplin 19 subjek.

Analisis data chi square menunjukan bahwa nilai chi square 8.623, sedangkan nilai probabilitas signifikansi 0.003. hal ini menunjukan bahwa jika dibandingkan dengan standar normal kemaknaan hipotesis pada tingkat kemaknaan α = 0.05 dapat disimpulkan bahwa hipotesis nol ditolak. Ini memberi arti bahwa terdapat perbedaan tingkat kedisiplinan karyawan antara laki-laki dan perempuan.

jeniskelamin * kategori kedisiplinan Crosstabulation Count 9 5 14 2 14 16 11 19 30 laiki-laki perempuan jeniskelamin Total

disiplin tidak disiplin kategori kedisiplinan Total Chi-Square Tests 8,623b 1 ,003 6,537 1 ,011 9,124 1 ,003 ,007 ,005 8,335 1 ,004 30 Pearson Chi-Square

Continuity Correc tiona Likelihood Ratio Fisher's Exact Tes t Linear-by-Linear Association N of Valid Cases Value df Asymp. Sig. (2-sided) Exact Sig. (2-sided) Exact Sig. (1-sided)

Computed only for a 2x2 table a.

0 cells (,0%) have expected count less than 5. The minimum expected count is 5,13.

(19)

19

Jika dilihat dari aspek risiko jenis kelamin mempunyai risiko untuk disiplin sebesar 12,6 kali jika disbanding dengan perempuan.

Kerjakan soal latihan dibawah ini

Di suatu sekolah pada bulan Juli diadakan pemilihan murid teladan. Sebelum pemilihan pihak

sekolah ingin mengetahui apakah murid perempuan mempunyai peluang yang sama dengan

murid laki-laki untuk dapat menjadi siswa teladan. Untuk tujuan tersebut guru-guru mengambil

sample yang terdiri dari 300 siswa dan ternyata 200 orang memilih siswa laki-laki dan 100

orang memilih siswa perempuan. Bagaimanakah kesimpulan pihak sekolah ?(𝝌

_𝒕𝒂𝒃𝟐

= 𝟑, 𝟖𝟒𝟏)

Calon Siswa

Frek. Observasi

Frek. Harapan

Laki-laki

200

150 Perempuan

100

150 Jumlah

300

Risk Estimate 12,600 1,999 79,436 5,143 1,328 19,916 ,408 ,197 ,844 30 Odds Ratio for

jeniskelamin (laiki-laki / perempuan) For cohort kategori kedisiplinan = disiplin For cohort kategori kedisiplinan = tidak disiplin

N of Valid Cases

Value Lower Upper

95% Confidence Interval