7. Counting Trees. Oleh : Ade Nurhopipah. Aldous, Joan M.,Wilson, Robin J Graph and Applications. Springer: UK.

(1)

1

7. Counting Trees

Oleh : Ade Nurhopipah

Pokok Bahasan :

1. Menghitung Labelled Tree 2. Menghitung Binary Tree 3. Menghitung Chemical Tree

Sumber :

Aldous, Joan M. ,Wilson, Robin J. 2004. Graph and Applications. Springer: UK.

Pada bagian ini kita akan menghitung banyaknya tree pada graph dengan sifat tertentu. Dua masalah berkaitan hal ini diberikan sebagai berikut.

Berapa banyak sistem kanal irigasi yang menghubungkan delapan lokasi dengan tujuh kanal? Berapa banyak molekul yang memiliki formula C6H14?

Kita dapat menyelesaikan masalah ini dengan menentukan banyaknya tree yang memiliki sifat tersebut. Kasus pertama merupakan masalah menghitung banyaknya tree berlabel dengan delapan vertex, dan kasus kedua merupakan menghitung banyaknya tree tidak berlabel dengan enam vertex yang masing-masing vertex memiliki derajat empat atau kurang.

Menghitung Tree Berlabel

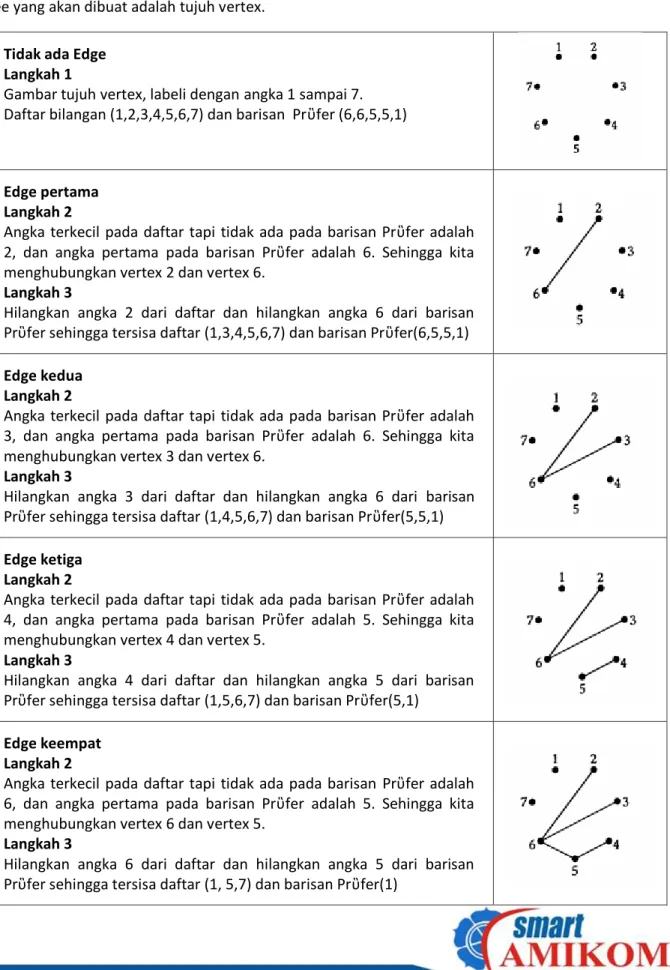
Menghitung graph berlabel lebih mudah daripada menghitung graph analognya yang tidak berlabel. Tabel 7.1 menunjukan jumlah tree berlabel dan tree tidak berlabel dengan n≤9 vertex. Pada kasus tree berlabel peningkatan jumlah n mengakibatkan meningkatnya jumlah tree berlabel dengan sangat cepat yang dikenal dengan combinatorial explosion. Gambar 7.1 menunjukan tree berlabel yang dapat dibuat dengan jumlah vertex 1, 2 dan 3.

Tabel 7.1 Jumlah tree berlabel dan tree tidak berlabel dengan vertex n≤9

(2)

2

Latihan 7.1

Gambarlah enam belas tree berlabel dengan empat buah vertex.

Petunjuk : Gambar dua buah tree tak berlabel dengan empat vertex (K1,3 dan P4) dan beri label

dengan semua cara yang mungkin.

Dengan memperhatikan Tabel 7.1, kita dapat menebak suatu rumus untuk jumlah tree berlabel dengan n titik. Ada tepat nn-2 tree berlabel yang dapat dibuat dengan n titik. Rumus ini dikenal dengan teorema Cayley. Untuk membuktikannya, kita dapat membangun korespondensi satu-satu antara tree berlabel dengan n vertex dan barisan bilangan sebanyak n-2 yang disebut barisan Prὓper. Konstruksi dari krespondensi satu-satu antara tree berlabel dan barisan Prὓper ini terdiri dari dua bagian. Pada konstruksi pertama kita membangun barisan Prὓper jika diketahui sebuah tree, dan pada konstruksi kedua kita membangun sebuah tree jika diketahui barisan Prὓper dari tree tersebut.

Pada bagian pertama, kita diberikan tree berlabel dengan n vertex, lalu kita membangun barisan Prὓper (a1,a2,a3,… an-2) di mana setiap ai adalah salah satu dari bilangan integer 1,2,3, …, n (pengulangan diperbolehkan). Konstruksi ini disajikan sebagai berikut.

Konstruksi A : Membangun barisan Prὓfer dari tree berlabel yang diberikan

Langkah 1

Temukan vertex dengan derajat 1 dan pilih vertex dengan label terkecil. Langkah 2

Perhatikan vertex yang bertetangga dengan vertex yang dipilih dan tempatkan label vertex tetangga tersebut pada barisan Prὓfer.

Langkah 3

Hilangkan vertex yang dipilih pada langkah 1 beserta edge yang insiden dengannya, maka terciptalah sebuah tree yang lebih kecil.

Ulang langkah 1-3 untuk sisa tree yang ada, teruskan sampai hanya ada dua vertex tersisa lalu berhentilah. Barisan Prὓper yang diinginkan telah terbangun.

Contoh konstruksi A

(3)

3 Tree tersebut memiliki 7 vertex, sehingga barisan Prὓper-nya memiliki lima buah angka.

Bagian pertama Langkah 1

Vertex dengan derajat 1 adalah titik 3,2,4 dan 7. Yang berlabel paling kecil adalah vertex 2.

Langkah 2 :

Vertex yang bertetangga dengan vertex 2 adalah vertex 6 sehingga angka pertama pada barisan Prὓper adalah 6. (6,?,?,?,?)

Langkah 3

Hilangkan vertex 2 dan edge 26 sehingga tersisa tree berikut.

Bagian kedua Langkah 1

Vertex dengan derajat 1 adalah titik 3,4 dan 7. Yang berlabel paling kecil adalah vertex 3.

Langkah 2 :

Vertex yang bertetangga dengan vertex 3 adalah vertex 6 sehingga angka kedua pada barisan Prὓper adalah 6. (6,6,?,?,?) Langkah 3

Bagian ketiga Langkah 1

Vertex dengan derajat 1 adalah titik 4,6 dan 7. Yang berlabel paling kecil adalah vertex 4.

Langkah 2 :

Vertex yang bertetangga dengan vertex 4 adalah vertex 5 sehingga angka ketiga pada barisan Prὓper adalah 5. (6,6,5,?,?) Langkah 3

Bagian keempat Langkah 1

Vertex dengan derajat 1 adalah titik 6 dan 7. Yang berlabel paling kecil adalah vertex 6.

Langkah 2 :

Vertex yang bertetangga dengan vertex 6 adalah vertex 5 sehingga angka keempat pada barisan Prὓper adalah 5. (6,6,5,5,?)

Langkah 3

(4)

4

Bagian kelima Langkah 1

Vertex dengan derajat 1 adalah titik 5 dan 7. Yang berlabel paling kecil adalah vertex 5.

Langkah 2

Vertex yang bertetangga dengan vertex 5 adalah vertex 1 sehingga angka terakhir pada barisan Prὓper adalah 1. (6, 6,5,5,1)

Langkah 3

Kita telah mendapatkan dua vertex sehingga proses selesai dan didapatkan barisan Prὓfer yaitu (6,6,5,5,1)

Latihan 7.2

Temukan barisan Prὓfer untuk setiap tree berlabel berikut.

Pada bagian kedua, kita diberikan barisan Prὓper (a1,a2,a3,… an-2) di mana setiap ai adalah salah satu dari bilangan integer 1,2,3, …, n (pengulangan diperbolehkan), lalu kita membangun sebuah tree berlabel dengan n vertex. Konstruksi ini disajikan sebagai berikut.

Konstruksi B : Membangun tree berlabel dari barisan Prὓfer yang diberikan

Langkah 1

Gambar n vertex, beri label dari 1 sampai n. Daftar suatu bilangan dari 1 sampai n Langkah 2

Temukan dua buah angka, angka pertama merupakan angka terkecil yang ada dalam daftar namun tidak ada pada barisan Prὓfer. Angka kedua merupakan angka pertama yang ada pada barisan Prὓfer. Tambahkan edge yang menghubungkan vertex yang memiliki label kedua angka yang dipilih.

Langkah 3

Hilangkan angka pertama yang ditemukan pada langkah 2 dari daftar, dan hilangkan angka kedua yang ditemukan dari barisan Prὓfer, sehingga tersisa daftar bilangan dan barisan Prὓfer yang lebih sedikit.

Ulangi langkah 2-3 untuk sisa daftar dan barisan Prὓfer, teruskan sampai hanya ada dua angka yang tersisa dalam daftar. Hubungkan kedua vertex dengan label angka pada daftar tersebut dan berhentilah. Tree berlabel yang diinginkan telah terbangun.

(5)

5 Contoh Konstruksi B

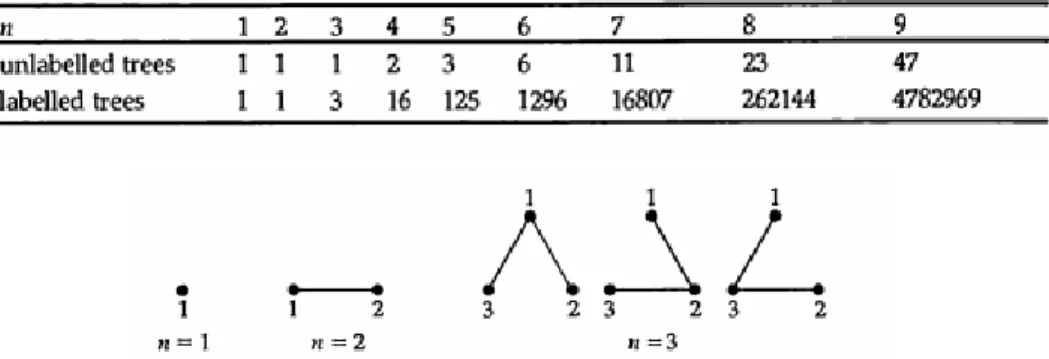
Diberikan barisan Prὓfer (6,6,5,5,1). Barisan ini memiliki lima angka, sehingga jumlah vertex pada tree yang akan dibuat adalah tujuh vertex.

Tidak ada Edge Langkah 1

Gambar tujuh vertex, labeli dengan angka 1 sampai 7. Daftar bilangan (1,2,3,4,5,6,7) dan barisan Prὓfer (6,6,5,5,1)

Edge pertama Langkah 2

Angka terkecil pada daftar tapi tidak ada pada barisan Prὓfer adalah 2, dan angka pertama pada barisan Prὓfer adalah 6. Sehingga kita menghubungkan vertex 2 dan vertex 6.

Langkah 3

Hilangkan angka 2 dari daftar dan hilangkan angka 6 dari barisan Prὓfer sehingga tersisa daftar (1,3,4,5,6,7) dan barisan Prὓfer(6,5,5,1)

Edge kedua Langkah 2

Langkah 3

Hilangkan angka 3 dari daftar dan hilangkan angka 6 dari barisan Prὓfer sehingga tersisa daftar (1,4,5,6,7) dan barisan Prὓfer(5,5,1)

Edge ketiga Langkah 2

Langkah 3

Hilangkan angka 4 dari daftar dan hilangkan angka 5 dari barisan Prὓfer sehingga tersisa daftar (1,5,6,7) dan barisan Prὓfer(5,1)

Edge keempat Langkah 2

Langkah 3

Hilangkan angka 6 dari daftar dan hilangkan angka 5 dari barisan Prὓfer sehingga tersisa daftar (1, 5,7) dan barisan Prὓfer(1)

(6)

6

Edge kelima Langkah 2

Langkah 3

Hilangkan angka 1 dari daftar dan hilangkan angka 5 dari barisan Prὓfer sehingga tersisa daftar ( 1,7) dan barisan Prὓfer()

Edge keenam

Pada daftar tersisa dua angka yaitu 1 dan 7, sehingga kita menghubungkan vertex 1 dengan vertex 7.

Proses selesai dan kita memperoleh tree berlabel yang diminta. Jika kita menggambar ulang graph yang diperoleh tanpa ada edge yang berpotongan, kita akan mendapatkan tree berikut.

Latihan 7.3

Temukan tree berlabel yang berkorespondensi dengan barisan Prὓfer berikut a. (2,1,1,3,5,5)

b. (1,1,4,4,4)

Catat bahwa barisan Prὓfer yang muncul dari tree berlabel pada contoh konstruksi A, memberikan hasil tree berlabel yang sama pada contoh konstruksi B. Hal ini terjadi secara umum. Jika kita memiliki tree berlabel, lalu kita mencari barisan Prὓfer dari tree tersebut, kemudian jika kita membangun suatu tree dari barisan Prὓfer yang telah didapatkan, maka kita akan membangun suatu tree berlabel yang sama dengan tree yang diberikan di awal. Dua konstruksi tersebut memberikan kita korespondensi satu-satu yang dibutuhkan antara tree berlabel dengan barisan Prὓfer. Korespondensi satu-satu ini dapat dipakai untuk membuktikan teorema Cayley berikut.

Teorema 7.1 : Teorema Cayley

(7)

7 Bukti

Kita mengasumsikan n≥3, karena hasil untuk n=1 dan n=2 sudah jelas.

Kita membangun korespondensi satu-satu antara himpunan tree berlabel dengan n vertex dan himpunan barisan Prὓfer dengan bentuk (a1,a2,a3,…,an-2), di mana setiap ai adalah bilangan integer 1,2,3,…, n (pengulangan diperbolehkan). Karena ada tepat n kemungkinan nilai untuk setiap bilangan integer ai, maka jumlah total dari barisan Prὓfer adalah :

n x n x … n = nn-2

(n-2 kali)

Sehingga dengan korespondensi satu-satu, antara barisan Prὓfer dengan tree yang dapat dibangun maka, jumlah tree berlabel dengan n vertex juga memiliki total nn-2.

Latihan 7.4

1. Bangunlah korespondensi satu-satu antara enam belas tree berlabel dengan empat vertex dan enam belas barisan Prὓfer-nya

2. Berapa banyak sitem kanal irigasi yang menghubungkan delapan lokasi dengan tujuh kanal?

Catatan sejarah

Pernyataan paling awal tentang teorema Cayley muncul pada artikel “A theorem on trees”, pada tahun 1889, walaupun hasil yang berkaitan pernah diterangkan sebelumnya. Namun pembuktian Cayley dianggap belum memuaskan, karena ia hanya mendiskusikannya dengan kasus n=6 dan argumennya tidak mudah digeneralisasikan untuk nilai n yang lebih besar. Sejak itu, beberapa pembuktian muncul. Pembuktian Prufer pada tahun 1918 dinilai sebagai pembuktian terbaik.

Menghitung Binary Tree

Pada bagian ini kita akan menghitung tree tak berlabel dengan menyajikan sebuah persamaan matematika untuk jumlah tree berdasarkan jumlah vertex yang diberikan dengan bantuan persamaan matematika untuk jumlah tree berdasarkan jumlah vertex lebih kecil. Persamaan ini disebut dengan hubungan recurrent. Kebanyakan masalah dengan jenis ini adalah masalah yang sangat kompleks untuk disajikan, namun pembahasan berikut tentang binary tree mengilustrasikan beberapa teknik yang dilibatkan.

Definisi 7.1

Binary tree adalah tree berakar (rooted tree) di mana jumlah edge yang turun dari vertex-nya paling banyak 2, dan cabang bagian kiri dengan cabang bagian kanan ditetapkan sebagai cabang yang berbeda.

(8)

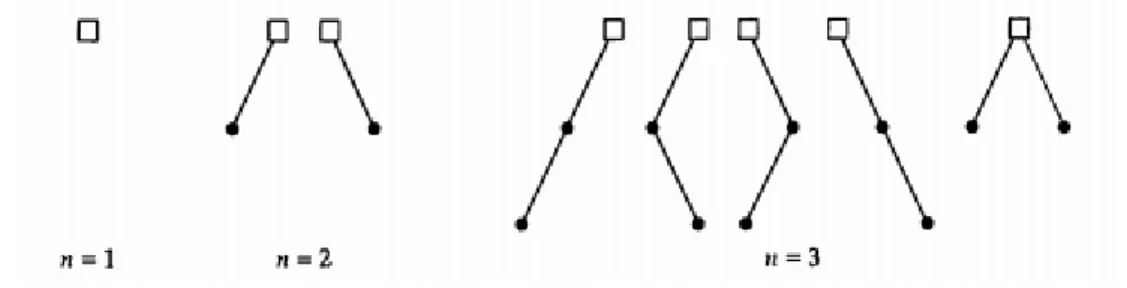
8 Gambar 7.2 menunjukan binarry tree dengan paling banyak tiga vertex (termasuk root). Root digambarkan dengan segiempat kecil.

Gambar 7.2 Binary Tree dengan n≥3

Tree yang memiliki cabang ke kanan dan cabang ke kiri merupakan binary tree yang berbeda. Sehingga ada lima binary tree yang diperoleh jika kita memiliki tiga vertex. Sedangkan pada rooted tree, secara umum hanya ada dua rooted tree yang diperoleh jika kita memiliki iga vertex seperti ditunjukan pada Gambar 7.3.

Gambar 7.3 Rooted Tree dengan n=3

Latihan 7.5

Gambarlah empat belas binary tree dengan empat vertex.

Selanjutnya muncul pertanyaan, berapa banyak binary tree jika kita diberikan n jumlah vertex tertentu? Misalnya un adalah notasi untuk jumlah binary tree dengan n vertex. Maka kita memperoleh nilai un sebagai berikut.

u1 = 1, u2 =2, u3=5 dan u4=14.

Untuk menemukan nilai un, secara umum kita membedakan binary tree sebagai berikut. 1. Trre yang memiliki cabang dari root ke sebelah kiri

2. Tree yang memiliki cabang dari root ke sebelah kanan

3. Tree yang memiliki cabang ke sebelah kiri dan ke sebelah kanan.

Sebagai contoh untuk n=3, terdapat dua binary tree yang memilliki edge ke sebelah kiri dari root, dua binary tree yang memilliki edge ke sebelah kanan dari root, dan satu binary tree yang memiliki edge ke sebelah kiri dan ke sebelah kanan root.

Misalnya an dinotasikan dengan jumlah binary tree dengan n vertex yang memiliki root edge ke kiri, dan bn dinotasikan dengan jumlah binary tree yang memilki root edge ke kanan, dan cn dinotasikan dengan jumlah binary tree yang memiliki keduanya, maka kita mendapatkan pola sebagai berikut.

(9)

9 Untuk binary tree dengan 1 vertex a1 = 0, b1=0, c1=0, u1=1

Untuk binary tree dengan 2 vertex a2 =1, b2=1, c2=0, u2=2 Untuk binary tree dengan 3 vertex a3 = 2, b3=2, c3=1, u3=5 Untuk binary tree dengan 4 vertex a4= 5, b4=5, c4=4, u4=14 Sehingga, untuk n≥2 kita mendapatkan

un = an+bn+cn

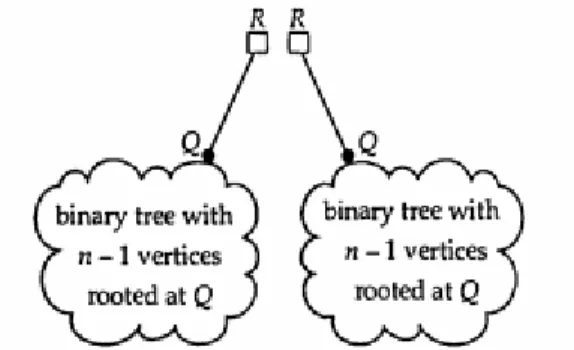
Perhatikan an dan bn. Binary tree dengan n vertex dan sebuah root memiliki satu dari bentuk sebagai berikut. Binary tree ini dapat diperoleh dari binary tree dengan n-1 vertex yang berakar di Q, dan menghubunkannya dengan root R dengan root edge RQ seperti ditunjukan pada Gambar 7.4.

Gambar 7.4 Konstruksi binary tree untuk memperoleh nilai an dan bn

Sehingga jumlah binary tree yang berakar di Q sama dengan un-1 atau,

an = un-1 , bn= un-1, untuk n≥2

Selanjutnya perhatikan nilai cn. Setiap binary tree dengan n vertex dan dua root edge pada

Gambar 7.5, dapat diperoleh dengan mengambil binary tree dengan k vertex yang berakar di P, dan binary tree dengan (n-1)-k vertex yang berakar di Q dan menghubungkan keduanya dengan root R dengan root edge RP dan RQ.

(10)

10 Karena uk sebagai binary tree yang berakar di P dan un-k-1 sebagai binary tree yang berakar di Q adalah Un-1, dan k dapat berupa angka 1,2,3,…, n-2, maka kita dapat kita mendapat kesempulan untuk n≥3 sebagai berikut.

cn = u1 un-2 + u2 un-3 + u3 un-3 + … + un-2 u1

Jika kita melakukan subtitusi nilai an , bn dan cn pada persamaan un maka kita akan

memperoleh hasil sebagai berikut.

un = 2un-1 + u1 un-2 + u2 un-3 + u3 un-3 + … + un-2 u1

Dengan menggunakan hubungan reccurent dengan n=5,6, …, kita dapat menemukan nilai u5,

u6, dan seterusnya. Sebagai contoh,

u5 = 2u4 + u1 u3 + u2 u2 + u3 u1

Latihan 7.6

Gunakan hubungan reccurent yang telah dipelajari untuk menentukan jumlah binary tree dengan enam titik.

Menghitung Chemical Tree

Kita telah mengetahui bahwa graph dapat merepresentasikan sebuah sebuah molekul, di mana vertex mewakili atom dan edge mewakili ikatan yang menghubungkan atom. Sebagai contoh ethanol dengan rumus fungsi C2H5OH dapat direpresentasikan oleh Gambar 7.6.

Gambar 7.6 Tree untuk molekul ethanol (C2H5OH)

Graph pada Gambar 7.6 tersebut, derajat dari setiap vertex secara sederhana dapat merepresentasikan valensi sebuah atom. Vertex atom karbon memiliki derajat 4, vertex oksigen memiliki derajat 2, dan vertex hidrogen memiliki derajat 1.

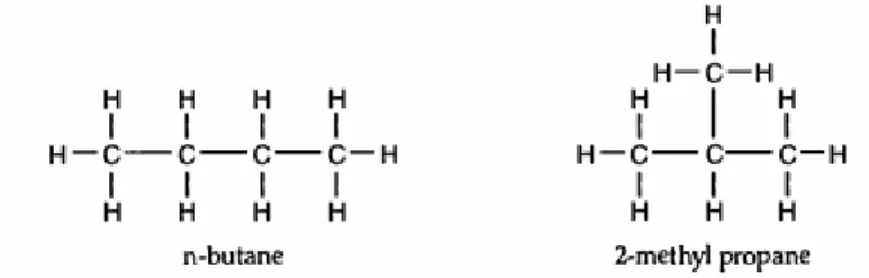
Tipe graph tersebut dapat dipakai untuk merepresentasikan susunan atom dalam molekul, graph tersebut juga dapat menjelaskan adanya isomer (molekul dengan rumus yang sama namun memiliki sifat yang berbeda). Sebagai contoh, molekul n-butana dan 2-methyl propana (secara formal disebut butana dan isobutana) keduanya memiliki rumus C4H10, namun atom di dalamnya disusun secara berbeda seperti ditunjukan pada Gambar 7.7.

(11)

11 Gambar 7.6 Tree untuk molekul n-butana dan molekul 2-methyl propana

Selanjutnya pertanyaan yang muncul adalah, apakan ada molekul lain dengan formula C4H10? Pertanyaan ini mengarah langsung pada masalah jumlah isomer (penentuan jumlah dari

molekul non-isomer dengan rumus yang diberikan). Masalah yang paling terkenal adalah menghitung jumlah alkana (paraffin) CnH2n+2. Untuk nilai n yang kecil, kita dapat mengkonstruksi

semua molekul tersebut seperti ditunjukan pada Tabel 7.2. Namun jika nilai n bertambah, masalahnya akan menjadi lebih rumit. Masalah perhitungan jumlah alkana adalah masalah perhitungan tree.

Kita dapat mensederhanakan masalah ini dengan menghilangkan semua atom hidrogen dan menyisakan graph karbon yang tidak isomorfik seperti ditunjukan pada Gambar 7.7. Graph karbon pada Gambar 7.8 adalah graph untuk n≥5.

Gambar 7.7 Membentuk graph karbon

(12)

12 Tabel 7.3 Molekul Alkana CnH2n+2 untuk n≤5

(13)

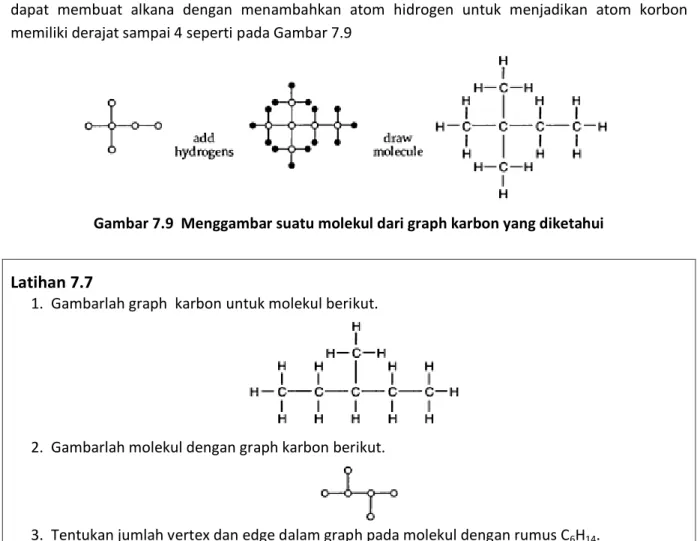
13 Setiap graph karbon memiliki struktur seperti tree dengan setiap vertex memiliki derajat titik 4 atau kurang. Sebaliknya dari suatu tree yang memiliki derajat vertex empat atau kurang kita juga dapat membuat alkana dengan menambahkan atom hidrogen untuk menjadikan atom korbon memiliki derajat sampai 4 seperti pada Gambar 7.9

Gambar 7.9 Menggambar suatu molekul dari graph karbon yang diketahui

Latihan 7.7

1. Gambarlah graph karbon untuk molekul berikut.

2. Gambarlah molekul dengan graph karbon berikut.

3. Tentukan jumlah vertex dan edge dalam graph pada molekul dengan rumus C6H14.

Dengan menggunakan daftar tree tidak berlabel dengan enam vertex, kita dapat menemukan semua alkana dengan rumus C6H14. Terdapat enam tree sepeti ditunjukan pada Gambar

7.10 berikut.

(14)

14 Lima tree pertama adalah graph karbon alkana yaitu : hexana, 2-methyl pentane, 2-methyl pentana, 2-3 dimethyl butana, dan 2-2 dimethyl butana. Tree keenam tidak dapat menjadi graph karbon karena memiliki derajat 5.

Latihan 7.8

Tentukan jumlah vertex dan edge pada graph dari semua alkana dengan rumus CnH2n+2.

Simpulkan bahwa graph tersebut merupakan tree.

Masalah umum dari menentukan jumlah alkana dengan rumus CnH2n+2 telah diselesaikan

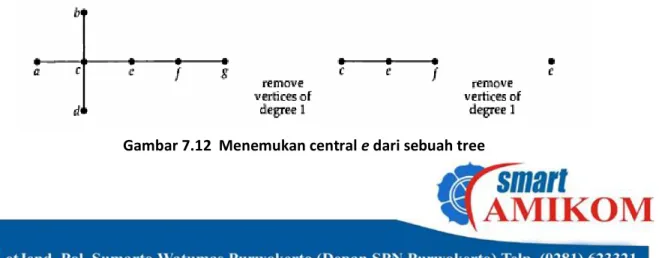
pada tahun 1870 oleh Arthur Cayley. Dalam menguraikan metode ini, kita diperkenalkan konsep “pusat” tree. Pada tree dengan bentuk simetris, kita dengan mudah dapat menentukan di mana pusatnya, misalnya tree pada Gambar 7.11. Namun bagaimanakah kita dapat menentukan pusat tree dari tree yang tidak beraturan?

Gambar 7.11 Pusat pada sebuah Tree

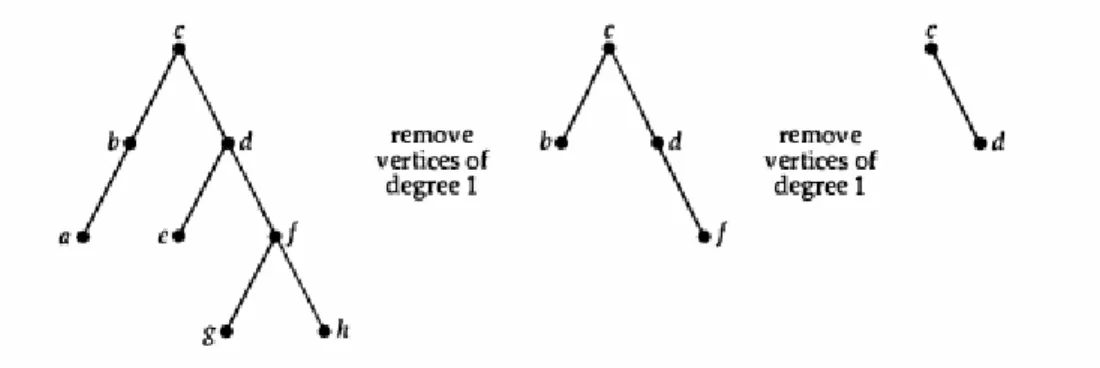
Untuk menjawab pertanyaan ini, kita ambil sebuah tree lalu kita hapus semua vertex yang memiliki derajat 1 secara bersama-sama dengan edge yang insiden dengannya. Lalu kita mengulangi proses tersebut sampai kita memperoleh pusat berupa sebuah vertex yang dinamakan dengan “center” atau dua vertex bertetangga yang disebut “bicenter”. Suatu tree dengan sebuah pusat disebut central tree dan tree dengan dua pusat disebut bicentral tree. Setiap tree merupakan satu dari jenis central tree atau bicentral tree, tapi tidak bisa menjadi keduanya. Sebagai contoh pada Gambar 7.12 menunjukan central tree dengan centre e dan Gambar 7.13 menunjukan tree dengan bicentral cd.

(15)

15 Gambar 7.13 Menemukan bicentral cd dari sebuah tree

Latihan 7.9

Klasifikasikan setiap tree dengan lima dan enam vertex sebagai central atau bicentral tree, dan posisikan center atau bicenter pada setiap kasus.

Pendekatan Cayley terhadap masalah menemukan jumlah alkana adalah dengan memperhatikan setiap molekul seperti sebuah tree dengan kemungkinan sebuah center (suatu vertex karbon dengan derajat 4) atau bicenter( dua vertex yang dihubungkan satu edge). Dengan menghapus center atau bicenter, akan dihasilkan jumlah tree yang lebih sedikit, sehingga diperoleh hubungan reccurent yang kompleks yang secara berurutan memberikan jumlah alkana dengan formula CnH2n+2. Tabel 7.3 menunjukan jumlah alkana yang berbeda dari molekul CnH2n+2 dengan n

atom karbon, untuk n=1,2,3, …,15.