14 Statistik Non Parametrik 2

(1)

STATISTIK NON PARAMETRIK (2)

14

Semester Ganjil 2018/2019 Jurusan Teknik Industri Universitas Brawijaya

(2)

Outline

21/11/18 www.debrina.lecture.ub.ac.id

2

(3)

Uji Korelasi Urutan Spearman

Statistik Non Parametrik

21/11/18

www.debrina.lecture.ub.ac.id 3

(4)

Uji Korelasi Urutan Spearman

Pertama kali

dikemukakan oleh Carl Spearman

4

(5)

Uji Korelasi Urutan Spearman

5

(6)

Contoh Soal 1

6

(7)

Solusi 1

Dengan taraf nyata 5% ujilah apakah ada korelasi antara peringkat yang diberikan oleh kedua pakar?

7

(8)

Solusi 1

8

(9)

Contoh Soal 2

M dan R, dua orang analis, merangking kualitas stok dengan n = 12 seperti pada tabel berikut.

Dengan tingkat signifikansi 5%, susunlah pengujian untuk menentukan

apakah ada kecenderungan

kecocokan pada ranking mereka.

Kode Stok Rank M Rank R M - R = d d²

A 5 4 1 1

B 8 6 2 4

C 3 1 2 4

D 10 8 2 4

E 7 9 -2 4

F 1 2 -1 1

G 9 5 4 16

H 2 7 -5 25

I 11 10 1 1

J 4 3 1 1

K 6 11.5 -5.5 30.25

L 12 11.5 0.5 0.25

∑d² 91.5

9

(10)

Solusi 2

Ada kecenderungan cocok berarti kita artikan bahwa ranking berkorelasi positif 1. H

₀

: ρ

_s

= 0

H

₁

: ρ

_s

> 0 2. α = 0,05

Berarti Z_0,05 = 1,64

3. Nilai hitung

Dengan demikian nilai statistik Z sampel

4. Daerah Kritis

Terima H₀ jika Z_sampel < Z_0,05=1,64 Tolak H₀ jika Z_sampel > Z_0,05=1,64

5. Kesimpulan

Karena Z_sampel = 2,26 > Z_0,05= 1,64, maka tolak H₀ dan terima H₁ yang artinya bahwa ada kecocokan dalam ranking M dan R

10

(11)

Uji Mann-Whitney (U Test)

Statistik Non Parametrik

21/11/18

www.debrina.lecture.ub.ac.id 11

(12)

Uji Mann-Whitney (U Test)

n Disebut juga pengujian U.

n Dikembangkan oleh H.B. Mann dan D.R. Whitney

n Digunakan untuk menguji rata-rata dari 2 sampel berukuran tidak sama

n Data ordinal

•  Uji Mann-Whitney merupakan alternatif bagi uji-t.

•  Uji Mann-Whitney digunakan untuk membandingkan dua mean populasi yang berasal dari populasi yang sama.

•  Uji Mann-Whitney juga digunakan untuk menguji apakah dua mean populasi sama atau tidak.

12

(13)

n Tahapan:

Menentukan n₁ dan n₂.

Menggabungkan kedua sampel dan

memberi urutan (ranking) tiap-tiap anggota

Menjumlahkan urutan masing-masing sampel

Menghitung statistik U

13

(14)

14

(15)

Uji Mann- Whitney (U Test)

Untuk sampel kecil

15

(16)

Jika sample size kecil (≤ 20)

21/11/18

www.debrina.lecture.ub.ac.id

16

1 1

1 2

1

2

) 1

. n ( n R

n n

U + −

+

=

2 2

1

2

) 1

. n ( n R

n n

U + −

+

=

(17)

Contoh Soal 1

17

(18)

Penyelesaian 1

18

Misalkan μ

₁

dan μ

₂

merupakan produktivitas padi dengan pupuk anorganik dan organik

1.  Hipotesis

¡  H₀ : μ₁ = μ₂ (produktivitas padi dengan pupuk anorganik dan organik adalah sama)

¡  H₁ : μ₁ ≠ μ₂(produktivitas padi dengan pupuk anorganik dan organik tidak sama atau berbeda)

2.  Tingkat signifikansi 5%

(19)

Penyelesaian 1 19

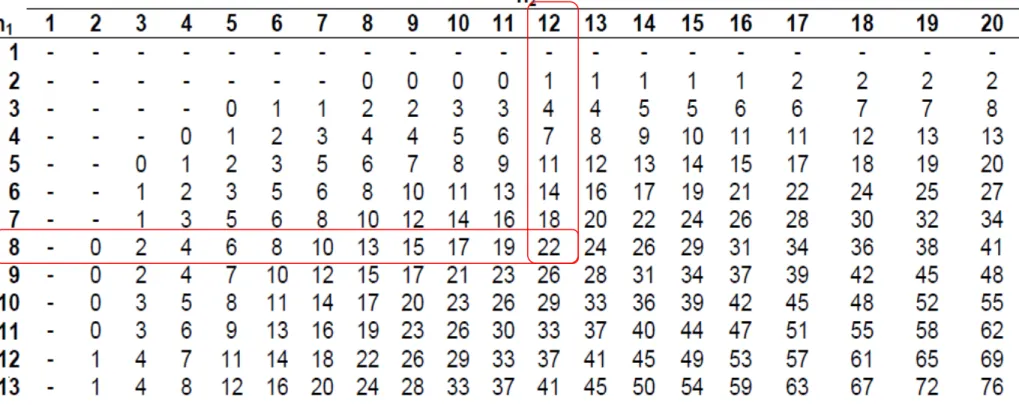
Dipakai adalah U terkecil

(20)

Tabel U / Mann-Whitney

20

21/11/18

(21)

Uji Mann- Whitney (U Test)

Untuk sampel besar

21

(22)

Jika sample size besar (> 20)

21/11/18

22

(23)

23

(24)

Contoh Soal 2 24

Berikut adalah nilai UAS Statistika 2 mahasiswa fakultas Ekonomi dan ilmu komputer

Catatan: jumlah sampel mahasiswa 20

(25)

Penyelesaian 2

25

Berdasarkan tabel tersebut, ujilah dengan taraf nyata 5%, apakah (peringkat) nilai mahasiswa fakultas ekonomi lebih besar dibanding mahasiswa ilmu komputer?

(26)

Penyelesaian 2

26

(27)

Contoh Soal 3

Untuk menguji tingkat rata- rata operasi antara perusahaan 1 dan 2. Diambil sampel random n₁ = 10 hari pada perusahaan 1 dan n₂

= 12 hari pada perusahaan 2. Jumlah n₁ + n₂ = 22, kemudian

tingkat rata-rata operasi diranking. Jumlah rank pada perusahaan 1 dan 2 berturut – turut adalah 145,5 dan 107,5. Pada α = 0,05

susunlah suatu pengujian untuk menentukan apakah tingkat rata- rata operasi perusahaan 1 lebih besar dari perusahaan 2?

27

Jawab

Misalkan μ₁ dan μ₂ merupakan tingkat rata – rata operasi perusahaan 1 dan 2 1. Hipotesis

H₀ : μ₁ = μ₂ (tingkat rata – rata operasi perusahaan 1 dan 2 sama)

H₁ : μ₁ > μ₂(tingkat rata – rata operasi perusahaan 1 lebih besar dari perusahaan 2)

2. Nilai kritis

Dengan α = 0,05, diperoleh:

Z_0,05 = 1,64

(28)

Penyelesaian 3

3. Nilai hitung

Standar deviasi populasi

Nilai statistik Z sampel

4. Kesimpulan

Karena nilai statistik

Z

_sampel

= 2,01 > Z

_0,05

= 1,64 maka tolak H

₀

.

Ini berarti tingkat rata – rata operasi perusahaan 1 lebih besar dari pada tingkat rata – rata

operasi perusahaan 2

28

(29)

Contoh Soal 4

29

(30)

Penyelesaian 4

1. Hipotesis

H₀ : μ₁ = μ₂ H₁ : μ₁ ≠ μ₂

2. Nilai kritis

Karena uji dua sisi, α = 0,10, maka harus dibagi dua menjadi (0,10/2 ) = 0,05. Sehingga Z_0,05 = 1,64

3. Nilai hitung

Standar deviasi populasi

𝜇_𝑅₁ = 𝑛₁(𝑛₁ + 𝑛₂ + 1)

2 = 14(14 + 11 + 1)

2 = 182

𝛿_𝑅 = $𝑛₁𝑛₂(𝑛₁ + 𝑛₁ + 1)

12 = $(14)(11)(14 + 11 = 1)

12 = 18,267

30

(31)

Penyelesaian 4

Nilai statistik Z

_sampel

4, Kesimpulan

Karena nilai statistik Z

_sampel

= 1,26 < Z

_0,05

= 1,64 maka terima H

₀

. Ini berarti taraf rata – rata kedua paket adalah sama.

𝑍_{𝑠𝑎𝑚𝑝𝑒𝑙} = 𝑅₁ − 𝜇_𝑅₁

𝜎_𝑅 = 205 − 182

18,267 = 1,26

Daerah penolakan H

₀

Daerah penolakan H

₀

31

14 Statistik Non Parametrik 2

STATISTIK NON PARAMETRIK (2)

Uji Korelasi Urutan Spearman

Solusi 2

Uji Mann-Whitney (U Test)

• Uji Mann-Whitney juga digunakan untuk menguji apakah dua mean populasi sama atau tidak.

Uji Mann- Whitney (U Test)

1. Hipotesis

Dipakai adalah U terkecil

Tabel U / Mann-Whitney

Contoh Soal 2 24

Berikut adalah nilai UAS Statistika 2 mahasiswa fakultas Ekonomi dan ilmu komputer

Penyelesaian 2

Jawab

Penyelesaian 3

Penyelesaian 4

Daerah penolakan H

•  Uji Mann-Whitney juga digunakan untuk menguji apakah dua mean populasi sama atau tidak.

1.  Hipotesis