Analisis Regresi

Disusun oleh:

FITRI

KURNIYAWATI

HALIMAH TUN SATDIAH

LISA RAHAYU

NUR KHASANAH

ANALISIS REGRESI

Dosen pengampu: Dr. Riswan Efendi, S. Si, M. Sc

JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SULTAN SYARIF KASIM RIAU

KATA PENGANTAR

Puji syukur penulis ucapkan kehadirat Allah Subhanahu wa Ta’ala. karena dengan rahmat, karunia, serta taufik dan hidayah-Nya penulis dapat menyelesaikan buku yang berjudul “Analisis Regresi” ini dengan baik meskipun masih banyak kekurangan didalamnya.

Penulis mengucapkan terima kasih kepada beberapa pihak yang telah banyak membantu dalam penyelesaian buku ini, diantaranya:

1. Dr. Riswan Efendi, S.Si, M.Sc., selaku dosen pengampu mata kuliah Analisis Regresi.

2. Seluruh dosen Program Studi Matematika yang telah memberikan ilmu-ilmu yang sangat bermanfaat bagi penulis.

3. Seluruh keluarga penulis yang senantiasa mendoakan dan memberikan semangat dalam menyelesaian buku ini.

4. Seluruh teman kelas IV B yang juga turut membimbing penulis.

Penulis sangat berharap buku ini dapat berguna selain memenuhi tugas mata kuliah Analisis Regresi juga dalam rangka menambah wawasan serta pengetahuan kita. Penulis menyadari sepenuhnya bahwa buku ini terdapat kekurangan dan jauh dari kata sempurna.

Oleh sebab itu, penulis berharap adanya kritik dan saran demi perbaikan di masa yang akan datang, mengingat tidak ada sesuatu yang sempurna tanpa saran yang membangun.

Semoga buku ini dapat dipahami bagi siapapun yang membacanya. Sekiranya buku yang telah disusun ini dapat berguna bagi kami penulis maupun para pembaca.

Sebelumnya penulis memohon maaf apabila terdapat kesalahan dan kata-kata yang kurang berkenan.

Pekanbaru, 28 Mei 2019

Penulis

DAFTAR ISI

KATA PENGANTAR ... i

DAFTAR ISI ... ii

BAB I PENDAHULUAN ... 1

1.1Latar Belakang ... 1

1.2Rumusan Masalah ... 1

1.3Tujuan Penulisan ... 1

1.4Manfaat Penulisan ... 1

BAB II KORELASI DAN REGRESI LINIER SEDERHANA ... 3

KORELASI 2.1 Pengeritan Korelasi ... 3

2.2 Koefesien Korelasi ... 3

2.3 Interpretasi Korelasi ... 3

2.4 Menghitung Korelasi dengan Aplikasi ... 4

REGRESI LINEAR SEDERHANA 2.5 Pengertian Regresi Linier Sederhana ... 6

2.6 Model Analisis Regresi Sederhana ... 7

2.7 Menghitung Regresi Linear dengan Aplikasi ... 8

CONTOH KASUS ... 12

BAB III METODE KUADRAT TERKECIL (OLS) DAN PENCILAN (OULIER) ... 17

3.1 Mengestimasi Parameter ... 17

Metode Ordinary Least Square (OLS) dalam Bentuk Matriks ... 19

Contoh Kasus ... 22

3.2 Pencilan (Outlier) ... 23

3.2.1 Pengaruh Pencilan ... 28

BAB IV REGRESI LINIER BERGANDA ... 29

4.1 Pengertian Regresi Linier Berganda ... 29

4.2 Model Regresi Linier Berganda ... 29

4.3 Derivasi dalam Bentuk Matriks ... 30

4.4 Contoh Kasus ... 30

BAB V REGRESI DUMMY ... 34

5.1 Pengertian Regresi Dummy ... 34

5.2 Model Regresi dengan Variabel Dummy ... 34

5.3 Prosedur Analisa ... 36

5.4 Contoh Kasus Regresi Dummy ... 36

BAB VI REGRESI LOGISTIK ... 42

6.1 Pengertian Regresi Logistik ... 42

6.1.1 Regresi Logistik Multinomial ... 43

6.1.2 Regresi Logistik Ordinal ... 48

6.1.3 Regresi Logistik Biner ... 52

BAB VII PENUTUP ... 58

7.1 Kesimpulan ... 58

7.2 Saran ... 58

DAFTAR PUSTAKA ... 59

BAB I

PENDAHULUAN

1.1 Latar Belakang

Istilah regresi dikemukakan untuk pertama kali oleh seorang antropolog dan ahli meteorology Francis Galton dala artikelnya “Family Likeness in Stature” pada tahun 1886. Ada juga sumber lain yang menyatakan istilah regresi pertama kali muncul dalam pidato Francis Galton di depan Section H of The British Associaton di Aberdeen, 1855 dan dalam makalah “Regression towards mediocrity in hereditary stature”, yang dimuat dalam Journal of The Anthropological Institute (Draper an Smith, 1992).¹

Studinya ini menghasilkan apa yang dikenal dengan hukum regresi universal tentang tingginya anggota suatu masyarakat. Hukum tersebut menyatakan bahwa distribusi tinggi suatu masyarakat tidak mengalami perubahan yang besar sekali antar generasi. Hal ini dijelaskan Galton berdasarkan fakta yang memperlihatkan adanya kecenderungan mundurnya (regress) tinggi rata- rata anak dari orang tua dengan tinggi tertentu menuju tinggi rata-rata seluruh anggota masyarakat. Ini berarti terjadi penyusutan ke arah keadaan sekarang. Tetapi sekarang istilah regresi telah diberikan makna yang jauh berbeda dari yang dimaksudkan oleh Gaston. Secara luas analisis regresi diartikan sebagai suatu analisis tentang ketergantungan suatu variabel kepada variabel lain yaitu variabel bebas dalam rangka membuat estimasi atau prediksi dari nilai rata-rata variabel tergantung dengan diketahuinya nilai variabel bebas.²

Analisis statistik yang digunakan untuk menyelesaikan masalah kausalitas atau sebab akibat adalah analisis regresi (Sembiring, 1995: 30). Metode yang sering digunakan dalam menyelesaikan masalah estimasi koefisien regresi adalah metode kuadrat terkecil, karena estimator yang didapat dari metode ini merupakan estimator yang tak bias (Neter, 1997: 37).

1.2 Rumusan Masalah

1. Apakah yang dimaksud dengan regresi linear sederhana?

2. Apakah yang dimaksud dengan OLS?

3. Apakah yang dimaksud dengan pencilan (outlier)?

4. Apakah yang dimaksud dengan regresi linear berganda?

1.3 Tujuan Penulisan

1. Menyempurnakan tugas mata kuliah analisis regresi.

2. Menjelaskan apa yang dimaksud dengan regresi linear sederhana.

3. Menjelaskan apa yang dimaksud dengan OLS dan pencilan (outlier).

4. Menjelaskan apa yang dimaksud dengan regresi linear berganda.

1.4 Manfaat Penulisan

Manfaat dari penulisan ini adalah sebagai berikut.

1 Agus Tri Basuki dan Nano Prawoto, Analisis Regresi Dalam Penelitian Ekonomi & Bisnis: Dilengkapi Aplikasi SPSS & Eviews, Ed. 1 (Cet. 1; Jakarta: Rajawali Pers, 2016), h. 1.

2 Ibid.

1. Menambah pengetahuan penulis tentang regresi linear sederhana.

2. Menambah pengetahuan penulis tentang ols dan pencilan (outlier).

3. Menambah pengetahuan penulis tentang regresi linear berganda.

4. Menambah referensi bagi mahasiswa mengenai analisis regresi serta sebagai dasar penelitian selanjutnya.

BAB II

KORELASI DAN REGRESI LINIER SEDERHANA

A.KORELASI

2.1 Pengertian Korelasi

Korelasi merupakan salah satu statistik infarensi yang akan menguji apakah dua variabel atau lebih mempunyai hubungan atau tidak. Terdapat tiga penggolongan berdasarkan jenis data dalam uji relasi yaitu sebagai berikut:

1. Data nominal: Uji Koefisien Kontingens, 2. Data ordinal: Uji Kendall, Spearman,

3. Data rasio dan interval: Uji Product Moment. ³

Kuat lemah hubungan diukur diantara jarak (range) 0 sampai 1. Korelasi mempunyai kemungkinan pengujian hipotesis dua arah. Korelasi searah jika nilai koefesiennya ditemukan positif, sebaliknya jika nilai koefesien korelasi negatif maka korelasi disebut tidak searah. Dalam korelasi sempurna tidak diperlukan lagi pengujian hipotesis, karena kedua variabel mempunyai hubungan linear yang sempurna. Artinya variabel X mempengaruhi variabel Y secara sempurna.

Jika korelasi sama dengan nol, maka tidak terdapat hubungan antara kedua variabel tersebut.

Kegunaan korelasi atau pengukuran asosiasi yaitu untuk mengukur kekuatan hubungan antar dua variabel atau lebih. Contohnya mengukur huungan antara variabel motivasi kerja dengan produktivitas, kualitas layanan dengan kepuasan pelanggan, dan lain sebagainya.

2.2 Koefesien Korelasi

Koefesien korelasi adalah pengukuran asosiasi antara dua variabel yang menunjukkan kekuatan hubungan linear dan arah hubungan dua variabel acak. Besarnya koefesien korelasi berkisar antara -1 sampai +1. Untuk memudahkan melakukan interpretasi mengenai kekuatan hubungan anntara dua variabel, penulis memberikan kriteria sebagai berikut (Sarwono: 2006):

1. 0: tidak ada korelasi antara dua variabel 2. 0 – 0.25: korelasi sangat lemah

3. 0.25 – 0.5: korelasi cukup 4. 0.5 – 0.75: korelasi kuat

5. 0.75 – 0.99: korelasi sangat kuat 6. 1: korelasi sempurna

2.3 Interpretasi Korelasi

Ada tiga penafsiran hasil anaisis korelasi, meliputi: (1) melihat kekuatan huungan dua variabel; (2) melihat signifikansi hubungan; dan (3) melihat arah hubungan.

Untuk melakukan interpretasi kekuatan hubungan antara dua variabel dilakukan dengan melihat angka koefesien korelasi hasil perhitungan dengan kriteria :

 Jika angka koefesien korelasi menunjukkan 0, maka kedua variabel tidak mempunyai hubungan.

 Jika angka koefesien korelasi mendekati 1, maka kedua variabel mempunyai hubungan semakin kuat.

3 V. Wiratna Sujarweni, Statistik Untuk Bisnis Dan Ekonomi, (Cet. 1; Yogyakarta: Pustaka Baru Press, 2015), h.

98.

 Jika angka koefesien korelasi mendekati 0, maka kedua variabel mempunyai hubungan semakin lemah.

 Jika angka koefesien korelasi menunjukkan 1, maka kedua variabel mempunyai hubungan linear sempurna positif.

 Jika angka koefesien korelasi menunjukkan -1, maka kedua variabel mempunyai hubungan linear negatif.

Interpretasi berikutnya melihat signifikansi hubungan antara dua variabel dengan didasarkan pada angka signifikansi yang dihasilkan dari penghitungan dengan ketentuan (dalam SPSS) :

 Jika angka signifikansi hasil riset < 0.05, maka hubungan kedua variabel signifikan.

 Jika angka signifikansi hasil riset > 0.05, maka hubungan kedua variabel tidak signifikan.

Interpretasi ketiga melihat arah korelasi yang dilihat dari angka koefesien korelasi. Jika koefesien positif, variabel X bernilai tinggi dan variabel Y juga tinggi maka arah korelasi searah.

Sedangkan jika koefesien korelasi negatif, variabel X bernilai tinggi sedangkan variabel Y rendah maka arah korelasi tidak searah.

Dalam kasus, misalnya hubungan antara kepuasan kerja dan komitmen terhadap organisasi sebesar 0.86 dengan angka signifikansi sebesar 0.2 akan mempunyai makna bahwa hubungan antar dua variabel tersebut sangat kuat, signifikan dan searah. Sebaliknya dalam kasus hubungan antara variabel mangkir kerja dengan produktivitas sebesar -0.86 dengan angka signifikansi sebesar 0.34, maka hubungan kedua variabel sangat kuat dan signifikan dan tidak searah.

2.4 Menghitung Korelasi dengan Aplikasi 1. Ms. Excel

Ketikkan rumus =CORREL(array1,array2)* lalu tekan tombol Enter. *array1 dan array2 dapat dilakukan dengan menandai seluruh data di kolom (mineral water (per day) dan CGPA last sem)

2. SPSS

 Pada bagian sudut kiri bawah pilih “Variable View” dan isi seperti gambar di bawah.

Gambar 1 : Variable View

 Selanjutnya pada bagian sudut kiri bawah pilih “Data View” dan masukkan data pada kolom yang sesuai.

 Lalu pilih menu Analyze-Correlate-Bivariate…

Gambar 2 : Analyze Data

 Kemudian akan muncul kotak dialog “Bivariate Correlations” dan pilih sesuai gambar dibawah dan pilih OK.

Gambar 3 : Bivariate Correlations

 Lalu akan muncul tampilan output SPSS “Correlations”.

3. Minitab

 Masukkan data ke dalam “Worksheet 1”.

Gambar 4 : Worksheet 1

 Pilih Stat-Basic Statistics-Correlation

Gambar 5 : Stat-Basic Statistics-Correlation

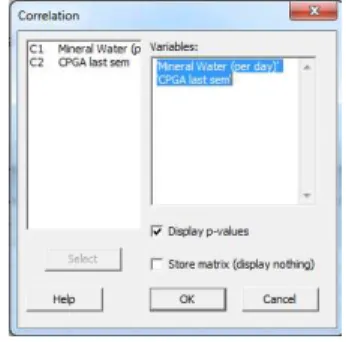
 Sehingga muncul kotak dialog “Correlation” dan isi sesuai gambar dibawah.

Gambar 6 : Correlation

*masukkan C1 dan C2 lalu klik “Select” sehingga kedua variabel tersebut muncul di kotak

“Variables”

 Selanjutnya akan muncul hasil output “Correlations” pada “Session”.

B.REGRESI LINIER SEDERHANA 2.5 Pengertian Regresi Linier Sederhana

Model regresi linier sederhana adalah model probabilistik yang menyatakan hubungan linier antara dua variabel di mana salah satu variabel dianggap memengaruhi variabel yang lain.

Variabel yang memengaruhi dinamakan variabel independen dan variabel yang dipengaruhi dinamakan variabel dependen. Sebagai contoh mungkin seorang peneliti tertarik untuk menyelidiki pengaruh (hubungan) linier dari Intelegency Quotient (IQ) terhadap hasil belajar statistika mahasiswa. Disini IQ adalah variabel independen, sedangkan hasil belajar adalah variabel dependen. Masih banyak contoh yang dapat dimodelkan dengan regresi linier sederhana, misalnya hubungan antara motivasi dan kinerja pegawai, hubungan antara usia dan tinggi badan manusia, hubungan antara pendapat dan pengeluaran rumah tangga, dan lain-lain.⁴

4 Suyono,Analisis Regresi untuk Penelitian, Ed.1, (Cet. 1; Yogyakarta: Deepublish, Februari-2018), hlm. 5.

Analisis regresi setidak-tidaknya memiliki tiga kegunaan, yaitu : ⁵

1. Untuk tujuan deskripsi dari fenomena data atau kasus yang sedang diteliti, regresi mampu mendeskripsikan fenomena data melalui terbentuknya suatu model hubungan yang bersifat numerik;

2. Untuk tujuan kontrol, regresi juga dapat digunakan untuk melakukan pengendalian (control) terhadap suatu kasus atau hal-hal yang sedang diamati melalui penggunaan model regresi yang diperoleh;

3. Sebagai prediksi, model regresi juga dapat dimanfaatkan untuk melakukan prediksi variabel terikat.

2.6 Model Analisis Regresi Sederhana

Model probabilistik untuk regresi linier sederhana adalah :

𝑌 = 𝛽0+ 𝛽1+ 𝜀 (1.1)

Dimana X adalah variabel independen, Y adalah variabel dependen, 𝛽0 dan 𝛽1 adalah parameter- parameter yang nilainya tidak diketahui yang dinamakan koefisien regresi, dan 𝜀 adalah kekeliruan atau galat acak (random error). Di sini variabel dependen diasumsikan bukan, dapat diobservasi atau diukur dengan kekeliruan yang dapat diabaikan, dan variasi dalam X dianggap dapat diabaikan dibanding dengan range dari X. Sebagai konsekuensi dari adanya suku galat acak 𝜀 maka variabel dependen Y juga merupakan variabel acak. Galat acak 𝜀 memiliki peranan yang sangat penting dalam analisis regresi. Galat acak 𝜀 digunakan untuk memodelkan variasi nilai-nilai Y untuk nilai X yang tetap. Karena kita hanya fokus pada pengaruh X terhadap Y maka akan selalu diasumsikan bahwa mean (harga harapan atau ekspektasi) galat acak 𝜀 sama dengan 0, ditulis 𝐸(𝜀) = 0. Ini berarti bahwa pengaruh semua faktor diluar X mean-nya dianggap sama dengan 0. Asumsi ini kiranya beralasan untuk mendapatkan model regresi linier sederhana yang baik.

Dengan asumsi bahwa mean galat acak sama dengan nol, maka mean variabel dependen Y dinotasikan dengan E(Y) adalah :

𝑬(𝒀) = 𝜷𝟎+ 𝜷𝟏𝑿 (1.2)

Dari rumus ini terlihat bahwa mean dari Y hanya dipengaruhi oleh X, parameter 𝛽0 dan 𝛽1

dan tidak dipengaruhi oleh faktor lain. Persamaan (1.2) merupakan persamaan garis lurus dengan gradien (kemiringan) 𝛽1 yang memotong sumbu vertikal di 𝛽0. Parameter 𝛽0 dinamakan intercept dan parameter 𝛽1 menyatakan perubahan pada mean E(Y) untuk setiap kenaikan satu satuan dalam X.

Jika (X1,Y1), (X2,Y2), ..., (Xn,Yn) adalah sampel dari pasangan variabel independen X dan variabel dependen Y yang memenuhi persamaan (1.1) maka,

𝑌1= 𝛽0+ 𝛽1𝑋1+ 𝜀1

𝑌2= 𝛽0+ 𝛽1𝑋2+ 𝜀2

5 Tri Basuki, Agus, Analisis Regresi dalam Penelitian Ekonomi & Bisnis,Ed.1, (Cet. 1; Jakarta: Rajawali Pers, 2016), hlm. 4

⋮

𝒀𝒏= 𝜷𝟎+ 𝜷𝟏𝑿𝒏+ 𝜺𝒏 (1.3)

Disini terdapat sejumlah-n galat acak 𝜀1, 𝜀2,.., 𝜀𝑛, semua galat acak ini diasumsikan memiliki mean 0.⁶

2.7 Menghitung Regresi Linear dengan Aplikasi 1. Ms. Excel

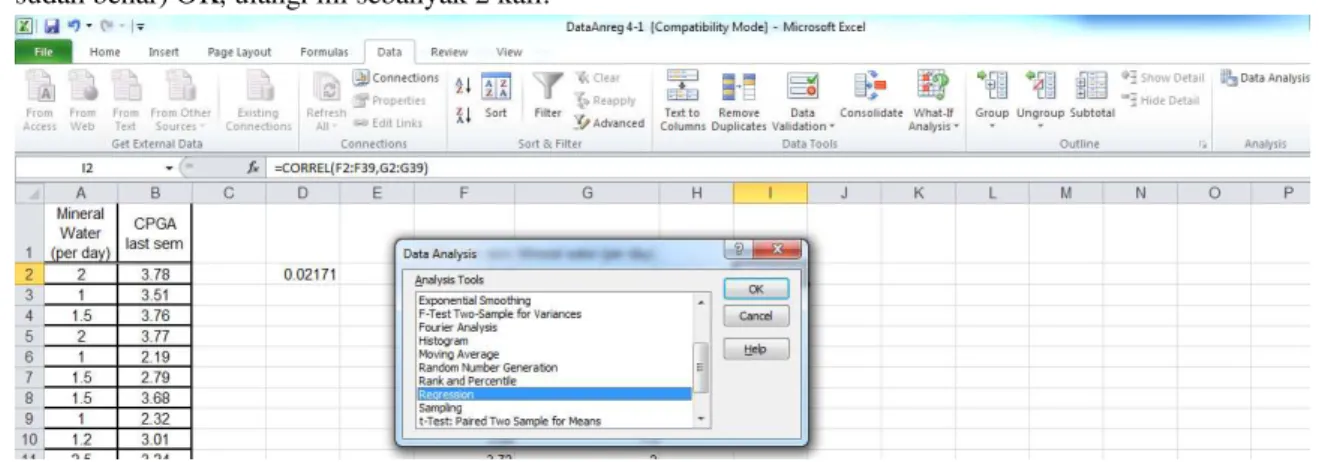
 Klik menu Data-Data Analysis. *jika Data Analysis belum muncul, aktifkan menu tersebut dengan klik menu File > Option > Add-Ins > centang Analysis Toolpak > Go > (pastikan centang sudah benar) OK, ulangi ini sebanyak 2 kali.

Gambar 7 : Data Analysis

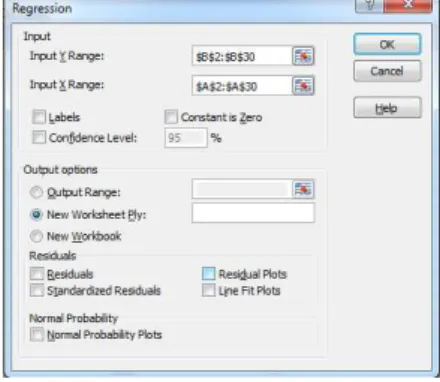
 Setelah muncul kotak dialog “Data Analysis” seperti pada gambar diatas, pilih Regression-OK. Kemudian muncul kotak dialog “Regression” dan input data sesuai variabel lalu tekan OK.

Gambar 8 : Kotak Dialog "Regression"

 Setelah itu, hasil output akan muncul di sheet sebelumnya.

2. SPSS

 Pada bagian sudut kiri bawah pilih “Variable View” dan isi seperti gambar di bawah.

6 Suyono,Analisis Regresi untuk Penelitian, Ed.1, (Cet. 1; Yogyakarta: Deepublish, Februari-2018), hlm. 5-7.

Gambar 9 : Data View

 Selanjutnya pada bagian sudut kiri bawah pilih “Data View” dan masukkan data pada kolom yang sesuai.

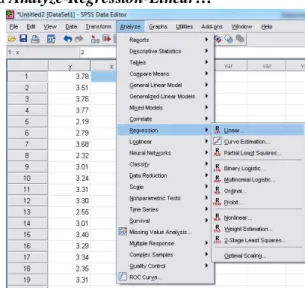
 Lalu pilih menu Analyze-Regression-Linear…

Gambar 10 : Menu Analyze

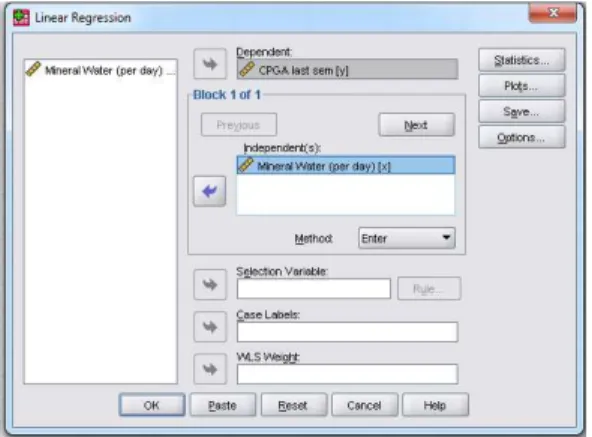
 Kemudian akan muncul kotak dialog “Linear Regressions” dan pilih sesuai gambar dibawah dan pilih OK.

Gambar 11 : Kotak Dialog "Linear Regressions"

*masukkan variabel Y ke kotak “Dependent” dan variabel X ke kotak “Independent(s)”.

 Lalu akan muncul tampilan output SPSS “Regression”.

4. Minitab

 Masukkan data ke dalam “Worksheet 1”.

Gambar 12 : Worksheet

 Pilih Stat-Basic Statistics-Regression-Regression…

Gambar 13 : Kotak Dialog "Linear Regressions"

 Sehingga muncul kotak dialog “Regression” dan isi sesuai gambar dibawah lalu tekan OK.

Gambar 14 : hasil output “Regressions

*kolom Response adalah untuk variabel terikat dan kolo Predictors adalah untuk variabel bebas.

 Selanjutnya akan muncul hasil output “Regressions:” pada “Session”.

CONTOH KASUS

1. KORELASI

(1) Hubungan antara kegiatan minum air mineral per hari dengan nilai IPK mahasiswa/i kelas IV B Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Sultan Syarif Kasim Riau.

No.

Mineral Water (per

day)

CPGA last sem

1 2 3.78

2 1 3.51

3 1.5 3.76

4 2 3.77

5 1 2.19

6 1.5 2.79

7 1.5 3.68

8 1 2.32

9 1.2 3.01

10 2.5 3.24

11 2 3.31

12 2 3.3

13 1.2 2.55

14 2.5 3.01

15 1 3.4

16 1.7 3.29

17 2 3.34

18 2 2.35

19 1.8 3.31

20 2 3.01

21 2 3

22 1.5 3.28

23 4 2.96

24 2.8 3.31

25 3 3.56

26 3 2.83

27 1.8 3.39

28 3 2.65

29 3 2.85

Tabel 1 : Data mengenai kegiatan minum air mineral per hari dengan nilai

Hasil output:

Ms. Excel:

0.02171

Hubungan Korelasi menunjukkan angka sebesar 0.02171

Mempunyai makna bahwa hubungan antar dua variabel tersebut sangat lemah dan searah.

SPSS:

Correlations

CPGA last sem Mineral Water (per day) CPGA last sem Pearson Correlation

Sig. (2-tailed) N

1 29

.022 .911 29 Mineral Water (per day) Pearson Correlation

Sig. (2-tailed) N

.022 .911 29

1 29

Tabel 2 : Hasil Output Correlationns SPSS Hubungan antara kegiatan minum air mineral per hari dengan nilai IPK:

1. Berdasarkan nilai signifikansi Sig. (2-tailed):

Dari Tabel 3 diketahui nilai Sig. (2-tailed) antara kegiatan minum air mineral per hari (X) dengan nilai IPK (Y) adalah sebesar 0.911 > 0.05 yang berarti tidak terdapat signifikan antara kegiatan minum air mineral per hari dengan nilai IPK.

2. Berdasarkan nilai r hitung (Pearson Correlations):

Diketahui r hitung untuk hubungan kegiatan minum air mineral per hari (X) dengan nilai IPK (Y) adalah sebesar 0.22 < r tabel = 0.3673, maka dapat disimpulkan bahwa tidak ada hubungan atau korelasi antar dua variabel tersebut.

Minitab:

Correlations: Mineral Water (per day), CPGA last sem

Pearson correlation of Mineral Water (per day) and CPGA last sem = 0.022 P-Value = 0.911

Hasil output diatas menunjukkan bahwa tidak ada korelasi yang signifikan antara kegiatan minum air mineral dan nilai IPK mahasiswa/i kelas IV B Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Sultan Syarif Kasim Riau.

(1) Hubungan antara kegiatan minum air mineral per hari dengan nilai IPK (berdasarkan data Raw Data Section 3).

No.

Mineral water (per

day) CGPA last sem

1 3 3.41

2 2 3.42

3 1.3 3.4

4 3 3.4

5 8 3.55

6 1.3 2.99

7 1 3.17

8 1.5 3.21

9 1.5 3.09

10 2 3.72

11 2 3.37

12 2 3.41

13 3 3.67

14 1 3.24

15 8 2.86

16 1 3.14

17 1.6 3.89

18 1.5 3.98

19 2 3.91

20 5 2.8

21 1 3.5

22 1 3.76

23 1.5 3.81

24 2 3.45

25 2 3.33

26 1.3 3.91

27 1 3.62

28 2.5 3.43

29 2 3.67

30 2 3.32

31 1.3 3.15

32 2 3.61

33 3 2.75

34 2 3.48

35 1.2 3.3

36 1 3.52

37 1.5 2.94

38 2.5 3.27

Tabel 4 : Data mengenai kegiatan minum air mineral per hari dengan nilai IPK Hasil output:

Ms. Excel:

-0.25699

Hubungan Korelasi menunjukkan angka sebesar -0.25699

Mempunyai makna bahwa hubungan antar dua variabel tersebut sangat lemah dan tidak searah.

SPSS:

Correlations

CPGA last sem Mineral Water (per day) CPGA last sem Pearson Correlation

Sig. (2-tailed) N

1 38

-.257 .119 38 Mineral Water (per day) Pearson Correlation

Sig. (2-tailed) N

-.257 .119 38

1 38

Tabel 5 : Hasil output correlations SPSS

Hubungan antara kegiatan minum air mineral per hari dengan nilai IPK:

1. Berdasarkan nilai signifikansi Sig. (2-tailed):

Dari table output diatas diketahui nilai Sig. (2-tailed) antara kegiatan minum air mineral per hari (X) dengan nilai IPK (Y) adalah sebesar 0.119 > 0.05 yang berarti tidak terdapat signifikan antara kegiatan minum air mineral per hari dengan nilai IPK.

2. Berdasarkan nilai r hitung (Pearson Correlations):

Diketahui r hitung untuk hubungan kegiatan minum air mineral per hari (X) dengan nilai IPK (Y) adalah sebesar -0.257 < r tabel = 0.3202, maka dapat disimpulkan bahwa tidak ada hubungan atau korelasi antar dua variabel tersebut.

Minitab:

Correlations: Mineral Water (per day), CPGA last sem

Pearson correlation of Mineral Water (per day) and CPGA last sem = -0.257 P-Value = 0.119

Hasil output diatas menunjukkan bahwa tidak ada korelasi yang signifikan antara kegiatan minum air mineral dan nilai IPK (berdasarkan data Raw Data Section 3).

2. REGRESI LINEAR SEDERHANA

1. Berdasrkan contoh soal nomor (1), hasil output regresi linear sederhana:

Ms. Excel:

Tabel 6 : Output Regression Statistics

Tabel 7 : ANOVA

Tabel 8 : Output Coefficients Regression

Dari informasi pada Tabel 8 didapat persamaan:

Y = 3.104 + 0123 X

SPSS:

Coefficients^a

Model Unstandardized Coefficients Standardized

Coefficients

t Sig.

B Std. Error Beta

1

(Constant)

Mineral Water (per day)

3.104 .013

.238 .112

.022 13.062 .113

.000 .911 a. Dependent Variable: CPGA last sem

Karena nilai b (angka koefesien regresi) bernilai positif, maka dapat dikatakan bahwa setiap penambahan 1% tingkat Mineral Water (X) berpengaruh positif terhadap CPGA las sem (Y).

sehingga persamaan regresinya

𝒀 = 𝟑. 𝟏𝟎𝟒 + 𝟎.𝟏𝟑𝑿 (1.4) Minitab:

Dari output diatas, persamaan yang didapat adalah:

CPGA las sem = 3.10 + 0.013 Mineral Water (per day)

Berarti kenaikan 1 liter mineral water (per day) memberikan pengaruh positif terhadap CPGA las sem sebesar 3.10.

2. Berdasarkan contoh soal (2) ), hasil output regresi linear sederhana:

Ms. Excel:

Tabel 9 : Output Regression Statistics

Tabel 10 : ANOVA

Tabel 11 : Output Coefficients Regression

Dari informasi pada Tabel 11 didapat persamaan:

Y = 3.515 – 0.050 X SPSS:

Coefficients^a

Model Unstandardized Coefficients Standardized

Coefficients

t Sig.

B Std. Error Beta

1 (Constant)

Mineral Water (per day)

3.515 -.050

.084 .031

-.257 41.660 -1.596

.000 .119 a. Dependent Variable: CPGA last sem

Karena nilai b (angka koefesien regresi) bernilai minus (-), maka dapat dikatakan bahwa Mineral Water (X) berpengaruh negatif terhadap CPGA las sem (Y). Sehingga

persamaan regresinya

𝑌 = 3.515 − 0.050𝑋 (1.5)

Minitab:

Dari output diatas, persamaan yang didapat adalah:

CPGA las sem = 3.52 – 0.0501 Mineral Water (per day)

Berarti kenaikan 1 liter mineral water (per day) memberikan pengaruh positif terhadap CPGA las sem sebesar 3.52.

BAB III

METODE KUADRAT TERKECIL (OLS) DAN PENCILAN (OUTLIER)

3.1 Mengestimasi Parameter

Estimasi model regresi linear sederhana dengan menggunakan metode kuadrat terkecil mempunyai prinsip meminimumkan jumlah kuadrat galat yang diuraikan sebagai berikut (Sembiring, 1995: 40). ⁷

Jumlah kuadrat galat adalah:





 











 ⁿ

i

i i

n

i

Q i

1

2 1 0 1

2 (   )

 . (2.1)

Untuk mengestimasi ₀ dan ₁, akan dipilih b0 dan b1 sebagai nilai estimator yang dapat meminimumkan Q.Nilai b0 dan b1 dapat ditentukan dengan mendiferensialkan persamaan (2.1) terhadap ₀ dan ₁. Sehingga didapatkan

 



     





 

 ⁿ

i

i i

n

i

ei

Q

1

1 0 0

1 2

0

) (

2  



 (2.2)

 



      





 

 ⁿ

i

i i

i n

i

ei

Q

1

1 0 1

1 2

1

) (

2  



 . (2.3)

Kemudian persamaan (2.2) dan (2.3) disamakan dengan nol, dan dengan mengganti ₀ dan

1 dengan nilai estimatornya, yaitu b0 dan b1, maka diperoleh:

0 ) (

2

1

1

0   









 n

i

i

i b b (2.4)

. 2 ( ) 0

1

1

0   











 n

i

i i

i b b

(2.5) Setelah disederhanakan, menjadi

0 ) (

1

1

0   







 n

i

i

i b b

7“Metode Kuadrat Terkecil”, eprints.uny.ac.id/1796/2/refisi.doc (diakses pada 25 mei 2019, pukul 03.12)

(2.6)















n 

i

i i

i b b

1

1

0 ) 0

( .

(2.7)

Dari persamaan (2.6) dan (2.7) dapat diperoleh persamaan normal

 

 







n 

i

n

i i

i nb b

1 1

1 0

(2.8)

  

  











n 

i

n

i i n

i i i

i b b

1 1

2 1 1

0 (2.9)

Dari persamaan (2.8), diperoleh nilai b₀:

b n b n

b n n b

b nb

n

i i n

i i

n

i i n

i i n

i

n

i i i









 









 





























1 1 1

0

1 1 0 1

1 1

1 0









 b₀ b₁

Nilai b1 dapat dicari dengan mensubstitusi nilai b0 ke dalam persamaan (2.9). Sehingga, hasilnya adalah

    

  



   











n 

i

n

i i n

i i n

i i n

i i i

i b

b n

1 n 1

2 1 1

1 1

1 )

( (2.10)



   



   



















 ⁿ

i i n

i

n

i i n

i i n

i i i

i b nb

n

1 2 1

1 1

2 1 1

1

.

   

   



















 ⁿ

i

n

i

i i i

n

i i n

i i

i n

n b

1 1 1

2 1 2

1( ( ) )

2 1 1

2

1 1

1

) (





 





 



















 _n

i i n

i i n

i

n

i i i i

i

n n b

n b n

n

i n i

i i

n

i i n

i n i

i i i

2

1 1

2

1 1 1

1



 



 



















 



 









 . (2.11)

Secara notasi, persamaan (2.11) dapat ditulis dalam bentuk

n n

n

n n

b n

n

i i n

i i n

i n i

i i

n

i i n

i i n

i i n

i i n

i i n

i n i

i i i

2

1 2

1 2

1 1

2

1 1 1

1 1

1 1

1



 



 





 



 





 



 



































 











 























2 2

1 2

1 2

1 1

2

2 1 1 1

1 1

1 1

1

n n n

n

n n n

b n

n

i i n

i i n

i n i

i i

n

i i n

i i n

i i n

i i n

i i n

i n i

i i i



 



 





 



 





 



 



































 











 























2

1 1

1 2

1 1

1 1













































  



















n n

b _n

i i n

i i n

i i

n

i i n

i i n

i i i

  

 





























 _n

i i n

i

i i

b

1

2 1

1 (2.12)

3.1.1 METODE ORDINARY LEAST SQUARE (OLS)DALAM BENTUK MATRIKS

Metode Ordinary Least Square (OLS) adalah suatu metode yang digunakan untuk menduga koefisien regresi klasik dengan cara meminimumkan jumlah kuadrat galat yaitu meminimumkan

∑𝑛 𝜀𝑖2

𝑖=1 . Estimator dalam metode OLS diperoleh dengan cara meminimumkan

∑ 𝜀𝑖2 = ∑ (𝑌 − 𝛽0− 𝛽1𝑋1− 𝛽2𝑋2− ⋯ − 𝛽𝑛𝑋𝑛)² (2.13) dengan n = 0, 1, 2, … dan ∑ 𝜀₁² adalah jumlah kuadrat galat (JKG). Pada notasi matriks JKG (∑ 𝜀12) dapat ditulis:

𝜺𝒊′𝜺𝒊 =



₁ ₂ ... n



















n



 ...

2 1

= 𝜺𝟏𝟐+ 𝜺𝟐𝟐+ ⋯ + 𝜺𝒏𝟐 = ∑𝜺𝒊𝟐 (2.14)

Berdasarkan, 𝑌1= 𝛽0+ 𝛽1𝑋1+ 𝜀1

𝑌2= 𝛽0+ 𝛽1𝑋2+ 𝜀2

… … … … 𝑌𝑛= 𝛽0+ 𝛽1𝑋𝑛+ 𝜀𝑛

(2.15)

Dalam matriks dapat ditulis:

















Yn

Y Y

...

2 1

= 



 





1 0





















Xn

X X

1 1 1

2 1



 ⁺

















n



 ...

2 1

yang juga dapat ditulis:

Y = Xβ + ε (2.16) Berdasarkan (2.16) diperoleh: ε = Y – Xβ (2.17) Sehingga matriks galat menjadi,

J = 𝜀𝑖′𝜀𝑖 = (Y – X𝛽)’ (Y – X𝛽)

= (Y’ – X’𝛽’) (Y – X𝛽)

= Y’Y – Y’X𝛽 – X’𝛽’Y + X’𝛽′ X𝛽

= Y’Y –2Y’X𝛽 + 𝛽X’X𝛽 (2.18)

Untuk meminimumkan 𝜀𝑖′𝜀𝑖, maka 𝜀𝑖′𝜀𝑖 harus diturunkan terhadap 𝛽 sehingga diperoleh persamaan normal

𝜕𝐽

𝜕𝛽0= −2 ∑(𝑌𝑖− 𝛽0− 𝛽1𝑋1− 𝛽2𝑋1− ⋯ − 𝛽𝑛𝑋𝑛) = 0

𝜕𝐽

𝜕𝛽1= −2∑(𝑌𝑖− 𝛽0− 𝛽1𝑋1− 𝛽2𝑋1− ⋯ − 𝛽𝑛𝑋𝑛)𝑋1= 0

𝜕𝐽

𝜕𝛽2= −2 ∑(𝑌𝑖− 𝛽0− 𝛽1𝑋1− 𝛽2𝑋1− ⋯ − 𝛽𝑛𝑋𝑛)𝑋2= 0

… … … …

𝜕𝐽

𝜕𝛽_𝑛 = −2 ∑(𝑌𝑖− 𝛽0− 𝛽1𝑋1− 𝛽2𝑋1− ⋯ − 𝛽𝑛𝑋𝑛)𝑋𝑛= 0 (2.19) ` Setelah disusun kembali dan mengganti semua perameter dengan estimatornya, didapat persamaan baru

𝑛𝛽̂0+ 𝛽̂1∑ 𝑋1+ 𝛽̂2∑𝑋2+ ⋯ + 𝛽̂𝑛∑ 𝑋𝑛= ∑𝑌𝑖

𝛽̂0∑𝑋1+ 𝛽̂1∑𝑋12+ 𝛽̂2∑ 𝑋2𝑋1+ … + 𝛽̂𝑛∑𝑋𝑛𝑋1= ∑ 𝑌𝑖𝑋1

𝛽̂0∑𝑋2+ 𝛽̂1∑ 𝑋1𝑋2+ 𝛽̂2∑ 𝑋22+ ⋯ + 𝛽̂𝑛∑ 𝑋𝑛𝑋2= ∑ 𝑌𝑖𝑋2

… … …

𝛽̂0∑ 𝑋𝑛+ 𝛽̂1∑ 𝑋1𝑋𝑛+ 𝛽̂2∑𝑋2𝑋𝑛+ ⋯ + 𝛽̂𝑛∑𝑋𝑛2= ∑ 𝑌𝑖𝑋𝑛 (2.20) Persamaan diatas dapat ditulis dalam bentuk matriks menjadi:



































       

2 2

1

2 2

2 2

1 2

1 1

2 2

1 1

2 1

n n

n n

n n n

X X

X X

X X

X X X

X X X

X X X

X X

X

X X

X n







































n







ˆ ˆ ˆ ˆ

2 1 0



=





















nm m

m

n n

X X

X

X X

X

X X

X

















2 1

2 22

12

1 21

11

1 1

1





















Yn

Y Y Y



3 2 1

(X’X) ^ˆ X’ Y

Atau dapat ditulis dalam notasi matriks menjadi:

(X’X) ^ˆ = X’Y (X’X)^-1(X’X) ^ˆ = (X’X)^-1X’Y

I^ˆ = (X’X)^-1X’Y

^ˆ = (X’X)^-1X’Y

Sehingga diperoleh estimator untuk OLS:

CONTOH KASUS

Tabel 12 Maka diperoleh OLS:

^ˆ = (X’X)^-1X’Y

= ¹

11.54[ 7 −21.6

−21.6 68.3 ] 



 





2 . 2 8 . 2 9 . 3 2 . 3 0 . 3 4 . 3 1 . 3

1 1 1 1 1 1 1

































3 . 2 1

5 . 2 1

0 . 4 1

9 . 2 1

0 . 3 1

2 . 3 1

5 . 3 1

= [−0.0050.992 ] Maka diperoleh persamaan:

Y = -0.005X+0.992

3.2 Pencilan (Outlier)

3.2.1 Pengertian Pencilan

Menurut Ferguson (1961), pencilan didefinisikan sebagai suatu data yang menyimpang dari sekumpulan data yang lain. Secara umum pencilan (oulier)

No. Y X

1 3.5 3.1

2 3.2 3.4

3 3.0 3.0

4 2.9 3.2

5 4.0 3.9

6 2.5 2.8

7 2.3 2.2

^ˆ= (X’X)^-1X’Y

adalah data yang tidak mengikuti pola umum model. Pencilan juga diartikan sebagai suatu keanehan atau keganjilan pada data amatan yang menunjukkan ketidaksesuaian dengan sisa data (Sembiring, 1995). Menurut Hair, dkk (1995) juga menyatakan bahwa data yang muncul memiliki karakteristik unik yang terlihat sangat jauh berbeda dari observasi lainnya dan muncul dalam bentuk nilai ekstrim baik untuk sebuah variabel tunggal ataupun variabel kombinasi.

3.2.2 Pendeteksian Pencilan

Terdapat banyak cara untuk mengidentifikasi adanya pencilan atau tidak pada sekumpulan data, diantaranya:

a. Diagram Pencar (Scatter Plot)

Untuk melihat apakah terdapat pencilan atau tidak pada sekumpilan data dapat dilakukan dengan memplot data dengan observasi ke-i (i=1,2,3,...,n) seperti pada gambar dibawah ini:

14 12 10 8 6 4 2 99

95 90 80 70 60 50 40 30 20 10 5

1

y

Percent

Mean 7.5

StDev 2.030

N 11

KS 0.193

P-Value >0.150

y Normal

Gambar 15 : Scatter Plot

*data pencilan terdapat pada y = 12.74

Kelemahan data dari metode in adalah keputusan bahwa data adalah suatu pencilan sangat tergantung pada kebijakan (judgment) peneliti. Oleh karena itu dibutuhkan seorang yang ahli dan berpengalaman dalam menginterpretasikan plot tersebut.

b. Boxplot

Pencilan dapat dideteksi dengan menggunakan boxplot. Metode ini sangat terkenal dalam mendeteksi pencilan. Metode ini menggunakan nilai quartil.

Quartil 1, 2 dan 3 akan membagi sebuah urutan data menjadi empat bagian.

Jangkauan (interrquatil (IQR) didefinisikan sebagai selisih antara quartil 1 dan quartil 3, atau IQR= Q3-Q1.

Menurut Soemartini (2007), data-data pencilan dapat ditentukan yaitu nilai yang kuang dari 1.5*IQR terhadap quartil 1 dan nilai yang lebih dari 1.5*IQR terhadap quartil 3.

Gambar 16 : Skema identifikasi pencilan menggunakan IQR atau boxplot

3.2.3 Pengaruh Pencilan

Pencilan berpengaruh terhadap proses analisa data, salah satunya terhadap nilai mean dan standar deviasi. Oleh karena itu, keberaaan pencilan dalam suatu pola data harus dihindari. Pencilan dapat menyebabkan hal-hal berikut:

1. Variance data menjadi besar.

2. Interval data dan range menjadi lebar.

3. Mean tidak dapat menunjukkan nilai yang sebenarnya.

4. Pada beberapa analisa data, pencilan dapat menyebabkan kesalahan dalam pengambilan keputusan dan kesimpulan.

BAB IV

REGRESI LINIER BERGANDA

4.1 Pengertian Regresi Linier Berganda

Regresi berganda adalah perpanjangan dari regresi linier sederhana. Ini digunakan ketika kita ingin memprediksi nilai suatu variabel berdasarkan pada nilai dua atau lebih variabel lainnya.

Variabel yang ingin kita prediksi disebut variabel dependen (atau kadang-kadang, hasil, target atau variabel kriteria). Variabel yang kami gunakan untuk memprediksi nilai variabel dependen disebut variabel independen (atau kadang-kadang, variabel prediktor, penjelas, atau regresi).

Dalam model regresi, variabel independen menjelaskan variabel dependen. Dalam analisis regresi sederhana, hubungan antar variabel bersifat linier, dimana perubahan pada variabel X akan diikuti oleh perubahan pada variabel Y secara permanen. Sedangkan dalam hubungan non- linear, perubahan variabel X tidak diikuti oleh perubahan variabel Y secara proporsional. seperti pada model kuadratik, perubahan x diikuti oleh kuadrat dari variabel X. Hubungan seperti itu tidak linier. Penyelesaian materi dalam regresi berganda dapat ditangani secara sistematis melalui proses penyelesaian dengan aturan matriks. Analisis regresi berganda lebih dari dua variabel bebas X lebih mudah diselesaikan dengan metode matriks.

4.2 Model Regresi Linier Berganda

Secara umum, kasus regresi berganda dapat ditulis sebagai,

t tk k 3

t 3 2 t 2 1

t x x x u

y     

di mana β adalah k parameter yang tidak diketahui, u adalah kesalahan atau istilah residu, t merujuk ke nomor pengamatan, dan xtk mengacu pada variabel independen ke-t untuk pengamatan t. Perhatikan penomoran variabel x dimulai dengan dua. Secara implisit, β1, parameter intersep, dikalikan satu. Nilai satu ini untuk x^t1 biasanya dihilangkan saat menulis persamaan. Namun, nilai untuk xt1 ini menjadi sangat penting nantinya dalam derivasi.

Persamaan individual untuk parameter k dan pengamatan n adalah

n nk k 3

n 3 2 n 2 1 n

3 k 3 k 33

3 32 2 1 3

2 k 2 k 23

3 22 2 1 2

1 k 1 k 13

3 12 2 1 1

u x x

x y

u x x

x y

u x x

x y

u x x

x y





























































































Poin kunci: derivasi estimator OLS dalam kasus regresi linier berganda adalah sama dengan kasus linear sederhana, kecuali aljabar matriks, bukan aljabar linier digunakan. Tidak ada yang baru ditambahkan, kecuali mengatasi faktor penyulit dari variabel independen tambahan.

Jumlah kesalahan kuadrat atau residu adalah skalar, satu angka. Dalam bentuk matriks, perkiraan jumlah kesalahan kuadrat adalah:

Dimana,

𝒆^′𝒆 = 𝒚^′𝒚– 2 β 𝑿^′ Y+ 𝐛^′𝑿^′𝑿β 4.3Derivasi dalam Bentuk Matriks

Berikut adalah langkah-langkah derivasi OLS dalam matriks :

No. Turunan dalam matematika Langkah-langkah 1. Min 𝒆^′𝒆 = 𝒚^′𝒚– 2 β 𝑿^′ Y+ 𝐛^′𝑿^′𝑿β Masalah asli, Min.SSR 2. SSR



 = - X’Y – X’Y + 2X’Xβ Persamaan yang akan diturunkan

SSR



 = – 2X’Y + 2X’Xβ = 0 Gunakan jumlah dan aturan daya untuk mengambil turunan parsial pertama dan atur sama dengan nol

3.

4.

2X’Xβ = 2X’Y

(𝑿^′𝑿)⁻¹X’Xβ = (𝑿^′𝑿)⁻¹X’Y

Hasil setelah langkah kedua dilakukan

Bagi kedua belah pihak X’ dengan 2 dan atur ulang dengan menambahkan X’Y ke kedua sisi

5. β = (𝑿^′𝑿)⁻¹X’Y Estimator OLS diperoleh dengan melakukan pra-evolusi kedua sisi dengan kebalikan dari X'X

4.4Contoh Kasus

Notasi Matriks dalam Persamaan Regresi Menggunakan OLS Class Attendance

(%) IQ LAST SCORE

60 110 65

70 120 70

75 115 75

80 130 75

80 110 80

90 120 80

95 120 85

95 125 95

100 110 90

100 120 98

Tabel 13

Dari data di atas adalah persamaan regresi berganda. Kemudian kami membuat persamaan regresi dalam bentuk notasi matriks

[ 6570 7575 8080 8595 9098]

=

[

1 110 60 1 120 70 11

11 11 11

115130 110120 120125 110120

7580 8090 9595 100100]

[𝛽₀ 𝛽₁ 𝛽2

]

Untuk memperoleh persamaan, kita perlu mencari nilai β β = (𝑿’𝑿)^−𝟏X’Y

𝑿^′𝑿 =[ 1 1 1 110 120 115

60 70 75 1 1 1 130 110 120

80 80 90 1 1 1 120 125 110

95 95 100 1 120100]

[

1 110 60 1 120 70 11

11 11 11

115130 110120 120125 110120

7580 8090 9595 100100]

= [ 10 1180 845

1180 139650 99900 845 99900 73075]

𝑿^′Y = [ 1 1 1 110 120 115

60 70 75 1 1 1 130 110 120

80 80 90 1 1 1 120 125 110

95 95 100 1 120100]

[ 6570 7575 8080 8595 9098]

= [ 813 96060 69925]

Masukkan ke dalam persamaan. Sehingga kita dapatkan :

β = (𝑿’𝑿)^−𝟏X’Y

β = [ 10 1180 845

1180 139650 99900 845 99900 73075]

−1

[ 813 96060 69925]

β =

[ 34.6220896671156 −0.279084086973254 −0.0188185491629786

−0.27908408697325 0.00257456224745045 −0.00029247642870887

−0.0188185491629786 −0.00029247642870887 0.000631133346161247] x [ 813

96060 69925]

= [ 23.054454492928

−0.034327496632983 0.737233019049548 ]

Kemudian kita masukkan ke dalam persamaan regressi berganda : Y= 23.0545 – 0.0343 X1 + 0.7372 X2

 Persamaan Regresi Menggunakan Aplikasi Minitab

Setelah mencari estimasi parameter dari fungsi regresi menggunakan OLS, kami juga harus membandingkan dengan hasil dari salah satu aplikasi statistik. Jadi kita dapat menyimpulkan apakah hasil manual kita benar atau tidak. Berikut ini adalah output dari hasil regresi linier dengan aplikasi Minitab.

Berdasarkan output diatas kita dapat simpulkan bahwa 𝛽0= −0.034 dan 𝛽1= 0.737 jadi hasil manual mencari estimasi parameter menggunakan metode OLS (Ordinary Least Square) memiliki hasil yang sama dengan menggunakan aplikasi Minitab.

BAB V

REGRESI DUMMY

5.1 Pengertian Regresi Dummy

Regresi memiliki beberapa persyaratan yang harus dipenuhi. Karena regresi masuk dalam statistik parametrik, tentunya variabel-variabel didalamnya memiliki skala interval atau rasio.

Selain itu data-data yang akan digunakan juga harus memenuhi kaidah asumsi klasik. Tetapi, dari beberapa variabel yang kita gunakan, bisa saja satu atau dua variabel tersebut berupa variabel dalam skala nominal atau ordinal. Variabel skala nominal atau ordinal di dalam regresi tersebut biasa dikenal sebagai variabel dummy.

Variabel dummy disebut juga variabel indikator, biner, kategorik, kualitatif, boneka, atau variabel dikotomi yang pada perinsipnya merupakan perbandingan karakteristik. Untuk menentukan variabel dummy yaitu dengan melihat kategori pada prediktor. Apabila prediktor memiliki kategori sebanyak r, maka variabel dummy yang terbentuk sebanyak (r-1). Kemudian simbolkan variabel dummy tersebut dengan simbol D (Gujarati, 2004: 340).

Beberapa penelitian kausal seringkali dibatasi oleh keberadaan variabel dependen yang terbatas. Metode regresi linier sederhana yang kita kenal hanya dapat mengakomodir data yang bersifat kontinu dan menyebar normal, tapi bagaimana data yang menyebar terbatas seperti mortalitas. Variabel dummy adalah variabel yang digunakan untuk mengkuantitatifkan variabel yang bersifat kualitatif (misal : jenis kelamin, ras, agama, perubahan kebijakan pemerintah, perbedaan situasi dan sebagainya).

Variabel kualitatif tersebut harus dikuantitatifkan atributnya (cirinya). Untuk mengkuantitatifkan atribut variabel kualitatif, dibentuk variabel dummy dgn nilai 1 dan 0. Jadi, inilah yang dimaksud dengan variabel dummy tersebut. Nilai 1 menunjukkan adanya, sedangkan nilai 0 menunjukkan tidak adanya ciri kualitas tsb. Misalnya variabel jenis kelamin. Jika nilai 1 digunakan untuk laki-laki maka nilai 0 menunjukkan bukan laki-laki (perempuan), atau sebaliknya. (Kategori yang diberi nilai 0 disebut kategori dasar, dalam artian bahwa perbandingan dibuat atas kategori tersebut).

5.2 Model Regresi dengan Variabel Dummy

Variabel-variabel dummy merupakan sebuah skala refleksibel yang dapat mengatasi berbagai masalah. Variabel dummy hanya mempunyai 2 (dua) nilai yaitu 1 dan 0, serta diberi simbol D.

Dummy memiliki nilai 1 (D=1) untuk salah satu kategori dan nol (D=0) untuk kategori yang lain.Variabel-variabel dummy merupakan sebuah skala refleksibel yang dapat