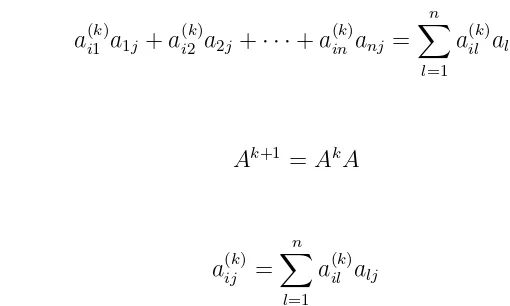SKRIPSI
RICHARD ALBERT NASUTION 010803013
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
2-EKSPONEN DARI 2-DIGRAPH DENGAN LOOP
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana
Sains
RICHARD ALBERT NASUTION 010803013
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
Judul : 2-EKSPONEN 2-DIGRAPH DENGAN LOOP
Kategori : SKRIPSI
Nama : RICHARD ALBERT NASUTION
Nomor Induk Mahasiswa : 010803013
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, September 2007
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Mardiningsih, M.Si Dr. Saib Suwilo, MSc.
NIP.131803344 NIP. 131796149
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
Dr. Saib Suwilo, MSc NIP. 131796149
PERNYATAAN
2-DIGRAPH DENGAN LOOP
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, September 2007
RICHARD ALBERT NASUTION 010803013
Setinggi puji dan sedalam syukur penulis serahkan kehadirat Allah SWT yang telah memberikan berkat dan rahmatNya sehingga penulis dapat menyelesaikan skrip-si yang berjudul” 2-EKSPONEN DARI 2-DIGRAPH DENGAN LOOP ”ini dengan baik. Skripsi ini sebagai salah satu mata kuliah wajib yang harus diselesaikan oleh seluruh mahasiswa Fakultas MIPA Departemen Matematika.
Pada kesempatan ini penulis mengucapkan terima kasih kepada Bapak Dr. Ed-dy Marlianto, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara. Bapak Dr. Saib Suwilo, M.Sc, dan Bapak Henry Rani S, M.Si selaku Ketua dan Sekretaris Departemen Matematika di FMIPA USU Medan. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Dra. Mardiningsih, M.Si selaku dosen pembimbing II yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini. Seluruh Staf Pen-gajar dan Staf Administrasi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara. Ibunda Ruminah tercinta yang se-lalu memberikan dukungan moril dan materiel serta doa yang tiada hentinya kepada penulis serta kepada Adinda Sudarno Hariadi tercinta yang telah memberikan doron-gan semangat kepada penulis.
Tak lupa, penulis juga mengucapkan terima kasih kepada para teman dan seniorku di Lab. Ekstension, yaitu b’Toni, b’Indra, Didi, Salman, Santri, Radhi, Andika yang telah membantu dalam penyelesaian skripsi ini, dukungan dan motivasi dalam pengerjaan skripsi ini. Juga buat seniorku di stambuk ’00 serta seluruh rekan-rekan ’01. Semoga Allah SWT memberikan balasan atas jasa-jasa mereka yang telah diberikan kepada penulis.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.
Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi yang membutuhkan.
ABSTRAK
Pada 2-digraphD, 2-eksponen didefinisikan sebagai bilangan bulat terkecil padah+k sehingga untuk setiap pasangan vertex u dan vdi D terdapat walk dari u kev dengan panjangh+k yang terdiri dariharc merah dank arc biru. 2-eksponen dari 2-digraph D dinotasikan oleh exp2(D). Shader dan Suwilo memperlihatkan eksponen dari
2-digraph primitif terletak pada interval ((n3 −5n2)/2,(3n3 + 2n2 −2n)/2). Tulisan
ini akan memberikan bentuk umum dari 2-digraph dengan 2-eksponen tepat 2n,2n− 1, dan2n−2
ABSTRACT
On 2-digraphD, 2-exponent being defined as smallest integerh+k therefore for every pairs of vertex u and v in D there is walk from u to v with legth h+k consist of h red arc and b blue arc. 2-exponent from 2-digraph D denoted by exp2(D)
Shader and suwilo show that 2-exponent from primitive 2-digraph lying on ((n3 −
5n2)/2,(3n3+2n2−2n))interval. This paper will give the general form of 2-digraphwith
2-exponent exactly 2n,2n-1,2n-2
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR viii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang Penelitian 1
1.2. Perumusan Masalah 3
1.3. Tinjauan pustaka 3
1.4. Tujuan penelitian 4
1.5. Manfaat penelitian 4
1.6. Metode penelitian 5
2. 2-DIGRAPH PRIMITIF 6
2.1. Notasi 6
2.2. Matriks Adjacency 12
2.3. Primitifitas Dari 2-Digraph Terhubung Kuat 14 2.4. Matriks tak negatif & Eksponen 2-digraph 19 2.5. Beberapa fakta tentang 2-digraph dengan loop 25
3. 2-DIGRAPH DENGAN LOOP 27
4. KESIMPULAN 34
4.1. Kesimpulan 34
DAFTAR PUSTAKA 36
DAFTAR GAMBAR
Gambar Halaman
2.1 Representasi grafis dari Digraph 7
2.2 Digraph dengan path, walk, cycle dan loop 8
2.3 Representasi grafis dari 2-Digraph 10
2.4 2-Digraph dengan path, walk, cycle dan loop 11
2.5 Digraph dengan 4 vertex, 6 arc 12
2.6 2-Digraph dengan 4 vertex, 3 arc merah, dan 4 arc biru 13
2.7 (a) digraph terhubung kuat ;(b) digraph tidak terhubung kuat 15
2.8 digraph terhubung kuat 16
2.9 (a) 2-digraph terhubung kuat ;(b) 2-digraph tidak terhubung kuat 17
2.10 2-digraph primitif 19
2.11 Representasi digraph 3 vertex dan 7 arc 21
2.12 Representasi 2-digraph dengan 3 vertex, 3 arc biru dan 3 arc merah 23
4.1 Representasi 2-digraph dengan 2-eksponen 2n 35
4.2 Representasi 2-digraph dengan 2-eksponen 2n-1 35
Pada 2-digraphD, 2-eksponen didefinisikan sebagai bilangan bulat terkecil padah+k sehingga untuk setiap pasangan vertex u dan vdi D terdapat walk dari u kev dengan panjangh+k yang terdiri dariharc merah dank arc biru. 2-eksponen dari 2-digraph D dinotasikan oleh exp2(D). Shader dan Suwilo memperlihatkan eksponen dari
2-digraph primitif terletak pada interval ((n3 −5n2)/2,(3n3 + 2n2 −2n)/2). Tulisan
ini akan memberikan bentuk umum dari 2-digraph dengan 2-eksponen tepat 2n,2n− 1, dan2n−2
2-DIGRAPH WITH LOOPS
ABSTRACT
On 2-digraphD, 2-exponent being defined as smallest integerh+k therefore for every pairs of vertex u and v in D there is walk from u to v with legth h+k consist of h red arc and b blue arc. 2-exponent from 2-digraph D denoted by exp2(D)
Shader and suwilo show that 2-exponent from primitive 2-digraph lying on ((n3 −
5n2)/2,(3n3+2n2−2n))interval. This paper will give the general form of 2-digraphwith
2-exponent exactly 2n,2n-1,2n-2
PENDAHULUAN
1.1 Latar Belakang Penelitian
Dalam kehidupan sehari-hari kita sering mendengar atau melihat sistem jalan
satu arah, arus listrik, jaringan kerja dll. Biasanya hal-hal tersebut diatas
direpresen-tasikan secara grafik dengan titik dan garis berarah, hubungan garis dan titik yang
demikian diamati oleh suatu objek di matematika yang disebut dengan digraph.
Suatu digraph terdiri dari titik-titik yang dihubungkan oleh garis berarah.
Secara formal, digraph adalah objek yang terdiri dari dua himpunan yaitu :
1. Himpunan hingga yang tak kosong V, dimana unsurnya disebut vertex dari
digraph D
2. HimpunanE yang merupakan himpunan bagian dari pasangan berurut V XV,
unsurnya disebut arc dari digraph D
vertex dalam digraph direpresentasikan oleh titik atau lingkaran kecil dan arc
direp-resentasikan oleh garis berarah dari suatu vertex ke vertex lainnya.
Suatu walk dari vertexuke vertexv yang panjangnyam adalah suatu barisan
arc dalam bentuk
2
walk diatas dapat direpresentasikan sebagai
u=v0 →v1 →v2 →. . .→ vm−1 →vm =v
Suatu digraphD dikatakan terhubung kuat bila untuk setiap pasangan vertexu dan
vdiD terdapat walk dariukev. DigraphD dikatakanministrong jika penghilangan
satu arc dari D mengakibatkan D tidak terhubung kuat. Suatu digraph terhubung
kuat D dikatakan primitif bila terdapat bilangan bulat k sehingga untuk setiap
pasangan vertex u dan v di D terdapat walk dari u ke v dengan panjang tepat k.
Bilangan bulat k terkecil yang demikian disebut disebut sebagai eksponen dari D
dan dinotasikan olehexp(D).
Studi tentang eksponen digraph primitif diprakarsai oleh Wielandt[5] yang
menyatakan bahwa untuk digraph primitif dengan n vertex, exp(D) ≤(n−1)2+ 1.
Holladay dan varga [4] memperlihatkan bahwa ila D adalah digraph primitif dengan
q loop maka exp(D)≤2n−q−1. Selanjutnya, Liu dan Shao [1] memberikan syarat
perlu dan bagi digraph terhubung kuatDdengannvertex danqloop yang mempunyai
exp(D) = 2n−q−1, sejalan itu dengan itu Dalimunthe dan Suwilo[10] memberikan
syarat cukup untuk digraph agar mempunyai eksponen tepat exp(D) = 2n−q−1.
Pada tahun 1997, fornasini dan Valcher[3] memperkenalkan konsep 2-digraph yakni
digraph dimana setiap arcnya diwarnai dengan merah atau biru. Sejalan dengan itu
Shader dan Suwilo[2] memperkenalkan konsep 2-eksponen dari 2-digraph. Shader
dan Suwilo mendefinisikan 2-eksponen dari 2-digraph sebagai bilangan bulat terkecil
h+k sehingga untuk setiap pasangan vertex u dan v di D terdapat walk dari u ke
v dengan panjang h+k dan terdiri dari h arc merah dan k arc biru. Shader dan
Suwilo memperlihatkan bahwa untuk 2-digraph D dengan n vertex, maka 2-eksponen
secara eksplisit memberikan formula bagi 2-eksponen dari 2-digraph yang terdiri dari
cycle (lihat[8]), dan memperlihatkan bahwa untuk 2-digraph yang asymetric maka
2 ≤ exp2(D) ≤ 4 (lihat[9]). Sejalan dengan hasil dari Holladay dan Varga[4] perlu
ditentukan 2-eksponen dari 2-digraph dengan loop.
1.2 Perumusan Masalah
Bula D adalah suatu 2-digraph primitif atas n vertex dan m ≥ 2 loop.
Dap-atkah ditemukan batas atas yang cukup ”baik” bagi 2-digraph dengan m≥2 loop.
1.3 Tinjauan pustaka
Shader dan Suwilo [2] memperlihatkan bahwa eksponen terbesar dari
2-digraph primitif terletak di interval [(n3−5n2)/2,(3n3+ 2n2−2n)/2]. Batas bawah
pada interval tersebut ditemukan dengan menggunakan 2-digraph yang terdiri dari
dua cycle dan batas atas ditemukan secara teoritis. Sehingga masih terdapat gap
an-tara batas empiris dan batas teoritis. Suwilo[8] memberikan formula bagi 2-eksponen
dari 2-digraph, yang terdiri atas cycle, dan memperlihatkan bahwa untuk 2-digraph
yang asymetric maka 2 ≤exp2(D)≤4.
Andaikan D adalah 2-digraph primitif yang terdiri dari dua cycle γ1 dan γ2
dengan panjang masing-masing ℓ(γ1) dan ℓ(γ2). Untuk sebarang pasangan vertex u
dan v, misalkan puv adalah sebuah path terpendek dari u ke vdan definisikan
ℓ′
r= limu,v
∈V{b(γ2)r(puv)−r(γ2)b(puv)}
ℓ′
b = lim
u,v∈V{r(γ1)b(puv)−b(γ1)r(puv)}
4
dengan sedikitnya terdapat satu arc untuk setiap warna, maka.
exp2(D) =ℓ(γ1)ℓ′r+ℓ(γ2)ℓ′b
Lee dan yang [7] secara khusus mendiskusikan 2-eksponen dari satu klas 2-digraph
ministrong yang terdiri dari cycle 1 → 2 → · · · → n −3 → n−2 → 1 dan path
n− 3 → n− 1 → n → 1 Andaikan D adalah digraph ministrong dengan banyak
vertex n ≥ 5 yang terdiri dari cycle 1 → 2· · · → n−3 → n −2 → 1 dan path
n−3 → n−1→ n → 1. Warnai paling sedikit satu arc untuk setiap warna, maka
2-eksponen dari 2-digraph terletak pada interval :
2n2−8n+ 7 ≤exp
2(D)≤2n2−5n+ 3
1.4 Tujuan penelitian
Menentukan 2-eksponen bagi 2-digraph yang terdiri dari sebuah cycle dengan
2 loop.
1.5 Manfaat penelitian
Penelitian ini bermanfaat untuk memperkaya literatur dibidang 2-eksponen
1.6 Metode penelitian
Metodologi penelitian ini bersifat literatur atau kepustakaan dengan langkah
- langkah sebagai berikut :
1. MenggunakanSoftwaresederhana untuk mendukung pengerjaan pengamatan.
2. Mencari kelas-kelas dari 2-digraph kemudian membandingkannya
3. Mencari bentuk umum dari masing-masing 2-eksponen dari 2-digraph
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR viii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang Penelitian 1
1.2. Perumusan Masalah 3
1.3. Tinjauan pustaka 3
1.4. Tujuan penelitian 4
1.5. Manfaat penelitian 4
1.6. Metode penelitian 5
2. 2-DIGRAPH PRIMITIF 6
2.1. Notasi 6
2.2. Matriks Adjacency 12
2.3. Primitifitas Dari 2-Digraph Terhubung Kuat 14 2.4. Matriks tak negatif & Eksponen 2-digraph 19 2.5. Beberapa fakta tentang 2-digraph dengan loop 25
3. 2-DIGRAPH DENGAN LOOP 27
4. KESIMPULAN 34
4.1. Kesimpulan 34
DAFTAR PUSTAKA 36
DAFTAR GAMBAR
Gambar Halaman
2.1 Representasi grafis dari Digraph 7
2.2 Digraph dengan path, walk, cycle dan loop 8
2.3 Representasi grafis dari 2-Digraph 10
2.4 2-Digraph dengan path, walk, cycle dan loop 11
2.5 Digraph dengan 4 vertex, 6 arc 12
2.6 2-Digraph dengan 4 vertex, 3 arc merah, dan 4 arc biru 13
2.7 (a) digraph terhubung kuat ;(b) digraph tidak terhubung kuat 15
2.8 digraph terhubung kuat 16
2.9 (a) 2-digraph terhubung kuat ;(b) 2-digraph tidak terhubung kuat 17
2.10 2-digraph primitif 19
2.11 Representasi digraph 3 vertex dan 7 arc 21
2.12 Representasi 2-digraph dengan 3 vertex, 3 arc biru dan 3 arc merah 23
4.1 Representasi 2-digraph dengan 2-eksponen 2n 35
4.2 Representasi 2-digraph dengan 2-eksponen 2n-1 35
PENDAHULUAN
1.1 Latar Belakang Penelitian
Dalam kehidupan sehari-hari kita sering mendengar atau melihat sistem jalan
satu arah, arus listrik, jaringan kerja dll. Biasanya hal-hal tersebut diatas
direpresen-tasikan secara grafik dengan titik dan garis berarah, hubungan garis dan titik yang
demikian diamati oleh suatu objek di matematika yang disebut dengan digraph.
Suatu digraph terdiri dari titik-titik yang dihubungkan oleh garis berarah.
Secara formal, digraph adalah objek yang terdiri dari dua himpunan yaitu :
1. Himpunan hingga yang tak kosong V, dimana unsurnya disebut vertex dari
digraph D
2. HimpunanE yang merupakan himpunan bagian dari pasangan berurut V XV,
unsurnya disebut arc dari digraph D
vertex dalam digraph direpresentasikan oleh titik atau lingkaran kecil dan arc
direp-resentasikan oleh garis berarah dari suatu vertex ke vertex lainnya.
Suatu walk dari vertexuke vertexv yang panjangnyam adalah suatu barisan
arc dalam bentuk
2
walk diatas dapat direpresentasikan sebagai
u=v0 →v1 →v2 →. . .→ vm−1 →vm =v
Suatu digraphD dikatakan terhubung kuat bila untuk setiap pasangan vertexu dan
vdiD terdapat walk dariukev. DigraphD dikatakanministrong jika penghilangan
satu arc dari D mengakibatkan D tidak terhubung kuat. Suatu digraph terhubung
kuat D dikatakan primitif bila terdapat bilangan bulat k sehingga untuk setiap
pasangan vertex u dan v di D terdapat walk dari u ke v dengan panjang tepat k.
Bilangan bulat k terkecil yang demikian disebut disebut sebagai eksponen dari D
dan dinotasikan olehexp(D).
Studi tentang eksponen digraph primitif diprakarsai oleh Wielandt[5] yang
menyatakan bahwa untuk digraph primitif dengan n vertex, exp(D) ≤(n−1)2+ 1.
Holladay dan varga [4] memperlihatkan bahwa ila D adalah digraph primitif dengan
q loop maka exp(D)≤2n−q−1. Selanjutnya, Liu dan Shao [1] memberikan syarat
perlu dan bagi digraph terhubung kuatDdengannvertex danqloop yang mempunyai
exp(D) = 2n−q−1, sejalan itu dengan itu Dalimunthe dan Suwilo[10] memberikan
syarat cukup untuk digraph agar mempunyai eksponen tepat exp(D) = 2n−q−1.
Pada tahun 1997, fornasini dan Valcher[3] memperkenalkan konsep 2-digraph yakni
digraph dimana setiap arcnya diwarnai dengan merah atau biru. Sejalan dengan itu
Shader dan Suwilo[2] memperkenalkan konsep 2-eksponen dari 2-digraph. Shader
dan Suwilo mendefinisikan 2-eksponen dari 2-digraph sebagai bilangan bulat terkecil
h+k sehingga untuk setiap pasangan vertex u dan v di D terdapat walk dari u ke
v dengan panjang h+k dan terdiri dari h arc merah dan k arc biru. Shader dan
Suwilo memperlihatkan bahwa untuk 2-digraph D dengan n vertex, maka 2-eksponen
secara eksplisit memberikan formula bagi 2-eksponen dari 2-digraph yang terdiri dari
cycle (lihat[8]), dan memperlihatkan bahwa untuk 2-digraph yang asymetric maka
2 ≤ exp2(D) ≤ 4 (lihat[9]). Sejalan dengan hasil dari Holladay dan Varga[4] perlu
ditentukan 2-eksponen dari 2-digraph dengan loop.
1.2 Perumusan Masalah
Bula D adalah suatu 2-digraph primitif atas n vertex dan m ≥ 2 loop.
Dap-atkah ditemukan batas atas yang cukup ”baik” bagi 2-digraph dengan m≥2 loop.
1.3 Tinjauan pustaka
Shader dan Suwilo [2] memperlihatkan bahwa eksponen terbesar dari
2-digraph primitif terletak di interval [(n3−5n2)/2,(3n3+ 2n2−2n)/2]. Batas bawah
pada interval tersebut ditemukan dengan menggunakan 2-digraph yang terdiri dari
dua cycle dan batas atas ditemukan secara teoritis. Sehingga masih terdapat gap
an-tara batas empiris dan batas teoritis. Suwilo[8] memberikan formula bagi 2-eksponen
dari 2-digraph, yang terdiri atas cycle, dan memperlihatkan bahwa untuk 2-digraph
yang asymetric maka 2 ≤exp2(D)≤4.
Andaikan D adalah 2-digraph primitif yang terdiri dari dua cycle γ1 dan γ2
dengan panjang masing-masing ℓ(γ1) dan ℓ(γ2). Untuk sebarang pasangan vertex u
dan v, misalkan puv adalah sebuah path terpendek dari u ke vdan definisikan
ℓ′
r= limu,v
∈V{b(γ2)r(puv)−r(γ2)b(puv)}
ℓ′
b = lim
u,v∈V{r(γ1)b(puv)−b(γ1)r(puv)}
4
dengan sedikitnya terdapat satu arc untuk setiap warna, maka.
exp2(D) =ℓ(γ1)ℓ′r+ℓ(γ2)ℓ′b
Lee dan yang [7] secara khusus mendiskusikan 2-eksponen dari satu klas 2-digraph
ministrong yang terdiri dari cycle 1 → 2 → · · · → n −3 → n−2 → 1 dan path
n− 3 → n− 1 → n → 1 Andaikan D adalah digraph ministrong dengan banyak
vertex n ≥ 5 yang terdiri dari cycle 1 → 2· · · → n−3 → n −2 → 1 dan path
n−3 → n−1→ n → 1. Warnai paling sedikit satu arc untuk setiap warna, maka
2-eksponen dari 2-digraph terletak pada interval :
2n2−8n+ 7 ≤exp
2(D)≤2n2−5n+ 3
1.4 Tujuan penelitian
Menentukan 2-eksponen bagi 2-digraph yang terdiri dari sebuah cycle dengan
2 loop.
1.5 Manfaat penelitian
Penelitian ini bermanfaat untuk memperkaya literatur dibidang 2-eksponen
1.6 Metode penelitian
Metodologi penelitian ini bersifat literatur atau kepustakaan dengan langkah
- langkah sebagai berikut :
1. MenggunakanSoftwaresederhana untuk mendukung pengerjaan pengamatan.
2. Mencari kelas-kelas dari 2-digraph kemudian membandingkannya
3. Mencari bentuk umum dari masing-masing 2-eksponen dari 2-digraph
BAB 2
2-DIGRAPH PRIMITIF
Pada bab ini diberikan beberapa konsep dasar seperti teorema dan beberapa definisi
sebagai landasan dalam penelitian ini. Konsep dasar ini berkaitan dengan masalah
yang dibahas dalam tulisan ini sepertidigraph, 2-digraph, terhubung kuat, 2-digraph
primitif, dan 2-eksponen dari 2-digraph.
2.1 Notasi
Pada bagian ini akan dibahas beberapa notasi digraph yang akan dipergunakan
dalam pembahasan 2-digraph.
2.1.1 Digraph.
Secara sederhana graph adalah kumpulan titik atau lingkaran kecil yang
di-hubungkan oleh garis tak berarah, jika garis penghubung diberi arah, maka graph
yang demikian disebut dengan digraph (directed graph).
AndaikanV adalah suatu himpunan objek berhingga yang tak kosong, sebuah
digraph adalah suatu objek yang dibentuk oleh himpunan V yang unsurnya disebut
vertexdari digraphD, dan himpunan A⊆V ×V yang unsurnya disebut denganarc
dari D. Jika diberikan a, b∈ V dengan (a, b) ∈ A, maka terdapat arc dari vertex a
ke vertexbdi digraph D. Vertex a disebut sebagai vertex awal dan vertex bdisebut
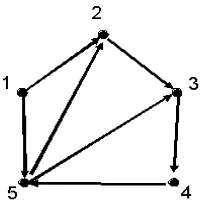
Contoh 2.1.1 Himpunan vertex V = {1,2,3,4,5} bersama dengan himpunan arc merah A = {(1,2),(1,5),(2,3),(3,4),(4,5),(5,2),(5,3)} adalah suatu digraph
de-ngan 5 vertex dan 7 arc.
Suatu digraph dapat direpresentasikan secara grafis dengan cara setiap vertex
direpresentasikan sebagai sebuah titik dan setiap arc (u, v) direpresentasikan sebagai
garis berarah dari titiku ke v.
Representasi dari digraph yang diberikan pada contoh 2.1.1 diatas diberikan
pada gambar berikut.
Contoh 2.1.2Representasi Grafis dari digraph
Gambar 2.1 : Representasi grafis dari Digraph
Diberikan D adalah digraph, u dan v adalah vertex di digraph D. Sebuah
walk dengan panjang m dari u ke v didefinisikan sebagai barisan arc dan dituliskan
sebagai berikut.
(v0, v1),(v1, v2), . . . ,(vm−1,m)
untuk m > 0, v0 = udanvm = v. Sebuah walk juga biasa dinotasikan u w
−→ v dan
panjangnya dinotasikan dengan ℓ(w). Sebuah path didefinisikan sebagai sebuah walk
8
cycle didefinisikan sebagai sebuah path tertutup, dan sebuah loop didefinisikan
seba-gai sebuah cycle dengan panjang satu. Berikut ini akan diberikan representasi dari
digraph untuk menjelaskan beberapa definisi diatas.
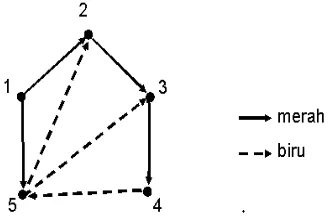
Contoh 2.1.3Diberikan digraph di bawah ini
Gambar 2.2 : Digraph dengan path, walk, cycle dan loop
Digraph pada gambar 2.2 diatas memiliki walk, path, cycle dan loop sebagai
berikut :
• 1→3→2 adalah sebuah path terbuka.
• 1→3→4→1 adalah sebuah path tertutup atau disebutcycle
• 1 → 3 → 2 → 5 → 3 → 4 adalah sebuah walk tetapi bukan path karena ada
perulangan vertex.
• 3→ 4→ 1→ 3→2 →5 →3 adalah sebuah walk tertutup dari 3 ke 3 tetapi
bukan cycle.
• 2→2 adalah sebuah loop
2.1.2 2-digraph.
Sekarang akan dibahas notasi - notasi digraph yang dijelaskan diatas dan
tak kosong, sebuah 2−digraph Dadalah suatu objek yang dibentuk oleh himpunan
V yang unsurnya disebut vertex dari D, bersama dengan himpunanA⊆V ×V yang
disebut arc merah dan himpunan B ⊆ V ×V yang disebut arc biru dari D. Jika
diberikan a, b, c, d ∈ V dengan a, b ∈ A dan c, d ∈ B maka terdapat arc merah dari
vertex a ke vertex b dan terdapat arc biru dari vertex c ke vertex d. Vertex a dan
c disebut vertex awal dan vertex bdan d disebut vertex akhir. Berikut ini diberikan
sebuah contoh 2-digraph
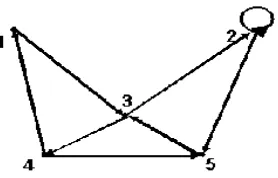
Contoh 2.1.4 Himpunan vertex V = {1,2,3,4,5} bersama dengan himpunan arc merah A = {(1,2),(2,3),(3,4),(5,1)} dan arc biru B = {(5,2),(5,3),(4,5)} adalah
suatu 2-digraph dengan 5 vertex, 4 arc merah dan 3 arc biru.
Suatu 2-digraph dapat direpresentasikan secara grafis dengan cara sebagai
berikut:
• Setiapvertexdirepresentasikan sebagai suatu titik.
• Setiap arc merah (a, b) direpresentasikan sebagai garis berarah tak putus dari
titika keb.
• Setiap arc biru (c, d) direpresentasikan sebagai garis berarah putus-putus dari
titikc ked
Berikut ini akan diberikan contoh representasi 2-digraph pada Contoh 2.1.3
10
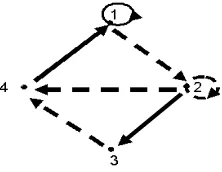
[image:30.612.241.406.140.251.2]Contoh 2.1.5Representasi Grafis dari 2-digraph
Gambar 2.3 : Representasi grafis dari 2-Digraph
Suatu (h, k) −walk dalam 2 −digraph adalah sebuah walk yang memuat
sebanyak h arc merah dan k arc biru.
Dari definisi yang diberikan diatas, suatu (h, k) −walk dari u ke v disebut
sebagai uv−walk, untuk sebuah walk w, r(w) dan b(w) adalah notasi jumlah dari
arc merah dan arc biru. Vektor
r(w) b(w)
disebut komposisi dari w
Suatu pathadalah suatu walk dengan semua vertex berbeda kecuali mungkin
vertex awal dan vertex akhir. Suatucycleadalah suatu path tertutup danloopadalah
suatu cycle dengan komposisi
0 1
atau
1 0
. Berikut ini akan diberikan representasi
Contoh 2.1.6Diberikan 2-digraph di bawah ini
Gambar 2.4 : 2-Digraph dengan path, walk, cycle dan loop
2-Digraph pada gambar 4 di atas memiliki path, walk, cycle dan loop sebagai
berikut :
• 1−→b 3−→r 2 adalah sebuah path terbuka dari 1 ke 2 dengan komposisi
1 1
.
• 1 −→b 3 −→b 4 −→r 1 adalah sebuah path tertutup atau cycle dari 1 ke 1 dengan
komposisi
1 2
.
• 1−→b 3−→r 2→−r 5−→b 3−→b 4 adalah walk dari 1 ke 4 dengan komposisi
2 3
, tetapi
bukan suatu path karena path adalah walk tanpa melalui lebih dari satu vertex
kecuali mungkin vertex awal dan akhir.
• 3−→b 4−→r 1−→b 3−→r 2−→r 5−→b 3 adalah sebuah walk tertutup dari 3 ke 3 dengan
komposisi
3 3
, tetapi bukan cycle.
• 2−→r 2 adalah sebuah loop dari 4 ke 4 dengan komposisi
1 0
.
• 1−→b 1 adalah sebuah loop dari 4 ke 4 dengan komposisi
0 1
12
Sebuah digraph atau 2-digraph dapat direpresentasikan kedalam sebuah
ma-triks, berikut ini diberikan hubungan antara digraph dan 2-digraph dengan matriks.
2.2 Matriks Adjacency
Pada subbab ini akan dibahas hubungan antara digraph, 2-digraph dengan
matriks. Sebuah digraph D dan 2-digraph D dengan n vertex dapat dinyatakan oleh
matriks, yang entri dari matriks tersebut adalah bilangan 1 atau 0, matriks yang
demikian disebut sebagai matriks adjacency.
2.2.1 Matriks Adjacency dari digraph.
Sebuah representasi grafis dari digraph D dapat dituliskan adjacency sebagai
berikut.
aij =
1,jika terdapat arc dari i kej
0,jika sebaliknya
Berikut ini diberikan contoh matriks adjacency dari sebuah representasi
di-graph.
[image:32.612.271.378.549.635.2]Contoh 2.2.1Representasi dari sebuah digraph
Dari representasi digraph diatas didapat matriks adjacency sebagai berikut.
1 1 0 0 0 0 1 1 0 0 0 1 1 0 0 0
Berikut ini akan diberikan sebuah matriks adjacency dari 2-digraph.
2.2.2 Matriks Adjacency 2-digraph.
Pada 2-digraph matriks adjacency dari sebuah representasi grafis dapat
dinya-takan sebagai berikut. Matriks adjacency merah, R = [rij] pada D adalah matriks
n×n dengan
rij =
1,jika terdapat arc merah
0,jika sebaliknya
matriks adjacency biru B = [bij] pada D adalah matriksn×n, dengan
bij =
1,jika terdapat arc biru
0,jika sebaliknya
Berikut ini akan diberikan sebuah 2-digraph dan direpresentasikan kedalam
matriks adjacencynya
[image:33.612.271.382.590.676.2]Contoh 2.2.2Representasi dari sebuah 2-digraph
14
Dari representasi 2-digraph diatas, dapat dibuat sebuah matriks adjacency
sebagai berikut.
R=
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0
. Adalah matriks adjacency merah
B =
0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0
. Adalah matriksadjacency biru
Berikut ini akan dibahas mengenai digraph dan 2-digraph terhubung kuat dan
keterhubungan dengan digraph dan 2-digraph primitif.
2.3 Primitifitas Dari 2-Digraph Terhubung Kuat
Pada bagian ini akan dibahas tentang digraph dan 2-digraph terhubung kuat
dan keterhubungan dengan primitifitas.
2.3.1 Digraph primitif.
Suatu digraphDdikatakan terhubung kuatstrongly connectedjika untuk setiap
walk berarah dari vertex u dan v dan walk berarah dari vertex v ke u. Berikut ini
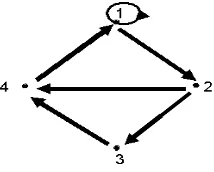
Contoh 2.3.1Representasi dari 2 buah digraph.
Gambar 2.7 : (a) digraph terhubung kuat ;(b) digraph tidak terhubung kuat
Pada gambar2.7 diatas menunjukkan bahwa (a) adalah terhubung kuat karena
terdapat walk dari satu vertex ke vertex lainnya, sedangkan (b) tidak terhubung kuat
karena tidak terdapat walk dari 1 ke 2.
Suatu digraph terhubung kuat dikatakan primitif jika terdapat bilangan bulat
positifk sehingga untuk setiap pasangan vertexu dan v diD terdapat uv-walk yang
panjangnya k.
Lemma 2.3.1 Andaikan D adalah digraph terhubung kuat maka setiap vertex v di D terletak pada cycle.
bukti : Ambil sebarang vertex v di D dan sebarang arc dari vertex u ke v di D. karenaD terhubung kuat, maka terdapat path darivken, akibatnya diperoleh suatu
path tertutup di D yang dibentuk oleh arc dari vertex v ke u di D. Oleh definisi,
path tertutup adalah suatu cycledari sebarang vertex di D, maka setiap vertexv di
D terletak pada suatu cycle.
Andaikan himpunan C = {c1, c2, . . . , ct} adalah himpunan semua cycle di D.
16
M adalah panjang cycleci(ℓ(ci)) misalkan< M >sebagai subgrup dari grup bilangan
bulat Z yang dibangun oleh kolom-kolom dariM yakni
< M > ={z1ℓ(c1) +z2ℓ(c2) +. . .+ztℓ(ct) :zi ∈Z, i= 1,2,3, . . . , t}
Andaikan D adalah digraph imprimitif dengan indeks imprimitifitas k, dan k =
gcd(ℓ(c1), ℓ(c2),· · · , ℓ(ct). Kemudian suatu digraph dikatakan primitif jika k = 1
dan imprimitf jika k 6= 1
Berikut ini diberikan representasi grafis digaph yang terhubung kuat dan
pri-mitif.
[image:36.612.264.383.408.529.2]Contoh 2.3.2Representasi dari digraph tehubung kuat
Gambar 2.8 : digraph terhubung kuat
Pada gambar 2.8 diatas, D adalah digraph terhubung kuat dengan dua cycle
yaitu 1 → 2 → 3 → 4 → 5 → 1 dengan panjang 5 dan cycle 1 → 3 → 4 → 5 → 1
dengan panjang 4. Oleh definisi diatas, maka pembagi persekutuan terbesar dari
2.3.2 2-digraph primitif.
Suatu 2-digraph D dikatakan terhubung kuat strongly connected jika untuk
setiap pasangan vertexudanvdiDterdapat walk berarah dari vertexukevdan walk
berarah dari vertexv keu, dengan mengabaikan komposisiarcyang ada. Berikut ini
diberikan contoh 2-digraph yang terhubung kuat dan 2-digraph yang tidak terhubung
kuat.
[image:37.612.206.438.308.422.2]Contoh 2.3.3Representasi dari 2 buah 2-digraph.
Gambar 2.9 : (a) 2-digraph terhubung kuat ;(b) 2-digraph tidak terhubung kuat
Pada gambar di atas menunjukkan bahwa (a) adalah 2-digraph terhubung kuat
karena terdapat walk dari satu vertex ke vertex lainnya. Sedangkan (b) adalah
2-digraph tidak terhubung kuat, karena tidak terdapat walk dari 1 ke 2.
Lemma 2.3.2 Andaikan D adalah suatu 2-digraph terhubung kuat maka setiap vertex terletak pada cycle.
Bukti. Ambil sebarang vertex v diD dan sebarang arc dari vertexu ke vertexv di D Karena terhubung kuat, maka terdapat path dari vertex v ke u dan dari vertex
18
vertexu ke v dan path dari vertex v keu di D. Oleh definisi vertex v terletak pada
suatu cycle.
Suatu 2-digraph terhubung kuat D dikatakan primitif jika terdapat bilangan
bulat tak negatifhdanksehingga untuk setiap pasangan vertexudanvdiDterdapat
(h, k)−walk dari u kev.
Andaikan komponen C ={γ1, γ2,· · · , γc} adalah himpunan semua cycle di D
adalah matrik dengan ckolom. M =
r(γ1) r(γ2) · · · r(γc)
b(γ1) b(γ2) · · · b(γc)
untuk kolom j pada
M adalah komposisi dari cycleγj kita definisikan sebagai < M >subgroup dari grup
bilangan bulat Z2 dibangun oleh kolom dari M.
Proposisi 2.3.1 Andaikan D adalah 2-digraph terhubung kuat, dan misalkan u dan v adalah vertex di D dan misalkan w1 dan w2 adalah walk dari u ke v di D. maka
r(w1)
b(w1)
−
r(w2)
b(w2)
∈< M >
Bukti: Karena D adalah 2-digraph terhubung kuat, maka terdapat walk wvu dari
v ke u. Misalkan w′
1 adalah walk tertutup yang dibentuk oleh u w1
−→ v wvu
−−→ u dan
misalkan w′
2 adalah walk tertutup yang dibentuk olehu w2
−→v wvu
−−→u. Karena untuk
setiap walk tertutup dapat dikomposisi menjadi cycle,
r(w′
1)
b(w′
1)
,
r(w′
2)
b(w′
2)
∈< M >
sehingga
r(w1)
b(w1)
−
r(w2)
b(w2)
=
r(w′
1)
b(w′
1)
−
r(w′
2)
b(w′
2)
∈< M >.
Diberikan D adalah sebuah 2-digraph dan z adalah vertex di D. Dua vertex
u dan v di D dikatakan equivalent, di u ∼2 v, bila terdapat sebuah walk wzu dari
z ke u dan sebuah walk wzv dari z ke v dengan komposisi yang sama. Dalam kasus
vertex equivalent, definisi dari equivalent vertex adalah vertex di D yang dipilih
secara bebas. Lebih lanjut, hal itu ditunjukkan oleh hubungan ∼2 adalah hubungan
kedalam kelas equivalent. Bilangan dari kelas equivalent k2 dari D disebut dengan
index imprimitivity dari D. Sebuah 2-digraph terhubung kuat dikatakan primitif
bila k2 = 1 dan imprimitif bila sebaliknya. Berikut ini kita berikan sebuah contoh
2-digraph primitif.
Contoh 2.3.2Representasi 2-digraph primitif
Gambar 2.10 : 2-digraph primitif
Perhatikan gambar diatas, kita mulai dengan arc nomor 2. Walk 2 −→b 3 dan
2−→b 1, adalah walk dari 2 ke 3 dan dari 2 ke 1 dengan komposisi yang sama. Sehingga
3 ∼2 1. Walk 2 b
−
→ 1 −→r 2 −→b 3 dan 2 →−b 3 −→b 1 −→r 2 adalah walk dari 2 ke 3 dan
dari 2 ke 2. Sehingga 3∼2 2. Dengan sifat transitif kita peroleh 1∼2 2 akibatnya,D
adalah primitif. Berikut ini akan diperlihatkan hubungan antara entri matriks hasil
representasi dengan eksponen dari 2-digraph.
2.4 Matriks tak negatif & Eksponen 2-digraph
Pada subbab ini akan dibahas pengertian matriks tak negatif dan
keterhubun-gannya dengan 2-digraph.
2.4.1 Matriks tak negatif.
Sebuah matriks dikatakan sebagai matriks tak negatif bila untuk setiap entri
matriksnyaaij adalah bilangan tak negatif, sebuah matriks dikatakan sebagai matriks
20
diberikan contoh dari matriks tak negatif dan matriks positif.
"0 1 0
0 0 1 1 0 0
#
, matriks tak negatif;
"1 2 1
2 1 1 1 1 2
#
, matriks positif
Selanjutnya akan dilihat pengertian dari eksponen dari 2-digraph dan hubungannya
dengan matriks tak negatif.
2.4.2 Eksponen digraph.
Pada digraph, eksponen dari digraph D didefinisikan sebagai bilangan bulat
terkecil k, sehingga untuk setiap pasangan vertexudanv terdapat walk berarah dari
u kev yang panjangnya k. Eksponen dari digraph D dinotasikan dengan exp(D).
Proposisi 2.4.1 Andaikan A adalah suatu matriks adjacency dari digraphD. Entri Ak
ij dari Ak menyatakan banyaknya walk dari vertex vi ke vj yang panjangnya k di
digraph D
Bukti: Andaikan A adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dariAmenyatakan arc dari vertexvi kevj di digraphD. Hal ini berakibat
untuk k = 1, maka setiap entri a1
ij dari A1 menyatakan banyaknya walk dari vertex
vi ke vj yang panjangnya satu
Asumsikan setiap entria(k)i,j dariAk menyatakan banyaknya walk dari vertexvi
ke vj yang panjangnya k di D, untuk k ≥ 1. Berikut ini diperlihatkan a(k+1)ij adalah
banyaknya walk dari vertexvi ke vj yang panjangnya k+ 1 di D, untuk k≥ 1.
Perhatikan setiap walk dari vertex vi ke vj di D dengan panjang k+ 1 yang
terdiri dari walk darivi kevldengan panjang k untukl = 1,2, . . . , n.dan dilanjutkan
dengan arc dari vertex vi kevj. Sehingga a(k)il alj adalah menyatakan walk yang
walk yang panjangnya k dari vertexvi kevj diD, makaa (k)
il = 0 sehinggaa (k)
il alj = 0.
Hal ini berarti tidak terdapat walk yang panjangnya k + 1 dari vertexvi ke vj yang
melalui vertex vl di D. Sehingga diperoleh banyaknya walk yang panjangnya k+ 1
dari vertexvi kevj diD adalah.
a(k)i1 a1j +a(k)i2 a2j+· · ·+a(k)inanj = n X
l=1
a(k)il alj
Karena
Ak+1 =AkA
maka
a(k)ij =
n X
l=1
a(k)il alj
hal ini berakibat a(k+1)ij adalah benar menyatakan banyaknya walk dari vertex vi ke
vj yang panjangnya k+ 1 di D.
Berikut ini diberikan contoh representasi grafis digraph yang akan dicari
ek-sponennya dengan menggunakan proposisi 2.4.1 diatas.
[image:41.612.176.431.205.358.2]Contoh 2.4.1representasi digraph dengan 3 vertex dan 5 arc.
Gambar 2.11 : Representasi digraph 3 vertex dan 7 arc
Dari representasi grafis digraph diatas didapat matriks adjacency A sebagai
berikut. A=
"0 1 0
0 1 1 1 0 1
#
22
vi kevj dengan panjang k adalah entri dari matriks A (k)
ij dari Ak. Dengan demikian
nilai k adalah eksponen dari digraph, bila matriks Ak adalah matriks positif.
Per-hatikan matriks Ak untuk k :
a. k = 1;A=
"0 1 0
0 1 1 1 0 1
#
bukan eksponen dari digraph pada contoh 2.4.1 diatas, karena tidak terdapat
walk dengan panjang satu, dari 1 ke 1, dari 1 ke 3, dari 2 ke 1 dan dari 3 ke 2
b. k = 2 ;A2 =
"0 1 1
1 1 2 1 1 1
#
bukan eksponen dari digraph contoh 2.4.1 diatas, karena tidak terdapat walk
dengan panjang dua, dari 1 ke 1.
c. k = 3;A3=
"1 1 2
2 2 3 1 2 2
#
Eksponen dari digraph pada contoh 2.4.1 diatas adalah 3, karena terdapat walk
dengan panjang tiga dari tiap pasangan vertex pada digraph D.
2.4.3 2-eksponen dari 2-digraph.
Pada 2-digraph D, eksponen didefisikan sebagai bilangan bulat terkecilh+k
sehingga untuk setiap pasangan vertexudanvdiD terdapat walk dariukevdengan
panjang h+k yang terdiri dariharc merah dan k arc biru. Eksponen dari 2-digraph
D dinotasikan olehexp2(D).
Lemma 2.4.1 Jika (R, B) adalah matriks adjacency dari 2-digraph D. Maka entri (i, j) dari (R, B)(h,k) adalah jumlah (h, k)-walk dari 2-digraph D
adalah walk dengan komposisi
0 1
di 2-digraph D. Dengan cara yang sama, jika
k = 0 maka (R, B)(1,0)=A adalah walk dengan entri (i, j) menyatakan walk dengan
komposisi
1 0
di 2-digraph D.
Andaikan lemma 2.4.1 benar untuk semua bilangan bulat tak negatif h′ dan
k′
dengan h′ +k′
≤ h+k akan diperlihatkan untuk h+k+ 1 adalah benar, dengan
catatan sebagai berikut.
(R, B)(h+1,k) =R(R, B)(h,k)+B(R, B)(h+1,k−1)
dengan induksi entri (i, j) pada R(R, B)(h,k) adalah walk dari i ke j diikuti
de-ngan sebuah arc merah dan diikuti oleh sebuah (h, k)-walk dari entri (i, j) pada
B(R, B)(h+1,k−1) adalah jumlah walk dari i ke j yang dimulai dengan sebuah arc
biru dan dikuti oleh sebuah (h+ 1, k −1)-walk sedemikian hingga entri (i, j) dari
(R, B)(h+1,k) adalah jumlah (h+ 1, k)-walk dari i kej
Berikut ini diberikan representasi grafis 2-digraph yang akan dicari
eksponen-nya.
[image:43.612.269.380.572.630.2]Contoh 2.4.2Representasi 2-digraph dengan 3 vertex, 3 arc biru dan 3 arc merah
24
Dari representasi 2-digraph diatas didapat matriks adjacency sebagai berikut.
Matriks adjacency merah R =
"0 1 0
0 0 0 1 1 0
#
dan
Matriks adjacency biru B =
"0 0 1
1 0 1 0 0 0
#
Dari contoh 2.4.2 kita cari eksponennya, yaitu dengan melihat penjumlahan h arc
biru dan k arc merahnya, dengan cara sebagai berikut:
a. untuk h+k = 1
1. (R, B)(1,0)=R =
"0 1 0
0 0 0 1 1 0
#
2. (R, B)(0,1)=B =
"0 0 1
1 0 1 0 0 0
#
b. untuk h+k = 2
1. (R, B)(2,0)=RR=
"0 0 0
0 0 0 0 1 0
#
2. (R, B)(1,1)=RB+BR=
"2 1 1
1 2 0 1 0 2
#
3. (R, B)(0,2)=BB =
"0 0 0
0 0 1 0 0 0
#
c. untuk h+k = 3
1. (R, B)(3,0)=RR2 =
"0 0 0
0 0 0 0 0 0
#
2. (R, B)(2,1)=R(R, B)(1,1)+BR2 =
"1 3 0
0 1 0 3 3 1
#
3. (R, B)(1,2)=RB2+B(R, B)(1,1)=
"2 0 3
3 1 3 0 0 1
4. (R, B)(0,3)=BB2 = "
0 0 0 0 0 0 0 0 0
#
d. untuk h+k = 4
1. (R, B)(4,0)=RR3 =
"0 0 0
0 0 0 0 0 0
#
2. (R, B)(3,1)=R(R, B)(2,1)+BR3 =
"0 1 0
0 0 0 1 4 0
#
3. (R, B)(2,2)=R(R, B)(1,2)+B(R, B)(2,1)=
"6 4 4
4 6 1 5 1 4
#
Untukh+k = 4 dengan komposisi arc
2 2
, 2 arc merah dan 2 arc biru, terdapat walk
dari tiap pasangan vertex u dan v di 2-digraph D sehingga 2-digraph pada contoh
2.4.2 diatas memiliki eksponen 4 dengan komposisi arc
2 2
, 2 arc merah dan 2 arc
biru.
2.5 Beberapa fakta tentang 2-digraph dengan loop
Dalam subbab ini akan diperlihatkan batas atas dan batas bawah dari eksponen
2-digraph exp2(D) dengan dua buah loop, satu dari masing-masing warna.
Teorema 2.5.1 Jika D adalah 2-digraph dengan n ≥2 vertex yang memuat sebuah loop merah dan sebuah loop biru, maka exp2(D)≤3n−3
Bukti. Diberikan i dan j vertex di 2-digraph D yang saling berhubungan di D, terdapat loop merah dan loop biru di 2-digraph D. Untuk setiap pasangan vertex
u dan v di D, selanjutnya walk wuv, u pui
−→ i −→pij j −p−jv→ v, adalah walk dari u ke v.
26
dari j ke v. Diberikan
lr = max
u∈V{r(pui)} dan lb = maxu∈V{b(pui)}
l′
r = maxv
∈V{r(pjp)} dan l
′
b= maxv
∈V {b(pjv)}
maka untuk setiap pasangan vertexu dan v adalah walk wuv dari u kev dengan
r(wuv)
b(wuv)
≤
lr+r(pij) +l′r
lb+b(pij) +l′b
adalah kejadian loop merah dan loop biru, karena walk wuv adalah kejadian loop
merah dan loop biru, walk wuv adalah sebuah walk dari u ke v dengan komposisi
lr+r(pij) +l′r
lb+b(pij) +l′b
disekitar loop merah dan loop biru adalah bilangan hasil perkalian,
sedemikian hingga
lr+lb, l′r+l
′
b, r(pij) +b(pij)≤n−1
akibatnya exp2(D) ≤3n−3
Teorema 2.5.2 Jika 2-digraphD terhubung kuat dengannvertex, sebuah loop merah dan sebuah loop biru pada vertex yang sama maka exp2(D)≤2n−2.
Bukti. Andaikan kedua loop berada pada vertex s, untuk 1 ≤ s ≤ n, dari setiap pasangan vertexi dan j di 2-digraph D, didapat Pis adalah path dari i kes dan Psj
adalah path dari s kej, jika :
lr = max
i {r(pui)} dan lb = maxi {b(pui)}
l′
r = maxj {r(pjp)} dan l′b= maxj {b(pjv)}
untuk setiap pasangan vertex i dan j di D didapat walk dari i ke j dimulai dari
vertex i, kemudian melalui path Pis sampai di vertex s kemudian diikuti path Psj
sampai ke vertex j maka :
r(wij)
b(wij)
≤
lr+l′r
lb+l′b
karena walk wij melalui kedua loop,
2-DIGRAPH DENGAN LOOP
Pada sebuah digraph dengan n vertex terdapat pernyataan bahwa eksponen
dari digraph yang demikian dinyatakan oleh exp(D) ≤ 2n−p−1, untuk p adalah
jumlah loop. Pada bab ini diberikan hasil utama tulisan ini, yakni 2-digraph dengan
sebuah cycle dan minimal sebuah loop dari masing-masing warna. Pada bab ini juga
akan diberikan batas atas dan bentuk umum eksponen 2-digraph dengan sebuah cycle
dan minimal sebuah loop dari masing-masing warna.
DiberikanD adalah 2-digraph terhubung kuat yang memiliki sebuah cycle dan
minimal sebuah loop dari masing-masing warna. Pada bagian ini diberikan syarat
agar 2-digraph yang memiliki eksponen tepat 2n-2.
Corollary 3.0.1 Jika D adalah 2-digraph terhubung kuat memiliki n vertex, sebuah cycle dan sebuah loop untuk masing-masing warna, terletak pada vertex yang sama
maka exp2(D) = 2n−2
Bukti. Dari corollary 3.1.1 didapat 2-digraph seperti berikut.
1−→2−→ · · · −→s−→ · · · −→(n−1)−→n −→1
adalah sebuah cycle γ dengan n vertex. Andaikan h dan k adalah bilangan bulat
tak negatif, sehingga untuk setiap pasangan vertex i dan j di 2-digraph D terdapat
28 Karena h k
-walk dari u ke u dengan panjang n, maka perlu mendapatkan
sebuah (h, k)-walk, w2,n walk dari 2 ke n dengan panjang minimal n+ 1. Jika walk
w2,n tidak melalui cycleγ, maka
h k =
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 0 1 +d 1 0
dengan c dan d adalah bilangan bulat tak negatif dan c+d > 2, dengan cara yang
sama walkws+1,s−1 dari vertexs+ 1 ke vertexs−1 tidak melalui cycleγ, akibatnya
h k =
r(γ) b(γ)
−
r(Ps−1,s+1)
b(Ps−1,s+1)
karena w2,n dan ws+1,s−1 tidak melalui cycleγ maka
r(γ) b(γ)
−
r(Ps−1,s+1)
b(Ps−1,s+1)
=
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 0 1 +d 1 0
r(Ps−1,s+1)
b(Ps−1,s+1)
−
r(Pn,2)
b(Pn,2)
=−c
0 1 −d 1 0 ,
Karena r(ps−1,s+1)−r(pn,2)≤2 dan b(ps−1,s+1)−b(pn,2)≤2 akibatnya 2 2 ≥ −d −c ,
atau c+d > −4, kontradiksi dengan c+d > 2. Sehingga w2,n atau ws+1,s−1 harus
melalui cycle γ. Karena path p2,n dan path ps+1,s−1 mempunyai panjang n −2,
dan p2,n harus melalui cycle γ maka h+k ≥ 1T
r(γ) b(γ)
+n−2 = 2n−2 sehingga
exp2(D) ≥ 2n−2. Dari teorema 2.5.2 didapat h+k ≤ 2n−2 sedemikian hingga
h+k= 2n−2. Akibatnyaexp2(D) = 2n−2
Corollary 3.1.1 menyatakan bahwa bila 2-digraph memiliki sebuah loop dari
masing-masing warna terletak pada vertex yang sama, maka eksponennyaexp2(D) =
2n−2. Berikut ini diberikan corollary yang menyatakan eksponenexp2(D) = 2n−1
dari tiap warna, Pn,2 adalah sebuah path dengan komposisi
2 0
, dan ps−1,s+1 adalah
path dengan komposisi
1 1
. Jika loopnya terletak pada vertex 1 dan vertex s maka
exp2(D) = 2n−1.
Bukti. Dengan tidak mengurangi keumuman, didapat 2-digraph sebagai berikut
1−m→2−→ · · · −→(s−1)−m→s−→b (s+ 1)−→ · · · −→n−m→1
adalah sebuah cycle γ dan Pn,2 adalah sebuah path dengan komposisi
2 0
, ps−1,s+1
adalah sebuah path dengan komposisi
1 1
,(s, s) adalah sebuah loop merah, dan (1,1)
adalah sebuah biru. Andaikan h dan k adalah bilangan bulat tak negatif, sehingga
untuk setiap pasangan vertexidan j di 2-digraphD terdapat (h, k)-walk dariikej.
Selanjutnya sebuah (h, k)-walk,w2,n walk dari 2 ken dengan panjang minimal
n+ 1. Jika walk w2,n tidak melalui cycleγ, maka
h k =
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 1 0
dengan c adalah bilangan bulat dan c > 2 dengan cara yang sama, karena ws+1,s−1
walk dari vertexs+ 1 ke vertexs−1 tidak melalui cycleγ, maka
h k =
r(γ) b(γ)
−
r(Ps−1,s+1)
b(Ps−1,s+1)
+d 0 1 ,
dengan d adalah bilangan bulat dand≥ 2. Bilaw2,n danws+1,s−1 tidak melalui cycle
γ maka
r(γ) b(γ)
−
r(Ps−1,s+1) b(Ps−1,s+1)
+d 0 1 =
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 1 0
r(Ps−1,s+1)
b(Ps−1,s+1)
−
r(Pn,2)
b(Pn,2)
=−c
30 2 2 ≥ −c d
, akibatnya d <2, kontradiksi dengan d >2. Sehingga w2,n atauws+1,s−1
harus melalui cycle γ. Walk w2,n dengan komposisi
2r(γ)−2 2b(γ)
dan walk ws+1,s−1
dengan komposisi
2r(γ)−1 2b(γ)−1
, dari komposisi kedua walk diatas didapath≥2r(γ)−1
dank ≥2b(γ) akibatnyah+k ≥2r(γ)−1+2b(γ) = 2n−1 sehingga exp2(D)≥2n−1
Untuk menunjukkanexp2(D)≤2n−1, maka harus ditunjukkan untuk setiap
vertexi dan j di 2-digraph D terdapat walkwi,j, dengan komposisi
r(wi,j)
b(wi,j
=
2r(γ)−1 2b(γ)
Untuk menunjukkan komposisi walk diatas, dapat dilakukan dengan membagi dalam
empat kasus. Untuk :
a) Terdapat dua buah loop diantara vertex i dan j
Dengan tidak mengurangi keumuman pembuktian, didapat 2−digraph sebagai
berikut, i −→ · · · −→m 1 −→ · · ·m −→m s −→ · · · −b → j adalah sebuah path. Karena D
adalah 2-digraph terhubung kuat, maka untuk setiap i dan j di 2-digraph D
terdapat walkwi,j dengan h k =
r(pi,j)
b(pi,j)
+ (2r(γ)−1)−b(pi,j)
0 1
+ 2b(γ)−
r(pi,j)
1 0
sehingga h+k= 2n−1.
b) Terdapat sebuah loop merah diantara vertexi dan j
Didapat 2−digraph sebagai berikut. i−→ · · · −→s−1−→m s−→b s+ 1→ · · · −→j
adalah sebuah path. Karena D adalah 2-digraph terhubung kuat, maka untuk
setiap i dan j di 2-digraph D terdapat (h, k)-walk. dengan
h k =
r(pi,j)
b(pi,j)
+
r(pj,i)
b(pj,i)
+(r(γ)−r(pi,j)−1)
1 0
+(b(γ)−b(pi,j)) 0 1 +
r(pi,j)
b(pi,j)
c) Terdapat sebuah loop biru diantara vertexidan j
Didapat 2-digraph sebagai berikut. i−→ · · · −→n −→m 1−→m 2 −→ · · · −→ j, adalah
sebuah path. Karena D adalah 2-digraph terhubung kuat, maka untuk setiap i
dan j di 2-digraph D terdapat (h, k)-walk. Dengan
h k =
r(pi,j)
b(pi,j)
+
r(pj,i)
b(pj,i)
+ (b(γ)−b(pi,j) 0 1 +
r(pi,j)
b(pi,j
+r(γ)−1−r(pi,j)
1 0
Sehingga h+k = 2n−1
d) Tidak terdapat kedua loop diantara vertexi dan j
Didapat 2−digraph sebagai berikut. i → · · · →j adalah sebuah path. Karena
D adalah 2-digraph terhubung kuat, maka untuk setiap i dan j di 2-digraph D
terdapat walk (h, k)-walk. dengan
h k =
r(pi,j)
b(pi,j)k
+r(γ)−1−r(pi,j)
1 0
+b(γ)−b(pi,j) 0 1 +
r(pj,i)
b(pj,i)
+
r(pi,j)
b(pi,j)
Sehingga h+k = 2n−1
Dari kasus a, b, c, dan d didapat h+k = 2n−1 sehingga exp2(D) ≤h+k = 2n−1
akibatnya exp2(D) = 2n−1
Corollary 3.1.2 diatas memberikan batasan agar 2-digraph memiliki eksponen
tepat 2n −1. Berikut ini akan dibahas batasan agar 2-digraph memiliki eksponen
tepat 2n
Corollary 3.0.3 Diberikan 2-digraph D terhubung kuat dengan n vertex, memiliki 1 cycle, 1 loop dari tiap warna, Pn,2 adalah path merah, dan Ps−1,s+1 adalah path biru.
32
Bukti. Dengan tidak mengurangi keumuman, didapat 2-digraph sebagai berikut
1−→m 2−→ · · · −→(s−1)−→b s−→b (s+ 1) −→ · · · −→n −→m 1
adalah sebuah cycle γ dan Pn,2 adalah sebuah path dengan komposisi
2 0
, ps−1,s+1
adalah sebuah path dengan komposisi
0 2
,(s, s) adalah sebuah loop merah, dan (1,1)
adalah sebuah biru. Andaikan h dan k adalah bilangan bulat tak negatif, sehingga
untuk setiap pasangan vertexidan j di 2-digraphD terdapat (h, k)-walk dariikej.
Selanjutnya sebuah (h, k)-walk,w2,n walk dari 2 ken dengan panjang minimal
n+ 1. Jika walk w2,n tidak melalui cycleγ, maka
h k =
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 1 0
dengan c adalah bilangan bulat dan c > 2 dengan cara yang sama, karena ws+1,s−1
walk dari vertexs+ 1 ke vertexs−1 tidak melalui cycleγ, maka
h k =
r(γ) b(γ)
−
r(Ps−1,s+1)
b(Ps−1,s+1) +d 0 1 ,
dengan d adalah bilangan bulat dand≥ 2. Bilaw2,n danws+1,s−1 tidak melalui cycle
γ maka
r(γ) b(γ)
−
r(Ps−1,s+1)
b(Ps−1,s+1)
+d 0 1 =
r(γ) b(γ)
−
r(Pn,2)
b(Pn,2) +c 1 0
r(Ps−1,s+1)
b(Ps−1,s+1)
−
r(Pn,2)
b(Pn,2)
=−c
1 0 +d 0 1 , 2 2 ≥ −c d
, akibatnya d <2, kontradiksi dengan d >2. Sehingga w2,n atauws+1,s−1
harus melalui cycle γ. Walk w2,n dengan komposisi
2r(γ)−2 2b(γ)
dan walk ws+1,s−1
dengan komposisi
2r(γ) 2b(γ)−2
, dari komposisi kedua walk diatas didapat h ≥ 2r(γ)
Untuk setiap pasangan vertex i dan j di 2-digraph D terdapat (2r,2b)-walk.
w(i,j) dariikej. Untuk setiap pasangan vertexidanj, sebuah walkwi,j dimulai dari
vertexidikuti olehpi,j kej adalah sebuah walk dariikej dengan komposisi dibatasi
oleh
2r 2b
. Selanjutnyawi,j melalui loop merah dan loop biru, dengan memanfaatkan
loop merah dan loop biru tersebut, untuk setiap pasangan vertex i dan j terdapat
(2r,2b)-walk dari i kej sehingga exp2(D)≤2n, akibatnyaexp2(D) = 2n
Pada bab ini telah didapat bentuk umum agar 2−digraph memiliki eksponen
exp2(D) tepat 2n−2,2n−1, dan 2n. Pada bab selanjutnya akan diberikan kesimpulan
BAB 4
KESIMPULAN
Pada bab ini akan diberikan kesimpulan yang didapat dari hasil tulisan dan
penelitian pada bab - bab terdahulu, selanjutnya akan diberikan saran untuk
diper-gunakan dalam penelitian lebih lanjut.
4.1 Kesimpulan
Kesimpulan yang didapat adalah syarat agar 2-digraph dengan 2-loop memiliki
eksponen tepat 2n, 2n−1, 2n−2 dengan n jumlah vertex. Eksponen dari 2-digraph
dengan 2-loop dan n vertex dapat diketahui dari komposisi warna arc yang adjacent
dengan loop merah maupun loop biru pada 2-digraph tersebut. Kesimpulan dari
tulisan ini adalah sebagai berikut :
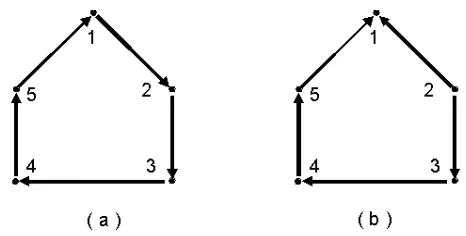
1. 2-digraph dengan eksponen tepat 2n didapat jika arc yang adjacent ke loop
merah adalah sepasang arc yang berwarna merah dan untuk loop biru adalah
sepasang arc yang berwarna biru, atau sebaliknya. Untuk lebih jelasnya
Representasi 2-digraph
Gambar 4.1 : Representasi 2-digraph dengan 2-eksponen 2n
2. 2-digraph dengan eksponen tepat 2n−1 didapat jika arc yangadjacentke loop
merah adalah sepasang arc berwarna merah dan arc yangadjacentke loop biru
adalah sepasang arc yang berbeda warna, atau sebaliknya. Untuk lebih jelasnya
perhatikan gambar berikut ini.
Representasi 2-digraph
Gambar 4.2 : Representasi 2-digraph dengan 2-eksponen 2n-1
3. 2-digraph dengan eksponen tepat 2n−2 didapat kedua loop terletak pada vertex
yang sama
4.2 Saran
Diperlukan penelitian lebih lanjut, untuk menentukanexp2(D) dengan
[image:55.612.212.438.456.519.2]36
DAFTAR PUSTAKA
[1] Bo Z, dan Liu B, Matrices with Maximum Exponents in The Class of Doubly Stochastic primitive matrices, Discrete Applied Mathematics. ,(199) vol 91, hal 53-56.
[2] B.L Shader and Suwilo, Exponent of nonnegatif pairs, Linear Algebra App. 363(2003), 275 -293
[3] E. Fornasini and M.E. Valcher, directed graphs, 2D state models and characteristic polinomials of irreducible matrix pairs. Linear Algebra App. 263(1997), 275-310.
[4] Holladay J. C and Varga R. S, On Powers of Nonnegative Matrices. Proc. Math. Amer. Soc. 9 (1958), vol 9 631–634.
[5] Schneider H, Wielandt’s Proof of The Exponent Inequality for Primitive Nonneg-ative Matrices, Linear Algebra Appl. 353 (2002), 5-10.
[6] R.A Brualdi and H.J Ryser,Combinatorial Matrix Theory,Cambridge University press, Cambridge, 1991
[7] S.G Lee and J.M Yang, Bound for 2-exponent of primitif extremal ministrong digraph, Commun. Korean. Math. Soc 20(2005), no1, 51-62
[8] S. Suwilo,2-exponent of two cycles,Procedings of the 12th National Conference of
Indonesian Mathematical Society,(2004),218-226
[9] S.Suwilo, Exponent set of complete asymetric 2-digraph, IRCMSA 2005 proced-ings, (2005), 51-56