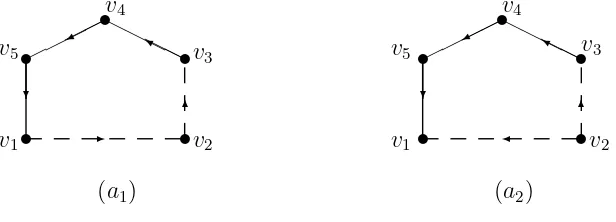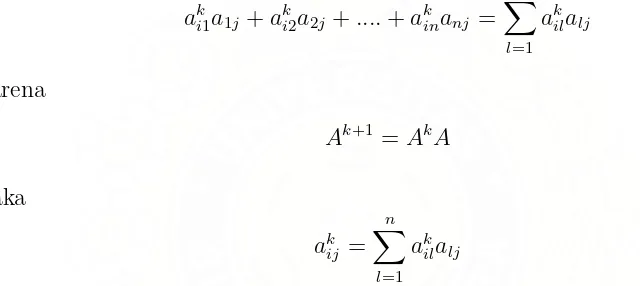EKSPONEN DIGRAPH DWI-WARNA DENGAN DUA CYCLE YANG BERSINGGUNGAN
SKRIPSI
Deni Ramadani Saragih 040803002
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana
Sains
DENI RAMADANI SARAGIH 040803002
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
i
PERSETUJUAN
Judul : EKSPONEN DIGRAPH DWI-WARNA
DEN-GAN DUA CYCLE YANG BERSINGGUNDEN-GAN
Kategori : SKRIPSI
Nama : DENI RAMADANI SARAGIH
Nomor Induk Mahasiswa : 040803002
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Febuari 2009
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Mardiningsih, M.Si Dr. Saib Suwilo, MSc.
NIP.131803344 NIP. 131796149
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
EKSPONEN DIGRAPH DWI-WARNA DENGAN DUA BUAH CYCLE YANG BERSINGGUNGAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Febuari 2009
iii
PENGHARGAAN
Setinggi puji dan sedalam syukur penulis serahkan kehadirat Allah SWT yang telah memberikan berkat dan rahmatNya sehingga penulis dapat menye-lesaikan skripsi yang berjudul ” EKSPONEN DIGRAPH DWI-WARNA DENGAN DUA BUAH CYCLE YANG BERSINGGUNGAN ”ini den-gan baik. Skripsi ini sebagai salah satu mata kuliah wajib yang harus diselesaikan oleh seluruh mahasiswa Fakultas MIPA Departemen Matematika.
Pada kesempatan ini penulis mengucapkan terima kasih kepada :
1. Bapak Dr. Eddy Marlianto, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
2. Bapak Dr. Saib Suwilo, M.Sc, dan Bapak Henry Rani S, M.Si selaku Ketua dan Sekretaris Departemen Matematika di FMIPA USU Medan.
3. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Dra. Mar-diningsih, M.Si selaku dosen pembimbing II yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini.
4. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.
5. Ayahanda Sarpanuddin Saragih dan Ibunda Sutini yang selalu memberikan dukungan moril dan materiel serta doa yang tiada hentinya kepada penulis serta kepada Abangda Sahdansyah Putra, S.Kom yang telah memberikan dorongan semangat kepada penulis.
Tak lupa, penulis juga mengucapkan terima kasih kepada para senior dan Ju-niordi di Lab. Ekstension, yang telah membantu dalam penyelesaian skripsi ini, Seluruh rekan-rekan ’04 khususnya Indra, Ramidin, Revin, Taufiq, Robby, Rajali, Gunyanto dan Hemi serta rekan-rekan lainnya yang tidak dapat disebutkan satu-persatu. Semoga Allah SWT memberikan balasan atas jasa-jasa mereka yang telah diberikan kepada penulis.
Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.
Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi yang membutuhkan.
Medan, Febuari 2009
Penulis,
ABSTRAK
v
2-EKSPONENTS OF TWO COLORED DIGRAPHS WITH TWO CYCLES WHOSE HAVE A COMMON VERTEX
ABSTRACT
Let D be a two-colored digraph whose two cycles are primitive on n ≥ 4 vertex which have a common vertex and the length of each cycle is m and m −1 with m≥ 3. This research will describe an upper bound and lowwer bound of exp2(D) such that 12(n2+n)≤exp2(D)≤ 1
2(2n
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
BAB
1. PENDAHULUAN 1
1.1. Latar Belakang Penelitian 1
1.2. Masalah Penelitian 2
1.3. Tinjauan Pustaka 2
1.4. Tujuan Penelitian 4
1.5. Desain dan Metodologi Penelitian 4
2. 2-DIGRAPH PRIMITIF 6
2.1. Notasi 6
2.2. Matriks Adjancency 10
2.3. Primitifitas Dari 2-digraph Terhubung Kuat 13
2.4. Matriks tak negatif dan Eksponen 2-digraph 16
2.5. Formula 2-eksponen 2-digraph dengan dua cycle 22
3. EKSPONEN 2-DIGRAPH DENGAN DUA CYCLE YANG
BERSINGGUNGAN 25
4. KESIMPULAN DAN SARAN 34
4.1. Kesimpulan 34
4.2. Saran 35
vii
DAFTAR GAMBAR
Gambar Halaman
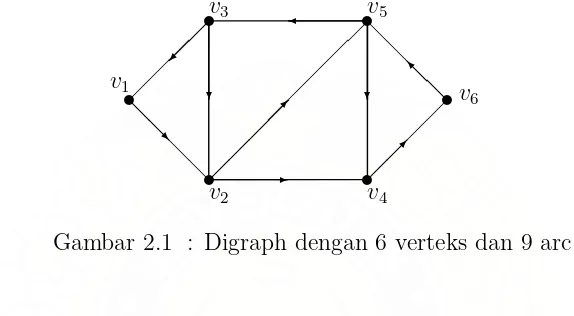
2.1 Digraph dengan 6 verteks dan 9 arc 7
2.2 Digraph dengan 5 verteks dan 7 arc 8
2.3 Representasi grafis dari 2-digraph. 9
2.4 2-Digraph dengan 9 verteks, 6 arc merah dan 4 arc biru. 10
2.5 Digraph dengan 4 verteks dan 4 arc. 11
2.6 Representasi dari sebuah 2-digraph. 12
2.7 Digraph primtif 14
2.8 Digraph dengan 3 verteks dan 5 arc. 17
2.9 2-Digraph dengan 4 verteks, 3 arc merah dan 2 arc biru 19
3.1 2-Digraph primitif dengan 5 arc merah dan 2 arc biru 31
3.2 2-Digraph primitif dengan 5 arc merah dan 2 arc biru 32
4.1 2-DigraphD yang memenuhi batas atas bagi exp2D 34
PENDAHULUAN
1.1 Latar Belakang Penelitian
Fornasini dan Valcher memberikan konsep digraph dwi-warna, yakni suatu
digraph yang setiap arcnya diwarnai merah atau biru (Fornasini dan Valcher,
1997). Suatu digraph-dwiwarna D adalah primitif jika terdapat bilangan bulat tak negatif h dan k sehingga untuk setiap pasangan verteks u dan v di D ada suatu (h, k) walk dari u ke v dan dari v keu. Eksponen dari digraph dwi-warna yang dinotasikan dengan exp2(D) adalah bilangan bulat positifh+k terkecil yang terdiri dari h arc berwarna merah dan k arc berwarna biru. Riset tentang ek-sponen dari digraph dwiwarna dimulai oleh Shader dan Suwilo (2003). Mereka
memperlihatkan bahwa bila D adalah digraph dwi-warna atas n verteks, maka eksponen terbesar dari D terletak pada interval [12(n3−5n2),1
2(3n3+ 2n2−2n)].
Penelitian pada 2-eksponen dari digraph dwi-warna lebih banyak dilakukan
untuk mencari suatu digraph dwi-warna primitif atas n verteks dengan eksponen lebih besar dari 12(n3 −5n2). Yakni dengan mencari 2-eksponen suatu digraph dwi-warna yang terhubung kuat dan mempunyai arc sesedikit mungkin.
Beberapa peneliti memfokuskan pada digraph dwi-warna yang terdiri dari
dua cycle dengan beberapa verteks persekutuan. Lee dan Yang (2005) mem-berikan batas bagi 2-eksponen dari ministrong 2-digraph dengan n − 3 verteks persekutuan, yakni bilaDadalah ministrong digraph primitif maka 2n2−8n+ 7 ≤ exp2(D) ≤ 2n2 −5n + 3. Shao dan Gao (2005) memberikan batas dan ekspo-nen dari 2-digraph dengan n +s verteks dan n −m verteks persekutuan, yakni andaikan D adalah 2-digraph atas n + s, s ≥ 0, m ≥ s + 1 verteks maka, 2n2−3n+1≤exp
2
Suwilo mendiskusikan dua kelas ministrong 2-digraph. Yakni bilaD adalah min-istrong 2-digraph atasn = 2m, m≥3 dann= 2m+ 1, m≥4 verteks dengann−5 verteks persekutuan, maka 2n2−10n+ 10≤exp2(D)≤ 1
2(2n3−5n2+ 7n−2) dan 2n2−14n+22≤exp2(D)≤ 1
2(n3−8n2+20n−15). Penelitian ini akan menentukan 2-eksponen serta batas atas dan batas bawah dari 2-eksponen digraph dwi-warna
primitif dengan dua cycle yang memiliki satu verteks persekutuan.
1.2 Masalah Penelitian
AndaikanDadalah suatu digraph dwi-warna primitif dengan dua buah cycle yang saling bersinggungan dan panjang masing-masing cycle adalahmdan m−1. Masalah dari penelitian ini adalah
1. Untuk menentukan fungsi F(n) dan G(n), sehingga memenuhi sifat F(n)≤ exp2(D)≤G(n).
1.3 Tinjauan Pustaka
Suatu graph berarah yang selanjutnya dikatakan digraph adalah suatu
him-punan tak kosong V = {v0, v1, ..., vm} yang elemen-elemen nya disebut verteks dan himpunan garis-garis berarah A yang elemen elemennya disebut arc. Suatu walk dengan panjang m dari sebuah digraph D yang menghubungkan verteks u dan verteks v adalah suatu barisan arc di Ddalam bentuk
u=v0 →v1 →v2 →, ...,→vm−1 →vm =v
dengan m > 0, v0 = u dan vm = v. Suatu walk dikatakan terbuka jika u 6= v dan tertutup jikau=v. Suatupath adalah suatuwalk tanpa perulangan verteks. Suatu digraph dikatakanterhubung kuat jika untuk setiap pasangan dari verteks
k. Eksponen dari D dan dinotasikan dengan exp(D) adalah bilangan positif k terkecil dari keseluruhan bilangan tak negatif k. Suatu digraph terhubung kuat adalah primitif jika dan hanya jika pembagi persekutuan terbesar dari panjang
cycle-cycle di D adalah 1 (Brualdi dan Ryser, 1991).
Fornasini dan Valcher (1997) memberikan konsep digraph-dwiwarna yang
selanjutnya dikatakan2-digraph, yakni suatu digraph yang setiap arcnya diwarnai
dengan warna merah atau biru, sehingga komponen terpenting dari suatu walk
tidak hanya panjangnya melainkan komposisinya, yakni banyaknya arc berwarna
merah dan arc berwarna biru pada walk tersebut. Suatu (h, k) -walk w pada suatu2-digraph D adalah suatu walk yang terdiri darih arc berwarna merah dan
k arc berwarna biru. Banyaknya h arc berwarna merah dank arc berwarna biru pada suatu walk w dinotasikan dengan r(w) dan b(w). Suatu vektor (r(w), b(w)) dikatakan komposisi dari walkw. Suatu 2-digraph dikatakan terhubung kuat jika digraph nya juga terhubung kuat.
Suatu2-digraph dikatakan primitif jika terdapat bilangan bulat tak negatif
h dan k sehingga untuk setiap pasangan verteks u dan v terdapat (h, k)-walk dari u ke v. Bilangan bulat tak negatif h + k yang terkecil dari keseluruhan bilangan tak negatifhdankdikatakan sebagai2-eksponen dariDyang dinotasikan denganexp2(D). AndaikanDadalah 2-digraph dan misalkan{γ1, γ2, ..., γl}adalah himpunan semua cycle yang berada diD. Suatu matriks cycle M dari D adalah
suatu matriks ber ordo 2×t, yakniM =
"
r(γ1) r(γ2) ... r(γl) bγ1) b(γ2) ... r(γl)
#
. Dengan kolom
ke-tdariM merupakan komposisi dari cycleγtdan 2 menyatakan banyaknya warna yang dipakai. Suatu 2-digraph D dikatakan primitif jika pembagi persekutuan terbesar dari minor-minor 2×2 dariM adalah 1 (Fornasini dan Valcher, 1997).
Suwilo dan Shader (2006) memberikan formula bagi 2-eksponen dari 2-digraph
yang terdiri atas dua cycle, yakni
exp2(D) =ℓ(γ1)ℓ′
r+ℓ(γ2)ℓ
′
4
Dengan ℓ(γ1) dan ℓ(γ2) adalah panjang masing-masing cycle di Ddan
ℓ′r = max
u,v∈V{b(γ2)r(Puv)−r(γ2)b(Puv)}. (1.2) ℓ′b = max
u,v∈V{r(γ1)b(Puv)−b(γ1)r(Puv)}. (1.3) Selanjutnya dengan formula tersebut, Suwilo dan Shader (2006) memperbaiki
batas 2-eksponen dari ekstremal ministrong digraph yang diberikan oleh Lee dan
Yang menjadi 2n2−8n+ 7≤exp
2(D)≤2n2−7n+ 3.
1.4 Tujuan Penelitian
Penelitian ini bertujuan untuk mencari batas bawah dan batas atas bagi
2-eksponen dari digraph-dwiwarna primitif dengan dua buah cycle yang saling
bersinggungan dan panjang masing-masing cycle adalahm danm−1. Yakni akan ditentukan FungsiF(n) dan G(n) sehingga F(n)≤exp2(D)≤G(n).
1.5 Desain dan Metodologi Penelitian
Metode penelitian ini bersifat literatur atau kepustakaan. Untuk
menen-tukan suatu fungsi F(n) dan G(n) sehingga F(n)≤exp2(D)≤G(n). Penentuan batas atas dan bawah dari digraph dwiwarna primitif dengan dua cycle yang
bers-inggungan dilakukan dengan menggunakan pendekatan berikut ini.
1. Dengan bantuan software two exp.
2. Dengan menggunakan formula yang diberikan Suwilo (Suwilo dan Shader,
2006), yakni exp2(D) = ℓ(γ1)ℓ′r+ℓ(γ2)ℓ
′
Pada penelitian ini b(γ1) = b(γ2) = 1. Sehingga ℓ′r dan ℓ′b dapat diseder-hanakan menjadi
ℓ′r = max
u,v∈V{r(Puv)−r(γ2)b(Puv)} (1.4)
ℓ′b = max
BAB 2
2-DIGRAPH PRIMITIF
Pada bab ini diberikan beberapa konsep dasar seperti teorema dan beberapa
defenisi sebagai landasan dalam penelitian ini. Konsep dasar ini berkaitan dengan
masalah yang dibahas dalam tulisan ini sepertidigraph, 2-digraph, terhubung kuat,
2-digraph primitif dan 2-eksponen dari 2-digraph.
2.1 Notasi
Pada subbab ini akan dibahas beberapa notasi digraph yang akan
dipergu-nakan dalam pembahasan 2-digraph.
2.1.1 Digraph.
Suatu digraph terdiri dari titik-titik yang dihubungkan oleh garis berarah.
Secara formal, digraph adalah objek yang terdiri dari dua himpunan yaitu.
1. Himpunan berhingga tak kosong V ={v0, v1, ..., vm}. Unsur dari V disebut verteks dari digraph D.
2. HimpunanAyang merupakan himpunan bagian dari pasangan berurutV×V dengan verteks-verteksnya tidak harus berbeda dan unsur-unsurnya disebut
arc dari digraphD.
Jika diberikan β = (u, v) adalah suatu arc di D, maka verteks u disebut sebagai verteks awal dan verteks v disebut sebagai verteks akhir. Suatu arc (u, v) dapat juga dinotasikan dengan u→v.
Suatu digraph dapat direpresentasikan secara grafis dengan cara setiap verteks
direpresentasikan sebagai sebuah titik dan setiap arc (u, v) direpresentasikan
se-bagai garis berarah dari titiku kev.
Representasi dari digraph yang diberikan pada Contoh 2.1 diberikan pada
gambar berikut.
Contoh 2.2Representasi Grafis dari digraph yang diberikan pada Contoh 2.1
t
v1
t
v2
t
v3
t
v5
❅ ❅
❅ ❅ ❅
❅ ❘
✲ ✠
t
v4
tv6 ❅
❅ ❅
❅ ✛
✒ ❄ ❄
✒ ❅
❅ ■
Gambar 2.1 : Digraph dengan 6 verteks dan 9 arc
Andaikan D adalah suatu digraph dan misalkan u dan v adalah verteks di digraphD. Suatu walk dengan panjangmdariukev didefinisikan sebagai barisan
arc dan dituliskan sabagai
v0 →v1 →v2 →...→vm−1 →vm
untuk m > 0, v0 = u dan vm =v. Suatu walk dikatakan terbuka jika u 6= v dan tertutup jika u=v. Suatupath adalah suatu walk tanpa perulangan verteks dan suatu cycle didefinisikan sebagai suatu path tertutup.
Berikut ini akan diberikan representasi dari digraph untuk menjelaskan
8
Contoh 2.3 Diberikan digraph dibawah ini.
t
t t
t
t ❙❙
❙ ❙
❙ ❙
❙ ❙ ❙
❙ ❙
❙
✇ ❄
✲
❏ ❏ ❏ ❏ ❏ ❏ ❏ ❏
❏ ❏ ❫
✟ ✟ ✟ ✟
✟ ✟ ✙ ❩ ❩ ❩ ❩ ❩ ❩ ❩ ❩
❩ ❩ ❩ ❩ ⑥ ✒
t
v1 tv2
tv3
t
v4
t
v5
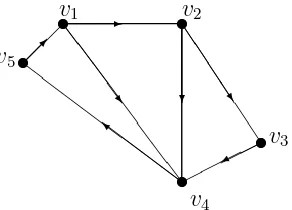
Gambar 2.2 : Digraph dengan 5 verteks dan 7 arc
Digraph pada gambar 2.2 memiliki walk, path dan cycle sebagai berikut :
a. Barisan arc berikut ini v1 → v4 → v5 → v1 →v2 →v4 adalah sebuah walk tetapi bukan path karena ada perulangan verteks.
b. Barisan arc berikut ini v2 →v3 →v4 adalah sebuah path terbuka.
c. Barisan arc berikut ini v1 →v4 →v5 →v1 adalah sebuah cycle.
2.1.2 2-Digraph.
Andaikan D adalah suatu digraph dengan m verteks v1, v2, ..., vm. Suatu digraph dwi-warna atau 2-digraph adalah suatu digraph D yang setiap arcnya diwarnai dengan dua warna, dalam hal ini merah atau biru. Suatu arc merah (u, v) dinotasikan dengan u −→r v dan suatu arc biru (u, v) dinotasikan dengan u−→b v.
Contoh 2.4 Himpunan verteks V = {v1, v2, v3, v4, v5, v6, v7, v8} bersama dengan himpunan arc merahR={(v1, v2),(v2, v3),(v4, v5),(v5, v6),(v5, v7),(v7, v8),(v8, v1)} dan arc biru B = {(v3, v4),(v6, v1)} adalah suatu 2-digraph dengan 8 verteks, 7 arc merah dan 2 arc biru.
Suatu 2-digraph dapat direpresentasikan secara grafis dengan cara sebagai
1. Setiap verteks direpresentasikan sebagai suatu titik.
2. Setiap arc merah direpresentasikan sebagai garis atau kurva berarah tak putus.
3. Setiap arc biru direpresentasikan sebagai garis atau kurva berarah putus-putus .
Berikut ini akan diberikan suatu contoh representasi 2-digraph pada Contoh
2.4 diperlihatkan pada gambar dibawah ini.
Contoh 2.5: Representasi grafis dari 2-digraph pada Contoh 2.4.
t
v2
t
v3
t
v4
t
v5
t
v6
t
v1
t
v8
t
v7
❆ ❆
❆
❆ ✁✁ ✁✁
❆ ❆ ❆ ❆ ✁
✁ ✁ ✁
❍ ❍ ❍ ❍ ✁ ✁ ✁ ✁ ✁ ✁ ✁ ✁
✲ ✁✁✕ ❆ ❆ ❆❑ ✻ ✛
✁ ✁ ✁☛
❍ ❍ ❍ ❨
❆ ❆❆❯
✁ ✁ ✁☛
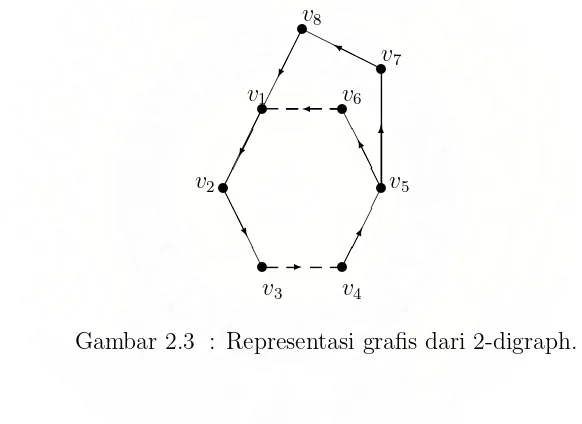
Gambar 2.3 : Representasi grafis dari 2-digraph.
Suatu (h, k)-walk w pada 2-digraphD adalah suatu walk yang panjangnya h+k, terdiri dari h arc merahdank arc biru. Banyaknya dari arc merah dan arc biru dari suatu walkw, masing-masing dinotasikan denganr(w) dan b(w). Vektor
"
r(w) b(w)
#
disebut komposisi dari walk w.
10
Contoh 2.6Diberikan 2-digraph dibawah ini.
t
t t
v1 v2
v3
v4
v5t t
t
t t t
✲
v6 ✡ v7✲ v8✲ ✡✡
✡✡ ✡
✡✡ ✡ ✣
✲ v9 ✲
❏ ❏
❏ ❏
❏ ❏ ❏
❏ ❏❫
✡ ✡ ✡ ✡ ✡ ✡
✡ ✡ ✡ ✢
✛ ❏
❏ ❏ ❏ ❏ ❏
❏ ❏ ❏ ❪
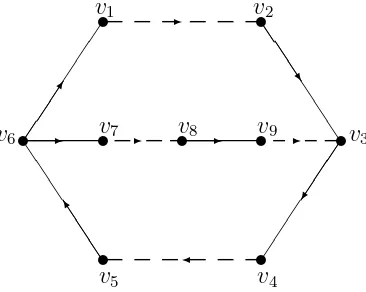
Gambar 2.4 : 2-Digraph dengan 9 verteks, 6 arc merah dan 4 arc biru.
2-Digraph pada Gambar 2.4 diatas memiliki path, walk dan cycle sebagai
berikut
a. Barisan arc berikut iniv1 −→b v2 −→r v3 −→r v4 −→b v5 adalah sebuah path terbuka dari v1 kev5 dengan komposisi walk
"
2 2
#
.
b. Barisan arc berikut ini v1 −→b v2 −→r v3 −→r v4 −→b v5 −→r v6 −→r v1 adalah sebuah path tertutup atau sebuah cycle dari v1 ke v1 dengan komposisi walk
"
4 2
#
.
c. Barisan arc berikut ini v3 −→r v4 →−b v5 −→r v6 −→r v7 −→b v8 −→r v9 −→b v3 −→b v4 adalah suatu walk dari v3 ke v4 dengan komposisi walk
"
4 4
#
.
Suatu digraph atau 2-digraph dapat di representasikan kedalam sebuah
ma-triks, berikut ini akan diberikan hubungan antara digraph dan 2-digraph dengan
matriks.
2.2 Matriks Adjancency
Pada sub bab ini akan dibahas hubungan antara digraph, 2- digraph dengan
oleh (0,1)-matriks, yang entri dari matriks itu adalah bilangan 0 atau 1. Matriks
yang demikian disebut sebagaimatriks adjacency.
2.2.1 Matriks Adjancency dari Digraph
Untuk setiap digraph D dengan m verteks dapat dituliskan suatu (0,1)-matriks A(D) = (aij) sebagai berikut.
aij =
1, jika terdapat arc darivi kevj di D
0, jika sebaliknya Untuk i, j = 1,2, ..., m
Matriks A(D) disebut sebagai matriks adjacency dari digraphD.
Berikut ini akan diberikan contoh matriks adjacency dari sebuah representasi
digraph.
Contoh 2.7Jika diberikan representasi dari sebuah digraph seperti berikut ini.
t
t
t
t
✑✑ ✑✑
✑✑
✑✑ ✑ ✸
◗◗ ◗
◗ ◗
◗ ◗◗
◗ s
✑ ✑ ✑ ✑ ✑ ✑
✑ ✑ ✑ ✰
◗ ◗ ◗ ◗ ◗ ◗
◗ ◗ ◗ ❦
v1 v3
v2
v4
Gambar 2.5 : Digraph dengan 4 verteks dan 4 arc.
Maka, dari representasi digraph pada Gambar 2.5 diatas diperoleh matriks
adja-cency sebagai berikut
0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0
12
2.2.2 Matriks Adjacency 2-digraph
Pada 2-digraph D atas m verteks, untuk menentukan (0,1)-matriks adalah sebagai berikut. Matriks adjacency merah, R = [rij] pada D adalah matriks ber ordo m×m dengan
rij =
1, jika terdapat arc merah dari vi ke vj diD
0, jika sebaliknya.
Matriksadjacency biru, B = [bij] pada Dadalah matriks ber ordo m×m dengan
bij =
1, jika terdapat arc biru dari vi ke vj diD
0, jika sebaliknya.
Berikut ini akan diberikan sebuah 2-digraph dan direpresentasikan kedalam
matriks adjacency.
Contoh 2.8 Bila representasi dari sebuah 2-digraph seperti berikut ini.
t
t
t t
✛ ✡✡
✡✡ ✡✡
✡✡ ✡
✣ ❫
✲
✛ ❏
❏ ❏ ❏ ❏ ❏
❏ ❏
v1
v2
v3 v4
Gambar 2.6 : Representasi dari sebuah 2-digraph.
Maka, representasi 2-digraph pada Gambar 2.6 diatas dapat dibuat kedalam
dua buah matriks adjacency sebagai berikut
Matriks adjacency ini, R =
0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0
matriks adjacency ini, B =
0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0
adalah matriks adjacency biru.
Berikut ini akan dibahas tentang digraph dan 2-digraph terhubung kuat dan
keterhubungan dengan digraph dan 2-digraph primitif.
2.3 Primitifitas Dari 2-digraph Terhubung Kuat
Pada bagian ini akan dibahas tentang digraph dan 2-digraph terhubung kuat
dan keterhubungan dengan primitifitas.
2.3.1 Digraph Primitif.
Suatu digraph D dikatakan terhubung kuat, jika untuk setiap pasangan verteks u dan v di D terdapat walk dariu ke v dan walk dari v keu. Berikut ini akan diberikan contoh digraph terhubung kuat dan digraph yang tidak terhubung
kuat.
Contoh 2.9Digraph terhubung kuat dan tidak terhubung kuat
t
v1 tv2
t
v4
t
v5 tv3
✲ ✻
❍ ❍ ❍ ❍
❍ ❍ ❨ ✟ ✟ ✟ ✟
✟ ✟ ✙
❄
(a)
t
v1 tv2
t
v4
t
v5 tv3
✛ ✻
❍ ❍ ❍ ❍
❍ ❍ ❨ ✟ ✟ ✟ ✟
✟ ✟ ✙
❄
(b)
Gambar pada Contoh 2.9 menunjukkan bahwa (a) adalah terhubung kuat
karena terdapat walk dari suatu verteks ke verteks lainnya, sedangkan (b) tidak
14
Andaikan himpunan C = {γ1,γ2,...,γt} adalah himpunan semua cycle di D. Maka panjang dari cycle - cycle pada digraphDdinotasikan denganℓ(γi) dimana i= 1,2,· · ·, t.
Suatu digraph terhubung kuat D adalah primitif jika dan hanya jika pem-bagi persekutuan terbesar dari panjang-panjang cycle diDadalah 1 (Brualdi dan Ryser, 1991). Berikut ini diberikan representasi grafis digraph yang terhubung
kuat dan primitif.
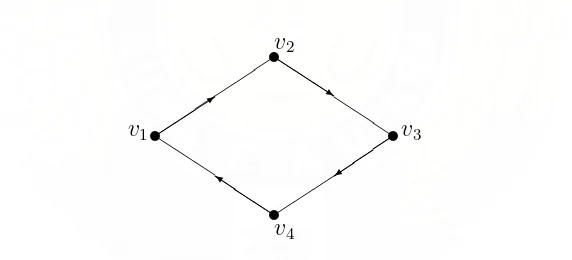
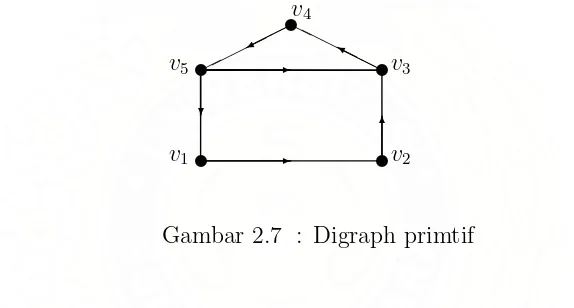
Contoh 2.10Digraph yang terhubung kuat di bawah ini adalah primitif.
✉
v1
✉
v2
✉
v3
✉
v4
✉
v5
✲
✻ ❍ ❍ ❍ ❍ ❍
❍ ❍ ❍ ❨ ✟ ✟ ✟ ✟ ✟
✟ ✟ ✟ ✙
❄
✲
Gambar 2.7 : Digraph primtif
Pada gambar 2.7 diatas,D adalah digraph terhubung kuat dengan dua cycle yaitu,v1 →v2 →v3 →v4 →v5 →v1 dengan panjang 5 dan cyclev3 →v4 →v5 → v3 dengan panjang 3. Oleh defenisi diatas, maka pembagi persekutuan terbesar dari cycle dengan panjang 5 dan 4 adalah 1, makaD adalah primitif.
2.3.2 2-Digraph Primitif.
Suatu 2-digraph D dikatakan terhubung kuat jika untuk setiap pasangan verteks udan v diD terdapat walk berarah dari verteks u kev dan walk berarah dari verteks v keu, dengan mengabaikan komposisi arc yang ada.
Berikut ini diberikan Contoh 2-digraph yang terhubung kuat dan 2-digraph
Contoh 2.112-Digraph terhubung kuat dan tidak terhubung kuat
t
v1 tv2
t
v4
t
v5 tv3
✻ ❍ ❍ ❍ ❍
❍ ❍ ❨ ✟ ✟ ✟ ✟
✟ ✟ ✙
❄
✲
(a1)
t
v1 tv2
t
v4
t
v5 tv3
✛ ✻
❍ ❍ ❍ ❍
❍ ❍ ❨ ✟ ✟ ✟ ✟
✟ ✟ ✙
❄
(a2)
Gambar pada contoh 2.11 diatas menunjukkan bahwa (a1) adalah terhubung
kuat karena terdapat walk dari suatu verteks ke verteks lainnya, sedangkan (a2)
tidak terhubung kuat karena tidak terdapat walk dari v1 kev2.
Andaikan D adalah 2-digraph yang terhubung kuat dan andaikan C = {γ1, γ2,· · ·, γt} merupakan himpunan semua cycle di D. Matriks cycle D adalah matriks berordo 2×t
M =
"
r(γ1) r(γ2) ... r(γt) b(γ1) b(γ2) ... b(γt)
#
dimana kolom ke-t dari M merupakan komposisi dari cycle γt dan 2 menyatakan banyak warna yang di pakai.
Suatu 2-digraphDterhubung kuat dikatakanprimitifjika terdapat bilangan bulat tak negatif h dan k sehingga untuk setiap pasangan verteks u dan v di D terdapat (h, k) walk dariu kev dan v keu. Suatu 2-digraph Ddikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari determinan-determinan
submatriks ber ordo 2×2 dari M adalah 1 (Fornasini dan Valcher, 1997).
Contoh 2.12Dari Gambar 2.6 diperoleh matriks cycle dari 2-digraph, yakni
M =
"
2 1 1 1
#
16
ordo 2×2 dari M adalah 1. Maka 2-digraph tersebut adalah primitif.
2.4 Matriks tak negatif dan Eksponen 2-digraph
Suatu matriks dikatakan sebagai matriks tak negatif bila untuk setiap
en-tri maen-triksnya aij adalah bilangan tak negatif, sebuah matriks dikatakan sebagai matriks positif bila untuk setiap entri matriksnyaaij adalah bilangan positif.
Berikut ini akan diberikan contoh dari matriks tak negatif dan matriks
posi-tif.
Contoh 2.13Matriks tak negatif dan matriks positif.
Matriks ini
0 1 2 0 1 0 1 0 1
adalah matriks tak negatif dan matriks ini
1 1 2 1 1 1 1 2 1
adalah
matriks positif.
Pada digraph D, eksponen dari suatu digraphDdidefenisikan sebagai bilan-gan bulat terkecilk, sehingga untuk setiap pasangan verteksudanvdiDterdapat walk berarah dariukev dengan panjangk. Eksponen dari digraphDdinotasikan denganexp(D).
Proposisi 2.1 AndaikanAadalah suatu matriks adjacency dari digraphD. Entri Ak
ij dari Ak menyatakan banyaknya walk dari verteks vi ke vj yang panjangnya k di D.
Bukti andaikan A adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dari A menyatakan arc dari verteks vi ke vj di digraph D. Hal ini berakibat untukk= 1, maka setiap entria1ij dari A1 menyatakan banyaknya walk dari verteks vi ke vj yang panjangnya satu.
Asumsikan setiap entriak
ak+1ij adalah banyaknya walk darivi kevj yang panjangnyak+ 1 diD, untukk ≥1
Perhatikan setiap walk dari verteks vi ke verteks vj di D dengan panjang k+ 1 yang terdiri dari walk vi ke vl dengan panjang k untuk l = 1,2, ..., n dan dilanjutkan dengan arc dari verteks vi ke vj. Sehingga ak
ilalj adalah walk yang panjangnya k + 1 dari verteks vi ke vj di D untuk k = 1,2, ..., n. Jika terdapat walk yang panjangnyak dari verteks vi ke verteksvj di D, maka ak
il = 0 sehingga ak
ilalj = 0. Hal ini berarti tidak terdapat walk yang panjangnyak+ 1 dari verteks vi ke vj yang melalui verteks vl di D. Sehingga diperoleh banyaknya walk yang panjangnyak+ 1 dari verteksvi ke verteksvj di D adalah.
aki1a1j +aki2a2j+....+akinanj = n
X
l=1 akilalj
Karena
Ak+1 =AkA
maka
akij = n
X
l=1 akilalj
Hal ini berakibat ak+1ij adalah benar menyatakan banyaknya walk dari verteks vi kevj yang panjangnya k+ 1 di D.
Berikut ini diberikan contoh representasi grafis digraph yang akan dicari
ek-sponennya dengan menggunakan Proposisi. 2.1 diatas.
Contoh 2.13Representasi digraph dengan 3 verteks dan 5 arc.
t t
t
✛ ✡✡
✡✡ ✡✡
✡✡ ✡ ✣
❏ ❏
❏ ❏
❏ ❏ ❏
❏ ❏ ❫
✒✑ ✓✏
✒✑ ✓✏ t
v1
t
v2
tv3
▼ ✍
Gambar 2.8 : Digraph dengan 3 verteks dan 5 arc.
18
sebagai berikut. A =
1 1 0 0 0 1 1 0 1
, dari Proposisi 2.1 untuk mencari banyak walk
dari verteks vi ke vj dengan panjang k adalah entri dari matriks Ak
ij dari Ak. Dengan demikian nilai k adalah eksponen dari digraph. Perhatikan matriks Ak untukk :
a. Untuk k = 1; diperoleh A =
1 1 0 0 0 1 1 0 1
, maka bukan merupakan eksponen
dari digraph pada Contoh 2.4.2, karena tidak terdapat walk dengan panjang
1 dari v2 kev1,v1 kev3, v2 kev2 dan dari v3 kev2.
b. Untuk k = 2; diperoleh A2 =
1 1 0 1 0 1 2 1 1
, maka bukan merupakan eksponen
dari digraph pada Contoh 2.4.2, karena tidak terdapat walk dengan panjang
dua dari v1 ke v3 dan v2 kev2.
c. Untuk k = 3; diperoleh A3 =
1 1 1 2 1 1 3 2 2
, karena terdapat walk dengan
panjang 3 dari tiap pasangan verteks pada digraph D, maka eksponen dari digraph pada Contoh 2.4.2 adalah 3.
AndaikanA danB adalah suatu matriks tak negatif ber ordom×m. Untuk bilangan tak negatif h dan k di definisikan (h, k)-Hurwitz product, (A, B)(h,k), dariA dan B adalah jumlah keseluruhan matriks dari hasil perkalianA sebanyak h kali dan B sebanyak k kali. Sebagai contoh, (A, B)(1,0) = A dan (A, B)(2,2) = A2B2+ABAB+AB2A+BABA+B2A2.
Lemma 2.2 jika (R, B) adalah matriks adjacency dari 2-digraph. Maka entri (i, j) dari (R, B)(h,k) adalah jumlah (h, k)-walk dari 2-digraph.
(R, B)(0,1) =B adalah walk dengan komposisi
"
0 1
#
di 2-digraph D. Dengan cara
yang sama, jikak = 0 maka (R, B)(1,0) =A adalah walk dengan entri (i, j)
meny-atakan walk dengan komposisi
"
1 0
#
di 2-digraph D.
Andaikan lemma 2.5 benar untuk semua bilangan bulat tak negatif h′ dan k′ denganh′+k′ ≤h+k akan diperlihatkan untukh+k+ 1 adalah benar dengan catatan sebagai berikut.
(R, B)(h+1,k) =R(R, B)(h,k)+B(R, B)(h+1,k−1)
dengan induksi entri (i, j) padaR(R, B)h,k adalah walk dari i kej diikuti dengan sebuah arc merah dan diikuti oleh sebuah (h, k) − walk dari entri (i, j) pada B(R, B)(h+1,k−1) adalah walk dari i ke j yang dimulai dengan sebuah arc biru
dan diikuti oleh sebuah (h+ 1, k −1)−walk sedemikian hingga entri (i, j) dari (R, B)(h+1,k) adalah jumlah h+ 1, k-walk dari i kej.
Berikut ini diberikan representasi grafis 2-digraph yang akan diberikan
ek-sponennya.
t
t
t t
✛ ✡✡
✡✡ ✡✡
✡✡ ✡ ✣
❏ ❏
❏ ❏
❏ ❏ ❏
❏ ❏ ❫
✲
✛ v1
v2
v3 v4
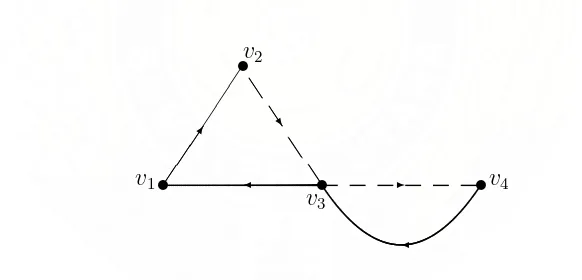
Gambar 2.9 : 2-Digraph dengan 4 verteks, 3 arc merah dan 2 arc biru
Dari representasi 2-digraph diatas, dapat dibuat dua buah matriksadjacency sebagai berikut
1. Matriks R =
0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0
adalah matriks adjacency merah pada Gambar
20
2. MatriksB =
0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0
adalah matriks adjacency biru pada Gambar 2.9.
Dari Lemma 2.2, entri (i, j) dari (R, B)(h,k) adalah banyaknya (h, k)-walk dari 2-digraph, makah+k terkecil adalah eksponen dari 2-digraph. Selanjutnya akan diperlihatkan matriks (R, B)(h,k) untuk beberapa h+k :
1. Untuk h+k = 2, maka diperoleh;
a. (R, B)(2,0) =R(R, B)(1,0)=
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
b. (R, B)(0,2) =R(R, B)(0,1)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
c. (R, B)(1,1) =R(R, B)(0,1)+R(R, B)(1,0)=
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
.
Untuk h+k = 2, maka bukan merupakan 2-eksponen dari 2-digraph pada Gambar 2.9 karena untuk setiap komposisi dari (R, B)(h,k) memuat (h,
k)-walk dengan panjang tidak sama dengan 2.
2. Untuk h+k = 3, maka diperoleh;
a. (R, B)(3,0) =R(R, B)(2,0)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
b. (R, B)(0,3) =B(R, B)(0,2)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
c. (R, B)(1,2) =R(R, B)(0,2)+B(R, B)(1,1)=
0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0
.
d. (R, B)(2,1) =R(R, B)(1,1)+B(R, B)(2,0)=
0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0
.
[image:30.595.115.443.362.772.2]Untuk h+k = 3, maka bukan merupakan 2-eksponen dari 2-digraph pada Gambar 2.9 karena untuk setiap komposisi dari (R, B)(h,k) memuat (h,
k)-walk dengan panjang tidak sama dengan 3.
Selanjutnya untukh+k= 10, maka diperoleh
a. (R, B)(10,0) =R10=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
.
b. (R, B)(0,10)=B10=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
.
c. (R, B)(9,1) =R(R, B)(8,1)+B(R, B)(9,0)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
.
d. (R, B)(1,9) =R(R, B)(0,9)+B(R, B)(1,8)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
22
e. (R, B)(2,8) =R(R, B)(1,8)+B(R, B)(2,7)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
.
f. (R, B)(8,2) =R(R, B)(7,2)+B(R, B)(8,1)=
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
.
g. (R, B)(3,7) =R(R, B)(2,7)+B(R, B)(3,6)=
0 0 0 0 0 0 0 0 38 0 0 38
0 0 0 0
.
h. (R, B)(6,4) =R(R, B)(5,4)+B(R, B)(4,5)=
3 1 1 3 3 3 4 3 1 3 6 1 3 3 4 3
.
Karena untuk setiap pasangan verteks u dan v di 2-digraph D terdapat walk dengan panjang 10 dengan 6 arc merah dan 4 arc biru, maka eksponen dari
2-digraphD adalah 10.
2.5 Formula 2-eksponen 2-digraph dengan dua cycle
Misalkan Dadalah suatu 2-digraph primitif dengan dua cycle γ1 dan γ2 dan
misalkan M =
"
r(γ1) r(γ2) b(γ1) b(γ2)
#
. Karena D adalah primitif maka det(M) = 1.
Untuk setiap pasangan verteks udan v, andaikanpuv adalah path terpendek dari uke v. Dan didefenisikan
ℓ′r = max
u,v∈V{b(γ2)r(puv)−r(γ2)b(puv)} (2.1) ℓ′b = max
Teorema 2.3 Andaikan D adalah suatu 2-digraph primitif yang terhubung kuat dengan dua cycle dengan paling sedikit satu arc pada masing-masing warna . Maka
exp2(D) = ℓ(γ1)ℓ′r+ℓ(γ2)ℓ
′
b.
Bukti Misalkan M adalah matriks cycle di D.Asumsikan det(M)=1. Anggap bahwa 2-eksponenD memuat (h, k)-walk. Akan ditunjukkan bahwa
" h k # =M "
ℓ′r ℓ′
b
#
(2.3)
Persamaan (2.3) mengakibatkan bahwa (h+k) = r(γ1)ℓ
′
r+r(γ2)ℓ
′
b+b(γ1)ℓ
′
r+ b(γ2)ℓ
′
b. Oleh karena itu exp2(D) = ℓ(γ1)ℓ
′
r+ℓ(γ2)ℓ
′
b.
Misalkan s dan t adalah bilangan non negatif sehingga
" h k # =M " s t # . (2.4)
Karena setiap (h, k) walk dari suatu verteks uke verteks v dapat berbentuk suatu perjalanan dariukev dengan mengelilingi cycleγ1 danγ2 kemudian menuju sebuah pathpuv dari uke v maka,
" h k # =M " z1 z2 # + " r(puv) b(puv) # (2.5)
untuk beberapa bilangan bulat tak negatif z1 dan z2. Persamaan (2.4) dan (2.3) mengakibatkan bahwa
" z1 z2 # = " s t #
- M−1
" r(puv) b(puv) # ≥ " 0 0 #
. Oleh karena itu,
"
s t
#
≥M−1
" r(puv) b(puv) # = "
b(γ2)r(puv)−r(γ2)b(puv) r(γ1)r(puv)−b(γ1)r(puv)
#
. (2.6)
24
"
h k
#
≥
"
ℓ′r ℓ′b
#
dan exp2(D)≥ℓ(γ1)ℓ′r+ℓ(γ2)ℓ
′
b.
Sekarang akan ditunjukkan bahwa exp2(D) ≤ ℓ(γ1)ℓ
′
r +ℓ(γ2)ℓ
′
b. Untuk be-berapa pasanga verteksu dan v, misalkan puv adalah path terpendek dariu ke v. Anggap suatu sistem persamaan diophantine
M
"
z1 z2
#
+
"
r(puv) b(puv)
#
=M
"
ℓ′r ℓ′b
#
(2.7)
Maka solusi dari sistem (2.7) adalah
"
z1 z2
#
=
"
ℓ′r−[b(γ2)r(puv)−r(γ2)b(puv)] ℓ′b−[r(γ1)b(puv)−b(γ1)r(puv)]
#
.
Oleh persamaan (2.1) dan (2.2) diperoleh ℓ′r ≥ b(γ2)r(puv) − r(γ2)b(puv) dan ℓ′b ≥ r(γ1)b(puv)− b(γ1)r(puv) untuk semua path terpendek puv, maka z1 ≥ 0 dan z2 ≥ 0. Oleh karena itu sistem (2.7) mempunyai solusi bilangan bulat tak negatif.
Hal ini mengakibatkan bahwa untuk setiap pasangan verteks u dan v, ter-dapat suatu uv −walk di D yang terdiri dari ℓ′rr(γ1) +ℓ′br(γ2) arc merah dan ℓ′rb(γ1) +ℓ′bb(γ2) arc biru. Yakni suatu walk yang berawal dari titik u, bergerak mengelilingiz1 kali cycleγ1 dan z2 kali cycleγ2, setelah kembeli keu menuju path
puv dan berakhir pada path v. Oleh karena itu exp2(D ≤ℓ(γ1)ℓ′
r+ℓ(γ2)ℓ
′
b. maka dapat disimpulkan bahwaexp2(D=ℓ(γ1)ℓ′
r+ℓ(γ2)ℓ
′
EKSPONEN 2-DIGRAPH DENGAN DUA CYCLE YANG BERSINGGUNGAN
Andaikan D adalah suatu 2-digraph primitif dengan m≥3 dann = 2m−2 verteks terdiri dari cycle 1 → 2 → 3 → ... → m −1 → m dan cycle m → m+ 1→ m+ 2 →...→ 2m−2 →m. Andaikan γ1 dan γ2 adalah cycle-cycle di D dengan pajang m dan m−1. Maka matriks cycle D mempuyai bentuk M =
"
m−a m−1−b
a b
#
untuk beberapa bilangan bulat a dan b sehingga 0≤ a≤m dan 0≤b ≤m−1. KarenaD adalah primitif dan berapa banyak warna diantara merah dan biru padaDdapat dipertukarkan, maka det(M) = (b−a)m+a=±1. Untuk det(M) = (b−a)m+a= 1 diperoleh a = 1 dan b= 1. Selanjutnya untuk det(M) = (b−a)m+a=−1 diperoleha =m−1 danb=m−2, sehingga diperoleh dua buah matriks cycleM =
"
m−1 m−2
1 1
#
atauM =
"
1 1
m−1 m−2
#
. Tanpa
menghilangkan keumumannya dapat diambil suatu matriksM =
"
m−1 m−2
1 1
#
.
Teorema 3.1 Andaikan D adalah 2-primitif digraph atas n = 2m− 2, m ≥ 3 verteks, dengan matriks cycle
"
m−1 m−2
1 1
#
, maka 12(n2 +n) ≤ exp2(D) ≤ 1
2(2n
2+n−2).
Bukti. Pertama sekali akan dibuktikan batas atas dari 2-eksponen D. Dari Teo-rema 2.6 mengakibatkan bahwa batas atas akan tercapai apabila ℓ′r dan ℓ′b besar. Hal ini terjadi ketika panjang path merah dan path biru pada digraphD adalah 2m−3 dan 2. Oleh persamaan 2.1 dan 2.2 maka diperoleh suatu persamaan baru, yakni
ℓ′r = max
26
ℓ′b = max
u,v∈V{(m−1)b(puv)−r(puv)} (3.2)
denganV adalah himpunan verteks di D
Sehingga ℓ′r akan besar apabila D memuat path merah r(puv) dari u ke v dengan panjang (2m−3) dan tidak memuat path birub(puv) dari u kev, ℓ′b akan besar apabilaDmemuat path biru b(puv) dariu kev dengan panjang 2 dan tidak memuat path merah r(puv) dari u ke v. Dari persamaan 3.1 dan 3.2 diperoleh ℓ′r = (2m−3) dan ℓ′b = (2m−2). Sehingga diperoleh
Exp2(D) =ℓ(γ1)ℓ
′
r+ℓ(γ2)ℓ
′
b =m(2m−3) + (m−1)(2m−2) = 4m2−7m+ 2 = 1
2(2n
2+n−2).
Selanjutnya akan dibuktikan batas bawah dari 2-eksponen D. Batas bawah bagi 2-eksponen D akan tercapai jika ℓ′r dan ℓ′b kecil. Hal ini terjadi apabila 2-digraphD mempunyai dua buah path merah terpisah dengan panjangm−1 dan m−2. Andaikan path puv adalah path dariu kev, karenaM =
"
m−1 m−2
1 1
#
maka masing-masing cycle dari digraph(D) memuat sebuah arc biru. Hal ini
berakibat setiap path puv haruslah memuat paling banyak 2 buah arc biru, oleh karena itu akan diperlihatkan kedalam dua kasus, yakni ketika path puv pada 2-digraph D mempunyai dua arc biru dan path puv pada 2-digraph D mempunyai sebuah arc biru.
Kasus 1. Path pada 2-digraph D mempunyai dua arc biru
Andaikan path x0 →x1 →, ...,→ xm−2 → xm−1 dan path y0 → y1 →, ...,→
ym−3 →xm−2 masing-masing adalah suatu path merah dengan panjangm−1 dan
m−2, maka masing-masing path mempunyai komposisi
"
m−1 0
#
dan
"
m−2 0
#
,
sehingga diperoleh ℓ′r = (m− 1). Selanjutnya kita perhatikan suatu path dari xm−1 ke x0 dan suatu path dari xm−2 ke x0 maka, masing-masing path memiliki
komposisi
"
2 m−1
#
dan
"
2 m−2
#
, dan diperoleh ℓ′b = (m), sehingga
Exp2(D) = ℓ(γ1)ℓ′
r+ℓ(γ2)ℓ
′
b = (m)(m−1) + (m−1)(m) = 2m2−2m= 12(n
Kasus 2. Path pada 2-digraph D mempunyai sebuah arc biru.
Andaikan path x0 →x1 →, ...,→ xm−2 → xm−1 dan path y0 → y1 →, ...,→ ym−3 →xm−2 masing-masing adalah suatu path merah dengan panjangm−1 dan m−2, maka path-path ini harus terletak pada masing-masing cycle γ1 dan γ2 dan mimiliki komposisi
"
m−1 0
#
dan
"
m−2 0
#
, sehingga diperoleh ℓ′r = (m−1). Selanjutnya kita perhatikan suatu path terpendek darixm−1 kex0 dan suatu path
terpendek dari xm−2 ke x0 maka, masing-masing path memiliki komposisi
"
0 1
#
,
sehingga diperolehℓ′b = (m−1) dan Exp2(D) = ℓ(γ1)ℓ
′
r+ℓ(γ2)ℓ
′
b = (m)(m−1) + (m−1)(m−1) = 2m2 −3m+ 1 = 1
2(n2+n).
Dari kasus 1 dan kasus 2 dapat disimpulkan batas bawah dari exp2(D) ≥ 1
2(n2+n). Sehingga diperoleh pembuktian bahwa 1
2(n2+n)≤exp2(D)≤ 1
2(2n2+ n−2).
Sekarang akan diperlihatkan karekteristik dari suatu 2-digraph sehingga
men-capai batas bawah dan batas atas dari Theorema 3.1.
Akibat 3.2 Andaikan D adalah 2-digraph primitif dan M =
"
m−1 m−2
1 1
#
,
denganm ≥3. Maka exp2(D) = 4m2−7m+ 2 jika dan hanya jika D mempunyai path merah dengan panjang2m−2 dan path biru dengan panjang 2.
28
Sekarang asumsikan bahwaexp2(D) = 4m2−7m+2 maka, akan ditunjukkan bahwa untuk setiap pasangan verteksudan v diD terdapat suatu (4m2−11m+ 7,4m−5)−walk dari ukev. Hal ini berakibat terdapat suatu pathpuv dari uke v dan bilangan bulat tak negatif z1 dan z2 sehingga
M " z1 z2 # + " r(Puv) b(Puv) # = "
4m2 −11m+ 7 4m−5
# dan diperoleh " z1 z2 # = "
(2m−3)−[r(puv)−(m−2)b(puv)] (2m−2)−[(m−1)b(puv)−r(puv)]
#
untuk beberapa pathpuv dari u kev.
Karena path puv memuat paling banyak 2 buah arc biru, maka akan diper-lihatkan kedalam 3 kasus yakni ketika path puv tidak memuat arc biru, memuat sebuah arc biru dan memuat dua buah arc biru.
• Path puv tidak memuat arc biru
Andaikan path puv tidak memuat arc biru, maka diperoleh penyelesaian z1 dan z2, yakni
" z1 z2 # = "
(2m−3)−r(puv) (2m−2) +r(puv)
#
, dengan r(puv) = 1,2, ...,2m−3
maka sebuah walk dimulai padau, mengelilingi ((2m−3)−r(puv)) kali cycle γ1, ((2m−2) +r(puv)) kali cycle γ2, setelah kembali ke umenuju sebuah path puv ke v. Mempunyai komposisi
((2m−3)−r(puv))
"
m−1 1
#
+ ((2m−2) +r(puv))
"
m−2 1 # + " r(puv) 0 # = "
4m2−11m+ 7 4m−5
#
.
• Path puv memuat sebuah arc biru
Andaikan pathpuv memuat sebuah arc biru, maka diperoleh penyelesaianz1 dan z2, yakni
" z1 z2 # = "
(3m−5)−r(puv) (m−1) +r(puv)
#
, dengan r(puv) = 0,1,2, ...,2m−3
v. Mempunyai komposisi
((3m−5)−r(puv))
"
m−1 1
#
+ ((m−1) +r(puv))
"
m−2 1
#
+
"
r(puv) 1
#
=
"
4m2−11m+ 7 4m−5
#
.
• Path puv memuat dua buah arc biru
Andaikan path puv memuat dua buah arc biru, maka diperoleh penyelesaian
z1 dan z2, yakni
"
z1 z2
#
=
"
(4m−7)−r(puv) r(puv)
#
, dengan r(puv) = 0,1,2, ...,2m−3
maka sebuah walk dimulai padau, mengelilingi ((4m−7)−r(puv)) kali cycle γ1, r(puv) kali cycleγ2, setelah kembali keumenuju sebuah pathPuv kev. Mempunyai komposisi
((4m−7)−r(puv))
"
m−1 1
#
+r(puv)
"
m−2 1
#
+
"
r(puv) 2
#
=
"
4m2−11m+ 7 4m−5
#
.
Dari ke tiga kasus diatas menunjukkan bahwaexp2(D) = 4m2−7m+ 2 jika dan hanya jikaDmemuat path biru dengan panjang 2 dan path merah dengan panjang 2m−2.
Selanjutnya akan diberikan suatu karakteristik sehingga D memenuhi batas bawah bagiexp2(D).
Akibat 3.3 AndaikanDadalah 2-digraph primitif dengan matriks cycle
"
m−1 m−2
1 1
#
,
denganm ≥3. Maka exp2(D) = 2m2−3m+ 1 jika dan hanya jika D mempunyai dua path merah terpisah dengan panjang m−1 danm−2dan path pada 2-digraph D memuat paling banyak sebuah arc biru.
Bukti. Anggap D adalah suatu 2-digraph dengan path pada D memuat paling banyak sebuah arc biru. Andaikan (i, j) dan (m, n) adalah masing-masing sebuah
30
merah terpisah dengan panjang m −1 dan m −2. Oleh karena itu diperoleh ℓ′r =m−1 danℓ′b =m−1 sehingga exp2(D) = 2m2−3m+ 1.
Sekarang asumsikan bahwaexp2(D) = 2m2−3m+1 maka, akan ditunjukkan bahwa untuk setiap pasangan verteks u dan v di D terdapat suatu (2m2−5m+ 3,2m−2)−walk dari u kev, berakibat terdapat suatu path puv dari u kev dan bilangan bulat tak negatifz1 dan z2 sehingga
M
"
z1 z2
#
+
"
r(Puv) b(Puv)
#
=
"
2m2 −5m+ 3 2m−2
#
dan diperoleh
"
z1 z2
#
=
"
(m−1)−[r(puv)−(m−2)b(puv)] (m−1)−[(m−1)b(puv)−r(puv)]
#
untuk beberapa pathpuv dari u kev.
Karena path puv memuat paling banyak sebuah arc biru, maka kita akan menganggap kedalam 2 kasus yakni ketika path (puv) tidak memuat arc biru dan
memuat sebuah arc biru.
• Path (puv) tidak memuat arc biru
Andaikan path (puv) tidak memuat arc biru, maka diperoleh penyelesaianz1 dan z2, yakni
"
z1 z2
#
=
"
(m−1)−r(puv) (m−1) +r(puv)
#
, dengan r(puv) = 1,2, ...,2m−3
maka sebuah walk dimulai pada u, mengelilingi ((m−1)−r(puv)) kali cycle γ1, ((m−1) +r(puv)) kali cycleγ2, setelah kembali ke u menuju sebuah path puv ke v. Mempunyai komposisi
((m−1)−r(puv))
"
m−1 1
#
+ ((m−1) +r(puv))
"
m−2 1
#
+
"
r(puv) 0
#
=
"
2m2−5m+ 3 2m−2
#
.
• Path (puv) memuat sebuah arc biru
Andaikan path (puv) memuat sebuah arc biru, maka diperoleh penyelesaian
"
z1 z2
#
=
"
(2m−3)−r(puv) r(puv)
#
, dengan r(puv) = 0,1,2, ...,2m−3
maka sebuah walk dimulai padau, mengelilingi ((3m−5)−r(puv)) kali cycle γ1, ((m−1) +r(puv)) kali cycleγ2, setelah kembali ke u menuju sebuah path puv ke v. Mempunyai komposisi
((2m−3)−r(puv))
"
m−1 1
#
+ (r(puv))
"
m−2 1
#
+
"
r(puv) 1
#
=
"
2m2−5m+ 3 2m−2
#
.
Argument diatas menunjukkan bahwa exp2(D) = 2m2 −3m + 1 jika dan hanya jika D mempunyai dua path merah terpisah dengan panjang m −1 dan m−2 dan path pada 2-digraph Dmemuat paling banyak sebuah arc biru.
Berikut ini akan diperlihatkan beberapa contoh batas atas dari 2-digraph
primitif dengan dua cycel yang bersinggungan, dengan suatu 2-digraph primitif
dengan setruktur yang lebih sederhana.
Contoh 3.12-Digraph primitif dengan 5 arc merah dan 2 arc biru.
t
v2
t
v3
t
v5
t
v1
t
v4 t
v6
■
✒ ❘
✠
✒ ❘
[image:40.595.112.467.387.549.2]✛
Gambar 3.1 : 2-Digraph primitif dengan 5 arc merah dan 2 arc biru
Digraph D mempunyai dua buah cycle yakni, suatu (3,1)-cycle dan (2,1)-cycle.
Matriks cycle dari D adalah M =
"
3 2 1 1
#
, sehingga diperoleh ℓ′r = 5 dan ℓ′b = 6
dan Exp2(D)≤ℓ(γ1)ℓ′
r+ℓ(γ2)ℓ
′
b = (4)(5) + (3)(6) = 38.
32
Contoh 3.2Akan diperlihatkan suatu (27,11)−walk dari verteks v1 ke verteks v2. Terdapat suatu pathpv1,v2 dariv1 kev2 yang mempunyai komposisi
"
1 0
#
yakni,
r(pv1,v2) = 1 dan b(pv1,v2) = 0. Selanjutnya akan ditemukan solusi tak negatif dari
z1 dan z2 untuk M " z1 z2 # + "
r(pv1,v2)
b(pv1,v2)
# = " 27 11 # . Karena " 27 11 # = 4 " 3 1 # + 7 " 2 1 # + " 1 0 #
maka, z1 = 4 dan z2 = 7. Oleh karena itu
suatu (27,11)−walk dari v1 kev2 adalah v1
r − →v2
r − →v3
r − →v4
7γ2
−−→v4 3γ1
−−→v4 b − →v1
r − →v2, denganv4
3γ1
−−→v4 adalah suatu walk yang bermula pada v4 dan berakhir pada v4 dan 3 kali mengelilingi cycleγ1.
Selanjutnya akan diperlihatkan batas bawah dari 2-digraph primitif dengan
dua cycel yang bersinggungan, dengan suatu 2-digraph primitif dengan setruktur
yang lebih sederhana.
Contoh 3.32-Digraph primitif dengan 5 arc merah dan 2 arc biru.
t v2 t v3 t v5 t v1 t v4
tv6
[image:41.595.107.470.370.583.2]■ ✒ ❘ ✠ ✒ ❘ ✛ ❅ ❅ ❅ ❅ ❅❅
Gambar 3.2 : 2-Digraph primitif dengan 5 arc merah dan 2 arc biru
Digraph D mempunyai dua buah cycle yakni, suatu (3,1)-cycle dan (2,
1)-cycle. Matriks cycle dari D adalah M =
"
3 2 1 1
#
, sehingga diperoleh ℓ′r = 3 dan
ℓ′b = 3 dan Exp2(D)≥ℓ(γ1)ℓ
′
r+ℓ(γ2)ℓ
′
Contoh 3.4 Akan diperlihatkan suatu (15,6)−walk dari verteks v4 ke verteks v4. Terdapat suatu pathpv4,v4 dariv4 kev4 yang mempunyai komposisi
"
3 1
#
yakni,
r(pv4,v4) = 3 dan b(pv4,v4) = 1. Selanjutnya akan ditemukan solusi tak negatif dari
z1 dan z2 untuk M
"
z1 z2
#
+
"
r(pv4,v4)
b(pv4,v4)
#
=
"
15 6
#
.
Karena
"
15 6
#
= 3
"
3 1
#
+ 2
"
3 1
#
+
"
3 1
#
maka, z1 = 3 dan z2 = 2. Oleh karena itu
suatu (15,6)−walk dari v4 ke v4 adalah v4 4γ1
−−→v4 2γ2
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Penelitian ini telah memperlihatkan batas bawah dan batas atas bagi 2-eksponen
dari digraph-dwiwarna primitif dengan dua buah cycle yang saling bersinggungan
dan panjang masing-masing cycle adalahmdanm−1, yaitu 1 2(n
2+n)≤exp2(D)≤ 1
2(2n
2+n−2) jika dan hanya jika D memenuhi syarat berikut ini: Batas atas dari exp2(D)
Batas atas akan tercapai apabila ℓ′r dan ℓ′b besar. Hal ini terjadi ketika panjang path merah dan path biru pada digraph D adalah 2m−3 dan 2. Berikut akan diperlihatkan representatif dari 2-digraph yang memenuhi batas atas dariexp2(D).
t t t t t t t t t t ◗ ◗ ◗ ◗ ◗ ◗ ❆ ❆ ❆ ❆ ✑ ✑✑ ✑✑ ✑ ✲ ❆ ❆❑ ◗ ◗ ◗ s ✰ ✛ ✑✑ ✑ ✸ ✲ ✛ ❦ ❄ qqq ❄ ✁✁ ✁✁✕
qqq✕✁✁
✑✑ ✑✑ ✑✑ ✑✑◗◗◗◗ ◗◗ ◗◗ 3 2 1
m−2 m−1
m
m+ 1 m+ 2
2m−1 2m−2
A1.
t t t t t t t t t t ◗◗ ◗◗ ◗◗ ◗◗✑✑ ✑✑ ✑✑ ❆ ❆ ❆ ❆ ❄ ❄ ✲ ❆ ❆❑ s ✰ ✛ ✸ ✲ ❦ qqq ✁✁ ✕ ✁✁ ✁✁✕ qqq 3 2 1
m−2 m−1
m
m+ 1 m+ 2
2m−1 2m−2
[image:43.595.149.447.412.716.2]A2.
Gambar 4.1 : 2-DigraphD yang memenuhi batas atas bagiexp2D
Batas bawah dari exp2(D)
Batas bawah akan tercapai apabila ℓ′r dan ℓ′b kecil. Hal ini terjadi apabila 2-digraphD mempunyai dua buah path merah terpisah dengan panjangm−1 dan m−2 dan Path pada 2-digraphDmemuat paling banyak sebuah arc biru. Berikut akan diperlihatkan representatif dari 2-digraph yang memenuhi batas bawah dari
exp2(D) t t t t t t t t t t ◗◗ ◗◗ ◗◗ ◗◗ ◗◗ ◗◗ ◗◗ ◗◗ ❆ ❆ ❆ ❆ qqq ✲ ❆ ❆❑ s ✰ ✛ ✸ ❦
qqq✕✁✁
✁✁ ✁✁✕ ❄ ❄ 3 2 1
m−2 m−1
m
m+ 1 m+ 2
2m−1 2m−2
B1. t t t t t t t t t qqq✕✁✁
✁✁ ✁✁✕ ❄ ❄ ❆ ❆ ❆ ❆ ✑✑ ✑✑ ✑✑ ✑✑✑ ✑ ✑✑ ✑✑ ✲ ❆ ❆❑ s ✰ ✛ ✸ ✲ ❦ qqq 3 2 1
m−2 m−1
m
m+ 1 m+ 2
2m−1 2m−2
[image:44.595.159.441.239.535.2]B2.
Gambar 4.2 : 2-DigraphD yang memenuhi batas bawah bagi exp2D
4.2 Saran
Diperlukan penelitian lebih lanjut untuk menentukan batas atas dan batas bawah
36
DAFTAR PUSTAKA
Beasley, L. B, dan Kirkland, S. 2003. A note onk-primitive digraphs.Linier Algebra Appl..373: hal. 67-74.
Brualdi, R. A dan Ryser, H. J. 1991. Combinatorial Matrix Theory. Cambridge : Cambridge University Press.
Fornasini, E. dan Valcher, M. E. 1997. Directed graphs, 2D State Models, and char-acteristic polinomials of irreducible matrix pairs. Linear Algebra Appl.. 263: hal. 275-310.
Gao, Y. dan Shao, Y. 2005. Exponents of two-colored digraph with two cycle.Linear Algebra Appl..407: hal. 263-276.
Gao, Y. dan Shao, Y. 2009. Exponents of 2-colorings of loopless, symmetric digraphs. Linear Algebra Appl..57(1): hal. 65-74.
Lee S. G dan Yang J. M. 2005. Bound for 2-exponents of primitive extremal digraph. Commun.Korean.Math.Soc.20(1): hal. 51-62.
Shader, B. L. dan Suwilo, S. 2003. Exponents of nonnegative matrix pairs. Linear Algebra Appl..363: hal. 275-293.