Estimating the Mean Function of a Compound Cyclic Poisson Process

(1)

PENDUGAAN FUNGSI NILAI HARAPAN PADA

PROSES POISSON PERIODIK MAJEMUK

RUHIYAT

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul Pendugaan Fungsi Nilai Harapan pada Proses Poisson Periodik Majemuk adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, April 2013

Ruhiyat

(4)

RINGKASAN

RUHIYAT. Pendugaan Fungsi Nilai Harapan pada Proses Poisson Periodik Majemuk. Dibimbing oleh I WAYAN MANGKU dan I GUSTI PUTU PURNABA.

Proses stokastik mempunyai peranan penting dalam memodelkan berbagai fenomena nyata. Salah satu bentuk khusus dari proses stokastik adalah proses Poisson majemuk. Banyak fenomena dalam berbagai bidang yang telah dimodelkan sebagai suatu proses Poisson majemuk, antara lain fenomena di bidang asuransi dan keuangan, fisika, demografi, geologi, serta biologi. Pengembangan model proses Poisson majemuk dapat dilakukan dengan memperumum proses Poisson yang digunakan. Salah satunya adalah dengan menggunakan proses Poisson periodik, sehingga modelnya menjadi proses Poisson periodik majemuk.

Penelitian ini memiliki empat tujuan, yaitu: (1) merumuskan penduga bagi fungsi nilai harapan pada proses Poisson periodik majemuk; (2) menganalisis kekonsistenan penduga; (3) menganalisis bias, ragam, dan mean squared error

(MSE) penduga; dan (4) mengamati perilaku penduga untuk kasus panjang interval waktu pengamatan yang terbatas.

Misalkan adalah suatu proses Poisson periodik dengan fungsi intensitas yang terintegralkan lokal dan tidak diketahui. Fungsi intensitas memiliki periode (diketahui) Fungsi intensitas tidak diasumsikan memiliki bentuk parametrik apapun kecuali berupa fungsi periodik, yakni

(5)

Misalkan untuk suatu , suatu realisasi tunggal dari proses yang terdefinisi pada suatu ruang peluang diamati pada suatu interval terbatas . Selanjutnya, untuk setiap titik data pada realisasi yang diamati, misalkan titik data ke- , 1, 2, , , peubah acak yang bersesuaian juga diamati.

Penduga bagi fungsi nilai harapan adalah

̂ ̂ ̂ ̂

dengan

̂

̂ ∑

dan

̂ ∑

dengan ̂ saat .

Penduga bagi fungsi nilai harapan dengan rumusan ini merupakan penduga yang konsisten lemah dan kuat, yaitu

̂ → dan

̂ →

untuk _→. Laju kekonvergenan bias, ragam, dan MSE penduga berturut-turut adalah

[ ̂ ] ( )

dan

[ ̂ ] ( )

untuk _→. Perilaku penduga belum cukup baik ketika interval waktu pengamatannya sepanjang 20 periode, tetapi sudah cukup baik ketika interval waktu pengamatannya sepanjang 40 periode yang merupakan interval yang terbatas.

(6)

SUMMARY

RUHIYAT. Estimating the Mean Function of a Compound Cyclic Poisson Process. Supervised by I WAYAN MANGKU and I GUSTI PUTU PURNABA.

A stochastic process has an important role in modeling various real phenomena. One special form of the stochastic process is a compound Poisson process. Many phenomena in different fields that have been modeled as a compound Poisson process, such as phenomena in the fields of insurance and finance, physics, demography, geology, and biology. A compound Poisson process model can be extended by generalizing the corresponding Poisson process. One of them is using cyclic Poisson process, so that the model becomes a compound cyclic Poisson process.

This research has four objectives as follows: (1) to formulate an estimator of the mean function of a compound cyclic Poisson process; (2) to analyze the consistency of the estimator; (3) to analyze the bias, variance, and mean squared error (MSE) of the estimator; and (4) to observe the behavior of the estimator in the case that the length of the observation time interval is bounded.

Let be a cyclic Poisson process with (unknown) locally integrable intensity function . We consider the case when the intensity function has a (known) period . We do not assume any (parametric) form of except that it is periodic, that is, the equality

(7)

Suppose that, for some , a single realization of the process defined on a probability space is observed, though only within a bounded interval . Furthermore, suppose that for each data point in the observed realization , say -th data point, 1, 2, , , its corresponding random variable is also observed.

The estimator of the mean function is given by ̂ ̂ ̂ ̂

where

̂

̂ ∑

and

̂ ∑

with the understanding that ̂ when .

The estimator of the mean function is both a weak and a strong consistent estimator, that is

̂ → and

̂ →

as _→. The rate of convergence of the bias, variance, and MSE of the estimator are respectively

[ ̂ ] ( )

and

[ ̂ ] ( )

as _→. The behavior of the estimator is not good enough when the length of the time interval of observations is 20 period, but it is good enough when the length of the time interval of observations is 40 period, which is a bounded interval.

(8)

© Hak Cipta Milik IPB, Tahun 2013

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

(9)

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

PENDUGAAN FUNGSI NILAI HARAPAN PADA

PROSES POISSON PERIODIK MAJEMUK

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2013

(10)

(11)

Judul Tesis : Pendugaan Fungsi Nilai Harapan pada Proses Poisson Periodik Majemuk

Nama : Ruhiyat

NIM : G551110101

Disetujui oleh Komisi Pembimbing

Dr Ir I Wayan Mangku, MSc Ketua

Dr Ir I Gusti Putu Purnaba, DEA Anggota

Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Ir Endar Hasafah Nugrahani, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

(12)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penelitian yang dilaksanakan sejak bulan Januari 2013 sampai April 2013 ini berjudul Pendugaan Fungsi Nilai Harapan pada Proses Poisson Periodik Majemuk.

Terima kasih penulis ucapkan kepada Dr Ir I Wayan Mangku, MSc dan Dr Ir I Gusti Putu Purnaba, DEA selaku pembimbing, atas semua ilmu, saran, kesabaran, dan motivasinya. Terima kasih juga penulis ucapkan kepada Dr Ir Hadi Sumarno, MS selaku penguji yang telah memberi saran. Di samping itu, penghargaan penulis sampaikan kepada keluarga besar Departemen Matematika FMIPA IPB yang telah membantu dalam penyusunan karya ilmiah ini. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, serta seluruh keluarga, atas doa, dukungan, dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, April 2013

(13)

DAFTAR ISI

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

PENDAHULUAN 1

Latar Belakang 1

Kerangka Pikir Penelitian 1

Tujuan Penelitian 3

PROSES POISSON PERIODIK MAJEMUK 3

PENDUGAAN FUNGSI NILAI HARAPAN 5

Perumusan Penduga 5

Kekonsistenan Penduga 6

Bias, Ragam, dan Mean Squared Error (MSE) Penduga 14

Ilustrasi Penyusunan Penduga dengan Data Bangkitan 23

SIMPULAN 26

DAFTAR PUSTAKA 27

LAMPIRAN 29

(14)

DAFTAR GAMBAR

1 Kerangka pikir penelitian 2

2 Grafik fungsi nilai harapan (—) beserta penduganya (–o–) menggunakan pengamatan pada interval waktu [0, 40] 25 3 Grafik fungsi nilai harapan (—) beserta penduganya (–o–)

menggunakan pengamatan pada interval waktu [0, 80] 25 4 Grafik fungsi nilai harapan (—) beserta penduganya (–o–)

menggunakan pengamatan pada interval waktu [0, 160] 26

DAFTAR LAMPIRAN

1 Bukti beberapa persamaan 29

2 Beberapa lema dan teorema teknis 33

(15)

PENDAHULUAN

Latar Belakang

Proses Poisson majemuk merupakan salah satu bentuk khusus proses stokastik yang memiliki banyak manfaat dalam memodelkan berbagai macam fenomena nyata. Bening dan Korolev (2002) menerapkan proses Poisson majemuk pada bidang asuransi dan keuangan. Sebagai contoh, proses Poisson majemuk digunakan untuk memodelkan besarnya klaim agregat, sehingga perusahaan asuransi dapat menduga besarnya keuntungan yang akan diperoleh pada masa yang akan datang. Sebelumnya, Byrne (1969) telah menggunakan proses Poisson majemuk pada beberapa permasalahan fisika. Selain itu, proses Poisson majemuk telah diterapkan pada bidang demografi (Kegler 2007), geologi (Özel dan İnal 2008), dan biologi (Puig dan Barquinero 2011).

Selama ini, kajian terhadap proses Poisson majemuk dilakukan dengan menggunakan proses Poisson homogen, yaitu proses Poisson yang fungsi intensitasnya konstan (tidak bergantung pada waktu). Apabila suatu kejadian memiliki peluang lebih besar untuk terjadi pada interval waktu tertentu dibandingkan pada interval waktu yang lain, maka asumsi ini tidak sesuai. Oleh karena itu, Proses Poisson majemuk kurang sesuai untuk memodelkan permasalahan tersebut. Untuk memperluas cakupan permasalahan yang dapat dimodelkan, asumsi tersebut harus diubah. Waktu dapat dianggap berpengaruh terhadap peluang terjadinya suatu kejadian, sehingga proses Poisson yang digunakan adalah proses Poisson takhomogen, yaitu proses Poisson yang fungsi intensitasnya merupakan fungsi dari waktu. Proses Poisson takhomogen ini merupakan perumuman dari proses Poisson homogen.

Kajian terhadap proses Poisson majemuk dengan menggunakan proses Poisson takhomogen sangatlah luas. Oleh karena itu, kajian dimulai dengan salah satu bentuk khusus dari proses Poisson takhomogen, yaitu proses Poisson periodik. Sesuai dengan namanya, fungsi intensitas dari proses Poisson periodik berupa fungsi periodik. Proses Poisson periodik ini cocok dalam menggambarkan fenomena yang terjadi secara periodik, seperti proses kedatangan pelanggan ke suatu pusat pelayanan dengan periode satu hari.

Kerangka Pikir Penelitian

(16)

2

Gambar 1 Kerangka pikir penelitian Pengembangan Model

Proses Poisson Majemuk Keterbatasan Model

Proses Poisson Majemuk

Fungsi Nilai Harapan pada Proses Poisson

Periodik Majemuk Model Proses Poisson

Periodik Majemuk Keperiodikan Fungsi

Intensitas

Pendugaan Fungsi Nilai Harapan

Perumusan Penduga

Kekonsistenan Penduga

Bias, Ragam, dan Mean Squared Error

(MSE) Penjabaran Fungsi

Nilai Harapan

Kekonsistenan

Lemah Kekonsistenan Kuat

(17)

3 Pada penelitian ini, fungsi intensitas dari proses Poisson periodik diasumsikan tidak diketahui karena apabila fungsi intensitas tersebut diketahui, fungsi nilai harapan dapat dengan mudah ditentukan. Dengan asumsi ini, diperlukan pendugaan terhadap fungsi nilai harapan. Pendugaan diawali dengan merumuskan penduga bagi fungsi nilai harapan. Suatu penduga merupakan penduga yang tidak baik apabila tidak dapat mendekati nilai yang diduganya ketika banyaknya sampel yang digunakan membesar. Oleh karena itu, penduga yang diperoleh harus dianalisis kekonsistenannya. Kekonsistenan yang dianalisis ada dua, yaitu kekonsistenan lemah dan kekonsistenan kuat. Berbeda dengan analisis kekonsistenan pada umumnya, analisis kekonsistenan pada penelitian ini dilakukan ketika interval waktu pengamatan memanjang. Nantinya, harus dibuktikan bahwa semakin panjang interval waktu pengamatan yang digunakan, semakin banyak pula sampel yang digunakan. Selain itu, untuk melihat perbedaan antara penduga dengan fungsi nilai harapan yang sebenarnya dilakukan analisis terhadap bias, ragam, dan mean squared error (MSE) dari penduga. Kemudian, pada penerapannya perlu diketahui seberapa panjang interval waktu pengamatan yang harus digunakan agar diperoleh penduga yang baik. Oleh karena itu, diperlukan pengamatan terhadap perilaku penduga untuk kasus panjang interval waktu pengamatan yang terbatas. Pengamatan ini dapat dilakukan dengan menggunakan data bangkitan.

Tujuan Penelitian

Tujuan dari penelitian ini adalah sebagai berikut:

1) merumuskan penduga bagi fungsi nilai harapan pada proses Poisson periodik majemuk,

2) menganalisis kekonsistenan penduga,

3) menganalisis bias, ragam, dan mean squared error (MSE) penduga, dan 4) mengamati perilaku penduga untuk kasus panjang interval waktu pengamatan

yang terbatas.

PROSES POISSON PERIODIK MAJEMUK

(18)

4

Selanjutnya, misalkan adalah suatu proses dengan ∑

(2) di mana adalah barisan peubah acak yang independent and identically distributed (i.i.d.) dengan nilai harapan dan ragam , yang juga

bebas terhadap proses . Proses disebut dengan proses Poisson periodik majemuk. Model dalam persamaan (2) adalah perumuman dari proses Poisson majemuk yang mengasumsikan bahwa adalah suatu proses Poisson homogen.

Fungsi nilai harapan dari , dinotasikan dengan , diberikan oleh

(3)

dengan

∫ (4)

Bukti persamaan (3) dapat dilihat pada Lampiran 1. Misalkan ⌊ ⌋

di mana untuk setiap bilangan real , menyatakan bilangan bulat terbesar yang lebih kecil dari atau sama dengan , dan misalkan pula

⌊ ⌋

maka untuk setiap bilangan real , dapat dinyatakan sebagai

(5)

dengan . Misalkan

∫ (6)

yaitu fungsi intensitas global dari proses , dan diasumsikan bahwa

(7)

maka untuk setiap yang diberikan,

(8)

Bukti persamaan (8) dapat dilihat pada Lampiran 1. Akhirnya, berdasarkan persamaan (3) dan (8), fungsi nilai harapan dari dapat dituliskan menjadi

(9)

(19)

5

PENDUGAAN FUNGSI NILAI HARAPAN

Pendugaan fungsi nilai harapan pada persamaan (9) dilakukan dengan menggunakan realisasi tunggal dari suatu proses Poisson periodik menjadi beberapa pendugaan, yaitu pendugaan fungsi intensitas global , pendugaan yang merupakan nilai harapan banyaknya kejadian yang terjadi pada interval waktu , dan pendugaan . Penduga bagi fungsi intensitas global telah dikaji pada Mangku (2001) dan rumusannya adalah sebagai berikut:

̂

Penduga ini merupakan rata-rata banyaknya kejadian yang terjadi pada interval waktu . Pendugaan fungsi intensitas global juga dilakukan pada Helmers dan Mangku (2012) serta Mangku (2010) untuk tujuan yang berbeda. Penduga bagi dirumuskan sebagai berikut:

̂ ∑

Penduga ini didapatkan dari rata-rata banyaknya kejadian yang terjadi pada setiap interval waktu , , yang termasuk dalam interval pengamatan

. Masing-masing interval waktu ini memiliki panjang yang sama dengan panjang interval waktu banyaknya kejadian yang diduga, yaitu , kecuali mungkin untuk satu interval. Selain itu, masing-masing interval waktu tersebut memiliki fungsi intensitas yang sama dengan interval waktu banyaknya kejadian yang diduga, kecuali mungkin untuk satu interval. Hal ini merupakan akibat dari sifat keperiodikan fungsi intensitas . Helmers dan Mangku (2012) serta Mangku (2010) juga melakukan pendugaan untuk tujuan yang berbeda. Penduga peubah acak yang bersesuaian untuk setiap titik data pada interval pengamatan

(20)

6

̂ ̂ ̂ ̂ (10)

dengan _̂ saat .

Kekonsistenan Penduga

Beberapa lema berikut digunakan dalam mengkaji kekonsistenan penduga bagi fungsi nilai harapan.

Lema 1

(21)

7

∫

Kemudian, karena ₍ ₎ untuk setiap , maka

( )

untuk _→, sehingga bagian pertama pada persamaan (11) adalah ( ) ( )

untuk _→. Kedua, karena terintegralkan lokal dan , untuk → , maka

∫

untuk _→, sehingga bagian kedua pada persamaan (11) adalah ∫

( )

untuk _→. Jadi,

[ ̂ ] ( )

untuk _→. Bu t eng p ■

Dalam tulisan ini, untuk setiap peubah acak dan dalam suatu ruang peluang , _→ menyatakan bahwa konvergen lengkap ke , untuk → . Peubah acak disebut konvergen lengkap ke , jika untuk setiap ,

∑ | |

(22)

8 Lema 2

Misalkan fungsi intensitas memenuhi persamaan (1) dan terintegralkan lokal, maka

Karena berlakunya (13) mengakibatkan berlakunya (12), maka cukup dibuktikan (13) saja. Untuk membuktikan (13), harus diperiksa bahwa untuk setiap ,

(23)

9

[ ̂ ]

Berdasarkan Lema 1, _{[ ̂} _] , untuk _→, sehingga untuk yang cukup besar,

| ̂ [ ̂ ]|

[ ̂ ]

Untuk penyederhanaan, misalkan . Selanjutnya, berdasarkan uji banding kembali, untuk membuktikan (16), cukup dibuktikan bahwa

∑

(17)

Perhatikan bahwa

∫

sehingga berdasarkan uji integral, diperoleh (17). Bu t eng p ■ Lema 3

[ ̂ ] ( )

untuk _→. Dengan kata lain, _̂ merupakan penduga yang tak bias asimtotik bagi .

Bukti:

Nilai harapan _̂ dapat dihitung seperti berikut:

[ ̂ ] [ ∑

]

∑

(24)

10

Karena merupakan fungsi periodik dengan periode , maka [ ̂ ] ∑ ∫

(25)

11 sehingga untuk yang cukup besar,

(| ̂ | ) | ̂ [ ̂ ]| (21) kanan pada pertidaksamaan (21) dapat dibatasi seperti berikut:

(26)

12

Berdasarkan Lema 3, _{[ ̂} ] , untuk _→, sehingga untuk yang cukup besar,

| ̂ [ ̂ ]|

[ ̂ ]

Dengan argumen yang sama pada bukti Lema 2, ∑

Oleh karena itu, berdasarkan uji banding, diperoleh (22). Bu t eng p ■ Lema 5

Misalkan fungsi intensitas memenuhi persamaan (1) dan terintegralkan lokal. Jika kondisi (7) dipenuhi, maka dengan peluang 1,

→ (23)

untuk _→. Bukti:

Berdasarkan Lema 1 dan kondisi (7),

∫ →

untuk _→. Kemudian, berdasarkan Teorema L.1 (Lema Borel-Cantelli), diperoleh (23). Bu t eng p ■

Kekonsistenan penduga fungsi nilai harapan disajikan dalam kedua teorema berikut. Hasil ini dapat juga dilihat pada Ruhiyat et al. (2013).

Teorema 1 (Kekonsistenan lemah)

Misalkan fungsi intensitas memenuhi persamaan (1) dan terintegralkan lokal. Jika memenuhi persamaan (2), maka

̂ → (24)

untuk _→. Jadi, _̂ merupakan penduga yang konsisten lemah bagi . Bukti:

Perhatikan kembali persamaan (10). Dengan menerapkan Lema L.2, untuk membuktikan (24), cukup diperiksa bahwa

̂ → (25)

̂ → (26)

(27)

13

sehingga dengan Teorema L.1 (Lema Borel-Cantelli), diperoleh

→ (| ̂ | )

(28)

14

Bias, Ragam, dan Mean Squared Error (MSE) Penduga

Berikut ini merupakan hasil analisis terhadap bias, ragam, dan mean squared error (MSE) dari penduga bagi fungsi nilai harapan.

Teorema 3 (Laju kekonvergenan bias)

[ ̂ ] [ ̂ ] ( )

untuk _→. Artinya, bias _̂ konvergen ke nol dengan laju jika → .

Bukti:

(29)

15 ( )

( )

untuk → . Oleh karena itu,

[ ̂ ] ∑ ( )

∑

( ) ∑

∑

( ) ( ∑

)

( ) ( ( ) )

( ) ( )

[ ̂ ] ( ) ( )

( ) ( ) (

)

( )

untuk _→. Jadi,

[ ̂ ] [ ̂ ] ( )

( )

(30)

16

Perhitungan ragam dari penduga bagi fungsi nilai harapan memerlukan beberapa hasil berikut.

Lema 6

[ ̂ ] ( )

Ragam _̂ dapat dihitung seperti berikut:

[ ̂ ]

Karena merupakan peubah acak Poisson, maka [ ̂ ]

[ ̂ ]

( )

Berdasarkan Lema 1 dan Lema 6, diperoleh akibat berikut. Akibat 1

[ ̂ ] ( )

(31)

17

( ) ( )

( ) ( ) ( )

( )

untuk _→. Bu t eng p ■ Lema 7

[ ̂ ] ( )

Ragam _̂ dapat dihitung seperti berikut:

[ ̂ ] [ ∑

]

∑

karena proses memiliki inkremen bebas. Kemudian, karena merupakan peubah acak Poisson, maka

[ ̂ ] ∑

∑

[ ∑

]

[ ̂ ]

( )

untuk → . Bu t eng p ■

(32)

18 Akibat 2

[ ̂ ] ( ) ( )

Momen kedua dari _̂ dapat ditentukan seperti berikut: [ ̂ ] [ ̂ ] ( [ ̂ ])

( ) ( )

( ) ( ) ( ) ( )

( ) ( )

Ragam dari penduga bagi fungsi nilai harapan disajikan dalam teorema berikut.

Teorema 4 (Laju kekonvergenan ragam)

[ ̂ ] ( )

untuk _→. Artinya, ragam _̂ konvergen ke nol dengan laju jika → .

Bukti:

Berdasarkan sifat dari ragam, ragam dari penduga bagi fungsi nilai harapan dapat diperoleh dari rumusan berikut:

[ ̂ ] [ ̂ ] ( [ ̂ ]) (32) Bagian kedua dari ruas kanan persamaan (32) telah diperoleh pada Teorema 1, sehingga tersisa bagian pertamanya yang perlu dihitung. Momen kedua dari penduga bagi fungsi nilai harapan dapat ditentukan melalui nilai harapan bersyarat berikut:

[ ̂ ] [ ̂ | ]

∑ [ ̂ | ]

(33)

19 [ ̂ | ]

∑ [ ̂ | ]

Berdasarkan rumusan dari ̂ , untuk , ̂ , sedangkan untuk ,

̂ ( ̂ ) ∑

sehingga untuk ,

[ ̂ | ]

[ ̂ ∑

]

̂ ( ∑

)

[ ̂ ] ( ∑

)

Pertama, dihitung

[ ̂ ]

̂ ̂

[ ̂ ] [ ̂ ]

Berdasarkan Lema 3 dan Akibat 2, diperoleh [ ̂ ]

( ) ( ) ( )

( ) ( )

(34)

(35)

21

∑

( ) ( ) ∑

untuk _→. Pada bukti Teorema 3 telah diperoleh ∑

(33)

dan

∑

₍₃₄₎

untuk _→. Dengan cara serupa, dapat diperoleh ∑

( ) (35)

Terakhir,

∑

( ) (36)

untuk _→. Bukti persamaan (36) dapat dilihat pada Lampiran 1. Dengan persamaan (33) – (36), diperoleh

[ ̂ ] ( )

( ₎

( ) ( ) ( ₎

( ) ( ) ( )

[ ]

(36)

22

( ) ( ) ( ₎

( ) ( ) ( )

[ ̂ ] [ ̂ ]

[ ̂ ] ( )

( ) ( ) ( ₎

( ) ( ) ( )

( ) ( )

( ) ( ) ( ₎

( ) ( ) ( )

( ) ₍ ₎

( ) ( )

( )

( ) ( )

untuk _→. Akhirnya, ragam dari penduga bagi fungsi nilai harapan adalah [ ̂ ] ( ) ( ) ( )

( )

(37)

23 Akibat 3 (Laju kekonvergenan MSE)

[ ̂ ] ( )

untuk _→. Artinya, MSE _̂ konvergen ke nol dengan laju jika → .

Bukti:

Berdasarkan Teorema 3 dan 4,

[ ̂ ] [ ̂ ] ( [ ̂ ])

( ) ( )

( )

Ilustrasi Penyusunan Penduga dengan Data Bangkitan

Ilustrasi ditujukan untuk mengamati perilaku penduga untuk kasus panjang interval waktu pengamatan yang terbatas. Penduga disusun dengan menggunakan data bangkitan. Pembangkitan data dan penyusunan penduga dilakukan dengan bantuan perangkat lunak R. Program R untuk proses ini terdapat pada Lampiran 3. Dalam ilustrasi ini, realisasi dibangkitkan dari proses Poisson periodik dengan rumusan fungsi intensitas

( )

Setelah didapatkan realisasi tersebut, dibangkitkan pula nilai-nilai dari peubah acak yang bersesuaian dengan setiap titik data. Nilai-nilai dari peubah acak tersebut dibangkitkan dengan menggunakan sebaran eksponensial dengan nilai harapan 2.

Proses Poisson periodik dengan fungsi intensitas demikian memiliki periode 4. Adapun fungsi intensitas globalnya adalah

∫

[ ]

(38)

24

Fungsi nilai harapan ini diduga dengan menggunakan rumusan penduga pada persamaan (10). Ada tiga pengamatan yang dilakukan yang panjang interval waktu pengamatannya masing-masing adalah 10, 20, dan 40 periode. Pengamatan pertama dilakukan pada interval waktu [0, 40], pengamatan kedua dilakukan pada interval waktu [0, 80], sedangkan pengamatan ketiga dilakukan pada interval waktu [0, 160]. Berdasarkan data pada masing-masing pengamatan tersebut, disusun penduga bagi fungsi nilai harapan pada interval waktu [0, 10].

(39)

25

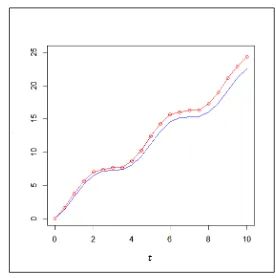
Gambar 2 Grafik fungsi nilai harapan (—) beserta penduganya (–o–) menggunakan pengamatan pada interval waktu [0, 40]

(40)

26

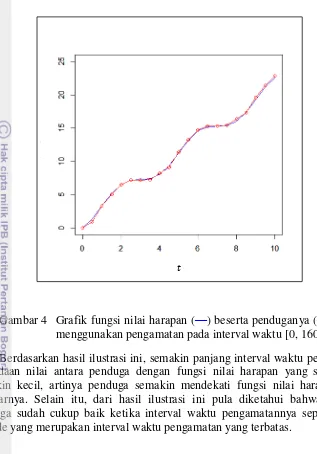
Gambar 4 Grafik fungsi nilai harapan (—) beserta penduganya (–o–) menggunakan pengamatan pada interval waktu [0, 160]

Berdasarkan hasil ilustrasi ini, semakin panjang interval waktu pengamatan, perbedaan nilai antara penduga dengan fungsi nilai harapan yang sebenarnya semakin kecil, artinya penduga semakin mendekati fungsi nilai harapan yang sebenarnya. Selain itu, dari hasil ilustrasi ini pula diketahui bahwa perilaku penduga sudah cukup baik ketika interval waktu pengamatannya sepanjang 40 periode yang merupakan interval waktu pengamatan yang terbatas.

SIMPULAN

Rumusan penduga bagi fungsi nilai harapan pada proses Poisson periodik majemuk adalah

̂ ̂ ̂ ̂

dengan

̂

̂ ∑

(41)

27 rumusan ini merupakan penduga yang konsisten, baik konsisten lemah, maupun konsisten kuat. Bias, ragam, dan MSE dari penduga bagi fungsi nilai harapan konvergen ke nol dengan laju jika → . Dari ilustrasi yang dilakukan dengan menggunakan data bangkitan, perilaku penduga belum cukup baik ketika interval waktu pengamatannya sepanjang 20 periode, tetapi sudah cukup baik ketika interval waktu pengamatannya sepanjang 40 periode.

DAFTAR PUSTAKA

Bening VE, Korolev VY. 2002. Generalized Poisson Models and Their Applications in Insurance and Finance. Boston (US): VSP International

Science Publishers.

Byrne J. 1969. Properties of compound Poisson processes with applications in statistical physics. Physica 41:575-587.

C p ńs M Kopp E 7 Measure, Integral and Probability. Ed ke-2. New

York (US): Springer.

DasGupta A. 2011. Probability for Statistics and Machine Learning: Fundamentals and Advanced Topics. New York (US): Springer.

Helmers R, Mangku IW. 2012. Predicting a cyclic Poisson process. Ann. Inst. Statist. Math. 64:1261-1279.

Helmers R, Mangku IW, Zitikis R. 2003. Consistent estimation of the intensity function of a cyclic Poisson process. J. Multivariate Anal. 84(1):19-39.

Hogg RV, McKean JW, Craig AT. 2005. Introduction to Mathematical Statistics. Ed ke-6. New Jersey (US): Prentice Hall.

Kegler SR. 2007. Applying the compound Poisson process model to reporting of injury-related mortality rates. Epidemiologic Perspectives & Innovations 4:1-9. Mangku IW. 2010. Consistent estimation of the distribution function and the intensity of waiting time of a cyclic Poisson process with linear trend. Far East J. Theor. Stat. 33(1):81-91.

Mangku IW. 2001. Estimating the Intensity of a Cyclic Poisson Process [disertasi]. Amsterdam (NL): University of Amsterdam.

Öze G İn C 2008. The probability function of the compound Poisson process and an application to aftershock sequence in Turkey. Environtmetrics 19:79-85. Puig P, Barquinero JF. 2011. An application of compound Poisson modeling to

biological dosimetry. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci.

467(2127):897-910.

(42)

28

Ruhiyat, Mangku IW, Purnaba IGP. 2013. Consistent estimation of the mean function of a compound cyclic Poisson process. Far East J. Math. Sci., siap

terbit.

(43)

29

Dengan menggunakan kembali asumsi kebebasan antara barisan peubah acak dengan proses ,

(44)

30

Bukti persamaan (8): Berdasarkan persamaan (4) dan (5), ∫

Bukti persamaan (36): Dari pembuktian Lema 5, diketahui bahwa →

untuk _→. Dari Lema 1, dapat diperoleh

(45)

(46)

(47)

33 Lampiran 2 Beberapa lema dan teorema teknis

Lema L.1 Bukti dapat dilihat pada Hogg et al. (2005).

Lema L.3

Misalkan _→ dan _→, maka

→ n → Bukti dapat dilihat pada Sokol dan Nielsen (2010).

Teorema L.1 (Lema Borel-Cantelli)

Misalkan adalah barisan kejadian pada ruang contoh . Jika ∑

(48)

34

Teorema L.2 (Hukum lemah bilangan besar)

Misalkan adalah peubah acak i.i.d. dengan nilai harapan dan ragam , maka

∑

→

untuk _→.

Bukti dapat dilihat pada C p ńs n Kopp ( 7) Teorema L.3 (Hukum kuat bilangan besar)

Misalkan Misalkan adalah peubah acak i.i.d. dengan nilai harapan , maka

∑

→

untuk _→.

(49)

35 Lampiran 3 Program R untuk ilustrasi

realisasi <- function(n, tau) contoh <- data[data >= bawah & data <= atas]

(50)

36

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 3 Maret 1989 dari ayah Kasmin dan ibu Jumi. Penulis merupakan putra kedua dari tiga bersaudara. Tahun 2011 penulis lulus sebagai sarjana sains dari Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor dan pada tahun yang sama diterima di program studi S2 Matematika Terapan, Sekolah Pascasarjana, Institut Pertanian Bogor.

Selama mengikuti perkuliahan, penulis menjadi asisten praktikum Metode Komputasi Matematik pada semester ganjil tahun akademik 2012-2013. Kegiatan yang pernah diikuti adalah International Actuarial Conference “Actuary… To Be

Left Behind or Trusted” yang diselenggarakan oleh Persatuan Aktuaris Indonesia pada tanggal 10-11 November 2011 di Bali, Indonesian-German Network for