LKS Matematika Kelas 7 Kurikulum 2013

Kompetensi Inti Pembelajaran Matematika Kelas VII

1

Menghargai dan menghayati ajaran agama yang 

dianutnya

2

Menghargai dan menghayati perilaku jujur, disiplin, 

tanggungjawab, peduli (toleransi, gotong royong), santun,

percaya diri, dalam berinteraksi secara efektif dengan 

lingkungan sosial dan alam dalam jangkauan pergaulan 

dan keberadaannya

3

Memahami pengetahuan (faktual, konseptual, dan 

prosedural) berdasarkan rasa ingin tahunya tentang ilmu

pengetahuan, teknologi, seni, budaya terkait fenomena 

dan kejadian tampak mata

4

Mencoba, mengolah, dan menyaji dalam ranah konkret 

(menggunakan, mengurai, merangkai, memodifikasi, dan 

membuat) dan ranah abstrak (menulis, membaca, 

BAB I

BILANGAN

KI KOMPETENSI DASAR

1 Menghargai dan menghayati ajaran agama yang dianutnya

2 Menunjukkan  sikap  logis,  kritis,  analitik, konsisten  dan  teliti,   bertanggung  jawab,  responsif dan tidak mudah menyerah dalam  memecahkan masalah.

Memiliki  rasa  ingin  tahu,  percaya  diri,  dan ketertarikan  pada  matematika  serta  memiliki rasa  percaya  pada  daya  dan  keguanaan  matematika,  yang  terbentuk  melalui pengalaman belajar.

3 Membandingkan dan mengurutkan berbagai  jenis  bilangan  serta   menerapkan  operasi hitung bilangan bulat dan bilangan pecahan  dengan  memanfaatkan  berbagai  sifat  operasi.

Kegiatan 1

Tujuan Pembelajaran

 Membandingkan dan mengurutkan sekelompok bilangan dari terkecil

 Menggambar garis bilangan dan menempatkan sekelompok bilangan pada garis  bilangan yang tepat

Perhatikan garis bilangan berikut ini

Tandailah bilangan bulat –4, 9, 1, ­2, 3 pada garis bilangan di atas

Perhatikan garis bilangan di bawah ini

.

Dapatkah kamu menuliskan beberapa pertanyaan dari gambar garis bilangan di atas?

-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10

-10 -5 0 5 10

 ABCD

Menga

mati

Pertanyaan Jawaban

1. Tulislah lawan dari setiap bilangan bulat berikut.

a. 16 lawannya ...

b. ­12 lawannya ...

c. 100 lawannya ... d. 75 lawannya ...

2. Membandingkan. Tulislah  <, >, atau = dalam    sehingga menjadi pernyataan  yang benar.

a. ­5  8 b. 13  ­14 c. –11  ­19

1. Tulislah sebuah bilangan bulat yang terletak di antara kedua bilangan bulat yang  diberikan.

a. ­2 dan 9 b. dan ­12  c. –7 dan ­11 

2.    Lengkapilah dengan sebuah bilangan bulat sehingga pernyataan menjadi benar.

a. ­9 > . . .

b. . . .  > 3 c. 0 > . . .

Mengump

ulkan

Informasi

Daftarlah suhu dari yang terkecil ke yang terbesar, jelaskan alasanmu kepada  teman­temanmu.  

 Suhu 25o_{F di bawah nol.}  Genangan air bersuhu 78o_F.  Air membeku pada suhu 32o_F.

 Suhu rendah dalam bulan Desember adalah ­3o_F.

Kegiatan 2

Tujuan Pembelajaran

 Menuliskan bentuk pengurangan dari bentuk penjumlahan yang diberikan atau  sebaliknya

 Menulis bentuk penjumlahan dan pengurangan dari pengambilan sejumlah  benda dari sekumpulan benda

Isilah titik­titik di bawah ini!

a. 2 + 3 = 5 ;   5  2 = . . . ;  5  3 = . . . b. 3 + 6 = . . .  ;   9  6 = . . . ;  9  3 = . . . c. 5 + 9 = . . . ;   14  9 = . . . ;  14  9 = . . . d. 12 + 7 = . . . ;   19  7 = . . . ;  19  12 = . . . e. 8 + 9 = . . .  ;   17  9 = . . . ;  17  8 = . . . f. 20 + 12 = . . . ;   32  12 = . . . ;  32  20 = . . . g. 16 + 17 = . . . ;   33  17 = . . . ;  33  16 = . . .

Amati hasil di atas, kemudian tulis dugaanmu dengan mengisi titik­titik di bawah ini     Jika  a + b = c, maka: 

c  a = . . .     b  a = . . .      Jika p  q = r, maka:         q + r = . . .         p  r = . . .

Pemecahan Masalah 

Sebuah   bus   dengan   kapasitas   27   tempat   duduk   penuh   sesak   dengan   penumpang

Komunika

si

Mengump

ulkan

Informasi

Mena

nya

P r o b l e m

yang turun dan 6 orang yang naik. Sesampainya di halte B ada 10 orang yang turun dan 3 orang yang naik. Semua penumpang yang tersisa akan turun di terminal. Ada berapa orang penumpang yang turun di terminal? Jelaskan.

... ... ... ...

Kegiatan 3

Tujuan Pembelajaran

 Menulis bentuk perkalian dari sejumlah benda yang terbagi ke dalam kelompok­ kelompok benda dengan jumlah yang sama dan menghitung hasilnya

 Menulis bentuk perkalian dari bentuk penjumlahan berulang dan menghitung hasilnya

 Mengingat dan mencongak perkalian bilangan sampai 100 dengan berbagai cara

Perhatikan masalah yang dihadapi Putu

Saat pergi ke dokter, Putu diberikan obat berbentuk syrup Aturan pakai  obat tersebut adalah   3 x 1 dan sebungkus pil dengan aturan pakai 2 x 1

Bagaimana putu harus meminum obatnya??

Dapatkah  kamu  membantu  Putu  menjelaskan  makna  3  x  1  yang  tertera  dalam obatnya.

... ... ... ...

Setiap   hari   Made   menabung   Rp   2000.   Dapatkah   kamu   menuliskan   banyak tabungan   Made   selama   1   minggu   dalam   bentuk   penjumlahan   yang   berulang? Berapa kali Made menabung selama 1 minggu? Coba tuliskan bentuk penjumlahan yang berulang tersebut dalam bentuk perkalian.

... ...

Menga

mati

Menan

ya

Menala

r

P r o b l e m

... ...

1. Tuliskan bentuk penjumlahan berikut dalam bentuk perkalian a. 4 + 4 + 4 = ...

b. 3 + 3 + 3 + 3 = ... c. 5 + 5  = ...

d. 2 + 2 + 2 + 2 + 2 = ...

2. Tuliskan dalam bentuk penjumlahan berulang a. 2 x 4 = ...

b. 3 x 6 = ... c. 4 x 8 = ...

d. 3 x m = ... e. p x 2 = ... f. a x b = ...

 

Kegiatan 4

Tujuan Pembelajaran

 Menulis   bentuk   pembagian   dari   sejumlah/sekelompok   benda   yang   diberikan kepada sejumlah orang dengan jumlah yang sama dan menghitung berapa orang yang mendapat bagian yang sama

 Menulis bentuk pembagian dari bentuk pengurangan berulang

 Menulis bentuk pembagian dari bentuk perkalian yang diberikan dan sebaliknya  Menyimpulkan sifat pembagian dengan satu, serta sisa hasil pembagian

1. Ibu mempunyai 40 kg beras, hari pertama beras tersebut dijual 5 kg, hari kedua 5  kg, hari ketiga 5 kg dan seterusnya sampai suatu hari beras Ibu habis terjual. Pada  hari ke berapa semua beras ibu habis?

Sisa beras hari 1 40 – 5 = .... Sisa beras hari 2 40 – 5 – 5 = ....

Mengump

ulkan

Informasi

Menalar

P r o b l e m

Sisa beras hari 3 40 – 5 – 5 – 5 = .... Sisa beras hari 4   ... Sisa beras hari 5   ... Sisa beras hari 6  ... ... ... ... ... 2. Andre memiliki 4 kantong berwarna merah, kuning, hijau dan biru. Jika di setiap  kantong dimasukkan 6 kelereng, berapa banyak kelereng Andre semuanya? ... ... ... 3. Andre memiliki 24 kelereng yang sama dan 4 kantong berwarna merah, kuning,  hijau dan biru. Jika semua kelereng akan dimasukkan ke dalam kantong secara  merata, berapa kelereng yang ada di tiap­tiap kantong? ... ... ...

Perhatikan   kembali   pekerjaanmu   di   nomor   2   dan   3.   Dapatkah   kamu   melihat hubungan   dua   kejadian   tersebut?   Dari   kegiatan   ini   coba   simpulkan   hubungan perkalian dan pembagian dua bilangan ... ... ... Kegiatan 5 Tujuan Pembelajaran

Menghitung   hasil   operasi   campuran   yang   melibatkan   penjumlahan,   pengurangan, perkalian dan pembagian bilangan cacah sesuai aturan

1. Seorang pedagang balon memiliki 20 buah balon. Karena pembeli sedang ramai pedagang   tadi   memutuskan   untuk   menambah   balon   yang   akan   dijual   dengan mengambil dagangan 5 temannya masing­masing 3 balon. Saat dijajakan, ternyata ada 7 balon yang meletus dan sisanya terjual habis. a. Tuliskan masalah tadi dalam operasi bilangan menggunakan tanda +, ­, x maupun : b. Tentukan berapa banyak balon yang terjual ... ... ...

Menalar

P r o b l e m

...

2. Adi, Budi, Cindi, dan Dedi adalah 4 bersaudara. Masing­masing dari 4 bersaudara ini memiliki uang Rp 3000. Ayah mereka ingin membagikan uang Rp 12.000 kepada 4 bersaudara ini secara merata. Setelah semua anak menerima uang, lalu mereka sepakat   untuk   membeli   bakso   dengan   Rp   2.500   setiap   anak.   Berapa   sisa   uang masing­masing anak saat ini?

a. Tuliskan masalah tadi dalam operasi bilangan menggunakan tanda +, ­, x maupun :

b. Berapa sisa uang masing­masing anak saat ini? c. Berapa sisa uang seluruhnya?

... ... ... ...

Kegiatan 6

Tujuan Pembelajaran

 Menjumlahkan dua bilangan bulat dengan bantuan garis bilangan atau cara  lainnya

Mengenal tanda dan bobot bilangan bulat

­5

Bobot 5 Tanda (­)

5

Bobot 5 Tanda (+)

3

Tanda ....

­10

Tanda ....

Menga

Permainan Kartu Merah Putih Alat :

Kartu Merah sebanyak 20 buah

 Dibuat dari kertas manila berwarna merah yang digunting membentuk segi  empat berukuran    4 x 2 cm

Kartu Putih sebanyak 20 buah

 Dibuat dari kertas manila berwarna putih yang digunting membentuk segi  empat berukuran    4 x 2 cm

1. Aturan Permainan

a) Kartu   merah   digunakan   untuk   melambangkan   1   satuan bilangan positif

b) Kartu   putih   digunakan   untuk   melambangkan   1   satuan bilangan negatif

c) Jika   1   kartu   merah   dan   1   kartu   putih   disatukan   maka keduanya akan saling menghilangkan nilai dengan kata lain hasilnya 0

d) Contoh 1 ; untuk menentukan hasil dari 7 + 5 digunakan 7 kartu merah dan 5 kartu merah ;

Dengan demikian terdapat 12 kartu merah (menunjukkan 7 + 5 = 12)

e) Contoh 2 ; untuk menentukan hasil dari ­3 + 4 digunakan 3  kartu putih dan 4 kartu merah

­4

Bobot .... Tanda ....

9

Bobot .... Tanda ....

Permainan

&

Karena ada tiga pasang kartu yang saling menghilangkan   (bernilai   0)   maka   hanya tersisa 1 kartu merah. Dengan demikian hasil dari ­3 + 4 adalah 1

Dengan menggunakan kartu merah putih, tentukan hasil dari penjumlahan berikut ini ;

A B C D

3+

1

 =

−3+(−1)

 =

3+(−1

)

 =

−3+

1

 =

3

+

2

 =

−

3

+(−

2

)

 =

3

+(−

2

)

 =

−

3

+

2

 =

3

+3

 =

−3+(−3

)

 =

3+(−3

)

 =

−3+

3

 =

3

+

4

 =

−

3

+(−

4

)

 =

3

+(−

4

)

 =

−

3

+

4

 =

4

+5

 =

−4+(−5)

 =

4

+(−5)

 =

−4+5

 =

4

+

8

 =

−

4

+(−

8

)

 =

4

+(−

8

)

 =

−

4

+

8

 =

5+

6

 =

−5+(−6

)

 =

5+(−6

)

 =

−5+

6

 =

7

+

8

 =

−

7

+(−

8

)

 =

7

+(−

8

)

 =

−

7

+

8

 =

Amati hasil penjumlahan di atas dan lengkapi tabel berikut ini Penjumlahan Tanda

Hasilnya

Bobot Hasilnya Penjumlahan bilangan 

bertanda (+) dengan (+) (kolom A)

Penjumlahan bilangan  bertanda (­) dengan (­) (kolom B)

Penjumlahan bilangan  bertanda (+) dengan (­) (kolom C)

Penjumlahan bilangan  bertanda (­) dengan (+) (kolom D)

Mengump

ulkan

Informasi

Menga

Dari hasil pengamatan tadi dapatkah kamu simpulkan cara menjumlahkan bilangan  bulat. Gunakan dua pertanyaan berikut untuk membantu membuat kesimpulanmu.

 Jika   dua   bilangan   bertanda   sama   dijumlahkan   maka   bagaimana   tanda   hasil penjumlahannya? Bagaimana cara menentukan bobot hasil penjumlahannya?  Jika dua bilangan bertanda berbeda dijumlahkan maka bagaimana tanda hasil

penjumlahannya? Kapan hasilnya bertanda (­) dan kapan hasilnya bertanda (+)? Bagaimana cara menentukan bobot hasil penjumlahannya?

 

PECAHAN

Kegiatan 1

Tujuan Pembelajaran

 Menuliskan nilai pecahan dari fenomena sehari­hari seperti pemotongan benda  menjadi beberapa bagian dan sebagainya 

 Menyatakan suatu pecahan ke dalam berbagai bentuk gambar dan sebaliknya  Menggambar garis bilangan dan menempatkan sekelompok pecahan pada garis 

bilangan yang tepat

 Menyatakan suatu pecahan ke bentuk pecahan lain yang senilai dengan  berbagai cara

 Membandingkan dan mengurutkan sekelompok pecahan dari terkecil melalui  representasi gambar atau kedudukannya dalam garis bilangan atau cara lainnya

Putu membelah sebuah jeruk bali menjadi dua bagian yang sama besar. Salah satu bagian  diserahkan kepada  Made. Kemudian  Made membelah  bagiannya menjadi dua bagian yang sama besar dan menyerahkan salah satu bagian kepada Komang. Berapa bagian jeruk yang diterima Komang?

Nyatakan   bagian   yang   diarsir   pada   gambar­gambar   berikut   ini   dengan   pecahan yang sesuai

No Gambar Pecahan

a

b

c

Menga

mati

Mengump

ulkan

[image:13.595.82.502.394.756.2]

d

e

Perhatikan kembali gambar dan pecahan yang ada pad nomor 2. Adakah arsiran pada   gambar   yang   menunjukkan   bagian   yang   sama   besar?   Jika   gambarnya menunjukkan bagian yang sama besar maka kedua pecahan tersebut dikatakan senilai. Coba tuliskan pecahan­pecahan senilai pada soal nomor 2.



1

3

senilai dengan

2

6



2

4

senilai dengan

…

…

Tambahkan   bagian   dari   gambar­gambar   berikut   sehingga   kamu   mendapatkan

pecahan lainnya yang senilai dengan 

1

3

? 

Menalar

P r o b l e m

Membandingkan pecahan yang penyebutnya sama

Perhatikan pecahan­pecahan berikut. Pecahan manakah yang nilainya paling kecil?

Jika penyebut beberapa pecahan sama, maka pecahan yang paling kecil dilihat dari ...

Menalar

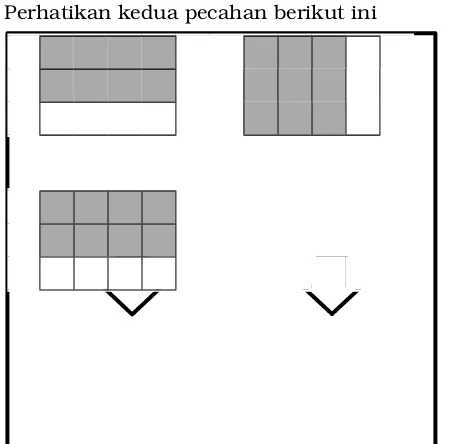
Membandingkan pecahan yang penyebutnya berbeda Perhatikan kedua pecahan berikut ini

Perhatikan   kedua   pecahan pada   gambar   di   samping. Potongan­potongan   yang berbeda seperti itu, akan sulit untuk   membedakan   mana yang   lebih   besar   dan   lebih kecil.

[image:16.595.106.336.84.306.2]

Agar lebih mudah, coba kamu buat   beberapa   garis   pada gambar,   sehingga   terbentuk potongan­potongan yang sama besar pada dua gambar.

Setelah   itu   kamu   akan melihat   pecahan   mana   yang lebih kecil

1

3       ₌       ...

21 _{,  sehingga}   1 3=

7 21

2

7       ₌       ...

21 _{,  sehingga}   2 7=

6 21

Tahap III :

Membandingkan pecahan yang penyebutnya sama pada Tahap II

Jika   sudah   dibandingkan   maka   kamu   akan   mendapatkan   jawaban   calon mana yang mendapat suara lebih banyak

Urutkanlah pecahan 

3

8

,

2

5

, dan

7

20

 _{dari yang terkecil ke yang terbesar.} Tahap I : Tentukan KPK dari 8, 5, Dan 20 (bisa menggunakan pohon faktor)

Tahap II : buat pecahan senilai yang penyebutnya sama dengan KPK 8, 5, dan 20

Tahap III : Urutkan dari yang terkecil

Mengump

ulkan

Kegiatan 2 Tujuan Pembelajaran  Menghitung hasil penjumlahan pecahan melalui representasi gambar  Menjumlah dan mengurang pecahan berpenyebut sama  Menjumlah dan mengurang pecahan berpenyebut tidak sama dengan mengubah pecahan­pecahan ke bentuk pecahan lain dengan penyebut sama

Erna   dan   Wati   membeli   roti   yang   telah   dipotong   menjadi   8   bagian   yang   sama.

Sambil duduk di halaman rumah, Erna makan  1 8  _{roti itu dan Wati makan}  3 8 _. Berapa bagian roti yang telah dimakan oleh mereka Gambarlah sebuah persegipanjang pada kertas berpetak seperti yang ditunjuk­ kan oleh gambar di bawah ini. Tiap persegipanjang ini menunjukkan  seperdelapanan. Warnailah satu bagian dari persegipanjang tersebut dengan pensil warna untuk  menyatakan  1 8 _{. Dengan menggunakan pensil warna yang lain, warnailah tiga} bagian yang lain dari persegipanjang itu untuk menyatakan  3 8 _. a. Berapa banyak bagian dari persegipanjang itu yang telah diwarnai? b. Pecahan apakah yang menyatakan banyaknya bagian dari persegipanjang yang telah diwarnai?

c. Jika   kamu   mewarnai   dua   bagian   lagi   dari   persegipanjang   itu,   pecahan apakah   yang   menyatakan   banyaknya   bagian   dari   persegipanjang   yang telah diwarnai? Kegiatan 3 Tujuan Pembelajaran  Menghitung hasil perkalian pecahan melalui representasi gambar, secara aljabar atau cara lainnya  Menemukan cara menghitung hasil pembagian pecahan dari bentuk  perkaliannya

P r o b l e m

S o l v i n g

Menan

ya

P r o b l e m

Pak Made mempunyai sebidang tanah untuk lahan perkebunan. Dia merencanakan menanami  separuh  lahannya dengan tanaman apotik hidup. Dia ingin  sepertiga

dari   lahan   yang   akan   ditanami   tanaman   apotik   hidup   itu   ditanami   temulawak. Berapakah dari lahan itu yang akan ditanami temulawak?

Untuk menyelesaikan masalah ini  dapat dikerjakan dengan gambar.

Bagian   yang   diwarnai   sekaligus   diarsir   adalah  

1

6   _{dari   lahan   semula.   Bagian   ini}

menunjukkan   bagian   dari   lahan   yang   ditanami   temulawak.   Luas   dari   bagian   tersebut

adalah   panjang    lebar,   yaitu  

1 2   _x  

1

3 _{.   Jadi,   bagian   yang   ditanami   temulawak}

menyatakan 

1 2  _x 

1 3  ₌ 

1 6 _.

Coba kamu lakukan kegiatan tadi untuk perkalian pecahan lainnya, diskusikan dengan  kelompokmu.

Kegiatan 4

Tujuan Pembelajaran

 Mengubah pecahan ke bentuk desimal dan persen

 Melakukan penjumlahan, pengurangan, perkalian dan pembagian pecahan  desimal dengan cara susun pendek atau cara lainnya

Saat di sekolah dasar, tentu kamu sudah pernah belajar pecahan desimal. Ubahlah  bentuk pecahan berikut ini menjadi pecahan desimal

Menga

mati

Bagian   apotik   hidup   yang ditanami temulawak

Bagian yang ditanami apotik hidup

a.

1

10

b.

3

5

c.

60

100

d.

12

20

Pecahan 

4

15

 dapat diubah menjadi pecahan desimal. Untuk mengubahnya,

kita   dapat   menggunakan   pembagian   susun.   Apa   kamu   masih   ingat?   Coba kamu perhatikan  pembagian susunnya 

¿

Jadi   4

15  ₌ 

0,26

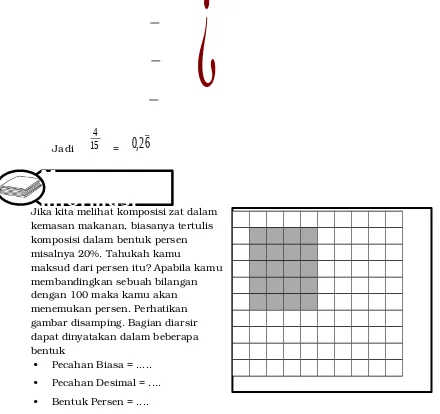
Jika kita melihat komposisi zat dalam kemasan makanan, biasanya tertulis komposisi dalam bentuk persen misalnya 20%. Tahukah kamu

[image:20.595.77.517.356.770.2]

maksud dari persen itu? Apabila kamu membandingkan sebuah bilangan dengan 100 maka kamu akan menemukan persen. Perhatikan gambar disamping. Bagian diarsir dapat dinyatakan dalam beberapa bentuk

 Pecahan Biasa = ...

 Pecahan Desimal = ....

 Bentuk Persen = ....

Menga

mati

Mengump

ulkan

1. Tulislah setiap persen berikut sebagai suatu pecahan dalam bentuk paling  sederhana.

   a.  15% b.  75% c.  88% d.  18%

2. Tulislah setiap pecahan berikut dalam permil

a.  

3

20

b.  

34

50

c.  

18

150

d.  

23

250

3. Sebanyak 35% dari anggota suatu kelompok mengatakan bahwa hobinya adalah  sepakbola. Berapa persen yang tidak hobi sepak bola?

POLA BILANGAN

Kegiatan 1

Tujuan Pembelajaran

 Mendiskusikan   dan   menjelaskan   alasan   dalam   memprediksi   berbagai   kemungkinan pola bilangan, pola geometris berdasarkan data yang disediakan

 Mendiskusikan   dan   menjelaskan   alasan   dalam   memprediksi   aturan   dari   barisan bilangan dan barisan geometris berdasarkan data yang disediakan

Alat dan Bahan : Satu lembar kertas. 

1. Lipatlah  satu  lembar  kertas  (berbentuk  persegipanjang)  sehingga  menjadi  2  bagian yang   sama.   Guntinglah   menurut   lipatan   tersebut.   Ada   berapa   banyak   potongan kertas?

2. Susunlah semua potongan kertas tersebut sehingga saling menutup. Lipatlah susunan kertas tersebut menjadi 2 bagian yang sama, kemudian guntinglah menurut lipatan tersebut.   Ada   berapa   banyak   potongan   kertas   sekarang?   Catatlahlah   banyaknya potongan kertas yang terjadi  pada tabel di bawah. 

3. Lakukan kegiatan nomor 2 sampai 6 kali.

4. Diskusikan dengan temanmu untuk menjawab pertanyaan berikut ini. a. Apakah banyaknya lembaran kertas yang terjadi mempunyai keteraturan? 

Jika ya, jelaskan keteraturannya!

Mengump

ulkan

Informasi

Banyaknya Lipatan Kertas

Banyaknya Potongan Kertas yang terjadi

1 2

2 4

3 8

4 ...

5 ...

6 ...

b. Apakah dapat ditentukan banyaknya lembaran kertas yang terjadi, jika  dilipat sebanyak 8 kali seperti cara di atas? Berapakah banyaknya lembar  kertas itu?

5. Banyaknya lembaran kertas yang terjadi, jika dilipat dengan cara di   atas membentuk  pola.  Pola 2,   4,   8,   ___,   ___,   ___,   ...       merupakan   salah   satu contoh   pola     bilangan.   Tanda   ___   isilah   dengan   bilangan­bilangan berikutnya dan tanda titik tiga (...) menunjukkan bahwa pola itu berlanjut untuk seterusnya.

6. Dengan   bahasamu   sendiri,   dapatkah   kamu   menjelaskan   arti   dari    pola

bilangan itu?

Bagian 2. Menentukan aturan suatu pola bilangan

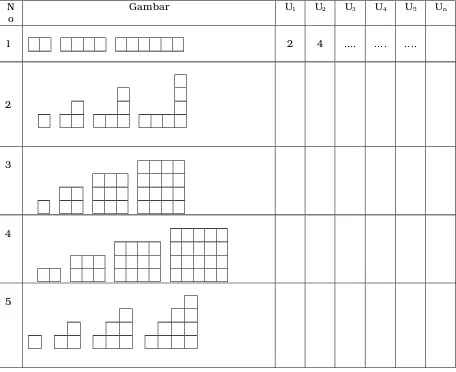
Tentukan  banyak  kotak  pada  setiap  pola  berikut,  banyak  kotak  pada  gambar  pertama adalah   suku   1   (U1),   gambar   kedua   adalah   suku   ke­2   (U2)   dan   seterusnya.   Perkirakan

banyak gambar­gambar selanjutnya jika dibuat gambar dengan pola yang sama

N

o Gambar U1 U2 U3 U4 U5 Un

1 2 4 .... .... ....

2

3

4

5

Mengump

ulkan

[image:23.595.73.529.366.738.2]

Kegiatan 2

Tujuan Pembelajaran

 Menyusun   atau   membuat   barisan   bilangan   dan   barisan   geometris   tertentu   dan meminta teman dalam kelompok untuk memprediksi aturan dan menjelaskan alasan logis yang dibuatnya

 Dengan permainan beberapa siswa memperagakan pola bilangan dengan alat peraga (kartu, batang korek api, kelereng, dll) secara kreatif.

Bersama kelompokmu lakukan kegiatan berikut ini

1. Siapkan   salah   satu   dari   alat­alat   berikut   ini   ;   lidi,   batang   korek   api,   kelereng, kerikil, atau benda lainnya yang mudah dicari dan dipindahkan

2. Susunlah   benda   yang   kalian   pilij   di   atas   meja   kerja   kelompok   kalian,   susunan benda haruslah berpola dan memungkinkan untuk dibuat susunan serupa dengan benda sejenis yang lebih banyak.

3. Gambarkan pola yang kalian buat dalam sebuah kertas kerja.

4. Jika sudah selesai, kalian bisa bertukar tempat dengan kelompok lain dan mencoba melanjutkan pola yang dibuat kelompok lain.

Kegiatan 3

Tujuan Pembelajaran

 Secara   berkelompok     melakukan   observasi   pada   barisan   aritmatika   dan   barisan geometri dengan teliti. Dari aktivitas itu Peserta Didik diharapkan dapat memahami pengetian   barisan   aritmatika,   barisan   geometri,   perbedaan   barisan   aritmatika   dan barisan   geometri   dan   unsur­unsurnya.   Selanjutnya   Peserta   Didik   dibimbing   untuk menentukan suku tertentu dari barisan aritmatika dan barisa geometri.

Bagian A. Barisan Aritmetika

1. Lanjutkan pola bilangan berikut ini sampai diperoleh pola bilangan dengan minimal 5   suku.   Tuliskan   bagaimana   kamu   mendapatkan   bilangan­bilangan   tersebut dengan menuliskannya sebagai aturan pola. 

a. 1, 4, 7, __ , __ , __

Permainan

&

Informasi

aturan : ... b. 3, 5, 7, __ , __ , __

aturan : ... c. 6, 10, 14, __ , __ , __

aturan : ... d. 25, 20, 15, __ , __ , __

aturan : ...

2. Perhatikan aturan dalam pola­pola bilangan di nomor 1. Adakah persamaan antara aturan keempat pola bilangan tersebut?

3. Pola   bilangan   yang   aturannya   dengan   cara   dijumlahkan   dengan   suatu   bilangan yang sama disebut sebagai barisan aritmetika

4. Kita bahas lebih jauh barisan aritmetika pada soal no 1a.

Suku ke­ Bilangan Cara mendapatkan Aturan

1 1 1 1

2 4 1+3 1+1.3

3 7 1+3+3 1+2.3

4 __ 1+3+3+3 1+3.3

5 __ ... ...

n 1+...

×

3

5. Kita bahas lebih jauh barisan aritmetika pada soal no 1c.

Suku ke­ Bilangan Cara mendapatkan Aturan

1 6 6 6

2 10 6+4 6+1.4

3 14 6+4+4 1+2.4

4 __ ... 1+3.4 5 __ ... ...

n 1+...

×

4

[image:25.595.87.529.237.677.2]

6. Jika suku pertama suatu barisan aritmetika adalah a dan bilangan yang digunakan untuk   menjumlahkan   satu   suku   ke   suku   berikutnya   adalah  b  (beda)   maka dapatkah   kamu  menuliskan   aturan  Un  dari   barisan  tersebut?   Jika  belum   isilah

tabel berikut

Suku ke­ Cara mendapatkan Aturan

1 a a + 0.b

2 a+b a + 1.b

3 a+b+b ... 4 a+b+b+b ... 5 ... ...

n A + (...).b

Bagian B. Barisan Geometri

aturan : ... b. 2, 6, 18, __ , __ , __

aturan : ... c. 3, 12, 48, __ , __ , __

aturan : ... d. 1, 5, 25, 125, __ , __ , __

aturan : ...

2. Perhatikan aturan dalam pola­pola bilangan di nomor 1. Adakah persamaan antara aturan keempat pola bilangan tersebut?

3. Pola bilangan yang aturannya dengan cara dikalikan dengan suatu bilangan yang sama disebut sebagai barisan geometri

4. Kita bahas lebih jauh barisan aritmetika pada soal no 1a.

Suku ke­ Bilangan Cara mendapatkan Aturan

1 1 1 1 x 20

2 2 1 x 2 1 x 21

3 4 1 x 2 x 2 1 x 22

4 __ 1 x 2 x 2 x 2 1 x 23

5 __ ... ...

n 1 x 2(...)

5. Kita bahas lebih jauh barisan aritmetika pada soal no 1c.

Suku ke­ Bilangan Cara mendapatkan Aturan

1 3 3 3 x 40

2 12 3 x 4 3 x 41

3 48 3 x 4 x 4 3 x 42

4 __ 3 x 4 x 4 x 4 3 x 43

5 __ ... ...

n 3 x 4(...)

6. Jika suku pertama suatu barisan geometri adalah a dan bilangan yang digunakan untuk mengalikan satu suku ke suku berikutnya adalah  r  (rasio) maka dapatkah kamu menuliskan aturan Un dari barisan tersebut? Jika belum isilah tabel berikut

Suku ke­ Cara mendapatkan Aturan

1 a a x r0

2 a x r a x r1

3 a x r x r a x r2

4 a x r x r x r a x r3

5 ...

BAB II

HIMPUNAN

KI KOMPETENSI DASAR

1 Menghargai dan menghayati ajaran agama yang dianutnya

2 Menunjukkan  sikap  logis,  kritis,  analitik, konsisten  dan  teliti,   bertanggung  jawab,  responsif dan tidak mudah menyerah dalam  memecahkan masalah.

memiliki  rasa  ingin  tahu,  percaya  diri,  dan ketertarikan  pada  matematika  serta  memiliki rasa  percaya  pada  daya  dan   keguanaan matematika,  yang  terbentuk  melalui pengalaman  belajar.

Kegiatan 1

Tujuan Pembelajaran  : 

 Menjelaskan, menguraikan, mendeskripsikan kriteria yang digunakan untuk 

mengkalisifikasi dan mengelompokkan benda­benda

 Menjelaskan himpunan melalui contoh dengan bantuan diagram, gambar atau cara

lainnya

 Menyebut dan menuliskan mana yang merupakan himpunan dan bukan himpunan

atau kumpulan benda dari berbagai kumpulan benda atau gambar benda dari hasil pengamatan

1. Bersama kelompokmu, tuliskanlah 20 nama hewan yang kamu ketahui

1) Ayam 6) ... 11) ... 16) ... 2) Bebek 7) ... 12) ... 17) ... 3) Angsa 8) ... 13) ... 18) ... 4) Burung 9) ... 14) ... 19) ...

Mengump

ulkan

5) Kelelawar 10) ... 15) ... 20) ... 2. Dari 20 nama hewan yang kamu sebutkan tadi, adakah diantaranya yang namanya

diawali dengan huruf yang sama? Kalau ada, coba kamu tuliskan.

... ... 3. Selain dilihat dari huruf awal yang membentuk namanya, adakah buah­buahan

yang kamu tuliskan tadi memiliki ciri­ciri lain yang sama, misalkan banyak kaki, jenis makanan, atau ciri­ciri lainnya? Coba kamu tuliskan dalam tabel berikut ini

No Ciri­ciri Nama Hewan

A Memiliki Sayap Ayam, Bebek, Angsa, Burung, Kelelawar B

C D E

4. Setiap kelompok hewan di atas, dapat diberi nama kelompok dengan huruf Kapital, misalnya A mewakili kelompok hewan yang memiliki sayap ditulis ;

A

=

{

Ayam , Bebek , Angsa , Burung , Kelelawar

}

B

=

¿

C

=

¿

D=

¿

E

=

¿

5. Jika   dilihat   dari   nama­nama   hewan   tadi,   dapatkah   kamu   menuliskan   anggota kumpulan hewan yang banyak makan? Diskusikan dengan anggota kelompokmu? Adakah perbedaan pendapat di antara kalian?

6. Kumpulan dengan ciri­ciri/kriteria yang jelas seperti yang sudah kalian tuliskan di nomor 4 dapat disebut sebagai himpunan, dengan himpunan nama­nama hewan sebagai himpunan semestanya.

7. Kumpulan   dengan   ciri­ciri/kriteria   yang   kurang   jelas   seperti   pada   nomor   5 seringkali menimbulkan perbedaan pendapat, sehingga kumpulan seperti itu tidak dapat dikategorikan sebagai himpunan .

Kegiatan 2

Tujuan Pembelajaran  : 

 Berdiskusi,   membahas,   menjelaskan   dan   menuliskan   cara   menyajikan

himpunan:   dengan   mendaftar   anggota­anggotanya,   dengan   kata­kata,   diagram   dan dengan   notasi   pembentuk   himpunan   berdasarkan   pengelompokan   dari   hasil pengamatan

 Berdiskusi,   membahas,   dan   memilih   cara   penyjian   himpunan   berdasarkan

karakteristik anggotanya

1. Jika A adalah himpunan bilangan Asli kurang dari 11, dapatkah kamu menuliskan anggota himpunan A?

A

={}

2. Selain dengan mendaftar anggotanya himpunan A juga dapat dituliskan dengan menyebutkan sifat/syarat anggota­anggotanya

A

=

¿

 ...

3. Himpunan   A   juga   dapat   dituliskan   dengan   menyebutkan   notasi   pembentuk himpunan. Notasi pembentuk himpunan dituliskan sebagai berikut

A

={a∨syarat yang harus dipenuhi a

}

Sehingga himpunan A dapat dituliskan

A

={a∨a<

11,

a adalahbilangan Asli

}

4. Misalkan himpunan G adalah himpunan bilangan genap diantara 0 dan 20. Coba kamu tuliskan himpunan G dengan tiga cara di atas.

a) Dengan mendaftar anggota G

... b) Dengan menyebutkan sifat anggota G

... c) Dengan menuliskan Notasi pembentuk himpunan G

...

Kegiatan 3

Tujuan Pembelajaran  : 

 Menentukan   anggota   dan   banyak   anggota   himpunan   dari   kelompok   tertentu

berdasarkan pengelompokan dari hasil pengamatan

 Menjelaskan,   mencontohkan   dan   menyatakan   himpunan   kosong,   nol,

berhingga, tak berhingga menggunakan konteks nyata

1. Misalkan H = Himpunan hari yang namanya berhuruf awal S. a) Sebutkan hari­hari apa sajakah yang merupakan anggota H?

... b) Hari­hari apa sajakah yang bukan merupakan anggota H? 

...

Untuk menyatakan anggota suatu himpunan digunakan lambang  



  dan untuk menyatakan   bukan   anggota   suatu   himpunan   digunakan   lambang  



.     Karena Senin   merupakan   anggota   himpunan   H,   maka   dapat   dituliskan:   Senin    H

Menga

mati

Mengump

ulkan

Informasi

Mengump

ulkan

Sedangkan Rabu bukan merupakan anggota himpunan H, maka dapat dituliskan: Rabu  H

c) Tentukan hubungan hari­hari lain dengan H

... ...

d) Berapakah banyak anggota H? Banyak anggota H dapat dituliskan sebagai n(H), sehingga kamu dapat tuliksan n(H) = ....

2. Misalkan I = Himpunan hari yang namanya berhuruf awal Vokal. 1. Sebutkan hari­hari apa sajakah yang merupakan anggota I?

...

2. Berapakah banyak anggota H? Banyak anggota H dapat dituliskan sebagai n(H), sehingga kamu dapat tuliksan n(H) = ....

... 3. I   merupakan   salah   satu   contoh   himpunan   kosong   (nol).   Dapatkah   kamu

menjelaskan karakteristik himpunan kosong  ... Himpunan kosong dapat dituliskan dengan { } atau 

∅

3. Perhatikan himpunan­himpunan berikut. P = { m, a, t, e, i, k} Q = { 1, 3, 5, 7, 9 } R = { 2, 4, 6, 8, . . . , 20 } S = { 0, 1, 2, 3, . . . } T = { 5, 10, 15, 20, . . . }  Dapatkah kamu menuliskan banyak anggota himpunan­himpunan di atas? n(P)   = n(S)   =

n(Q)   = n(T)  = n(R)  =

 Perhatikan himpunan P, Q dan R. Dapatkah kamu memastikan banyak anggota himpunan­himpunan   tersebut?   Himpunan   P,   Q   dan   R   merupakan   contoh

himpunan   berhingga.   Dapatkah   kamu   menjelaskan   bagaimana   karakteristik himpunan berhingga?

... ...  Perhatikan  himpunan  S  dan  T.  Dapatkah  kamu  memastikan  banyak  anggota

himpunan­himpunan   tersebut?   Himpunan   S   dan   T   merupakan   contoh

himpunan   tak   berhingga.   Dapatkah   kamu   menjelaskan   bagaimana karakteristik himpunan tak berhingga?

... ...

P r o b l e m

1. Perhatikan kumpulan­kumpulan berikut ini, tentukan apakah kumpulan tersebut “dapat”  atau  “tidak  dapat”  membentuk  suatu  himpunan  dengan  memberi  tanda rumput KUMPULAN DAPAT MEMBENTUK HIMPUNAN TIDAK DAPAT MEMBENTUK HIMPUNAN

b. kumpulan   bunga­bunga   yang indah.

c. kumpulan   siswa­kelas   I   SMP yang   berulang   tahun   pada tanggal 1 Juli.  

d. kumpulan guru­guru SMP yang berusia kurang dari 40 tahun. e. kumpulan guru­guru SMP yang

bijaksana.

f. kumpulan   bilangan   genap antara 1 dan 10.

g. kumpulan   bilangan   prima kurang dari 20.

h. kumpulan   siswa   kelas   I   SMP yang pandai.

i. kumpulan walimurid SMP yang sabar.

j. kumpulan   buku   paket matematika SMP.

1. kumpulan   orang­orang   yang rajin belajar

2. Jika  S adalah  himpunan nama­nama  bulan dalam  satu tahun,  dapatkah kamu menuliskan himpunan S dengan mendaftar anggotanya, menyebutkan sifatnya dan menuliskan notasi pembentuk himpunannya? ... ... ... 3. Dapatkah kamu menuliskan dengan mendaftar anggotanya, himpunan J yaitu him himpunan nama­nama bulan dalam satu tahun yang diawali dengan huruf J ...

4. Dapatkah   kamu   menuliskan   dengan   menyebutkan   syarat­syarat   anggotanya

himpunan 

R=

{

September , Oktober , Nopember , Desember

}

...

5. Dapatkah   kamu   menuliskan   notasi   pembentuk   himpunan

R=

{

September , Oktober , Nopember , Desember

}

... 6. Diketahui P = { bilangan pembagi dari 24 }

Tuliskan  semua  anggota  P  dan  periksalah  apakah  pernyataan  berikut  ini  benar atau salah.

i. 10  P j. 12  P k. 20  P l. 24  P

Kegiatan 4

Tujuan Pembelajaran  : 

 Menjelaskan, mencontohkan dan menyatakan jenis, cakupan dan karakteristik

himpunan   semesta   dari   kelompok   benda/   himpunan   bilangan   berdasarkan pengelompokan dari hasil pengamatan

 Menjelaskan karakteristik dan menentukan himpunan bagian dan banyaknya

himpunan bagian dari kelompok benda/ himpunan berdasarkan pengelompokan dari hasil pengamatan

Misalkan 

A  = { merah, kuning, hijau }.

B  = { merah, kuning, hijau, ungu, biru}.

C  = { merah, jingga, kuning, hijau, biru, nila, ungu}

Perhatikan himpunan di atas. B memuat semua anggota A, maka dikata­kan bahwa B merupakan himpunan semesta dari himpunan A.

a) Coba kamu selidiki apakah C himpunan semesta dari A? Jelaskan ... b) Coba kamu selidiki apakah B himpunan semesta dari A? Jelaskan

...

Coba kamu diskusikan definisi dari himpunan semesta

Himpunan Semesta adalah ... ... ... ... Sebutkan dua himpunan semesta yang mungkin untuk masing­masing himpunan  berikut ini.

K  =  { kerbau, kuda }.

L =  { Indonesia, Malaysia, Singapura }.

Menga

mati

Menan

ya

M =  { merah, kuning, hijau }. N =  { jeruk, mangga, nanas }. O  =  { Juni, Juli }.

P  =  { ayam, itik, angsa }.

Kegiatan 5

Tujuan Pembelajaran  : 

 Mendeskripsikan   dan   menentukan   komplemen   dari   kelompok   benda/

himpunan berdasarkan pengelompokan dari hasil pengamatan

 Menjelaskan karakteristik keanggotaan dan menentukan karakteristik 

keanggotaan dan hasil irisan dari dua atau lebih dari kelompok benda/himpunan   Menjelaskan karakteristik keanggotaan dan menuliskan hasil gabungan dari 

dua atau lebih dari kelompok benda/himpunan

 Menjelaskan karakteristik keanggotaan  dan menuliskan hasil pengurangan 

atau selisih dari dua atau lebih dari kelompok benda/himpunan

1. Menjelang Ulangan Akhir Semester, semua siswa kelas 7 harus menyiapkan diri dan   mempelajari   dengan   baik   sebanyak   12   mata   pelajaran   yang   akan   diujikan, yaitu:  PKn, Agama, Bahasa Indonesia, Matematika, IPA, IPS, Bahasa Inggris, Penjaskes,   Seni   Budaya,   TIK,   Budi   Pekerti,   dan   Bahasa   Daerah.  Seminggu sebelum ujian, Putu sudah mempelajari dengan baik 5 mata pelajaran, yaitu: PKn, Bahasa Indonesia, TIK, IPS dan Matematika. Sedangkan Made baru mempelajari dengan baik 4 mata pelajaran, yaitu: IPA, Matematika, Bahasa Inggris, dan IPS.

Dari keterangan di atas, kita dapat membentuk himpunan­himpunan antara lain:

S =  Himpunan mata pelajaran pada Ulangan Akhir Semester.

A =  Himpunan  mata  pelajaran  pada  Ulangan Akhir Semester yang 

sudah dipelajari Putu.

B =  Himpunan  mata  pelajaran  pada  Ulangan Akhir Semester yang 

sudah dipelajari Made

.

a) Coba kamu tuliskan himpunan­himpunan di atas dengan cara mendaftar 

anggota­anggotanya.

S = ... ... A = ... ... B = ... ...

P r o b l e m

b) Misalkan P = Himpunan mata   pelajaran   pada   Ulangan Akhir Semester yang belum dipelajari Putu. Dapatkah kamu mendaftar anggota P?

P = ... ... c) Perhatikan   anggota­anggota   himpunan   P,   semua   anggota   P   merupakan

elemen S yang bukan anggota A. Dengan demikian P dapat juga dituliskan sebagai  Ac  _{atau A’  (dibaca : komplemen himpunan A). Dengan demikian}

coba kamu tuliskan anggota Ac

Ac _= ...

...

d) Coba kamu tuliskan, dengan mendaftar anggotanya, himpunan Bc

Bc _= ... 

... e) Dari   contoh   tadi,   jika   Q   merupakan   suatu   himpunan,   coba   jelaskan   dengan

kalimatmu sendiri pengertian dari himpunan Qc

... ...

Perhatikan   kembali   soal   pada   nomor   1.   Jika   D   merupakan   himpunan   mata pelajaran     pada     Ulangan   Akhir   Semester   yang   sudah   dipelajari   Putu   dan   juga sudah dipelajari Made.

a) Dapatkah kamu menuliskan anggota D

A = ... ... B = ... ... D = ... ... b) Coba kamu jelaskan karateristik/ciri­ciri anggota D jika dibandingkan dengan A

dan B. 

... ... Himpunan   D   dapat   juga   dikatakan   sebagai   Irisan   A   dan   B,   yang   dituliskan

A ∩B

c) Jika P dan Q suatu himpunan, maka berdasarkan karakteristik di atas coba jelaskan definisi dari 

P∩ Q

...      ...

Perhatikan   kembali   soal   pada   nomor   1.   Jika   E   merupakan   himpunan   mata pelajaran   pada   Ulangan Akhir Semester yang sudah dipelajari Putu atau sudah dipelajari Made.

A = ... ... B = ... ... E = ... ... b) Coba kamu jelaskan karateristik/ciri­ciri anggota E jika dibandingkan dengan A

dan B. 

... ... Himpunan E dapat juga dikatakan sebagai Gabungan A dan B, yang dituliskan

A

∪

B

c) Jika P dan Q suatu himpunan, maka berdasarkan karakteristik di atas coba jelaskan definisi dari 

P

∪

Q

...      ...

2. Perhatikan   kembali   soal   pada   nomor   1.   Jika   F   merupakan   himpunan   mata pelajaran  pada  Ulangan Akhir Semester yang sudah dipelajari Putu tetapi belum dipelajari Made.

a) Dapatkah kamu menuliskan anggota F

A = ... ... B = ... ... F = ... ... b) Coba kamu jelaskan karateristik/ciri­ciri anggota F jika dibandingkan dengan A

dan B. 

... ... Himpunan   F   dapat   juga   dikatakan   sebagai   Selisih   A   dan   B,   yang   dituliskan

A

−

B

c) Jika P dan Q suatu himpunan, maka berdasarkan karakteristik di atas coba jelaskan definisi dari 

P

−

Q

...      ...

Kegiatan 5

Tujuan Pembelajaran  : 

 Menggambar berbagai bentuk diagram venn dari dua atau lebih dari kelompok

 Menjelaskan dan menyebutkan hubungan himpunan dari dua atau lebih dari

kelompok benda/himpunan

 Diskusi   menyelesaikan  masalah  dari   dua   atau   lebih   dari   kelompok

benda/himpunan permasalahan dalam keseharian yang melibatkan konsep himpunan

Cara yang memudahkan kita untuk menyatakan dan melihat hubungan antara beberapa himpunan adalah dengan meng­gunakan diagram atau gambar himpunan yang disebut dengan  Diagram   Venn.   Dalam   membuat   suatu   Diagram   Venn,   perlu   diperhatikan beberapa hal, antara lain:

1. Himpunan semesta biasanya digambarkan dengan bentuk persegipanjang.

2. Setiap   himpunan   lain   yang   sedang   dibicarakan   digambarkan   dengan  lingkaran

atau kurva tertutup sederhana.

3. Setiap anggota masing­masing himpunan digambarkan dengan noktah atau titik. 4. Jika banyak anggota himpunannya tak berhingga, maka masing­masing anggota

himpunan tidak perlu digambarkan dengan suatu titik.

Contoh

Jika diketahui himpunan semesta S = { a, b, c, d, e, f, g } dan  A = { b, d, f, g }, maka  diagram Venn dari S sebagai berikut:

Sedangkan diagram Venn dari himpunan S dan A adalah

S

A

      b     d a      e

   c       f    g

Menga

mati

S

a

      b     d

      e    c        f    g

Mengump

ulkan

1. Dengan memperhatikan contoh di atas, coba gambarlah diagram Venn dari himpunan­himpunan berikut.

a) S  = { 1, 2, 3, . . . , 10 }    A  = { 3, 5, 7 }

b) S  = { 1, 2, 3, . . . , 10 }

A  = Himpunan bilangan cacah genap antara 1 dan 10 

c) S  = { a, b, c, d, . . . , j } A  = { a, i, e }

B  = { b, c, d, i, e }

2. Misal A = { 1, 2, 3, 4 } dan B = { 2, 3, 5, 7, 8 }. Jika kedua himpunan tersebut dinyatakan dalam diagram venn, maka ada beberapa hal yang perlu diperhatikan.

Perhatikan   bahwa  

A ∩B

={

2,3

}

,   dengan   demikian   kedua   himpunan   tersebut dalam diagram  venn akan  saling berpotongan  (bagian yang  diarsir). Coba  kamu tuliskan anggota himpunan A maupun B pada diagram venn berikut. 

Dari kegiatan ini dapat disimpulkan bahwa jika 

A ∩B ≠

∅

 maka A dan B  merupakan dua himpunan yang saling berpotongan

3. Misalkan

P  = Himpunan 6 abjad Latin yang pertama Q  = Himpunan 3 abjad Latin yang pertama a) Tuliskan semua anggota P dan Q

P = ... Q = ... b) Tuliskan anggota 

P∩ Q

P∩ Q=

¿

 ... c) Perhatikan P, Q, dan 

P∩ Q

, adakah diantara himpunan tersebut yang 

sama?

d) Coba nyatakan himpunan­himpunan di atas dengan diagram venn

S

A B

Dari   kegiatan   ini   dapat   disimpulkan,   jika  

P∩ Q

=

P

  maka   P   merupakan himpunan bagian dari Q dengan kata lain semua anggota P merupakan anggota Q, kejadian seperti ini dapat dituliskan 

P

⊂

Q

BAB III

GARIS DAN SUDUT

KI KOMPETENSI DASAR

1 Menghargai dan menghayati ajaran agama yang dianutnya

2 Memiliki  sikap  terbuka,  santun,  objektif, menghargai  pendapat   dan  karya  teman dalam interaksi kelompok maupun aktiftas   sehari­hari

3 Memahami  berbagai  konsep  dan  prinsip garis  dan  sudut  dalam   pemecahan masalah nyata;

Kegiatan 1

Tujuan Pembelajaran

 Menentukan titik, garis, dan bidang

 Mengidnetifikasi sinar garis dan ruas garis (segmen)

 Mengidentifikasi dan menjelaskan benda­benda yang melibatkan sudut dan garis yang  bersifat alamiah ataupun buatan manusia untuk kepentingan estetik, fungsi, manfaat,  ataupun fungsi ergonomisnya 

Kegiatan 2

Tujuan Pembelajaran

 Menentukan kedudukan kedua garis

1. Lukislah sebuah garis yang melalui titik A dan B (garis AB) 2. Lukislah sebuah garis yang melalui titik E dan D (garis ED)

3. Apakah AB dan ED bertemu(berpotongan)? Di mana perpotongan AB dan ED? 4. Lukislah sebuah garis yang melalui titik A dan G  (garis AG)

5. Apakah AB dan AG bertemu(berpotongan)? Di mana perpotongan AB dan AG? 6. Lukislah sebuah garis yang melalui titik C dan D  (garis CD)

7. Apakah AB dan CD bertemu(berpotongan)? 

8. Dari garis­garis yang kamu buat tadi, yang manakah merupakan garis yang saling  berpotongan?

9. Dari garis­garis yang kamu buat tadi, yang manakah merupakan garis yang saling  berhimpit?

10. Dari garis­garis yang kamu buat tadi, yang manakah merupakan garis yang saling  Sejajar?

Kegiatan 3

 Menggambar atau melukis garis dan sudut dengan menggunakan penggaris, jangka dan busur derajat

Bagian A. Titik, Garis dan Bidang

Alat : Selembar kertas, pensil, penggaris

Langkah kerja 1. Gambarlah sebuah titik pada kertasmu. Melalui sebuah titik ini buatlah sebuah garis. Dapatkah kamu membuat garis lain yang juga melalui titik tadi? Ada berapa banyak garis yang dpat dibuat melalui satu titik? 2. Gambarlah dua buah titik. Dapatkah kamu membuat sebuah garis yang melalui kedua titik tersebut? Ada berapa garis yang dapat dibuat? 3. Gambarlah tiga buah titik. Gambarlah garis yang melalui masing­masing dua titik dari ketiga titik yang kamu gambar tadi. Ada berapa garis yang dapat dibuat? Bagian B. Melukis dan Mengukur Besar Sudut Dapatkah kamu mengukur besar sudut PQR pada gambar di bawah ini?      Alat apakah yang dapat kamu gunakan untuk mengukur?

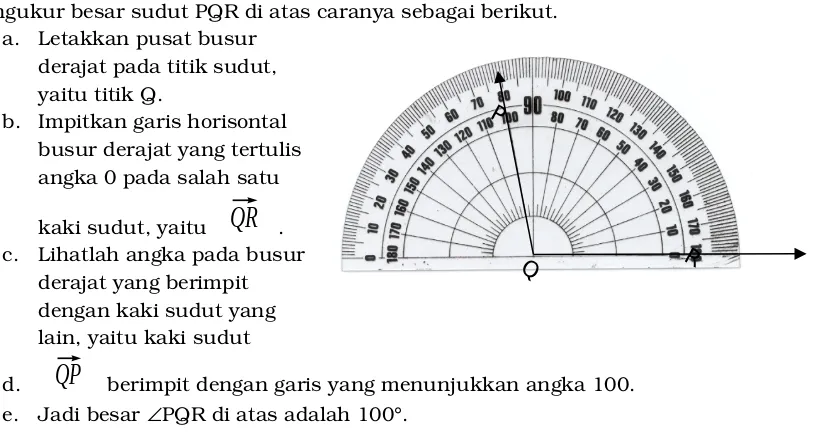
Salah   satu   alat   yang   dapat digunakan   untuk   mengukur besar suatu sudut adalah busur derajat    Pada   busur   derajat terdapat   dua   deretan   angka yaitu   bagian   atas   dan   bagian bawah.   Pada   bagian   atas,   dari kiri   ke   kanan   tertulis   angka   0, 10,   20,   30,     .   .   .   ,   180, sedangkan di bagian bawah dari kiri ke kanan tertulis 180, 170,

160,  . .  . ,  0. Perpotongan  antara garis  horisontal dengan  garis vertikal  disebut  pusat busur.  Untuk mengukur besar sudut PQR di atas caranya sebagai berikut. a. Letakkan pusat busur derajat pada titik sudut, yaitu titik Q. b. Impitkan garis horisontal busur derajat yang tertulis angka 0 pada salah satu

kaki sudut, yaitu 

⃗

QR

. c. Lihatlah angka pada busur

derajat yang berimpit dengan kaki sudut yang lain, yaitu kaki sudut

d.

⃗

QP

 berimpit dengan garis yang menunjukkan angka 100. e. Jadi besar PQR di atas adalah 100.

Garis horisontal

Pusat busur

Garis vertikal

[image:42.595.125.532.509.726.2]

Dengan menggunakan busur derajat, lukislah sebuah sudut yang besarnya 1. 300

2. 450

3. 600

4. 900

5. 1200

Untuk memeriksa pemahamanmu dan untuk melatih keterampilan dalam menggunakan  busur derajat, ukurlah besar setiap sudut berikut ini. Jelaskan caramu mengukur!

1.       2. 

3.       4. 

Kegiatan 4

Tujuan Pembelajaran

 Mengidentifikasi sudut lancip  Mengidentifikasi sudut tumpul  Mengidentifikasi sudut siku­siku

Terampil

Matematik

a

1. Sudut berapakah yang dibentuk jarum jam dan menit ketika pukul 03.00?

2. Pada pukul berapa akan terbentuk sudut yang sama besarnya dengan sudut pada pukul 03.00?

... 3. Sebutkan   beberapa   kondisi   waktu   sehingga   jarum   jam   dan   jarum   menit

membentuk sudut yang kurang dari sudut pada pukul 03.00

... 4. Sebutkan   beberapa   kondisi   waktu   sehingga   jarum   jam   dan   jarum   menit

membentuk sudut yang lebih dari sudut pada pukul 03.00

...

Dalam masalah di atas terdapat 3 jenis sudut, dapatkah kamu menghubungkannya dengan peta konsep berikut ini?

Kegiatan 4

Tujuan Pembelajaran

 Menentukan hubungan antar sudut jika dua buah garis sejajar dipotong oleh sebuah  garis lainnya

Menga

mati

Menan

ya

Dengan menggunakan busur derajat ukurlah besar masing­masing sudut yang ada pada gambar di atas. Adakah sudut­sudut yang besarnya sama? Coba kamu pasangkan sudut­ sudut yang besarnya sama.

Dengan melihat hasil di atas, tanpa menggunakan busur derajat, coba tandai sudut­sudut yang besarnya sama pada gambar berikut.

BAB IV

SEGIEMPAT DAN SEGITIGA

Menga

mati

Mengump

ulkan

KI KOMPETENSI DASAR

1 Menghargai dan menghayati ajaran agama yang dianutnya

2 Menunjukkan   sikap   logis,   kritis,   analitik, konsisten   dan   teliti, bertanggung   jawab,   responsif dan tidak mudah menyerah dalam memecahkan masalah.

Memiliki   rasa  ingin  tahu,   percaya  diri,  dan ketertarikan  pada matematika     serta     memiliki   rasa     percaya     pada     daya     dan keguanaan   matematika,     yang     terbentuk     melalui   pengalaman belajar.

3 Memahami   sifat­sifat   bangun   datar   dan   menggunakannya     untuk menentukan  keliling  dan luas;

menaksir  dan  menghitung  luas  permukaan  bangun  datar  yang tidak  beraturan  dengan  menerapkan prinsip­prinsip geometri; 4 Menyelesaikan  permasalahan  nyata  yang  terkait  penerapan  sifat­

sifat  persegipanjang, persegi, trapesium, jajargenjang, belahketupat, dan layang­layang.

Kegiatan 1

 Mengidentifikasi dan menjelaskan benda­benda dengan permukaaan berbentuk segitiga atau   segiempat   yang   bersifat   alamiah   ataupun   buatan   manusia   untuk   kepentingan estetik, fungsi, manfaat, ataupun fungsi ergonomisnya 

 Menggambar atau melukis segitiga dan segi empat dengan berbagai ukuran sisi, sudut dan modelnya. Mengukur sudutnya dengan dengan menggunakan busur derajat

 Menentukan jenis, sifat dan karakteristik  segitiga  dan segiempat  berdasarkan  ukuran dan hubungan antar sudut dan sisi­sisi

1. Perhatikan   benda­benda   yang   ada   di   sekitarmu,   adakah   yang   permukaannya berbentuk segitiga atau segi empat? Carilah setidaknya masing­masing 5 benda.

Benda yang permukaannya

Berbentuk Segitiga Benda yang permukaannyaBerbentuk Segiempat

 

2. Dari benda­benda yang kamu catat tadi, coba gambarkan bentuk permukaannya menggunakan penggaris

Menga

mati

Mengump

ulkan

Informasi

3. Dengan menggunakan penggaris ukurlah unsur­unsur dari segi empat berikut ini. a. Panjang sisi ;

AB = ...., CD = .... AD = ...., BC = .... b. Panjang diagonal

AC = ...., BD = .... c. Perpotongan

diagonal

AE = ...., EC = .... BE = ...., ED = .... d. Besar sudut

∠

A

=

¿

 ...., 

∠

B

=

¿

 ....

∠

C

=

¿

 ...., 

∠

D=

¿

 ....

Sifat­sifat Jajar Genjang Panjang sisi : Panjang diagonal : Perpotongan 

diagonal

:

Besar sudut :

4. Bandingkan   sifat   jajar   genjang   tadi   dengan   persegi   panjang   berikut   ini.   Sifat manakah yang berlaku pada persegi panjang? Adakah sifat yang dapat dijelaskan lebih spesifik, misalnya besar sudut dengan ukuran tertentu?

Panjang sisi :

Panjang diagonal :

Perpotongan diagonal :

Besar Sudut :

5. Bandingkan   sifat   persegi   panjang   tadi dengan persegi berikut ini. Sifat manakah yang berlaku pada persegi? Adakah sifat yang dapat dijelaskan lebih spesifik, misalnya besar sudut atau ukuran sisinya?

Menalar

Panjang sisi ;

Panjang diagonal :

Perpotongan diagonal :

Besar Sudut :

6. Dengan menggunakan penggaris ukurlah unsur­unsur dari segi empat berikut ini. a. Panjang sisi ;

AB = ...., CD = .... AD = ...., BC = .... b. Panjang diagonal

AC = ...., BD = .... c. Perpotongan diagonal

AE = ...., EC = .... BE = ...., ED = .... d. Besar sudut

∠

A

=

¿

 ....,

∠

B

=

¿

 ....

∠

C

=

¿

 ....,

∠

D

=

¿

 ....

Sifat­sifat Layang­layang Panjang sisi : Panjang diagonal : Perpotongan 

diagonal

:

Besar sudut :

7. Bandingkan   sifat   layang­layang   tadi   dengan   belah   ketupat   berikut   ini.   Sifat manakah yang berlaku pada belah ketupat? Adakah sifat yang dapat dijelaskan lebih spesifik, misalnya besar sudut atau ukuran sisinya?

Panjang sisi ;

Panjang diagonal :

Perpotongan diagonal :

Besar Sudut :

Kegiatan 2

Tujuan Pembelajaran

 Mendiskusikan  dan menemukan  rumus untuk  menghitung keliling  dan luas  persegi panjang dan segitiga melalui pengamatan atau eksperimen

 Menggambar, mendemonstrasikan atau memperagakan berbagai bangun segitiga dan persegi panjang dengan luas atau keliling tertentu dengan bantuan alat atau tanpa alat peraga

1. Tentukan   luas   daerah   dan   keliling   persegi panjang   berikut   ini.   (Luas   daerah   dapat dihitung   dengan   menghitung   banyak   persegi satuan pada bangun datar tersebut)

Panjang  = Lebar  = Luas  =  Keliling  =

2. Tanpa   menghitung   semua   persegi   satuan, dapatkah kamu menentukan luas dan keliling persegi panjang berikut ini? Jelaskan.

Luas  =  Keliling  =

Kesimpulan

Jika  p = panjang dan l = lebar  maka rumus Luas (L) dan Keliling (K) adalah sebagai berikut

L = ... K = ...

3. Karena persegi adalah persegi panjang yang semua sisinya sama panjang, luas persegi dapat diperoleh dengan menggunakan rumus luas persegi panjang

Luas Persegi Panjang = ...

Karena pada persegi ukuran p = l = sisi persegi (s) Sehingga Luas Persegi =...

Mengump

ulkan

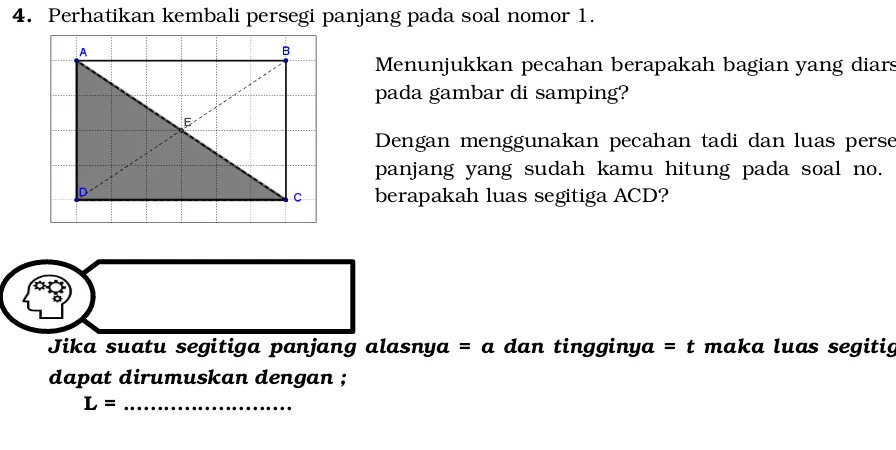
4. Perhatikan kembali persegi panjang pada soal nomor 1. 

Menunjukkan pecahan berapakah bagian yang diarsir pada gambar di samping?

Dengan menggunakan pecahan tadi dan luas persegi panjang   yang   sudah   kamu   hitung   pada   soal   no.   1, berapakah luas segitiga ACD?

Jika suatu segitiga panjang alasnya = a dan tingginya = t maka luas segitiga dapat dirumuskan dengan ;

L = ...

Kegiatan 3

Tujuan Pembelajaran

 Mendiskusikan dan menjelaskan cara menghitung luas segi empat lainnya (trapesium, jajargenjang,   belah   ketupat,   dan   layang­layang)   atau   bangun   gabungan   melalui pengamatan atau eksperimen

1. Luas   jajar   genjang   dapat   ditentukan   dengan   menggunakan   pendekatan   persegi panjang. Lakukan kegiatan berikut ini;

[image:51.595.66.514.83.308.2]

a. Guntinglah gambar jajar genjang seperti gambar   di   samping   (ada   di   halaman terakhir   bab   ini)   sehingga   kamu memperoleh   selembar   kertas   berbentuk jajar genjang

b. Gunting   bagian   yang   diarsir,   kemudian pindahkan   tempatnya   agar   kamu membentuk   bangun   baru   yang berbentuk persegi panjang

c. Jika sudah berhasil membentuk persegi panjang, maka dapat disimpulkan Luas Jajar Genjang = Luas Persegi Panjang = 

p× l

Dengan menghubungkan  p dan l  dengan  alas (a)  dan  tinggi (t)  jajar  genjang, diperoleh Luas Jajar Genjang = ...

Menalar

Permainan

&

2. Luas   layang­layang   juga   dapat   ditentukan   dengan menggunakan pendekatan persegi panjang. 

a.   Guntinglah gambar layang­layang seperti gambar di samping (ada di halaman terakhir bab ini) sehingga

kamu   memperoleh   selembar   kertas   berbentuk layang­layang

b. Gunting   setiap   diagonalnya   (garis   putus­putus) sehingga kamu memperoleh 4 buah segitiga

c. Dengan 4 segitiga tadi, coba kamu bentuk kembali sebuah bangun persegi panjang.

Jika diagonal layang­layang tadi adalah d1

dan d2, maka bagaimana hubungan panjang dan lebar persegi panjang 

dengan d1 dan d2?  (*)

d. Jika sudah berhasil membentuk persegi panjang, maka dapat disimpulkan

Luas layang­layang = Luas Persegi Panjang = 

p× l

(**) Berdasarkan (*) dan (**) dapat disimpulkan

Luas layang­layang = ...

3. Dengan langkah yang sama dengan nomor 6, coba kamu temukan rumusan luas belah ketupat.

Luas belah ketupat = ...

4. Menemukan luas trapezium dapat dilakukan dengan pendekatan luas persegi panjang dan segitiga.

Luas Trapezium=

L

_I

+

L

_II

+

L

_III Luas segitiga I

LI = ...

Luas segitiga III

LIII = ...

Luas persegi panjang II LII = ...

Dengan demikian luas trapesium = ...

Karena   (p   +   a   +   a)   +   p   merupakan   jumlah   kedua   sisi   sejajar   dan   t   adalah   tinggi trapezium, maka 

Luas Trapezium = 

1

2

× Jml sisi sejajar ×t

Kompetensi Dasar

3.1 Menaksir  dan  menghitung  luas  permukaan  bangun  datar  yang  tidak  beraturan dengan menerapkan prinsip­prinsip geometri 

Kegiatan 

Tujuan Pembelajaran

 Mendiskusikan cara menaksir luas bangun datar tidak beraturan 

1. Tentukan   keliling   bangun   disamping,   jelaskan   cara menghitunya dengan kata­katamu sendiri

2. Dengan menghitung banyaknya persegi satuan, tentukan luas daerah bangun datar berikut ini

3. Luas daerah bangun datar seperti di atas juga dapat dicari dengan cara menggunting beberapa   bagian   bangun   itu   dan   menyusunnya   kembali   menjadi   beberapa   persegi panjang. Coba kamu lakukan hal ini (bangun yang harus digunting ada di halaman terakhir bab ini) 

P r o b l e m

4. Sebelumnya   kamu   sudah   mempelajari   rumus­rumus   luas   bangun   datar.   Dengan menggunakan rumus­rumus ini kamu juga dapat menentukan luas daerah bangun datar yang tidak beraturan.

Bangun I (Trapezium) LI

= ...        ...

Bangun II (Persegi Panjang)

LII = ...

       ...

Bangun III (Segitiga)

LIII = ...

       ...

Bangun IV (Jajar Genjang)

LIV = ...

       ...

BAB V

PERBANDINGAN DAN SKALA

KI KOMPETENSI DASAR

1 Menghargai dan menghayati ajaran agama yang dianutnya

2 Memiliki  sikap  terbuka,  santun,  objektif, menghargai  pendapat   dan  karya  teman dalam interaksi kelompok maupun aktiftas   sehari­hari

3 Memahami  konsep  perbandingan  dan  menggunakan  bahasa   perbandingan  dalam  mendeskripsikan  hubungan  dua besaran; 4 Menggunakan konsep perbandingan untuk menyelesaikan  masalah 

Kegiatan 1

Tujuan Pembelajaran

 Menggambar denah atau peta letak suatu benda/rumah dengan benda­benda lain tanpa skala dan dengan skala dilengkapi dengan unsur­unsur pelengkap peta  Mendiskusikan,  membahas dan  menentukan nilai  perbandingan atau  skala dari

peta,   serta   menghitung   ukuran   sebenarnya   benda   dalam   peta/denah/foto berdasarkan skalanya

 Melakukan   pengukuran     pada   model   (gambar,   denah,   peta)  untuk   menentukan jarak atau ukuran sebenarnya

1. Coba kamu gambarkan (dalam sebuah kertas tambahan) denah menuju rumahmu jika sekolah sebagai patokannya. Buatlah dengan keterangan yang sejelas­jelasnya agar denah yang kamu buat mudah dipahami orang lain.

2. Kalimantan   Utara   (Kaltara)   adalah   salah   satu   Provinsi   termuda   di   Indonesia. Perhatikan peta Provinsi Kaltara berikut ini

Terampil

Matematik

a

Peta di atas dibuat dengan skala 1 : 6.000.000

Artinya   setiap   1   cm   pada   peta   di   atas,   bermakna   6.000.000   cm   pada   jarak (keadaan) sebenarnya. Dengan demikian jika ada dua kota pada peta di atas yang jaraknya 2 cm maka jarak sesungguhnya dari kedua kota tersebut adalah ;

2

×

6.000 .000=

¿

... cm = ... Km

3. Coba kamu ukur (menggunakan penggaris) jarak kota Tarakan ke 4 kota lainnya yang terdapat pada peta di atas. Selanjutnya dengan menggunakan skala peta di atas, coba kamu tentukan jarak sebenarnya dari kota Tarakan ke kota­kota lainnya tersebut.

4. Dari   kegiatan   di   atas   coba   kamu   rumuskan   kembali   makna   dari   sebuah   skala 1 : 400.000. Bagaimana cara menentukan sebuah skala jika dihubungkan dengan jarak sebenarnya dan jarak pada peta?

... ... ...

5. Perhatikan kembali denah menuju rumahmu yang telah kamu buat di nomor 1. Apakah denah tersebut sudah menggunakan skala? Jika sudah, berapa skalanya? Jika belum, coba kamu ulangi sekali lagi menggunakan skala yang sesuai.

Kegiatan 2

Tujuan Pembelajaran

 Mendiskusikan,   membahas   dan   menentukan   nilai   perbandingan   dari   komposisi bahan makanan, bahan obat pada resep, bahan bangunan dsb serta menghitung bahan yang diperlukan dalam resep/gedung dsb berdasarkan nilai perbandingan.

Mengump

ulkan

Informasi

1. Pak Ketut mempunyai 5 ekor kambing dan 2 ekor sapi. Tentukan perbandingan  dari:

a. banyaknya kambing dengan  banyaknya sapi ...

b. banyaknya kaki kambing dengan banyaknya kaki sapi! ...

2. Untuk membuat secangkir kopi diperlukan 2 sendok teh bubuk kopi dan 3 sendok teh gula pasir.

a. Tentukan   perbandingan  banyaknya   kopi  terhadap   banyaknya  gula   untuk membuat secangkir kopi!

Banyak kopi : banyak gula = .... : ....

b. Misalnya kamu disuruh membuat 2 cangkir kopi, berapa banyaknya gula dan   kopi   yang   kamu   perlukan?   Tentukan   perbandingan   banyaknya   kopi terhadap banyaknya gula untuk membuat  2 cangkir kopi!

c. Dapatkah kamu menentukan perbandingan banyaknya gula dan kopi untuk membuat 5 cangkir kopi?

... ... ...

d. Tanpa   menghitung   banyaknya   gula   dan   kopi   yang   diperlukan,   dapatk