LKS Matematika Kelas X Semester

Created by Mukhlisah Zulfa Nadiya 1

NAMA : ………

KELAS : ………

Matematika itu mudah

dan menyenangkan!

SEMANGAT!!!

Lembar Kerja Siswa 1

A. EKSPONEN

a. Menemukan Konsep Eksponen

Seorang peneliti bidang mikrobiologi di sebuah lembaga penelitian sedang mengamati pertumbuhan suatu bakteri di sebuah

laboratorium mikrobiologi. Pada kultur bakteri tersebut, satu bakteri membelah menjadi r

bakteri setiap jam. Hasil pengamatan menunjukkan bahwa jumlah bakteri pada akhir 3 jam adalah 10.000 bakteri dan setelah 2 jam kemudian, jumlah bakteri tersebut menjadi 40.000 bakteri. Peneliti tersebut ingin mengetahui banyak bakteri sebagai hasil pembelahan dan mencari tahu banyak bakteri dalam waktu 8 jam.

Sebelum mempelajari lebih jauh serta mengenal, memahami dan menyelesaikan beberapa permasalahan matematika yang menyangkut pangkat/eksponen dan bentuk akar diharapkan peserta didik menggali informasi dan pengalaman belajar terdahulu dari beberapa sumber referensi / media interaktif.

Diskusikan dengan kelompok belajar anda, guna menentukan beberapa hubungan yang pasti dian- tara beberapa pola berikut ini:

Masalah 1

1 . Tentukan dan jabarkan bentuk : a. 35 _{b. 5}6 _{c. 10}4

Penyelesaian :

a. 35 _{= 3 x …. x ….. x ….. x ….. = 243}

b. 56 _{= …. x …. x ….. x ….. x ….. x …… = …….}

c. 104 _{= …. x ….. x ….. x ….. = ………}

an _{= …. x ….. x ….. x …… x ….. x a , di mana : a}n _{dibaca a pangkat n}

n factor a disebut bilangan pokok atau basis. n disebut pangkat atau eksponen an _{disebut bilangan berpangkat.}

Apa yang dapat kalian simpulkan dari beberapa penyelesaian di atas?

... b. Sifat-Sifat Pangkat Bulat Positif

Diskusikan dengan kelompok belajar anda, guna menentukan beberapa hubungan yang pasti di antara beberapa pola berikut ini:

Masalah 2 :

Tentukan nilai dari: a. 43 _{x 4}2 _{b. 2}4 _{x 2}5

Penyelesaian :

a. 43 _{x 4}2 _{= ( 4 x …. x 4 ) x ( 4 x ….. ) = ( 4 x ….. x ….. x ….. x ….) = 4}3 + 2 _{= 4}…..

3 faktor 2 faktor (3 + 2) factor b. 24 _{x 2}5 _{= ( 2 x …. x …. x …. ) x ( 2 x …. x …. x …. x 2 )}

= ( …. x …. x …. x …. x …. x …. x …. x …. x …. ) = 2…..

Penarikan kesimpulan:

ap _{. a}q _{= ( a x a x a x … x a ) ( a x a x a x … x a) = ( a x a x a x .. x a ) = a} … + ….

…. Factor …. Factor ( … + …. ) factor Apa yang dapat kalian simpulkan dari uraian penyelesaian masalah di atas?

Buktikan bahwa sifat 1 berlaku untuk : ap . aq = a …. + ……

Masalah 3 :

Tentukan nilai dari: a5 _{: a}3

Penyelesaian :

a5 _{: a}3 _{= ( a x... x... x … x a ) : ( a x... x...)}

5 faktor 3 faktor

=(a x...x...x...x... ) : (a x...x...) = 1 x ( a x ….. ) = a2 _{= a}5 - 3

5 faktor 3 faktor 2aktor Penarikan kesimpulan:

ap _{: a}q _{= (a x...x...x...) : (a x...x...x...)}

p faktor q faktor

= 1 x ( a x …..x…..x a ) = a x a x …. x a = a…. - …

(p - …. ) faktor

Apakah benar bahwa dalam sifat ke-2 dari bilangan bulat positif adalah ap _{: a}q _{= a}…-…

Apa yang dapat kalian simpulkan dari urain di atas?

... ...

Masalah 4 :

Tentukan nilai dari: ( 2 x 5 )3

Penyelesaian :

( 2 x 5 )3 _{= ( 2 x 5 ) x ( … x … ) x ( …x 5 ) = ( 2 x … x 2 ) x ( 5 x …x … ) = 2} … _{. 5} ….

3 faktor 3 faktor 3 faktor Penarikan kesimpulan:

( a . b )p _{= ( a x b ) x ( … x … )x … x ( … x b ) = ( a x … x … x a ) x ( b x .…x … x b)}

p factor p factor p factor = a…_{. b}….

Sifat 3 : ( a . b )p = a… . bp

Masalah 5 :

Tentukan nilai dari: (53₎4

Penyelesaian :

(53₎4 _{= 5}3 _{x 5}… _{x … x 5}3 _{= ( 5 x ….x 5 ) x ( 5 x ….x …. ) x ( 5 x ….x …. ) x ( 5 x ….x …. )}

4 faktor 4 faktor

= 5 x …. x …. x ….. x …. x …. x ….. x ….. x ….. x …. x …. x 5 = 5 …. x … _{= 5}…

3 faktor 3 faktor 3 faktor 3 faktor Apa yang dapat kalian simpulkan dari uraian di atas?

... Sifat 4 : ( ap₎q _{= a}… x …

Masalah 6 :

Tentukan nilai dari:

(

2 3

)

4

Penyelesaian :

(

2

3

)

4

= ... x … x ... x ... = ... 4 faktor

Created by Mukhlisah Zulfa Nadiya 3

Kesimpulan: an _{= ... x ... x ... x ...}

(n faktor)

Sifat 1 : ap _{. a}q _{= a} …. + ……

Sifat 2 : ap _{: a}q _{= a}…-…

Sifat 3 : ( a . b )p _{= a}… _{. b}....

Sifat 4 : ( ap₎q _{= a}… x …

Sifat 5 :

(

a

b

)

n

Sifat 5 :

(

a

b

)

n

= ...

c. Pangkat Nol

Bakteri E. Coli membelah diri setiap 12,5 menit. Hal ini berarti jumlah bakteri E. Coli

menjadi berlipat .... kali lipat dari sebelumya. Lengkapilah.

Waktu 0 12,5 25 37,5 50 ...

Jumlah 1 2 4 ... ... ...

2... ₂... ₂... _{... ... ...}

Pada saat 0 menit, banyak bakteri = .... Banyak bakteri = 2 .... _{= ....}

Mari kita buktikan bahwa a0 _{= 1}

Cara 1: Cara 2:

ap _{: a}p _{= 1 a}0_{x a}p _{= a} 0 + p

a p –p _{= .... a}0_{x a}p _{= ....}

a ... _{= .... a}0 _{= a} ... _{: x a}p

(terbukti) a0 _{= .... (terbukti)}

d. Pangkat Bulat Negatif Lengkapilah

104 ₁₀3 ₁₀2 ₁₀1 ₁₀0 ₁₀-1 ₁₀-2 ₁₀-3 ₁₀-4 _...

10.00 0

...

Amati pola bilangan tersebut. Dengan pola tersebut, dapat dilihat bahwa: 10 -1 ₌ 1

10 = 1

10…… 10

-2 ₌ 1

… … … … . =

1 10…… 10 -1 ₌ 1

… … … … =

1 10…… Mari kita buktikan bahwa a –n ₌ 1

an

Bukti: a0 _{: a}n _{= 1 : a}n

a 0 – ... ₌ 1

an

a ... _{= .... (terbukti)}

Latihan

Ubahlah menjadi pangkat positif dan hitunglah hasilnya

No Pangkat Negatif Pangkat Positif Hasil

1 5-2

2 2a-4

3 1

4−2

4 1

5p−1

Kesimpulan:

a

0

= ....

5

(

1 3

)

−3

6

(

2 7

)

−4

7 _2a−3

p−7

❑

e. Pangkat Pecahan 1) Misalkan n

√

a=ab

Kedua ruas dipangkat n sehingga diperoleh

(

n

√

a

)

n=

(

ab

)

n

a1 _{= a} ...

1 = b. ... b = ...

Jadi, dapat disimpulkan bahwa n

√

a=ab = a ...

2) _amn₌

(

_am

)

1

n

=

√

n… …… … …

Latihan

1. Lengkapi tabel berikut

Bentuk Pangkat Bentuk Akar

y

1 2

s

3 5

(3r) 1 4

5

√

a2

4

√

2b3

5

6

√

h

2. Hitunglah nilainya

a. ₄32

b.

₂₇23

c.

₁₆−41

d.

₂₅−23

3. Nyatakan dalam bentuk pangkat dengan bilangan pokok 2 a.

√

34

b.

√

564

4. Sederhanakan bentuk pangkat berikut dan nyatakan dalam bentuk akar a. _a12_{x a}32

b. _a12_:a13

c.

(

_a23_b 9 2

)

6 7

Created by Mukhlisah Zulfa Nadiya 5

Kesimpulan: n

√

a=a… ….

a

m n₌n

√

… …

d.

(

a

2 3

b

8 3

)

3 4

Lembar Kerja Siswa 2

Topik : Bilangan Rasional, Bilangan Irasional dan Bentuk Akar A. Bilangan Rasional

Bilangan Rasional yaitu bilangan yang dapat dinyatakan dalam bentuk ... dengan a dan b bilangan bulat dan b ≠ 0. Bilangan Rasional dilambangkan dengan ....

Bilangan Rasional dibedakan menjadi dua, yakni: a. Bilangan bulat, seperti -3, -2, 0, 5, 8, ...

b. Bilangan pecahan seperti: 1₂

,

1₄

,

3₅

, ...

Ciri-ciri Bilangan Rasional:

a. Bilangan desimal yang terputus/terbatas, misal: 1₄

=

0,25 dan 3₅

= 0,6

b. Bilangan desimal yang tidak terputus/terbatas tapi berulang, misal: ₆1

=

0,16666... dan 1

9

= 0,1111...

B. Bilangan Irasional

Bilangan Irasional yaitu bilangan yang tidak dapat dinyatakan dalam bentuk ... dengan a dan b bilangan bulat dan b ≠ 0.

Ciri: Bilangan desimal yang tidak terputus/terbatas dan tidak berulang, misal: 0,1435486495....

Manakah yang termasuk bilangan rasional dan irasional?

1.

√

25 2.

√

12 3.

√

6 4.

√

16

5. π 6. 3

√

4 7. 3

√

8 8.

√

0,25

Bilangan irasional disebut bilangan bentuk akar karena tidak dapat bisa diperoleh akarnya yang rasional.

C. Bentuk Akar

22 _{= 4 maka}

√

_{4=¿ ...}

23 _{= ... maka} 3

√

8 = ... 24 _{= ... maka} 4

√

….. = ...

Secara umum: Diketahui n bilangan bulat dan n ≥ 2 X disebut akar ke – n dari a apabila xn _{= ....}

X = … …

√

….. apabila xn _{= ....}

D. Menyederhanakan Bentuk Akar

Untuk setiap a dan b bilangan bulat positif berlaku n

√

a x b=

√

na x

√

n b

Sederhanakan:

1.

√

8 =

√

… x …=

√

… x

√

… = ...

√

… .

2.

√

48 =

√

… x …=

√

… x

√

… = ...

√

… .

3. 3

√

294 = 3

√

… x …=

√

… x

√

… = ...

√

… .

4. 3

5. 3

√

135 =

√

3… x …=

√

3…x

√

3…=…

√

3…

E. Operasi Aljabar pada Bentuk Akar 1. a

√

n c+b

√

nc

=

(…+…)

√

n…

2. a

√

n c−b

√

nc

=

(…−…)

√

n…

3. a

√

n c x b

√

n d

=

(… x …)

√

n… x …

4. a n

√

c b

√

nd=

…...

….. n

√

… … … … .

5.

√

a2

=

√

a x

√

a=… …

6.

√

a x

√

b=

√

…….

7.

√

a

√

b=

√

… … . … …

Soal Latihan

1. 3

√

5 + 4

√

5 = (... + ...)

√

5 = ... 2. 5

√

2 - 7

√

2 = (... - ...)

√

2 = ...

3.

√

18+

√

8 =

√

… x … +

√

… x … = ....

√

…+…

√

… = ... 4.

√

12−

√

27=

√

… x … -

√

… x … = ....

√

…−…

√

… = ... 5.

√

6x

√

3=

√

… x … =

√

… . = ...

6.

√

12 3 =

√

… … .

… … =… … …..

7. 5

√

2 x 4

√

6 = (... x ...)

√

… x … = ... 8. 10

√

10

2

√

5 =

… ….

……

√

…….

…… = ...

9.

√

2 (

√

6+

√

3 ) =

√

2x

√

6+

√

2x

√

…=

√

… …+

√

… ….. = ... 10. (

√

2+

√

3)2=¿ (

√

2+

√

3 )(

√

2+

√

3 )

= (

√

2 )2 _{+ 2 .... x.... + (...)}2

= .... + 2

√

… …. + ...= (... + ...) + 2

√

… … = ... 11. (

√

7−

√

5)2=¿ (

√

7−

√

5 )( ... - … )

= (

√

7 )2 _{– 2 .... x.... + (...)}2

= .... – 2

√

… …. + ... = (... + ...) - 2

√

… … = ... 12. (

√

2+

√

5 ) (

√

2−

√

5 ) = (

√

2 )2 _{+ ... - ... - (...)}2

= .... - ... =...

F. Menyederhanakan Bentuk

√

(a+b)+2

√

ab dan

√

(a+b)−2

√

ab

1. (

√

a+

√

b)2 = (

√

a )2 _{+ 2 .... x.... + (...)}2

= .... + 2

√

… …. + ...

= (... + ...) + 2

√

… … (tarik akar kedua ruas)

(

√

a+

√

b) =

√

(…+…)+2

√

… … .

2. (

√

a−

√

b)2 = (

√

a )2 _{- 2 .... x.... + (...)}2

= .... - 2

√

… …. + ...

= (... + ...) - 2

√

… … (tarik akar kedua ruas)

(

√

a−

√

b) =

√

(…+…)−2

√

… … .

Created by Mukhlisah Zulfa Nadiya 7

Kesimpulan:

√

(a+b)+2

√

ab=(

√

…+

√

…)

√

(a+b)−2

√

ab=(

√

…−

√

…)

Soal Latihan

1.

√

7+2

√

10=(

√

…+

√

…)

A + b = 7

Ab = 10 , maka a = ... dan b = .... Sehingga

√

7+2

√

10=(

√

…+

√

…)

2.

√

8−2

√

7=(

√

…−

√

…)

A + b = ...

Ab = .... , maka a = ... dan b = .... Sehingga

√

8−2

√

7=(

√

…−

√

…)

3.

√

8−

√

60=

√

8−

√

… x …=

√

8−2

√

… .

A + b = ....

Ab = ... , maka a = ... dan b = .... Sehingga

√

8−

√

60=(

√

…−

√

…)

4.

√

₁₁+

√

72=

√

11+

√

… x …=

√

11+2

√

….

A + b = ....

Ab = ... , maka a = ... dan b = .... Sehingga

√

11+

√

72=(

√

…−

√

…)

G. Merasionalkan Penyebut

1) Bentuk

a

√

b

dikali dengan ...

Contoh:

a)

3

√

5= 3

√

5x

√

5

√

5=¿

...

b)

14

√

7= 14

√

7x

√

… .

√

… .=¿

...

2) Bentuk

c

a+

√

b

dikali dengan ...

a)

5

3+

√

2= 5 3+

√

2x

3−

√

2 3−

√

2

=

5(3−

√

2)

(3+

√

2)(3−

√

2)=

… … …−… …..

… … … …..… … … …=

… … …−… …..

… … … …

b)

₂ 6 +

√

3=

6 2+

√

3x

… … … … …

… … … … …

=

6(… … … … …)

(2+

√

3)(… … … … …..)=

… … …−… …..

… … … …..… … … …=

… … …−… …..

… … … …

3) Bentuk

c

a)

√

5

3−

√

3=

√

5 3−

√

3x

3+

√

3

… … … …

=

√

5(3+

√

3)

(3−

√

3)(… … … …)=

… … …+… …..

… … … …..… … … …=

… … …+… …..

… … … …

b)

4

5−

√

2= 4 5−

√

2x

… … … …

… … … …

=

4(… … … .)

(5−

√

2)(… … … …)=

… … …+… …..

… … … …..… … … …=

… … …+… …..

… … … …

4) Bentuk

c

√

a+

√

b

dikali dengan ...

a)

6

√

2+

√

5= 6

√

2+

√

5 x

… … … .

√

2−

√

5

=

6(… … … …)

(… … … … …)(… … … … …...)= … … …−… ….. … … … …= … … …−… ….. … … … …

b)

10

√

3+

√

6= 10

√

3+

√

6x

… … … … …

… … … … …

=

10(… … … … …) (… … … …...)(… … … …..)=

… … …−… …..

… … … …..… … … …=

… … …−… …..

… … … …

5) Bentuk

c

√

a−

√

b

dikali dengan ...

a)

12

√

7−

√

5= 12

√

7−

√

5x

… … … .

√

7+

√

5

=

12(… … … …)

(… … … … …)(… … … … …...)= … … …−… ….. … … … …= … … …−… ….. … … … …

b)

9

√

3−

√

6= 9

√

3−

√

6x

… … … … …

… … … … …

=

9(… … … … …)

(… … … …...)(… … … …..)=

… … …−… …..

… … … …..… … … …=

… … …−… …..

… … … …

Lembar Kerja Siswa3

Topik : Logaritma dan sifat-sifatnya A. RINGKASAN MATERI

Ayo pikirkan?

Bakteri E. Coli membelah diri setiap 12,5 menit. Hal ini berarti jumlah bakteri E. Coli

menjadi berlipat .... kali lipat dari sebelumya. Dapatkah kamu menentukan berapa waktu yang diperlukan agar bakteri itu berjumlah 100?

Logaritma adalah invers (kebalikan) dari perpangkatan.

 Definisi Logaritma:

a disebut basis (bilangan pokok), y disebut numerus, dan x dinamakan hasil logaritma. Contoh:

Bentuk logaritma Bentuk pangkat

2_{log 8 = 3 2}3 _{= ...} 3_{log 27 = 3 3}... _{= 27} 10_{log 10.000 = 4 10}4 _{= ...}

Untuk basis 10 boleh tidak dituliskan. Misalnya 10_{log b boleh ditulis log b.}

 Sifat-sifat logaritma: 1. a_{log 1 = 0}

Bukti:

Misal a_{log 1 = x , maka a}x _{= 1. Jadi x = ... karena a}0 _{= 1}

2. a_{log a = 1}

Bukti:

Misal a_{log a =y , maka a}y _{= a. Jadi y = ... karena a}1 _{= a}

3. a_{log (x . y) =} a_{log x +} a_{log y}

Bukti:

Misalkan: a_{log x = m, maka x = ...} a_{log y = n, maka y = ...}

xy = a... _{x a} ... _{= a}...

Berdasarkan definisi logaritma, xy = a... , maka

a_{log xy = ...}

= a_{log ...+} a_{log ...}

4. a_log x

y = alog x - alog y

Bukti:

Misalkan: a_{log x = m, maka x = ...} a_{log y = n, maka y = ...}

x

y = a...: a ... = a...

Berdasarkan definisi logaritma, xy = a... , maka Untuk setiap a > 0 dan a ≠ 1

a_log x

y = ...

= a_{log ... -} a_{log ...}

5. a_{log x}n _{= n} a_{log x}

Bukti:

a_{log x}n ₌

a_{log(x.x.x. ....x)}

⏟

ada....faktor (perpangkatan merupakan perkalian berulang)

=

...+...+...+...

⏟

...suku _(Sifat a_{log xy =} a_{log x +} a_{log y)}

= ... a

log x

6. ❑log

am

bn = _mn a_{log b}

7. a_{log b =} ❑log c

b

log ❑

c

a

8. a_{log b =} 1 log

❑

b _a

9. a_{log b x} b_{log c =} a_{log c}

10. a❑logb a

= b

B. Lembar Kerja Siswa

1. Nyatakan bentuk pangkat berikut ke dalam bentuk logaritma dan bentuk logaritma ke dalam bentuk pangkat

a) Perhatikan bilangan berpangkat berikut ini 52 _{= 25}

5 disebut ………….., 2 disebut ………., 25 disebut ……… Nyatakan bentuk pangkat tersebut dalam bentuk logaritma dengan: Basis adalah … , numerus adalah … , dan hasil logaritma adalah … Bentuk logaritma dari 52 _{= 25 adalah} … _{log … = …}

b) 10-3 _{= 0,001 Bentuk logaritmanya adalah ...}

c)

(

1 6

)

2 =

(

1

36

)

Bentuk logaritmanya adalah ... d) Perhatikan bentuk logaritma berikut

2_{log 32 = 5}

2 disebut ………….., 32 disebut ………., 5 disebut ……… Nyatakan bentuk logaritma tersebut ke dalam bentuk pangkat dengan: Basis adalah ... , pangkat adalah ... , dan numerus adalah ...

Bentuk pangkat dari 2_{log 32 = 5 adalah …}

e) 4_log 1

64 = -3 Bentuk pangkatnya adalah ... f) 8_{log 1 = 0 Bentuk pangkatnya adalah ...}

2. Hitunglah

(a) 4_{log 8 = log}

❑

2….

2… . ₌ ….

….. 2log 2 = ... (b) 216_log 1

36 = ❑log

6… .

6…. ₌ ….

….. 6log 6 = ... (c) 2 3_{log 2 + 3} 3_{log 3 –} 3_{log 36 =} 3_{log 2}2 ₊ 3_{log 3}... _– 3_{log 36}

= 3_{log 4 +} 3_{log ... –} 3_{log 36}

= 3_log 4x …..

……… …

= 3_{log ... = ...}

(d) 2 3_{log 4 -} 1

2 3log 25 + 3log 10 – 3log 32 = 3_{log 4}... _- 3

log 2512 + 3log 10 – 3log 32

= 3_{log ... -} 3_{log ... +} 3_{log 10 –} 3_{log 32}

= 3_log (… … x … … … .) (…… … … x … … …..)

= 3_{log ...}

= ... (e) 5❑log7

5

=

(f) log 30 - 1

log ❑ 48 10+ 1 log ❑ 16

10

= log 30 – log ... + log ...

= log

_{…… ……}30x ….. = log ... = ...

(g) Diketahui2_{log 3 = a dan} 3_{log 5 = b. Nyatakan logaritma berikut dalam bentuk a dan b}

1) 5_{log 2 2)} 4_{log 10 3)} 15_{log 6}

Penyelesaian:

1) Diketahui 2_{log 3 = a maka} 3_{log 2 = ...} 5_{log 2 =} ❑log

3 … log ❑ 3 …

=

… … … . … … … .

= ...

2) 4_{log 10 =} 4_{log (... x ...) =} 4_{log ... +} 4_{log ... =} 1

log ❑ 2 ….

+

log ❑ 3 …. log ❑ 3 ….

=

_…1_..

+

….

2 log❑

3 _{… .}

=

1

…..

+

… .

2x … .

=

1

…..

+ ...

3) 15_{log 6 =} ❑log

3 6 log ❑ ….. … .

=

log ❑ 3

(… x … .)

log ❑

3

(… x … .)=

log ❑

3

…+_❑3log… .

log ❑ …..

… .+ ❑log… .

… .

=

… …+1

… .+1

=

0

X Y

0

LEMBAR KERJA SISWA 1

Topik: Memahami dan Menemukan Konsep Nilai Mutlak Menggambar Grafik Nilai Mutlak

Masalah:

Seorang anak bermain di halaman rumah. Dia melompat ke depan 1 langkah, lalu ke belakang 2 langkah, ke depan 3 langkah dan ke belakang 4 langkah.

a. Gambarkan sketssa lompatan anak itu dalam garis bilangan real

b. Hitung berapa banyak langkah yang dilakukan anak tersebut

Banyak langkah adalah konsep nilai mutlak karena hanya menghitung banyak langkah, bukan arahnya. Banyak langkah selalu dinyataakan dengan bilangan bulat ...

Ke depan 1 langkah = │1│ = ... Ke belakang 2 langkah = │-2│ = ... Ke depan 3 langkah = │3│ = ... Ke belakang 4 langkah = │-4│ = ... Banyak langkah seluruhnya = │1│ + │-2│ + │3│+ │-4│ = ... Kesimpulan:

Nilai mutlak suatu bilangan adalah jarak antara bilang tersebut dengan ... pada garis bilangan real.

Definisi: x ∈R

|x|=

{

… , jika x ≥0

…, jika x<0

Menggambar Grafik Nilai Mutlak 1) f(x) = |x|

Lengkapi tabel berikut

x -3 -2 -1 0 1 2 3

y = f(x) 3 (x, y) (-3, 3)

Gambarkan titik (x, y) pada koordinat Cartesius

Created by Mukhlisah Zulfa Nadiya 13

BAB 2.

Persama

an dan

Pertidaks

X Y

0

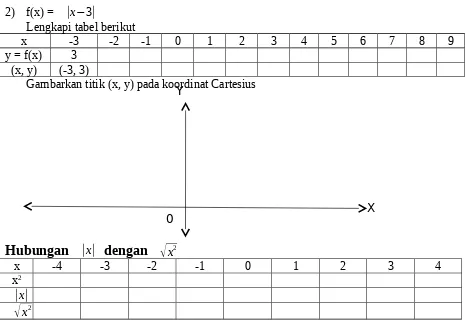
2) f(x) = |x−3|

Lengkapi tabel berikut

x -3 -2 -1 0 1 2 3 4 5 6 7 8 9

[image:14.595.67.533.150.474.2]

y = f(x) 3 (x, y) (-3, 3)

Gambarkan titik (x, y) pada koordinat Cartesius

Hubungan

|x|

dengan

√

x2

x -4 -3 -2 -1 0 1 2 3 4

x2

|x|

√

x2

Kesimpulan: ...

LEMBAR KERJA SISWA 2

Topik: Persamaan dan Pertidaksamaan Linear Masalah 1:

1) Tuti mempunyai sejumlah uang, kemudian Ayay memberikan uang pada Tuti sebanyak 1

3 dari uang Tuti semula. Uang Tuti sekarang Rp 12.000,00. Berapa uang Tuti semula?

Penyelesaian:

a. Nyatakan hal yang diketahui menjadi suatu variabel Misal: Uang Tuti semula = x

b. Buat model matematika dari masalah

Uang Tuti semula + 1₃ Uang Tuti semula = 12.000 ... + 1

3 ... = 12.000

X Y

0

... + 1₃ ... = 12.000 ... x = 12.000

X = _{… … … …}12.000 = ... Jadi. Uang Tuti semula adalah ... 2) Empat tahun yang lalu usia Iwan adalah 1

2 dari usianya sekarang. Sedangkan 5 tahun lagi, usia Iwan sama dengan usia kakak sekarang. Berapakan usia Iwan dan kakak sekarang?

Penyelesaian:

a. Misal: Usia Iwan skarang = x Usia kakak sekarang = y

Usia Iwan 4 tahun yang lalu = ... Usia Iwan 5 tahun lagi = ... b. Model matematika dan penyelesaiannya:

Empat tahun yang lalu usia Iwan adalah 1

2 dari usianya sekarang : x - ... = ...

x - ... = 4 ... x = 4

X = _{… … … …}4 = ... Jadi, usia Iwan sekarang adalah ...

5 tahun lagi, usia Iwan sama dengan usia kakak sekarang: X + ... = ...

... + ... = y

Y = ... Jadi, usia kakak sekarang adalah ... Definisi:

Bentuk umum Persamaan Linier Satu Variabel: ax + b = 0 a, b ∈R dan a ≠ 0 di mana

a : ... x : ... b : ... Bentuk umum Persamaan Linier Dua Variabel: ax + by + c = 0 a, b ∈R dan a , b ≠ 0 di mana

x, y : ... a : ... b : ... c : ...

Menentukan Himpunan Penyelesaian Persamaan Linier Satu Variabel dan Dua Variabel serta Menggambar Grafiknya

Contoh: 1) x = 3

a) Lengkapilan tabel berikut

x ... ... ... ... ... ...

y -2 -1 0 1 2 3

(x, y)

b) Gambarkan titik (x, y) pada koordinat Cartesius

X Y

0

X Y

c) HP = {...} 2) y = -2

a) Lengkapilan tabel berikut

x -2 -1 0 1 2 ...

y (x, y)

b) Gambarkan titik (x, y) pada koordinat Cartesius

c) HP = {...}

3) x + 2y = 4

a) Lengkapilan tabel berikut

x -2 -1 0 1 2 ...

y (x, y)

0

0

0

0

0

c) HP = {...} Himpunan penyelesaian persamaan linier ax + by = c adalah himpunan semua pasangan (x, y) yang memenuhi persamaan linier tersebut.

Masalah 2:

Uang Adi lebih banyak dari uang Bayu, tetapi lebih sedikit dari uang Cici. Uang Cici lebih sedikit Rp 3000 dari uang Dina dan uang Dina lebih banyak Rp 5.000 dari uang Adi.

Urutkan dari jumlah uang yang paling banyak! Penyelesaian:

Misalkan: Uang Adi = A Uang Bayu = B Uang Cici = C Uang Dina = D

a) Uang Adi lebih banyak dari uang Bayu : A ... B b) Uang Adi lebih sedikit dari uang Cici : A .... C

c) Uang Cici lebih sedikit Rp 3000 dari uang Dina : C + ... = D , maka C .... D d) Uang Dina lebih banyak Rp 5.000 dari uang Adi : D = A + ... , maka A .... D

Jadi, urutannya dari yang terbesar adalah ...

Menggambar Daerah Himpunan Penyelesaian Pertidaksamaan Linear Satu Variabel 1) x < 2

2) x > -4

3) 1 < x <3

4) x ≤ 4

5) x ≥ -1

6) -2 ≤ x ≤ 4

0

LEMBAR KERJA SISWA 1

Topik : Sistem Persamaan Linear Dua Variabel

1. Dona membeli tiga buah jeruk dan sebuah apel seharga Rp. 5.000,-sedangkan Doni membeli dua buah jeruk dan dua buah apel seharga Rp. 6.000,- Berapa harga sebuah jeruk dan apel?

Cara Substitusi:

Misalkan x = jeruk dan y = apel ...x + y = 5.000 (1) ...x + ...y = 6.000 (2) Diselesaikan dengan substitusi .... x + y = 5.000

y = 5.000 – ....x (1) substiusikan ke persamaan (2) ... x + ... y = 6.000 (2)

.... x + ... (5.000 – 3x) = 6.000 .... x + ... – .... x = 6.000 ...x =...

X = ...

Jadi harga sebuah jerukadalah... ... x + ... y = 6.000 (2)

... x = 6.000 - ... y

x = ... substitusikan ke persamaan (1) .... x + y = 5.000

... + y = 5000 .... y = ...

Y = ...

Jadi harga sebuah apel adalah... Cara eliminasi:

Misalkan x = jeruk dan y = apel 3x + y = 5.000 (1) 2x + 2y = 6.000 (2) Eliminasi x :

BAB 3.

Sistem

Persamaan

dan

(kalikan dengan suatu bilangan agar koefisien x pada persamaan (1) dan (2) sama 3x + y = 5.000 x ...x + ....y = ...

2x + 2y = 6.000 x ...x + ....y = ... -...x = ...

x = ... Jadi harga sebuah jeruk adalah ...

Eliminasi y :

(kalikan dengan suatu bilangan agar koefisien y pada persamaan (1) dan (2) sama 3x + y = 5.000 x ...x + ....y = ...

2x + 2y = 6.000 x ...x + ....y = ... -...y = ...

y = ...

Jadi harga sebuah apel adalah ... Cara Gabungan Eliminasi dan Substitusi:

Misalkan x = jeruk dan y = apel 3x + y = 5.000 (1) 2x + 2y = 6.000 (2) Eliminasi x :

(kalikan dengan suatu bilangan agar koefisien x pada persamaan (1) dan (2) sama 3x + y = 5.000 x ...x + ....y = ...

2x + 2y = 6.000 x ...x + ....y = ... -...x = ...

x = ... Jadi harga sebuah jeruk adalah ...

Substitusi x = ... ke salah satu persamaan (1) atau (2) Misal ke persamaan (1)

3x + y = 5.000

3 (...) + y = ... ... + y = ... Y = ...

Jadi harga sebuah apel adalah ...

2. Ani membeli makanan camilan yang terdiri 4 bungkus wafer dan satu bungkus kripik di toko Serba Enak harus membayar Rp. 13.000,-. Anisa ditoko yang sama membeli sebungkus wafer dan 3 bungkus kripik membayar Rp. 17.000,-. Anita ditoko yang sama membeli 2 bungkus wafer dan 2 bungkis kripik membayar dengan uang Rp. 20.000,-. Berapa uang kembalian yang akan diterima Anita?

Silahkan dijawab dengan cara yang menurutmu paling mudah!

LEMBAR KERJA SISWA 2

Topik : Sistem Persamaan Linear Tiga Variabel 1. Tentukan penyelesaian permasalah berikut

Ada tiga orang siswa berbelanja ke toko. Siswa pertama membeli 1 buku, 1pensil dan 1 panggaris membayar uang sebesar Rp 1.800,- , siswa kedua membeli 2 buku dan 1pensil

membayar uang sebesar Rp 25.000,- dan siswa ketiga beli 1 penggaris membayar uang sebesar Rp3.000,-

Penyelesaian: Misalkan:

Buku = x, pensil = y dan penggaris = z Model matematika dari permasalah: x + y + z = …….. (1)

2 x + y = ... (2) Z = ... (3)

Menggunakan cara campuran:

Dari persamaan (1) dan (2) eliminasi y x + y + z = 1800

2 x + y = 25000 -... + .... = -...-... (4)

Dari persaman (3) disubtitusikan ke persamaan (4) -x + 3000 = ...

-x = ...

x = ... (5)

dari persamaan (3) dan (5) ke persamaan (1) x + y + z = 1800

... + y + ... = 1800 y = 1800 - ... y = ...

Jadi harga 1 buku = ... 1 pensil = ...

1 penggaris = ...

2. Ada orang ibu namanyaDewi, Anggun dan Melinda pergi bersama-sama kepasar Ramadhan, pada salah satu tempat ibu-ibu membeli makan untuk persiapan berbuka puasa. Ibu Dewi beli dua kotak kurma, satu kue bingka dan satu gelas es buah, ibu Anggun beli satu kotak kurma, dua kue bingka dan satu gelas es buah, dan Ibu Melinda beli tiga kotak kurma, dua kue bingka dan satu gelas es buah.Dari belanjaan mereka masing-masing mengaluarkan uang. Ibu Dewi sebesar Rp125.000, ibu Anggun sebesar Rp 120.000 dan ibu Melinda sebesar Rp200.000.Dari permasalah diatas berapa harga dari masing-masing makanan tersebut ?

a. Penyelesaian cara subtitusi:

Langkah pertama : Dengan memisalkan kurma = x, bingka= y dan es buah = z buat permasalah diatas dalam bentuk model matematika. …. x + ….y + …. z = ….. (1) …. x + ….y + …. z = ….. (2) …. x + ….y + …. z = ….. (3)

Langkah kedua : Pilih satu persamaan sederhana dari persamaan (1), (2) atau (3), kemudian nyatakan x sebagai fungsi y dan z, atau y sebagai fungsi x dan z, atau z sebagai fungsi x dan y.

Langkah ketiga : subtitusikan y atau x atau z yang diperoleh dari langkah kedua persamaan lainnyasehinggga didapat persamaan dua variabel.

y = …... - .... x - … z masukan ke persamaan (2) diperoleh ….x + ( …... - .... x - … z) + … z = …... (5) ... = ...

y = …... - .... x - … z masukan ke persamaan (3) diperoleh ….x + (-..x - … z + …) + … z = …. (6)

... = ...

Persamaan (5) dan (6) adalah persamaan linear dua variabel maka selesaikan cara sistem persamaan linear dua variabel (5) ………= ………… (6) ………= ………… Didapat x = ….. z = …..

Langkah keempat : Subtitusikan x = … dan z = … ke salah satu persamaan (1) atau (2) atau (3) didapat y = ….

Langkah kelima: Buat kesimpulan Harga satu kotak korma = Rp … Harga satu biji bingka = Rp … Harga satu gelas es buah = Rp … b. Penyelesaian cara Eliminasi:

Langkah pertama : Dengan memisalkan kurma = x, bingka= y dan es buah = z buat permasalah diatas dalam bentuk model matematika. …. x + ….y + …. z = ….. (1) …. x + ….y + …. z = ….. (2) …. x + ….y + …. z = ….. (3)

Langkah kedua : eliminasi salah satu variabel x atau y atau z dari persamaan (1), (2) dan (3) dengan mengkombinasikan persamaan (1), (2) dan (2), (3) atau lainnya

Misal eliminasi z dari persamaan (1) dan (2) serta (2) dan (3)

…. x + ….y + …. z = ….. (1) …. x + ….y + …. z = ….. (2) _______________________

… x + … y = …. (4) …. x + ….y + …. z = ….. (2) …. x + ….y + …. z = ….. (3) _______________________

… x + … y = …. (5) Langkah ketiga : dari langkah dua didapat persamaan linear dua variabel (4) dan (5) … x + … y = …. (4)

… x + … y = …. (5) ______________ eliminasi y

x = ….

… x + … y = …. (4) … x + … y = …. (5) ______________ eliminasi x

y = …. Langkah keempat :

Dari hasil langkah tiga masukan x dan y ke salah persamaan (1), (2) atau (3) Misal ke persamaan (1):…. x + ….y + …. z = ...….. (1)

... + ... + ... z = ... z = ………... - ... = ... Langkah kelima : Buat kesimpulan

Jadi harga satu kotak korma = Rp … Harga satu biji bingka = Rp … Harga satu gelas es buah = Rp …

3. Tentukan himpunan penyelesaian dari sistem persamaan linear berikut. x + 3y - z = 3 (1)

x + 2y + 3z = -2 (2) x + y - z = 1 (3)

Penyelesaian: Cara Campuran

Eliminasi x dari persamaan (1) dan (2) x + 3y - z = 3

x + 2y + 3z = -2 -... - -... = 5 -... ( 4 ) Eliminasi x dari persamaan (2) dan (3

x + 2y + 3z = -2 ...(2) x + y - z = 1 ....(3)

.... + ... = - 3 ...(5) Eliminasi y dari persamaan (4) dan (5) .... - .... = 5

... + .... = - 3

- 8 z = .... Z = ...

Untuk z = .... maka y - 4z = 5 y - 4(... ) = 5

y + ... = 5 y = ...

Untuk z = ... dan y = ... , maka x + 3y - z = 3 X + 3( ... ) - ( ... ) = 3

X + .... + .... = 3 X + ... = 3 X = ...

Jadi , Himpunan penyelesaiannya adalah { ( .... , .... , ....) }

BAB 4. MATRIKS

LEMBAR KERJA SISWA 1

A. Pengertian Matriks

Matriks adalah susunan beberapa bilangan dalam bentuk ... yang diatur menurut ... dan ...

Setiap bilangan disebut ...

A=

(

a11 a12 … a1n

a21 a22 … a2n

… … … …

am1 am2 … amn

)

aijadalah elemen pada baris ke... dan kolom ke ...

Ordo matriks adalah banyak baris dan banyak kolom

Matriks A punya ... baris dan ... kolom. Ordo matriks A = ... x ... ditulis A…x…

Banyak elemen matriks = … x … Contoh:

A=

(

1

−2 3

2 6 −3 4 0 7 5 8 −6

)

a. Banyak baris = … e. a11 = … i. a22 = …

b. Banyak kolom = … f. a23 = … j. a33 = …

c. Ordo matriks A = … g. a31 = …

d. Banyak elemen = … h. a14 = …

B. Jenis-Jenis Matriks

1. Matriks baris, jika hanya ada … baris. Ordo = 1 x n A1 x 3 = ( 1 2 3)

2. Matriks kolom, jika hanya ada … kolom. Ordo = m x 1 B2 x1 =

(

4

−2)

3. Matriks persegi, jika banyak baris ....banyak kolom. Ordo = n x n C2 x 2 =

(

1 23 4)

C. Transpos Matriks

Transpos matriks ditulis AT _{yang diperoleh dengan cara mengubah susunan ... menjadi}

... dan sebaliknya. Contoh:

A=

(

1 −2 3 0 6 −1

)

AT

=

(

… … …

… … …

)

D. Kesamaan Dua Matriks

A = B jika kedua matriks berordo ... dan elemen-elemen yang seletak (bersesuaian) juga ...

Created by Mukhlisah Zulfa Nadiya 23 baris ke …. baris ke …. baris ke ….

kolom ke ….

kolom ke ….

A =

(

1 2

−3 0) B =

(

2 2

6 3

−12 4 0

)

Apakah A = B?

Latihan!

Tentukan nalai a dan b jika: 1.

(

2 3

1 a

)

=

(

b 3

1 −2) a = ... b = ....

2.

(

a+2 6

−5 9)=

(

4 6

−5 2b−1)

a + 2 = ... 2b – 1 = ... a = ... b = ... 3.

(

a+b

a−b

)

=

(

4 6

)

a + b = ... a – b = ...

dengan eliminasi atau substitusi didapatkan a = .... dan b = ....

LEMBAR KERJA SISWA 2

Topik : Operasi Aljabar Matriks 1. PENJUMLAHAN MATRIKS

Jika A dan B berordo ..., A + B diperoleh dengan menjumlah elemen A dan B yang ...

A =

(

1 −2

4 6

)

B =

(

3 0

−1 5)

A + B =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

- Matriks Nol = matriks yang semua elemennya .... O2 x 2 =

(

… …

… …

)

- Lawan matriks

b = -A, B adalah ... matriks A LENGKAPILAH!

A =

(

−4 2

3 1) B =

(

−5 4

−1 0) C =

(

6 3 0 −2)

a) A + B =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

B + A =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

B + C =

(

… … … …

)

+

(

… … … …

)

=

(

… … … …

)

b) Dari hasil (a)

(A + B) + C =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

A + (B + C) =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

c) A + O =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

O + A =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

d) A + (-A) =

(

… …

… …

)

+

(

… … … …

)

=

(

… …

… …

)

2. PENGURANGAN MATRIKS

Jika A dan B berordo ..., maka pengurangan A dengan B dinyatakan A – B = A + (-B)

Contoh:

A =

(

−4 2

3 1) B =

(

−5 4

−1 0)

A – B =

(

… …

… …

)

-

(

… … … …

)

=

(

… … … …

)

+

(

… … … …

)

=

(

… … … …

)

B – A =

(

… …

… …

)

-

(

… … … …

)

=

(

… … … …

)

+

(

… … … …

)

=

(

… … … …

)

Apakah A – B = B – A ?

3. PERKALIAN MATRIKS DENGAN BILANGAN REAL

Jika k bilangan reak, maka kA adalah matriks yang diperoleh dengan mengalikan k dengan ...

A =

(

a b

c d

)

kA = k

(

… … … …

)

=

(

… …

… …

)

LENGKAPILAH!

A =

(

1 23 4) B =

(

2 3

5 −1) p = -1 q = 2 dan r = 4

a) (q + r) A = (…+…)

(

… …

… …

)

= ...

(

… … … …

)

=

(

… …

… …

)

b) qA + rA = …

(

… …

… …

)

+…

(

… … … …

)

=

(

… … … …

)

+

(

… … … …

)

=

(

… … … …

)

Created by Mukhlisah Zulfa Nadiya 25 KESIMPULAN:

1) A + B = ... + ... (sifat ...)

c) r(A + B) = …

[

(

… … … …

)

+

(

… … … …

)

]

= …

(

… … … …

)

=

(

… … … …

)

d) rA + rB = …

(

… …

… …

)

+…

(

… … … …

)

=

(

… … … …

)

+

(

… … … …

)

=

(

… … … …

)

e) p(qA) = …

[

…

(

… …

… …

)

]

= …

(

… … … …

)

=

(

… …

… …

)

f) (pq) A = (…x…)

(

… …

… …

)

= ...

(

… … … …

)

=

(

… …

… …

)

LEMBAR KEGIATAN SISWA 3

Topik : Perkalian Dua Matriks

Misalkan ada dua matriks A dan B masing-masing berordo m x r dan r x n. Hasil kalinya: Am x r x Br x n = C… x …

Untuk mendapat elemen matriks C (cij) ikuti langkah berikut:

1. Pilih baris ... dari matriks A dan kolom ... dari matriks B 2. Kalikan elemen yang bersesuaian dan jumlahkan

A.B =

(

a b

c d

)

.

(

p q r s

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

LENGKAPILAH!

1)

(

2 1 4 −2).

(

3 6

5 7)=

(

… …+… … … …+… …

… …+… … … …+… …

)

=

(

…+… …+…

…+… …+…

)

=

(

… …

… …

)

2) A=

(

3 −2 1

0 1 5

−4 3 2

)

B=

(

2 4

−1 1 0 3

)

Ordo A = ... Ordo B = .... Ordo AB = …

AB =

(

3

−2 1

0 1 5

−4 3 2

)(

2 4

−1 1 0 3

)

=

(

… …… …++… … … …… … … …++… …… … … …+… … … …+… …

)

=

(

…+… …+… …+… …+… …+… …+…

)

=

(

… …… … … …

)

Hitunglah BA? Apakah AB = BA?

MENEMUKAN SIFAT PERKALIAN MATRIKS

A=

(

0 31 2)B=

(

−1 2

1 3)C=

(

2 3

−1 −4

)

Tentukan:

a) AB dan BC A.B =

(

… …

… …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

B.C =

(

… … ... …

)

.

(

… … … …

)

=

(

… …+…… … …+… … … …+…… … …+… …

)

=

(

… … … …

)

b) Dari jawaban (a) hitunglah (AB)C dan A(BC) (AB).C =

(

… …

… …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

A.(BC) =

(

… … ... …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

Dari jawaban bagian (b), apakah hasilnya sama? Apa kesimpulanmu? ... c) B + C dan AC

B + C =

(

… …

… …

)

+

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

A.C =

(

… … ... …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

d) Dari jawaban (a) dan (c) hitunglah A(B + C) dan AB + AC A.(B + C) =

(

… …

… …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

AB + AC =

(

… … ... …

)

+

(

… … … …

)

=

(

……+…… … …+…… ……+…… … …+……

)

=

(

… … … …

)

Dari jawaban (d), apakah hasilnya sama? Apa kesimpulanmu?

... e) BA dan CA

BA =

(

… …

… …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

CA =

(

… … ... …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

f) Dari jawaban (c) dan (e), hitunglah (B + C)A dan BA + CA (B + C).A =

(

… …

… …

)

.

(

… … … …

)

=

(

… …+…… … …+… … … …+…… … …+… …

)

=

(

… … … …

)

BA + CA =

(

… … ... …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

Dari jawaban (f), apakah hasilnya sama? Apa kesimpulanmu?

... g) 3(BC) , (3B)C dan B(3C)

3(BC) = 3.

(

… … … …

)

=

(

3x … 3x …

3x … 3x …

)

=

(

… …

… …

)

(3B)C =

[

3

(

… … ... …

)

]

.

(

… … … …

)

=

(

… … ... …

)

.

(

… … … …

)

¿

(

……+… … … …+… … ……+… … … …+… …

)

=

(

… … … …

)

B(3C) =

(

… …

… …

)

.

[

3

(

… … ... …

)

]

=

(

… … … …

)

.

(

… … … …

)

¿

(

……+… … … …+… … ……+… … … …+… …

)

=

(

… … … …

)

Apakah hasilnya sama? Apa kesimpulanmu?

... h) Dari jawaban (a), tentukan (AB)T

AB =

(

… …

… …

)

maka (AB)T =

(

… …

… …

)

i) BT_{dan A}T_{serta hasil kali B}T_AT

A=

(

0 31 2)B=

(

−1 2

1 3) Maka AT ₌

(

… …

… …

)

dan BT =

(

… …

… …

)

BT_AT ₌

(

… …

… …

)

.

(

… … … …

)

=

(

… …+… … … …+… … … …+… … … …+… …

)

=

(

… … … …

)

Dari jawaban (h) dan (i), apakah hasilnya sama? Apa kesimpulanmu? ... j) 2A, (2A)T_{, A}T_{, dan 2A}T

2A = 2

(

… …

… …

)

=

(

… …

… …

)

(2A)T₌

(

… …

AT ₌

(

… …

… …

)

2AT _{= 2}

(

… …

… …

)

=

(

… …

… …

)

Apakah (2A)T _{= 2A}T _{?Apa kesimpulanmu?}

... KESIMPULAN:

a. Asosiatif : (AB)C = A(...) b. Distributif Kiri : A(B + C) = AB + ...

A(B – C) = ... - AC c. Distributif Kanan : (B + C) A = ... + CA

(B – C) A = BA - ... d. k (BC) = (k...)C = B(k...)

e. (AB)T _{= ...}T _...T

f. (kA)T _{= k...}

LEMBAR KEGIATAN SISWA 4

Topik : Determinan dan Invers Matriks, Persamaan Matriks 1. Determinan

Matriks 2 x 2

A =

(

a b

c d

)

det A = |A|=

|

a b

c d

|

=¿ …….………

Matriks 3 x 3

A=

(

a₁₁ a₁₂ a₁₃ a₂₁ a₂₂ a₂₃ a31 a32 a33

)

Metode Sarrus

|A|=

|

a₁₁ a₁₂ a₁₃ a₂₁ a₂₂ a₂₃ a31 a32 a33

|

… … … … … …

det A = |A|=¿

……… - Matriks Singular jika det A = 0

- Matriks nonsingular jika det A ≠ 0

LENGKAPILAH!

1) A =

(

2 −1 5 3

)

det A = |A|=

|

… …

… …

|

=¿ …x ... - ... x ... = ... - … = …

2) A =

(

4 3 12 5 4 3 2 1

)

|A|=

|

4 3 1 2 5 4 3 2 1

|

… … … … … …

= ... + ...+ ... – ... – ... – ... = ... + ... + ... - ... - ... - ... = ...

SOAL:

1) Tentukn determinan matriks berikut

a) A =

(

7 −5

−4 3

)

b) B =

(

3 2 4 0 1 −3

−1 2 2

)

2) C =

(

x 5

1 x−2) dan D =

(

2 3x−2

x −5

)

Jika |C|=|D| , maka tentukan nilai x yang memenuhi! 2. Invers Matriks

Invers Matriks 2 x 2

A =

(

a b

c d

)

I adalah matriks identitas

AB = BA = I I2 x 2 =

(

1 00 1)

A adalah invers B A. A-1 = _A-1_{. A = I}

A-1 ₌ 1

|A|. Adj A Matriks persegi yang punya invers disebut …

= 1

|A|

(

… …

… …

)

Syarat punya invers: ...

LENGKAPILAH! 1) A =

(

4 21 1)

|A|=

|

… …

… …

|

=¿ …x ... - ... x ... = ... - … = …

A-1 ₌ 1

|A|. Adj A =

1

…

(

… …

… …

)

=

(

… …

… …

)

2) A =

(

5 −10

|A|=

|

… …

… …

|

=¿ …x ... - ... x ... = ... - … = …

A-1 ₌ 1

|A|. Adj A =

1

…

(

… …

… …

)

=

(

… …

… …

)

3. PERSAMAAN MATRIKS

Jika A, B, dan X matriks persegi, A matriks nonsingular, maka 1) AX = B ⟺ X = ……….

2) XA = B ⟺ X = ……... LENGKAPILAH!

1) A=

(

4 52 3)B=

(

2 8

4 −6)

AX = B |A|=

|

… …

… …

|

=¿ …x ... - ... x ... = ... - … = …

X = ... A-1 ₌ 1

|A|. Adj A =

1

…

(

… …

… …

)

=

(

… …

… …

)

X = 1

…

(

… …

… …

)(

… …

… …

)

= 1

…

(

… …

… …

)

=

(

… …

… …

)

2) XA = B

X = ………

=

(

… …

… …

)

1

…

(

… …

… …

)

= 1

…

(

… …

… …

)(

… …

… …

)

= 1

…

(

… … … …

)

=

(

… …

… …

)

4. PENGGUNAAN MATRIKS

MENYELESAIKAN SISTEM PERSAMAAN LINEAR DUA VARIABEL

{

ax+by=c px+qy=r

(

… …

… …

)(

x y

)

=

(

… …

)

a. Dengan Invers Matriks

AX = B X = ...

b. Determinan (Aturan Cramer)

D=

|

… …

… …

|

Dx =

|

… …

… …

|

x =

… …

Dy =

|

… …

… …

|

y =

… …

SOAL

Ani membeli 2 buah pensil dan 1 buku tulis seharga Rp 5750. Sedangkan Iwan membeli 1 buah pensil dan 2 buku tulis seharga Rp 5500

Tentukan harga pensil dan buku tulis dengan invers matriks dan aturan Cramer!

BAB 5. RELASI DAN FUNGSI

LEMBAR KERJA SISWA 1

Topik :Relasi dan Fungsi MATERI

Pengertian Produk Cartesius

Jika A dan B adalah dua himpunan yang tidak kosong, maka produk Cartesius himpunan A dan himpunan B adalah himpunan semua pasangan terurut (x,y) dengan x  A dan y  B dan ditulis AxB = {(x,y) | x A dan y  B}.

Contoh :

Misal A : {a, b, c} dan B : {1, 2}, tentukan : a. A x B c. A x A b. B x A d. B x B Jawab:

A x B = {(a,1), (b,1), (c,1), (a,2), (b,2), (c,2)} B x A = {(1,a), (1,b), (1,c), (2,a), (2,b), (2,c)}

A x A = {(a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c)} B x B = {(1,1), (1,2), (2,1), (2,2)}

Relasi Misal :

A x B adalah produk Cartesius himpunan A dan B, maka relasi atau hubungan R dari A ke B adalah sembarang himpunan bagian dari produk Cartesius A x B.

Pada relasi R = {(x,y)| x  A dan x  B} dapat disebutkan bahwa :

a. Himpunan ordinat pertama dari pasangan terurut (x,y) disebut daerah asal (domain).

b. Himpunan B, disebut daerah kawan (kodomain).

c. Himpunan bagian dari B yang bersifat Ry dengan y  B disebut daerah hasil (range) relasi R.

1 2 3 4

0 1 2 3

1 2 3 4

1

0 2 3

b. Grafik pada bidang Cartesius Contoh :

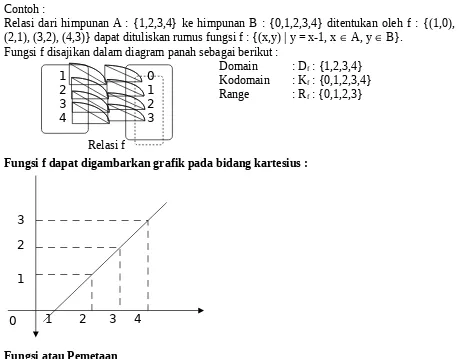
Relasi dari himpunan A : {1,2,3,4} ke himpunan B : {0,1,2,3,4} ditentukan oleh f : {(1,0), (2,1), (3,2), (4,3)} dapat dituliskan rumus fungsi f : {(x,y) | y = x-1, x  A, y  B}.

Fungsi f disajikan dalam diagram panah sebagai berikut :

Domain : Df : {1,2,3,4}

Kodomain : Kf : {0,1,2,3,4}

Range : Rf : {0,1,2,3}

Fungsi f dapat digambarkan grafik pada bidang kartesius :

Fungsi atau Pemetaan

Relasi dari himpunan A ke himpunan B disebut fungsi atau pemetaan, jika dan hanya jika tiap unsur dalam himpunan A berpasangan tepat hanya dengan sebuah unsur dalam himpunan B. f adalah suatu fungsi dari himpunan A ke himpunan B, maka fungsi f dilambangkan dengan f : A  B

[image:33.595.68.527.98.457.2]

B

A jika x A dan y  B, sehingga (x,y)  f, maka y

disebut peta atau bayangan dari x oleh fungsi f dinyatakan dengan lambang y : f (x)

(ditunjukkan dalam gambar disamping)

y = f (x) : rumus untuk fungsi f x disebut variabel bebas

y disebut variabel tak bebas Contoh :

Diketahi f : A  B dan dinyatakan oleh rumus f (x) = 2x – 1. Jika daerah asal A ditetapkan A : {x | 0  x  4. x  R} a. Tentukan f (0), f (1), f (2), f (3) dan f (4).

b. Gambarkan grafik fungsi y : f (x) = 2x – 1 dalam bidang kartesius. c. Tentukan daerah hasil dari fungsi f.

Jawab : a. f (x) = 2x – 1, maka :

f (0) = -1 f (1) = 1 f (2) = 3 f (3) = 5 f (4) = 7

b. Grafik fungsi y : f (x) = 2x – 1

y = f (x) = 2x – 1

Daerah asal

c. Daerah hasil fungsi f  Rf = {y | -1  y  7, y  R}

Jika daerah asal dari suatu fungsi f tidak atau belum ditentukan, maka dapat diambil daerah asalnya himpunan dari semua bilangan real yang mungkin, sehingga daerah hasilnya merupakan bilangan real. Daerah asal yang ditentukan dengan cara seperti itu disebut daerah asal alami (natural domain).

Contoh :

Tentukan daerah asal dari fungsi berikut :

1. f (x) =

4

x+1

Jawab :

f (x) =

4

x+1 _{, supaya f (x) bernilai real maka x + 1  0 atau x  -1}

Jadi Df : {x | x  R, dan x  -1} 2. g (x) =

√

4

−

x

2

Jawab :

g (x) =

√

4

−

x

2 , supaya g (x) bernilai real maka : 4 – x2_{ 0}

x2 _{– 4  0}

(x-2) (x+2)  0  -2  x  2 Jadi Dg = {x | -2  x  2, x  R}

Kerjakan Soal berikut

1. Perhatikan himpunan A dan B berikut ini

A = {Rupiah, Rupee, Baht, Ringgit} B = {Indonesia, India, Thailand, Malaysia} Dapatkah Anda melihat adanya hubungan antara himpunan A dan B?

Jelaskan :

... ... ... 2. Perhatikan empat himpunan berikut ini

C={Jakarta, London, Cairo, Beijing} , D={Indonesia, Inggris, Mesir, China} E={Indonesia, Brazil, Nigeria, Swiss},F={Asia,Amerika,Afrika,Eropa} Tentukan pasangan himpunan yang dapat mempunyai hubungan dan jelaskan hubungannya

Jawab:

... ... ... ... 3. Isilah diagram Venn A dengan anggota himpunan A dan diagram venn B dengan

anggota himpunan B dai soal no 1

A B

A B

Selanjutnya buatlah hubungan anggota himpunan A dengan menggunakan dengan anggota himpunan B

4. Ulangi kembali seperti no 3 dengan himpunan-himpunan pada soal no 2

Jawab : A B

5. Tentukan titik titik pada kordinat kartesius berikut sehingga memperlihatkan hubungan pada jawaban soal no 3

Malaysia Thailand India Indonesia

Rupiah Rupee Bath Ringgit

6. Buatlah Himpunan pasangan berurutan dari”Koordinat kartesius” pada jawaban soal no 5

Jawab :

... ... ... ... ... ... 7. Ria, Budi, dan Edy gemar bermain bulu tangkis. Eko dan Andi gemar bermain bola

basket. Ali gemar bermain bulu tangkis dan bola basket.

a. Jika A adalah himpunan nama anak dan B adalah himpunan permainan, maka : Tunjukkanlah relasi di atas dengan diagram panah!

A x B = {(Ria, ... ), (Budi, ...), (... , Bulu tangkis), (... , ...), (... , ...),

(... , ...)}

8. Tuliskan” hubungan” dari setiap diagram panah berikut ini

9. Buatlah kesimpulan bagaimana dapat terjadinya hubungan antara 2 himpunan!

... ... ... 10. Perhatikan diagram panah

a. Tentukan hubungan dari setiap diagram panah berikut!

b. Diagram panah mana yang semua anggotanya mendapat pasangan anggota himpunan B?

11. Diagram panah yang setiap anggota himpunan A mendapat pasangan tepat satu pada anggota himpunan B dinamakan fungsi atau dengan simbol f . Manakah diagram panah pada soal no 9 yang merupakan fungsi , berikan alasannya

Jawab :

... ... ... 12. Dalam fungsi himpunan A dinamakan Domain , himpunan B dinamakan kodomain ,

himpunan anggota himpunan B yang mendapat pasangan dinamakan range Tentukan Domain, Kodomain dan range dari setiap fungsi pada soal no 10 Jawab:

... ... ... ... ... ... ... ... ... ... ... ... ... 13. Sebuah fungsi aljabar dapat dinyatakan dengan

f

(

x

) =

√

x

atau

y

=

√

x

a. Isilah tabel berikut untuk fungsi

f

(

x

) =

√

x

x 9 8 7

f(x) 3

b. Berapa nilai x yang berakibat nilai y atau f(x) tidak dapat ditentukan Jawab :

... ... Dalam fungsi aljabar himpunan setiap nilai x yang yang menghasilkan nilai y yang

merupakan bilangan riil merupakan daerah asal atau Domain dari fungsi dan himpunan nilai y yang merupakan bilangan riil dinamakan daerah hasil atau Range dari fungsi.

14. Perhatikan diagram berikut.

(a) (b) (c)

Diagram manakah yang mendefinisikan fungsi? Jelaskan.

... ... ... ... ... 15. Suatu fungsi f dari himpunan A ke himpunan B dinyatakan dengan aturanx2 _{- 4x + 3,}

dengan x ∈ A. Jika diketahui A = {1, 2, 3, 4} dan B = {-2, -1, 0, 1, 2, 3, 4}, tentukan:

a. Himpunan pasangan berurutan dalam f

b. Daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range) dari f

Jawab:

x 1 2 3 4

f(x ) Df = ... Kf = ... Rf = ...

16. Tentukan domain dan range dari soal no 12 Jawab :

... ... 17. Diketahui fungsi f =

√

2x−1 tentukan domain dan range fungsi tersebut agar

fungsi mempunyai nilai (peta). Jawab:

Agar f(x) bernilai real maka 2x – 1 ≥ 0 2x ≥ ...

x ≥ ...

Jadi, D = {x │ ...} R = {x │ ...} 18. Diketahui fungsi f = 3x+6

2x−5 tentukan domain dan range fungsi tersebut agar fungsi mempunyai nilai (peta).

Jawab:

Agar f(x) bernilai real maka penyebut dari pecahan tersebut ≠ 0 ... ≠ 0

x ≠ ...

Jadi, D = {x │ ...} R = {x │ ...}

19. Diberikan fungsi f memetakan x ke y dengan rumus y =

2x−1

x+3 _{, x - 3. Tuliskan}

rumus fungsi g yang memetakan y ke x. Jawab:

y =

2x−1

x+3

0 X

Y Y

X 0

y (x + 3) = ... xy + ... = ... xy - ... = -3y – 1

x (... - ...) = ...

x = … … … …_{… … … …} , y ≠ ... 20. Diketahui fungsi f(x)=3x−2 , hitunglah :

a. f(2) b. f(-2) c. f(x+1) d. f(2x+5) Jawab :

a. f(2) = 3 (....) – 2 = .... - .... = ... b. f(-2) = 3 (....) – 2 = .... - .... = ...

c. f(x + 1) = 3 (...) – 2 = ... - .... = ... d. f(2x + 5) = 3 (...) – 2 = ... - .... = ... 21. Diketahui f(2x – 3) = 4x – 7. Hitunglah nilai dari f(7).

Jawab: 2x – 3 = .... 2x = .... + 3 = .... x = ....

f(7) = 4 (...) – 7 = ...

Latihan

1. Relasi-relasi himpunan A : {a,b,c,d} ke himpunan B : {1,2,3,4} berikut ini manakah yang merupakan fungsi / pemetaan (gambarkan terlebih dulu diagram panahnya).

a. f = {(a,1), (b,2), (c,3), (d,4)} b. g = {(a,2), (b,2), (c,3), (d,3)} c. h = {(a,4), (b,1), (b,3), (c,2), (d,4)}

d. i = {(a,1), (a,2), (a,3), (a,4)} e. j = {(a,1), (b,1), (c,1), (d,1)}

2. Relasi-relasi yang disajikan dalam bentuk grafik kartesius manakah yang merupakan pemetaan atau fungsi ?

Y

0 X X

Y

0

c. d.

3. Diketahui fungsi f : R  R dinyatakan dengan rumus f (x) = x2 _{– 1.}

Jika daerah asal f adalah Df : {x | -3  x  3, x  R}

a. Tentukan f (-3), f (-2), f (0), f (1), f (2), f (3).

b. Gambarkan grafik fungsi f (x) = x2 _{– 1 dalam bidang kartesius.}

c. Tentukan daerah hasil fungsi f.

d. Tentukan nilai a jika diketahui f (a) = 3. 4. Tentukan daerah asal alami pada fungsi berikut !

a. f (x) =

√

5

x

−

2

b. g (x) =

1

4x−3 _{c. g (x) =}

1

√

x

+

1

BAB 6. BARISAN DAN DERET

LEMBAR KERJA SISWA 1

Topik: Barisan dan Deret Aritmatika

A. MENEMUKAN KONSEP BARISAN ARITMETIKA

Jika tinggi anak tangga pertama adalah 20 cm, maka tinggi anak tangga kedua bertambah 15 cm sehingga menjadi 35, anak tangga ketiga tingginya adalah 50, dan seterusnya selalu bertambah tinggi 15 cm untuk tangga selanjutnya. Jika di susun urutan bilangan tersebut adalah 20, 35, 50, …., . Beda setiap dua bilangan yang berdekatan pada barisan adalah tetap yaitu 15.

Dengan demikian barisan tersebut disebut BARISAN ...

Definisi: Barisan aritmetika adalah barisan bilangan yang beda setiap dua suku yang berurutan adalah ...

B. MENEMUKAN RUMUS SUKU KE-n DARI BARISAN ARITMETIKA

Dari gambar tinggi tia