BAB 2
TINJAUAN TEORITIS
2.1 Pengertian Regresi Linier
Pengertian regresi secara umum adalah sebuah alat statistik yang memberikan
penjelasan tentang pola hubungan (model) antara dua variabel atau lebih.. Dalam
analisis regresi dikenal 2 jenis variabel yaitu:
1. Variabel Respon disebut juga variabel dependen yaitu variabel yang
keberadaannya dipengaruhi oleh variabel lainnya dan dinotasikan dengan
variabel .
2. Variabel Prediktor disebut juga dengan variabel independen yaitu variabel
yang bebas (tidak dipengaruhi oleh variabel lainnya) dan dinotasikan dengan
Untuk mempelajari hubugan – hubungan antara variabel bebas maka regresi linier
terdiri dari dua bentuk, yaitu:
1. Analisis regresi sederhana (simple analysis regresi) 2. Analisis regresi berganda (Multiple analysis regresi).
Analisis regresi sederhana merupakan hubungan antara dua variabel yaitu
Sedangkan analisis regresi berganda merupakan hubungan antara 3 variabel atau
lebih, yaitu sekurang-kurangnya dua variabel bebas dengan satu variabel tak bebas.
Tujuan utama regresi adalah untuk membuat perkiraan nilai suatu variabel
(variabel dependen) jika nilai variabel yang lain yang berhubungan dengannya (variabel lainnya) sudah ditentukan.
2.2 Analisis Regresi Linier Sederhana
Regresi linier sederhana digunakan untuk mendapatkan hubungan matematis dalam
bentuk suatu persamaan antara variabel tak bebas tunggal dengan variabel bebas
tunggal. Regresi linier sederhana hanya memiliki satu peubah yang dihubungkan
dengan satu peubah tidak bebas . Bentuk umum dari persamaan regresi linier untuk
populasi adalah
Di mana:
= Variabel takbebas
= Variabel bebas
= Parameter Intercep
= Parameter Koefisisen Regresi Variabel Bebas
Menentukan koefisien persamaan a dan b dapat dengan menggunakan metode
kuadrat terkecil, yaitu cara yang dipakai untuk menentukan koefisien persamaan
dan dari jumlah pangkat dua (kuadrat) antara titik-titik dengan garis regresi yang
2.3 Regresi Linier Berganda
Regresi linier berganda adalah analisis regresi yang menjelaskan hubungan antara
peubah respon (variabel dependen) dengan faktor-faktor yang mempengaruhi lebih dari satu prediktor (variabel independen).
Regresi linier berganda hampir sama dengan regresi linier sederhana, hanya
saja pada regresi linier berganda variabel bebasnya lebih dari satu variabel penduga.
Tujuan analisis regresi linier berganda adalah untuk mengukur intensitas hubungan
antara dua variabel atau lebih dan membuat prediksi perkiraan nilai atas
Secara umum model regresi linier berganda untuk populasi adalah sebagai berikut:
Model regresi linier berganda untuk populasi diatas dapat ditaksir berdasarkan
sebuah smpel acak yang berukuran n dengan model regresi linier berganda untuk
sampel, yaitu:
Dengan:
= Nilai taksiran bagi variabel
= Taksiran bagi parameter konstanta
= Taksiran bagi parameter koefisien regresi
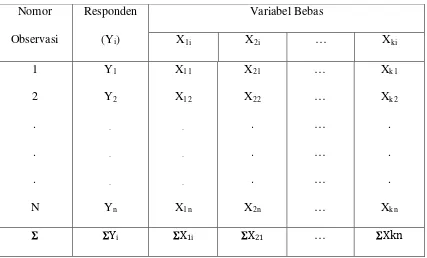
Bentuk data yang akan diolah ditunjukkan pada table berikut:
Tabel 2.1 Bentuk Umum Data Observasi
Nomor
Dalam regresi linier berganda variabel tak bebas tergantung kepada dua atau lebih
variabel bebas . Bentuk persamaan regresi linier berganda yang mencakup dua
atau lebih variabel dapat ditulis sebagai berikut:
Dengan:
= 1, 2, …,
= ukuran sampel
= variabel kesalahan (galat)
Untuk rumus diatas, dapat diselesaikannya dengan empat persamaan oleh
empat variabel yang terbentuk:
Dengan adalah koefisien yang ditentukan berdasarkan data hasil
pengamatan.
2.5 Koefisien Determinasi
Koefisien determinasi dinyatakan dengan untuk pengujian regresi linier berganda
yang mencakup lebih dari dua variabel. Koefisien determinasi adalah untuk
mengetahui proporsi keragaman total dalam variabel tak bebas yang dapat
dijelaskan atau diterangkan oleh variabel – variabel bebas yang ada di dalam model
persamaan regresi linier berganda secara bersama-sama. Maka akan ditentukan
dengan rumus:
Dengan:
= Jumlah kuadrat regresi
Harga yang diperoleh sesuai dengan variasi yang dijelaskan masing–masing
variabel yang tinggal dalam regresi. Hal ini mengakibatkan variansi yang dijelaskan
penduga yang disebabkan oleh variabel yang berpengaruh saja (yang bersifat nyata)
2.6 Koefisien Korelasi
Korelasi adalah derajat hubungan linier antara dua variabel atau lebih dari data hasil
variabel diikuti oleh perubahan variabel lain, baik yang searah maupun tidak.
Hubungan antara variabel dapat dikelompokkan menjadi tiga jenis :
1) Terjadinya korelasi positif apabila perubahan antara variabel yang satu diikuti
oleh variabel lainnya dengan arah yang sama (berbanding lurus). Artinya
apabila variabel yang satu meningkat, maka akan diikuti peningkatan variabel
lainnya.
2) Korelasi Negatif
Terjadinya korelasi negative apabila perubahan antara variael yang astu diikuti
oleh variabel lainnya dengan arah yang berlawanan (berbanding terbalik).
Artinya apabila variabel yang satu meningkat, maka akan diikuti penurunan
variabel lainnya.
3) Korelasi Nihil
Terjadinya korelasi nihil apabila perubahan antara variabel yang satu diikuti
oleh variabel lainnya dengan arah yang tidak teratur (acak). Artinya apabila
variabel yang satu meningkat, kadang diikuti dengan peningkatan pada
variabel lain dan kadang diikuti dengan penurunan pada variabel lain.
Berdasarkan hubungan antar variabel yang satu dengan variabel lainnya
dinyatakan dengan koefisien korelasi yang disimbolkan dengan ” ”. Besarnya
korelasi berkisar antara
Untuk mencari korelasi antara variabel dengan dapat dirumuskan sebagai
Untuk hubungan empat variabel tersebut dapat dihitung dengan menggunakan rumus
sebagai berikut:
1. Koefisien korelasi antara dan
2. Koefisien korelasi antara dan
3. Koefisien Korelasi antara dan
Nilai koefisien korelasi adalah Jika dua variabel berkorelasi
negative maka nilai koefisien korelasinya akanmendekati -1, jika dua variabel tidak
berkorelasi maka nilai koefisien korelasinya akan mendekati 0, sedangkan jika dua
variabel berkorelasi positif maka nilai koefisien korelasinya akan mendekati 1.
Untuk lebih mengetahui seberapa jauh derajat antara variabel-variabel
tersebut, dapat dilihat dalam perumusan berikut:
-0,79 ≤ r ≤ -0,50 berarti korelai sedang secara negatif
-0,49 ≤ r ≤ 0,49 berarti korelasi lemah
0,50 ≤ r ≤ 0,79 berarti berkorelasi sedang secaaara positif
0,80 ≤ r ≤ 1,00 berarti berkorelasi kuat secara positif
2.7 Uji Regresi Linier Berganda
Uji regresi linier ganda perlu dilakukan untuk mengetahui apakah sekelompok
variabel bebas secara bersamaan mempunyai pengaruh terhadap variabel tak bebas.
Pada dasarnya pengujian hipotesis tentang parameter koefisien regresi secara
keseluruhan atau pengujian persamaan regresi dengana menggunakan statistik F yang
dirumuskan sebagai berikut:
Dengan:
=
Statistik F yang menyebar mengukuti distribusi F denagan derajatkebebasan dan
=
Jumlah Kuadrat regresi , dengan derajat kebebasanDalam pengujian persamaan regresi terutama menguji hipotesis tentang parameter
koefisien regresi secara keseluruhan melibatkan intersep serta buah variabel
penjelasan sebagai berikut:
Dengan persamaan penduganya adalah:
Dengan merupakan penduga bagi parameter
Langkah-langkah yang dibutuhkan dalam pengujian hipotesis ini adalah sebagai
berikut:
a. Menentukan formulasi hipotesi
( tidak mempengaruhi
Minimal ada satu parameter koefisien regresi yang tidak sama dengan nol
atau mempengaruhi .
b. Menentukan taraf nyata α dan dengan derajat kebebasan dan
Pilih taraf nyata α yang diinginkan.
c. Menentukan kriteria pengujian
diterima bila
ditolak bila
d. Menentukan nilai statistik F