Lampiran 1: Iterasi Newton
1 format long % agar memberikan nilai sebanyak 15 bilangan decimal 2
3 % nilai perkiraan awal 4 x= xguess;
5 y= yguess; 6
7 % input jumlah iterasi yang diinginkan 8 Niter=input('jumlah iterasi= ');
9 iterasiold(1) = x; 10 iterasiold(2) = y; 11 for n=1:Niter 12 f1=xˆ2-yˆ2-y; 13 f2=yˆ2+xˆ2-x;
14 j=[2*x-2*y-1; 2*x-1 2*y];
15 iterasi = [x; y]-inv(j)*[f1; f2] 16 galat = norm(iterasi-iterasiold') 17 x = iterasi(1);
18 y = iterasi(2);
Lampiran 2: Aliran Satu Fase
1 maxk = 10000; % jumlah waktu 2 tfinal = 200;
3 dt = tfinal/maxk;
4 n = 30; % jumlah diskritisasi
5 dx = 1/n; 6 b=dt/2*dx; 7
8 % Initial condition 9 x(1) = 0.0;
10 u(1,1) = 1.0; 11
12 for i = 2:n+1
13 x(i) =x(i-1) + dx; 14 u(i,1) =1-[x(i)*x(i)]; 15 end
16
17 for k=1:maxk+1
18 time(k) = (k-1)*dt; 19 end
20
21 % metode eksplisit 22 for k=2:maxk+1
23 u(1,k)=1;
24 for i=2:n+1
25 u(i,k) =b * u(i-1,k-1) * u(i-1,k-1) + u(i,k-1) *
26 (1-b*u(i,k-1));
27 end
28 end 29
30 hold on;
31 plot(x,u(:,maxk/2+1),'r--'); 32 plot(x,u(:,1),'blue');
33 title('explicit method') 34 xlabel('X')
Lampiran 3: Aliran Dua Fase
1 % input parameter
2 L = 1; %panjang domain
3 tfinal = a;
4 maxk = t; %jumlah perputaran waktu
5 n = d; %jumlah diskritisasi
6 dt = tfinal/maxk; 7 dx = L/n;
8 b=dt/dx; 9
10 % kondisi awal 11 x(1) = 0.0; 12 u=zeros(n+1,1); 13 u(1,1) = 1.0; 14
15 for i = 2:n+1
16 x(i) =x(i-1) + dx; 17 u(i,1) = 0.0; 18 end
19
20 for k=1:maxk+1
21 time(k) = (k-1)*dt; 22 end
23
24 % metode eksplisit 25 F = zeros(n+1,1); 26 for k = 2:maxk+1
27 u(1,k)=1;
28 v = velocity(u(:,k-1),dx); 29 F = Fflux(u(:,k-1))*v; 30 Fkanan = F(2:n+1,1); 31 Fkiri = F(1:n,1);
32 u(2:n+1,k) = u(2:n+1,k-1) - b*(Fkanan - Fkiri); 33 end
34
35 % representasi grafik 36 hold on;
40 title('Profile Saturation') 41 xlabel('x')
42 ylabel('S(x,t)') 43 hold off;
fungsi yang diimplementasikan pada code Aliran dua fase diatas
1 % subfungsi fungsi flux 2 function value = Fflux(u)
3 vr = k; % nilai viskositas
4 value=(vr*u.*u)./(vr*u.*u+(1-u).*(1-u));
1 % subfungsi velocity
2 function vel = velocity(u,dx) 3 m = size(u);
4 laval = 0.0; 5 for j=2:m
6 increment = (1/lamda(u(j-1))+1/lamda(u(j)))*0.5*dx; 7 laval = increment+ laval;
8 end
9 vel = 1/laval;
fungsi lamda diimplementasikan pada subfungsi velocity
1 function val = lamda(u)
2 vr = k; % nilai viskositas
Lampiran 4: Aliran Dua Fase Nonekuilibrium
1 L = 1.0; % Panjang domain
2 M = 400; % jumlah diskritisasi
3 dx = L/M;
4 x = linspace(0,L,M+1)'; 5
6 dt = 0.001 7
8 tau = 0.02; 9 b = dt/dx; 10 c = tau/dt; 11 cc = tau/dx;
12 maxt = 100; % jumlah waktu
13
14 sigma = initialsigma(cc, M); % kondisi awal untuk sigma 15
16 U = zeros(2*M,1); 17 U(1:M,1) = 0.0;
18 U(M+1:2*M,1) = sigma(2:M+1,1); 19
20 for k = 1:maxt+1
21 Uold = U;
22 U = iterasiU(U, Uold, b, c, dx); 23 end
24
25 sat = [1; U(1:M,1)];
26 effsat = [1; U(M+1:2*M,1)]; 27 figure(1);
28 hold on;
29 plot(x,sigma,'b--');
30 plot(x,sat, 'k', x,effsat,'r');
31 legend('sigma awal', 'saturation', 'sigma');
Terdapat beberapa subfungsi yang diimplementasikan pada M-File diatas yaitu
1 %subfungsi initialsigma akan menghasilkan nilai awal sigma 2 function sigma = initialsigma(c, M)
4 sigma = zeros(M+1,1); 5 sigma(1) = 1.0;
6 si = 0.2; %Initial Guess
7 % Implementation of Newton's Iteration 8 for i = 2:M+1
9 ss = sigma(i-1);
10 fluxfunold = fluxfunc(ss); 11 for k=1:Niter
12 fluxfun = fluxfunc(si);
13 derfluxfun = derfluxfunc(si); 14 Fsi=si+c*(fluxfun-fluxfunold); 15 Fsi2=1+c*derfluxfun;
16 Delta = -Fsi/Fsi2;
17 si = si + Delta;
18 if (Delta<1.0e-8)
19 break;
20 end
21 end
22 sigma(i) = si; 23 end
24 end
1 %subfungsi iterasi newton pada U
2 function [U] = iterasiU(U, Uold, b, c, dx)
3 Niter = 100; % jumlah iterasi
4
5 for m = 1:Niter
6 F = Fvektor(U, Uold, b, c, dx); 7 jacobi = matriksjacobian(U, b, c); 8 Delta = -jacobi \ F;
9 U = U + Delta;
10 if (norm(Delta)<1.0e-8)
11 m;
12 break;
13 end
14 end 15 end
1 % subfungsi untuk menghitung F(U)
2 function [F] = Fvektor(U, Uold, b, c, dx) 3
4 tt = length(U); 5 F = zeros(tt,1); 6 M = tt/2;
7 v = velocity(U(1:M+1), dx); 8
9 F(1) = U(1) - Uold(1) + v*b*(fluxfunc(0.5*(U(1+M) + 10 Uold(M+1)))) - (v*b*(0.5*(1+1)));
11 F(M+1) = 0.5*(U(M+1) U(1) + Uold(M+1) Uold(1))
-12 c*(U(1)-Uold(1));
13
14 for i=2:M
15 F(i) = U(i) - Uold(i) + v*b*(fluxfunc(0.5*(U(i+M)+ 16 Uold(M+i)))) - v*b*(fluxfunc(0.5*(U(i+M-1)+
17 Uold(M+i-1))));
18 F(M+i) = 0.5*(U(M+i) U(i) + Uold(M+i) Uold(i))
-19 c*(U(i)-Uold(i));
20 end 21 end 22 %
Pada subfungsi iterasiU dihitung matriks jacobian F(U) yang diimplementasikan oleh subfungsi berikut
1 %fungsi matriksjacobi
2 function [jacobian] = matriksjacobian(U, b, c) 3
4 tt = length(U); 5 M = tt/2;
6 jacobian = zeros(tt); 7 for l=1:M
8 jacobian(l,l) = 1;
9 jacobian(l+M,l+M) = 0.5; 10 jacobian(l+M, l) = -c-0.5; 11 end
12
14 jacobian(l,l+M) = 0.5*b*derfluxfunc(U(l+M)); 15 end
16
17 for l=2:M
18 jacobian(l,M+l-1) = -0.5*b*derfluxfunc(U(M+l-1)); 19 end
20
21 jacobian = sparse(jacobian); 22 end
Pada subfungsi Fvektor terdapat fungsi fluxfunc dan velocity
1 % subfungsi fungsi flux
2 function new = fluxfunc(sigma) 3 vr = 7;
4 new=(vr.*sigma.*sigma)/(vr.*sigma.*sigma+(1-sigma).*(1-sigma));
1 % subfungsi velocity sebagai nilai persamaan Darcy 2 function vel = velocity(u,dx)
3 m=size(u); 4 laval = 0.0; 5 for j=2:m
6 increment = (1/lamda(u(j-1))+1/lamda(u(j)))*0.5*dx; 7 laval = increment+ laval;
8 end
9 vel=1/laval; 10 end
pada fungsi matriksjacobi terdapat subfungsi derflux
1 %subfungsi untuk menghitung turunan fungsi flux 2 function val=derfluxfunc(sigma)
3 vr = 7;
Apsley, D. 2005. Computational fluid dynamic.
Choiron, M. A. Pengantar Analisa Numerik. Universitas Brawija, Malang.
Depriandi. 2010. Penggunaan Data Special Core Analysis (SCAL) untuk Menentukan Kurva Permeabilitas Relatif pada Lapangan X. Fakultas Teknik, Universitas Islam Riau.
He, J. 2008. Numerical Integration. University of Houston, Amerika.
Holden, L. 1997. The buckley–leverett equation with spatially stochastic flux function. SIAM Journal on Applied Mathematics, 57(5):1443–1454.
IATMI SM STT MIGAS Balikpapan. 2011. Pengantar Studi Water Floo-ding. https://iatmismmigas.wordpress.com/2012/06/07/pengantar-studi-water-flood/. [Online; accesed 04 - Februari - 2015].
Juanes, R. 2008.Nonequilibrium effects in models of three-phase flow in porous media. Advances in Water Resources, 31(4):661 – 673.
LeVeque, R. 2002. Finite Volume Methods for Hyperbolic Problems. Cambridge Texts in Applied Mathematics. Cambridge University Press.
Munir, R. 2003. Metode numerik. Informatika, Bandung. Praveen, C. 2013. Finite Volume Method on Unstructured Grid.
Putra, M. A. A. 2011. Simulasi Pemindahan Fluida 2 fasa didalam Coalescer dengan Menggunakan CFD. Fakultas Teknik, Universitas Diponegoro.
Shaw, C. T. 1992. Using computational fluid dynamics. Prentice Hall Hemel Hemps-tead. England.
Thomas, J. W. 2013. Numerical partial differential equations: conservation laws and elliptic equations, volume 33. Springer Science & Business Media.
Tulus, A. K. A. and dan Muhamad Norhamidi, A. S. Numerical simulation of in-cylinder gas dynamic of two-stroke linear engines using finite volume method. InPr oceedings of the 2nd International Conference on Research and Educaton in Mathematics (ICREM2), pages 25–27.
HASIL DAN PEMBAHASAN
Tujuan dilakukannya injeksi air yaitu mengoptimalkan produksi minyak yang
terperangkap di dalam reservoir dengan melakukan desakan oleh media air.
Se-belum melakukan perhitungan numerik pada persoalanwaterflooding, maka dapat
diperhatikan proses injeksi berikut
Gambar 3.1: Proses Injeksi
Pada saat injeksi dilakukan air dimasukkan kedalam sumur injeksi dengan
seba-gai fluida yang didorong. Ketika air masuk kedalam reservoir, maka terjadi interaksi
antara fluida dan batuan dimana sifat batuan telah dijelaskan pada pembahasan
se-belumnya yaitu porositas, permeabilitas, dan saturasi.
Air dan minyak memiliki viskositas yang berbeda sehingga jelas bahwa
mi-nyak dan air tidak akan pernah tercampur atau dikenal dengan sebutanimmiscible.
Oleh karenanya ketika terjadi interaksi antara batuan dan air, secara tidak langsung
akan terjadi interaksi antara air dan minyak sehingga pada tahap ini, besar nilai
mobilitas dan viskositas akan memberi pengaruh.
Oleh proses tersebut, maka minyak dapat diangkat oleh sumur produksi
se-hingga minyak tersebut siap untuk dilakukan proses selanjutnya yaitu proses
pe-nyulingan. Oleh penjelasan diatas, maka jelas bahwa perhitungan perlu dilakukan
agar dapat diperkirakan nilai keekonomisan dan efisiensi kinerja yang dilakukan
pada daerah tertentu. Dengan demikian, maka perhitungan dapat dijelaskan pada
pembahasan berikut
3.1 Solusi Persamaan Hiperbolik Orde Satu Menggunakan Upwinding
Persamaan diferensial parsial adalah suatu fungsi yang bergantung pada lebih
da-ri satu vada-riabel. Hal ini menyebabkan persamaan diferensial memegang peranan
sangat penting dalam menggambarkan suatu permasalahan secara fisik. Salah
sa-tu jenis persamaan diferensial parsial yang banyak diimplementasikan adalah
per-samaan hiperbolik yang biasanya berhubungan dengan getaran atau sesuatu yang
berhungan dengandiscontinu dalam waktu, seperti gelombang kejut yang
dinya-takan pada persamaan Burger, ketidak-kontinuan dalam kecepatan, tekanan dan
ra-pat massa. Contoh dari bentuk persamaan hiperbolik adalah persamaan gelombang,
persamaan transportasi, mekanika gelombang, dinamika gas, aliran supersonik, dan
sebagainya.
Salah satu bagian dari persamaan hiperbolik adalah persamaan transportasi
atau dikenal juga dengan persamaan adveksi. Persamaan adveksi merupakan
fluida lainnya. Persamaan yang paling sederhana merepresentasikan hukum
keke-kalan massa yang diekspresikan sebagai
∂tu=−c∂xu.
Pada skripsi ini, persamaan yang akan dicari solusinya adalah persamaan hiperbolik
pada aliran fluida dua fase yang juga mengilustrasikan kekekalan massa.
3.1.1 Aliran Dua-Fase Fluida
Fluida dapat dinyatakan pada suatu zat yang dapat mengalir, contohnya zat cair dan
gas. Dikatakan aliran dua fasa fluida yaitu jika terdapat dua fluida yang memiliki
densitas dan viskositas yang berbeda saling berpadu, misalnya cair-gas dan cair-cair.
Aliran dua-fase merupakan bentuk paling sederhana dari aliran multi-fase (Putra,
2011).
Dalam hal ini, banyak persoalan yang dapat digambarkan pada kehidupan
nyata, baik dalam bidang industri ataupun kehidupan sehari-hari. Seperti pada ketel
uap, kondensor, alat penukar panas, reaktor nuklir, pencairan gas alam, pipa saluran
dan lain-lain.
Telah disebutkan sebelumnya bahwawaterfloodingmerupakan salah satu
tek-nik pengangkatan minyak bumi dari reservoir yang berkaitan dengan aliran dua fase
dimana aliran yang dimaksud adalah air-minyak, kedua aliran ini memiliki interaksi
yang akan menjadi salah satu faktor yang mempengaruhi analisis dan juga tingkat
kekentalan (viskositas) yang dimiliki oleh tiap aliran.
Formula klasik dari aliran multifasa menggambarkan flux fluida makro
de-ngan perkembade-ngan langsung dari persamaan Darcy untuk satu fasa yang pertama
kali diajukan oleh Muskat (Juanes, 2008). Perkembangan multifasa dari persamaan
Darcy dapat digambarkan sebagai relasi quasi-linear, karena flux fluida bergantung
linear pada tenaga pendorong yang meliputi viskositas, kapiler dan gravitasi.
Kenyataan ini dimodelkan sebagai fungsi nonlinear permeabilitas relatif dan
mema-sukkan efek nonekuilibrium atau efek dinamik. Model untuk dua-fase aliran dapat
diekspresikan pada persamaan diferensial parsial berikut
∂S ∂t +
∂
∂x(vf(S)) = 0 inR×(0, T) (3.1)
Dari persamaan diatas terdapatSyang merupakan saturasi pada media berpori yang
didefinisikan sebagai perbandingan antara pori volume batuan yang berisi fase
flui-da tertentu (air, minyak) terhaflui-dap total volume pori batuan. Sehingga, perhitungan
saturasi berfungsi untuk menghitung konsntrasi fase fluida yang ada dalam
reservo-ir. Adapunvsebagai suatu kecepatan aliran pada media berpori dan dikenal sebagai
hukum Darcy yang telah dibahas pada penjelassan sebelumnya. Persamaan Darcy
direpresentasikan oleh
v =−k(x)λ(S)dP
dx.
Dengan menggabungkan hukum Darcy dan hukum kekekalan flux dv
dx = 0, maka diperoleh
− d dx
k(x)λ(S)dP
dx
= 0 in(0, L) (3.2)
dengan kondisi batasP(0) =P0danP(L) = 0, dimanak(x)adalah permeabilitas,
λ sebagai mobilitas yang ditulis secara matematis sebagai λ(S) = krα
µα dengan krα merupakan permeabilitas relatif α sedangkan α adalah jenis fasa, µα sebagai
viskositas, P sebagai tekanan. Dari persamaan Darcy diatas dapat dilihat bahwa
terdapat kebergantunganvterhadap nilai viskositas, permeabilitas dan tekanan yang
menjadi penyebab terbentuknya aliran dua fase.
Oleh karenanya, perlu dilakukan perhitungan karena dapat mempengaruhi
ha-sil dari solusi persamaan Buckley-Leverett. Dengan mengintegrasikan (3.2)
terha-dapx, diperoleh
v =−k(x)λ(S)dP
dx =C sehingga
dP dx =−
Integralkan terhadapxsepanjang(0, L)
karenaC tidak bergantung kepadaxdapat ditunjukkan bahwa Z L
oleh kondisi awal diperoleh
C = Z L P0
nilaiv dapat diselesaikan melalui aturan trapezoidal dengan menggunakan
kuadra-tik relatif permeabilitaskrw =S2dankro = (1−S)2 sehinggaλ(S) =
Radalah viskositas relatif danvR = µ0
µw. Konsentrasi saturasi memiliki nilai antara [0,1], andaikan S = 1 maka λ(S) = vR
µo dan S = 0 maka λ(S) = 1
µo. Untuk mendapatkan nilai minimum dan maximum dari λ(S), maka akan dicari titik stationer yaitu pada saat λ′
(S) = 0, sehingga S = 1 titik minimum danvRmerupakan titik ujung yang menjadi titik maximum. Secara
umumvR>1, sehingga dapat ditunjukkan bahwa
vR Integralkan setiap suku terhadapxsepanjang [0,L]
sehingga diperoleh
dengan mengasumsikank(x)adalah konstanta, maka
P0vR
Pada aliran dua-fase, sifat viskositas pada fluida memiliki peran yang cukup
penting, Sehingga untuk mengekspresikan persamaan aliran fluida dua-fase,
diper-lukan suatu variabel yang dapat meggambarkan sifat tersebut. Viskositas adalah
kekentalan yang dimiliki oleh fluida, dalam hal ini fluida yang dimaksud adalah
air dan minyak. Kedua fluida ini memiliki derajat viskositas yang berbeda, hal ini
merupakan salah satu penyebab air dan minyak tidak tercampur (immiscible) ketika
berada pada wadah yang sama dan dalam keadaan setimbang. Biasanya diukur oleh
perbandingan viskositas minyak dan air yang direpresentasikan olehvR = µo
µw di-manavR>1karena viskositas minyak lebih besar dari pada air hal ini ditunjukkan
oleh kejadian alam yang nyata dimana minyak lebih kental dari pada air. Terdapat
f yang merupakan fungsi fraksi aliran air
f(S) = λw
3.1.2 Metode Volume Hingga
Tidak selamanya kasus persamaan diferensial dapat diselesaikan dengan metode
analisis, metode analisis hanya dapat dilakukan pada kasus-kasus tertentu saja. Oleh
karena itu jika suatu permasalahan tidak dapat diselesaikan dengan cara tersebut,
Telah disebutkan sebelumnya bahwa metode volume hingga sesuai
diterapk-an pada permasalahditerapk-an alirditerapk-an fluida dditerapk-an aerodiamika dditerapk-an diketahui bahwa
water-floodingmerupakan suatu permasalahan aliran fluida pada media berpori, sehingga
pada kasus ini akan dilakukan pendekatan numerik dengan menggunakan metode
volume hingga. Model Buckley-Leverett dengan tanpa saturasi efektif dapat
di-ekspresikan oleh persamaan berikut
∂tS+∂xvf(S) = 0 (3.5)
dengan batas kiri
S =S0(x) padat= 0 (3.6)
Dengan mengimplementasikan metode volume hingga yang telah dijelaskan
sebe-lumnya, maka dapat ditunjukkan bahwa
e
Si,n=Si,ne −1− v∆ti
∆xi [f(Si,ne −1)−f(Sie−1,n−1)] (3.7) dari penjelasan diatas, dengan mensubstitusikanf(S)terhadap persamaan (3.7)
di-peroleh
Oleh pendekatan numerik, besar nilai galat dapat diabaikan dengan mengasumsikan S(xi, tn) = Sei,ndanS(xi, tn−1) = Sei,n−1
3.1.3 Kondisi CFL
Dalam penyelesaian numerik, terdapat beberapa cara untuk menilai seberapa baik
hasil perhitungan dan seberapa dekat nilai numerik terhadap nilai eksak.
Diantara-nya adalah nilai konvergen dan stabilitas, dimana stabilitas akan bergantung pada
kondisi CFL (Courant, Friedrichs, dan Lewy). Selama kondisi CFL terpenuhi,
ma-ka stabilitas ama-kan dapat dipertahanma-kan (Leveque, 2002). Jima-ka terdapat persamaan
adveksiqt+ ¯uqxmaka kondisi CFL dapat didefinisikan
rasiozpada (3.8) biasa disebut bilangan Courant. Pada kasus ini, kondisi CFL dapat
Telah diketahui nilaivoleh persamaan (3.3) dan diketahuif(S)pada (3.4) sehingga
diperoleh
f′(S) = 2vRS[(1−S)
2+vRS2]−vRS2[−2(1−S) + 2vRS]
[(1−S)2+vRS2]2 (3.10)
dengan demikian, akan diperoleh maksimumf′
(S)yang bergantung padaSdanvR
sehingga dapat ditunjukkan bahwa
oleh persamaan (3.9) diperoleh
maks|f′
Konvergensi sangat dipengaruhi oleh nilai∆xdan ∆t, jika∆x dan∆t
me-nuju 0 (grid diperhalus), maka konvergensi akan tercapai sehingga nilai pendekatan
numerik akan menuju nilai eksak. Oleh karenanya, untuk memenuhi kondisi diatas,
maka pada haruslah diaturv∆t <∆xsehingga v∆∆xt <1. Agar lebih mudah
difaha-mi, perhatikan contoh berikut
Contoh
Terdapat suatu persamaan diferensial parsial ∂S
∂t + ∂
∂x(vf(S)) = 0 inR×(0, T)
Untuk mendapat perumusan secara numerik, maka nilai v yang memenuhi
persa-maan tersebut harus dihitung terlebih dahulu sehingga dapat dilakukan penurunan
yang ditunjukkan oleh persamaan berikut
dengan kondisi batas P(0) = 1 dan P(1) = 0 dan v = −k(x)λ(S)dP
dx. Dari pembahasan sebelumnya, maka diketahui bahwa
vR
µo(vR+ 1) < v <
vR
µo (3.11)
Telah diketahui nilaivoleh persamaan (3.11) dan diketahuif′
(S)pada (3.10)
dengan demikian, akan diperoleh maksimumf′
(S) = 2, minimumf′
(S) = 0dan
diasumsikanv = 1, oleh persamaan (3.9) diperoleh
maks|f′
(S)|vR∆t
∆x ≤1
dengan nilai maks|f′
(S)|= 2sehingga
∆t
∆x ≤
1 2vR.
Karena nilai maksf′
(S) = 2maka diperoleh ∆t
∆x ≤
1 2vR
. Akan tetapi hal tersebut
berlaku jika v = 1, namun pada kenyataannya v bernilai
1, vR sehingga jika
v < vR maka ∆t
∆x dapat bernilai sedikit lebih besar dari
1
2, dikarenakan adanya
kebergantungan setiap variabel v, f′
(S),∆∆xt namun tetap mempertahankan kondisi
<1. Andaikan viskositasvR =ksehingga
f(S) = vRS
2
(1−S)2+vRS2 =
kS2
(1−S)2+kS2
Nilaivakan diperoleh dengan mengimplementasikan aturan trapezoidal.
Ke-mudian ambilk = 5,10maka dapat ditunjukkan oleh Gambar 3.2 dan 3.3 dimana
grafik tersebut diperoleh dari perhitungan dengan menggunakan MATLAB pada
Lampiran 3.
3.1.3.1 Penjelasan Grafik
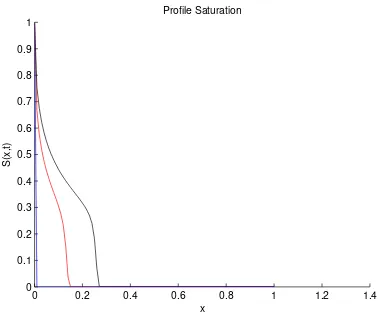
Grafik tersebut menggambarkan perhitungan nilai saturasi ketika air
0 0.2 0.4 0.6 0.8 1 1.2 1.4 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Profile Saturation
x
S(x,t)
Gambar 3.2: Aliran Dua fase denganvR = 5
S(x, t) = 1 menunjukkan bahwa air secara keseluruhan dan ketika S(x, t) = 0
menunjukkan minyak secara keseluruhan. Adapunxmerupakan jarak antara sumur
injesi dengan sumur produksi dimanax = 0 merupakan sumur injeksi danx = 1
merupakan sumur produksi.
Pada kedua Gambar dilakukan perhitungan saturasi dengan 3 waktu yang
ber-beda yaitu jika dilakukan injeksi sebanyak maxt kali (t=maxt), maka oleh grafik
diperlihatkan perhitungan pada saat t = 0, t = maxt
2 , dan t =maxt. Sehingga
dapat diketahui bahwa semakin lama waktu injeksi, maka minyak akan terus
ber-gerak menuju sumur produksi atau grafik akan menunjukkan nilaix = 1. Dengan
demikian, diketahui bahwa minyak dapat diangkat secara keseluruhan oleh sumur
produksi.
visko-0 0.2 0.4 0.6 0.8 1 1.2 1.4 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Profile Saturation
x
S(x,t)
Gambar 3.3: Aliran Dua Fase denganvR= 10
sitas minyak (µo) dan air (µw) dimana minyak sebagai fase fluida yang didorong dan
air sebagai pendorong. Sehingga dapat digambarkan bahwa jika nilai viskositas air
semakin kecil sedangkan viskositas konstan, maka waktu yang dibutuhkan dalam
proses injeksi akan semakin cepat.
3.1.4 Saturasi Efektif
Model Barenblatt merupakan pemodelan dari tekanan kapiler nonekuilibrium pada
permeabilitas relatif, hal ini didasari oleh perpindahan multifase pada media
ber-pori yang menunjukkan penyusunan kembali pada skala berber-pori. Sedangkan
ka-rakteristik waktu yang berfungsi untuk menyusun kembali aliran jaringan menjadi
substansial sehingga flux setiap fase tidak bergantung pada saturasi aktual.
Untuk menyelesaikan fungsi Buckley-Leverett (BL) dengan fungsi flux
dan saturasi efektif (σ). Dengan menggunakan analisis dimensi dan penalaran
se-cara fisik, Barenblatt mengajukan relasi evolusi yang direpresentasikan oleh model
berikut
σ−S =τ ∂tS (3.12)
Saturasi efektif dianggap sebagai sebuah saturasi yang akan datang dan bergantung
pada saturasi aktual dengan pendekatan
σw ≈Sw(t+τ)
dimanaτ adalah koefisienphenomenologicalyang bergantung pada saturasi aktual
dan bernilai positif. Persamaan (3.12) dapat diurai menjadi suatu persamaan
al-jabar dengan melakukan pendekatan metode volume hingga dengan menggunakan
pendekatanmid pointpada integrasi terhadap batasx Z tn+1
kemudian gunakan pendekatantrapezoidal ruleuntuk integrasi terhadap batast
1
3.1.5 Aliran Dua Fase dengan Saturasi Efektif
Telah disebutkan sebelumnya bahwa skripsi ini akan melakukan perhitungan
nume-rik pada persamaan Buckley-Leverett yang dihubungkan dengan model Barenblatt.
Dengan mengikuti penurunan sebelumnya, akan dilakukan perhitungan terhadap
kondisi awal untuk σ(x,0) = σ0(x) dengan pendekatan volume hingga terhadap
σ0 +τ ∂xf(σ0) = S0(x). Integrasi persamaan ini sepanjang [xi−1
Dengan mengaplikasikan pendekatanmid point rulepadaσdanS, diperoleh
σ0(xi)∆x+τ
Kemudian gunakan pendekatan upwind pada fungsi flux sehingga diperoleh
σ0(xi)∆x+τ
h
f(σ0(xi))−f(σ0(xi−1)) i
=S0(xi)∆x+G1+G2
/ Dengan mengabaikan kedua galat tersebut diperoleh satu persamaan aljabar yang
mengaturσe0(xi)≈σ0(xi)
Persamaan diatas merupakan persamaan nonlinier, sehingga dapat diselesaikan
de-ngan menggunakan iterasi Newton. Dalam hal ini akan dicariσ0(xi)dengan
meng-aturG(eσ0(xi)) = 0, dimana
Adapun turunan dariGterhadapzadalah
G′
(z) = 1 + τ ∆xf
′
(z)
Dengan demikian, iterasi Newton untuk persamaan diatas adalah
zn=zn−1−
G(zn−1) G′
untukn= 1,2,3, ..., dan diharapkanlimn→∞zn=eσ0(xi). Adapun perhitungannya ditunjukkan oleh Lampiran 4 sebagai subfungsi.
Dapat dilihat bahwa persamaaan (2.1) merupakan persamaan diferensial
par-sial, sedangkan pada persamaan (2.2) merupakan persamaan diferensial biasa. Oleh
karena itu, persoalan diatas akan diuraikan secara terpisah. Untuk persamaan
dife-rensial parsial, lakukan integrasi numerik yang telah dijelaskan pada pembahasan
aliran dua fase. Namun karena akan dilakukan perhitungan dengan menggabungkan
saturasi dan saturasi efektif, maka ada pendekatan yang dilakukan dengan metode
yang berbeda.
Adapun cara pendekatan integrasi numerik yang dilakukan pada
persama-an (3.5) dengpersama-an mengambil batas integrasi ypersama-ang sama seperti sebelumnya yaitu
[xi−1 2, xi+
1
2] pada pias ruang dan [tn, tn+1] pada pias waktu yang ditunjukkan se-bagai berikut
Pendekatanmidpoint rulepada batasxuntuk suku pertama menghasilkan Z xi+ 12
Adapun pada suku kanan, dilakukan pendekatanupwindpada batasx Z tn+1
Dari uraian diatas, maka diperoleh
σi,n+1. Dengan mengasumsikan semua galat berada pada pendekatanSi,n ≈ Sei,n, Si,n+1 ≈Sei,n+1,σi,n≈eσi,ndanσi,n+1≈σei,n+1
Untuk persamaan diferensial biasa, telah diuraikan oleh persamaan (3.13),
diasumsikan bahwaτe(S(xi, tn))adalah konstanta sehingga
Dari persamaan (3.14) dan (3.15), asumsikan bahwa semua variabelS danσ
padatn+1 sebagai sebuahunknownyang harus dicari nilainya. Karena persamaan
diatas nonlinier, maka dapat diselesaikan dengan menggunakan iterasi Newton pada
sistem aljabar yang telah dijelaskan pada Bab sebelumnya. Untuk itu, misalkan
[U1,· · · , UM, UM+1,· · · , U2M] ⊤
=U ∈R2M
sedemikian sehingga
Ui =Si,ne +1danUM+i =σi,ne +1, untuki= 1,2,· · · , M.
Kemudian berdasarkan penurunan diatas, dibentuk F : R2M → R2M, sedemikian
sehingga
F(U)=0,
yang direpresentasikan oleh persamaan berikut
FM+i(U) =
Solusi persamaan aljabar nonlinear di atas dicari dengan metode iterasi Newton:
jika diberikan U(0) sebagai vektor initial guess, maka U(k) untuk k = 1,2,· · ·,
sampai konvergensi tercapai diberikan oleh
U(k)=U(k−1)−[F′(U(k−1))]−1F(U(k−1))
Dapat dilihat bahwa metode iterasi Newton membutuhkan matriks Jacobian
F′(U)=
Matriks jacobian yang dihasilkan adalah matriks bujur sangkar(2M ×2M)
yaitu memiliki jumlah baris dan kolom tergantung padai(jumlah diskritisasi yang
dibentuk). Oleh matriks jacobian diatas, maka perlu dilakukan penurunan parsial
pada (3.16) sebagai berikut
∂Fi(U)
sedangkan pada (3.17) diperoleh turunan parsial
dan
dimanaeσ0,n+1 merupakan suatu nilai awal yang telah diketahui nilainya. Sehingga
diperoleh turunan
Jika pada persamaan (2.1) dan (2.2) dengan domain (0, L), dibagi menjadi M subinterval. Maka dapat dilakukan diskretisasi pada kedua persamaan tersebut
dimanai= 1,2,3,· · · , M. Andaikanb = ∆t
2 oleh penurunan parsial yang telah dijelaskan sebelumnya, maka diperoleh matriks jacobian berikut
F′(U)=
Dari uraian diatas, maka dapat dilakukan perhitungan dengan menggunakan
MATLAB dengan code pada lampiran 4.
3.1.5.1 Penjelasan Grafik
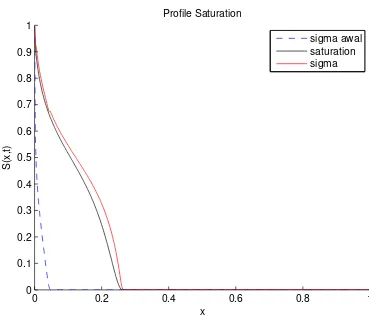
Hasil perhitungan dapat diperlihatkan oleh Gambar 3.4 dan 3.5 berikut
Oleh kedua gambar diperlihatkan bahwaS(x, t)sebagai sumbuyyang
0 0.2 0.4 0.6 0.8 1 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x
S(x,t)
Profile Saturation
sigma awal saturation sigma
Gambar 3.4: Aliran Dua Fase dengan Efek Nonekuilibrium dimana vR = 3dan τ = 0.01
dan dan sumur produksi dimana ketika x = 0menunjukkan sumur injeks
sedang-an pada x = 1 menunjukkan tempat sumur produksi. Grafik tersebut merupakan
gambaran terhadap kondisi efek dari permeabilitas relatif pada fluida yang
dinon-dimensionalkan. Ditunjukkan bahwa sigma awal adalah nilai awal yang diberikan
oleh pasangan Buckley-Leverett dan Barenblatt, saturation merupakan saturasi
ak-tual (saturasi saat ini) dan sigma merupakan efektif saturasi (saturasi yang akan
datang).
Kedua grafik merupakan hasil perhitungan dengan nilai waktu yang sama,
adapun pada setiap grafik dapat dibandingkan hasil perhitungan saturasi efektif dan
saturasi aktual dimana diharapkan bahwa pada perhitungan dengan memasukkan
efek nonequilibrium dapat dilakukan perhitungan teknik waterflooding yang lebih
0 0.2 0.4 0.6 0.8 1 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
sigma awal saturation sigma
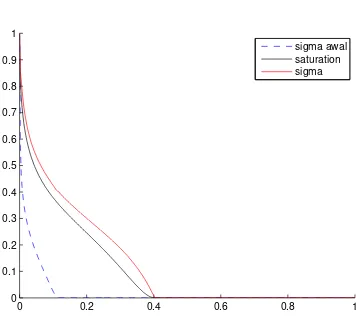
Gambar 3.5: Aliran Dua Fase dengan Efek Nonekuilibrium dimana vR = 7dan τ = 0.02
Grafik pada Gambar 3.4 memiliki nilaivR = 3danτ = 0.01sedangkan
gra-fik pada Gambar 3.5 memiliki nilaivR = 7 danτ = 0.02, dapat dilihat perubahan
yang terjadi ketika nilai parameter yang dimasukkan berbeda, sehingga dapat
di-simpulkan bahwa kedua parameter tersebut memberikan pengaruh terhadap proses
pendesakan. Telah dijelaskan sebelumnya bahwavR adalah viskositas relatif yang
merupakan perbandingan dari viskositas minyak dan air danτadalah koefisien
phe-nomenologi. Semakin besar viskositas relatif yang berarti ketika nilai viskositas
fluida pendorong semakin kecil dan viskositas minyak konstan, maka waktu yang
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Teknikwaterfloodingtelah banyak dimodelkan secara numerik oleh para peneliti,
namun biasanya perhitungan dilakukan pada efek equilibrium atau hanya
menca-ri solusi pada persamaan Buckley-leverett saja. Namun, pada kenyataannya
bah-wa teknik bah-waterflooding adalah suatu kejadian interaksi antara fluida dan batuan
dengan adanya efek nonequilibrium pada permeabilitas relatif. Dengan demikian,
diharapkan pemodelan yang dihasilkan akan lebih efisien.
Hasil perhitungan pada persoalan waterflooding memperlihatkan gambaran
kondisi minyak yang didorong oleh air dapat dihitung disepanjang waktu, sehingga
ketika diukur semua kondisi fisik yang menjadi parameter perhitungan, maka dalam
jangka waktu tertentu dapat dipertimbangkan besar tekanan yang diberikan untuk
mendorong minyak agar sampai ke sumur produksi dengan lebih optimal. Dengan
demikian, maka perhitungan dapat dijadikan sebagai acuan bagi pelaku kinerja
la-pangan dalam mengaplikasikan teknik tersebut.
4.2 Saran
Ketika melakukan pendekatan numerik pada persamaan differensial parsial dan
per-samaan diferensial biasa terdapat galat yang bergantung pada besar dan jumlah grid
yang dibentuk. Sehingga diperlukan ketelitian yang lebih untuk melakukan
pende-katan agar perhitungan lebih akurat. Oleh karena itu, penelitian ini dapat
diting-katkan dengan tujuan memperkecil galat yang tentunya dibutuhkan suatu metode
TINJAUAN PUSTAKA
2.1 Model Aliran Dua-Fase Nonekulibrium pada Media Berpori
Penelitian ini merupakan kajian ulang terhadap penelitian yang telah dilakukan oleh Juanes (2008), dalam tulisannya yang berjudulNonequilibrium effects in models of three-phase flow in porous media. Pada tulisan tersebut dilakukan simulasi wa-terfloodingdengan melakukan pendekatan diskritisasi menggunakancell-centered finite volumeyaitu solusi disimpan pada pusat setiap grid yang dibentuk, sedangkan pada skripsi ini, penulis melakukan diskritisasi dengan menggunakanvertex cente-red finite volumeyaitu solusi yang disimpan pada simpul (vertex) dari mesh dimana setiap vertexiharus dibangun cell (Praveen, 2013).
Juanes menyatakan bahwa model aliran dua fase dengan efek nonekuilibri-um pada media berpori telah diajukan sebelnonekuilibri-umnya oleh Barenblatt dengan bebas kapilaritas. Kemudian dipasangkan dengan model Buckley-Leverett dengan bebas kapilaritas dimana fluks merupakaan fungsi saturasi efektif yang direpresentasikan dengan persamaan
∂tS+∂xvf(σ) = 0 (2.1)
dan persamaan evolusi
σ−S =τ ∂tS (2.2)
Sistem ini harus dilengkapi denngan kondisi batas fluks pada batas kirix= 0dalam bentukf(σ) = ¯f(t). Selain itu juga diberikan kondisi awal padat= 0dalam bentuk
S =S0(x)
σ0+τ ∂xf(σ0) = S0(x)
(2.3)
dimanaSadalah saturasi aktual (saturasi saat ini) danτ adalah saturasi efektif (sa-turasi yang akan datang).
Sedangkan model Barenblatt menggambarkan dua fase aliran pada media berpori dengan efek dinamik (nonekuilibrium) pada relatif permeabilitas. Pada kasus ini,
water flooding yang ditunjukkan oleh persamaan (2.1) yang dipasangkan dengan persamaan (2.2) akan diselesaikan melalui analisis numerik, yang akan dijelaskan pada Bab selanjutnya
2.2 Deret Taylor
Biasanya metode numerik diturunkan berdasarkan hampiran fungsi terhadap bentuk polinomial sehingga fungsi akan menjadi lebih sederhana. Deret Taylor dapat digu-nakan pada hampir setiap pendekatan numerik yang didefinisikan sebagai berikut Definisi
Andaikan terdapat f dan semua turunannya f′
, f′′
n+1merupakan galat denganlim
n→∞
f(n+1)(tx)
(n+1)! h
n+1= 0
2.3 Metode Iterasi Newton Pada Sistem Aljabar
Metode iterasi Newton merupakan suatu metode yang berfungsi untuk mencari ni-lai akar dari suatu persamaan, yaitu mencarir ∈ Ryang memenuhi f(r) = 0. Pe-nurunan metode ini dapat diperoleh dari deret Taylor yang direpresentasikan oleh persamaan (2.5). Untukn= 1, persamaan (2.5) menjadi
dimana f′′(tx)
2! h
2 merupakan galat. Jika dimisalkan x+h merupakan pendekatan
untukr, maka dengan mengabaikan galat tersebut diperoleh
0 =f(x) +f′
yang diharapkan limn→∞xn = r. Penurunan diatas dapat dipakai untuk menda-patkan metode iterasi yang mencari r ∈ Rn yang memenuhi F(r) = 0, dimana F :Rn →Rn. Dalam hal ini,
0=F(x)+F′(x)h
dimanaF′(x)merupakan matrix Jacobian dengan ordon×n
F′(x)=
Sehingga dapat ditunjukkan bahwa
h=−[F′
(x)]−1
F(x).
Jika terdapat nilai dugax0maka secara umum metode iterasi Newton untuk system
aljabar dapat ditulis sebagai berikut
xn+1 =xn−[F
diselesaikan dengan cara analitik. Oleh karena itu, diperlukan suatu metode nume-rik dimana penyelesaian integrasi dapat diselesaikan dengan bantuan perhitungan komputer (integrasi numerik) dengan batas integral tertentu yang direpresentasikan oleh
I =
Z b
a
f(x)dx.
Rinaldi Munir (2003) dalam bukunyaIntegrasi Numerikmenjelaskan bahwa terdapat 3 cara dalam melakukan pendekatan dalam menurunkan rumus integrasi numerik yaitu metode pias, metodeNewton-Codes danKuadratur Gauss. Penulis akan membatasi pembahasan hanya pada integrasi numerik dengan metode pias.
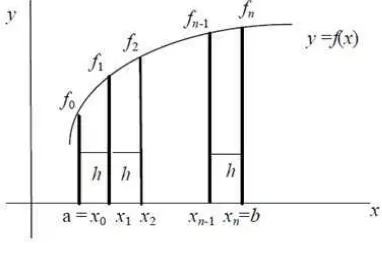
Perhatikan Gambar 2.1, andaikan[a, b] merupakan interval pada luas kurva f(x), maka dibentuk n partisi sepanjang interval [a, b], dimana lebar setiap pias adalah
h= b−a
n .
Dengan demikian, titik pias dinyatakanxi =a+ihdimanai= 0,1, ..., n
Gambar 2.1: Metode Pias
2.4.1 Aturan Trapesium
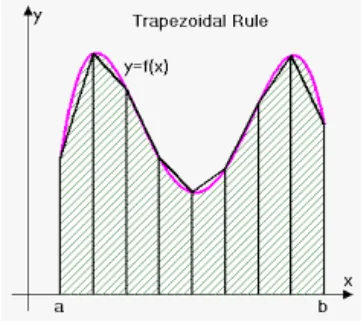
Pada pendekatan trapesium dapat digunakan rumus luas trapesium pada setiap pi-as. Perhatikan Gambar 2.2. Secara umum, luas dibawah kurva pada pias(xi, xi+1
Gambar 2.2: Trapezoidal
didekati oleh
Z xi+1
xi
f(x)dx≈f(xi) +f(xi+1)h 2
dimanai= 0,1,2, ..., n−1. Dengan demikian,
Z b
a
f(x)dx≈ n−1
X
i=0
f(xi) +f(xi+1)
h
2.
2.4.2 Aturan Titik Tengah
Luas daerah pias dapat digambarkan sebagai luas persegi panjang dimanahsebagai lebar danf(xi+1
2)sebagai panjang yang dapat ditunjukkan oleh Gambar 2.3, Secara
umum, pendekatan ini dapat ditulis sebagai Z xi+1
xi
f(x)dx≈f(xi+1+xi 2 )h
dimanai= 0,1,2, ..., n−1, sehingga Z b
a
f(x)dx≈ n−1
X
i=0
f(xi+1+xi 2 )h.
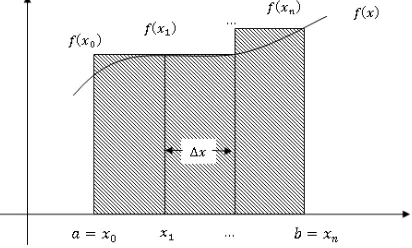
2.4.3 Aturan Titik Kanan
Pada pendekatan aturan titik kanan dapat dianggaphsebagai lebar pias danf(xi+1)
sebagai panjang. perhatikan Gambar 2.4, Secara umum, pendekatan ini dapat ditulis
Gambar 2.4: Aturan Titik Kanan
sebagai
Z xi+1
xi
f(x)dx≈f(xi+1)h,
dimanai= 0,1,2, ..., n−1, sehingga Z b
a
f(x)dx≈ n−1
X
i=0
f(xi+1)h.
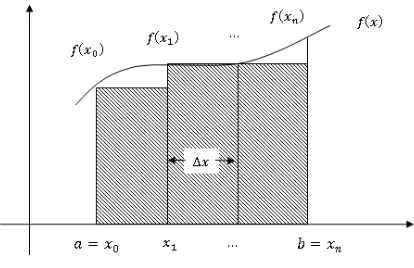
2.4.4 Aturan Titik Kiri
Pada pendekatan aturan titik kiri dapat dianggap h sebagai lebar pias dan f(xi) sebagai panjang. perhatikan Gambar 2.5, Secara umum dapat ditulis sebagai
Z xi+1
xi
f(x)dx≈f(xi)h,
dimanai= 0,1,2, ..., n−1, sehingga Z b
a
f(x)dx≈ n−1
X
i=0
Gambar 2.5: Aturan Titik Kiri
2.5 Galat
Penyelesaian numerik akan selalu memiliki nilai galat, karena metode numerik me-rupakan suatu pendekatan terhadap nilai eksak. Jika nilai galat mendekati nol, ma-ka penyelesaian numerik ama-kan mendema-kati nilai eksak. Hal itu ama-kan terjadi jima-ka jarak pias (∆xdan∆t) diperkecil, namun perhitungan yang dilakukan akan semakin ba-nyak. Kita tahu bahwa nilai eksak merupakan jumlahan dari nilai hampiran dan galat, yang berarti galat adalah selisih antara nilai eksak dan hampiran yang dinya-takan oleh
ε=r−x
dimanaxadalah nilai hampiran danradalah nilai eksak.
Besar galat tidak memperhatikan nilai positif atau negatif, sehingga ditulis dalam harga mutlak yang ditunjukkan oleh
|ε|=|r−x|.
Untuk mengetahui sebarapa besar pengaruh nilai galat terhadap nilai eksak, maka nilai galat dapat dinormalkan terhadap nilai eksak yang disebut dengan galat relatif yang representasikan oleh
εR = r−x
x .
2.5.1 Galat Iterasi Newton
Dalam menentukan nilai akar, iterasi Newton merupakan salah satu metode yang sering digunakan karena konvergensinya lebih cepat (jika nilai iterasi konvergen) dari pada metode yang lain. Pada kasus tertentu, metode Newton bisa bersifat di-vergen sehingga tidak selamanya metode Newton dapat digunakan untuk mencari nilai suatu akar. Metode ini dikatakan konvergen jika
(x)6= 0. Adapun pada orde konvergensi dinyatakan
εr+1 = f
′′
(xr)ε2r
2f′(x
r)
denganxr merupakan nilai hampiran terhadap akar. Dalam perhitungan menggu-nakan komputer, perlu bagi kita untuk membatasi jumlah perhitungan agar kom-puter dapat menghentikan perhitungan. Sehingga dapat ditentukan bahwa iterasi akan berhenti pada saat |xn+1 − xn| < ε adapun untuk menghitung galat relatif
dinyatakan oleh
|xn+1−xn|
|xn+1|
< δ
dimanaε, δmerupakan toleransi galat yang diinginkan. Adapun pada sistem aljabar, galat dapat direpresentasikanεi =r−x(i)dan norm Euclidean galat adalah
kǫi k=
2.5.2 Galat Aturan Trapesium
Integrasi numerik menggunakan pendekatan trapesium memiliki galat yang ditun-jukkan sebagai berikut
Andaikan terdapat dua titik yaitux0 = 0danh = x, dengan menggunakan deret
sehingga
jadi, nilai eksak diperoleh Z h
0
f(x)dx= h
2(f(x0) +f(x1)) +O(h
3)
Dapat disimpulkan bahwa galat total dari pendekatan trapesium berbanding lurus dengan kuadrat lebar pias (h). semakin kecil lebar pias, maka ukuran galat akan semakin kecil.
2.5.3 Galat Aturan Titik Tengah
Pendekatan titik tengah diperoleh galat untuk satu pias
G=
Z h
0
f(x)dx−hf(x1 2)
Dengan metode yang sama pada aturan trapesium diperoleh
Gtotal =− h3
24(f
′′
(x0) +f′′(x1) +f′′(x2) +...f′′(xn−1))
Adapun untuk beberapa pias, diperoleh
Gtotal =
dari uraian diatas dapat disimpulkan bahwa galat yang dihasilkan pada pendekatan aturan titik tengah dua kali lebih kecil dari pada aturan trapesium, sehingga die-tahui bahwa metode in lebih efisien dari aturan trapesium. Adapun galat untuk pendekatan aturan titik kanan dan titik kiri telah dijelaskan oleh Jiwen He (2008) yang iuraikan sebagai berikut
2.5.4 Galat Aturan Titik Kanan
Telah dijelaskan pendekatan integrasi numerik pada aturan titik kanan pada pem-bahasan sebelumnya, maka untuk galat yang dihasilkan dapat ditunjukkan sebagai berikut
G=
Z h
0
dimanai= 0,1, ..., n−1. Sehingga diperoleh galat untuk satu pias
G= h
2
2 f
′
(x1)
Adapun pias sebanyak n diperoleh
Gtotal = 1
2(b−a)f
′
(xi)
≈O(h)
2.5.5 Galat Aturan Titik Kiri
Dapat ditunjukkan galat dari aturan titik kiri sebagai berikut
G=
Z h
0
f(x)dx−hf(xi)
dimanai= 0,1, ..., nsehingga diperoleh galat untuk satu pias
G= h
2
2 f
′
(x0)
Adapun pias sebanyak n diperoleh
Gtotal =
1
2(b−a)f
′
(xi)
≈O(h)
Dapat dilihat bahwa pendekatan aturan titik kanan dan aturan titik kiri me-miliki besar galat yang sama, namun berbeda pada pendekatan trapesium dan titik tengah. Diketahui bahwa pendekatan yang memiliki galat yang paling kecil diantara keempat pendekatan diatas adalah aturan titik tengah. Sehingga dapat disimpulkan bahwa pendekatan aturan titik tengah yang memiliki efisiensi yang cukup cepat dari jumlah diskritisasi yang dilakukan. Namun ada beberapa kondisi yang menyebabk-an pendekatmenyebabk-an ymenyebabk-ang dilakukmenyebabk-an harus disesuaikmenyebabk-an dengmenyebabk-an permasalahmenyebabk-an ymenyebabk-ang sedmenyebabk-ang dijalankan. Oleh karenanya perlu bagi kita untuk mempelajari lebih mendalam ten-tang pendekatan numerik.
Contoh
x2−y2 =y,x2+y2 =xdenganinisial guessx0 = 0.8dany0 = 0.4.
maka solusi pada iterasi pertama yaitu:
Perhitungan dapat dilakukan dengan menggunakan MATLAB dimana code dapat dilihat pada lampiran 1. Jika dilakukan iterasi sebanyak 5 kali, maka akan didapat hasil yang ditunjukkan oleh tabel berikut
i xi yi error
0 0.8 0.4
-1 0.772881355932203 0.420338983050847 0.033898305084746 2 0.771845967451467 0.419644283432102 0.001246850779495 3 0.771844506348887 0.419643377608757 1.719109270156545e-006 4 0.771844506346038 0.419643377607081 3.304913436759251e-012 5 0.771844506346038 0.419643377607081 0
Dari penyelesaian diatas dapat kita ketahui bahwa pada iterasi ke-5 nilai galat telah mencapai 0, sehingga diketahui nilai akar dari x = 0.771844506346038dan y = 0.419643377607081
2.6 Solusi Numerik pada Persamaan Diferensial Partial
komputer diprogram untuk melakukan perhitungan operasi sederhana seperti pen-jumlahan, pengurangan, perkalian, pembagian, dan perulangan.
Oleh karena itu persamaan diferensial harus ditransformasikan kedalam per-samaan yang hanya terdiri dari bilangan, kombinasi dari bilangan tersebut dapat digambarkan oleh operasi yang sederhana. Untuk melakukan transformasi pada persamaan tersebut maka dapat dilakukan suatu cara yang disebut diskritisasi ya-itu setiap suku dalam persamaan diferensial harus diterjemahkan kedalam sebuah bentuk numerik yang dapat diprogram oleh komputer untuk dihitung. Berbagai tek-nik dapat dilakukan diantaranya metode beda hingga, metode elemen hingga, dan metode volume hingga.
Metode beda hingga merupakan suatu teknik yang didasari pada deret Taylor yang menggambarkan turunan dari variabel sebagai selisih antara nilai-nilai dari va-riabel dari berbagai titik dalam ruang dan waktu. Teknik kedua yaitu metode elemen hingga, dalam metode ini domain dari persamaan diferensial parsial yang berlaku dibagi menjadi sejumlah elemen berhingga. Namun pada metode ini, proses diskri-tisasi yang dilakukan lebih sulit dibandingkan dengan metode beda hingga. Teknik yang ketiga adalah metode volume hingga, teknik ini cukup popular digunakan un-tuk persoalan komputasi fluida dinamik.
Menurut Apsley (2005) metode volume hingga sesuai diterapkan pada ma-salah aliran fluida dan aerodinamika. Pada metode volume hingga harus diketahui domainnya dengan jelas, dari domain tersebut dibagi menjadi grid-grid baik ters-truktur maupun tidak (unstrustured), pada masing-masing grid memenuhi persama-an matematika ypersama-ang terbentuk.
2.6.1 Metode Volume Hingga
Metode Volume Hingga (MVH) merupakan salah satu teknik diskritisasi pada per-samaan diferensial parsial, dan biasanya diimplementasikan pada hukum konser-vasi. Pada dasarnya metode ini mengatur persamaan diferensial agar dikonversi kedalam bentuk numerik yaitu dengan membagi domainΩmenjadi himpunan dari volume berhingga yang saling lepas. Domain yang dipartisi sebanyakiyang disebut grid atau mesh.
Tulus, Ariffin, Abdullah dan Norhamidi (2005) telah melakukan peneliti-an mengenai aplikasi Computational Fluid Dinamic(CFD) dengan menggunakan metode volume hingga dalam tulisannya yang berjudulNumerical Simulation of In-Cylinder Gas Dynamic of Two-Stroke Linear Engines using Finite Volume Method.
Thomas J.W (2013) dalam bukunyaNumerical Partial Differential Equation Conservation Law and Elliptic Equation mengemukakan suatu formulasi umum dari hukum konservasi berikut
∂u ∂t +
∂f(u)
∂x = 0 inR×(0, T)
persamaan tersebut dapat diselesaikan dengan menggunaka metode volume hingga, dimana akan dicari solusiU(xi, tn)atau dapat dinotasikan sebagaiUinyang kemu-dian dibentuk suatu grid terhadap domain xdan waktut. Andaikan terdapat suatu interval [a, b], maka untuk mencari solusinya dapat dipartisi sebanyak n, dimana n ∈N, sehingga∆x= (b−a)
n . Maka untukxi =a+i∆xdan kemudian terdapat∆t sehinggatn =n∆t. Dalam hal ini, dibentukcontrol volumepada diskritisasi yaitu suatu bidang dengan batasxyaituxi−1
2 danxi+ 1
2 sedangkan batas terhadaptyaitu
tn−1 dantnyang dapat ditunjukkan oleh Gambar 2.6 sehingga dapat direpresenta-sikan oleh
Gambar 2.6: Control Volume
pada suku pertama integralkan terhadap batast, pada suku kedua integralkan terha-dap batasxsehingga diperoleh
Z xi+ 1
dengan mengaplikasikan pendekatanmid pointdapat ditunjukkan bahwa
Z xi+ 1
sedangkan pada fungsi flux dilakukan pendekatanleft pointdapat diperlihatkan bah-wa
Lakukan pendekatan upwind yang diilustrasikan oleh Gambar 2.7, dimana pende-katan upwind dapat direpresentasikan oleh
f(u(xi+1
2, tn−1))≈f(u(xi, tn−1))
f(u(xi−1
Gambar 2.7: Upwinding
Seperti yang telah disebutkan sebelumnya, terdapat galat pada setiap pendekatan numerik sehingga
u(xi, tn)∆xi−u(xi, tn−1)∆xi+f(u(xi, tn−1))∆ti
−f(u(xi−1, tn−1))∆ti+Galat1+Galat2 = 0
(2.6)
dengan Galat1= galat integrasi numerik dan Galat2=galat upwinding. Dalam hal
ini∆xi dan∆ti merupakan pias yang dapat ditentukan besarnya, jika∆xi dan∆ti menuju nol, maka galatnya pun akan menuju nol sehingga solusi numerik akan mendekati solusi eksak. Oleh karenanya dapat kita lakukan pendekatanu(xi, tn)≈ U(xi, tn)sehingga persamaan (2.6) dapat ditulis
U(xi, tn)∆xi−U(xi, tn−1)∆xi+f(U(xi, tn−1))∆ti
−f(U(xi−1, tn−1))∆ti = 0
jadi,
U(xi, tn) =U(xi, tn−1)−
∆ti
∆xi
f(U(xi, tn−1))−f(U(xi−1, tn−1))
(2.7)
Contoh
Terdapat suatu persamaan yang direpresentasikan oleh persamaan berikut ∂u
∂t +
1 2
∂u2
∂x = 0 inR×(0, T) (2.8) dengan kondisi batas u(x,0) = 1−x2, tentukan solusi numerik dari persamaan
Penyelesaian
Persamaan (2.8) merupakan persamaan transport yang dikenal dengan sebutan per-samaan Burger inviscid yang merupakan bentuk sederhana dari perper-samaan diferen-sial pardiferen-sial nonlinier. Persamaaan Burger terkenal dengan solusinya berupa gelom-bang kejut dan merupakan bentuk khusus dari model Buckley-Leverett.
Permasalahan ini dapat diselesaikan oleh beberapa metode, namun dalam hal tulisan ini penulis akan menyelesaikan persamaan tersebut dengan menggu-nakan metode volume hingga yang telah dijelaskan sebelumnya dengan melakukan langkah-langkah yang dijelaskan sebelumnya yaitu dengan melakukan integrasi se-perti persamaan (2.6.1)
pada suku pertama integralkan terhadaptdan pada suku kedua integralkan terhadap x
pada suku pertama digunakan pendekatanmid pointdan pada suku kedua digunakan pendekatanleft pointsehingga diperoleh
u(xi, tn)∆xi−u(xi, tn−1)∆xi+
dengan menggunakan upwinding diperoleh
∆xi[u(xi, tn)−u(xi, tn−1)] +
1 2∆ti[u
2(x
i, tn−1)−u2(xi−1, tn−1)] = 0
dengan melakukan perhitungan al-jabar diperoleh
u(xi, tn) = u(xi, tn−1)−
∆ti
2∆xi[u
2(x
i, tn−1)−u2(xi−1, tn−1)]
persamaan (2.8) dapat diselesaikan secara numerik dengan menggunakan metode volume hingga yang menjadi rujukan pada penelitian ini.
0 0.2 0.4 0.6 0.8 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
explicit method
X
u(x,t)
PENDAHULUAN
1.1 Latar Belakang
Kebutuhan terhadap Bahan Bakar Minyak (BBM) pertama kali muncul pada tahun
1858 ketika minyak mentah ditemukan oleh Edwin L. Drake di Titusville (IATMI
SM STT MIGAS Balikpapan, 2012). Seiring perkembangan zaman, kebutuhan
ma-nusia terhadap minyak bumi semakin meningkat, sedangkan ia merupakan sumber
alam yang tidak dapat diperbarui. Pada awal ditemukan minyak bumi, teknik yang
dilakukan untuk pengambilan minyak bumi hanya bergantung pada kondisi alam
yang dikenal dengan istilahprimary recoveryatau metode primer yaitu minyak
bu-mi yang dihasilkan dengan kondisi alabu-mi yang normal.
Namun kondisi alam tidak dapat mengangkat minyak bumi secara
keseluruh-an dari sumber bumi (reservoir) sehingga minyak bumi yang dihasilkan
diperki-rakan hanya dapat bertahan sekitar sepuluh tahun kedepan. Jika hal ini dibiarkan,
maka kita tidak dapat memproduksi bahan bakar minyak sedangkan kebutuhan
se-makin meningkat, sehingga akan menghambat laju pertumbuhan ekonomi dan akan
berdampak pada laju pertumbuhan lainnya. Karena minyak bumi merupakan
sa-lah satu faktor pendorong pertumbuhan dunia. Oleh karena itu, pihak pemerintah
maupun pihak swasta melakukan berbagai usaha dalam mencari solusi dari
perma-salahan tersebut.
Pada awal 1880-an, J.F. Carll mengajukan suatu cara untuk meningkatkan
produksi minyak bumi dengan menggunakan teknik injeksi air yang dinamai
secon-dary recoveryatau metode sekunder (IATMI SM STT MIGAS Balikpapan, 2012).
Teknik injeksi air (water flooding) merupakan salah satu cara pendesakan minyak
bumi menuju sumur produksi yang bertujuan untuk memberikan tambahan energi
ke dalam reservoir. Dalam proses ini, air akan mendesak minyak mengikut
produksi (IATMI SM STT MIGAS Balikpapan, 2012). Teknik injeksi air dapat
diilustrasikan oleh gambar berikut.
Eksperimen pertama dilakukan di lapangan Bradford, Pennsylvania, AS. Dari
eksperimen ini dapat dibuktikan bahwa teknik injeksi air atau dikenal dengan
sebut-anwater flooding dapat meningkatkan produksi minyak darireservoir. Pada awal
tahun 1890-an Amerika mulai menggunakan metode ini, dan pada tahun 1921
pene-rapannya mulai meningkat, misalnya di Oklahoma pada tahun 1931, di Kansas pada
tahun 1935, dan di Texas pada tahun 1936.Water floodingsangat banyak digunakan
karena berbagai alasan antara lain:
1. mobilitas yang cukup rendah,
2. air mudah didapatkan,
3. pengadaaan air cukup murah,
4. berat kolom air dalam sumur injeksi turut memberikan tekanan, sehingga
cu-kup banyak mengurangi tekanan injeksi yang perlu diberikan di permukaan,
5. mudah tersebar ke daerah reservoir, sehingga efisiensi penyapuannya cukup
tinggi,
Teknikwater flooding dapat digambarkan sebagai hubungan dua fase aliran
yangimmiscible(tidak tercampur). Suatu fluida dikatakan tidak bercampur jika
ter-dapat lapisan yang kasat mata ketika kedua fluida tersebut disatukan pada suhu dan
tekanan tertentu, hingga mencapai suatu titik kesetimbangan kimia yang dalam hal
ini fase minyak-air. Efisiensi pendesakan dipengaruhi oleh faktor interaksi antara
fluida dan media yang menampungnya yaitu batuan pada reservoir. Oleh karena itu
perlu bagi kita untuk mengetahui sifat bebatuan tersebut diantaranya
1.1.1 Sifat Fisik Batuan Reservoir
Reservoir dapat didefinisikan sebagai suatu lapisan yang berada dibawah
permu-kaan bumi yang memiliki strukutur tertentu yang menjadi wadah untuk
menam-pung minyak bumi dan gas bumi dalam jumlah yang cukup besar. Lapisan tersebut
berbentuk perangkap yang berisi batuan-batuan yang memiliki sifat-sifat tertentu,
dan biasanya tergantung pada komposisi, temperatur dan tekanan tempat
terjadi-nya akumulasi hidrokarbon didalam reservoirterjadi-nya. Tekanan yang dimiliki reservoir
akan sangat berpengaruh terhadap pendesakan minyak, oleh karena dilakukan
tek-nik -tektek-nik tertentu untuk mempertahankan tekanan sehingga minyak bumi yang
terperangkap dapat diproduksi secara maksimal. Biasanya didalam reservoir
terda-pat lebih dari satu fase fluida yaitu minyak, air dan gas.
1.1.1.1 Porositas
Porositas didefinisikan sebagai perbandingan antara volume pori batuan
terha-dap total volume batuan. Ukuran porositas suatu batuan akan menentukan kapasitas
penyimpanan fluida didalam reservoir. Porositas terbagi dua yaitu
1 prorositas absolut merupakan perbandingan antara rongga pori yang saling
berhubungan dengan volume total batuan
2 porositas efektif merupakan perbandingan antara rongga pori yang saling
secara matematis dapat ditulis
φ = Vb −Vs Vb
dimanaφ= porositas,Vb= volume total batuan danVs= volume bersih total batuan
1.1.1.2 Permeabilitas
Permeabilitas merupakan kemampauan batuan dalam menyalurkan fluida.
Apa-bila media berpori tidak ssaling berhubungan, maka batuan tersebut tidak memiliki
permeabilitas. Oleh karenanya diketahui bahwa terdapat hubungan antara
permea-bilitas dengan porositas efektif. yang terbagi tiga yaitu
1 permeabilitas absolut : kemampuan batuan dalam medistribusikan semua fasa
fluida yang dikandungnya,
2 permeabilitas efektif : kemampuan batuan dalam mendistribusikan salah satu
fasa fluida jika batuan tersebut mengandung lebih dari satu fasa fluida,
3 permeabilitas relatif : perbandingan antara permebilitas efektif dan absolut
yang dipengaruhi oleh sejarah saturasi dan wettabilitas.
Sekitar tahun 1856, Henry Darcy seorang ahli hidrologi dari Prancis mempelajari
aliran air yang melewati suatu lapisan batu pasir, dimana hasil temuannya
diformu-lasikan kedalam hukum aliran fluida yang disebut hukum Darcy yang
direpresenta-sikan oleh
Q= kA µ ×
dP dL
dimanaQ = laju alir (cc/sec),k = permeabilitas (darcy), µ =viskositas (cp), A =
luas penampang (cm2
), dan dPdL = gradien tekanan (atm/cm). Persamaan Darcy
berlaku pada kondisi
• alirannya mantap (steady state),
• kondisi isothermal,
• formasinya homogen dan arah alirannya horizontal,
• fluidanyaincompressible.
1.1.1.3 Saturasi
Saturasi didefinisikan sebagai perbandingana antara volume pori-pori
batu-an ybatu-ang berisi fluida formasi terhadap total volume pori-pori batubatu-an atau jumlah
kejenuhan fluida dalam reservoir persatuan volume pori. Karena dianggap bahwa
dalam reservoir terdapat fluida air dan minyak, maka perhitungan saturasi terbagi
dua yaitu
• saturasi minyak
So =
volume pori batuan yang diisi oleh minyak volume pori total ,
• saturasi air
Sw =
volume pori batuan yang diisi oleh air volume pori total ,
karena pori-pori batuan berisi air dan minyak, maka berlaku hubunganSo+Sw = 1.
1.1.1.4 Pembasahan Batuan (Wettability)
Wettabilitas merupakan kemampuan fluida dalam membasahi batuan atau
ke-cenderungan fluida untuk menyebar atau melekat ke permukaan batuan. Jika dua
fluida ditempatkan pada permukaan zat padat, maka salah satu fasa akan tertarik
lebih kuat dibanding fasa yang lain sehingga cenderung akan membasahi zat
pa-dat. Wettabilitas memiliki peranan yang cukup penting karena akan menimbulkan
tekanan kapiler akibat dari gaya tarik - menarik (adhesi) dari kedua zat tersebut,
sehingga akan mendorong minyak agar dapat bergerak. Faktor yang mempengaruhi
• jenis mineral yang terkandung dalam batuan,
• ukuran butir batuan, semakin halus butiran batuan maka semakin besar gaya
adhesi yang terjadi,
• jenis kandungan hidrokarbon yang terdapat didalam minyak mentah.
Pada reservoir, air biasa cenderung membasahi batuan dan minyak tidak
mempu-nyai gaya tarik dengan batuan sehingga minyak akan lebih mudah bergerak
(mega-lir).
1.1.1.5 Tekanan Kapiler
Tekanan kapiler dapat didefinisikan sebagai perbedaan tekanan antara fluida
yang dapat membasahi batuan dengan fluida yang tidak dapat membasahi batuan.
Hubungan tekanan kapiler didalam rongga pori batuan dapat digambar oleh
kena-ikan air pada pipa yang memiliki diameter sangat kecil, hal ini diakibatkan adanya
gaya adhesi pada permukaan tabung. Sehingga tekanan kapiler merupakan
kecen-derungan rongga pori batuan untuk mengisi setiap pori batuan dengan fluida yang
bersifat membasahi.
1.1.1.6 Mobility Ratio
Besarnya kemampuan fluida untuk bergerak sebagai fungsi dari permeabilitas
relatif terhadap viskositas dikenal dengan sebutan mobilitas. Semakin tinggi
mobili-tas fluida, akan semakin mudah bagi fluida untuk bergerak melewati media berpori.
Dalam proses injeksi perbandingan antar kemampuan bergerak fluida pendesak dan
fuida yang didesak sangat perlu diperhitungkan agar dapat memperkirakan efisiensi
pendesakan yang terjadi. Mobility ratio dapat ditunjukkan sebagai berikut
λ= kw/µw ko/µo
diketahui bahwaλ=mobilitas fluida,kw =permeabilitas air danko =permeabilitas
minyak. Dalam waterflood yang bertindak sebagai pendesak adalah air yang
Adapun sifat yang dimiliki fluida diantaranya
1.1.1.7 Viskositas (Kekentalan)
Viskositas adalah ketahanan internal suatu fluida untuk mengalir. Besar
ni-lai suatu viskositas dipengaruhi oleh temperatur dimana nini-lai kenaikan temperatur
akan menurunkan nilai viskositas suatu fluida. Pada permasalahan waterflooding
terdapat hubungan viskositas dari kedua fluida yang disebut viskositas relatif yang
didefinisikan sebagai perbandingan antara viskositas fluida yang didorong (minyak)
terhadap viskositas fluida pendorong (air).
1.1.1.8 Massa jenis (Density)
massa jenis disebut juga kerapatan suatu benda yang didefinisikan sebagai
perbandingan massa terhadap volum.
Water floodingmerupakan suatu permasalahan yang berkaitan dengan fluida
yang dideskripsikan dengan persamaan differensial parsial dimana akan sangat
su-lit jika diselesaikan secara anasu-litis, sehingga harus diselesaikan dengan melakukan
suatu pendekatan numerik. Oleh karena itu, perlu bagi kita untuk melakukan suatu
analisa numerik. Analisa numerik adalah analisa mempergunakan algoritma dari
metode numerik, sedangkan Metode numerik adalah teknik yang digunakan untuk
memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi
perhitungan atau aritmatika biasa (Choiron).
Penyelesaian suatu persoalan matematika dengan metode numerik umumnya
dapat diselesaikan dengan lebih dari satu metode, sehingga dipilih metode terbaik
yang dapat menghasilkan penyelesaian yang efisien dan efektif serta tidak
meng-hasilkan galat yang besar. Dalam hal ini, metode yang dilakukan adalah metode
volume hingga. Metode volume hingga merupakan suatu metode untuk
menyelesa-ikan persamaan differensial parsial dengan melakukan pendekatan numerik dimana
solusinya akan medekati nilai analitis, nilai ataupun tingkat akurasi yang dihasilkan
Dari uraian di atas, teknikwater floodingmemiliki beberapa keunggulan dari
sisi ekonomis dan efisiensi kerja, namun pada kenyataannya teknik ini hanya
mam-pu meningkatkan 10-20% dari keseluruhan minyak bumi yang terdapat di
reservo-ir. Karena kebutuhan minyak bumi semakin meningkat, tentunya harus ada usaha
yang dilakukan dalam meningkatkan produksi minyak secara lebih maksimal. Hal
ini memotivasi penemuanEnhanced Oil Recovery(EOR) yang merupakantertiary
recovery atau metode tersier, dimana metode ini dapat mengangkat minyak bumi
sekitar 30-60% dari reservoir. EOR terbagi atas 3 teknik yaitu injeksi kimia, injeksi
gas tercampur dan injeksi panas (Usman, 2011).
Penulis tidak akan membahas secara detail terkait metode EOR
dikarena-kan tulisan ini hanya adikarena-kan membahas teknik water flooding dalam pengangkatan
minyak bumi dari reservoir. Persoalanwaterflooding pada dasarnya digambarkan
oleh persamaaan Buckley-Leverett dengan efek equilibrium, adapun pada tulisan
ini akan dilakukan perhitungan persamaaan Buckley-Leverett dengan memasukkan
efek nonequilibrium dan permeabilitas relatif yang direpresentasikan oleh
persama-an Barenblatt.
Persamaan Buckley-Leverett dan Barenblatt merupakan suatu pasangan
per-samaan diferensial parsial dan persamaaan diferesial biasa yang dapat
diselesai-kan dengan menggunadiselesai-kan metode volume hingga. Oleh karena itu, tulisan ini
akan menguraikan permasalahan tersebut dengan mencari solusi numerik
persama-an Buckley-Leverett ypersama-ang paspersama-angkpersama-an dengpersama-an persamapersama-an Barenblaat.
1.2 Perumusan Masalah
Rumusan masalah yang akan diteliti adalah bagaimana merumuskan secara
nume-rik teknikwater floodingdengan mengggunakan metode volume hingga.
1.3 Batasan Masalah
flooding menggunakan metode volume hingga dengan mengasumsikan porositas,
viscositas dan permeabilitas adalah konstan
1.4 Tujuan Penelitian
Penelitian ini bertujuan untuk melakukan analisis numerik pada persoalan water
floodingdengan mengimplementasikan metode volume hingga sehingga dapat
di-ketahui waktu injeksi dan laju produksi dari hasil perhitungan yang dilakukan.
1.5 Manfaat Penelitian
Manfaat dari penelitian ini yaitu memberikan suatu gambaran mengenai teknik
wa-ter flooding pada proses pengangkatan minyak dari reservoir yang dapat
dijadik-an suatu pertimbdijadik-angdijadik-an ataupun acudijadik-an dalam melakukdijadik-an kinerja lapdijadik-angdijadik-an dibiddijadik-ang
produksi minyak bumi.
1.6 Metodologi Penelitian
Untuk melakukan analisis numerik pada teknik water flooding maka dilakukan
langkah-langkah berikut:
1. Mengumpulkan berbagai informasi terkait tentangwater floodingdan Metode
Volume Hingga,
2. Terdapat suatu persamaan diferensial parsial hiperbolik orde satu dari model
Buckley-Leverett yang direpresentasikan oleh
∂tS+∂xvf(σ) = 0
yang dipasangkan oleh persamaan diferensial biasa atau persamaan evolusi
σ−S =τ ∂tS
kondisi awal yang diberikan
S =S0(x) padat = 0
σ0+τ ∂xf(σ0) = S0(x)
permasalahan diatas merupakan gambaran dari dua-fase aliran dengan
meng-gunakan model Barenblatt dengan mengabaikan tekanan kapler sehingga
le-bih berfokus pada efek dinamik dalan permeabilitas relatif hal tersebut
di-gambarkan oleh persamaan evolusi diatas,
3. Lakukan simulasi numerik dengan menggunakan pendekatan volume hingga.
Oleh pendekatan ini, dilakukan diskritisasi sepanjang n sehingga
mengha-silkan
F :R2n →R2n
dimana
F(U) =0
danU merupakan vektor yang berisikanSei,ndaneσi,n,
4. Pada kasus diatas, fluks merupakan fungsi saturasi efektif, bukan saturasi
ak-tual. Sehingga dalam penyelesaiannya digunakan iterasi Newton untuk solusi
sistem aljabar,
5. Menggunakan bantuan software MATLAB untuk melakukan perhitungan
METODE VOLUME HINGGA
ABSTRAK
Simulasiwaterfloodingbiasanya dilakukan dengan menggunakan persamaan
Buck-ley-Leverett (BL), yaitu persamaan transportasi pada fluida dinamik yang
meng-gambarkan dua fase aliran fluida yang immisciblepada media berpori. Dalam hal
ini, penulis memfokuskan diri pada efek nonekuilibrium dalam permeabilitas relatif dengan mengabaikan tekanan kapiler yang dapat digambarkan oleh model Baren-blatt yaitu model dari tekanan kapiler nonekuilibrium dan permeabilitas relatif. Pa-da kasus ini, flux Pa-dari setiap fase paPa-da persamaan BL tiPa-dak bergantung paPa-da saturasi saat ini saja (saturasi aktual), akan tetapi juga bergantung pada saturasi efektif (sa-turasi yang akan datang). Sehingga pada penyelesaiannya diperlukan persamaan evolusi yang diajukan oleh Barenblatt. Tulisan ini merupakan kajian ulang dari apa yang telah dilakukan oleh Juanes. Namun, penulis melakukan diskritisasi dengan
menggunakanvertex centered finite volumepada hukum kekekalan masa
(persama-an diferensial parsial) d(persama-an persama(persama-an evolusi (persama(persama-an diferensial biasa).
ABSTRACT
Waterflooding simulation is usually done using Buckley-Leverett (BL) equation, which is the transport equation on dynamic fluid that describe two phase flow im-miscible in porous media. In this case, we focus on nonequilibrium effect in the relative permeability with neglible capillary pressure, described by Barenblatt mo-del, which includes both nonequilibrium capillary pressure and relative permeabili-ty. In this case, flux fluid of each phase on BL equation does not only depend on the current saturation (actual saturation) but also on the so called effective saturation. This paper is a review of what has been done by Juanes. However, the numerical discretization employs vertex centered finite volume for conservation laws (partial differential equation) and evolution relation (ordinary differential equation).
METODE VOLUME HINGGA
SKRIPSI
NUR AISYAH
110803010
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
METODE VOLUME HINGGA
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai
gelar Sarjana Sains
NUR AISYAH
110803010
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
Judul : Analisis Numerik untuk Persoalan Water Flo-oding dengan Menggunakan Metode Volume Hingga
Kategori : SKRIPSI
Nama : Nur Aisyah
Nomor Induk Mahasiswa : 110803010
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETA-HUAN ALAM
Medan, Agustus 2015
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dr. Esther S.M. Nababan, M.Sc Dr. Mardiningsih, M.Si NIP. 19610318 198711 2 001 NIP. 19630405 198811 2 001
Diketahui oleh :
Departemen Matematika FMIPA USU
Ketua,
Prof. Dr. Tulus, M.Si
ANALISIS NUMERIK UNTUK PERSOALAN WATER FLOODING
DENGAN MENGGUNAKAN METODE VOLUME HINGGA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa
kutipan dan ringkasan penting yang masing-masing disebutkan sumbernya.
Medan, Agustus 2015
NUR AISYAH