Model Pemrograman Kuadratik Dalam Pembagian Daerah Pemilihan Umum .

MODEL PEMROGRAMAN KUADRATIK DALAM PEMBAGIAN

DAERAH PEMILIHAN UMUM

SKRIPSI

HERYANTO SEMBIRING

050803054

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MODEL PEMROGRAMAN KUADRATIK DALAM PEMBAGIAN

DAERAH PEMILIHAN UMUM

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

HERYANTO SEMBIRING

050803054

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : MODEL PEMROGRAMAN KUADRATIK DALAM

PEMBAGIAN DAERAH PEMILIHAN UMUM

Kategori : SKRIPSI

Nama : HERYANTO SEMBIRING

Nomor Induk Mahasiswa : 050803054

Program Studi : SARJANA (S-1) MATEMATIKA

Diluluskan di Medan, Oktober 2009

Komisi Pembimbing:

Pembimbing II Pembimbing I

Drs. Liling Perangin - angin, M.Si Prof. Dr. Herman Mawengkang NIP. 19470714 198403 1 001 NIP. 19461128 197403 1 001

Diketahui/Disetujui oleh:

Departemen Matematika FMIPA USU

PERNYATAAN

MODEL PEMROGRAMAN KUADRATIK DALAM PEMBAGIAN DAERAH PEMILIHAN UMUM

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan langsung yang masing-masing disebutkan sumbernya.

Medan, Oktober 2009

PENGHARGAAN

Rasa syukur dan terimakasih penulis panjatkan kehadirat Tuhan Yang Maha Esa atas berkat dan karuniaNya penulis dapat menyelesaikan skripsi ini.

Penulis menyadari bahwa penyusunan skripsi ini mendapat dukungan dan bantuan dari berbagai pihak. Oleh karena itu, saya mengucapkan terimakasih kepada:

- Bapak Prof. Dr. Herman Mawengkang, selaku Dosen Pembimbing I dan Bapak Drs. Liling Perangin - angin, M.Si , selaku Dosen Pembimbing II yang telah mendidik dan memberikan arahan dalam penyususnan skripsi ini.

- Bapak Drs. H. Haludin Panjaitan dan Ibu Dra. Elly Rosmaini, M.Si selaku dosen pembanding yang senantiasa memberikan saran dan dorongan dalam penyusunan skripsi ini.

- Bapak Dr. Saib Suwilo, M.Sc selaku ketua Departemen Matematika FMIPA USU.

- Bapak Prof. Dr. Eddy Marlyanto M.Sc selaku Dekan FMIPA USU.

- Pegawai Badan Pusat Statistik Sumatera Utara.

- Orang tua tercinta N. Sembiring dan R. Nainggolan, yang senantiasa mendukung penulis dalam doa dan selalu memberikan dorongan baik secara moril dan material hingga terselesainya skripsi ini.

- Semua pihak keluarga yang mendukung

- Teman-teman math ’05 dan ‘07 USU dan

Penulis menyadari bahwa skripsi ini masih banyak memiliki kekurangan dan kesilapan, oleh karena itu penulis sangat mengharapkan saran yang membangun dari semua pihak pembaca demi kesempurnaan skripsi ini.

Akhir kata penulis mengucapkan terimakasih dengan harapan semoga skripsi ini bermanfaat bagi semua pihak yang membaca.

ABSTRAK

ABSTRACT

2.7 Harga Eigen 19 2.8 Bentuk Kuadratik 20 2.9 Bentuk Umum Pemrograman kuadratik 21 2.10 Masalah Pembagian Graph Berbobot Ganda 20

BAB III PEMBAHASAN

3.1 Model Pemrograman kuadratik Dalam Pembagian Daerah

Pemilihan Umum 24

3.2 Proses Penggambaran Batas – batas Daerah Pemilihan 25

BAB IV KESIMPULAN DAN SARAN

4.1 Kesimpulan 35

4.2 Saran 35

DAFTAR PUSTAKA

LAMPIRAN

DAFTAR GAMBAR

Halaman

GAMBAR 2.1. Himpunan Konvek 6

GAMBAR 2.2. Fungsi Konvek 7

GAMBAR 2.3. Fungsi Konkaf 7

GAMBAR 2.4. Konstruksi untuk bukti 9

GAMBAR 2.5. Graph dengan tujuh sisi dan lima titik 11

GAMBAR 2.6. Graph tak berbobot 11

GAMBAR 2.7. Graph berbobot 12

GAMBAR 2.8. Graph berarah 13

GAMBAR 2.9. Graph berbobot dan berarah 13

GAMBAR 2.10. Graph tempat wisata scenic valley 14

GAMBAR 2.11. Contoh denah kabupaten serta graph yang diekstrak dari denah tersebut 20

DAFTAR TABEL

Halaman

TABEL 1. Jumlah penduduk di lima kabupaten di provinsi Sumatera

Utara tahun 2007 24 TABEL 2. Harga peubah yang diperoleh dari hasil LINDO 30

LAMPIRAN

ABSTRAK

ABSTRACT

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Daerah - daerah pemilihan sangat berperan penting didalam suatu pemilihan umum, khususnya ketika suatu aturan pemungutan suara diberlakukan, karena hal ini turut serta didalam penentuan dari suara ke tempat duduk didalam parlemen. Sebagai contoh, menurut aturan perundang-undangan Amerika Serikat, banyaknya tempat duduk dari masing-masing provinsi untuk Dewan Perwakilan (biasanya sama dengan banyaknya daerah-daerah pemilihan di masing-masing provinsi) bergantung terhadap ukuran relatif dari populasi provinsi dibandingkan terhadap provinsi lain. Setelah banyaknya tempat duduk ditetapkan di setiap provinsi, tugas dari penggambaran daerah-daerah pemilihan yang baru secara umum ditunjukkan oleh setiap badan pembuat undang - undang provinsi.

1.2 Perumusan Permasalahan

Perumusan permasalahan dari penelitian ini adalah memodelkan permasalahan pembagian wilayah secara politik dengan kendala-kendala yang terdapat didalamnya untuk menghasilkan solusi optimal yang mana permasalahan tersebut untuk memperoleh daerah pembagian yang lebih dapat diterima dan kemudian diselesaikan dengan menggunakan perangkat lunak LINDO atau LINGO.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menyelesaikan permasalahan pembagian wilayah dengan menggunakan metode pemograman kuadratik untuk menghasilkan solusi yang lebih baik.

1.4 Kontribusi Penelitian

Adapun kontribusi dari penelitian ini adalah untuk menambah wawasan para pembaca pada umumnya dan khususnya untuk membantu pemerintah, partai-partai politik maupun pihak-pihak yang terkait menyangkut permasalahan pembagian wilayah untuk kepentingan politik agar mencegah terjadinya “gerrymandering“ atau pemberian kesempatan secara curang terhadap suatu partai politik, keadilan, sehingga hasil pembagian wilayah dapat mengurangi keluhan-keluhan dan kemarahan-kemarahan dari orang-orang yang memiliki hak dalam memilih.

1.5 Tinjauan Pustaka

Zhenping li, Rui-Sheng Wang dan Yong Wang, journal 2007 sebagai

rujukan utama dalam penulisan ini. Sebenarnya terdapat beberapa pendekatan-pendekatan secara matematik dan numerik untuk permasalahan ini. Dalam tulisan tersebut permasalahan pembagian wilayah pemilihan umum dirumuskan sebagai

3. Dij menyatakan panjang dari lintasan terpendek antara titik vi ke vj

Adapun kesatuan secara geografi disini berarti bahwa setiap unit pada suatu daerah pemilihan terhubung satu sama lain melalui unit-unit yang juga terdapat dalam daerah pemilihan tersebut. Kesatuan secara geografi adalah salah satu kendala yang membuat permasalahan daerah pemilihan umum untuk parlemen menjadi agak rumit. Dalam jurnal ini disebutkan bahwa kesetaraan populasi sendiri kadang-kadang mengarahkan pada masalah kesatuan dan keteraturan geografi yang mengakibatkan

. 4. q menyatakan banyaknya daerah pemilihan yang ditetapkan.

daerah pemilihan dengan bentuk yang tidak alami dan juga disebutkan bahwa ada banyak cara untuk mendefinisikan keteraturan secara geografi, akan tetapi belum ada definisi secara umum yang dapat diterima.

Drawing political districts by heuristics combine with weighted voronoi

regions. Jurnal ini bertujuan untuk memperoleh daerah-daerah yang teratur dan

seimbang dalam pembagiannya dan hasilnya telah diuji didalam kehidupan nyata dan telah dibandingkan dengan heuristic-heuristic yang lain seperti pada permasalahan pembagian wilayah di negara Italia pada tahun 1996.

1.6 Metode Penelitian

Tulisan ini bersifat literatur dan melakukan pengumpulan data riset. Dalam penelitian ini metode yang digunakan adalah metode dokumentasi. Metode dokumentasi adalah metode pengumpulan data yang diperlukan dalam permasalahan yang menyangkut :

- Data lima kabupaten di Sumatera Utara tahun 2005.

- Data jarak antar kabupaten di Sumatera Utara yang berdekatan.

Adapun tulisan ini disusun dengan langkah – langkah sebagai berikut:

Langkah pertama: Mengonsepsikan suatu graph H dari suatu daerah atau provinsi yang diberikan, yang mana setiap titik dari H mewakili suatu

daerah yang lebih kecil dari H atau dapat disebut sebagai suatu kabupaten dan satu sisi yang menghubungkan titik u dan

v yang mengindikasikan bahwa titik u dan v adalah titik yang berdekatan pada graph H.

Langkah ketiga : Merumuskan permasalahan yang dinyatakan oleh langkah

ketiga kedalam model pemrograman kuadratik dengan data - data yang diperoleh dari hasil pengimpulan data riset.

Langkah keempat : Menyelesaikan permasalahan oleh langkah keempat dengan menggunakan perangkat lunak LINDO ataupu LINGO.

Langkah kelima : Mengambil kesimpulan.

BAB 2

LANDASAN TEORI

2.1 Himpunan Konvek

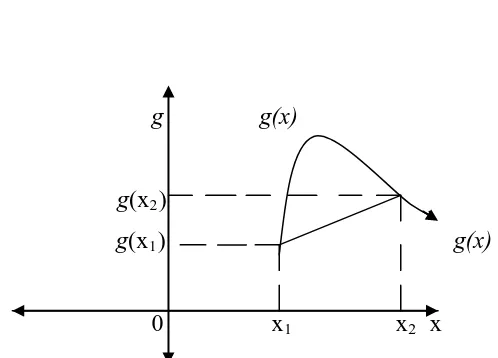
Definisi 2.1.1. Suatu himpunan C di Rn dikatakan konvek jika untuk setiap x, y ∈ C dan setiap bilangan real α, 0 < α < 1, titik αx + (1 - α)y ∈ C atau garis penghubung antara dua titik sebarang di himpunan tersebut masih terletak di dalam himpunan tersebut.

Berikut adalah contoh suatu himpunan konvek:

•x2 •x1

GAMBAR 2.1 Himpunan Konvek

2.2 Fungsi Konvek

Definisi 2.2.1. Suatu fungsi ƒ dikatakan konvek jika untuk setiap x1, x2

ƒ(αx + (1 - α)y) ≤αƒ(x) + (1- α)ƒ(y)

Definisi 2.2.2. Suatu fungsi g dikatakan konkaf jika fungsi ƒ = - g

Teorema 2.2.2. Anggap ƒ adalah suatu fungsi kontinu dan dapat diturunkan sekali. Jika ƒ adalah suatu fungsi konvek yang terdefinisi pada suatu himpunan konvek C

Bukti. Fungsi ƒ adalah fungsi konvek. Untuk semua α, 0 ≤ α ≤ 1, ƒ(αx + (1 - α)y) ≤αƒ(x) + (1- α)ƒ( y) atau ƒ(αx + (1 - α)y) ≤αƒ(x) - αƒ( y) +ƒ( y)

ƒ(αx + (1 - α)y) ≤α[ƒ(x) - ƒ( y)] +ƒ( y) ƒ(αx + y - αy) ≤α[ƒ(x) - ƒ( y)] +ƒ( y) ƒ(y + α(x - y)) ≤α[ƒ(x) - ƒ( y)] +ƒ( y) untuk 0 < α≤ 1, ≤ƒ(x) - ƒ( y) dan

jika α→ 0 akan diperoleh ƒ(y) ≥ƒ(x) + ∇ƒ(x)(y – x) untuk semua x, y ∈ C. ฀

2.3 Syarat Perlu Orde Pertama

2.3.1 Definisi Titik Minimum Relatif dan Titik Minimum Global

Definisi 2.3.1.1. Suatu titik x* dinamakan sebagai titik minimum relatif dari fungsi ƒ di C jika terdapat ε > 0 sehingga ƒ(x) ≥ƒ(x*) untuk semua x ∈ C dalam jarak ε dari x*.

Definisi 2.3.1.2. Suatu titik x* dinamakan sebagai titik minimum global dari fungsi ƒ di C jika ƒ(x) ≥ƒ(x*) untuk semua x ∈ C.

2.3.2 Arah layak

Untuk menurunkan syarat perlu orde pertama oleh titik minimum relatif, ide dasarnya adalah memperhatikan pergerakan titik tersebut dengan diberikan beberapa arah dan sepanjang arah yang diberikan fungsi tujuan dapat dipandang sebagai fungsi dari satu variabel. Dengan diberikan diberikan x ∈ C dan diberi d sebagai arah layak di x dan jika terdapat suatu > 0 sehingga x + αd ∈ C untuk semua 0 ≤α≤ .

Teorema 2.3.2.1 (Syarat perlu orde pertama). Anggap C adalah himpunan konvek dan fungsi ƒ∈ C1 terdefinisi di C. Jika x* adalah titik minimum relatif dari ƒ

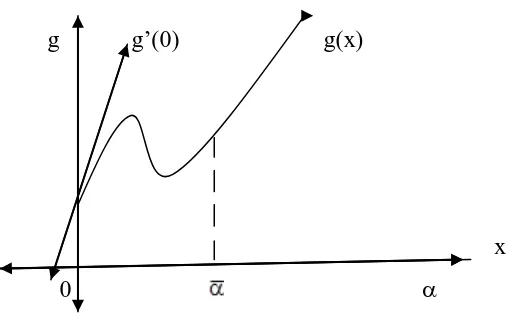
Bukti. Untuk sebarang α, 0 ≤α≤ , titik x(α) = x* + αd ∈ C juga definisikan fungsi g(α) = ƒ(x(α)), maka fungsi g memiliki minimum relatif di α = 0.

Dari kalkulus biasa

g(α) – g(0) = g’(0)α + o(α) (4)

Jika g’(0) < 0 maka untuk harga α yang cukup kecil α > 0, sisi kanan dari (4) adalah negatif sehingga g(α) – g(0) < 0. Hal ini kontradiksi dengan minimal dari g(0).

Dengan demikian g’(0) = ∇ƒ(x*

)d ≥ 0. ฀

g g’(0) g(x)

x 0 α

GAMBAR 2.4. Konstruksi untuk bukti

Teorema 2.3.2.2. Anggap fungsi ƒ adalah fungsi kontinu dan dapat diturunkan dua kali. Jika fungsi ƒ adalah konvek didalam daerah definisi himpunan

konvek dan berisi satu titik interior jika dan hanya jika Hessian matriks H dari ƒ

adalah semidefinit positif diseluruh C

Bukti. Dari teorema Taylor, ƒ(y) = ƒ(x) + ∇ƒ(x)(y – x) + (y – x)TH(x + α(y –

ƒ(y) ≥ƒ(x) + ∇ƒ(x)(y – x) (5)

dari teorema 2.2.2 yang mengakibatkan fungsi ƒ adalah konvek. Sekarang anggap Hessian tidak semidefinit positif di beberapa titik x ∈ C. Anggap y ∈ C sehingga (y – x)TH(x)(y – x) < 0 yang mana y dapat dipilih sehingga untuk semua α, 0 ≤α≤ 1, (y – x)TH(x + α(y – x))(y – x) < 0. Dalam hal ini menurut teorema Taylor, (5) tidak terpenuhi dan mengakibatkan fungsi ƒ tidak konvek. ฀

Dari teorema 2.3.1 diperoleh ƒ(y) ≥ ƒ(x) + ∇ƒ(x)(y – x). Anggap terdapat

suatu titik x∗ sehingga untuk semua y ∈ C berlaku ∇ƒ(x∗)(y – x∗) ≥ 0 maka ƒ(y) ≥ ƒ(x∗) + ∇ƒ(x∗)(y – x∗) ≥ ƒ (x∗) dalam hal ini fungsi ƒ memiliki minimum

global. ∇ƒ(x∗)(y – x∗) ≥ 0 oleh teorema syarat perlu titik minimum relatif dapat bahwa

y – x∗ = d.

Jika suatu fungsi ƒ yang kontinu dan dapat diturunkan dua kali maka terdapat

suatu α, 0 ≤α≤ 1 sehingga ƒ(y) = ƒ(x) + ∇ƒ(x)(y – x) + (y – x)TH(αx + (1 - α)y)(y –

x) disebut sebagai teorema Taylor orde dua.

Jika fungsi ƒ adalah fungsi yang kontinu dan dapat diturunkan dua kali maka matriks Hessi dari ƒ di x adalah matriks n x n dan dinotasikan dengan ∇2ƒ(x) atau H(x) sebagai

H(x) =

Karena = sehingga terlihat bahwa matriks Hessi adalah simetri dan

2.4 Graph

Definisi 2.4.1. Suatu graph G adalah suatu himpunan terbatas, takkosong dari himpunan vertices atau titik V beserta dengan sehimpunan edge atau sisi E. Suatu graph G dinotasikan dengan G = (V,E).

Berikut adalah contoh gambar graph G.

• v1 e1 •v2

e2 e3 •v5 e4 e5 e6 •v3 v4• e7

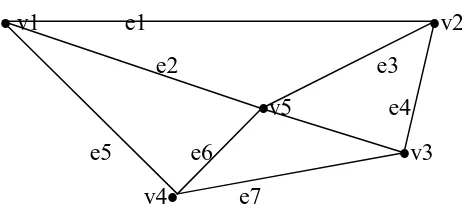
GAMBAR 2.5. Graph dengan tujuh sisi dan lima titik

Dari gambar graph G diatas terdapat lima titik dan tujuh sisi yaitu V = {v1, v2, v3, v4, v5}dan E = {e1, e2, e3, e4, e5, e6, e7

1• •2

}

Definisi 2.4.2. Suatu graph G ditinjau berdasarkan bobotnya terdiri atas dua yaitu:

1. Graph berbobot yaitu graph yang memiliki nilai di sisinya dan 2. Graph tak berbobot yaitu graph yang tidak memiliki nilai di sisinya.

Berikut adalah graph tak berbobot

•6 3• •5

Berikut adalah graph berbobot:

Definisi 2.4.3. Suatu graph G dibagi atas dua berdasarkan arahnya yaitu 1. Graph berarah yaitu graph yang memiliki arah pada sisi-sisinya dan

2. Graph tak berarah yaitu graph yang tak memiliki arah pada sisi-sisinya.

Dari gambar 2.6 dan 2.7 diatas merupakan graph tak berarah sebab tidak didapati arah pada sisi-sisinya.

1. Graph berbobot dan berarah yaitu graph yang memiliki arah dan bobot pada sisi-sisinya dan

2. Graph berbobot dan tak berarah yaitu graph yang memiliki bobot pada sisinya dan tidak memiliki arah pada sisi-sisinya.

Dari gambar 2.7 diatas merupakan graph berbobot dan tak berarah sebab terdapat bobot pada sisinya tetapi tidak memiliki arah pada sisinya.

Berikut adalah contoh graph berbobot dan berarah:

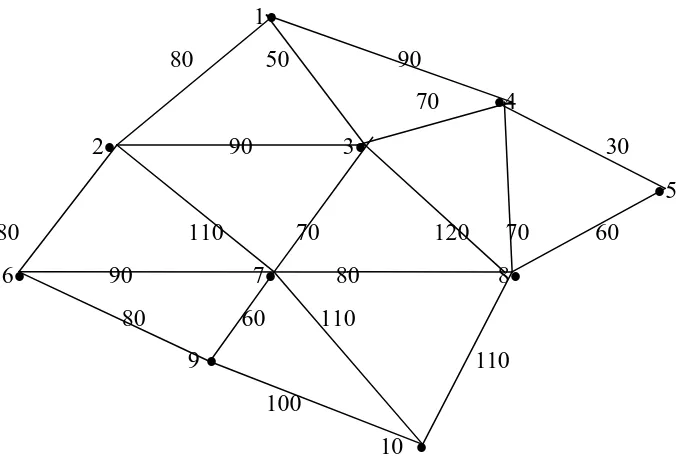
Langkah 2: Anggap u adalah suatu titik di T yang mana L(u) adalah minimum dan

Solusi.

Iterasi 10 u = j berhenti

sehingga jarak terpendek dari 1 ke 10 adalah 230 Km.

2.6 Matriks

2.6.1 Matriks secara umum

Definisi 2.6.1 (Definisi umum dari matriks). Suatu matriks adalah himpunan dari elemen-elemen yang disusun berdasarkan baris dan kolom dalam bentuk bujur sangkar atau persegi panjang yang diberi kurung siku atau kurung biasa. Suatu matriks A dapat dinotasikan sebagai berikut:

ij menyatakan elemen pada baris ke-i dan kolom ke-j. Dan matriks diatas adalah matriks dengan m baris dan n kolom.

2.6.2 Mariks Identitas

In =

2.6.3 Mariks Simetri

Definisi 2.6.3.1. Suatu matriks persegi A dikatakan simetri jika

A = AT .

Contoh 2.6.3.1.1

Jika diketahui matriks A

A = dan AT =

Terlihat bahwa matriks A memiliki angka-angka yang sama pada baris dan kolomya, sehingga matriks A adalah matriks simetri.

2.6.4 Mariks Adjency

Definisi 2.6.4.1. Matriks adjency A = (aij

1 jika v

) dari suatu graph G dengan p titik adalah suatu matriks simetrik ukuran p x p yang mana

i dan vj berdekatan dan ai,j =

Contoh 2.6.4.1

Dari gambar 2.7 sebelumnya maka matriks adjency dari graph tersebut adalah

Jelas dari matriks diatas bahwa matriks tersebut adalah matriks simetri karena matriks tersebut sama dengan transposnya.

2.7 Harga Eigen .

Definisi 2.7.1. Jika A adalah matriks berukuran n x n, maka suatu vektor tak nol x di Rn dinamakan vektor eigen dari A jika Ax adalah perkalian skalar dari x yaitu Ax = λx untuk beberapa skalar λ. Skalar λ dinamakan harga eigen dari A dan x dikatakan vektor eigen terhadap λ. Untuk memperoleh harga eigen dari matriks A

berukuran n x n adalah dengan cara sebagai berikut: Ax = λIx atau ekuivalen dengan (λI – A)x = 0. dengan mencari determinan dari (λI – A)x = 0 atau det (λI – A) = 0 akan memberikan solusi bagi λ. (λI – A) = 0 dinamakan persamaan karakteristik sedangkan det (λI – A) dinamakan polinomial karakteristik.

Contoh 2.7.1

Tentukan harga eigen dari matriks

Solusi.

Karena

λI – A = λ -

polinomial karakteristik dari A adalah

det (λI – A) = det = λ2 - 3λ + 2

dan persamaan karakteristik dari A adalah

λ2

- 3λ + 2 = 0.

Serta solusi dari persamaan ini adalah λ = 1 dan λ = 2 yang merupakan harga eigen dari A.

2.8 Bentuk Kuadratik

Definisi 2.8.1. Suatu bentuk kuadratik dalam x1, x2, ..., xn adalah suatu pernyataan yang dapat ditulis sebagai

[x1 x2 ... xn] A

yang mana A adalah matriks simetri n x n.

ditulis dalam bentuk perkalian keluar adalah

xTAx = a11 + a22 + ... + ann + .

Berikut adalah contoh bentuk kuadratik dalam x dan y :

2x2 + 6xy – 7y2 = [x y]

Definisi 2.8.2. Suatu bentuk kuadratik xTAx adalah semidefinit positif jika xTAx ≥ 0 untuk semua harga x.

Teorema 2.8.3. Jika A adalah matriks simetri maka matriks A adalah semidefinit positif jika harga eigen dari A adalah nonnegatif.

Bukti. Asumsikan bahwa matriks A adalah semidefinit postif. Anggap λ adalah harga eigen yang berkenaan terhadap vektor eigen x, maka 0 ≤ xTAx = xTλx = λxTx = λ|| x ||2. Karena || x ||2 > 0 maka λ positif. ฀

2.9 Bentuk Umum Pemrograman Kuadratik

Definisi 2.9.1. Bentuk umum pemrograman kuadratik dapat dituliskan sebagai berikut:

Minimumkan xTAx + xTc

Dengan kendala x = bi, i ∈ E x ≤ bi

yang mana E dan I adalah himpunan-himpunan indeks untuk kendala-kendala persamaan dan kendala-kendala pertidaksamaan. Matriks A adalah matriks semidefinit positif. Jika A adalah matriks semidefinit positif, maka fungsi ƒ adalah

2.10 Masalah Pembagian Graph Berbobot Ganda

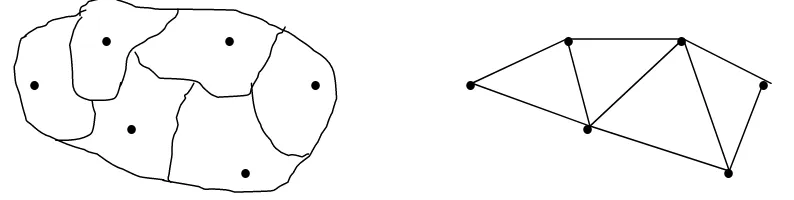
Masalah pembagian wilayah dapat dirumuskan sebagai suatu partisi graph berbobot ganda dan dapat dikonversi kedalam model pemrograman kuadratik, yang mana n kabupaten dari suatu provinsi dibagi kedalam q daerah pemilihan sehingga topologi dari masing-masing daerah pemilihan secara geografi adalah teratur dan setiap daerah memiliki ukuran populasi yang sama. Perhatikan gambar berikut:

• • • • • • • •

• •

• •

GAMBAR 2.11. Gambar yang disebelah kiri diatas merupakan denah gambar peta suatu provinsi dengan enam kabupaten dan tanda • merupakan ibukota dari masing-masing kabupaten; dan gambar yang disebelah kanan merupakan suatu graph T yang diekstrak dari gambar disampingnya dengan cara menghubungkan garis pada titik-titik yang berdekatan.

Anggap n adalah total kabupaten dalam suatu provinsi, q adalah total daerah untuk dibagi dan pi adalah ukuran populasi kabupaten ke-i. Untuk menyelesaikan masalah pembagian wilayah pertama konsepsikan suatu graph adjacent dari H yang mana setiap titik menyatakan suatu kabupaten. Terdapat suatu sisi antara kabupaten vi dan vj

1 jika v

berdekatan dalam peta. Matriks adjacent dari H adalah A yang mana,

i dan vj berdekatan dan ai,j =

0 untuk yang lain.

Dengan menggunakan algoritma Dijkstra, dapat ditemukan lintasan terpendek dari sebarang titik. Anggap D menyatakan matriks lintasan terpendek, Dij adalah panjang lintasan terpendek dari titik vi ke vj.

Kemudian konsepsikan graph berbobot ganda G(V,E,P(v),D(e)). Dalam graph ini masing-masing titik di V menyatakan suatu kabupaten dari provinsi dan bobot dari P(vi) = pi dari suatu titik vi mewakili ukuran populasi dari kabupaten. Untuk sebarang pasangan titik vi dan vj terdapat suatu edge (vi,vj)∈ E. Bobot Dij dari edge vi,vj adalah panjang dari lintasan terpendek antara vi dan vj dalam graph H. Jika tidak ada lintasan antara titik vi dan vj yakni graph H adalah tak terhubung dan bobot dari vi dan vj adalah tak hingga. Dengan perkataan lain, jika graph H itu terhubung maka graph G adalah graph berbobot ganda lengkap. Graph berbobot ganda dapat dinyatakan sebagai lintasan terpendek matriks D.

BAB 3

PEMBAHASAN

3.1 Model Pemrograman Kuadratik Dalam Pembagian Daerah Pemilihan Umum

Masalah pemrograman kuadratik dalam pembagian daerah pemilihan umum dapat dinyatakan dengan diberikan suatu provinsi dengan n kabupaten dan ukuran populasinya, bagaimana cara untuk membagi suatu provinsi kedalam k wilayah menurut beberapa kendala yang diberikan.

Anggap diberikan: 1. xik

2.

∈[0,1] menyatakan persentasi dari populasi kabupaten ke-i untuk dikelompokkan kedalam daerah pemilihan ke-k.

= (p1 + p2 + ... + pn) . menyatakan rata-rata populasi dari masing-masing daerah

pemilihan umum.

3. Dij menyatakan panjang dari lintasan terpendek antara titik vi ke vj 4. q menyatakan banyaknya daerah pemilihan yang ditetapkan

.

sehingga permasalahan ini dapat dirumuskan ke dalam bentuk model pemrograman kuadratik sebagai berikut:

pemilihan umum parlemen dari provinsi. Kendala ketiga mengindikasikan batas-batas dari peubah.

Adapun banyak peubah yang muncul dari model tersebut adalah sebanyak daerah pemilihan yang berbanding lurus terhadap banyaknya kabupaten yang ada dan banyaknya kendala yang ada dari model tersebut adalah sebanyak dua kali dari penjumlahan daerah pemilihan terhadap banyaknya kabupaten.

3.2 Proses Penggambaran Batas-batas Pembagian Daerah

Contoh Soal

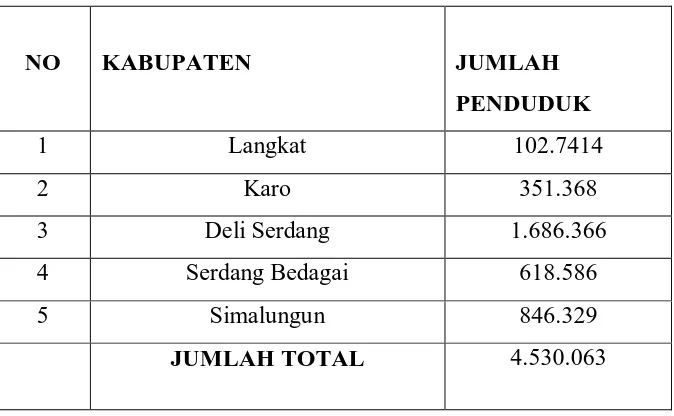
Diberikan data lima kabupaten di provinsi Sumatera Utara pada tahun 2007 dari sumber Badan Pusat Statistik Provinsi Sumatera Utara sebagai berikut:

TABEL 1. Jumlah penduduk di lima kabupaten tahun 2007 di provinsi Sumatera Utara

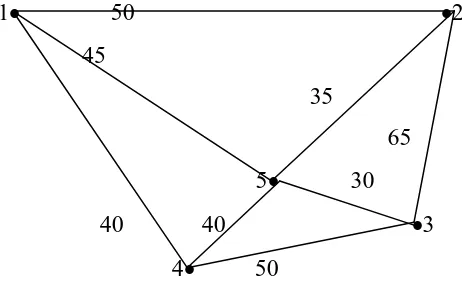
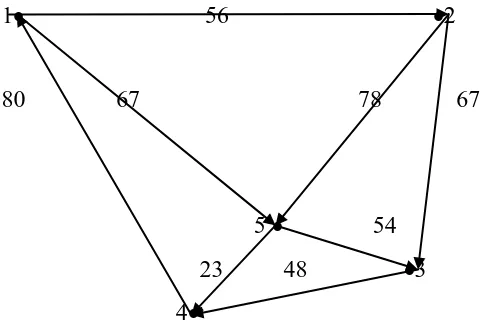
Adapun graph dari lima kabupaten tersebut yang diekstrak dari peta (dari lampiran.... ) sebagai berikut

Jika lima kabupaten tersebut akan dibagi kedalam tiga daerah pemilihan umum maka

Dengan menggunakan metode Dijkstra dapat dicari jarak terpendek antar kabupaten sebanyak dengan n =5 dan r =2 (prinsip kombinasi terjadi dikarenakan bahwa jarak dari kabupaten ke - i terhadap kabupaten ke - j sama dengan jarak

terpendek dari kabupaten ke – j ke kabupaten ke – i, dengan

=

=

10.

Adapun dari graph G diatas didapat jarak terpendek antar dua kabupaten yang berdekatan sebagai berikut:

Jarak terpendek dari Langkat ke Karo dan sebaliknya adalah 109 Km Jarak terpendek dari Langkat ke Deli Serdang dan sebaliknya adalah 67 Km Jarak terpendek dari Deli Serdang ke Karo dan sebaliknya adalah 92 Km

Jarak terpendek dari Deli Serdang ke Serdang Bedagai dan sebaliknya adalah 30 Km Jarak terpendek dari Deli Serdang ke Simalungun dan sebaliknya adalah 92 Km Jarak terpendek dari Karo ke Simalungun dan sebaliknya adalah 88 Km

Adapun jarak terpendek dari Langkat ke Simalungun dapat dicari dengan menggunakan metode Dijkstra. Anggap dari graph G diatas angka – angka 1, 2, 3, 4, dan 5 diganti menjadi a, b, c, d, e. Dengan menggunakan metode Dijkstra maka

Iterasi 3

Iterasi u = e berhenti, sehingga jarak terpendek dari ake e atau Langkat ke Simalungun adalah 159 Km.

Iterasi 2

Iterasi 2

u = d berhenti, sehingga jarak terpendek dari b ke d atau dari Karo ke Serdang Bedagai adalah 122 Km.

Dari data-data dan hasil-hasil diatas maka permasalahan dalam model pemrograman kuadratik adalah

Minimumkan f =

Dengan kendala

x51 + x52 + x53 = 1 xik

Adapun banyak peubah yang digunakan dalam model diatas adalah sebanyak 15 peubah yaitu x

≥ 0, untuk i = 1,2,...5 dan k = 1,2,3

Dengan menggunakan perangkat Lunak LINDO, penyelesaian permasalahan diatas sampai pada iterasi kedelapan (lihat lampiran....dan memberikan hasil seperti pada tabel berikut:

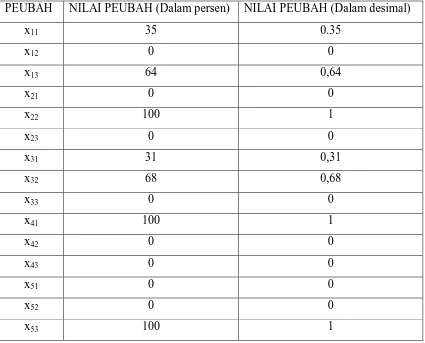
TABEL 2. Harga peubah yang diperoleh dari perangkat Lunak LINDO

11, x12, x13, x21, x22, x23, x31, x32, x33, x41, x42, x43, x51, x52, dan x53 atau banyak kabupaten n berbanding lurus terhadap daerah pemilihan q

PEUBAH

Dari tabel diatas didapati harga – harga untuk masing – masing peubah. Misalkan peubah x11 = 35 % artinya bahwa 35% dari populasi penduduk di kabupaten pertama atau Langkat dikelompokkan kedalam daerah pemilihan umum pertama.

Dari tabel diatas dapat dilihat bahwa daerah – daerah yang dikelompokkan kedalam daerah pemlihan umum pertama adalah kabupaten Langkat sebanyak 35%, kabupaten Deli Serdang 31%, dan kabupaten Serdang Bedagai sebanyak 100% dari banyaknya populasi masing – masing kabupaten tersebut.

Dari tabel diatas dapat dilihat bahwa daerah – daerah yang dikelompokkan kedalam daerah pemlihan umum kedua adalah kabupaten Karo sebanyak 100% dan kabupaten Deli Serdang 68% dari banyaknya populasi masing – masing kabupaten tersebut.

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dalam tulisan ini diteliti masalah pembagian wilayah untuk kepentingan politik. Pertama, masalah ini diubah kedalam bentuk masalah pembagian graph berbobot ganda kemudian diformulasikan dalam model pemrograman kuadratik. Dengan menggunakan perangkat lunak LINDO, dapat dicari solusi optimal. Seperti yang telah dipaparkan sebelumnya dengan diberikan populasi dan jarak lima kabupaten di provinsi Sumatera Utara kemudian dari data – data tersebut diolah yaitu mencari jarak terpendek antar kabupaten, rata – rata populasi di masing – masing daerah pemilihan umum dan mensubstitusikan angka – angka tersebut kedalam model pemrograman kuadratik. Dengan menggunakan perangkat lunak LINDO didapati hasil untuk permasalahan tersebut pada iterasi kedelapan seperti yang ditampilkan pada tabel 2 serta penjelasan dari tabel tersebut. Metode ini deterministik dan memiliki nilai optimal yang global.

4.2 Saran

DAFTAR PUSTAKA

Anton, H. 1984. Linear Algebra and Its Application. John Wiley and Sons, Inc: New York

C. Chou dan S Li. 1984. Taming The Gerrymander – Statistical Physics Approach to Political Districting Problem. Physics A, 369(2005), 799 - 808

Foulds, L, R. 1973.Combinatorial Optimization for undergraduate. Springer, Inc: New York

Luenberger, G, David. 1973. Introduction to Linear and Nonlinear Programming Springer, Inc: New York

Ricca Andrea, Isabella Lari dan Bruno S. 1996. Drawing Political Districs by Voronoi Regions and local Search. Journal

Sarkar, S. 2003. A Textbook for Discrete Mathematic.S Chand and Company: New Delhi