Penyelesaian Permasalahan Transshipment dengan Metode North West Corner dan Metode Stepping Stone

(1)

DAFTAR PUSTAKA

Aminudin. 2005. Prinsip-prinsip Riset Operasi. Erlangga. Jakarta

Bajalinov, Erik B. 2003. Linear-Fractional Programming : Theory, Methods,

Applications and Software. Springer Science+Bussiness Media. New

York.

Bronson, Richard. 1988. Teori dan Soal-soal Operations Research. Erlangga.

Jakarta

Dantzig, George B & Mukund N Thapa. 2003. Linear Programming: Theory and

Extentions. Springer Science+Bussiness Media. New York.

Hillier, Frederick S Gerald. 1994. Perngantar Riset Operasi. Erlangga. Jakarta

Nasution, M.N. 2008. Manajemen Transportasi. Ghalia Indonesia. Jakarta.

Prawirosentono, Suyadi. 2005. Riset Operasi dan Ekonofisika. Bumi Aksara.

Jakarta

Siagian, P. 2006. Penelitian Operasional. UI-Press. Jakarta

Simarmata, A. 1991. Operations Research: Sebuah Pengantar. PT Gramedia

Pustaka Utama. Jakarta.

Sitorus, Parlin. 1997. Program Linier. Universitas Trisakti, Jakarta.

Subagyo, Pangestu., Asri, Marwan., Handoko, Tani. 1984. Dasar-dasar Operations

Research. BPFE. Yogyakarta

Supranto, J. 1980. Linear Programming. Fakultas Ekonomi Universitas Indonesia.

Jakarta.

Supranto, Johannes. 1988. Riset Operasi untuk Pengambilan Keputusan.

(2)

Syaripuddin, 2012. Penyelesaian Masalah Transshipment Menggunakan Vogels’s Approximation Method (VAM) . Jurnal Eksponensial 3: 2.

Taha, Hamdy A. 1992. Operation Research an Intoduction. Macmillan Publishing

Company. New York

Wijaya, Andi. 2012. Pengantar Operasi riset. Mitra Wacana Media. Bogor

(3)

(4)

BAB 3

HASIL DAN PEMBAHASAN

3. 1 Model Transshipment

Model transshipment adalah perluasan dari model transportasi. Perbedaannya adalah pada model transshipment semua simpul berpotensi menjadi tempat persinggahan barang atau titik transshipment, sedang pada model transportasi pengiriman barang langsung dari gudang yang kelebihan barang ke gudang yang

membutuhkan barang.

Masalah transshipment merupakan suatu problema transportasi di mana sebagian atau seluruh barang diangkut dari tempat asal tidak langsung dikirim ke

tempat tujuan tetapi melalui tempat transit. Hal ini sering terjadi dalam dunia

nyata. Jadi, sebelum didistribusikan ke tempat tujuan akhir disimpan dahulu di

suatu lokasi (tempat penyimpanan sementara). Dengan demikian tujuan utama

masalah transshipment adalah untuk menentukan jumlah unit barang yang akan dikirim dari tempat asal ke tempat tujuan akhir meskipun melalui tempat transit

(dengan ketentuan bahwa seluruh permintaan di tempat akhir dapat dipenuhi)

dengan total biaya angkutan yang dikeluarkan seminimal mungkin (Parlin Sitorus

,1997). Dalam bukunya, Erik B. Bajalinov (2003) menggambarkan skema

permasalahan transshipment:

Gambar 3. 1 Permasalahan Transshipment

(5)

Dalam transshipment pengiriman tidak harus dilakukan secara langsung tetapi boleh melalui satu atau beberapa perantara (Hamdy A Taha , 1992). Pada

gambar di atas dapat dilihat bahwa titik transshipment dapat bertindak sebagai sumber maupun tujuan.

Dalam masalah transshipment, barang dari sumber sebagian atau seluruhnya akan berhenti di tempat transit kemudian dilanjutkan ke tempat tujuan.

Pernyelesaian awal akan diselesaikan menggunakan metode North West Corner dan kemudian akan dioptimalkan menggunakan metode Stepping Stone.

3. 2 Aplikasi Masalah Transshipment

PT. Hakasima merupakan perusahaan penjualan peralatan rumah tangga yang

telah memiliki banyak cabang di Indonesia. Dalam kasus ini, data yang diambil

adalah distribusi barang pada PT. Hakasima cabang Bukittinggi (Sumatera Barat).

Pada permasalahan ini, produk yang diteliti adalah distribusi panci.

Perusahaan ini melakukan pengiriman dari dua gudang yang terletak di

Jakarta Pusat dan Jakarta Barat yang akan didistribusikan ke tempat di daerah

Bukittinggi dan sekitarnya yaitu Sinarmas Bukittinggi, Payakumbuh, Stainlist Bukittinggi dan Batu Sangkar. Sebelum sampai di tempat tujuan, barang tersebut

singgah (transit) di Padang Utara, Padang Barat dan Padang Timur.

Hubungan antara jumlah pemasokan dari tempat asal dan jumlah

permintaan di tempat tujuan akhir sebagai berikut :

Tabel 3. 1 Jumlah Unit yang akan Dikirim dari Tempat Asal

NO Lokasi gudang Jumlah yang akan dikirim

1 Jakarta Pusat 3012 unit

(6)

Tabel 3. 2 Jumlah Permintaan di Tempat Tujuan

Tabel 3. 3 Biaya Angkut Per Unit (dalam rupiah)

Ke

NO Lokasi Tujuan Jumlah Permintaan

1 Sinarmas Bukittinggi 1256 unit

2 Payakumbuh 1256 unit

3 Stainlist Bukittinggi 1000 unit

(7)

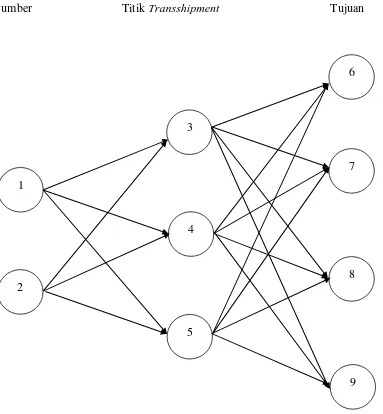
Sumber Titik Transshipment Tujuan

Gambar 3. 2 Jalur Transportasi

Dari gambar 3. 2 dapat dibuat tabel pendistribusian barang dengan dua sumber,

tiga tempat transit dan empat lokasi tujuan. Jumlah persediaan dari masing-masing

sumber adalah sebagai berikut:

Jakarta Pusat = 3012 unit

Jakarta Selatan = 2012 unit

Total = 5024 unit

Jumlah permintaan dari masing-masing lokasi adalah sebagai berikut:

Sinarmas Bukittinggi = 1256 unit

6

3

7

1

4

2

8

5

(8)

Payakumbuh = 1256 unit

Stainlist Bukittinggi = 1000 unit Batu Sangkar = 1512 unit

Total = 5024 unit

Terlihat bahwa jumlah persediaan = jumlah permintaan. Masalah transshipment di atas adalah masalah transshipment seimbang.

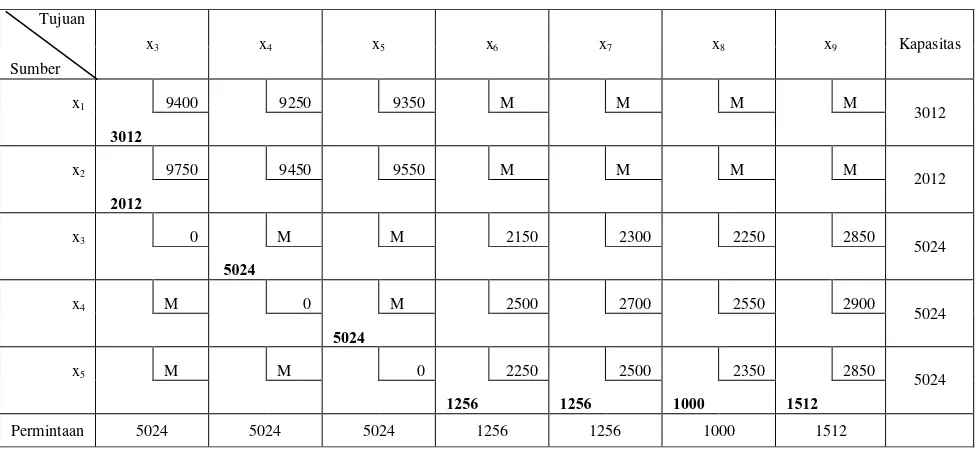
Selanjutnya dapat dibuat tabel transportasi yang sesuai untuk contoh

masalah transshipment di mana x1 dan x2 merupakan sumber, x3, x4 dan x5

merupakan titik transshipment dan x6, x7, x8 dan x9 merupakan tujuan. Jika tidak

ada jalur langsung (misal dari x1 ke x6) maka biaya transportasinya sebesar M

(M=100000 atau bilangan positif terbesar) artinya biaya transportasi bisa melebihi

dari perkiraan, sedangkan biaya transportasi ke titik itu sendiri (misal x3 ke x3)

adalah 0.

3. 2. 1 Penyelesaian Awal dengan Metode North West Corner

a. Tahap 1

Untuk dapat menyelesaikan permasalahan transshipment ini, langkah awal yang harus dilakukan adalah membuat tabel transportasi.

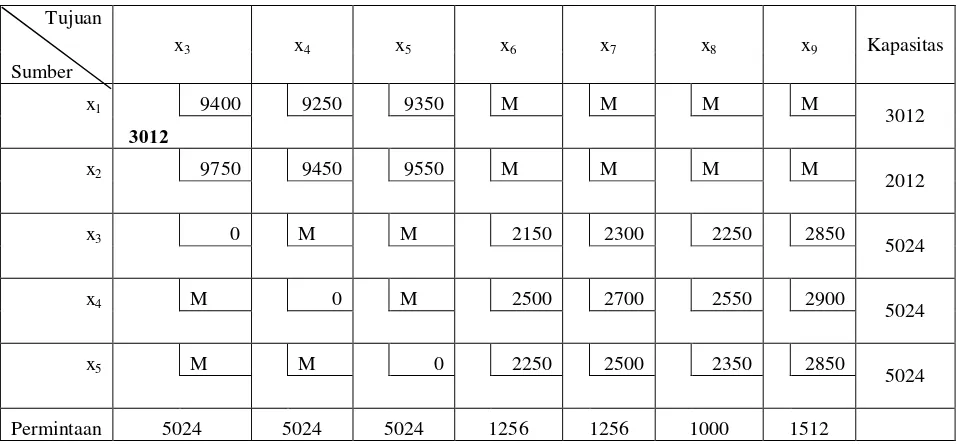
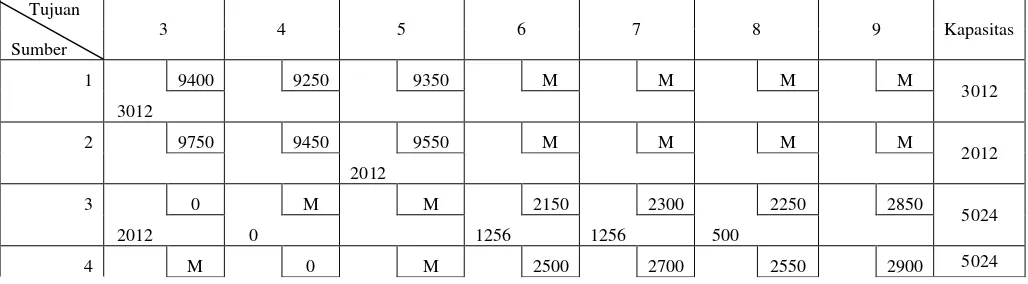
Tabel 3.4 Tabel Awal Transportasi dengan Biaya Transportasinya

(9)

b. Tahap 2

Langkah selanjutnya dimulai dari sel pada sudut kiri atas yang diisi dengan angka

sebanyak-banyaknya yang disesuaikan dengan kapasitas dan permintaan.

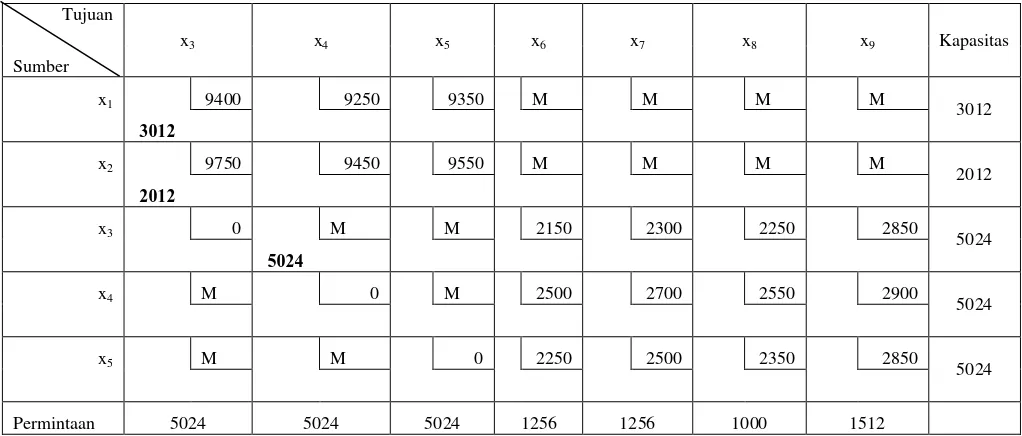
Tabel 3. 5 Hasil Tahap 1

kapasitas namun belum memenuhi permintaan. Untuk itu dilanjutkan pengisian

pada sel x21 agar permintaan terpenuhi dengan memperhatikan kapasitas yang ada.

(10)

(11)

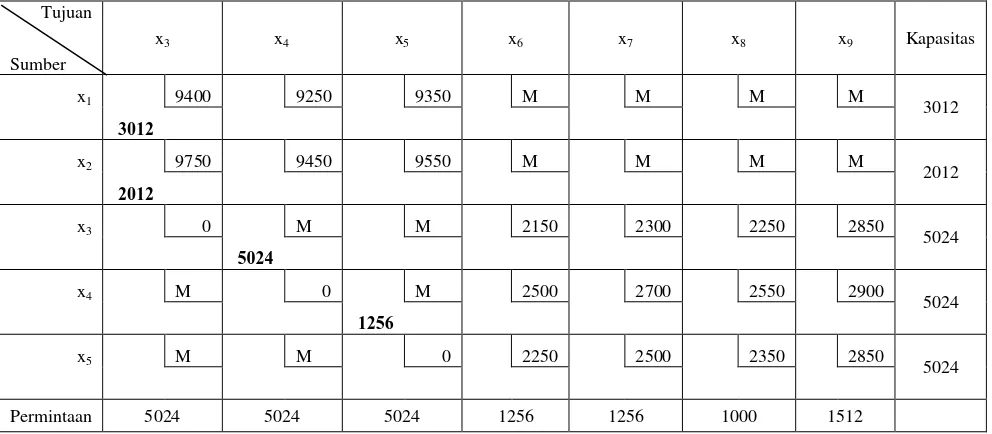
e. Tahap 5

Permintaan dan kapasitas pada baris x3 dan kolom x4 telah terpenuhi. Selanjutnya

isi sel x45.

Langkah selanjutnya mengisi sel pada kolom berikutnya yaitu pada sel x46.

(12)

g. Tahap 7

Sel x56 telah memenuhi permintaan namun belum memenuhi kapasitas yang ada.

Untuk memenuhi kapasitas maka sel x57 hingga x59 harus diisi hingga kapasitas

terpenuhi.

Tabel 3. 10 Hasil Tahap Akhir

Setelah semua kapasitas dan permintaan terpenuhi, berarti penyelesaian awal

dengan metode North West Corner telah terpenuhi.

h. Tahap 8

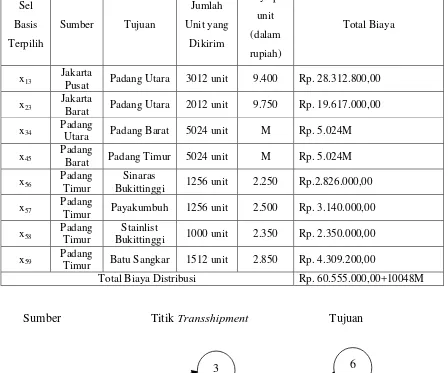
Dengan demikian besarnya biaya transportasi dari penyelesaian awal yang telah

diperoleh adalah sebagai berikut :

(13)

Tabel 3. 11 Alokasi dan Total Biaya Distribusi dengan Metode North west Corner

Pusat Padang Utara 3012 unit 9.400 Rp. 28.312.800,00

x23

Jakarta

Barat Padang Utara 2012 unit 9.750 Rp. 19.617.000,00

x34

Bukittinggi 1256 unit 2.250 Rp.2.826.000,00

x57

Padang

Timur Payakumbuh 1256 unit 2.500 Rp. 3.140.000,00

x58

Padang Timur

Stainlist

Bukittinggi 1000 unit 2.350 Rp. 2.350.000,00

x59

Padang

Timur Batu Sangkar 1512 unit 2.850 Rp. 4.309.200,00

Total Biaya Distribusi Rp. 60.555.000,00+10048M

(14)

3. 2. 2 Penyelesaian Optimal dengan Metode Stepping Stone

Persyaratan yang harus dipenuhi untuk penyelesaian optimal dengan

menggunakan metode Stepping Stone adalah bahwa jumlah sel berisi pada tabel transportasi sebanyak m+n-1 sel. Dari tabel 3. 10 ternyata jumlah sel yang terisi

sebanyak 8 buah di mana seharusnya jumlah sel berisi sebanyak 11 buah. Dengan

demikian harus ditambahkan nilai 0 ke sel yang kosong hingga syarat m+n-1

terpenuhi.

a. Tahap 1

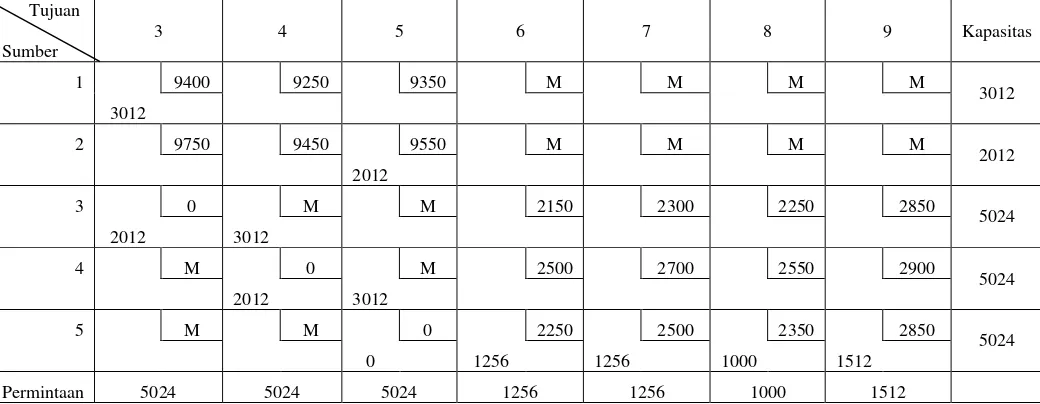
Tabel 3. 12 Pemecahan Persoalan Degenerasi

Untuk dapat melanjutkan penyelesaian ke tahap optimal, pada kasus degenerasi

harus ditambahkan nilai nol hingga jumlah sel yang terisi sebanyak m+n-1.

b. Tahap 2

Dari Tabel 3.12 pilih sel-sel yang kosong untuk mencari nilai indeks perbaikannya

dengan cara melakukan loncatan searah jarum jam dengan pijakannya berupa sel

basis sehingga terbentuk sebuah loop terdekat yang memungkinkan untuk kembali

(15)

sudut sel dari loop tersebut. Mulai dengan tanda (+) pada sel kosong terpilih. Setelah semua sel-sel kosong dievalusi dan didapat nilai indeks perbaikannya

selanjunya dilihat apakah masih ada nilai yang < 0. Jika tidak ada, maka

pemecahan awal sudah optimal tetapi bila masih ada nilai yang negatif pilih sel

yang mempunyai nilai negatif terbesar (penurunan biaya terbesar) untuk dilakukan

perbaikan jalur.

Tabel 3. 13 Indeks Perbaikan untuk Sel Kosong Tabel 3.12

Sel

Kosong Jalur Tertutup Biaya Δ Biaya

(16)

x48 _x₄₈_-x₅₈_+x₅₅_-x₄₅ _{2550-2350+0-M} 200-M

x49 _x₄₉_-x₅₉_+x₅₅_-x₄₅ _{2900-2850+0-M} 50-M

x53 _x₅₃_-x₃₃_+x₃₄_-x₄₄_+x₄₅_-x₅₅ _M-0+M-0+M-0 3M

x54 _x₅₄_-x₄₄_+x₄₅_-x₅₅ _M-0+M-0 2M

Dari Tabel 3.13 sel x25 dan sel x37 memiliki nilai indeks perbaikan dengan

nilai negatif terbesar. Pilih salah satu sel untuk dilakukan perbaikan. Sel yang

Perbaikan sel dilakukan dengan mengalokasikan jumlah barang terkecil dari isi sel

bertanda negatif dan tambahkan terhadap sel bertanda positif. Pada gambar 3.4

terlihat bahwa sel bertanda negatif yang memiliki jumlah barang yang paling kecil

(17)

adalah sel x23 = 2012. Diperoleh alokasi yang baru terlihat pada Gambar 3. 5.

Terlihat bahwa sel x25 berubah menjadi sel non basis (sel tak kosong).

a. Tahap 3

Evaluasi kembali sel kosong pada tabel 3. 14. Lakukan seperti tahap 2.

Tabel 3. 15 Indeks Perbaikan Sel Kosong Pada Tabel 3. 14

Sel

(18)

x24 _x₂₄_-x₂₅_+x₄₅_-x₄₄ _{9450-9550+M-0} -100-M

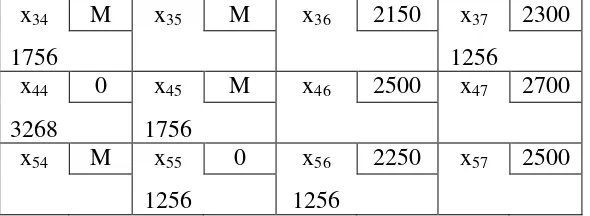
dilakukan perbaikan pada sel X37 karena memiliki indeks perbaikan negatif

(19)

x34 M x35 M x36 2150 x37 2300

Gambar 3.7 Hasil Perbaikan Sel x37

b. Tahap 4

Kembali lakukan perbaikan sel kosong pada tabel 3. 16 untuk mengetahui apakah

masih ada sel dengan nilai negatif.

(20)

Tabel 3. 17 Indeks Perbaikan Sel Kosong pada Tabel 3. 16

Sel

x14 _x₁₄_-x₃₄_+x₃₃_-x₁₃ _{9250-M+0-9400} -150-M

Ternyata masih ada indeks perbaikan sel bertanda negatif. Sel yang dipilih adalah

(21)

Gambar 3. 8 Loop Pada Sel x36

Gambar 3. 9 Hasil Perbaikan Sel x36

(22)

Evaluasi kembali sel kosong pada tabel 3. 18 untuk mengetahui nilai indeks

perbaikannya.

Tabel 3. 19 Indeks Perbaikan Sel Kosong pada Tabel 3. 18

Sel

(23)

Pada tabel 3.19 terlihat bahwa masih ada nilai indeks perbaikan bertanda negatif.

Sel x38 dipilih untuk dilakukan perbaikan karena memiliki nilai indeks perbaikan

negatif terbesar.

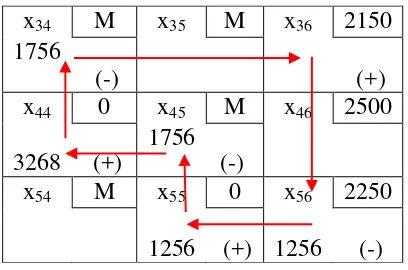
Gambar 3. 10 Loop Pada Sel x38

(24)

Lakukan kembali evaluasi sel kosong pada tabel 3. 20 untuk mengetahui nilai

indeks perbaikannya.

Sel

(25)

x53 _x₅₃_-x₃₃_+x₃₈_-x₅₈ _{M-0+2250-2350} M-100

x54 _x₅₄_-x₃₄_+x₃₈_-x₅₈ _{M-M+2250-2350} 100

x56 _x₅₆_-x₃₆_+x₃₈_x₅₈ _{2250-2150+2250-2350} 0

x57 _x₅₇_-x₃₇_+x₃₈_-x₅₈ _{2500-2300+2250-2350} 100

Ternyata masih ada nilai indeks perbaikan bertanda negatif. Maka dilakukan

perbaikan pada sel dengan nilai indeks perbaikan negatif terbesar yaitu sel x24.

x24 9450 x25 9550 x26 M x27 M x28 M

(26)

e. Tahap 7

Lakukan kembali evaluasi sel kosong pada tabel 4. 21 untuk mengetahui nilai

indeks perbaikannya.

Sel

(27)

9250-9450+9550-0+2350-x28 _x₂₈_-x₅₈_+x₅₅_-x₂₅ _{M-2350+0-9550} M-11900

Masih ada sel bertanda negatif. Maka akan dilakukan perbaikan pada sel dengan

nilai indeks perbaikan negatif terbesar yaitu pada sel x49.

(28)

x24 9450 x25 9550 x26 M x27 M x28 M x29 M

f. Tahap 8

Untuk mengetahui apakah masih ada sel dengan nilai indeks perbaikan bertanda

(29)

Sel

(30)

9250-9450+9550-0+2350-Perhitungan indeks perbaikan sel kosong pada Tabel 4.24 menunjukkan

bahwa semua sel telah bernilai positif. Artinya pemecahan masalah tersebut sudah

optimal.

Tabel 3. 26 Hasil Akhir Menggunakan Metode Stepping Stone

Tujuan

Biaya total dalam pemecahan optimal persoalan transshipment sebagai berikut :

Tabel 3. 27 Alokasi dan Total Biaya Distribusi dengan Metode Stepping Stone

Sel Basis

Terpilih Sumber Tujuan

(31)

X36

Padang

Utara

Sinarmas

X37

X49

Padang

Barat

Batu

Sangkar 1512 unit 2.900 Rp. 4.384.800,00

X58

Padang

Timur

Stainlist

Total Biaya Transportasi Rp. 59.560.200,00

(32)

3. 3 Pembahasan

Dari perhitungan di atas terlihat bahwa proses pengerjaan pada metode North West Corner mengalokasikan jumlah maksimum yang dapat diperbolehkan oleh permintaan dan kapasitas kepada sel x13. Sel ini berada pada sudut kiri atas atau

arah sudut barat laut sesuai dengan namanya. Jika masih ada permintaan dan

kapasitas yang tersisa, maka dilanjutkan dengan berpindah satu sel ke kanan atau

ke bawah sesuai dengan kapasitas dan permintaan yang diperbolehkan.

Jumlah sel yang terisi pada tabel transportasi harus berjumlah m+n-1 (m

adalah jumlah baris dan n adalah jumlah kolom) dari penyelesaian permasalahan

di atas menggunakan metode North West Corner telah terjadi persoalan degenerasi. Untuk mengatasi persoalan ini harus ditambahkan niai 0 hingga

jumlah sel yang terisi memenuhi syarat untuk melanjutkan ke penyelesaian

optimal.

Penyelesaian optimal dilakukan dengan menggunakan metode Stepping Stone. Metode ini mendasarkan solusi persoalan transportasi dengan melakukan perbaikan bertingkat dari solusi awal yang telah disusun. Lintasan Stepping Stone dapat melintasi (melompati) sel kosong atau sel berisi.

Dari perhitungan yang telah dilaukan terihat bahwa penyelesaian optimal

menggunakan metode Stepping Stone menghasilkan total biaya yang lebih optimal dibandingkan dengan penyelsaian awal menggunakan metode Noth West Corner. Proses pada metode Stepping Stone dilakukan berulang-ulang hingga indeks perbaikan seluruhnya bernilai positif. Dengan demikian, semua rute yang

memungkinkan akan dievaluasi hingga mendapatkan hasil yang optimal. Biaya

distribusi panci yang optimal menggunakan metode Stepping Stone pada Perusahaan Hakasima adalah Rp. 59.560.200,00, lebih optimal dibandingkan

(33)

BAB 4

KESIMPULAN DAN SARAN

4. 1 Kesimpulan

Berdasarkan pembahasan pada bab-bab sebelumnya, penulis menyimpulkan

bahwa :

1. Kombinasi metode North West Corner dan metode Stepping Stone dapat menyelesaikan masalah transshipment.

2. Metode Stepping Stone dapat digunakan untuk mengoptimalkan penyelesaian awal yag dihasilkan oleh metode North West Corner di mana hasil yang di dapat menjadi lebih optimal.

4. 2 Saran

1. Penelitian masalah transshipment dapat dilakukan pada kasus tidak seimbang yaitu dengan menambahkan variabel dummy.

2. Untuk pengembangan selanjutnya bisa dicoba dengan data yang lebih

(34)

BAB 2

LANDASAN TEORI

2. 1 Masalah Transportasi

Salah satu permasalahan khusus dalam program linier adalah masalah transportasi.

Untuk menyelesaikan permasalahan ini digunakan metode transportasi. Dikatakan

khusus, karena terletak pada karakteristik utama, yaitu bahwa masalah-masalah

tersebut cenderung membutuhkan sejumlah pembatas dan variabel yang sangat

banyak sehingga penggunaan komputer dalam menyelesaikan metode

simpleksnya akan sangat mahal dibandingkan secara manual (Fien Zulfikarijah,

2003).

Secara umum arti transportasi adalah adanya perpindahan barang dari satu

tempat ke tempat lain. Tempat atau tempat-tempat asal barang disebut juga dengan

istilah sumber atau sumber-sumber. Sedangkan tempat atau tempat-tempat tujuan

disebut destination. Hal ini merupakan bagian dari kehidupan nyata manusia untuk memindakan barang dari satu tempat ke tempat lain sesuai dengan

kebutuhannya. Misalnya di suatu tempat asal barang mempunyai jumlah produk

yang berlebih sehingga perlu ditransportasikan ke tempat lain yang

memerlukannya (Suyadi Prawirosentono, 2005).

Tabel 2.1. Tabel Untuk Persoalan Transportasi

(35)

Suatu model dikatakan seimbang jika total jumlah penawaran sama dengan

jumlah permintaan (Aminudin, 2004).

∑ ∑

Prosedur penyelesaian masalah transportasi dengan menggunakan metode

penyelesaian program linier adalah (Parlin Sitorus, 1997) :

1. Definisikan masalah yang dihadapi ke dalam model matematika program

linier.

2. Susunlah tabel transportasi awal.

3. Kembangkan penyelesaian awal dengan menggunakan salah satu metode

di bawah :

(36)

4. Cari penyelesaian optimal dengan menggunakan salah satu metode di

bawah :

a. Metode Stepping Stone

b. Metode Modified Distribution 5. Evaluasi penyelesaian optimal.

2. 2 Masalah Transshipment

Transshipment adalah masalah transportasi yang memungkinkan dilakukannya pengiriman barang dengan cara tidak langsung, di mana barang dari suatu sumber

dapat berada pada sumber lain sebelum mencapai tujuan akhir. Pada model

transshipment ini suatu sumber sekaligus dapat berperan sebagai tujuan dan sebaliknya, suatu tujuan dapat juga berperan sebagai sumber. Dengan kata lain,

proses pendistribusian barang dari suatu sumber ke tujuan harus melalui agen

terlebih dahulu.

Syaripuddin (2012) mengatakan dalam model ini setiap sumber maupun

tujuan dipandang sebagai titik potensial bagi demand maupun supply. Oleh karena itu untuk menjamin bahwa tiap titik potensial tersebut mampu menampung

total barang di samping jumlah barang yang ada di titik tersebut, maka perlu

ditambahkan kepada titik-titk itu kuantitas supply dan demandnya masing-masing sebesar B.

∑ ∑

(37)

2. 3 Metode Transportasi

2. 3. 1 Pengertian Metode Transportasi

Metode transportasi merupakan bagian dari program linier yang digunakan untuk

mengatur dan mendistribusikan sumber-sumber yang menyediakan produk ke

tempat-tempat yang membutuhkan untuk mencapai efisiensi biaya transportasi.

Alokasi produk harus memperhatikan biaya distribusi dari satu tempat ke tempat

lain, hal ini dikarenakan adanya perbedaan dari biaya-biaya tersebut. Syarat dari

metode transportasi adalah besarnya kebutuhan (permintaan) sama dengan

kapasitas, apabila kebutuhan tidak sama dengan kapasitas maka untuk

menyamakannya ditambahkan variabel dummy dengan biaya distribusi sebesar nol (Andi Wijaya, 2012).

Terdapat dua solusi dalam metode transportasi, yaitu : solusi awal, yang

terdiri dari metode North West Corner, metode Least Cost Combination, Vogel Approximation Method dan solusi optimal, yang terdiri dari metode Stepping Stone dan metode Modified Distribution.

2. 3. 2 Metode Transportasi Menggunakan Solusi Awal

a. Metode North West Corner

Langkah-langkah pada metode North West Corner adalah (Andi Wijaya, 2012) :

a. Membuat tabel transportasi.

b. Dimulai dari sel pada sudut kitri atas yang diisi dengan angka

sebanyak-banyaknya yang disesuaikan dengan kapasitas dan

permintaan (pilih yang paling kecil).

c. Lakukan langkah yang sama pada langkah 2 untuk mengisi sel-sel lain

yang disesuaikan dengan kapasitas dan permintaan sampai seluruh

(38)

b. Metode Least Cost Combination

Langkah-langkah pada metode Least Cost Combination adalah (Andi Wijaya, 2012) :

a. Membuat tabel transportasi.

b. Dimulai dari mengisi sel pada biaya terendah dengan angka

sebanyak-banyaknya yang disesuaikan dengan kapasitas dan permintaan (pilih

yang paling kecil).

c. Lakukan langkah yang sama pada langkah b untuk mengisi sel-sel lain

yang disesuaikan dengan kapasitas dan permintaan sampai seluruh

kapasitas permintaan terpenuhi.

c. Vogel Approximation Method

Langkah-langkah pada metode Vogel Approximation Method adalah (Andi Wijaya, 2012) :

a. Cari dua biaya terendah dari masing-masing baris dan kolom.

b. Selisihkan dua biaya terndah tersebut.

c. Pilih selisi biaya terbesar pada baris atau kolom tersebut (apabila

terdapat selisih sebesar yang sama, maka dapat dipilih salah satunya).

d. Alokasikan produk sebanyak-banyaknya (disesuaikan dengan kapasitas

dan permintaan) di sel yang memiliki biaya terendah pada baris atau

kolom yang memiliki selisih terbesar tersebut.

e. Baris atau kolom yang telah diisi penuh tidak dapat diikutsertakan

kembali dalam proses perhitungan pencarian selisih biaya berikutnya.

f. Lakukan kembali pada langkah a sampai semua produk dialokasikan

(39)

2. 3. 3 Metode Transportasi Menggunakan Solusi Optimal

a. Metode Stepping Stone

Langkah-langkah metode Stepping Stone adalah (Andi Wijaya, 2012) : a. Mencari sel yang kosong

b. Melakukan loncatan pada sel yang terisi

Keterangan :

1. Loncatan dapat dilakukan secara vertikal atau horizontal.

2. Dalam suatu loncatan tidak boleh dilakukan lebih dari satu kali

loncatan pada baris atau kolom yang sama tersebut.

3. Loncatan dapat dilakukan melewati sel lain selama sel tersebut

terisi.

4. Setelah loncatan pada baris langkah selanjutnya pada kolom dan

sebaliknya.

5. Jumlah loncatan bersifat genap.

6. Perhatikan sel yang terisi pada loncatan berikutnya untuk

memastikan proses tidak terlambat

c. Lakukan pehitungan biaya pada sel yang kosong tersebut, dimulai dari

sel yang kosong.

d. Perhitungan dilakukan dengan cara menghitung biaya, sel yang kosong

diberi tanda positif selanjutnya negatif, positif, negatif, dst.

e. Apabila semua telah bernilai positif berarti solusi awal yang telah

dikerjakan sebelumnya telah menghasilkan biaya transportasi minimum,

tetapi apabila masih terdapat nilai negatif, maka dicari nilai negatif

terbesar (penghematan terbesar).

f. Apabila terdapat tanda negatif, alokasikan produk dengan melihat proses

e,akan tetapi yang dilihat adaah isi dari sel tersebut. Tambahkan dan

kurangkan dengan isi sel negatif terkecil pada seluruh sel.

g. Lakukan langkah yang sama dengan mengulang dari langkah b sampai

(40)

b. Metode Modified Distribution

Langkah-langkah metode Modified Distribution adalah (Andi Wijaya, 2012) :

a. Menghitung nilai indeks pada masing-masing baris dan kolom, dengan

menggungakan rumus Ri + Kj – Cij, di mana Ri adalah nilai indeks pada baris i, Kj merupakan nilai indeks pada kolom j dan Cij adalah biaya transportasi dari sumber i ke tujuan j. Pemberian nilai indeks ini harus berdasarkan pada sel yang telah terisi atau digunakan. Sebagai

alat bantu untuk memulai pencarian nilai indeks, maka nilai baris

pertama (R1) ditetapkan sama dengan nol.

b. Nilai indeks seluruh baris dan kolom diperoleh dengan rumus Ri + Kj =

Cij.

c. Mencari sel-sel yang kosong atau sel yang belum terisi

d. Mengitung besarnya nilai pada sel-sel kosong tersebut dengan rumus Iij

= Cij– Ri– Kj.

e. Apabila nilai sel-sel kosong tersebut keselutuhannya bernilai positif

berarti proses tersebut telah menghasilkan biaya transportasi minimum.

f. Apabila masih terdapat nilai negative berarti masih terdapat sel yang

memiliki angka negatif.

g. Proses pengalokasian dilakukan menggunakan pendekatan yang serupa

dengan metode Stepping Stone.

h. Lakukan langkah a untuk memastikan semua nilai sel kosong tidak ada

yang bernilai negatif.

2. 4 Degenerasi

Degenerasi (turun derajat) terjadi apabila jumlah sel yang terisi pada tabel

transportasi kurang dari m+n-1 (m merupakan jumlah baris dan n merupakan

jumlah kolom). Hal ini dapat diatasi dengan melakukan penambahan set terisi

(41)

jumlah sel yang terisi mencapai m+n-1. Pemilihan ini sembarang dan biasanya

diberikan pada variabel-variabel dengan biaya pengiriman terendah. Memperbaiki

suatu pemecahan yang turun derajat dapat berkesudahan dengan penggantian

suatu variabel dasar yang bernilai nol dengan variabel dasar lain yang juga bernilai

nol. Meskipun kedua pemecahan yang turun derajat ini secara efektif adalah sama

(hanya penamaan variabel-variabel dasar yang telah berubah sedangkan nilainya

tetap) tetapi iterasi tambahan ini perlu agar metode transportasi dapat dilanjutkan

(42)

BAB 1

PENDAHULUAN

1.1Latar Belakang

Masa perkembangan transportasi terwujud dalam bentuk kemajuan alat angkut

yang selalu mengikuti dan mendorong kemajuan teknologi transportasi. Pada

umumnya masalah transportasi berhubungan dengan distribusi suatu barang dari

beberapa sumber dengan penawaran terbatas menuju beberapa tujuan dengan

permintaan tertentu pada biaya transport minimum. Karena hanya ada satu macam

barang, suatu tempat tujuan dapat memenuhi permintaannya dari satu atau lebih

sumber.

Persoalan transportasi terpusat pada pemilihan rute dalam jaringan

distribusi produk antara pusat industri dan distribusi gudang atau antara distribusi

gudang regional dan distribusi pengeluaran lokal. Dalam menggunakan metode

transportasi, pihak manajemen mencari rute distribusi atau penugasan yang akan

mengoptimumkan tujuan tertentu. Misalnya tujuan meminimumkan total biaya

transportasi, memaksimumkan laba, atau meminimumkan waktu yang digunakan.

Metode transportasi merupakan suatu metode yang digunakan dalam

pendistribusian barang dari sumber-sumber yang menyediakan barang yang sama

ke tempat-tempat yang membutuhkan secara optimal. Pendistribusian barang

harus diatur sedemikian rupa karena terdapat perbedaan biaya-biaya distribusi dari

satu sumber ke tempat-tempat tujuan. Metode transportasi bermanfaat untuk

memperlancar pendistribusian barang, memaksimalkan pengalokasian dari sumber

ke tujuan dan berguna dalam usaha menekan total biaya transportasi. Dengan

penerapan metode transportasi, biaya, waktu dan tenaga dapat dioptimalkan serta

meningkatkan efisiensi perusahaan. Dengan demikian, pada dasarnya perhitungan

biaya transportasi dengan menggunakan metode transportasi berupaya untuk

(43)

mana sehingga akan dapat diperoleh jumlah biaya angkut yang paling minimal

dan memaksimalkan keuntungan. Metode transportasi juga dapat digunakan untuk

memecahkan masalah dalam dunia usaha. Salah satu masalahnya adalah masalah

transshipment.

Masalah tansshipment merupakan persoalan transportasi transisi atau persoalan transportasi yang termodiﬁkasi. Tempat transit ini dapat menerima

pasokan dan dapat mengirimkan barang. Tujuan utama masalah transshipment adalah meminimumkan biaya distribusi barang yang dikirim dari tempat asal ke

tempat tujuan meskipun melalui tempat transit.

Ada beberapa metode transportasi yang dapat digunakan untuk

menyelesaikan masalah transshipment yaitu, Metode North West Corner, Metode Least Cost Combination, Vogel Approximation Method, Metode Modified Distribution dan Metode Stepping Srone. Metode transportasi yang digunakan untuk mencari solusi layak dasar awal dalam penelitian ini adalah Metode North West Corner (NWC) yang kemudian dilanjutkan dengan pengujian solusi optimum dengan menggunakan Metode Stepping Stone untuk membuktikan bahwa proses pengalokasian hasil produksi yang dilakukan sudah optimal dengan

biaya transportasi yang minimum.

Metode North West Corner atau metode pojok barat laut merupakan metode awal dalam penyelesaian masalah transportasi. Sesuai dengan namanya,

penyelesaian dengan metode ini dimulai dari sel paling kiri atas. Metode ini

memperlihatkan bahwa tiap langkah yang dilakukan akan memenuhi satu kendala.

Metode Stepping Stone adalah metode yang digunakan untuk mendapatkan solusi optimal dalam masalah transportasi. Metode ini bersifat trial and error, yaitu dengan mencoba-coba memindahkan sel yang ada isinya (stone) ke sel yang kosong (water). Tentu saja pemindahan ini harus mengurangi biaya. Untuk itu harus dipilih sedemikian rupa sel-sel kosong yang biaya transportasinya kecil dan

memungkinkan dilakukan pemindahan.

Berdasarkan uraian di atas, penulis membuat judul mengenai Metode

(44)

Permasalahan Transshipment dengan Metode North West Corner dan Metode Stepping Stone.

1.2Perumusan Masalah

Berdasarkan latar belakang di atas, maka permasalahan dari penelitian ini

dirumuskan bagaimana mengatasi masalah transshipment menggunakan kombinasi Metode North West Corner (NWC) dan Metode Stepping Stone.

1.3Batasan Masalah

Batasan masalah yang akan dibahas dalam penelitian ini adalah :

1. Metode transportasi yang digunakan adalah metode Metode North West Corner dan Metode Stepping Stone.

2. Masalah transshipment dalam tulisan ini adalah masalah transshipment seimbang.

1.4Tinjauan Pustaka

Persoalan transportasi merupakan persoalan program linier. Bahkan aplikasi dari

teknik program linier pertama kali ialah dalam merumuskan persoalan transportasi

dan memecahkannya. Persoalan transportasi yang dasar pada mulanya

dikembangkan oleh F. L. Hitchcock pada tahun 1941 dalam studinya yang

berjudul The distribution of a product from several sources to numerous locations (Johannes Supranto, 1988).

Mengirim barang dari satu tempat ke tempat lain memerlukan alat transportasi,

(45)

memerlukan biaya pengiriman. Besarnya biaya pengiriman barang dipengaruhi

oleh dua variabel, yaitu jumlah barang yang akan dikirimkan dan biaya angkut per

unit (Suyadi Prawirosentono, 2005).

Menurut P. Siagian (2006) gambaran umum dari persoalan transportasi

dapat dijelaskan sebagai berikut :

 Sebuah perusahaan yang menghasilkan barang atau komoditi tertentu

melalui sejumlah pabrik pada lokasi yang berbeda, akan mengirim barang

ke berbagai tempat yang memerlukan dengan jumlah kebutuhan yang

sudah tertentu, atau

 Sejumlah barang atau komoditi hendak dikirim dari sejumlah pelabuhan

asal kepada sejumlah pelabuhan tujuan, masing-masing dengan tingkat

kebutuhan yang sudah diketahui.

Masalah transportasi berkenaan dengan penyusunan suatu program distribusi

serta pengangkutan satu jenis barang tertentu dari beberapa sumber ke beberapa

tempat tujuan, sehingga dengan program itu diperoleh jumlah ongkos angkut yang

sekecil-kecilnya (D. A Simarmata, 1991). Menurut J. Supranto (1980), masalah

transportasi untuk mencari nilai minimum dapat dirumuskan sebagai berikut:

(46)

Keterangan:

xij = jumlah barang yang harus diangkut dari tempat asal i ke tempat tujuan j

cij = biaya angkut per unit barang dari tempat asal i ke tempat tujuan j

si= banyaknya barang yang tersedia di tempat asal i

dj= banyaknya permintaan terhadap barang dari tempat tujuan j

i = sumber ke i

j = tujuan ke j

Dalam masalah transportasi, pengiriman tidak berlangsung antara tempat

asal dan tempat tujuan, maupun dari tempat tujuan ke tempat asal. Metode terbaik

distribusi adalah melalui titik tengah pengiriman yang disebut transshipment (George B Dantzig dan Mukund N Thapa, 2003).

Metode transportasi merupakan bagian dari program linier yang digunakan

untuk mengatur dan mendistribusikan sumber-sumber yang menyediakan produk

ke tempat-tempat yang membutuhkan untuk mencapai efisiensi biaya transportasi.

Metode transportasi digunakan untuk memecahkan masalah dalam dunia usaha

seperti masalah pembelanjaan modal, analisis lokasi dan alokasi dana untuk

investasi. Metode transportasi diharapkan mampu meminimumkan biaya tempat

tujuan dengan biaya yang paling minimum. Masing-masing sumber tersebut

mempunyai kapasitas pengiriman tertentu, sedangkan masing-masing tempat

tujuan ini mempunyai permintaan dalam jumlah tertentu pula (M. N. Nasution,

2008).

Menurut Fien Zulfikarijah (2003), ciri-ciri khusus metode transportasi

adalah

a) Terdapat sejumlah sumber dan sejumlah tujuan tertentu.

b) Jumlah yang didistribusikan dari setiap sumber dan yang diminta oleh

(47)

c) Jumlah yang dikirim atau diangkut dari suatu sumber ke suatu tujuan

sesuai dengan permintaan atau kapasitas sumber. Jumlah permintaan

dan penawaran seimbang dan apabila jumlah permintaan tidak sama

dengan jumlah penawaran, maka harus ditambahkan variabel dummy. d) Biaya transportasi dari suatu sumber ke suatu tujuan adalah tertentu.

e) Jumlah variabel dasar m+n-1, di mana m adalah jumlah baris dan n

adalah jumlah kolom. Apabila jumlah variabel dasar kurang dari

m+n-1 yang disebut degenerasi, maka harus ditambahkan variabel dasar

dengan nilai nol.

Metode North West Corner atau metode pojok barat laut diperkenalkan oleh Charnes dan Cooper, kemudian dikembangkan oleh Danzig. (P. Siagian,

2006). Metode ini digunakan untuk mencari penyelesaian layak pada variabel

dasar (Fien Zulfikarijah, 2003). Sedangkan metode Stepping Stone merupakan metode yang digunakan untuk menguji solusi awal yang telah dilakukan

sebelumnya. Metode Stepping Stone ditemukan oleh W. W Cooper dan A. Charnes (Pangestu Subagyo dkk, 1984). Menurut Parlin Sitorus (1997) ciri-ciri

metode Stepping Stone (Batu Loncatan) adalah

a. Jumlah sel berisi pada tabel penyelesaian awal sama dengan m+n-1 (m

adalah jumlah baris dan n adalah jumlah kolom).

b. Arah tujuan transportasi harus dimulai dari tempat asal ke tempat tujuan,

dan tidak boleh lebih dari satu tempat tujuan ke tempat tujuan lainnya.

c. Lintasan Steping Stone dapat melintasi sel kosong atau berisi.

1.5 Tujuan Penelitian

(48)

1.6Kontribusi Penelitian

Manfaat dari penelitian ini adalah sebagai berikut:

1. Membantu menyelesaikan masalah transshipment dengan Metode North West Corner (NWC) dan Metode Stepping Stone.

2. Sebagai informasi bagi penelitian selanjutnya yang berhubungan dengan

masalah transshipment.

1.7Metodologi Penelitian

Langkah-langkah yang akan dilakukan dalam menyelesaikan penelitian ini adalah:

1. Mencari literatur dari beberapa buku, jurnal dan karya tulis yang

berhubungan dengan Metode North West Corner (NWC) dan Metode Stepping Stone.

2. Menjelaskan definisi Metode Transportasi, transshipment, Metode North West Corner (NWC) dan Metode Stepping Stone.

3. Menyelesaikan permasalahan transshipment dengan penyelesaian awal

menggunakan Metode North West Corner Method (NWC) dan

pengoptimalan menggunakan Metode Stepping Stone.

4. Menyimpulkan hasil dan informasi dari penyelesaian permasalahan yang

(49)

PENYELESAIAN PERMASALAHAN TRANSSHIPMENT DENGAN METODE NORTH WEST CORNER DAN

METODE STEPPING STONE

ABSTRAK

Masalah tansshipment merupakan persoalan transportasi transisi atau persoalan transportasi yang termodifikasi. Tempat transit ini dapat menerima pasokan dan dapat mengirimkan barang. Tujuan utama masalah transshipment adalah meminimumkan biaya distribusi barang yang dikirim dari tempat asal ke tempat tujuan meskipun melalui tempat transit. Permasalahan dalam penelitian ini adalah bagaimana pengaruh metode North West Corner yang dilanjutkan dengan metode Stepping Stone terhadap peminimuman biaya transportasi pada Perusahaan penjualan peralatan rumah tangga. Tujuan penelitian ini adalah untuk mengetahui berapa biaya minimum yang dikeluarkan Perusahaan dalam pendistribusian produk perusahaan. Solusi layak dasar awal yaitu North West Corner yang kemudian dilanjutkan dengan pengujian solusi optimum dengan menggunakan Stepping Stone.

(50)

TRANSSHIPMENT PROBLEM SOLVING WITH NORTH WEST

CORNER’S METHOD AND STEPPING STONE METHOD

ABSTRACT

Tansshipment problem is transportation problem of transition or modified transportation problem. This transit area can receive supply and can deliver the goods. The main purpose of transshipment problem is to minimize the cost of distribution delivered goods from the place of origin to destination via transit point though. The problem in of this study are how the North West Corner method continued with method Stepping Stone to the optimization of transportation costs on the company's sales of household appliances. The purpose of this study was to determine the minimum costs incurred in the company's product distribution company. Initial basic feasible solution using the North West Corner Method followed by testing the optimum solution by using Stepping Stone Method.

Keywords : Transshipment Problem, North West Corner Method, Stepping Stone

(51)

PENYELESAIAN PERMASALAHAN TRANSSHIPMENT

DENGAN METODE NORTH WEST CORNER DAN

METODE STEPPING STONE

SKRIPSI

MEGAYANTI NADAPDAP

120803030

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(52)

PENYELESAIAN PERMASALAHAN TRANSSHIPMENT

DENGAN METODE NORTH WEST CORNER DAN

METODE STEPPING STONE

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar

Sarjana Sains

MEGAYANTI NADAPDAP

120803030

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(53)

PERSETUJUAN

Judul : Penyelesaian Permasalahan Transshipment dengan

Metode North West Corner dan Metode Stepping Stone

Kategori : Skripsi

Nama : Megayanti Nadapdap

Nomor Induk Mahasiswa : 120803030

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika Dan Ilmu Pengetahuan Alam

(FMIPA) Universitas Sumatera Utara

Diluluskan di

Medan, Juni 2016

Komisi Pembimbing:

Pembimbing 2, Pembimbing 1,

Drs. Marihat Situmorang, M.Kom Drs.Agus Salim Harahap, M.Si NIP. 19631214 198903 1 001 NIP. 19540828 198103 1 004

Disetujui oleh:

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si.

(54)

PERNYATAAN

PENYELESAIAN PERMASALAHAN TRANSSHIPMENT DENGAN METODE NORTH WEST CORNER DAN METODE

STEPPING STONE

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2016

MEGAYANTI NADAPDAP

(55)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus dengan kasih dan

berkatNya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul

Penyelesaian Permasalahan Transshipment dengan Metode North West Corner dan Metode Stepping Stone.

Terima kasih juga penulisa sampaikan kepada :

1. Bapak Drs. Agus Salim Harahap, M. Si selaku pembimbing 1 dan Bapak

Drs. Marihat Situmorang, M. Kom selaku pembimbing 2 yang telah

membimbing penulis selama penulisan skripsi ini.

2. Ibu Dra. Normalina Napitupulu, M. Sc dan Ibu Asima Manurung, S. Si,

M. Si selaku dosen penguji yang telah memberikan kritik dan saran yang

membangun dalam penyempurnaan skripsi ini.

3. Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dr. Mardiningsih, M.Si

selaku Ketua dan Sekretaris Departemen Matematika FMIPA-USU

Medan.

4. Bapak Dr. Kerista Sebayang, M. S selaku Dekan FMIPA USU serta

seluruh civitas akademika di lingkungan FMIPA USU.

5. Ayahanda Padang Nadapdap dan Ibunda Sarilla Panjaitan (Almh) serta

saudari penulis Ria Astuti Nadapdap yang selama ini memberikan

bantuan dan dorongan kepada penulis.

6. Teman-teman grup “Sama Wisuda” yaitu Sahata, Agustina, Goklim,

Oka, Willy, Daniel, Purnomo, Artha, Ayen, Fransiskus, Desi, dan

Yosephin atas motivasi, nasehat, semangat dan bantuannya kepada

penulis.

7. Kakanda Endang Tampubolon, S. Si dan Helena Nababan yang telah

menjadi motivator bagi penulis untuk memulai skripsi ini.

8. Teman-teman mahasiswa matematika stambuk 2012 dan teman-teman

(56)

PENYELESAIAN PERMASALAHAN TRANSSHIPMENT DENGAN METODE NORTH WEST CORNER DAN

METODE STEPPING STONE

ABSTRAK

Masalah tansshipment merupakan persoalan transportasi transisi atau persoalan transportasi yang termodifikasi. Tempat transit ini dapat menerima pasokan dan dapat mengirimkan barang. Tujuan utama masalah transshipment adalah meminimumkan biaya distribusi barang yang dikirim dari tempat asal ke tempat tujuan meskipun melalui tempat transit. Permasalahan dalam penelitian ini adalah bagaimana pengaruh metode North West Corner yang dilanjutkan dengan metode Stepping Stone terhadap peminimuman biaya transportasi pada Perusahaan penjualan peralatan rumah tangga. Tujuan penelitian ini adalah untuk mengetahui berapa biaya minimum yang dikeluarkan Perusahaan dalam pendistribusian produk perusahaan. Solusi layak dasar awal yaitu North West Corner yang kemudian dilanjutkan dengan pengujian solusi optimum dengan menggunakan Stepping Stone.

(57)

TRANSSHIPMENT PROBLEM SOLVING WITH NORTH WEST

CORNER’S METHOD AND STEPPING STONE METHOD

ABSTRACT

Tansshipment problem is transportation problem of transition or modified transportation problem. This transit area can receive supply and can deliver the goods. The main purpose of transshipment problem is to minimize the cost of distribution delivered goods from the place of origin to destination via transit point though. The problem in of this study are how the North West Corner method continued with method Stepping Stone to the optimization of transportation costs on the company's sales of household appliances. The purpose of this study was to determine the minimum costs incurred in the company's product distribution company. Initial basic feasible solution using the North West Corner Method followed by testing the optimum solution by using Stepping Stone Method.

Keywords : Transshipment Problem, North West Corner Method, Stepping Stone

(58)

DAFTAR ISI

1. 6 Kontribusi Penelitian 7

1. 7 Metodologi Penelitian 7

BAB 2 LANDASAN TEORI 8

2. 1 Masalah Transportasi 8

2. 2 Masalah Transshipment 10

2. 3 Metode Transportasi 11

2. 3. 1 Pengertian Metode Transportasi 11

2. 3. 2 Metode Transportasi Menggunakan Solusi Awal 11 2. 3. 3 Metode Transportasi Menggunakan Solusi Optimal 13

2. 4 Degenerasi 14