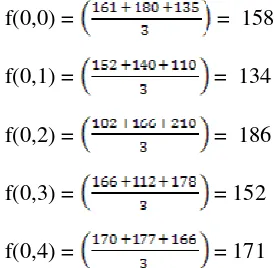Kombinasi Algoritma Jaringan Syaraf Tiruan Learning Vector Quantization (LVQ) Dan Self Organizing Kohonen Pada Kecepatan Pengenalan Pola Tanda Tangan

KOMBINASI ALGORITMA JARINGAN SYARAF TIRUAN

LEARNING VECTOR QUANTIZATION (LVQ) DAN SELF

ORGANIZING KOHONEN PADA KECEPATAN

PENGENALAN POLA TANDA TANGAN

TESIS

EMNITA BR GINTING

117038071

PROGRAM STUDI S2 TEKNIK INFORMATIKA

FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI

UNIVERSITAS SUMATERA UTARA

MEDAN

KOMBINASI ALGORITMA JARINGAN SYARAF TIRUAN

LEARNING VECTOR QUANTIZATION (LVQ) DAN SELF

ORGANIZING KOHONEN PADA KECEPATAN

PENGENALAN POLA TANDA TANGAN

TESIS

Diajukan untuk melengkapi tugas dan memenuhi syarat memperoleh

ijazah Magister Teknik Informatika

EMNITA BR GINTING

117038071

PROGRAM STUDI S2 TEKNIK INFORMATIKA

FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI

UNIVERSITAS SUMATERA UTARA

MEDAN

PERSETUJUAN

JUDUL : KOMBINASI ALGORITMA JARINGAN

SYARAF TIRUAN LEARNING VECTOR QUANTIZATION (LVQ) DAN SELF ORGANIZING KOHONEN PADA KECEPATAN PENGENALAN POLA TANDA TANGAN

NAMA : EMNITA BR GINTING

NOMOR INDUK MAHASISWA : 117038071

PROGRAM STUDI : MAGISTER TEKNIK INFORMATIKA

FAKULTAS : ILMU KOMPUTER DAN TEKNOLOGI INFORMASI

UNIVERSITAS SUMATERA UTARA Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dr. Zakarias Situmorang Prof. Dr. Muhammad Zarlis

Diketahui/disetujui oleh Ketua Program Studi,

PERNYATAAN

KOMBINASI ALGORITMA JARINGAN SYARAF TIRUAN LEARNING

VECTOR QUANTIZATION (LVQ) DAN SELF ORGANIZING KOHONEN PADA

KECEPATAN PENGENALAN POLA TANDA TANGAN

TESIS

Saya mengakui bahwa tesis ini adalah hasil karya saya sendiri, kecuali beberapa

kutipan dan ringkasan yang masing-masing telah disebutkan sumbernya.

Medan, Oktober 2013

Emnita br Ginting

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN

AKADEMIS

Sebagai sivitas akademika Universitas Sumatera Utara, saya yang bertanda tangan

dibawah ini:

Nama : Emnita br Ginting

NIM : 117038071

Program Studi : Teknik Informatika

Demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada

Universitas Sumatera Utara Hak Bebas Royalti Non-Eksklusif (Non-Exclusive Royalty

Free Right) atas tesis saya yang berjudul:

KOMBINASI ALGORITMA JARINGAN SYARAF TIRUAN LEARNING VECTOR QUANTIZATION (LVQ) DAN SELF ORGANIZING KOHONEN PADA

KECEPATAN PENGENALAN POLA TANDA TANGAN

Beserta perangkat yang ada (jika diperlukan). Dengan Hak Bebas Royalti

Non-Eksklusif ini, Universitas Sumatera Utara berhak menyimpan, mengalih media,

memformat, mengelola dalam bentuk database, merawat dan mempublikasikan tesis

saya tanpa meminta izin dari saya selama tetap mencantumkan nama saya sebagai

penulis dan sebagai pemegang dan/ atau sebagai pemilik hak cipta.

Demikian pernyataan ini dibuat dengan sebenarnya.

Medan, Oktober 2013

Emnita br Ginting

Telah diuji pada

Tanggal: Oktober 2013

PANITIA PENGUJI TESIS

Ketua : Prof.Dr.Muhammad Zarlis

Anggota : 1. Dr.Zakarias Situmorang

2. Prof.Dr.Herman Mawengkang

3. Prof.Dr.Tulus

RIWAYAT HIDUP

DATA PRIBADI

Nama Lengkap : Emnita br Ginting, S.Kom.

Tempat dan Tanggal Lahir : Juhar, 09 Februari 1987

Alamat Rumah : Jl. Setia Budi No. 285 A Tanjung Sari

Telepon/ Faks/ HP : (061) 8211129/ -/ 081375356664

E-mail : emnita_ginting@yahoo.com

Instansi Tempat Bekerja : -

Alamat Kantor : -

DATA PENDIDIKAN

SD : SDN No: 043944 Juhar TAMAT: 1999

SLTP : SLTP Negeri 1 Juhar TAMAT: 2002

SLTA : SMA Swasta Santo Thomas 1 Medan TAMAT: 2005

S1 : Ilmu Komputer Universitas Sumatera Utara TAMAT: 2010

KATA PENGANTAR

Puji syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa atas berkat, rahmat

dan karunianya berupa pengetahuan, kesehatan dan kesempatan yang diberikan

kepada penulis sehingga dapat menyelesaikan tesis dengan judul “KOMBINASI ALGORITMA JARINGAN SYARAF TIRUAN LEARNING VECTOR

QUANTIZATION (LVQ) DAN SELF ORGANIZING KOHONEN PADA

KECEPATAN PENGENALAN POLA TANDA TANGAN”.

Penulis dalam penyusunan untuk menyelesaikan tesis ini banyak mendapati

kesulitan dan kendala–kendala yang dihadapi, namun berkat bantuan, dorongan,

nasehat dari berbagai pihak terutama dari dosen pembimbing serta dari para dosen,

maka tugas tesis ini dapat diselesaikan dengan baik. Terutama tidak lepas dari

dorongan orang tua, kakak, adik yang juga telah banyak memberikan bantuan dan

dorongan hingga penulis dapat sampai pada TESIS ini.

Untuk itu penulis ingin menyampaiakan ucapan terimakasih yang sebesar–

besarnya kepada :

1. Kedua Orangtua saya Ayahanda Sebastianus Derom Ginting dan Ibunda

Sulaweti br Tarigan tercinta yang telah memberikan kasih sayangnya, doa

yang tak pernah putus serta dorongan moril maupun materil kepada saya

sehingga dapat menyelesaikan tesis ini dengan baik.

2. Bapak Prof. Dr. Muhammad Zarlis, selaku Ketua Program Studi

Pascasarjana Teknik Informatika Fakultas Ilmu Komputer dan Teknologi

Informasi Sumatera Utara Medan sekaligus Pembimbing I yang telah

bersedia memberikan bimbingan serta pengarahan hingga selsesainya

penulisan tesis ini.

3. Bapak Dr. Zakarias Situmorang selaku Dosen Pembimbing II yang telah

bersedia memberikan bimbingan serta pengarahan hingga selesainya

penulisan tesis ini.

4. Bapak Dosen Penguji yang telah memberikan saran untuk perbaikan dan

5. Bapak dan Ibu Dosen yang telah memberikan materi perkuliahan dan ilmu

pengetahuan selama penulis menyelesaikan Program Studi Pascasarjana

Teknik Informatika.

6. Segenap sivitas akademika Program Studi Pascasarjana Teknik

Informatika Sumatera Utara.

7. Teman – teman seperjuangan Angkatan 2011 Kom-C yang telah

memberikan dukungan dalam penyelesaian tesis ini.

8. Kakak saya Raskarina Ginting dan Rehlitna Ginting, adik saya Ingan

Pulungta Ginting, serta sepupu saya Nopita Tarigan yang telah banyak

memberikan dorongan dan bantuan kepada saya sehingga dapat

menyelesaikan tesis ini dengan baik.

Penulis menyadari bahwa masih ada kekurangan dalam penulisan tesis ini, untuk

itu, penulis mengharapkan kritik dan saran dari pembaca demi kesempurnaan

penelitian selanjutnya.

Akhir kata penulis berharap semoga karya ilmiah ini dapat bermanfaat bagi semua

pihak, khususnya dalam bidang pendidikan.

Medan, Oktober 2013

Penulis

Emnita br Ginting

ABSTRAK

Tanda tangan adalah sebuah bentuk khusus dari tulisan tangan yang mengandung karakter khusus dan bentuk-bentuk tambahan yang sering digunakan sebagai bukti verifikasi identitas seseorang. Sebagian tanda tangan dapat dibaca, namun banyak pula tanda tangan yang tidak dapat dibaca. Kendati demikian, sebuah tanda tangan dapat ditangani sebagai sebuah citra sehingga dapat dikenali dengan menggunakan aplikasi pengenalan pola pada pengolahan citra. Karena tanda tangan merupakan mekanisme primer untuk authentication dan authorization dalam transaksi legal, maka kebutuhan akan penelitian pada pengembangan aplikasi pengenalan dan verifikasi tanda tangan secara otomatis dan efisien meningkat dari tahun ke tahun. Metode yang banyak digunakan dalam pengenalan tanda tangan adalah metode jaringan syaraf tiruan. Pada jaringan syaraf tiruan terdapat proses pembelajaran serta pengenalan. Salah satu algoritma jaringan syaraf tiruan adalah Learning Vector Quantization (LVQ) dan Self Organizing Kohonen. Proses-proses yang terjadi pada metode jaringan syaraf tiruan memerlukan waktu yang relatif lama. Hal ini dipengaruhi banyaknya sampel data yang digunakan sebagai alat update bobot yang dilatih. Semakin banyak dan besar ukuran dari pola yang dilatih, semakin lama pula waktu yang dibutuhkan jaringan. LVQ adalah suatu metode pelatihan pada lapisan kompetitif terawasi yang akan belajar secara otomatis untuk mengklasifikasikan vektor-vektor input kedalam kelas-kelas tertentu. Kelas-kelas-kelas yang dihasilkan tergantung pada jarak antara vektor-vektor input. Jika ada 2 vektor input yang hampir sama maka lapisan kompetitif akan mengklasifikasikan kedua vektor input tersebut ke dalam kelas yang sama. Jaringan Self Organizing Kohonen merupakan salah satu model jaringan syaraf tiruan yang menggunakan metode pembelajaran tanpa supervisi atau tak terbimbing yang menyerupai model jaringan syaraf manusia. Untuk mempercepat proses komputansi pada training dan recognition maka dibangun sebuah algoritma kombinasi antara LVQ dengan Self Organizing Kohonen dengan memodifikasi pemberian bobot sehingga diperoleh waktu yang lebih singkat dalam proses training serta recognition.

COMBINATION ALGORITHM OF NEURAL NETWORK LEARNING legible signature, but many signatures that can not be read. However, a signature can be handled as an image so that it can be recognized using pattern recognition applications in image processing. Because the signature is the primary mechanism for authentication and authorization in legal transactions, the need for research on the development of recognition applications and automatic signature verification and efficiently increases from year to year. The method is widely used in signature recognition is a method of artificial neural network. On artificial neural networks are learning and recognition. One neural network algorithm is Learning Vector Quantization ( LVQ ) and Self Organizing Kohonen. Processes that occur in the neural network method requires a relatively long time. It is influenced by the number of data samples are used as a means of weight training update. The more and the large size of the pattern being trained, the longer the time it takes the network. LVQ is a method of training the unsupervised competitive layer will automatically learn to classify input vectors into certain classes. The classes are generated depends on the distance between the input vectors. If there are 2 input vectors are nearly as competitive layer will then classify both the input vectors into the same class. Kohonen Self Organizing Network is one of the neural network model which uses learning methods or unguided unsupervised neural network model that resembles humans. To speed up the computing process in the training and recognition is then developed an algorithm and a combination of LVQ and Self Organizing Kohonen by modifying the weight given to obtain a shorter time in the process of training and recognition.

4.2.2 Proses Recognition 63

BAB 5 KESIMPULAN DAN SARAN 66

5.1 Kesimpulan 66

5.2 Saran 66

Gambar 3.14 Flow Chart Pengenalan Tanda Tangan Metode Self Organizing

Kohonen ………...…. 39

Gambar 3.15 Flow Chart Proses Pengenalan Tanda Tangan dengan Jaringan

New JST ………. 40

Gambar 3.16 Flow Chart Pengenalan Tanda Tangan Metode New JST… 41

Gambar 3.17 Flow Chart Pengenalan Tanda Tangan Metode New JST

(Lanjutan) ……….. 42

Gambar 4.1 Tampilan Menu Utama Aplikasi ………... 56

Gambar 4.2 Tampilan Proses Training Tanda Tangan Metode LVQ ….. 57

Gambar 4.3 Tampilan Proses Training Tanda Tangan Metode Self Organizing

Kohonen ……… 57

Gambar 4.4 Tampilan Proses Training Tanda Tangan Metode New JST. 58

Gambar 4.5 Tampilan Pengenalan Tanda Tangan Metode LVQ ……… 59

Gambar 4.6 Tampilan Pengenalan Tanda Tangan Metode Self Organizing

Kohonen ……….. 59

Gambar 4.7 Tampilan Pengenalan Tanda Tangan Metode New JST .... 60

Gambar 4.8 Tampilan Training Tanda Tangan Metode LVQ ……….... 61

Gambar 4.9 Tampilan Training Tanda Tangan Metode Self Organizing

Kohonen ……….. 62

Gambar 4.10 Tampilan Training Tanda Tangan Metode New JST …... 62

Gambar 4.11 Tampilan Pengenalan Tanda Tangan Metode LVQ ….... 63

Gambar 4.12 Tampilan Pengenalan Tanda Tangan Metode Self Organizing

Kohonen ………..… 64

DAFTAR TABEL

Halaman

Tabel 2.1 Perbedaan Jaringan Syaraf Biologis dengan JST ... 14

Tabel 3.1 Data Matrik Input Gambar ... 43

Tabel 3.2 Data Bobot ……….. 43

ABSTRAK

Tanda tangan adalah sebuah bentuk khusus dari tulisan tangan yang mengandung karakter khusus dan bentuk-bentuk tambahan yang sering digunakan sebagai bukti verifikasi identitas seseorang. Sebagian tanda tangan dapat dibaca, namun banyak pula tanda tangan yang tidak dapat dibaca. Kendati demikian, sebuah tanda tangan dapat ditangani sebagai sebuah citra sehingga dapat dikenali dengan menggunakan aplikasi pengenalan pola pada pengolahan citra. Karena tanda tangan merupakan mekanisme primer untuk authentication dan authorization dalam transaksi legal, maka kebutuhan akan penelitian pada pengembangan aplikasi pengenalan dan verifikasi tanda tangan secara otomatis dan efisien meningkat dari tahun ke tahun. Metode yang banyak digunakan dalam pengenalan tanda tangan adalah metode jaringan syaraf tiruan. Pada jaringan syaraf tiruan terdapat proses pembelajaran serta pengenalan. Salah satu algoritma jaringan syaraf tiruan adalah Learning Vector Quantization (LVQ) dan Self Organizing Kohonen. Proses-proses yang terjadi pada metode jaringan syaraf tiruan memerlukan waktu yang relatif lama. Hal ini dipengaruhi banyaknya sampel data yang digunakan sebagai alat update bobot yang dilatih. Semakin banyak dan besar ukuran dari pola yang dilatih, semakin lama pula waktu yang dibutuhkan jaringan. LVQ adalah suatu metode pelatihan pada lapisan kompetitif terawasi yang akan belajar secara otomatis untuk mengklasifikasikan vektor-vektor input kedalam kelas-kelas tertentu. Kelas-kelas-kelas yang dihasilkan tergantung pada jarak antara vektor-vektor input. Jika ada 2 vektor input yang hampir sama maka lapisan kompetitif akan mengklasifikasikan kedua vektor input tersebut ke dalam kelas yang sama. Jaringan Self Organizing Kohonen merupakan salah satu model jaringan syaraf tiruan yang menggunakan metode pembelajaran tanpa supervisi atau tak terbimbing yang menyerupai model jaringan syaraf manusia. Untuk mempercepat proses komputansi pada training dan recognition maka dibangun sebuah algoritma kombinasi antara LVQ dengan Self Organizing Kohonen dengan memodifikasi pemberian bobot sehingga diperoleh waktu yang lebih singkat dalam proses training serta recognition.

COMBINATION ALGORITHM OF NEURAL NETWORK LEARNING legible signature, but many signatures that can not be read. However, a signature can be handled as an image so that it can be recognized using pattern recognition applications in image processing. Because the signature is the primary mechanism for authentication and authorization in legal transactions, the need for research on the development of recognition applications and automatic signature verification and efficiently increases from year to year. The method is widely used in signature recognition is a method of artificial neural network. On artificial neural networks are learning and recognition. One neural network algorithm is Learning Vector Quantization ( LVQ ) and Self Organizing Kohonen. Processes that occur in the neural network method requires a relatively long time. It is influenced by the number of data samples are used as a means of weight training update. The more and the large size of the pattern being trained, the longer the time it takes the network. LVQ is a method of training the unsupervised competitive layer will automatically learn to classify input vectors into certain classes. The classes are generated depends on the distance between the input vectors. If there are 2 input vectors are nearly as competitive layer will then classify both the input vectors into the same class. Kohonen Self Organizing Network is one of the neural network model which uses learning methods or unguided unsupervised neural network model that resembles humans. To speed up the computing process in the training and recognition is then developed an algorithm and a combination of LVQ and Self Organizing Kohonen by modifying the weight given to obtain a shorter time in the process of training and recognition.

BAB 1 PENDAHULUAN

1.1Latar Belakang

Jaringan Syaraf Tiruan (JST) adalah sebuah alat pemodelan data statistik non-linier.

JST dapat digunakan untuk memodelkan hubungan yang kompleks antara input dan

output untuk menemukan pola-pola pada data. Jaringan Syaraf Tiruan merupakan

salah satu sistem pemrosesan informasi yang didesain dengan menirukan cara kerja

otak manusia dalam menyelesaikan suatu masalah dengan melakukan proses

pembelajaran melalui perubahan bobot sinapsisnya. Sebuah JST dikonfigurasikan

untuk aplikasi tertentu seperti pengenalan pola atau klasifikasi data, melalui proses

pembelajaran. Pada proses pembelajaran, kedalam jaringan saraf tiruan dimasukkan

pola-pola input atau output lalu jaringan akan diajari untuk memberikan jawaban yang

bisa diterima.

Pada penelitian Prabowo dengan judul Perbandingan Antara Metode Kohonen

Neural Network dengan Metode Learning Vector Quantization pada Pengenalan Pola

Tandatangan memberikan hasil bahwa dengan menggunakan pola-pola yang sudah

disediakan, metode LVQ lebih akurat dalam mengklasifikasikan tanda tangan dengan

rata-rata keberhasilan sebesar 93.80 % dibanding dengan metode Kohonen (89.59%).

Hal ini disebabkan proses update faktor pembobot metode LVQ yang menggunakan

banyak pola untuk proses pelatihan dibandingkan metode Kohonen yang bobot

awalnya diambil secara acak dan di-update hingga dapat mengklasifikasikan diri

sejumlah kelas yang diinginkan (Prabowo, 2006).

Proses pembelajaran menggunakan metode LVQ memerlukan waktu yang relatif

lebih lama daripada metode Kohonen. Hal ini dipengaruhi banyaknya sampel pola

yang digunakan sebagai alat update bobot yang dilatih. Semakin banyak dan besar

ukuran dari pola yang dilatih, semakin lama pula waktu yang dibutuhkan metode LVQ

untuk proses pelatihan.

Dari hasil perbandingan diatas didapat bahwa metode Kohonen dapat melakukan

proses pembelajaran lebih cepat untuk mengklasifikasikan tandatangan dibanding

metode LVQ meskipun dari faktor keberhasilan dalam mengklasifikasikan pola,

JST terdiri dari beberapa metode yaitu metode Hebb Rule, Perceptron, Delta Rule,

Backpropagation, Heteroassociative Memory (BAM), Learning Vector Quantization

serta Self Organizing Kohonen. Jaringan syaraf yang digunakan oleh penulis adalah

jaringan syaraf tiruan dengan metode Learning Vector Quantization (LVQ) dan

metode Backpropagation. Disini penulis ingin mengkombinasikan kedua metode di

atas untuk mempercepat proses pengenalan tanda tangan.

LVQ adalah suatu metode pelatihan pada lapisan kompetitif terawasi yang akan

belajar secara otomatis untuk mengklasifikasikan vektor-vektor input kedalam

kelas-kelas tertentu. Kelas-kelas-kelas yang dihasilkan tergantung pada jarak antara vektor-vektor

input. Jika ada 2 vektor input yang hampir sama maka lapisan kompetitif akan

mengklasifikasikan kedua vektor input tersebut ke dalam kelas yang sama.

Jaringan Self Organizing Kohonen merupakan salah satu model jaringan syaraf

tiruan yang menggunakan metode pembelajaran tanpa supervisi atau tak terbimbing

(unsupervised learning) yang menyerupai model jaringan syaraf manusia. Sifat

antropometric tersebut ditunjukkan dengan kemampuan menerima masukan dan

reaksinya yang lazim dimiliki manusia (Valenturf, 1995). Keunggulan lain dari

algoritma Self Organizing Kohonen adalah mampu untuk memetakan data berdimensi

tinggi kedalam bentuk peta berdimensi rendah. Proses pemetaan terjadi apabila sebuah

pola berdimensi bebas diproyeksikan dari ruang masukan ke posisi pada array

berdimensi satu atau dua.

Tanda tangan adalah sebuah bentuk khusus dari tulisan tangan yang mengandung

karakter khusus dan bentuk-bentuk tambahan yang sering digunakan sebagai bukti

verifikasi identitas seseorang. Sebagian tanda tangan dapat dibaca, namun banyak pula

tanda tangan yang tidak dapat dibaca (unreadable). Kendati demikian, sebuah tanda

tangan dapat ditangani sebagai sebuah citra sehingga dapat dikenali dengan

menggunakan aplikasi pengenalan pola pada pengolahan citra (Qur’ani, 2010).

Karena tanda tangan merupakan mekanisme primer untuk authentication dan

authorization dalam transaksi legal, kebutuhan akan penelitian pada pengembangan

aplikasi pengenalan dan verifikasi tanda tangan yang otomatis dan efisien meningkat

pada tahun-tahun terakhir ini (Qur’ani, 2010).

Pengenalan dan verifikasi tanda tangan meliputi dua bagian yang berbeda tetapi

berkaitan erat satu sama lain. Yang pertama adalah identifikasi dari pemilik tanda

atau dipalsukan. Selain itu, bergantung pada kebutuhannya, pengenalan tanda

tangan dibagi menjadi dua kelas yang berbeda yaitu pengenalan dan verifikasi tanda

tangan online dan offline. Pada pengenalan secara on line, dibutuhkan beberapa alat

bantu khusus yang digunakan untuk mengukur kecepatan dan tekanan tangan ketika

membuat tanda tangan. Dilain pihak, hampir semua sistem pengenalan tanda tangan

offline bergantung pada teknik pengolahan citra dan feature extraction (Qur’ani,

2010).

Dengan melihat penelitian Prabowo diatas, maka penulis berniat melakukan

melakukan kombinasi dari kedua algoritma dengan mengambil kelebihan dari

masing-masing algoritma diatas dan memberi judul tesis ini dengan Kombinasi Algoritma

Jaringan Syaraf Tiruan Learning Vector Quantization (LVQ) dengan Self Organizing

Kohonen pada Kecepatan Pengenalan Pola Tanda Tangan.

1.2Rumusan Masalah

Berdasarkan latar belakang, maka yang menjadi rumusan masalah pada penelitian ini

adalah:

Bagaimana peningkatan kecepatan proses pengenalan pola tanda tangan dengan

mengkombinasikan algoritma Learning Vector Quantizatin dan Self Organizing

Kohonen.

1.3Tujuan Penelitian

Penelitian ini bertujuan untuk mengkombinasikan algoritma Learning Vector

Quantization dan Self Organizing Kohonen untuk mempercepat pengenalan pola tanda

tangan.

1.4Batasan Masalah

Adapun batasan masalah pada tesis ini adalah:

a. Input data pelatihan dan pengujian berupa file citra tanda tangan hasil scan

b. Proses kecepatan pengenalan pola tandatangan dilakukan dengan

mengkombinasi algoritma Learning Vector Quantization dengan Self

Organizing Kohonen.

1.5Metodologi Penelitian

Metode penelitian dalam penyusunan tugas ini dibagi menjadi dua tahap yaitu, tahap

pengumpulan data serta pembangunan perangkat lunak.

1.5.1 Tahap Pengumpulan Data

Teknik pengumpulan yang dilakukan adalah study pustaka atau study literatur.

Pengumpulan data dengan cara mengumpulkan literatur, jurnal, paper dan

bacaan-bacaan yang ada kaitannya dengan judul penelitian.

1.5.2 Tahap Pembangunan Perangkat Lunak

Pada tahap ini dilakukan penulisan program yang sesuai dengan algoritma yang sudah

BAB 2

LANDASAN TEORI

2.1 Citra Digital

Citra merupakan fungsi kontinyu dari intensitas cahaya pada bidang dua dimensi.

Intensitas cahaya merupakan hasil kali antara jumlah pancaran (illuminasi) cahaya

yang diterima objek dengan derajat kemampuan obyek memantulkan cahaya. Citra

digital umumnya direpresentasikan dalam bentuk matriks 2 dimensi dengan ukuran

NxM. Elemen terkecil dalam citra digital (elemen matriks) disebut pixel. Setiap nilai

pixel pada citra merepresentasikan nilai intensitas cahaya (Budi, 2009).

Nilai fungsi intensitas f(x,y) memiliki rentang nilai yang disebut skala keabuan, yaitu:

l min < f(x,y) < l max atau 0 f(x,y) L-1 ... (1)

Dimana:

f(x,y) : nilai intensitas pada posisi x,y.

lmax = L : nilai max intensitas (skala keabuan)

l min : nilai min intensitas

Suatu citra dapat didefinisikan sebagai fungsi f(x,y), berukuran M baris dan N

kolom, dengan x dan y adalah koordinat spasial dan amplitudo f di titik kordinat f(x,y)

dinamakan intensitas atau tingkat keabuan dari citra pada titik tersebut. Apabila nilai

x, y dan nilai amplitudo f secara keseluruhan berhingga (finite) dan nilai bernilai

Kordinat citra digital dapat dilihat pada Gambar 2.1.

Gambar 2.1 Kordinat Citra Digital

Sebuah citra digital dapat diwakili oleh sebuah matriks dua dimensi f(x,y) yang

terdiri dari M kolom dan N baris, dimana perpotongan antara kolom dan baris disebut

piksel (pixel = picture element) atau elemen terkecil dari sebuah citra. Citra digital

dapat ditulis dalam bentuk matrik sebagai berikut (Kusumanto,, 2011).

………... (2)

Suatu citra ƒ(x,y) dalam fungsi matematis dapat dituliskan sebagai berikut:

0 x M-1

0 y N-1

0 ƒ(x,y) G-1

dimana :

M = jumlah piksel baris (row) pada array citra

G = nilai skala keabuan (graylevel)

Besarnya nilai M, N dan G pada umumnya merupakan perpangkatan dari dua.

M = 2m ; N = 2n; G = 2k ... (3)

Dimana:

Nilai m, n dan k adalah bilangan bulat positif. Interval (0,G) disebut skala keabuan

(grayscale). Besar G tergantung pada proses digitalisasinya. Biasanya keabuan 0 (nol)

menyatakan intensitas hitam dan 1 (satu) menyatakan intensitas putih. Untuk citra 8

bit, nilai G sama dengan 28 = 256 warna (derajat keabuan).

Gambar 2.2 Representasi Citra Digital Dalam 2 Dimensi (Kusumanto, 2011)

Jenis citra berdasarkan nilai pikselnya adalah sebagai berikut (Putra, 2010):

1. Citra Biner

Citra biner adalah citra digital yang hanya memiliki dua kemungkinan nilai piksel

yaitu hitam dan putih. Citra biner juga disebut sebagai citra black and white (B&W)

atau citra monokrom. Hanya dibutuhkan 1 bit untuk mewakili nilai setiap piksel dari

citra biner. Citra biner sering kali muncul sebagai hasil dari proses pengolahan seperti

Gambar 2.3 Citra Biner (Putra, 2010)

2. Citra Grayscale

Citra grayscale merupakan citra digital yang hanya memiliki satu nilai kanal pada

setiap pikselnya, dengan kata lain nilai bagian RED=Green=Blue. Nilai tersebut

digunakan untuk menunjukkan tingkat intensitas. Warna yang dimiliki adalah warna

dari hitam, keabuan dan putih. Tingkatan keabuan disini merupakan warna abu

dengan berbagai tingkatan dari hitam hingga mendekati putih. Citra grayscale berikut

memiliki kedalaman warna 8 bit (256 kombinasi warna keabuan).

Gambar 2.4 Citra Keabuan (Putra, 2010)

3. Citra Warna (8 bit)

Setiap piksel dari citra warna (8 bit) hanya diwakili oleh 8 bit dengan jumlah warna

maksimum yang dapat digunakan adalah 256 warna. Ada dua jenis citra warna 8 bit.

Pertama, citra warna 8 bit dengan menggunakan palet warna 256 dengan setiap

paletnya memiliki pemetaan nilai (colormap) RGB tertentu. Model ini lebih sering

digunakan. Kedua, setiap pixel memiliki format 8 bit sebagai berikut.

Bit-7 Bit-6 Bit-5 Bit-4 Bit-3 Bit-2 Bit-1 Bit-0

R R R G G G B B

Gambar 2.5 8 bit true color

Gambar 2.6 Citra Warna 8 bit (Putra, 2010)

4. Citra Warna (16 bit)

Citra warna 16 bit (biasanya disebut sebagai citra highcolor) dengan setiap pikselnya

diwakili dengan 2 byte memory (16 bit). Warna 16 bit memiliki 65536 warna.

Gambar 2.7 Citra Warna 16 bit (Putra, 2010)

5. Citra Warna (24 bit)

2.2Pengolahan Data Citra

Data yang digunakan dalam penelitian ini adalah sekumpulan citra untuk

pembelajaran (learning data set) dan sekumpulan citra untuk pengujian (testing

data set) yang diperoleh dari hasil scanning tanda tangan. Citra tanda tangan yang

digunakan berukuran 340 x 272 pixel. Citra tersebut mengalami proses konversi

ke gray scaling jika merupakan citra true color, selanjutnya citra akan dikenai proses

deteksi tepi berbasis gradien dengan operator Roberts, yang dilanjutkan dengan proses

operasi negasi. Citra analisis merupakan citra grayscale dengan skala 8 bit yang

memiliki intensitas warna berkisar antara 0 sebagai nilai minimum sampai 255 yang

merupakan nilai maksimum. Citra analisis kemudian dikonversi ke dalam barisan

bilangan biner sepanjang 340 x 272 untuk masing-masing citra. Untuk setiap pixel

dengan nilai intensitas warna 237 diberi nilai 1, sedangkan untuk nilai intensitas

warna > 237 diberi nilai 0, sehingga akan diperoleh barisan nilai yang terdiri

dari 0 dan 1 sepanjang 92480 elemen. Kemudian dilakukan proses pembagian

region (wilayah) sehingga menghasilkan 10 x 8 region yang berisi penjumlahan nilai

pixel dalam region yang masing-masingnya berukuran 34x34 pixel.

2.3Edge Detection Method

Edge detection atau deteksi tepi digunakan untuk melihat apakah suatu edge atau tepi

melewati atau berada di dekat suatu titik (pixel) dalam sebuah citra (Sigit,dkk.,2005).

Tepi adalah batas antara dua daerah dengan sifat tingkat keabuan yang relatif berbeda.

Tujuan dari deteksi tepi adalah menandai bagian yang menjadi detil citra, dan

memperbaiki detil citra yang kabur karena error atau efek proses akuisisi citra (Sigit,

dkk.,2005). Batas suatu obyek semakin nampak bersamaan dengan ketidak

kontinuitasan intensitas dalam suatu citra. Eksperimen pada sistem penglihatan

manusia menunjukkan bahwa suatu citra sangat penting, bahkan suatu obyek dapat

dikenali hanya dari garis bentuk kasarnya saja (croude outline). Kenyataan ini

merupakan konsep prinsip untuk merepresentasikan suatu obyek melalui batasnya.

Tepi lokal (local edge) adalah daerah kecil dalam suatu citra yang tingkat keabuan

lokalnya berubah dengan sangat cepat dengan cara yang sederhana (misalnya

monotonik). Operator tepi (edge operator) adalah operator matematis (atau yang hasil

komputasinya ekuivalen), yang dengan perluasan kecil, didesain untuk mendeteksi

keberadaan tepi lokal dalam suatu fungsi citra (Low, 1991). Pada intinya, ide yang

mendasari sebagian algoritma pendeteksian tepi adalah perhitungan suatu operator

derivatif lokal. Dalam teknik deteksi tepi ini, diasumsikan bahwa tepi adalah pixel

yang memiliki nilai gradien tinggi. Gradien itu sendiri adalah ukuran besarnya

perubahan intensitas yang terjadi.

Pada citra digital f(x,y) turunan berarah sepanjang sekian obyek akan bernilai

maksimum pada arah normal dari kontur tepian yang bersesuaian. Sifat ini

dipergunakan sebagai dasar pemanfaatan operator gradien sebagai deteksi tepi.

Gradien suatu citra f(x,y) pada lokasi x,y data didefinisikan sebagai vektor.

... (2.1)

Operator gradien menghitung intensitas perubahan tingkat keabuan dan arah dimana

bertetangga. Operator Robert Cross adalah operator gradien yang sederhana berukuran

2 x 2. Operator ini menyediakan pendekatan paling sederhana dari magnitude gradien,

yang dapat ditunjukkan dengan fungsi matematis berikut ini, yaitu:

... (2.2)

Mask konvolusi untuk Operator Roberts adalah:

Gambar 2 menunjukkan algoritma deteksi tepi dengan operator Robert yang diikuti

dengan proses negasi. Pengurangan 255 terhadap nilai hasil penjumlahan 2 konvolusi

dari citra dimaksudkan untuk menegasikan, karena hasil konvolusi biasanya berada di

sekitar nilai 0 (nilai kecil), sehingga jika ditampilkan, citra tepi kebanyakan berwarna

gelap (hitam).

2.4Jaringan Syaraf Biologi

Otak manusia memiliki struktur yang sangat kompleks dan memiliki kemampuan

yang luar biasa. Otak terdiri dari neuron-neuron dan penghubung yang disebut

sinapsis. Neuron bekerja berdasarkan impuls/sinyal yang diberikan pada neuron.

Neuron meneruskannya pada neuron lain. Diperkirakan manusia memiliki 1012 neuron

dan 6x1018 sinapsis. Dengan jumlah yang begitu banyak, otak mampu mengenali pola,

melakukan perhitungan, dan mengontrol organ-organ tubuh dengan kecepatan yang

lebih tinggi dibandingkan komputer digital (Puspitaningrum, 2006). Sebagai

perbandingan, pengenalan wajah seseorang yang sedikit berubah misal memakai topi,

memiliki jenggot tambahan dan lainnya akan lebih cepat dilakukan manusia

dibandingkan komputer. Pada waktu lahir, otak mempunyai struktur yang

menakjubkan karena kemampuannya membentuk sendiri aturan-aturan/pola

berdasarkan pengalaman yang diterima. Jumlah dan kemampuan neuron berkembang

seiring dengan pertumbuhan fisik manusia, terutama pada umur 0-2 tahun. Pada 2

Gambar 2.10 Susunan Neuron Biologis [Puspitaningrum, 2006]

Menurut Medsker dan Liebowitz dalam Septiani (2005) perbedaan terminologis

antara jaringan syaraf biologis dan tiruan disajikan pada Tabel 2.1.

Tabel 2.1 Perbedaan Jaringan Syaraf Biologis dengan JST [Septiani, 2005]

Neuron memiliki 3 komponen penting yaitu dendrit, soma dan axon. Dendrit

menerima sinyal dari neuron lain. Sinyal/tersebut berupa impuls elektrik yang dikirim

melalui celah sinaptik melalui proses kimiawi. Sinyal tersebut dimodifikasi

(diperkuat/diperlemah) di celah sinaptik. Berikutnya, soma menjumlahkan semua

sinyal-sinyal yang masuk. Kalau jumlahan tersebut cukup kuat dan melebihi batas

ambang (threshold), maka sinyal tersebut akan diteruskan ke sel lain melalui axon.

Frekuensi penerusan sinyal berbeda-bedaantara satu sel dengan yang lain. Neuron

biologi merupakan sistem yang "fault tolerant" dalam 2 hal. Pertama, manusia dapat

mengenali sinyal input yang agak berbeda dari yang pernah kita terima sebelumnya.

Sebagai contoh, manusia sering dapat mengenali seseorang yang wajahnya pernah

dilihat dari foto, atau dapat mengenali seseorang yang wajahnya agak berbeda karena

sudah lama tidak dijumpainya. Kedua, otak manusia tetap mampu bekerja meskipun

neuron lain kadang-kadang dapat dilatih untuk menggantikan fungsi sel yang rusak

tersebut.

2.5Jaringan Syaraf Tiruan (Neural Network (NN))

Jaringan Syaraf Tiruan (JST) adalah suatu metode pembelajaran yang diinspirasi dari

jaringan sistem pembelajaran biologis yang terjadi dari jaringan sel syaraf (neuron)

yang terhubung satu dengan yang lainnya (Silvia, 2007).

Berikut adalah beberapa definisi JST :

a. JST adalah suatu teknik pemrosesan informasi berbasis komputer yang

mensimulasikan dan memodelkan sistem syaraf biologis.

b. Suatu model matematik yang mengandung sejumlah besar elemen pemroses

yang diorganisasikan dalam lapisan-lapisan.

c. Suatu sistem komputasi yang dibuat dari sejumlah elemen pemroses yang

sederhana dan saling diinterkoneksikan untuk memproses informasi melalui

masukan dari luar dan mampu inresponsi keadaan yang dinamis.

d. JST adalah suatu teknologi komputasi yang berbasis hanya pada model syaraf

biologis dan mencoba mensimulasikan tingkah laku dan kerja model syaraf.

e. JST adalah sistem pemroses informasi yang memiliki karakteristik mirip

dengan jaringan syaraf biologi. JST dibentuk sebagai generalisasi model

matematika dari jaringan syaraf biologi, dengan asumsi bahwa :

1. Pemrosesan informasi terjadi pada banyak elemen sederhana (neuron).

2. Sinyal dikirirnkan diantara neuron-neuron melalui penghubung-penghubung.

3. Penghubung antar neuron memiliki bobot yang akan memperkuat atau

memperlemah sinyal.

4. Untuk menentukan output, setiap neuron menggunakan fungsi aktivasi

(biasanyabukan fungsi linier) yang dikenakan pada jumlahan input yang

diterima. Besarnya output ini selanjutnya dibandingkan dengan suatu batas

ambang.

2.5.1 Arsitektur Jaringan Syaraf

Ada beberapa arsitektur jaringan syaraf (Silvia, 2007), antara lain:

Pada jaringan ini, sekumpulan masukan neuron dihubungkan langsung dengan

sekumpulan keluarannya. Sinyal mengalir searah dari layar (lapisan) masukan

sampai layar (lapisan) keluaran. Setiap simpul dihubungkan dengan simpul

lainnya yang berada diatasnya dan dibawahnya, tetapi tidak dengan simpul yang

berada pada lapisan yang sama.

Model yang masuk kategori ini antara lain : ADALINE, Hopfield, Perceptron,

LVQ, dan lain-lain. Pada gambar berikut diperlihatkan arsitektur jaringan layar

tunggal dengan n buah masukan (x1, x2,..., xn) dan m buah keluaran (y1, y2,...,

ym)

Gambar 2.11 Jaringan Syaraf Tiruan dengan Lapisan Tunggal [Puspitorini, 2008]

b. Jaringan dengan Banyak Lapisan (Multiple Layer Network)

Jaringan dengan banyak lapisan memiliki 1 atau lebih lapisan yang terletak

diantara lapisan input dan lapisan output. Seperti terlihat gambar dibawah ada

lapisan lapisan yang terletak diantara 2 lapisan yang bersebelahan. Jaringan

dengan banyak lapisan ini dapat menyelesaikan permasalahan lebih sulit dari pada

jaringan lapisan tunggal, tentu saja dengan pembelajaran yang lebih rumit.

Namun demikian, pada banyak kasus, pembelajaran pada jaringan dengan banyak

lapisan ini lebih sukses dalam menyelesaikan masalah. Model yang termasuk

kategori ini antara lain : MADALINE, backpropagation.

Pada Gambar 2.3 diperlihatkan jaringan dengan n buah unit masukan (x1, x2,...,

xn), sebuah layar tersembunyi yang terdiri dari m buah unit (z1,z2,...,zm) dan 1

Gambar 2.12 Jaringan Syaraf Tiruan dengan Banyak Lapisan [Puspitorini, 2008]

c. Jaringan Reccurent

Model jaringan reccurent (reccurent network) mirip dengan jaringan layar

tunggal ataupun jamak. Hanya saja, ada simpul keluaran yanng memberikan

sinyal pada unit masukan (sering disebut feedback loop). Dengan kata lain sinyal

mengalir dua arah, yaitu maju dan mundur. Contoh : Hopfield network, Jordan

network, Elmal network.

2.5.2 Keuntungan Menggunakan Komputasi dengan JST

Kemampuan dan proses komputasi pada JST memberikan keuntungan-keuntungan

sebagai berikut :

1. JST bersifat adaptif terhadap perubahan parameter yang mempengaruhi

karakteristik sistem, sehingga pada proses belajar, JST mampu belajar secara

adaptif dan melaksanakan tugas berbasis pada data yang diberikan saat

pelatihan.

2. JST memiliki kekebalan atau toleran terhadap kesalahan. Artinya, JST tetap

berfungsi walaupun ada ketidak-lengkapan data yang dimasukkan. JST

mempunyai kemampuan mengisi bagian masukan yangkurang lengkap

sedemikian rupa sehingga tetap diperoleh keluaran yang lengkap.

3. JST dapat dilatih memberikan keputusan dengan memberikan set pelatihan

sebelumnya untuk mencapai target tertentu, sehingga JST mampu

membangun dan memberikan jawaban sesuai dengan informasi yang diterima

pada proses pelatihan.

4. JST mempunyai struktur paralel dan terdistribusi. Artinya, komputasi dapat

5. JST mampu mengklasiflkasi pola masukan dan pola keluaran. Melalui proses

penyesuaian, pola keluaran dihubungkan dengan masukan yang diberikan

oleh JST.

6. JST mengurangi derau, sehingga dihasilkan keluaran yang lebih bersih.

7. JST dapat dimanfaatkan pada proses optimisasi penyelesaian suatu masalah.

8. JST dapat digunakan pada proses pengendalian sistem agar masukan

memperoleh tanggapan yang diinginkan.

2.5.3 Algoritma Umum Jaringan Syaraf Tiruan

Algoritma pembelajaran/pelatihan jaringan syaraf tiruan adalah sebagai berikut:

Dimasukkan n contoh pelatihan ke dalam jaringan saraf tiruan.

Lakukan :

1. Inisialisasi bobot-bobot jaringan. Set i = 1.

2. Masukkan contoh ke-i (dari sekumpulan contoh pembelajaran yang terdapat

dalam set pelatihan) ke dalam jaringan pada lapisan input.

3. Cari tingkat aktivasi unit-unit output menggunakan algoritma aplikasi.

If kinerja jaringan memenuhi standar yang ditentukan

sebelumnya (memenuhi syarat berhenti)

then exit.

4. Update bobot-bobot dengan menggunakan aturan pembelajaran jaringan.

If i=n, then reset i = 1.

Else i = i - 1.

Ke langkah 2.

Algoritma aplikasi/inferensi jaringan saraf tiruan :

Dimasukkan sebuah contoh pelatihan ke dalam jaringan saraf tiruan. Lakukan:

1. Masukkan kasus ke dalam jaringan pada lapisan input.

2. Hitung tingkat aktivasi node-node jaringan.

3. Untuk jaringan koneksi umpan maju, jika tingkat aktivasi dari semua unit

output-nya telah dikalkulasi, maka exit. Untuk jaringan koneksi balik, jika

tingkat aktivasi dari semua unit output menjadi konstan atau mendekati

konstan, maka exit. J jika tidak, kembali ke langkah 2. Jika jaringannya tidak

stabil, maka exit dan fail.

Ada beberapa fungsi aktivasi yang sering digunakan dalam jaringan saraf tiruan,

antara lain (Puspitorini, 2008):

a. Fungsi Undak Biner Hard Limit

Jaringan dengan lapisan tunggal sering menggunakan fungsi undak (step function)

untuk mengkonversikan input dari suatu variabel yang bernilai kontinu ke suatu

output biner (0 atau 1).

Fungsi undak biner hard limit dirumuskan sebagai berikut:

y =

Gambar 2.13 Fungsi aktivasi: Undak Biner Hard Limit [Puspitorini, 2008]

b. Fungsi Undak Biner Threshold

Fungsi undak biner dengan menggunakan nilai ambang sering juga disebut

dengan nama fungsi nilai ambang (threshold) atau fungsi Heaviside. Fungsi

undak biner (dengan nilai ambang ) dirumuskan sebagai berikut:

y =

Sumber: Puspitorini, 2008

Gambar 2.14 Fungsi aktivasi: Undak Biner Threshold [Puspitorini, 2008]

2.6Sejarah Jaringan Syaraf Tiruan

Jaringan syaraf tiruan sederhana pertama kali diperkenalkan oleh McCulloch dan Pitts

di tahun 1943. McCulloch dan Pitts menyimpulkan bahwa kombinasi beberapa neuron

sederhana menjadi sebuah sistem neural akan meningkatkan kemampuan

komputasinya. Bobot dalam jaringan yang diusulkan oleh McCulloch dan Pitts diatur

untuk melakukan fungsi logika sederhana. Fungsi aktivasi yang dipakai adalah fungsi

model jaringan yang disebut Perceptron. Metode pelatihan diperkenalkan untuk

mengoptimalkan hasil iterasinya.

Widrow dan Hoff (1960) mengembangkan perceptron dengan memperkenalkan

aturan pelatihan jaringan, yang dikenal sebagai aturan delta (atau sering disebut

kuadrat rata-rata terkecil). Aturan ini akan mengubah bobot perceptron apabila

keluaran yang dihasilkan tidak sesuai dengan target yang diinginkan. Apa yang

dilakukan peneliti terdahulu hanya menggunakan jaringan dengan layer tunggal

(single layer). Rumelhart (1986) mengembangkan perceptron menjadi

Backpropagation, yang memungkinkan jaringan diproses melalui beberapa layer.

Selain itu, beberapa model jaringan syaraf tiruan lain juga dikembangkan oleh

Kohonen (1972), Hopfield (1982) dan lainnya. Pengembangan yang ramai dibicarakan

sejak tahun 1990an adalah aplikasi model-model jaringan syaraf tiruan untuk

menyelesaikan berbagai masalah di dunia nyata.

Jaringan Syaraf Tiruan ditentukan oleh tiga hal :

1. Pola hubungan antar neuron (disebut arsitektur jaringan)

2. Metode untuk menentukan bobot penghubung (disebut metode

learning/training).

3. Fungsi aktivasi

2.7Paradigma Pembelajaran

Berdasarkan cara memodifikasi bobotnya, ada 2 macam pelatihan yang dikenal yaitu

dengan supervisi (supervised) dan tanpa supervisi (unsupervised). Dalam pelatihan

dengan supervisi, terdapat sejumlah pasangan data (masukan-target keluaran) yang

dipakai untuk melatih jaringan hingga diperoleh bobot yang diinginkan. Pasangan data

tersebut berfungsi sebagai "guru" untuk melatih jaringan hingga diperoleh bentuk

yang terbaik. "Guru" akan memberikan informasi yang jelas tentang bagaimana sistem

harus mengubah dirinya untuk meningkatkan unjuk kerjanya. Pada setiap kali

pelatihan, suatu input diberikan ke jaringan. Jaringan akan memproses dan

mengeluarkan keluaran. Selisih antara keluaran jaringan dengan target (keluaran yang

diinginkan) merupakan kesalahan yang terjadi. Jaringan akan memodifikasi bobot

sesuai dengan kesalahan tersebut. Jaringan perceptron, ADALINE dan

Backpropagation merupakan model-model yang menggunakan pelatihan dengan

ada "guru" yang akan mengarahkan proses pelatihan. Dalam pelatihannya, perubahan

bobot jaringan dilakukan berdasarkan parameter tertentu dan jaringan dimodifikasi

menurut ukuran parameter tersebut.

Sebagai contoh, dalam model jaringan kompetitif, jaringan terdiri dari 2 layar,

yaitu layar input dan layar kompetisi. Layar input menerima data eksternal. Layar

kompetitif berisi neuron-neuron yang saling berkompetisi agar memperoleh

kesempatan untuk merespon sifat-sifat yangada dalam data masukan. Neuron yang

memenangkan kompetisi akan memperoleh sinyal yang berikutnya ia teruskan. Bobot

neuron pemenang akan dimodifikasi sehingga lebih menyerupai data masukan.

Sebagai ilustrasi, pelatihan dengan supervisi dapat diandaikan sebagai skripsi yang

dibimbing oleh seorang dosen. Pada setiap kali pengumpulan berkas skripsi, dosen

akan mengkritik, mengarahkan dan meminta perbaikan agar kualitas skripsi

meningkat. Sebaliknya, Dalam pelatihan tanpa supervisi dapat dibayangkan sebagai

skripsi tanpa dosen pembimbing. Mahasiswa mengerjakan skripsi sebaik-baiknya

berdasarkan ukuran tertentu (misal dibandingkan dengan skripsi yang sudah ada

sebelumnya atau dibandingkan dengan hasil skripsi temannya). Berdasarkan hasil

yang pernah dilaporkan, model pelatihan dengan supervisi lebih banyak digunakan

dan terbukti cocok dipakai dalam berbagai aplikasi. Akan tetapi kelemahan utama

pelatihan dengan supervisi adalah dalam hal pertumbuhan waktu komputasinya yang

berorde eksponensial. Ini berarti untuk data pelatihan yang cukup banyak, prosesnya

menjadi sangat lambat.

2.7.1 Pelatihan Dengan Supervisi

Jaringan memberikan tanggapan dengan mendapatkan target tertentu. Sebelum

jaringan mengubah sendiri bobotnya untuk mencapai target, bobot interkoneksi

diinisialisasi. Proses belajar JST dengan pengawasan adalah proses belajar dengan

memberikan latihan untuk mencapai suatu target keluaran yang ditentukan. JST

mendapatkan latihan untuk mengenal pola-pola tertentu. Dengan memberikan target

keluaran, perubahan masukan akan diadaptasi oleh keluaran dengan mengubah bobot

interkoneksinya mengikuti algoritma belajar yang ditentukan. Set pelatihan dipilih

dari fungsi keluaran maksimum setiap keadaan parameter yang diubah. Dengan

menginisialisasi bobot tiap sel, JST akan mencari error terkecil, sehingga bentuk

dilakukan, kita perlu memperhatikan beberapa hal dalam menyusun set pelatihan,

yaitu:

a. Pemberian urutan pola yang akan diajarkan

b. Kriteria perhitungan error

c. Kriteria proses belajar

d. Jumlah iterasi yang harus dilalui

e. Inisialisasi bobot dan parameter awal

Pelatihan dilakukan dengan memberikan pasangan pola-pola masukan dan

keluaran. Untuk keperluan pengendalian, pasangan pola tidak mengikuti rumusan

tertentu. JST harus dapat mengadaptasi masukan yang acak supaya keluaran tetap

mengikuti target. Lebih lanjut, proses pelatihan dilakukan dengan memberikan pola

yang menggunakan masukan acak dan bobot interkoneksi yang besar. Dengan

pemberian bobot yang besar, perbedaan target dan keluaran berkurang lebih cepat,

sehingga proses adaptasi akan lebih cepat pula. Salah satu proses belajar dengan

pengawasan adalah proses belajar menggunakan algoritma propagasi balik. Proses

belajar jaringan umpan balik dituliskan dalam bentuk algoritma propagasi balik yang

dikenal sebagai JPB. Jaringan Propagasi Balik (JPB) kadang-kadang dikenal sebagai

Multilayer Perceptron (MLP). Anda dapat menggunakan algoritma propagasi balik

untuk melatih jaringan lapis banyak.

2.7.2 Pelatihan Tanpa Supervisi

Pada pelatihan tanpa supervisi, jaringan tidak mendapatkan target, sehingga JST

mengatur bobot interkoneksi sendiri. Belajar tanpa pengawasan kadang-kadang diacu

sebagai Self-Organizing Learning, yakni belajar mengklasifikasikan tanpa dilatih.

Pada proses belajar tanpa pengawasan, JST akan mengklasifikasikan contoh pola-pola

masukan yang tersedia ke dalam kelompok yang berbeda-beda. Contoh JST dengan

belajar tanpa pengawasan adalah jaringan Kohonen.

2.8Jaringan Syaraf Learning Vector Quantization (LVQ)

Menurut Jang, et al. (1997) LVQ merupakan metode klasifikasi data adaptif

berdasarkan pada data pelatihan dengan informasi kelas yang diinginkan. Walaupun

merupakan suatu metoda pelatihan supervised tetapi LVQ menggunakan teknik data

clustering unsupervised untuk pra proses set data dan penentuan cluster center-nya.

Arsitektur jaringan LVQ hampir menyerupai suatu jaringan pelatihan kompetitif

tertentu. Kusumadewi dan Hartai (2006) menyatakan LVQ merupakan metoda untuk

melakukan pelatihan terhadap lapisan-lapisan kompetitif supervised. Lapisan

kompetitif akan belajar secara otomatis untuk melakukan klasifikasi terhadap vektor

input yang diberikan. Apabila beberapa vektor input memiliki jarak yang sangat

berdekatan, maka vektor-vektor input tersebut akan dikelompokkan dalam kelas yang

sama. Pemrosesan yang terjadi pada setiap neuron adalah mencari jarak antara suatu

vektor input ke bobot yang bersangkutan (w1 dan w2). Dimana w1 adalah vektor

bobot yang menghubungkan setiap neuron pada lapisan input ke neuron pertama pada

lapisan output, sedangkan w2 adalah vektor bobot yang menghubungkan setiap

neuron pada lapisan input ke neuron yang kedua pada lapisan output. Fungsi aktivasi

F1 akan memetakan y_in1 ke y1 = 1 apabila:

|X – w1| < |X – w2|, dan y1 = 0 jika sebaliknya.

Demikian pula dengan yang terjadi pada fungsi aktivasi F2, akan memetakan

y_in1 ke y1 = 1 apabila |X – w2| < |X – w1|, dan y1 = 0 jika sebaliknya.

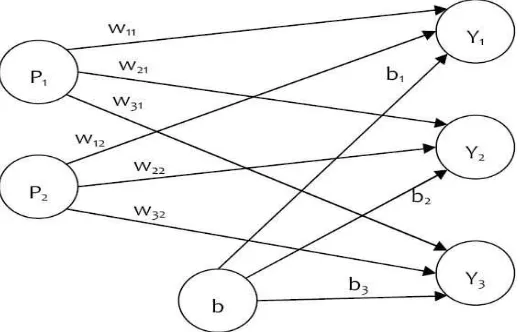
Gambar 2.15 menunjukan jaringan LVQ dengan unit pada lapisan input, dan 2 unit

(neuron) pada lapisan output.

Gambar 2.15 Arsitektur Jaringan Learning Vector Quantization [Kusumadewi,2006]

Algoritma untuk LVQ adalah sebagai berikut:

Notasi x : training vector (X1, X2, ..., Xn)

T : kategori dari training vector yang benar

Wj : Vektor bobot untuk kategori j !

Cj : Kategori j (hasil training)

||X – Wj|| : jarak Euclidian.

Step 0 Inisialisasi

Step 1 Jika kondisi stop salah, lakukan step 2 s.d. step 6

Step 2 Untuk setiap vector training, lakukan step 3 s.d. step 4

Step 3 dapatkan j sehingga ||X – Wj|| minimum

Step 4 Update Wj

nantinya akan digunakan untuk melakukan simulasi atau pengujian data yang lain.

2.9Jaringan Syaraf Kohonen Self Organizing

Pada metode pembelajaran yang tak terawasi ini tidak memerlukan target output. Pada

metode ini, tidak dapat ditentukan hasil yang seperti apakah yang diharapkan selama

proses pembelajaran. Selama proses pembelajaran, nilai bobot disusun dalam suatu

range tertentu tergantung pada nilai input yang diberikan. Tujuan pembelajaran ini

adalah mengelompokkan unit-unit yang hampir sama dalam suatu area tertentu

(Puspitorini, 2008).

Jaringan Syaraf Kohonen Self Organizing termasuk dalam pembelajaran tak

terawasi (unsupervised learning). Pertama kali diperkenalkan oleh Prof. Teuvo

Kohonen pada tahun 1982. Pada jaringan ini, suatu lapisan yang berisi neuron-neuron

akan menyusun dirinya sendiri berdasarkan input nilai tertentu dalam suatu kelompok

yang dikenal dengan istilah cluster. Selama proses penyusunan diri, cluster yang

memiliki vektor bobot paling cocok dengan pola input (memiliki jarak yang paling

dekat) akan terpilih sebagai pemenang. Neuron yang menjadi pemenang beserta

neuron-neuron tetangganya akan memperbaiki bobot-bobotnya (Tae, 2010).

Tujuan pembelajaran dari algoritma ini adalah untuk mentransformasikan suatu

pola sinyal masukan yang mempunyai dimensi yang berubah-ubah ke suatu peta yang

berdimensi satu atau dua. Sifat pemetaan yang dimiliki jaringan syaraf Kohonen Self

Organizing meniru pada otak manusia yang tidak terdapat pada jaringan syaraf tiruan

dimensi dan sinyal-sinyal masukan sejumlah n. Vektor bobot untuk suatu unit

kelompok disediakan satu eksemplar dari pola-pola masukan yang tergabung dengan

kelompok tersebut. Selama proses pengorganisasian sendiri, unit kelompok yang

memiliki vektor bobot paling cocok dengan pola masukan (ditandai dengan jarak

Euclidean paling minimum) dipilih sebagai pemenang. Unit pemenang dan unit

tetangganya diperbaharui bobotnya. Untuk susunan unit kelompok linier, tetangga

dengan radius R di sekitar unit kelompok jaringan terdiri atas semua unit jaringan

yang memenuhi maksimal fungsi Aj : ( 1, J-R < = j,= min (J+R, m) (Tae, 2010).

Arsitektur Jaringan Saraf Kohonen ditunjukkan pada Gambar 2.16.

Gambar 2.16 Arsitektur Jaringan Self OrganizingKohonen

[Kusumadewi,2006]

Algoritma pengelompokkan pola jaringan Self Organizing Koh (Tae, 2010) adalah

sebagai berikut:

Step 0 Inisialisasi awal

Bobot wij (random)

Nilai parameter learning rate ( ) dan faktor penurunannya

Bentuk dan jari-jari (R) topologi sekitarnya

Step 1 Selama kondisi penghentian bernilai salah, lakukan langkah 2 – 7

Step 2 Untuk setiap input vektor x, (i = 1, 2, …, n) lakukan langkah 3 – 5

Step 4 Tentukan indeks J sedemikian sehingga D(j) minimum

Step 5 Untuk setiap unit j di sekitar J, modifikasi bobot

Step 6 Modifikasi parameter learning rate

Step 7 Uji kondisi penghentian

Kondisi penghentian iterasi adalah selisih antara wij saat itu dengan wij pada iterasi

sebelumnya. Apabila semua wij hanya berubah sedikit saja, berarti iterasi sudah

mencapai konvergensi sehingga dapat dihentikan.

2.10 Jaringan Syaraf New JST

Pada metode pembelajaran pada JST ini merupakan jaringan yang tak terawasi serta

tidak memerlukan target output. Proses pembelajaran, nilai bobot disusun dalam suatu

range tertentu tergantung pada nilai input yang diberikan. Vektor-vektor input tersebut

akan dikelompokkan dalam kelas yang sama. Pemrosesan yang terjadi pada setiap

neuron adalah mencari jarak antara suatu vektor input ke bobot yang bersangkutan

(w1 dan w2). w1 adalah vektor bobot yang menghubungkan setiap neuron pada

lapisan input ke neuron pertama pada lapisan output, sedangkan w2 adalah vektor

bobot yang menghubungkan setiap neuron pada lapisan input ke neuron yang kedua

BAB 3

METODOLOGI PENELITIAN

Learning Vector Quantization (LVQ) adalah suatu metode untuk melakukan

pembelajaran pada lapisan kompetitif yang terawasi (dengan supervisi) dimana

jaringan akan secara otomatis belajar untuk mengklasifikasikan vektor-vektor input.

Kelas-kelas yang didapatkan sebagai hasil dari lapisan kompetitif ini hanya tergantung

pada jarak antara vektor-vektor input. Jika dua vektor input mendekati sama, maka

lapisan kompetitif akan meletakkan kedua vektor input tersebut ke dalam kelas yang

sama.

Pada pelatihan tanpa supervisi, jaringan tidak mendapatkan target, sehingga jaringan mengatur bobot interkoneksi sendiri. Belajar tanpa pengawasan

kadang-kadang diacu sebagai Self-Organizing Learning, yakni belajar mengklasifikasikan

tanpa dilatih. Pada proses belajar tanpa pengawasan, jaringan akan mengklasifikasikan

contoh pola-pola masukan yang tersedia ke dalam kelompok yang berbeda-beda.

Berdasarkan hasil yang pernah dilaporkan, model pelatihan dengan supervisi lebih banyak digunakan dan terbukti cocok dipakai dalam berbagai aplikasi. Akan tetapi

kelemahan utama pelatihan dengan supervisi adalah dalam hal pertumbuhan waktu

komputasinya yang berorde eksponensial. Ini berarti untuk data pelatihan yang cukup

banyak, prosesnya menjadi sangat lambat.

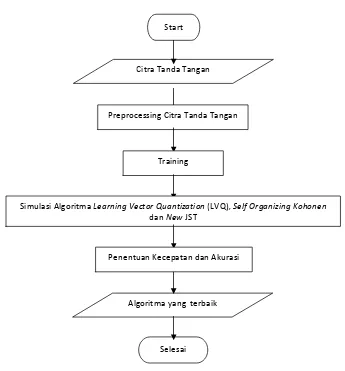
3.1 Rancangan Penelitian

Dalam melakukan kombinasi algoritma Learning Vector Quantization dengan Self Organizing

Kohonen untuk mempercepat proses pengenalan pola tandatangan penulis menyusun langkah

Gambar 3.1 Flow Chart Rancangan Penelitian

3.2 Bahan Penelitian

Bahan yang digunakan pada penelitian ini adalah tanda tangan berupa citra digital hasil akusisi dengan alat digital berupa scanner yang akan digunakan untuk pembelajaran (learning data set) dan sekumpulan citra untuk pengujian (testing data set). Proses praproses

(preprocessing)citra merupakan kumpulan proses – proses yang digunakan untuk

menyiapkan citra input untuk dijadikan masukan ke dalam jaringan. Proses praproses pada penelitian ini terbagi menjadi tiga tahap yaitu:

1. Proses scaling citra dengan dimensi 350 x 250 pixel. 2. Proses grayscaling

3. Proses edges detection 4. Proses Binerisasi

" # # $

% & $ " # # $

# $

' ( $ '

)*+,-. #

( $ ' / $

Pada proses scaling citra tanda tangan yang digunakan di-crop menjadi ukuran

350 x 250 pixel dan selanjutnya citra tersebut mengalami proses konversi ke

grayscaling jika merupakan citra true color, selanjutnya citra akan dikenai proses

deteksi tepi berbasis gradien dengan operator Sobel. Citra analisis merupakan citra

grayscale dengan skala 8 bit yang memiliki intensitas warna berkisar antara 0 sebagai

nilai minimum sampai 255 yang merupakan nilai maksimum.

Citra analisis kemudian dikenakan proses binerisasi yaitu dikonversikan ke dalam

bilangan biner dengan proses threshold (pengambangan) sepanjang 350 x 250 untuk

masing-masing citra. Untuk setiap pixel dengan nilai intensitas warna 128 diberi

nilai 0, sedangkan untuk nilai intensitas warna > 128 diberi nilai 1, sehingga akan

diperoleh barisan nilai yang terdiri dari 0 dan 1 sepanjang 87.500 piksel elemen.

Sebagai contoh citra tanda tangan seperti pada Gambar 3.2.

Gambar 3.2 Citra Tanda Tangan

3.3 Pembacaan File Citra

Pada citra warna 24-bit (true color) tidak terdapat palet RGB, karena nilai RGB

langsung diuraikan dalam data bitmap berbentuk biner. Untuk membaca nilai

RGB-nya, dilakukan mencari header-header serta data bitmap yang berisi informasi

dimensi, format dan nilai piksel citra. Setiap elemen data bitmap panjangnya 3 byte,

masing-masing byte menyatakan komponen R, G, dan B. Setiap byte data

merepresentasikan 8 bit, jadi pada citra warna ada 3 byte x 8 bit = 24 bit kandungan

warna.

Pada citra warna, tiap pixel-nya mengandung 24-bit kandungan warna atau 8-bit untuk masing-masing warna dasar (R, G, dan B), dengan kisaran nilai kandungan

antara 0 (00000000) sampai 255 (11111111) untuk tiap warna. Sebagai contoh suatu

Gambar 3.3 Contoh Nilai Piksel Citra Warna

Pada contoh citra Gambar 3.2 di atas, data pertama adalah header yang berisi informasi nama file, jenis format dan dimensi citra. Di bawah data bitmap terdapat pixel pertama mempunyai nilai = 100001111011010010100001.

Untuk mendapatkan nilai RGB setiap piksel dengan menggunakan rumus sebagai berikut: Nilai R = c and 255 ... (3.1)

Nilai G = (c and 65,280)/256 ... (3.2)

Nilai B = ((c and 16,711,680)/256)/256 ... (3.3)

Dimana c adalah nilai piksel citra

Pada Gambar 3.2 di atas, nilai piksel (0,0) adalah 111100001011010010111001

(24 bit). Nilai R dihitung dengan persamaan 3.1 sebagai berikut:

Nilai R = 100001111011010010100001 and 11111111 = 10100001 (Biner)

= 161 Desimal

Nilai komponen G dihitung dengan persamaan (3.2):

Nilai G = (100001111011010010100001 and 1111111100000000)/ 100000000

Sehingga diperoleh nilai piksel (0,0) 11110000 11110000 11111111:

Dalam analisa ini jumlah piksel yang dihitung sebanyak 25 piksel saja dan untuk

mendapatkan nilai RGB piksel selanjutnya dilakukan sama seperti cara di atas dan

selanjutnya nilai RGB semua nilai piksel pada citra dimasukkan ke dalam matriks

seperti pada Gambar 3.4.

161,180,135 152,140,110 182,166,210 166,112,178 170,177,166

202,189,134 201,180,111 140,173,110 192,120,200 112,167,162

133,200,152 165,100,155 124,110,167 140,180,126 200,160,200

141,204,104 134, 80,144 140,110,115 150,180,150 160,210,220

56,100,110 147,140,165 143,230,173 140,212,210 150,212,150

Gambar 3.4 Matriks Nilai RGB Citra Warna

3.4 Menghitung Nilai Grayscale Citra

Matriks citra warna pada Gambar 3.3 di atas ditransformasikan menjadi citra

grayscale dengan menghitung rata-rata warna Red, Green dan Blue. Secara matematis

penghitungannya adalah sebagai berikut.

f₀ (x,y) = ……… (3.4)

Sebagai contoh menghitung nilai grayscale citra pada Gambar 3.3 di atas

menggunakan persamaan (3.6) adalah sebagai berikut:

f(0,0) = = 158

f(0,1) = = 134

f(0,2) = = 186

f(0,3) = = 152

f(0,4) = = 171

Untuk menghitung nilai grayscale piksel selanjutnya dilakukan sama seperti cara

di atas, selanjutnya hasil nilai grayscale matriks citra warna dimasukkan ke dalam

158 134 186 152 171

110 164 111 170 0

166 100 155 114 125

47 155 172 174 200

175 0 47 90 144

Gambar 3.5 Matriks Nilai Grayscale

3.5 Deteksi Tepi

Deteksi tepi berfungsi untuk mempertegas batas batas citra atau untuk meningkatkan

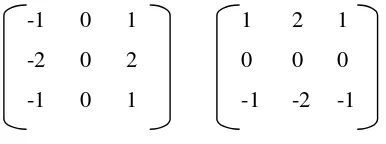
penampakan garis batas garis tanda tangan. Pada penelitian ini digunakan operator

Sobel dengan dua buah kernel seperti pada Gambar 3.6.

-1 0 1 1 2 1

-2 0 2 0 0 0

-1 0 1 -1 -2 -1

Gambar 3.6 Dua Buah Matriks Kernel

Pada citra tanda tangan dilakukan deteksi tepi dengan mengambil 1 blok citra 3 x 3

Pixel seperti pada Gambar 3.7.

158 134 186 -1 0 1 1 2 1

110 164 111 -2 0 2 0 0 0

166 100 155 -1 0 1 -1 -2 -1

Gambar 3.7 Matriks citra 3x3 Pixel dengan Dua filter

sx = 158(-1) + 134(-2) + 186(-1) +166(1) +100(2) + 155(1)

= 478

sy = 158(1)+110(2)+166(1)+186(-1)+111(-2)+ 155(-1)

Perhitungan nilai magnitudo (M) adalah sebagai berikut:

M = |sx| + |sy|

M = |478| + |452|

M = 930

Citra hasil konvolusi yang diperoleh dari perhitungan deteksi tepi untuk pixel blok 3 x

3 adalah seperti pada Gambar 3.8.

* * *

* 930 * * * *

Gambar 3.8 Nilai Konvolusi (M) Sekitar Piksel 3x3

Dari hasil konvolusi, maka nilai magnitudo dibagi secara rata untuk ke 9 piksel yaitu

930 : 9 = 103 dan dimasukkan ke dalam matriks citra 3x3 seperti pada Gambar 3.9.

103 103 103

103 103 103

103 103 103

Gambar 3.9 Matriks Hasil Deteksi Tepi Citra 3x3

3.6 Binerisasi

Pemisahan citra grayscale diatas berfungsi untuk mengambil bagian citra yang

merupakan titik gelap (0) dan putih (1). Binerisasi dilakukan dengan membagi citra

menjadi 8x8 bagian subcitra, nilai intensitas rata-rata dari subcitra yang paling rendah

digunakan menjadi nilai threshold T. Setelah itu dilakukan proses binarisasi citra

menggunakan nilai threshold T. Persamaan yang digunakan untuk melakukan

binarisasi citra adalah sebagai berikut.

Dari matriks Gambar 3.4 dilakukan perhitungan Threshold untuk proses binerisasi

dimana jika nilai grayscale < 128 maka akan dimasukkan ke nilai 0, sedangkan jika

nilai grayscale > T akan dimasukkan ke nilai 1.

Nilai piksel (0,0) = 158, nilai piksel 158 > 128, maka nilai biner = 1

Nilai piksel (0,1) = 134, nilai piksel 134 >128, maka nilai biner = 1

Nilai piksel (0,2) = 186, nilai piksel 186 > 128, maka nilai biner = 1

Nilai piksel (0,3) = 152, nilai piksel 152 > 128, maka nilai biner = 1

Nilai piksel (1,0) = 171, nilai piksel 171 > 128, maka nilai biner = 1

Dari hasil perhitungan nilai threshold diatas dimasukkan ke dalam matriks citra

biner seperti pada Gambar 3.10.

1 1 1 1 1

0 1 0 1 0

1 0 1 0 1

0 1 1 1 1

1 0 0 0 1

Gambar 3.10 Matriks Citra Biner

Dengan g(x,y) adalah citra biner hasil proses binarisasi dari citra tanda tangan

dengan skala keabuan f(x,y), dengan nilai threshold T. Citra hasil threshold ini

menghasilkan tanda tangan biner seperti pada Gambar 3.11.

Citra grayscale tanda tangan Citra biner tanda tangan

Dengan diperolehnya citra tanda tangan biner, maka tahap preprocessing citra

sudah selesai dan selanjutnya citra biner pada Gambar 3.11 dilakukan proses

pengenalan pola dengan meode jaringan syaraf tiruan.

3.7Flow Chart Pengenalan Tanda Tangan dengan JST LVQ

Adapun flow chart proses pengenalan tanda tangan dengan jaringan syaraf Tiruan

(JST) dengan metode LVQ dapat dilihat seperti pada Gambar 3.12.

Gambar 3.12 Flow Chart Pengenalan Tanda Tangan metode LVQ

" # $ %

% 2 3 4 5 # $

% ' . $ *+,

6# 7 8 4.' 4) 9.' - : 6 ). '

--% % ' %

; 6 & 7

; 6 7 ;

;< &6 7 ;

% .' 4 .' 4 6

% 8 (= )

>-7 4 4;;;4 ; >>-7 4 4;;;4' >7

3 8 (= >(= 7

Gambar 3.13 Flow Chart Pengenalan Tanda Tangan metode LVQ (Lanjutan)

3.8Flow Chart Proses Pengenalan Tanda Tangan dengan JST Self Organizing Kohonen

Adapun flow chart proses pengenalan tanda tangan dengan jaringan syaraf tiruan

(JST) dengan metode Self Organizing Kohonen dapat dilihat seperti pada Gambar

3.14.

# $

6 & 76 & ?

@ % $

6 0 6

6 & 1 6 &

% 8 >

. # 7 "> ' >7 >? 6 ) % -. # 01 "> ' >7 > 6 ) %

Gambar 3.14 Flow Chart Pengenalan Tanda Tangan metode Self Organizing Kohonen < %

% 2 3 4 5

6A + B

6 & 76 & ?

3 ' 8 < $ C '

' ' 8 + ) %

-% ' * $ C ) 6 & 4 6 4 < &6

-' $ $ ' '

/ $ 2 $ 9( 2D