Studi Metode Regresi Ridge Dan Metode Analisis Komponen Utama Dalam Menyelesaikan Masalah Multikolinearitas

(1)

STUDI METODE REGRESI RIDGE DAN METODE ANALISIS

KOMPONEN UTAMA DALAM MENYELESAIKAN

MASALAH MULTIKOLINEARITAS

SKRIPSI

OCKTAVALANNI SIREGAR

100803011

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

STUDI METODE REGRESI RIDGE DAN METODE ANALISIS

KOMPONEN UTAMA DALAM MENYELESAIKAN

MASALAH MULTIKOLINEARITAS

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

OCKTAVALANNI SIREGAR 100803011

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : STUDI METODE REGRESI RIDGE DAN

METODE ANALISIS KOMPONEN UTAMA DALAM MENYELESAIKAN MASALAH MULTIKOLINEARITAS

Kategori : SKRIPSI

Nama : OCKTAVALANNI SIREGAR

Nomor Induk Mahasiswa : 100803011

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juli 2014 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dr. Suwarno Ariswoyo, M.Si Drs. Pengarapen Bangun, M.Si NIP. 19500321198003 1 001 NIP. 195608151985031005

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

(4)

PERNYATAAN

STUDI METODE REGRESI RIDGE DAN METODE ANALISIS KOMPONEN UTAMA DALAM MENYELESAIKAN MASALAH MULTIKOLINEARITAS

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2014

(5)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang telah memberikan rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Studi Metode Ridge Dan Metode Analisis Komponen Utama Dalam Menyelesaikan Masalah Multikolinearitas.

Terima kasih penulis sampaikan kepada Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU. Bapak Drs. Pengarapen Bangun, M.Si dan Bapak Dr. Suwarno Ariswoyo, M.Si selaku pembimbing yang telah memberikan panduan, petunjuk, dan bimbingan berharga kepada penulis untuk menyempurnakan skripsi ini. Penulis juga mengucapkan terima kasih kepada Bapak Prof. Dr. Tulus, M.Si, selaku ketua Departemen Matematika, Ibu Dra. Mardiningsih, M.Si selaku sekretasis Departemen Matematika, Bapak Drs. Henry Rani Sitepu, M.Si dan Bapak Drs. Gim Tarigan, M.Si selaku penguji skripsi, dan staf pengajar Matematika di FMIPA USU, beserta pegawai Administrasi.

Penulis juga mengucapkan terima kasih kepada kedua orang tua yang tercinta Ibunda Robianna Harahap dan Ayahanda Dasrin Siregar serta adik penulis yang penulis sayangi Dasliana Siregar dan Arifin Siregar yang telah memberikan dorongan dan doa dalam menyelesaikan skripsi ini. Akhirnya penulis juga mengucapkan terima kasih kepada Dewi Harni Nst, Ida Husna, Fitriana, Tri ananda puteri, Nusaibah Kholilah, Ayu Widyani, Rika Listya Sari, kak Silvi dan teman-teman lain yang tidak dapat disebutkan satu persatu atas bantuannya dalam menyelesaikan skripsi ini.

Semoga segala bentuk bantuan yang telah diberikan mendapat balasan yang jauh lebih baik dari Tuhan Yang Maha Esa.

Sebagai seorang mahasiswa, penulis menyadari bahwa masih banyak kekurangan di dalam menyelesaikan skripsi ini. Untuk itu, kritik dan saran yang membangun sangat diharapkan demi perbaikan tulisan ini.

Medan, Juli 2014

(6)

ABSTRAK

(7)

ABSTRACT

(8)

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak iv

Abstract v

Daftar Isi vi

Daftar Tabel viii

Bab 1 Pendahuluan 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 3

1.3. Pembatasan Masalah 4

1.4. Tujuan Penelitian 4

1.5. Kontribusi Penelitian 4

1.6. Metodologi Penelitian 5

Bab 2 Tinjauan Pustaka 6

2.1. Matrik 6

2.1.1. Definisi Matriks 6

2.1.2. Jenis-Jenis Matriks 7

2.1.3. Penjumlahan Matriks dan Perkalian Skalar Matriks 10

2.1.4. Determinan 11

2.1.5. Invers Matriks 11

2.2. Nilai Eigen dan Vektor Eigen 12

2.3. Matriks Korelasi 13

2.4. Multikolinearitas 15

2.5. Konsekuensi Multikolinearitas 17

2.6. Pendeteksian Multikolinearitas 18

2.7. Regresi Linear Berganda 18

2.8. Metode Regresi Ridge 19

2.9. Ridge Trace 21

2.10. Analisis Komponen Utama 22

Bab 3 Metode Penelitian 29

3.1. Bidang Penelitian 29

3.2. Metode dan Desain Penelitian 29

(9)

3.4. Variabel Penelitian 30

3.5. Teknik Analisis Data 31

Bab 4 Pembahasan 35

4.2. Metode Regresi Linear Berganda 40

4.3. Pendeteksian Multikolinearitas 41

4.5. Uji Keberartian Regresi 47

4.6. Metode Analisis Komponen Utama 54

Bab 5 Kesimpulan dan Saran 66

5.1. Kesimpulan 68

5.2. Saran 68

(10)

DAFTAR TABEL

Halaman Tabel 4.1: Data Banyaknya Serangan Virus Pada penggerek Batang 39

Padi Afrika di Pantai Gading Afrika Barat dan Faktor-faktor yang Mempengaruhinya

Tabel 4.2: Penaksir Parameter Metode Kuadrat Terkecil 40

Tabel 4.3: ANAVA untuk Data Awal 41

Tabel 4.4: Nilai Toleransi dan VIF 41

Tabel 4.5: Nilai Korelasi Antar Variabel Bebas 42

Tabel 4.6: Hasil Pemusatan dan Penskalaan 43

Tabel 4.7: Nilai VIF β( c ) Dengan Berbagai Nilai c 44 Tabel 4.8: Nilai β ( c ) Dengan Berbagai Nilai c 45

Tabel 4.9: ANAVA Ridge 47

Tabel 5.0: Penaksir Parameter Regresi Ridge 48

Tabel 5.1: Matriks Korelasi 55

Tabel 5.2: Communalities 55

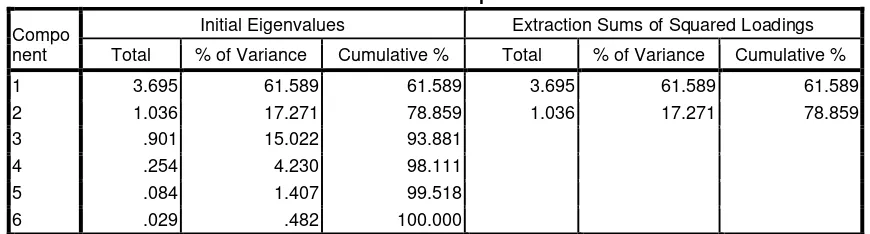
Tabel 5.3: Nilai Eigen Analisis Komponen Utama 56

Tabel 5.4: Matriks Komponen 57

Tabel 5.5: Koefisien Komponen Utama 57

Tabel 5.6: Skor Faktor Komponen Utama 59

Tabel 5.7: Koefisien Regresi Komponen Utama 60

(11)

ABSTRAK

(12)

ABSTRACT

(13)

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Banyak metode yang dapat digunakan untuk menganalisis data atau informasi pada suatu pengamatan. Salah satu metode statistik yang paling bermanfaat dan paling sering digunakan adalah analisis regresi. Metode ini digunakan untuk mengetahui sejauh mana ketergantungan atau hubungan sebuah variabel tak bebas dengan sebuah atau lebih variabel bebas. Jika dalam analisisnya hanya melibatkan sebuah variabel bebas, maka analisis yang digunakan adalah Analisis Regresi Linier Sederhana. Sedangkan bila dalam analisisnya melibatkan dua atau lebih variabel bebas, maka analisis yang digunakan adalah Analisis Linier Berganda.

Analisis regresi linier berganda adalah hubungan secara linear antara dua atau lebih variabel independen (X1, X2,….Xn) dengan variabel dependen (Y). Analisis ini untuk mengetahui arah hubungan antara variabel independen dengan variabel dependen apakah masing-masing variabel independen berhubungan positif atau negatif dan untuk memprediksi nilai dari variabel dependen apabila nilai variabel independen mengalami kenaikan atau penurunan.

(14)

diantaranya adalah koefisien regresi menjadi lebih tidak stabil, Standard Error menjadi besar dan variabel terlihat memiliki pengaruh yang kecil secara individual tetapi kuat secara kelompok selain itu multikolinieritas juga dapat mengakibatkan tanda dari koefisien regresi berlawanan arah dengan koefisien korelasi . Untuk mengatasi masalah tersebut terdapat beberapa metode yang biasa digunakan, diantaranya adalah penggunaan informasi apriori dari hubungan beberapa variabel yang saling berhubungan, menghubungkan data cross sectional dan data time 2 series, mengeluarkan suatu variabel atau beberapa variabel prediktor yang terlibat hubungan kolinier (Soemartini, 2008). Akan tetapi pada prakteknya prosedur penanggulangan tersebut sangat tergantung sekali pada kondisi penelitian. Dan metode lainnya yaitu metode regresi ridge dan metode analisis komponen utama.

Metode regresi ridge merupakan salah satu metode yang dianjurkan untuk memperbaiki masalah multikolinearitas, prosedur ini di tujukan untuk mengatasi kondisi buruk yang diakibatkan oleh korelasi yang tinggi antara beberapa peubah peramal di dalam model, sehingga matriks XtX nya hampir singular, yang pada gilirannya menghasilkan nilai dugaan parameter model yang tidak stabil.

Regresi ridge merupakan modifikasi dari metode kuadrat terkecil dengan cara menambah tetapan bias c yang kecil kepada nilai diagonal matriks XtX. Besarnya tetapan bias c mencerminkan besarnya bias dalam koefisien penduga ridge dan c

yang bernilai nol merupakan implementasi dari metode kuadrat terkecil. Metode ini bertujuan untuk memperkecil variansi estimator koefisien regresi.

(15)

Selanjutnya variabel baru ini dinamakan komponen utama (principal component). Tujuan metode ini untuk menyederhanakan variabel yang diamati dengan cara mereduksi data asli/awal menjadi sedikit mungkin komponen, akan tetapi mampu menyerap sebagian besar jumlah varian dari data asli/awal (menyerap informasi sebanyak mungkin dari informasi data asli).

Analisis komponen utama menghasilkan kombinasi linear dari variabel-variabel yang diperoleh dari mereduksi variabel-variabel asli/awal yang banyak sekali. Di dalam proses mereduksi, diperoleh variabel yang lebih sedikit akan tetapi masih mengandung informasi yang termuat dalam data asli/awal. Variabel hasil mereduksi tersebut dinamakan faktor yang juga disebut komponen atau faktor komponen.

Dari uraian di atas, maka dalam penelitian tugas akhir ini peneliti mengkaji metode regresi ridge dan metode analisis komponen utama untuk menyelesaikan masalah multikolinearitas. Oleh karena itu penulis mengangkat judul untuk penelitian ini yaitu “Studi Metode Regresi Ridge Dan Metode Analisis Komponen Utama Dalam Menyelesaikan Masalah Multikolinearitas”.

1.2. Perumusan Masalah

Berdasarkan latar belakang diatas, masalah yang akan dibahas adalah sebagai berikut :

1. Bagaimana mendeteksi adanya multikolinearitas pada suatu data?

(16)

1.3. Pembatasan Masalah

Ruang lingkup dalam penelitian ini dibatasi pada data yang diambil dari buku atau internet, dan antar variabel bebas pada data diduga memiliki korelasi (multikolinearitas). kemultikolinearitasan data akan dideteksi, lalu ditanggulangi dengan metode regresi ridge dan analisis komponen utama.

1.4. Tujuan Penelitian

Tujuan dari penelitian ini adalah sebagai berikut:

1. Untuk mendeteksi ada tidaknya multikolinearitas dalam suatu data.

2. Untuk mengetahui prosedur penanggulangan masalah multikolinearitas dengan Metode Regresi Ridge dan Metode Principal Component Analysis (Komponen Utama).

1.5 Kontribusi Penelitian

Manfaat dari penelitian ini adalah:

1. Memberikan pengetahuan tentang tindakan yang harus dilakukan dalam mengidentifikasi dan menanggulangi keberadaan multikolinearitas.

2. Memberikan pengetahuan dasar tentang analisis regresi, metode ridgedan analisis komponen utama..

(17)

1.6 Metodologi Penelitian

Dalam penelitian ini penulis melakukan studi literatur dan mencari bahan dari buku dan internet yang membahas mengenai multikolinearitas, regeresi ridge dan analisis komponen utama (principal component analysis). Kemudian mengambil sampel data yang multikolinearitas dari buku atau internet. Adapun langkah-langkahnya adalah sebagai berikut:

a. Menguraikan penyelesaian masalah multikolinearitas dengan regresi ridge.

b. Menguraikan penyelesaian masalah multikolinearitas dengan analisis komponen utama.

c. Melakukan pendeteksian ada tidaknya multikolinearitas dalam suatu data. d. Menanggulangi multikolinearitas dengan metode regresi ridge.

e. Menanggulangi multikolinearitas dengan metode analisis komponen utama.

(18)

BAB 2

TINJAUAN PUSTAKA

2.1. Matriks

2.1.1. Definisi Matriks

Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga berbentuk persegi panjang, dimana panjang dan lebarnya ditunjukkan oleh banyaknya kolom dan baris serta dibatasi tanda ”[ ]” atau “( )” (Anton, 1987).

Matriks A adalah susunan segiempat dari skalar-skalar yang biasanya dinyatakan dalam bentuk sebagai berikut:

                      = mn m m m n n n a a a a a a a a a a a a a a a a A . . . . . . . . . . . . . . . 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11

Baris-baris dari matriks A semacam ini adalah m deretan horizontal yang terdiri dari skalar-skalar:

(

a11,a12,...,a1n

) (

, a21,a22,...,a2n

) (

,..., am1,am2,...,amn

)

Dan kolom-kolom dari A adalah n deretan vertikal yang terdiri dari skalar-skalar:

(19)

Elemen a_ijyang disebut entri ij atau elemen ij, muncul pada baris i dan kolom j. Matriks tersebut seringkali dituliskan hanya sebagai A=[aij] (Schaum’s, 2006).

2.1.2. Jenis jenis matriks

1. Matriks Bujursangkar

Matriks bujursangkar adalah matriks yang memiliki baris dan kolom yang sama banyak. Matriks bujursangkar n x n dikatakan sebagai matriks dengan orde n.

Contoh:

      =

1 3

4 2

A

2. Matriks Nol

Matriks nol adalah suatu matriks yang semua elemennya mempunyai nilai nol.

      =

0 0

A

3. Matriks Diagonal

Matriks diagonal adalah suatu matriks bujursangkar dimana semua elemen diluar diagonal utama mempunyai nilai nol dan paling tidak ada satu elemen diagonal utama

≠ 0 disimbol D. Contoh :

  

 

  

  =

5 0 0

0 2 0

0 0 4

D

4. Matriks Segitiga Atas

(20)

Contoh:           = 8 0 0 7 2 0 3 5 4 A

5. Matriks Segitiga Bawah

Matriks segitiga bawah adalah matriks dimana semua entri diatas diagonal utama bernilai nol. Contoh:           = 8 3 6 0 2 7 0 0 4 A

6. Matriks Identitas

Matriks identitas atau matriks satuan bujursangkar-n ditulis In atau hanya I adalah matriks bujursangakar-n dengan bilangan 1 pada diagonalnya dan 0 pada entri-entri lainnya. Contoh:           = 1 0 0 0 1 0 0 0 1 I

7. Matriks Skalar

Skalar ialah suatu bilangan konstan. Jika k suatu bilangan konstan maka hasil kali k I

dinamakan scalar matriks. Contoh:

k I3, k=3

(21)

8. Matriks Simetri

Apabila matriks A yang berisikan aij

Dimana i=j=1,2,…,n. dan berlaku aij= aji maka matriks A disebut matriks simetri Contoh:           − − − = 8 7 5 7 6 3 5 3 2 A

Keterangan: melalui pengamatan, elemen-elemen simetri di dalam A sama, atau AT=A. Jadi A adalah matriks simetri.

9. Transpos Matriks

Transpos dari suatu matriks A=(aij) ialah suatu matriks baru dengan menukarkan baris menjadi kolom dan kolom menjadi baris. Apabila suatu matriks ditranspos kepada dirinya sendiri maka disebut matriks simetri.

Contoh:           = →           = 8 7 5 3 7 3 5 4 2 8 3 5 7 7 4 5 3 2 T A A

10. Matriks Ortogonal

Matriks real A disebut matriks ortogonal jika AT=A-1, yaitu, jika AAT= ATA=I. Jadi A haruslah matriks bujursangkar dan dapat dibalik.

Contoh: Misalkan                 − − − = 9 4 9 1 9 8 9 7 9 4 9 4 9 4 9 8 9 1

A . Mengalikan A dengan AT menghasilkan I, yaitu

AA-T

(22)

11. Matriks Trace

Misalkan A=[aij] adalah matriks bujursangkar-n, diagonal dari A terdiri dari elemen-elemen subskrip bilangan kembar yaitu:

a11, a22, a33, …, ann

Trace dari A ditulis tr(A) adalah jumlah dari elemen-elemen diagonal yaitu: tr(A) = a11 + a22 + a33 + … +ann

contoh :           − − − = 8 7 5 7 8 3 5 3 2 A

Maka tr(A) = a11 + a22 + a33 = 2 + 8 + (-8) = 2

2.1.3. Penjumlahan matriks dan perkalian skalar matriks

Misalkan A=[aij] dan B=[bij] adalah dua matriks dengan ukuran yang sama, misalnya matriks mxn. Jumlah A dan B ditulis A+B adalah matriks yang diperoleh dengan menjumlahkan elemen-elemen yang bersesuaian dari A dan B. Yaitu

            + + + + + + + + + = + mn mn m m m m n n n n b a b a b a b a b a b a b a b a b a B A ... ... ... ... ... ... ... 2 2 1 1 2 2 22 22 21 21 1 1 12 12 11 11

Hasilkali dari matriks A dengan suatu skalar k ditulis k.A atau hanya kA adalah matriks yang diperoleh dengan cara mengalikan setiap elemen A dengan k. Yaitu

(23)

2.1.4. Determinan

Setiap matriks bujursangkar-n A=(aij) memiliki skalar khusus yang disebut determinan A, dilambangkan dengan det(A) atau |A| atau

nn n

n

n n

a a

a

a a

a

a a

a

... ... ... ... ...

... ...

2 1

2 22

21

1 12

11

Sifat-sifat determinan:

1. Jika AT merupakan transpos dari matriks A maka det(A)=det(AT ).

2. Jika semua elemen dari suatu baris atau kolom dari matriks kuadrat A mempunyai nilai nol maka det(A)=0.

3. Jika 2 baris atau 2 kolom dipertukarkan maka nilai determinan matriks tersebut berubah tanda.

4. Jika 2 baris atau 2 kolom mempunyai elemen yang sama maka nilai determinan=0.

2.1.5. Invers Matriks

Jika pada matriks bujur sangkar A terdapat matriks B sehingga AB = I, dengan I

adalah matriks identitas, maka B dinamakan invers matriks A dan ditulis sebagai Jadi jika A adalah matriks bujur sangkar tak singular berorde-n, maka terdapat satu

invers sehingga

Invers matriks memiliki sifat:

1. ; yaitu invers dari perkalian dua matriks adalah perkalian inversnya dalam urutan yang terbalik.

(24)

2.2. Nilai Eigen dan Vektor Eigen

Kata “vektor eigen” adalah ramuan bahasa Jerman dan Inggris. Dalam bahasa Jerman “eigen” dapat diterjemahkan sebagai “sebenarnya” atau “karakteristik”. Oleh Karena itu, nilai eigen dapat juga dinamakan nilai sebenarnya atau nilai karakteristik. Dalam literatur lama kadang-kadang dinamakan akar-akar latent.

Jika A adalah matriks n x n, maka vektor taknol x di dalam Rn dinamakan vektor eigen (eigenvector) dari A jika Ax adalah kelipatan skalar dari x; yakni, Ax =

λx untuk suatu skalarλ. Skalarλdinamakan nilai eigen (eigenvalue) dari A dan x dikatakan vektor eigen yang bersesuaian denganλ (Anton, 1987) .

Nilai eigen dan vektor eigen mempunyai tafsiran geometrik yang bermanfaat dalam R2 dan R3. Jikaλadalah nilai eigen dari A yang bersesuaian dengan x. maka Ax = λx, sehingga perkalian oleh A akan memperbesar x, atau membalik arah x, yang bergantung pada nilaiλ. Untuk mencari nilai eigen matriks A yang berukuran n x n

maka dituliskan kembali Ax = λx sebagai

Ax = λI x

atau secara ekivalen

(λI – A)x = 0 Supayaλ menjadi nilai eigen, maka harus ada pemecahan tak nol dari persamaan ini. Akan tetapi persamaan ini akan mempunyai pemecahan tak nol jika dan hanya jika det(λI – A) = 0 ini dinamakan persamaan karakteristik A, skalar yang memenuhi persamaan ini adalah nilai eigen dari A. Bila diperluas, maka determinan det(λI – A) adalah polinom λ yang dinamakan polinom karakteristik dari A (Anton, 1987).

Jika A adalah matriks n x n, maka polinom karakteristik A harus terpenuhi sebanyak n dan koefisienλn adalah 1. Jadi, polinom karakteristik dari matriks n x n

mempunyai bentuk det(λI – A) = n n _n

c

c + +

+ −

...

1 1λ

(25)

Jika A matriks n x n, maka pernyataan-pernyataan berikut ekivalen satu sama lain: 1. λ adalah nilai eigen dari A.

2. Sistem persamaan (λI – A)x = 0 mempunyai pemecahan yang taktrivial. 3. Ada vektor taknol x di dalam Rn sehingga Ax =λx.

4. λ adalah pemecahan riil dari persamaan karakteristik det(λI – A) = 0.

Vektor eigen A yang bersesuaian dengan nilai eigen λ adalah vektor taknol x yang memenuhi Ax =λx. Secara ekivalen, vektor eigen yang bersesuaian denganλ adalah vektor taknol dalam ruang pemecahan dari (λI – A)x = 0. Ruang pemecahan ini dinamakan sebagai ruang eigen (eigenspace) dari A yang bersesuaian denganλ.

2.3. Matriks Korelasi

Misalkan persamaan

ε β

β

β + + + +

= X _pX_p

Y ₀ ₁ ₁ ...

(1) Keterangan: Y = peubah tak bebas

Xj = peubah bebas β_i= parameter ε_i = galat error dinyatakan sebagai

ε β

β β

β

+ −

+ + − +

− +

+ + +

=

) (

... ) (

) (

) ...

( ₀ ₁ ₁ ₁ ₁ ₁ ₂ ₂ ₂

p p p

p p

X X

X X X

X X

X Y

(2) dengan X_j = nilai tengah yang dihitung dari data

j = 1, 2, ..., p

Andaikan β =β +β X + +β_pX_p ∧

... 1 1 0 0

Maka persamaan (2) dapat ditulis

ε β

β β

β + − + − + + − +

= ∗

) (

... ) (

)

( ₁ ₁ ₂ ₂ ₂

1

0 X X X X p Xp Xp

(26)

atau ε β β β β = − + − + + − + − ∗ ) ( ... ) ( )

( ₁ ₁ ₂ ₂ ₂

1

0 X X X X p Xp Xp

Y

(3) Jika β₀∗ =Y , maka

ε β

β

β − + − + + − +

=

−Y ₁(X₁ X₁) ₂(X₂ X₂) ... _p(X_p X_p)

Y

(4) Matriks XtX untuk model ini adalah

                      = PP p p p p p p t S S S S S S S S S S S S S S S S X X . . . . . . . . . . . . . . . 3 2 1 3 33 32 31 2 23 22 21 1 13 12 11 dengan 2 1 ) ( jj j ij ij S x x

z = − dimana

∑

= − = n i j ij

jj x x

S 1 2 , ) ( dan 2 1 yy i i S y y

y∗ = − dimana

∑

= −

= n

i i

yy y y

S 1 2 , ) (

dengan i = 1, 2, …, n j = 1, 2, …, p

Ini akan mengubah persamaan (4) menjadi

ε β β β + + + + = ∗ p PP p

yy S Z S Z S Z

S y 2 1 2 2 1 22 2 1 2 1 11 1 2 1

1 ... ₍₅₎

dengan bj= , 1,2,..., .

2 1 p j S S yy jj

j  =

      β

Dengan metode kuadrat terkecil, nilai dugaan parameter (

∧

b) pada persamaan di atas dapat ditentukan yaitu

∧

(27)

matriks ZtZ merupakan matriks korelasi yaitu:                       = 1 . . . . . . . . . 1 . . . 1 . . . 1 3 2 1 3 32 31 2 23 21 1 13 12 p p p p p p T r r r r r r r r r r r r Z Z

dengan

∑

=         ₋         ₋ = n i jj j nj ii i ni ij S x x S x x r 1

hubungan antara koefisien regresi data awal ( _j)

∧

β dengan koefisien regresi yang

dibakukan (bj

∧ ) adalah 2 1         =∧ ∧ jj yy j j S S b

β dan

∑

= ∧ ∧ − = n j j jx y 1 0 β β

dengan j = 1, 2, ..., p y= rata-rata dari y

x= rata-rata dari x.

2.4. Multikolinearitas

Multikolinearitas adalah hubungan linear antara beberapa atau semua variabel independen didalam model regresi. Salah satu asumsi model regresi linear klasik adalah bahwa tidak terdapat multikolinearitas diantara variabel-variabel independen yang masuk dalam model. Salah satu indikator yang dapat digunakan dalam mendeteks multikolinearitas adalah nilai VIF yang lebih dari 10 (Gujarati, 2004).

(28)

X2,…,Xk (dimana X1 = 1 untuk semua pengamatan untuk memungkinkan unsur intersep), suatu hubungan linear yang pasti dikatakan ada apabila kondisi berikut ini dipenuhi:

0 ...

2 2 1

1X +λ X + +λkXk =

λ (6)

dimana X1, X2, …, Xk = variabel ke 1, 2, …, k

λ₁,λ₂,...,λ_k = konstanta sedemikian rupa sehingga tidak semuanya secara simultan sama dengan nol.

Tetapi, saat ini istilah multikolinearitas digunakan dalam pengertian yang lebih luas untuk memasukkan kasus multikolinearitas sempurna, seperti ditunjukkan oleh (6) maupun kasus dimana variabel X berkorelasi tetapi tidak secara sempurna, seperti kondisi berikut :

0 ...

2 2 1

1X +λ X + +λkXk +vi =

λ (7)

dimana vi = unsur kesalahan stokhastik (Gujarati, 1978).

Untuk melihat perbedaan antara multikolinearitas yang sempurna dan kurang sempurna, asumsikan, sebagai contoh, bahwa λ₂ ≠0. Maka (7) dapat ditulis sebagai

k k _X

X X

X

2 3

2 3 1 2 1

2 ... _λ

λ λ

λ

− − −

−

= (8)

yang menunjukkan bagaimana X2 berhubungan linear secara sempurna dengan variabel lain atau bagaimana X2 dapat diperoleh dari kombinasi linear variabel X lain. Dalam keadaan ini, koefisien korelasi antara variabel X2 dan kombinasi linear di sisi kanan dari (8) akan menjadi sama dengan satu (Gujarati, 1978).

Serupa dengan itu, jika λ2 ≠0, persamaan (7) dapat ditulis sebagai

i k

k _X _v

X X

X

2 2

3 2 3 1 2 1 2

1 ...

λ λ

λ

− −

−

= (9)

(29)

2.5. Konsekuensi Multikolinearitas

Jika asumsi model regresi linear klasik dipenuhi, penaksir kuadrat-terkecil biasa (OLS) dari koefisien regresi adalah linear, tak bias, dan mempunyai varians minimum, ringkasnya penaksir tadi adalah penaksir tak bias kolinear terbaik (Best Linear Unbiased Estimator/BLUE). Jika sekarang dapat ditunjukkan bahwa multikolinearitas sangat tinggi, penaksir OLS masih tetap memiliki sifat BLUE.

Ketidakbiasan adalah sifat multi sampel atau penyampelan berulang. Jika seseorang mendapatkan sampel berulang dan menghitung penaksir OLS untuk tiap sampel ini, maka rata-rata nilai sampel akan menuju ke nilai populasi yang sebenarnya dari penaksir, dengan meningkatnya jumlah sampel. Tetapi hal ini tidak mengatakan sesuatu mengenai sifat penaksir dalam sampel.

Dalam kasus multikolinearitas sempurna penaksir OLS tak tertentu dan varians atau kesalahan standarnya tak tertentu. Jika kolinearitas tajam tetapi tidak sempurna, maka dapat terjadi konsekuensi berikut ini:

1 Meskipun penaksir OLS mungkin bisa diperoleh, kesalahan standarnya cenderung semakin besar dengan meningkatnya tingkat korelasi antara peningkatan variabel. 2. Karena besarnya kesalahan standar, selang keyakinan untuk parameter populasi

yang relevan cenderung untuk lebih besar.

3. Dalam kasus multikolinearitas yang tinggi, data sampel mungkin sesuai dengan sekelompok hipotesis yang berbeda-beda. Jadi probabilitas untuk menerima hipotesis yang salah meningkat.

4. Selama multikolinearitas tidak sempurna, penaksiran koefisien regresi adalah mungkin tetapi taksiran dan kesalahan standarnya menjadi sangat sensitif terhadap sedikit perubahan dalam data.

(30)

2.6. Pendeteksian Multikolinearitas

Menurut Gujarati (1978) ada beberapa cara untuk mendeteksi ada tidaknya multikolinearitas diantaranya yaitu :

1. Menghitung koefisien korelasi sederhana (simple correlation) antara sesama variabel bebas, jika terdapat koefisien korelasi sederhana yang mencapai atau melebihi 0.8 maka hal tersebut menunjukkan terjadinya masalah multikolinearitas dalam regresi.

2. Menghitung nilai Toleransi atau VIF (Variance Inflation Factor), jika nilai Toleransi kurang dari 0.1 atau nilai VIF melebihi 10 maka hal tersebut menunjukkan bahwa multikolinearitas adalah masalah yang pasti terjadi antar variabel bebas.

3. Lakukan regresi antar variabel bebas dan menghitung masing-masingR2 , kemudian melakukan uji–F dan bandingkan dengan F tabel. Jika nilai F hitung melebihi nilai F tabel berarti dapat dinyatakan bahwa X_i kolinier dengan X yang lain.

2.7. Regresi Linear Berganda

Regresi linear berganda adalah regresi dimana variabel terikatnya (Y) dihubungkan atau dijelaskan dengan lebih dari satu variabel bebas (X1, X2……..Xn) dengan syarat variabel bebas masih menunjukkan hubungan yang linear dengan variabel tak bebas. Hubungan fungsional antara variabel dependen (Y) dengan variabel independent (X1,

X2……..Xn) secara umum dapat dituliskan sebagai berikut: Y = f(X1, X2……..Xn)

(31)

Model regresi linear berganda merupakan suatu model yang dapat dinyatakan dalam persamaan linear yang memuat peubaha dan parameter. Parameter ini pada umumnya tidak diketahui dan dapat ditaksir. Hubungan linear lebih dari dua peubah bila dinyatakan dalam bentuk persamaan matematis adalah:

Ŷ = b0 + b1X1 + b2X2 + … + biXi

dengan

∧

Y = nilai estimasi Y Xi = peubah bebas bi = parameter

Koefisien-koefisien b₀,b₁,...,bi dapat ditentukan dengan menggunakan metode kuadrat terkecil (least square method). Metode kuadrat terkecil untuk menentukan persamaan linear estimasi, berarti memilih satu kurva linear dari beberapa kemungkinan kurva linear yang dapat dibuat dari data yang ada yang mempunyai error paling kecil dari data aktual dengan data estimasinya.

2.8. Metode Regresi Ridge

Metode regresi ridge merupakan salah satu metode yang dianjurkan untuk memperbaiki masalah multikolinearitas dengan cara memodifikasi metode kuadrat terkecil, sehingga dihasilkan penduga koefisien regresi lain yang bias. Modifikasi metode kuadrat terkecil dilakukan dengan cara menambah tetapan bias c yang relatif kecil pada diagonal matriks X’X , sehingga penduga koefisien regresi dipengaruhi oleh besarnya tetapan bias k. pada umumnya nilai c terletak antara 0 dan 1.

(32)

regresi ridge ini adalah masih memungkinkan untuk melakukan seleksi terhadap variabel asal.

Dalam regresi ridge variabel bebas x dan variabel tak bebas y

ditransformasikan dalam bentuk variabel baku Z dan Y*, dimana transformasi variabel bebas dan variabel tak bebas ke bentuk variabel baku diperoleh dari

(10)

dengan Z = nilai variabel yang di bakukan

x = nilai variabel x

x = nilai rata-rata x

x

S = simpangan baku x

(11) dengan Y∗= nilai variabel y yang dibakukan

y = nilai variabel y y = nilai rata-rata y

y

S = simbangan baku y

Selanjutnya

(12)

(13)

Sementara itu, rumus dari korelasi

(14)

Sehingga persamaan normal kuadrat terkecil (XX)b=X’y akan berbentuk (rxx)b=rxy, dengan rxxadalah matriks korelasi variabel x dan rxyadalah matriks korelasi variabel y

x

S x x

Z = −

   

  −    

  − =

x

x S

x x

S x x Z

Z' .

y

S y y Y∗ = −

    

   −    

  − =

y

x S

y y S

x x y

Z' .

(

)(

)

x x xx

S S

x x x x

(33)

dan masing-masing variabel x. Akibat dari transformasi matriks X ke Z dan vektor y

ke y*, maka akan menjadikan persamaan normal regresi ridge yaitu: (rxx+kI) * ∧

b ₌rxy. Sehingga penduga koefisien regresi ridge menjadi :

*

∧

b _{= (}rxx+kI)-1rxy. (15)

Dengan *

∧

b _{= vektor koefisien regresi ridge}

rxx = matriks korelasi variabel x berukuran pxp

rxy = vektor korelasi antara variabel x dan y berukuran px1 k = tetapan bias

I = matriks identitas berukuran pxp

Masalah yang dihadapi dari regresi ridge adalah penentuan nilai dari c. prosedur yang cukup baik untuk menentukan nilai c ini adalah dengan menggunakan nilai statistik CP-Mallows yaitu Ck. statistik CP-Mallows adalah suatu criteria yang berkaitan dengan rata-rata kuadrat error (mean square error) dari nilai kesesuaian model. Nilai k yang terpilih adalah yang meminimumkan nilai Ck (Mayers, 1990).

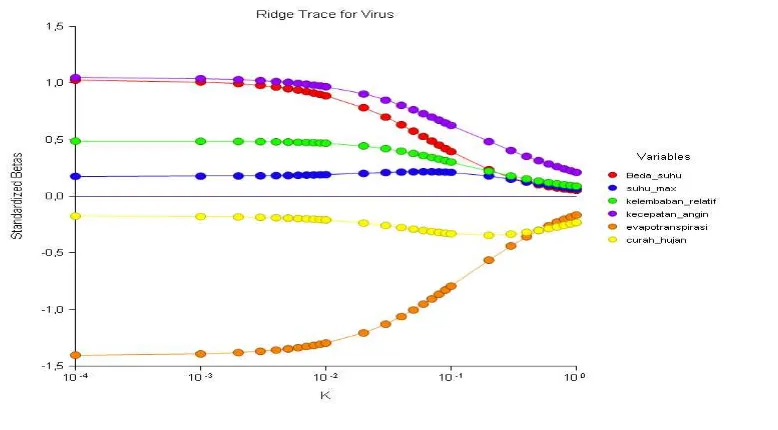
2.9. Ridge Trace

Ridge Trace adalah plot dari estimator Regresi Ridge dengan berbagai kemungkinan nilai tetapan bias c, konstanta c mencerminkan jumlah bias dalam estimator (c)

∧

β .

Bila c = 0 maka estimator (c)

∧

β akan bernilai sama dengan kuadrat terkecil β, tetapi cenderung lebih stabil dari pada estimator kuadrat terkecil.

(34)

Nilai dari c berada pada interval (0.1). Pemilihan tetapan bias c merupakan masalah yang perlu diperhatikan. Tetapan bias yang diinginkan adalah tetapan bias yang menghasilkan bias relatif kecil dan menghasilkan koefisien yang relatif stabil.

Tahapan penaksiran koefisien regresi ridge:

1. Lakukan transformasi tehadap matriks X menjadi Z dan vektor Y menjadi YR, melalui centering and rescaling.

2. Hitung matriks Z'Z => matriks korelasi dari variable bebas, serta hitung Z'YR

=> korelasi dari variable bebas terhadap variable tak bebas y.

3. Hitung nilai penaksir parameter β dengan berbagai kemungkinan tetapan bias c.

4. Hitung nilai VIF dengan berbagai nilai c (0<c<1)

5. Tentukan nilai c dengan mempertimbangkan nilai VIF dan β.

Tentukan koefisien penduga (estimator) regresi ridge dari nilai c yang terpilih..

6. Buat persamaan model regresi ridge

7. Uji Hipotesis secara Simultan dengan ANOVA regresi ridge dan Parsial . 8. Transformasikan ke bentuk asal.

2.10. Analisis Komponen Utama

Analisis komponen utama merupakan suatu teknik mereduksi data multivariat (banyak data) untuk mengubah (mentransformasi) suatu matrik data awal/asli menjadi suatu set kombinasi linear yang lebih sedikit akan tetapi menyerap sebagian besar jumlah varian dari data awal.

(35)

antara peubah asal, analisis komponen utama tidak akan memberikan hasil yang di inginkan, karena peubah baru yang diperoleh hanyalah peubah asal yang ditata berdasarkan besarnya keragamannya. Makin erat korelasi (baik positif maupun negatif) antara peubah, maka baik pula hasil yang diperoleh dari analisis komponen utama.

Analisis komponen utama mengekstrak dengan cara yaitu komponen pertama menyerap varian matriks korelasi paling banyak. kemudian diikuti komponen kedua yang menyerap varian terbanyak kedua terhadap sisa varian dan begitu seterusnya, sampai komponen yang terakhir menyerap varian matriks korelasi paling sedikit. Setiap komponen yang berikutnya juga harus orthogonal yaitu tidak berkorelasi sama sekali dengan komponen sebelumnya atau yang mendahuluinya. Akhirnya, ketika p mendekati k, jumlah varian yang dijelaskan oleh setiap komponen semakin kecil. Tujuannya ialah untuk mempertahankan sejumlah komponen yang diperoleh bisa dipergunakan sebagai variabel bebas (predictor) dalam analisis regresi/diskriminan atau analisis varian, yang sudah bebas dari multikolinearitas.

Kalau Wi = komponen ke i, maka diperoleh m persamaan berikut : W1 = γ11z1+γ12z2 +...+γ1jzj +...+γ1pzp

W2 = γ21z1 +γ22z2 +...+γ2jzj +...+γ2pzp

. . .

Wi = γ_i₁z₁+γ₁₂z₂ +...+γ_ijz_j +...+γ_ipz_p .

. .

Wm = γm1z1 +γm2z2 +...+γmjzj +...+γmpzp.

(36)

γ = vektor eigen

z = nilai standar variabel

Komponen yang ke-i yaitu Wi merupakan kombinasi linear dari X1, X2, …, Xj, …, Xp dengan timbangan (weight) yaitu γ1_j,γ2_j,...,γ_ij,...,γ_ip yang pemilihannya harus

sedemikian rupa, sehingga memaksimumkan rasio dari varian komponen pertama (W1) dengan jumlah varian (total variance) data asli/awal. Komponen berikutnya yaitu W2, juga kombinasi linear yang ditimbang dari seluruh variabel asli, tidak berkorelasi dengan komponen atau faktor pertama (W1) dan harus menyerap secara maksimum sisa varian yang ada (Supranto, 2004).

Langkah awal yang dilakukan dalam Analisis Komponen Utama adalah menentukan nilai eigen dan vektor eigen dari matriks R, matriks korelasi dari X. Dengan terlebih dahulu mengubah data yang distribusi normal umum menjadi distribusi normal baku dengan rumus

Dengan : Z = nilai variabel yang di bakukan x = nilai data berdistribusi normal nilai rata-rata variabel

σ = standar deviasi

Nilai eigen matriks korelasi ini adalah r solusi λ₁,λ₂,...,λ_r dari persamaan determinan

= 0

(37)

Untuk setiap akar ciri λ_j terdapat vector ciri (Characteristic vector) γ_j yang memenuhi sistem persamaan homogen

0 )

( − j j =

T

I Z

Z λ γ .

Vektor ciri solusinya γ_j =(γ₁_j_,γ₂_j,...,γ_rj)', yang dipilih dari sekian banyak solusi sebanding yang ada untuk setiap j, merupakan solusi yang ternormalkan sedemikian rupa sehingga γ'jγj =1. juga dapat diperlihatkan bahwa jika semua λj berbeda,

maka setiap pasangan vector ciri akan saling orthogonal sesamanya. Vektor γ_j digunakan untuk membentuk Z ke dalam suku-suku komponen utama yaitu:

r rj j

j

j z z z

W =γ₁ ₁+γ₂ ₂ +...+γ

sehingga jumlah kuadrat setiap peubah baru W_j, yang unsur-unsurnya W_ji dengan n

i=1,2,..., , adalah λj. Dengan kata lain, Wj mengambil sejumlah λj dari

keragaman totalnya. Perhatikan bahwa

∑

=

= r

j

j r

1

λ sehingga jumlah kuadrat totalnya

∑

= =

= n

i ji r

j

r W 1

2 1

seperti semula (Draper and Smith, 1992).

Jadi, prosedur ini menciptakan peubah-peubah baru W_j dari peubah-peubah asalnya

j

Z , melalui suatu transformasi linear pada persamaan

r rj j

j

j z z z

W =γ1 1+γ2 2 +...+γ

sedemikian rupa sehingga vektor-vektor W itu orthogonal sesamanya. Peubah W_j padanan nilai λ_j yang terbesar disebut komponen utama pertama. Komponen ini menjelaskan bagian terbesar dari keragaman yang dikandung oleh gugusan data yang telah dibakukan. Komponen-komponen W_j yang lain menjelaskan proporsi keragaman yang semakin lama semakin kecil sampai semua keragaman datanya terjelaskan, jadi

∑

=

= p

j

j r

1

(38)

Biasanya semua W_j tidak digunakan melainkan mengikuti suatu aturan seleksi tertentu. Komponen-komponen dapat dihitung sampai sejumlah tertentu proporsi keragaman data yang cukup besar (mungkin 75 persen atau lebih) telah dijelaskan”, dengan kata lain, kita pilih k penyumbang terbesar yang menghasilkan 0,75.

1

>

∑

=

k

j j

r

λ

Aturan-aturan semacam ini secara otomatis memberi k peubah W yang merupakan hasil trasformasi terhadap peubah asal Z_i. Selanjutnya prosedur kuadrat terkecil digunakan untuk memperoleh persamaan peramalan bagi Y sebagai fungsi dari peubah-peubah W_j yang terpilih itu. Urutan masuknya pada peubah W_j tidak ada pengaruhnya dalam hal ini, sebab semua yaitu orthogonal satu sama lain. Bila persamaan regresi dalam Wj telah diperoleh, persamaan ini dapat dikembalikan

menjadi fungsi peubah semula Z_i bila dikehendaki, atau ditafsirkan berdasarkan peubah-peubah W_j tadi (Draper and Smith, 1992).

(39)

Algoritma analisis komponen utama :

1. Mencari nilai rata-rata dari masing-masing variabel, dengan rumus :

Keterangan : i = 1, 2, 3, …, n

i

X = nilai rata-rata variabel ke i

i

X = nilai data variabel ke i

n = jumlah sampel.

2. Mencari standar deviasi setiap variabel dengan rumus :

Keterangan : j = 1, 2, 3, …, n

S_i= standar deviasi ke i.

3. Menstandarkan masing-masing variabel bebas , dengan rumus :

4. Menentukan rata-rata setiap variabel yang telah distandarisasi, dengan rumus :

dengan Zi = rata-rata variabel ke i yang telah distandarisasi.

5. Mencari koefisien korelasi dari variabel yang distandarkan, dengan rumus :

dengan rij = koefisien korelasi kolom ke i dan baris ke j.

6. Menentukan matriks korelasi, jika ZTZ adalah matriks korelasi, maka n

X Xi =

∑

i

(

)

1

2

− −

=

∑

n X X

Si ij i

i i ij ij

S X X

Z = −

n Z Zi =

∑

i

∑

− −

=

2 2

) (

) )(

(

j jk i

ik

j jk i ik ij

Z Z Z

Z

(40)

7. Mencari nilai eigen (λ) yang lebih besar dari 1. Nilai eigen dicari dengan menggunakan persamaan

dengan I = matriks identitas.

8. Mencari vektor eigen dari nilai eigen yang lebih besar dari satu dengan menggunakan persamaan :

dengan j = 1, 2, 3, …, n

γ_j= vektor eigen ke j.

9. Komponen utama ke j untuk standar Z didapatkan yaitu : .

Maka model regresi komponen utama dapat dirumuskan sebagai :

Keterangan : Y_{= variabel tak bebas}

j

W = variabel bebas komponen utama yang merupakan kombinasi linier dari semua variabel baku Z(j=1, 2,….,m)

0

k = konstanta

j

k = koefisien model regresi ( j = 1, 2,….,m)

v = galat

                      = 1 . . . . . . . . . 1 . . . 1 . . . 1 3 2 1 3 32 31 2 23 21 1 13 12 p p p p p p T r r r r r r r r r r r r Z Z 0 = − I Z ZT λ

0 ) (ZTZ −λ_jI γ_j =

r rj j

j

j Z Z Z

W =γ1 1+γ2 2+...+γ

v W k W k W k k

(41)

BAB 3

METODE PENELITIAN

3.1. Bidang Penelitian

Penelitian ini dikelompokkan dalam penelitian tinjauan literatur pada bidang ilmu statistika matematika. Obyek yang diteliti menyangkut pada data yang diambil dari buku maupun internet yang disebutkan sumbernya.

3.2. Metode dan Desain Penelitian

1. Metode Penelitian

Metode penelitian yang digunakan adalah metode penelitian kuantitatif literatur dengan pengambilan data pada buku maupun internet.

2. Desain Penelitian

(42)

3.3. Sumber Data

Sumber data yang diambil yaitu data sekunder. Data sekunder adalah data yang diperoleh peneliti bukan dari cara peneliti sendiri tetapi dikumpulkan oleh orang lain, seperti dari dokumen perusahaan, brosur, internet, dan dari riset kepustakaan yang dimaksud untuk mendapatkan informasi penting lainnya, dasar pengaturan, serta dasar teori agar diperoleh kerangka pikir dan pemecahan secara teoritis terhadap apa yang diteliti. Data yang digunakan untuk studi ini yaitu data dari buku yang sudah tersedia.

3.4. Variabel Penelitian

1. Variabel

Variabel adalah konsep yang mempunyai variabilitas, sedangkan konsep adalah penggambaran atau abstraksi dari suatu fenomena tertentu. Konsep yang berupa apapun, asal mempunyai ciri yang bervariasi, maka dapat disebut sebagai variabel. Dengan demikian, variabel dapat diartikan sebagai segala sesuatu yang bervariasi. Variabel pada penelitian ini terdiri dari:

a. Variabel X/Bebas/Independent/ yang mempengaruhi adalah :

(43)

b. Variabel Y/terikat/dependent/yang dipengaruhi yakni : serangan Virus (Y) pada penggerek batang padi Afrika di Pantai Gading Afrika Barat.

3.5. Teknik Analisis Data

Agar dapat mempermudah, mempercepat dan memastikan keakuratan perhitungan dan penyajian data, maka dirancang suatu program statistik yang mampu mengolah data staistik secara cepat dan akurat, yaitu dengan NCSS dan SPSS.

1. Analisis regresi linier

Menurut (Algifari, 2000), analisis regresi adalah studi mengenai ketergantungan variabel dependent (terikat) dengan satu atau lebih variabel independent dengan tujuan untuk mengestimasi atau memprediksi rata-rata populasi atau nilai rata-rata variabel dependent berdasarkan nilai variabel independent yang diketahui.

Ŷ = b0 + b1X1 + b2X2 + … + biXi

dengan

∧

Y = nilai estimasi Y Xi = peubah bebas bi = parameter

2. Uji koefisien regresi linier

(Algifari, 2000) menguraikan uji koefisien regresi linier terdiri dari :

1. Uji Statistik F

a. Merumuskan hipotesis

(44)

H1 : b1, b2, b3, b4, b5, b6 ≠ 0 atau sig Fhitung > Ftabel, maka Ho ditolak dan H1 diterima (ada pengaruh signifikan variabel X1, X2, X3, X4, X5, X6 terhadap variabel Y).

b.Memilih uji statistik F karena ingin mengetahui apakah ada pengaruh signifikan antar variabel independent secara bersama-sama terhadap variabel dependent. c. Menentukan tingkat signifikan, yaitu α = 5%, "derajat kebebasan (df) dengan

rumus df1(N1) = k-1, df2(N2) = n-k, k adalah konstruk (jumlah variabel X dan Y), sedangkan n adalah jumlah sampel, untuk menentukan Ftabel.

d. Menghitung Fhitung dengan bantuan sarana komputer program "SPSS for Ms. Windows."

e. Membuat simpulan membandingkan Fhitungdengan Ftabel, dan membandingkan sig Fdengan signifikan α = 5% (0,05 ).

2. Uji Statistik t

Secara parsial (masing-masing variabel X) menggunakan uji statistik t dengan langkah-langkah sebagai berikut :

a. Merumuskan hipotesis

Ho : b1, b2, b3, b4, b5, b6 = 0 atau thitung ≤ttabel, maka Ho diterima dan H1 ditolak (tidak ada pengaruh signifikan variabel X1, X2, X3, X4, X5, X6 terhadap variabel Y). H1 : b1, b2, b3, b4, b5, b6 ≠ 0 atau thitung > ttabel, Ho ditolak dan H1 diterima (ada pengaruh signifikan variabel X1, X2, X3, X4, X5, X6 terhadap Y).

b. Memilih uji statistik t karena ingin mengetahui apakah ada pengaruh signifikan masing-masing variabel independent terhadap variabel dependent.

c. Menentukan tingkat signifikan, yaitu α= 5%, "derajat kebebasan (df) = n-k, n adalah jumlah sampel, k adalah konstruk (jumlah variabel X dan Y) untuk menentukan ttabel.

(45)

e. Membuat simpulan membandingkan thitung dengan ttabel dan membandingkan signifikansi tdengan signifikan α = 5% (0,05).

3. Koefisien Determinasi

Analisis ini digunakan untuk mengetahui perubahan variabel terikat yang disebabkan adanya perubahan variabel bebas, dan digunakan dalam presentase. Koefisien ini juga digunakan sebagai pendekatan atas suatu hubungan linier antar variabel (X) lebih dari 2, digunakan rumus sebagai berikut :

Dimana :

R2 = Besar koefisien determinasi.

b = Slope garis estimasi yang paling baik.

X = Nilai variabel X Y = Nilai variabel Y n = Banyaknya data.

Nilai koefisien determinasi berganda ini adalah lebih besar dari 0 tetapi lebih kecil dari 1, maka apabila :

a. Nilai koefisien determinasi menunjukkan angka mendekati 1, berarti variabel bebas (X) memiliki pengaruh yang besar terhadap variabel terikat (Y).

b. Nilai koefisien determinasi mendekati 0, berarti bahwa perubahan variabel terikat (Y) banyak dipengaruhi oleh faktor-faktor lain diluar variabel yang diteliti.

2 2 2 1 1

2 ...

Y

Y x b Y

x b Y x b

(46)

4. Koefisien Beta Standar

Koefisien beta standar digunakan untuk menentukan variabel bebas (independent) yang paling berpengaruh signifikan terhadap variabel terikat (dependent). Koefisien yang dihasilkan dari regresi linier yang telah dinormalisasikan akan menunjukkan variabel bebas dengan tingkat signifikan yang paling tinggi, artinya variabel tersebut merupakan variabel yang paling besar pengaruhnya terhadap variabel terikat.

5. Koefisien Korelasi

Dari data yang ada akan disajikan matriks koefisien korelasi. Matriks tersebut dapatmenggambarkan korelasi diantara peubah bebas (x).

6. Variance Inflation Factor (VIF)

Setelah data matriks korelasi disajikan, selanjutnya akan disajikan perhitungan Variance Inflation Factor (VIF) dengan bantuan program SPSS 16. Perhitungan VIF dimaksudkan untuk mendeteksi adanya multikolinearitas diantara peubah-peubah bebas (x).

7. Regresi Ridge

(47)

8. Analisis Komponen Utama

Analisis komponen utama merupakan suatu teknik mereduksi data multivariat (banyak data) untuk mengubah (mentransformasi) suatu matrik data awal/asli menjadi suatu set kombinasi linear yang lebih sedikit akan tetapi menyerap sebagian besar jumlah varian dari data awal. Perhitungan dengan analisi kompnen utama ini menggunakan bantuan program SPSS 16.

(48)

BAB 4

PEMBAHASAN

4.1.Metode Regresi Ridge

Metode regresi ridge merupakan salah satu metode yang dianjurkan untuk memperbaiki masalah multikolinearitas dengan cara memodifikasi metode kuadrat terkecil, sehingga dihasilkan penduga koefisien regresi lain yang bias. Modifikasi metode kuadrat terkecil tersebut dilakukan dengan cara menambah tetapan bias c yang relatif kecil pada diagonal matriks X’X , sehingga penduga koefisien regresi dipengaruhi oleh besarnya tetapan bias k. pada umumnya nilai c terletak anatara 0 dan 1. Pada dasarnya metode ini juga merupakan metode kuadrat terkecil. Perbedaannya adalah bahwa pada metode regresi ridge, nilai variabel bebasnya ditransformasikan dahulu melalui prosedur centering and rescaling. Kemudian pada diagonal utama matriks korelasi variable bebas ditambahkan biasing constant (c) dimana nilainya antara 0 dan 1. Metode regresi ridgedapat digunakan dengan asumsi matriks korelasi dari variable bebasnya dapat diinverskan. Akibatnya nilai dugaan koefisien regresi dan variable tak bebasnya mudah didapat.

Model Regresi berganda dengan OLS

bc + b1Xi1 + b2Xi2 + . . . + bp-1 Xip-1 (16) b = ( X 'X)-1X'Y (17) Model Standardized Regression

b1*Xi1* + b2*Xi2* + . . . + bp-1* Xip-1* (18) b* = ( rxx)-1rxy matriks korelasi

Model Ridge regression

(49)

bR = ( rxx + c I)-1rxy matriks korelasi dimana:

c = biasing constant I = identity matrix

bR [(p-1) x 1] =

Tahapan dalam metode regresi ridge :

1. Lakukan transformasi tehadap matriks X menjadi Z dan vektor Y menjadi YR, melalui centering and rescaling.

2. Hitung matriks Z'Z => matriks korelasi dari variable bebas, serta hitung Z'YR => korelasi dari variable bebas terhadap variable tak bebas y.

3. Hitung nilai penaksir parameter bR dengan kemungkinan tetapan bias c. 4. Hitung nilai VIF dengan berbagai nilai c (0<c<1)

5. Tentukan nilai c dengan mempertimbangkan nilai VIF dan bR.

Tentukan koefisien penduga (estimator) regresi ridge dari nilai c yang terpilih.. 6. Buat persamaan model regresi ridge

7. Uji Hipotesis secara Simultan dengan ANOVA regresi ridge dan Parsial . 8. Transformasikan ke bentuk asal.

a. Metode Centering and Rescaling

Dalam persamaan regresi yang memiliki model :

Yi = β0 + β1Xi1 + β2Xi2 + εi

Persamaan tersebut di atas dapat dibentuk menjadi :

Yi = β0 + β1 (Xi1 – ) + β1 + β2(Xi2 - ) + β2 + εi

= (β0 + β1 + β2 ) + β1 (Xi1 - ) + β2 (Xi2 - ) + εi

menurut rumus untuk mendapatkan β0 yaitu :

(50)

= β0 + β1 + β2

Sehingga Yi – (β0 + β1 + β2 ) = β1 (Xi1 - ) + β2(Xi2 - ) + εi

Yi - = β1 (Xi1 - ) + β2(Xi2 - ) + εi

Jika yi = Yi - xi1 = Xi1 - xi2 = Xi2 -

maka didapat persamaan baru yaitu :

yi = β1xi1 + β2xi2 + εi

Prosedur untuk membentuk persamaan pertama menjadi persamaan terakhir disebut

dengan prosedur centering. Prosedur ini mengakibatkan hilangnya β0 (intercept) yang

membuat perhitungan untuk mencari model regresi menjadi lebih sederhana.

Bila dari persamaan di atas dibentuk persamaan : Yi R= β1Zi1 + β2Zi2 + εi’ YiR= =

Zi1 = =

Zi2 = =

Keterangan:

: nilai variabel tak bebas ke-i hasil trasformasi

: nilai variabel tak bebas ke-i : rata-rata variabel tak bebas

: Jumlah Observasi

:

: nilai variabel bebas 1 ke-i hasil trasformasi : nilai variabel bebas 1 ke i

(51)

:

maka prosedur ini disebut dengan prosedur Rescaling. Keseluruhan dari prosedur di atas

disebut prosedur centering and rescaling.

b. Menentukan tetapan bias / biasing constant (c)

Ridge trace merupakan plot dari estimator ridge regresi secara bersama dengan berbagai kemungkinan nilai tetapan bias c. Konstanta c mencerminkan jumlah bias dalam estimator ( c ). Saat c bernilai 0 maka estimator ( c ) akan bernilai sama dengan estimator kuadrat terkecil yang telah dalam bentuk standardized. Ketika c > 0 estimator ridge regression akan bias tetapi cenderung menjadi lebih stabil daripada estimator kuadrat terkecil. Umumnya nilai c terletak pada interval 0<c<1.

Pemilihan besarnya tetapan bias c merupakan masalah yang perlu diperhatikan. Tetapan bias yang diinginkan adalah tetapan bias yang relative kecil dan menghasilkan koefisien estimator yang relatif stabil.

Suatu acuan yang digunakan untuk memilih besarnya c, dengan melihat besarnya VIF dan melihat pola kecenderungan Ridge Trace. VIF merupakan faktor yang mengukur seberapa besar kenaikan variansi dari koefisien estimator dibandingkan terhadap variable bebas lain yang saling orthogonal. Bila diantara variabel bebas tersebut terdapat korelasi yang tinggi, nilai VIF akan besar. VIF memiliki nilai mendekati 1 jika variabel bebas X tidak saling berkorelasi dengan variabel-variabel bebas lainnya.

Nilai VIF untuk koefisien ridge regression adalah element diagonal pada matriks (p-1) x (p-(p-1) berikut:

(52)

Cara pemilihan ini memang bersifat subyektif, artinya jika ada 2 orang pemilih memilih nilai c dengan data yang sama mungkin akan mendapatkan nilai c yang tidak sama (Myers, 1990).

Contoh kasus :

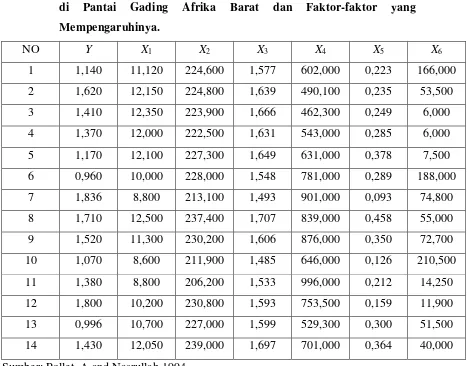
[image:52.612.111.578.333.699.2]

Untuk mengetahui penggunaan metode regresi ridge dan analisis komponen utama dalam menyelesaikan masalah multikolinearitas, akan digunakan suatu contoh kasus yang terdapat multikolinearitas diantara variabel-variabel bebasnya. Data yang akan dibahas adalah data yang tertera pada tabel berikut ini :

Tabel 4.1. Data Banyaknya Serangan Virus Pada penggerek Batang Padi Afrika di Pantai Gading Afrika Barat dan Faktor-faktor yang Mempengaruhinya.

NO Y X1 X2 X3 X4 X5 X6

(53)

Keterangan :

Y = Virus (mikron)

X1 = rerata selisih suhu harian tertinggi dan suhu harian terendah( 0C ) X2 = rerata suhu harian tertinggi ( 0C )

X3 = logaritma kelembaban relatif maksimum (Kg/m3) X4 = kecepatan angin (knot)

X5 = logaritma evepotranspirasi ( mm) X6 = curah hujan (mm)

4.2. Metode Regresi Linier Ganda

Langkah-langkah untuk mendapatkan koefisien regresi dengan data awal adalah sebagai berikut :

1. Hitung nilai penaksir parameter β, kemudian hitung galat baku dan hitung t, buat suatu model.

2. Hitung ŷ dan menganalisa dengan tabel ANAVA.

Hasil Analisis Regresi dengan menggunakan Metode Kuadrat Terkecil terhadap data pada tabel 4.1.

Pengujian keberartian model regresi ganda yang dilakukan secara parsial atau individu , dengan hipotesis

H0 : βi = 0, untuk i=1,2,3 (variabel regressor X secara individu tidak berpengaruh secara signifikan terhadap nilai taksiran Y)

H1 : βi ≠ 0,untuk i=1,2,3 (variabel regressor X secara individu tidak perpengaruh secara signifikan terhadap nilai taksiran Y)

(54)

[image:54.612.109.505.126.283.2]

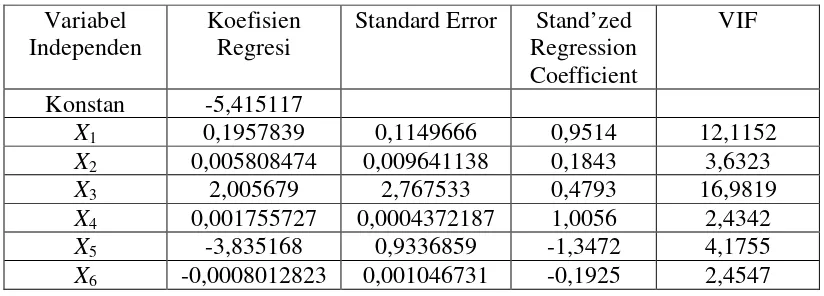
Tabel 4.2. Penaksir Parameter Metode Kuadrat Terkecil Coefficientsa

Model

Unstandardized Coefficients

Standardized Coefficients

T Sig.

Collinearity Statistics

B Std. Error Beta Tolerance VIF

1(Constant) -5.591 3.165 -1.766 .121

x1 .211 .122 1.026 1.724 .128 .064 15.570

x2 .006 .010 .176 .582 .579 .248 4.033

x3 2.037 3.030 .487 .672 .523 .043 23.059

x4 .002 .000 1.048 4.261 .004 .376 2.659

x5 -3.994 .917 -1.403 -4.357 .003 .219 4.558

x6 .000 .001 -.175 -.693 .511 .356 2.805

a. Dependent Variable: y

Tabel 4.3. Tabel ANAVA Untuk Data Awal

ANOVAb

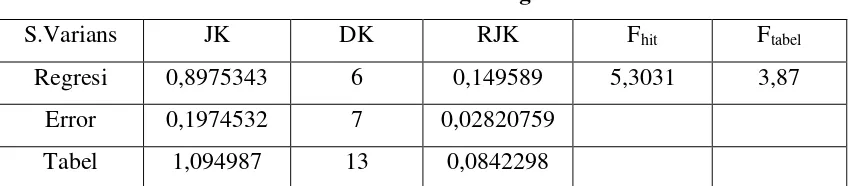
Model Sum of Squares Df Mean Square F Sig.

1 Regression .921 6 .153 6.160 .015a

Residual .174 7 .025

Total 1.095 13

a. Predictors: (Constant), x6, x4, x2, x5, x1, x3 b. Dependent Variable: y

Dari tabel 4.2. diatas diperoleh model regresi sebagai berikut: Ŷ = -5,591 + 0,211 X1 + 0,006 X2 + 2,037 X3 + 0,002 X4 - 3,994 X5

4.3. Pendeteksian Multikolinearitas

Dalam pendeteksian multikolinearitas ada beberapa cara yang dapat digunakan yaitu sebagai berikut:

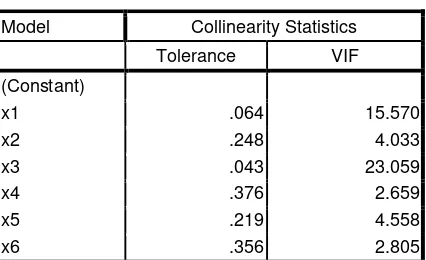
1. Faktor Variansi Inflasi (Variance Inflation Faktor, VIF)

[image:54.612.125.522.355.427.2]

(55)

variabel bebas. (Variance Inflation Factor ke-j /

2

1 1 )

j j

R VIF

−

= , dan Toleransi =

) 1 (

1 2

j

R

VIF = − . Dengan : 2

j

R adalah koefisien determinasi antara X_j dengan variabel bebas lainnya pada persamaan/model dugaan regresi; dimana j = 1,2,…, p.

[image:55.612.215.428.250.380.2]

Dengan bantuan software SPSS 16.0, diperoleh nilai Toleransi atau VIF untuk data di atas pada tabel berikut ini.

Tabel 4.4. Nilai Toleransi dan VIF

Model Collinearity Statistics

Tolerance VIF

(Constant)

x1 .064 15.570

x2 .248 4.033

x3 .043 23.059

x4 .376 2.659

x5 .219 4.558

x6 .356 2.805

Hasil uji melalui variance inflation factor (VIF) pada hasil output tabel coefficients masing-masing variabel independent memiliki nilai VIF lebih dari 10 dan nilai tolerance kurang dari 0,1. Maka dapat dinyatakan data pada tabel 4.1 terdapat masalah multikolinearitas.

2. Nilai Korelasi

Tabel 4.5. Nilai Korelasi Antar Variabel Bebas

X1 X2 X3 X4 X5 X6

X1 0,731870 1,000000 0,786021 0,191961 0,726467 0,169565

X₂ 0,942984 0,786021 1,000000 0,355660 0,794605 0,560393

X3 0,520302 0,191961 0,355660 1,000000 0,032919 0,055715

X4 0,739453 0,726467 0,794605 0,032919 1,000000 0,276299

X5 0,448261 0,169565 0,560393 0,055715 0,276299 1,000000

[image:55.612.110.517.580.707.2]

(56)

Sehingga nilai korelasi antar variabel dapat dibuat dalam bentuk matriks korelasi c

sebagai berikut :

                    = 0,491544 0,115551 0,343377 0,203488 0,119203 0,109933 1,000000 0,276299 0,055715 0,560393 0,169565 0,448261 0,276299 1,000000 0,032919 0,794605 0,726467 0,739453 0,055715 0,032919 1,000000 0,355660 0,191961 0,520302 0,560393 0,794605 0,355660 1,000000 0,786021 0,942984 0,169565 0,726467 0,191961 0,786021 1,000000 0,731870 C

Dari matriks korelasi c dapat dilihat bahwa nilai korelasi antar variabel bebas terdapat nilai korelasi yang lebih besar dari 0,8. Hal ini menunjukkan bahwa terdapat masalah multikolinearitas antar variabel bebasnya.

3. Determinan matriks korelasi

Dari matriks korelasi c dapat dihitung nilai determinannya sebagai berikut :

0040 , 0 0,491544 0,115551 0,343377 0,203488 0,119203 0,109933 1,000000 0,276299 0,055715 0,560393 0,169565 0,448261 0,276299 1,000000 0,032919 0,794605 0,726467 0,739453 0,055715 0,032919 1,000000 0,355660 0,191961 0,520302 0,560393 0,794605 0,355660 1,000000 0,786021 0,942984 0,169565 0,726467 0,191961 0,786021 1,000000 0,731870 =                     = C C

Nilai determinan dari matriks korelasi c mendekati nol ini menunjukkan terdapat masalah multikolinearitas yang tinggi.

(57)

[image:57.612.107.535.88.350.2]

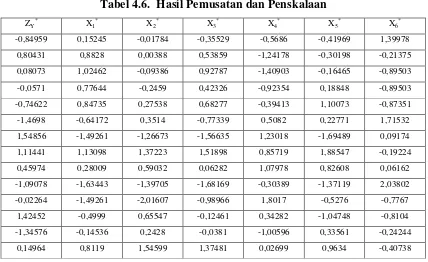
Tabel 4.6. Hasil Pemusatan dan Penskalaan ZY

*

X1 *

X2 *

X3 *

X4 *

X5 *

X6 *

-0,84959 0,15245 -0,01784 -0,35529 -0,5686 -0,41969 1,39978

0,80431 0,8828 0,00388 0,53859 -1,24178 -0,30198 -0,21375

0,08073 1,02462 -0,09386 0,92787 -1,40903 -0,16465 -0,89503

-0,0571 0,77644 -0,2459 0,42326 -0,92354 0,18848 -0,89503

-0,74622 0,84735 0,27538 0,68277 -0,39413 1,10073 -0,87351

-1,4698 -0,64172 0,3514 -0,77339 0,5082 0,22771 1,71532

1,54856 -1,49261 -1,26673 -1,56635 1,23018 -1,69489 0,09174

1,11441 1,13098 1,37223 1,51898 0,85719 1,88547 -0,19224

0,45974 0,28009 0,59032 0,06282 1,07978 0,82608 0,06162

-1,09078 -1,63443 -1,39705 -1,68169 -0,30389 -1,37119 2,03802

-0,02264 -1,49261 -2,01607 -0,98966 1,8017 -0,5276 -0,7767

1,42452 -0,4999 0,65547 -0,12461 0,34282 -1,04748 -0,8104

-1,34576 -0,14536 0,2428 -0,0381 -1,00596 0,33561 -0,24244

0,14964 0,8119 1,54599 1,37481 0,02699 0,9634 -0,40738

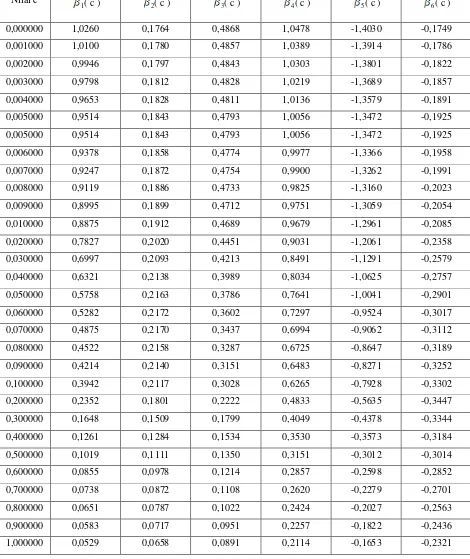
[image:57.612.109.581.508.698.2]

Dalam peroses pendugaan regresi ridge, pemilihan tetapan bias c merupakan suatu yang penting dalam penelitian ini, penentuan tetapan bias c ditempuh melalui pendekatan nilai VIF dan gambar Ridge Trace. Nilai koefisien dari ( c ) dengan berbagai kemungkinan tetapan bias c dapat dilihat pada tabel 4.7.