Pemodelan Pemakaian Energi Listrik Persektor Pelanggan Dengan Menggunakan Metode Analisis Regresi Komponen Utama Pada PT. PLN (PERSERO) Cabang Padangsidimpuan

PEMODELAN PEMAKAIAN ENERGI LISTRIK PERSEKTOR

PELANGGAN DENGAN MENGGUNAKAN METODE

ANALISIS REGRESI KOMPONEN UTAMA PADA

PT. PLN (PERSERO) CABANG

PADANGSIDIMPUAN

SKRIPSI

YUNIAR ZEIN LUBIS

080803001

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PEMODELAN PEMAKAIAN ENERGI LISTRIK PERSEKTOR PELANGGAN DENGAN MENGGUNAKAN METODE ANALISIS REGRESI KOMPONEN

UTAMA PADA PT. PLN (PERSERO) CABANG PADANGSIDIMPUAN

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

YUNIAR ZEIN LUBIS 080803001

DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAMUNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : PEMODELAN PEMAKAIAN ENERGI LISTRIK PERSEKTOR PELANGGAN DENGAN

MENGGUNAKAN METODE ANALISIS

REGRESI KOMPONEN UTAMA PADA PT. PLN (PERSERO) CABANG PADANGSIDIMPUAN

Kategori : SKRIPSI

Nama : YUNIAR ZEIN LUBIS

Nomor Induk Mahasiswa : 080803001

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juli 2013 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Djakaria Sebayang, M.Si Drs. Gim Tarigan, M.Si NIP. 19511227198503 1 002 NIP. 19550201198601 1 001

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

PERNYATAAN

PEMODELAN PEMAKAIAN ENERGI LISTRIK PERSEKTOR PELANGGAN DENGAN MENGGUNAKAN METODE ANALISIS REGRESI KOMPONEN

UTAMA PADA PT. PLN (PERSERO) CABANG PADANGSIDIMPUAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2013

PENGHARGAAN

Assalamua’laikum Wr. Wb.

Puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah melimpahkan rahmat dan karuniaNya sehingga penulis dapat menyelesaikan skripsi ini dengan. Oleh karena itu dengan segala kerendahan hati dalam kesempatan ini, penulis ingin mengucapkan terima kasih kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini, ucapan terima kasih sampaikan kepada:

Bapak Drs. Djakaria Sebayang, M.Si dan Bapak Drs. Gim Tariga, M.Si sebagai Dosen Pembimbing 1 dan 2 yang telah banyak memberikan arahan, motivasi, waktu, ilmu pengetahuan dan kepercayaan kepada penulis dalam mengerjakan skripsi ini. Bapak Drs Marihat Situmorang M.Si dan Ibu Asima Manurung, S.Si, M.Si sebagai Dosen Pembanding yang banyak memberikan saran dan masukan dalam penyelesaian skripsi ini.

Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dra. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika Fakultas Matematika dan ilmu Pengetahuan Alam Universitas Sumatera Utara. Bapak Dr. Sutarman, M.Sc selaku Dekan Fakultas Matematika dan ilmu Pengetahuan Alam Universitas Sumatera Utara. Semua Dosen dan Staff pegawai Matematika FMIPA USU.

Kedua orang tua saya tercinta ayahanda Zairil Zein Lubis, S.Pd dan ibunda Hawani nasution serta saudara-saudara penulis Nisa, Zizah, Iat, Purnama, Yuni, Miftah dan keluarga besar dari Udak Sutan Napsan Nasution atas nasehat dan doa, dukungan moril dan materil, yang menjadi sumber motivasi bagi penulis untuk tetap semangat dalam penulisan skripsi ini. Serta para sahabat-sahabat Silvi, Fitri, Alvi, Syelviana, Ulan, Fika, Ugi, dan semua teman-teman seperjuangan di Matematika stambuk 2008.

Medan, Juni 2013 Penulis,

ABSTRAK

PRINCIPAL COMPONENT ANALYSIS AS A METHOD TO OVERCOME THE PROBLEM OF MULTICOLLINEARITY

ABSTRACT

The number of usage energi of electrics influenced by the usage of energi of electrics per sector of client covering domestic, social, business, industrial, government, and

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak iv

Abstract v

Daftar Isi vi

Daftar Tabel vii

Bab 1 Pendahuluan 1

1.1. Latar Belakang 2

1.2. Perumusan Masalah 3

1.3. Pembatasan Masalah 3

1.4. Tujuan Penelitian 3

1.5. Metodologi Penelitian 3

1.6. Tinjauan Pustaka 4

Bab 2 Landasan Teori 7

2.1. Analisis Korelasi 7

2.2. Matriks Korelasi 8

2.3. Nilai Eigen dan Vektor Eigen 8

2.4. Determinan 9

2.5. Analisis Komponen utama 10

2.6. Regresi Linear Berganda 14

Bab 3 Pembahasan 15

3.1. Pembakuan Data 20

3.2. Menghitung Koefisien Korelasi 23

3.3. Menghitung Nilai Eigen 24

3.4. Menghitung Vektor Eigen 25

Bab 4 Penutup 32

4.1. Kesimpulan 32

4.2. Saran 32

DAFTAR TABEL

Halaman Tabel 3.1: Pemakaian Energi Listrik Persektor Pelanggan Pada

PT. PLN (Persero) Area Padangsidimpuan

Januari 2007 s/d September 2012 16

Tabel 3.2: Data Pembakuan 21

Tabel 3.3: Matriks Korelasi 23

Tabel 3.4: Nilai Eigen dan Proporsi Kumulatif 24

Tabel 3.5: Vektor Eigen 25

Tabel 3.6: Nilai Komponen Utama 26

Tabel 3.7: Besaran-besaran Untuk Menghitung 28

ABSTRAK

PRINCIPAL COMPONENT ANALYSIS AS A METHOD TO OVERCOME THE PROBLEM OF MULTICOLLINEARITY

ABSTRACT

The number of usage energi of electrics influenced by the usage of energi of electrics per sector of client covering domestic, social, business, industrial, government, and

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Pada zaman modern seperti saat sekarang ini, energi listrik merupakan kebutuhan primer bagi manusia, baik masyarakat yang tinggal di perkotaan maupun masyarakat yang tinggal di pedesaan. Listrik tidak bisa dipisahkan dengan kehidupan manusia karena hampir semua kegitan manusia menggunakan listrik. Dengan tidak ada energi listrik, dunia akan sangat sulit berkembang, bisa jadi monoton.

Pada era globalisasi seperti saat ini, khususnya di bidang industri yang semakin berkembang didukung dengan perkembangan teknologi yang semakin canggih sangat dibutuhkan banyak hal dalam mendukung kemajuan pendidikan dan teknologi termasuk energi listrik. Kalau tidak ada listrik semua akan terasa sulit, dan dimalam hari dunia akan menjadi gelap gulita. Seiring dengan perkembangan zaman yang semakin canggih dan modern semakin banyak pula alat-alat elektronik yang membutuhkan tenaga listrik, sehingga kebutuhan akan listrik semakin hari semakin meningkat.

Sumber energi listrik utama diberikan oleh lembaga listrik negara. Organisasi ini bertanggung jawab untuk menghasilkan tenaga listrik di pusat-pusat tenaga listrik, dan disalurkan kepada pemakai melalui kabel-kabel penghantar. Para pemakai listrik diantaranya adalah : rumah tangga, industri, lembaga masyarakat, badan sosial, bisnis, gedung pemerintahan, dan multiguna. Semua itu disebut dengan pelanggan.

Berdasarkan uraian di atas penulis ingin menganalisa dan melakukan penelitian tentang pemodelan pemakaian energi listrik yang terjadi di Padangsidimpuan dengan menggunakan Analisi Komponen Utama. Analisis Komponen Utama adalah merupakan suatu teknik mereduksi data multivariate (banyak data) yang mengubah (mentransformasi) data awal menjadi suatu set kombinasi linier yang lebih sedikit, tetapi menyerap sebagian besar jumlah varian dari data awal. Analisis Komponen Utama bertujuan untuk mengubah dari sebagian besar variabel asli yang digunakan yang saling berkolerasi satu dengan lainnya, menjadi satu set variabel baru yang lebih kecil dan saling bebas (tidak berkolerasi lagi), dan merupakan kombinasi linier dari variabel asal. Secara umum tujuan dari Analisis Komponen Utama adalah mereduksi dimensi data sehingga lebih mudah menginterpretasikan data-data tersebut.

Oleh sebab itu penulis memilih judul “Pemodelan Pemakaian Energi Listrik Persektor Pelanggan Dengan Menggunakan Metode Analisis Regresi Komponen Utama Pada PT. PLN ( Persero ) Cabang Padangsidimpuan”.

1.2. Perumusan Masalah

1.3. Pembatasan Masalah

Penelitian dibatasi pada data pemakaian energi listrik yang diperoleh dari PT. PLN Cabang Padangsidimpuan dari Januari 2007 sampai dengan September 2012.

1.4. Tujuan Penelitian

Tujuan dari penelitian ini adalah :

1. Untuk mengetahui model pendugaan dari pemakaian energi listrik dari beberapa sektor pelanggan pada PT. PLN Cabang Padangsidimpuan dengan menggunakan Analisis Komponen Utama (AKU).

2. Hasil penelitian ini dapat dijadikan sebagai bahan referensi untuk peneliti - peneliti berikutnya dalam data yang akan dianalisis.

1.5. Metodologi Penelitian

Penelitian yang dilakukan melalui beberapa tahap seperti yang diuraikan berikut ini : 1. Menetapkan variabel–variabel penelitian.

2. Pengumpulan data meliputi data–data pemakaian energi listrik pelanggan di wilayah distrubusi PT. PLN.

3. Membakukan variabel-variabel penelitian dengan menggunakan rumus

Dengan : Z = nilai variabel yang di bakukan x = nilai data berdistribusi normal nilai rata-rata variabel

σ = standar deviasi



5. Menghitung nilai eigen dari matrik kolerasi dengan menggunakan

persamaan

= 0.

6. Menghitung proforsi komulatif.

7. Menghitung eigen vektor dengn menggunakan persamaan :

= 0

8. Menghitung komponen-komponen yang direduksi.

9. Memasukkan nilai-nilai data awal kedalam transformasi komponen utama yang dihasilkan.

10.Membuat model dengan menggunakan metode kuadrat terkecil 11.Membuat tabel analisis ragam.

12.Penarikan kesimpulan.

1.6. Tinjauan Pustaka

segugus data peubah ganda yang besar serta dapat memerinkatkan urutan terbesar dari variabel yang digunakan.

Siswadi (1998, hal 23) menyatakan Analisis Komponen Utama (AKU) digunakan untuk :

1. Mengidentifikasi peubah baru yang mendasari peubah ganda.

2. Mengurangi banyaknya dimensi himpunan peubah yang biasa terdiri atas peubah yang banyak yang saling berkolerasi menjadi peubah–peubah baru yang tidak berkolerasi dengan mempertahankan sebanyak mungkin keragaman dalam himpunan data tersebut.

3. Menghilangkan peubah–peubah asal yang mempunyai sumbangan informasi yang relatif kecil.

Tujuan utama Analisis Komponen Utama ialah menjelaskan sebanyak mungkin jumlah varian data asli dengan sedikit mungkin komponen utama. Banyaknya komponen yang bisa di ekstrak dari data awal/asli ialah sebanyak variabel yang ada. Katakan ada m komponen yang bisa di ekstrak dari p variabel asli, maka paling banyak m = p, artinya banyaknya komponen sama dengan banyaknya variabel. Hal ini tidak diinginkan, sebab menjadi tidak hemat (parsimonious), maka m harus lebih kecil dari p, artinya banyaknya komponen yang harus dipertahankan (to retain) harus sedikit mungkin, akan tetapi sudah mencakup sebagian besar informasi yang terkandung di dalam data asli. Data asli harus direduksi dengan sedikit mungkin komponen akan tetapi masih memuat sebagian besar variasi dari data asli/awal, katakana lebih dari 80% (Supranto, 2004).

Analisi Komponen Utama merupakan suatu teknik analisis satistik untuk mentranformasi peubah-peubah asli yang masih berkolerasi satu dengan yang lain menjadi satu set peubah baru yang tidak berkolerasi lagi. Peubah-peubah baru itu disebut sebagai komponen utama (Jhonson dan Wichern, 1982)

BAB 2

LANDASAN TEORI

2.1. Analisis Korelasi

Analisis korelasi adalah alat statistik yang dapat digunakan untuk mengetahui derajat hubungan linear antara satu variabel dengan variabel lain (Algifari, 1997). Umumnya analisis korelasi digunakan, dalam hubungannya dengan analisis regresi, untuk mengukur ketepatan garis regresi dalam menjelaskan variasi nilai variabel dependen.

Ukuran yang digunakan untuk mengukur derajat korelasi (hubungan) antara satu variabel dengan variabel lain dinamakan koefisien korelasi (correlation coefficient) yang disimbolkan dengan r. Jika koefisien korelasi dikuadratkan (r2) maka akan menjadi koefisien determinasi. Dalam konteks regresi, koefisien determinasi merupakan ukuran yang lebih bermakna dibandingkan koefisien korelasi. Koefisien determinasi mampu memberikan informasi mengenai variasi nilai variabel dependen yang dapat dijelaskan oleh model regresi yang digunakan. Sedangkan koefisien korelasi hanya merupakan ukuran mengenai derajat hubungan antara dua variabel.

(semakin mendekati nol) maka tingkat keeratan hubungan antara dua variabel tersebut semakin lemah.

Koefisien korelasi dapat juga digunakan untuk mengetahui arah hubungan antara dua variabel. tanda minus (-) pada nilai r menunjukkan hubungan yang berlawanan arah. artinya, apabila nilai vaariabel yang satu naik maka nilai variabel yang lain turun. Tanda plus (+) pada nilai r menunjukkan hubungan yang searah. Artinya, apabila nilai variabel yang satu naik, maka nilai variabel yang lain juga naik (Algifari, 1997).

2.2. Matriks Korelasi

Matriks korelasi n peubah acak X1, ..., Xn adalah n × n matrik dimana i,j adalah corr(Xi, Xj). Jika ukuran korelasi yang digunakan adalah koefisien momen-produk, matriks korelasi akan sama dengan matrik kovarian peubah acak yang telah distandarkan Xi /SD(Xi) untuk i = 1, ..., n. Sehingga, matriks korelasi merupakan matriks definit tak-negatif.

Matriks korelasi selalu simetris, yakni korelasi antara X_idan X_j adalah sama dengan korelasi antara Xj dan Xi.

2.3. Nilai Eigen dan Vektor Eigen

Kata “vektor eigen” adalah ramuan bahasa Jerman dan Inggris. Dalam bahasa Jerman “eigen” dapat diterjemahkan sebagai “sebenarnya” atau “karakteristik”. Oleh Karena itu, nilai eigen dapat juga dinamakan nilai sebenarnya atau nilai karakteristik. Dalam literatur lama kadang-kadang dinamakan akar-akar latent.

Ax = λx

untuk suatu skalarλ . Skalarλ dinamakan nilai eigen (eigenvalue) dari A dan x dikatakan vektor eigen yang bersesuaian denganλ (Anton, 1987) .

Nilai eigen merupakan bilangan real, yang berarti dapat bernilai nol, negatif, dan positif, sedangkan vektor eigen x merupakan anggota dari Rn untuk An x n dan x bukan vektor nol ( Mahmud, 2009 ).

Jikaλadalah nilai eigen dari A yang bersesuaian dengan x. maka Ax = λx, sehingga perkalian oleh A akan memperbesar x, atau membalik arah x, yang bergantung pada nilaiλ. Untuk mencari nilai eigen matriks A yang berukuran n x n maka dituliskan kembali Ax = λx sebagai

Ax = λI x

atau secara ekivalen (λI – A)x = 0

Supayaλ menjadi nilai eigen, maka harus ada pemecahan taknol dari persamaan ini. Akan tetapi (λI – A)x = 0 akan mempunyai pemecahan tak nol jika dan hanya jika det(λI – A) = 0

Ini dinamakan persamaan karakteristik A, skalar yang memenuhi persamaan ini adalah nilai eigen dari A. Bila diperluas, maka determinan det(λI – A) adalah polinom λ yang dinamakan polinom karakteristik dari A (Anton, 1987).

Vektor eigen A yang bersesuaian dengan nilai eigen λ adalah vektor taknol x yang memenuhi Ax =λx. Secara ekivalen, vektor eigen yang bersesuaian denganλ adalah vektor taknol dalam ruang pemecahan dari (λI – A)x = 0. Ruang pemecahan ini dinamakan sebagai ruang eigen (eigenspace) dari A yang bersesuaian denganλ (Anton, 1987).

2.4. Determinan

A ) sebagai jumlah semua hasil kali elementer bertanda dari A. Jumlah det(A) dinamakan determinan A (Anton, 1987).

Determinan A secara simbolis ditulis sebagai

∑

±

=

n nj j

ja a

a

A) ...

det(

2 1 2

1

dimana

∑

menunjukkan bahwa suku-suku tersebut harus dijumlahkan terhadap semua permutasi ( j₁, j₂,..., j_n) dan simbol + atau – dapat dipilih dalam masing-masing suku sesuai dengan apakah permutasi itu genap atau ganjil (Anton, 1987).

Jika A adalah matriks kuadrat, maka minor entri a_ij dinyatakan oleh M_ij dan didefenisikan menjadi determinan submatriks yang tetap setelah baris ke i dan kolom ke j dicoret dari A. Bilangan (−1)i+jM_ij dinyatakan oleh C_ij dan dinamakan kofaktor entri a_ij.

Determinan matriks A yang berukuran n x n dapat dihitung dengan mengalikan entri-entri dalam suatu baris atau kolom dengan kofaktor-kofaktornya dan menambahkan hasil-hasil kali yang dihasilkan; yakni, untuk setiap 1≤i≤n dan

n j≤ ≤

1 , maka

det (A) = a_1jC_1j +a_2jC_2j +...+a_njC_nj (ekspansi kofaktor sepanjang kolom ke j) det (A) = a_i1C_i1 +a_i2C_i2 +...+a_inC_in (ekspansi kofaktor sepanjang baris ke i) (Anton, 1987).

2.5. Analisis Komponen Utama

Analisis komponen utama tidak selalu bermanfaat. Analisis komponen utama digunakan untuk mereduksi banyaknya peubah asal menjadi beberapa peubah baru yang dapat menjelaskan dengan baik keragaman data asal. Bila tidak ada korelasi antara peubah asal, analisis komponen utama tidak akan memberikan hasil yang di inginkan, karena peubah baru yang diperoleh hanyalah peubah asal yang ditata berdasarkan besarnya keragamannya. Makin erat korelasi (baik positif maupun negatif) antara peubah, maka baik pula hasil yang diperoleh dari analisis komponen utama.

Analisis komponen utama mengekstrak dengan cara yaitu komponen pertama menyerap varian matriks korelasi paling banyak. kemudian diikuti komponen kedua yang menyerap varian terbanyak kedua terhadap sisa varian dan begitu seterusnya, sampai komponen yang terakhir menyerap varian matriks korelasi paling sedikit. Setiap komponen yang berikutnya juga harus orthogonal yaitu tidak berkorelasi sama sekali dengan komponen sebelumnya atau yang mendahuluinya. Akhirnya, ketika p mendekati k, jumlah varian yang dijelaskan oleh setiap komponen semakin kecil. Tujuannya ialah untuk mempertahankan sejumlah komponen yang diperoleh bisa dipergunakan sebagai variabel bebas (predictor) dalam analisis regresi/diskriminan atau analisis varian, yang sudah bebas dari multikolinearitas.

Kalau Ki = komponen ke i, maka diperoleh m persamaan berikut : K1 = γ11z1+γ12z2 +...+γ1jzj +...+γ1pzp

K2 = γ21z1+γ22z2 +...+γ2jzj +...+γ2pzp .

. .

Ki = γi1z1+γi2z2 +...+γijzj +...+γipzp .

. .

γ = vektor eigen

z = nilai standar variabel

Komponen yang ke-i yaitu Ki merupakan kombinasi linear dari X1, X2, …, Xj, …, Xp dengan timbangan (weight) yaitu γ_1j,γ_2j,...,γ_ij,...,γ_ip yang pemilihannya harus sedemikian rupa, sehingga memaksimumkan rasio dari varian komponen pertama (K1) dengan jumlah varian (total variance) data asli/awal. Komponen berikutnya yaitu K2, juga kombinasi linear yang ditimbang dari seluruh variabel asli, tidak berkorelasi dengan komponen atau faktor pertama (K1) dan harus menyerap secara maksimum sisa varian yang ada (Supranto, 2004)..

Langkah awal yang dilakukan dalam Analisis Komponen Utama adalah menentukan nilai eigen dan vektor eigen dari matriks R, matriks korelasi dari X. Dengan terlebih dahulu mengubah data yang distribusi normal umum menjadi distribusi normal baku dengan rumus

Dengan : Z = nilai variabel yang di bakukan x = nilai data berdistribusi normal nilai rata-rata variabel

σ = standar devias

Nilai eigen matriks korelasi ini adalah r solusi λ₁,λ₂,...,λ_r dari persamaan determinan

= 0.

dapat ditunjukkan bahwa jumlah akar-akar ciri matriks korelasi ini sama dengan tras (trace) matriks ZTZ.

Untuk setiap akar ciri λ_j terdapat vector ciri (Characteristic vector) γ_j yang memenuhi sistem persamaan homogen

0 )

Vektor ciri solusinya γ _j =(γ_1j,γ_2j,...,γ_rj)', yang dipilih dari sekian banyak solusi sebanding yang ada untuk setiap j, merupakan solusi yang ternormalkan sedemikian rupa sehingga γ'jγ j =1. juga dapat diperlihatkan bahwa jika semua λj berbeda, maka setiap pasangan vector ciri akan saling orthogonal sesamanya. Vektor γ_j digunakan untuk membentuk Z ke dalam suku-suku komponen utama yaitu:

r

Biasanya semua K_j tidak digunakan melainkan mengikuti suatu aturan seleksi tertentu. McGraw-Hill, New York, 1976, menyarankan (hlm. 273) bahwa”… komponen-komponen dapat dihitung sampai sejumlah tertentu proporsi keragaman data yang cukup besar (mungkin 75 persen atau lebih) telah dijelaskan”, dengan kata lain, kita pilih k penyumbang terbesar yang menghasilkan 0,75.

1 aturan semacam ini secara otomatis memberi k peubah K yang merupakan hasil trasformasi terhadap peubah-peubah asal Zi. Selanjutnya prosedur kuadrat terkecil digunakan untuk memperoleh persamaan peramalan bagi Y sebagai fungsi dari peubah-peubah Kj yang terpilih itu. Urutan masuknya Kj tidak ada pengaruhnya dalam hal ini, sebab semuanya orthogonal satu sama lain. Bila persamaan regresi dalam K_j telah diperoleh, persamaan ini dapat dikembalikan menjadi fungsi peubah semula Z_i bila dikehendaki, atau ditafsirkan berdasarkan peubah-peubah K_j tadi (Draper and Smith, 1992).

2.6. Regresi Linear Berganda

Regresi linear berganda adalah regresi dimana variabel terikatnya (Y) dihubungkan atau dijelaskan dengan lebih dari satu variabel bebas (X1, X2……..Xn) dengan syarat variabel bebas masih menunjukkan hubungan yang linear dengan variabel tak bebas. Hubungan fungsional antara variabel dependen (Y) dengan variabel independent (X1, X2……..Xn) secara umum dapat dituliskan sebagai berikut:

Y = f(X1, X2……..Xn)

dengan : Y = variabel dependen X1, X2……..Xn = variabel independent.

Model regresi linear berganda merupakan suatu model yang dapat dinyatakan dalam persamaan linear yang memuat peubaha dan parameter. Parameter ini pada umumnya tidak diketahui dan dapat ditaksir. Hubungan linear lebih dari dua peubah bila dinyatakan dalam bentuk persamaan matematis adalah:

pi pi i

i X X

X

Y =β +β +β + +β ∧

...

2 1 1 1 0

dengan ∧

Y = nilai estimasi Y Xj = peubah bebas β_i= parameter

BAB 3

PEMBAHASAN

Seiring dengan perkembangan zaman yang semakin canggih dan modren, banyak alat-alat elektronik yang menggunakan tenaga listrik, sehingga kebutuhan akan listrik semakin lama semakin meningkat. Para pemakai energi listrik disebut juga pelanggan. Banyaknya energi listrik yang dibutuhkan tergantung pada pemakaian energi listrik persektor pelanggan itu sendiri.

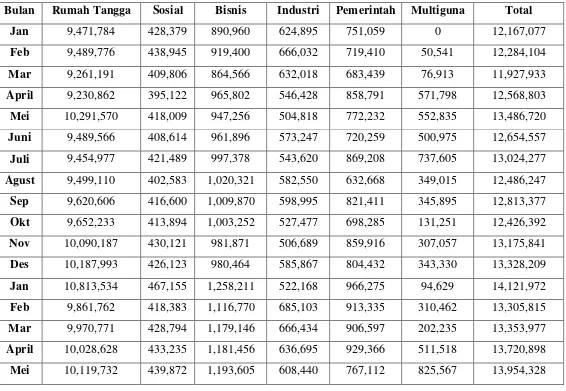
Tabel 3.1 Pemakaian Energi Listrik Persektor Pelanggan Pada PT. PLN (Persero) Area Padangsidimpuan Januari 2007 s/d September 2012

Bulan Rumah Tangga Sosial Bisnis Industri Pemerintah Multiguna Total

Jan 9,471,784 428,379 890,960 624,895 751,059 0 12,167,077

Feb 10,290,817 620,021 2,087,213 378,891 1,056,524 24,148 14,457,614 Mar 10,418,453 595,391 2,021,427 424,173 991,727 14,087 14,465,258 April 12,490,067 803,898 2,196,654 582,264 1,054,610 93,358 17,220,851 Mei 12,355,243 684,827 2,439,701 486,382 1,068,531 257,256 17,291,940 Juni 13,109,320 612,927 2,490,825 459,542 1,054,780 344,461 18,071,855 Juli 12,448,128 509,827 2,379,275 432,344 1,087,928 546,150 17,403,652 Agust 12,970,826 576,701 2,197,913 461,138 1,090,907 494,074 17,791,559 Sep 14,264,684 631,287 2,304,935 533,317 1,110,021 22,489 18,866,733 Okt 14,024,901 690,435 2,268,958 510,199 1,082,364 96,835 18,673,692 Nov 14,380,566 626,515 2,192,844 611,424 1,033,314 189,100 9,033,763

Variabel-variabel penelitian secara lengkap dapat dituliskan sebagai berikut: Y = Jumlah pemakaian energi listrik

X1 = Pemakaian energi listrik untuk rumah tangga (KWh) X2 = Pemakaian energi listrik untuk sosial (KWh)

X3 = Pemakaian energi listrik untuk bisnis (KWh) X4 = Pemakaian energi listrik untuk industri (KWh) X5 = Pemakaian energi listrik untuk pemerintahan (KWh) X6 = Pemakaian energi listrik untuk multiguna (KWh)

Analisis dilakukan dengan dugaan bahwa rumah tangga (X1), sosial (X2), bisnis (X3), industri (X4), pemerintahan (X5), dan multiguna (X6) dapat mempengaruhi jumlah pemakaian energi listrik (Y).

3.1. Pembakuan Data

Langkah awal yang dilakukan sebelum pembakuan data adalah 1. Mencari rata-rata setiap variabel bebas dengan rumus:

n X

∑

= µ

dengan µ = nilai rata-rata variabel X = nilai data variabel n = jumlah populasi.

2. Mencari standar deviasi setiap variabel dengan rumus :

(

)

n X

∑

−

=

2

µ σ

dengan σ = standar deviasi.

Setelah rata-rata dan standar deviasi diperoleh, maka pembakuan data dapat dilakukan dengan rumus:

nilai rata-rata variabel σ = standar deviasi

Sehingga diperoleh data yang telah dibakukan sebagai berikut:

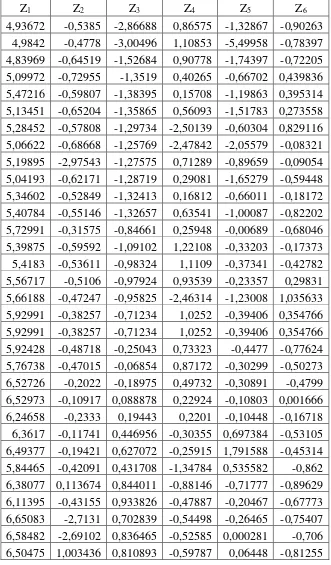
Tabel 3.2 Data Pembakuan

Z1 Z2 Z3 Z4 Z5 Z6

3.2. Menghitung Koefisien Korelasi

Koefisien korelasi digunakan untuk mengetahui hubungan antara satu variabel dengan variabel yang lain. Koefisien korelasi dapat ditentukan dengan menggunakan persamaan

Kemudian, koefisien-koefisien korelasi ini dimasukkan ke dalam bentuk matriks korelasi dengan persamaan:



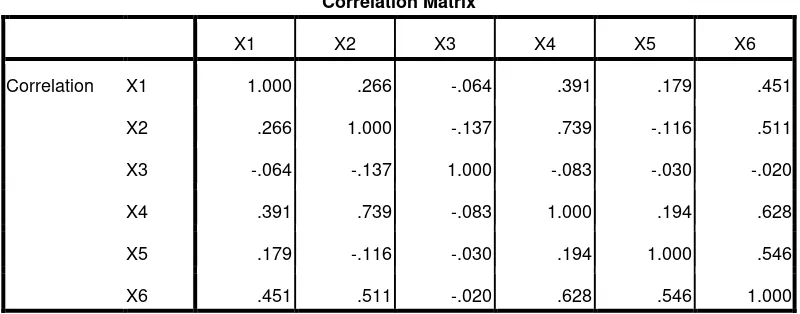
Dengan menggunakan SPSS diperoleh matriks korelasi sebagai berikut: Tabel 3.3 Matriks Korelasi



3.3. Menghitung Nilai Eigen

Nilai Eigen (Eigen values) menunjukkan kepentingan relatif masing-masing faktor dalam menghitung varians keenam variabel yang dianalisis. Susunan eigenvalues selalu diurutkan dari yang terbesar sampai ke yang terkecil, dengan syarat bahwa nilai eigen di bawah 1 tidak digunakan dalam menghitung jumlah komponen yang terbentuk.

Untuk menentukan nilai eigen digunakan persamaan:

= 0

Dengan bantuan SPSS diperoleh nilai eigen sebagai berikut:

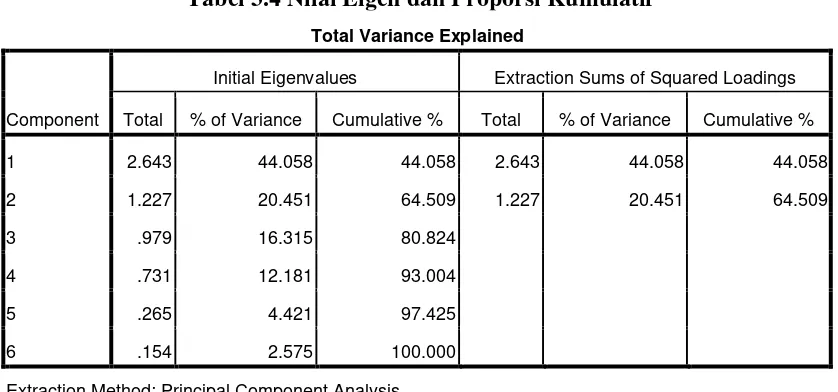
Tabel 3.4 Nilai Eigen dan Proporsi Kumulatif

Total Variance Explained

Component

Initial Eigenvalues Extraction Sums of Squared Loadings

Total % of Variance Cumulative % Total % of Variance Cumulative %

Extraction Method: Principal Component Analysis.

Sedangkan untuk empat komponen lainnya, angka eigenvalues sudah di bawah satu. Komponen 1 memiliki eigenvalue sebesar 2,643 artinya komponen 1 ini dapat menjelaskan 2,643 dari total communalities dengan persentase keragaman sebesar 44,058%. Komponen 2 memiliki eigenvalue sebesar 1,227, artinya komponen 2 ini dapat menjelaskan 1,227 dari total communalities dengan persentase keragaman sebesar 20,451%. Sehingga, dapat disimpulkan bahwa diperolehnya dua komponen utama pertama telah mampu menerangkan keragaman data sebesar persentase kumulatif, yaitu 64,509%.

3.4. Menghitung Vektor Eigen

Untuk menghitung vektor eigen digunakan persamaan

0 )

(ZTZ −λ_jI γ_j = .

Diperoleh hasilnya sebagai berikut:

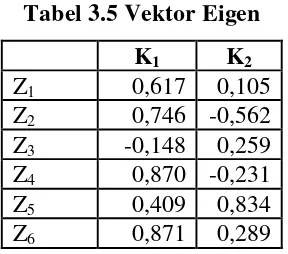
Tabel 3.5 Vektor Eigen

K1 K2

Z1 0,617 0,105 Z2 0,746 -0,562 Z3 -0,148 0,259 Z4 0,870 -0,231 Z5 0,409 0,834 Z6 0,871 0,289 Angka-angka pada tabel 3.5 di atas dapat ditafsirkan sebagai: K1 = 0,617Z1 + 0,746Z2 - 0,148Z3 + 0,870Z4 + 0,409Z5 + 0,871Z6 K2 = 0,105Z1 – 0,562Z2 + 0,259Z3 – 0,231Z4 + 0,834Z5 + 0,289Z6. dengan K1 = vektor eigen komponen pertama

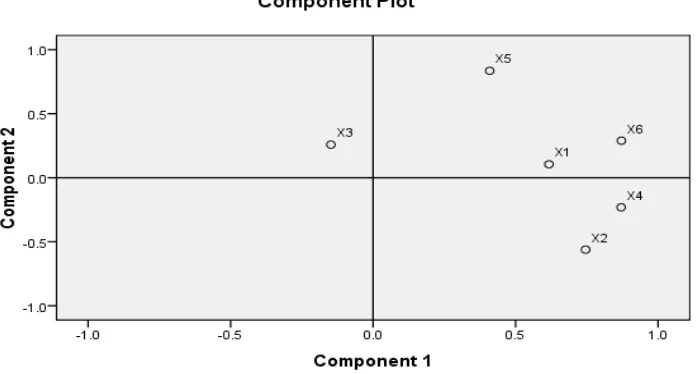
Berdasarkan tabel vektor eigen dan komponen plot di atas, komponen K1 dilandasi variabel X1, X2, X4, X6, maka bisa diberi nama: pemakaian dominan. Sedangkan K2 dilandasi variabel X2, X5, maka bisa diberi nama: pemakaian sosial dan pemerintah.

Nilai-nilai komponen utama Kj selanjutnya dihitung untuk setiap titik data asal dan dicantumkan bersama-sama nilai peubah responnya, dan diperoleh hasil sebagai berikut:

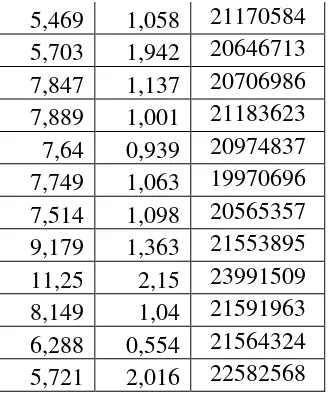
Tabel 3.6 Nilai Komponen Utama

K1 K2 Y

5,469 1,058 21170584

Untuk membentuk model persamaan regresinya, kita asumsikan bahwa modelnya adalah linear:

2

dengan konstanta b0, b1, dan b2 dapat ditaksir berdasarkan pengamatan data K1 dan K2 yang diperoleh.

Tabel 3.7 Besaran-besaran Untuk Menghitung

2

2,492 -1,49 12167077 6,21 2,2201 30320355,88 -18128944,73 -3,71308 1,196 -5,056 12284104 1,43 25,563 14691788,38 -62108429,82 -6,046976 2,178 -1,398 11927933 4,744 1,9544 25979038,07 -16675250,33 -3,044844 3,263 0,073 12568803 10,65 0,0053 41012004,19 917522,619 0,238199 3,126 -0,369 13486720 9,772 0,1362 42159486,72 -4976599,68 -1,153494 2,988 -0,763 12654557 8,928 0,5822 37811816,32 -9655426,991 -2,279844 1,321 0,858 13024277 1,745 0,7362 17205069,92 11174829,67 1,133418 -0,27 -0,574 12486247 0,073 0,3295 -3371286,69 -7167105,778 0,15498 1,352 0,949 12813377 1,828 0,9006 17323685,7 12159894,77 1,283048 1,897 -1,072 12426392 3,599 1,1492 23572865,62 -13321092,22 -2,033584 2,818 -0,126 13175841 7,941 0,0159 37129519,94 -1660155,966 -0,355068 2,549 -0,685 13328209 6,497 0,4692 33973604,74 -9129823,165 -1,746065 3,055 0,297 14121972 9,333 0,0882 43142624,46 4194225,684 0,907335 3,823 0,01 13305815 14,62 0,0001 50868130,75 133058,15 0,03823

1,539 0,454 13954328 2,369 0,2061 21475710,79 6335264,912 0,698706 4,519 0,19 14614904 20,42 0,0361 66044751,18 2776831,76 0,85861 4,519 0,19 14614904 20,42 0,0361 66044751,18 2776831,76 0,85861 3,108 0,064 14601022 9,66 0,0041 45379976,38 934465,408 0,198912 3,414 0,253 14214332 11,66 0,064 48527729,45 3596225,996 0,863742 3,793 0,239 16087137 14,39 0,0571 61018510,64 3844825,743 0,906527 4,091 0,627 16093224 16,74 0,3931 65837379,38 10090451,45 2,565057 3,654 0,651 15395364 13,35 0,4238 56254660,06 10022381,96 2,378754 3,33 1,348 15679109 11,09 1,8171 52211432,97 21135438,93 4,48884 3,882 2,376 16004591 15,07 5,6454 62129822,26 38026908,22 9,223632 1,524 1,471 14404783 2,323 2,1638 21952889,29 21189435,79 2,241804 2,056 0,171 15726109 4,227 0,0292 32332880,1 2689164,639 0,351576 2,222 0,87 15068501 4,937 0,7569 33482209,22 13109595,87 1,93314 0,736 2,092 16391687 0,542 4,3765 12064281,63 34291409,2 1,539712 0,859 2,338 16229000 0,738 5,4662 13940711 37943402 2,008342 3,44 0,286 16031667 11,83 0,0818 55148934,48 4585056,762 0,98384 3,258 0,466 16407531 10,61 0,2172 53455736 7645909,446 1,518228 1,818 1,293 16866821 3,305 1,6718 30663880,58 21808799,55 2,350674 5,132 0,044 17152489 26,34 0,0019 88026573,55 754709,516 0,225808 3,128 1,193 16311016 9,784 1,4232 51020858,05 19459042,09 3,731704 1,428 1,653 16511498 2,039 2,7324 23578419,14 27293506,19 2,360484 2,929 0,799 14457614 8,579 0,6384 42346351,41 11551633,59 2,340271 2,863 0,439 14465258 8,197 0,1927 41414033,65 6350248,262 1,256857 5,562 0,132 17220851 30,94 0,0174 95782373,26 2273152,332 0,734184 4,885 0,941 17291940 23,86 0,8855 84471126,9 16271715,54 4,596785 4,765 1,255 18071855 22,71 1,575 86112389,08 22680178,03 5,980075 3,536 1,52 17403652 12,5 2,3104 61539313,47 26453551,04 5,37472

5,02 1,513 17791559 25,2 2,2892 89313626,18 26918628,77 7,59526 4,95 1,11 18866733 24,5 1,2321 93390328,35 20942073,63 5,4945 5,128 0,835 18673692 26,3 0,6972 95758692,58 15592532,82 4,28188 2,662 0,143 9033763 7,086 0,0204 24047877,11 1291828,109 0,380666 5,042 0,891 18625373 25,42 0,7939 93909130,67 16595207,34 4,492422 5,519 3,338 20685122 30,46 11,142 114161188,3 69046937,24 18,422422 4,718 1,09 18343802 22,26 1,1881 86546057,84 19994744,18 5,14262

4,9 1,004 17722067 24,01 1,008 86838128,3 17792955,27 4,9196 3,367 2,91 19778614 11,34 8,4681 66594593,34 57555766,74 9,79797 5,121 1,08 19300947 26,22 1,1664 98840149,59 20845022,76 5,53068 7,467 1,938 21187934 55,76 3,7558 158210303,2 41062216,09 14,471046

5,703 1,942 20646713 32,52 3,7714 117748204,2 40095916,65 11,075226 7,847 1,137 20706986 61,58 1,2928 162487719,1 23543843,08 8,922039 7,889 1,001 21183623 62,24 1,002 167117601,8 21204806,62 7,896889 7,64 0,939 20974837 58,37 0,8817 160247754,7 19695371,94 7,17396 7,749 1,063 19970696 60,05 1,13 154752923,3 21228849,85 8,237187 7,514 1,098 20565357 56,46 1,2056 154528092,5 22580761,99 8,250372 9,179 1,363 21553895 84,25 1,8578 197843202,2 29377958,89 12,510977 11,25 2,15 23991509 126,6 4,6225 269904476,3 51581744,35 24,1875 8,149 1,04 21591963 66,41 1,0816 175952906,5 22455641,52 8,47496 6,288 0,554 21564324 39,54 0,3069 135596469,3 11946635,5 3,483552 5,721 2,016 22582568 32,73 4,0643 129194871,5 45526457,09 11,533536 288,834 49,149 1153755652 1546 126,26 5238116787 981819470,4 268,621819

Harga b0, b1, dan b2 diperoleh dari persamaan:

Dapat disubstitusikan ke dalam nilai - nilai yang sesuai sehingga diperoleh: 1153755652 = 69b0 + 288,834 b1 + 49,149 b2

5238116787 = 288,834b0 + 1546b1 + 268,621819b2 981819470,4 = 49,149b1 + 268,621819b1 + 126,26b2

Dalam bentuk matriks, persamaan di atas dinyatakan dengan:



b0 = 11723492,43 b1 = 1014091,079 b2 = 1361636,804

Jadi, persamaan regresinya adalah:

2 1 1361636,804

079 , 1014091 11723492

ˆ _{K K}

Y = + +

Artinya,

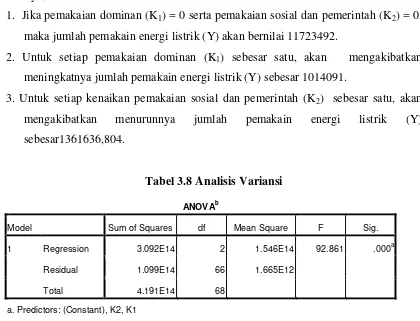
1. Jika pemakaian dominan (K1) = 0 serta pemakaian sosial dan pemerintah (K2) = 0, maka jumlah pemakain energi listrik (Y) akan bernilai 11723492.

2. Untuk setiap pemakaian dominan (K1) sebesar satu, akan mengakibatkan meningkatnya jumlah pemakain energi listrik (Y) sebesar 1014091.

3. Untuk setiap kenaikan pemakaian sosial dan pemerintah (K2) sebesar satu, akan mengakibatkan menurunnya jumlah pemakain energi listrik (Y) sebesar1361636,804.

Tabel 3.8 Analisis Variansi

ANOVAb

Model Sum of Squares df Mean Square F Sig.

1 Regression 3.092E14 2 1.546E14 92.861 .000a

Residual 1.099E14 66 1.665E12

Total 4.191E14 68

a. Predictors: (Constant), K2, K1

b. Dependent Variable: Y

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Dari penelitian ini dapat disimpulkan bahwa:

1. Dengan menggunakan analisis komponen utama diperoleh dua komponen K1 dan K2 yang bermamfaat dalam pendugaan persamaan regresi untuk pemakaian energi listrik persektor pelanggan pada PT. PLN (persero) Area Padangsidimpuan.

2. Model pemakaian energi listrik pada PT. PLN (persero) Area Padangsidimpuan adalah

Yˆ =11723492+1014091,079K₁ +1361636,804K₂. Artinya,

1. Jika pemakaian dominan (K1) = 0 serta pemakaian sosial dan pemerintah (K2) = 0, maka jumlah pemakain energi listrik (Y) akan bernilai 11723492.

2. Untuk setiap pemakaian dominan (K1) sebesar satu, akan mengakibatkan meningkatnya jumlah pemakain energi listrik (Y) sebesar 1014091.

3. Untuk setiap kenaikan pemakaian sosial dan pemerintah (K2) sebesar satu, akan mengakibatkan menurunnya jumlah pemakain energi listrik (Y) sebesar1361636,804.

4.2. Saran

1. Penelitian ini tidak terlepas dari berbagai kelemahan, untuk itu diperlukan suatu teori-teori yang lebih mendukung.

DAFTAR PUSTAKA

Algifari. 2000. Analisis Regresi Teori, kasus, dan solusi. Yogyakarta : BPFE Yogyakarta.

Anton, Howard. 1992. Aljabar Linear Elementer. Edisi 5. Jakarta : Penerbit Erlangga.

Draper, N. and Smith, H. 1992. Analisis Regresi Terapan. Edisi 2. Jakarta : PT Gramedia Pustaka Utama.

Imrona, Mahmud. 2009. Aljabar Linear Dasar. Jakarta: Penerbit Erlangga.

Iswardono. 1981. Sekelumit Analisis Regresi dan Korelasi. Yogyakarta : BPFE Yogyakarta.

Siswadi dan Suharjo, 1998, Analisis Regresi dan Kolerasi Data Peubah Ganda, Jurusan Matematika, FMIPA IPB.

Sudjana, 1996 Teknik Analisis Regresi dan Kolerasi, Penerbit Tarsiti Bandung.