SKRIPSI
LEONARDO SILALAHI
070803049
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
ANALISIS REGRESI KOMPONEN UTAMA UNTUK MENGATASI MASALAH MULTIKOLINIERITAS
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
LEONARDO SILALAHI 070803049
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : ANALISIS REGRESI KOMPONEN UTAMA
UNTUK MENGATASI MASALAH
MULTIKOLINIERITAS
Kategori : SKRIPSI
Nama : LEONARDO SILALAHI
Nomor Induk Mahasiswa : 070803049
Program Studi : SARJANA (SI) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Djakaria Sebayang, M.Si. Drs. Henry Rani Sitepu, M.Si. NIP. 195112271985031002 NIP. 195303031983031002
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
ANALISIS REGRESI KOMPONEN UTAMA UNTUK MENGATASI
MASALAH MULTIKOLINIERITAS
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juni 2011
PENGHARGAAN
Puji dan syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa atas berkat dan anugrah yang dilimpahkanNya sehingga skripsi ini dapat diselesaikan.
Skripsi ini merupakan salah satu syarat yang harus dipenuhi dan diselesaikan oleh seluruh mahasiswa Fakultas FMIPA Departemen Matematika. Pada skripsi ini penulis mengambil judul skripsi tentang Analisis Regresi Komponen Utama Untuk
Mengatasi Masalah Multikolinieritas.
Dalam penyusunan skripsi ini banyak pihak yang membantu, sehingga dengan segala rasa hormat penulis mengucapkan terima kasih kepada:
1. Bapak Dr. Sutarman, M.Sc. selaku Dekan FMIPA USU.
2. Bapak Prof. Dr. Tulus M.Si dan Ibu Dra. Mardiningsih, M.Si selaku ketua dan sekretaris Departemen Matematika FMIPA USU.
3. Bapak Drs. Henry Rani Sitepu, M.Si. selaku dosen dan pembimbing I yang berkenan dan rela mengorbankan waktu, tenaga dan pikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
4. Drs. Djakaria Sebayang, M.Si. selaku dosen dan pembimbing II yang juga berkenan dan rela mengorbankan waktu, tenaga dan pikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
5. Bapak Prof . Dr. Tulus, M.Si dan Drs. Ujian Sinulingga selaku komisi penguji atas masukan dan saran yang telah diberikan demi perbaikan skripsi ini.
6. Seluruh Staf pengajar departemen matematika dan pegawai FMIPA USU
7. Alm Bapak U. Silalahi, Ibunda tercinta R.S. br Manurung yang penulis sayangi. Terima kasih atas segala pengertian, kesabaran, dan kasih sayang yang telah diberikan serta dukungan selama penulis masih dibangku perkuliahan hingga akhirnya menyelesaikan tugas ini.
8. Saudara-Saudara ku, K’Lenni Silalahi, Amd, K’Lestarina Silalahi, Spd, B’Lamhot
Silalahi, Sth, K’Lusiana Silalahi, Spsi serta adik ku Lorencius Silalahi. Terima kasih buat kasih saying motivasi serta semangat yang selalu diberikan kepada
penulis “you are my spirit”.
9. Terima kasih buat Opung ku Biv. R. br Gultom, buat doa serta kasih sayang yang setiap saat diberikan kepada penulis.
Penulis juga mengucapkan terima kasih kepada teman-teman yang banyak membantu penulis dalam perkuliahan hingga pada penyelesaian skripsi ini. Buat Enrico, Erbin, Magdalena, Rolina, Dewi, Imelda, Desri, Riris, Jojor, Siska serta semua teman-teman satu satmbuk 2007, buat kawan-kawan pengurus HMM juga buat junior
2008, 2009, hingga “adik kandung” 2010 yang telah memberi semangat, penulis
Penulis juga menyadari masih banyak kekurangan dalam penulisan ini. Oleh karena itu, penulis meminta saran dari pembaca guna menyempurnakan tulisan ini.
Demikian yang dapat penulis sampaikan, atas perhatian serta kerjasamanya penulis ucapkan terima kasih. Semoga tulisan ini bermanfaat bagi yang membutuhkan.
Medan, Juni 2011 Penulis
ABSTRAK
THE PRINCIPAL COMPONENT REGRESSION ANALYSIS FOR SOLVING MULTICOLLINEARITY
ABSTRACT
DAFTAR ISI
2.2Nilai Eigen dan Vektor Eigen 13
2.3Matriks Korelasi 15
2.4Analisis Regresi Linier Berganda 18
2.4.1 Asumsi Regresi Linier Berganda 18
2.4.2 Metode Kuadrat Terkecil 19
2.4.3 Sifat Penduga Kuadrat Terkecil 21
2.5Uji Regresi Linier 22
2.6Koefisien Determinasi 23
2.7Multikolinieritas 24
2.7.1 Pendeteksian Multikolinieritas 25
2.7.2 Pengaruh Multikolinieritas 26
2.8Analisis Komponen Utama 27
2.8.1 Menentukan Komponen Utama 28
2.8.1.1Komponen Utama Berdasarkan Matriks Kovariansi 28 2.8.1.2Komponen Utama Berdasarkan Matriks Korelasi 32 2.8.2 Kriteria Pemilihan Komponen Utama 33
2.8.3 Kontribusi Komponen Utama 34
Bab 3 Pembahasan 35
2.1Regresi Komponen Utama 35
2.3Ilustrasi Regresi Komponen Utama Mengatasi Multikolinieritas 38 3.3.1 Analisis Dengan Regresi Linier Berganda 39
3.3.2 Pendeteksian Multikolinieritas 40
3.3.3 Analisis Dengan Regresi Komponen Utama 42 3.3.4 Uji Signifikansi Koefisien Regresi Variabel Baku 46
Bab 4 Kesimpulan dan Saran
4.1Kesimpulan 47
4.2Saran 48
Daftar Pustaka 49
DAFTAR TABEL
Halaman
Tabel 3.1 Data Gas Mileage pada 30 Mobil 38
Tabel 3.2 Uji Signifikansi Koefisien Regresi Linier Berganda 40
Tabel 3.3 Nilai Korelasi Data Gas Mileage 41
Tabel 3.4 Nilai Faktor Variansi Inflasi 41
Tabel 3.5 Nilai Eigen, Proporsi Total Variansi dan Proporsi Variansi Kumulatif 43 Tabel 3.6 Koefisien Komponen Utama (Vektor Eigen) 43
Tabel 3.7 Skor Faktor Komponen Utama 44
ABSTRAK
THE PRINCIPAL COMPONENT REGRESSION ANALYSIS FOR SOLVING MULTICOLLINEARITY
ABSTRACT
Bab 1
PENDAHULUAN
1.1Latar Belakang
Regresi merupakan suatu teknik statistika yang dapat digunakan untuk
menggambarkan hubungan fungsional antara suatu variabel tak bebas (respon) dengan
satu atau beberapa variabel bebas (deterministik). Menurut Drapper and Smith (1992)
analisis regresi merupakan metode analisis yang dapat digunakan untuk menganalisis
data dan mengambil kesimpulan yang bermakna tentang hubungan ketergantungan
variabel terhadap variabel lainnya.
Analisis regresi yang sering digunakan dalam pemecahan suatu permasalahan
adalah regresi linier. Dalam perkembangannya terdapat dua jenis regresi yang sangat
terkenal, yaitu regresi linier sederhana dan regresi linier berganda. Regresi linier
sederhana digunakan untuk menggambarkan hubungan antara satu variabel bebas (X)
dengan satu variabel tak bebas (Y). Sedangkan jika variabel bebas (X) yang digunakan
lebih dari satu, maka persamaan regresinya adalah persamaan regresi linier berganda.
Secara umum persamaan regresi linier dengan k variabel bebas dinyatakan
dengan :
+ + + … + +
dengan :
Y = variable tak bebas (respon)
= variable bebas (deterministik) , …, = parameter regresi
Parameter regresi pada persamaan diatas dicari penduganya dengan
menggunakan metode kuadrat terkecil (MKT). Penduga yang dihasilkan oleh MKT
bersifat BLUE (best linear unbiased estimation) apabila asumsi–asumsi pada analisis
regresi dipenuhi, yang disebut dengan asumsi klasik. Asumsi klasik regresi linier
tersebut adalah nilai variabel bebas (X) tetap pada sampel berulang dan bebas terhadap
kesalahan pengganggu, nilai rata-rata kesalahan pengganggu adalah nol,
homoskedastisitas sama untuk setiap observasi, tidak ada otokorelasi antar kesalahan
pengganggu dan tidak ada multikolinieritas diantara variabel bebas.
Salah satu dari asumsi yang harus dipenuhi untuk melakukan pengujian
hipotesis terhadap parameter pada analisis regresi linier berganda adalah tidak terjadi
multikolinieritas diantara variabel bebas. Jika terdapat multikolinieritas di dalam
regresi linier berganda maka akan mengakibatkan penggunaan MKT dalam menduga
parameter terganggu. Meskipun MKT dapat digunakan tetapi galat yang dihasilkan
akan menjadi besar, variansi dan kovariansi parameter tidak terhingga. Sehingga
parameter yang dihasilkan tidak bersifat BLUE lagi.
Menurut Montgomery dan Peck (dalam naftali, 2007) adanya multikolinieritas
dalam analisis regresi linier berganda disebabkan oleh berbagai hal antara lain metode
pengumpulan data yang digunakan, kendala model pada populasi yang diamati,
spesifikasi model, dan penentuan jumlah variabel bebas yang lebih banyak dari jumlah
observasi. Oleh karena itu, dalam suatu penelitian harus benar-benar diperhatikan
metode, model, spesifikasi model dan jumlah variabel bebas yang digunakan.
Ada beberapa cara yang dapat digunakan untuk mengatasi masalah
multikolinieritas, diantaranya ialah :
1. Penambahan data baru yang bertujuan untuk memperkecil standar error.
Namun penambahan data baru seringkali hannya memberikan efek
penanggulangan yang kecil pada masalah multikolinieritas.
2. Mengeluarkan suatu variabel atau beberapa variabel bebas yang terlibat
hubungan kolinier, namun prosedur ini akan mengurangi obyek penelitian
spesifikasi terjadi karena salah dalam menentukan variabel yang tepat/benar
dalam suatu model regresi.
3. Analisis regresi komponen utama, pada analisis regresi komponen utama
semua peubah bebas masuk ke dalam model, tetapi sudah tidak terjadi
multikolinieritas karena sudah dihilangkan pada tahap analisis komponen
utama.
Dari beberapa cara mengatasi masalah multikolinieritas, analisis regresi komponen
utama merupakan cara yang sangat ampuh (Drapper and Smith, 1981). Berdasarkan
hal tersebut maka peneliti tertarik untuk melakukan penelitian terhadap suatu kasus
yang mengalami masalah multikolinieritas dan metode untuk mengatasi masalah
multikolinieritas ini, yaitu dengan menggunakan analisis regresi komponen utama.
Penelitian ini dibuat berupa tulisan yang diberi judul “Analisis Regresi Komponen
Utama Untuk Mengatasi Masalah Multikolinieritas”.
1.2Perumusan Masalah
Multikolinieritas merupakan masalah yang serius dalam menduga parameter pada
analisis regresi linier berganda. Multikolinieritas menyebabkan ketidakstabilan pada
parameter dugaan, pengujian hipotesis menjadi kurang kuat (less powerfull), artinya
yang seharusnya ditolak menjadi diterima atau sebaliknya. Oleh karena itu pada
penelitian ini akan dibahas bagaimana cara mengatasi masalah multikolinieritas
menggunakan analisis regresi komponen utama.
1.3Pembatasan Masalah
Peneliti membatasi permasalahan yang akan membahas mengenai masalah
multikolinieritas yang terjadi pada analisis regresi linier berganda dan menganggap
1.4Tinjauan Pustaka
Montgomery (1976) mengatakan pendugaan parameter regresi dengan menggunakan metode kuadrat terkecil adalah dengan meminimumkan jumlah kuadrat
galat (JKG) dimana JKG dirumuskan sebagai berikut :
∑ ∑
Supranto, J (1992) dalam bukunya mengatakan istilah multikolinieritas merupakan
hubungan linier yang sempurna atau pasti diantara variabel–variabel bebas dalam
model regresi linier berganda. Istilah kolinieritas sendiri berarti hubungan linier
tunggal, sedangkan multikolinieritas menunjukkan adanya lebih dari satu hubungan
linier yang sempurna.
Gasperz (1991) dalam bukunya mengatakan permasalahan terjadinya multikolinieritas diantara penjelas yang banyak maka teknik pendugaan berdasarkan
metode kuadrat terkecil (MKT) menjadi tidak tepat karena akan menimbulkan
konsekuensi yang serius. Maka analisis yang tepat adalah model regresi komponen
utama.
Drapper and Smith (1981) dalam bukunya mengatakan cara lain yang digunakan
untuk mengatasi masalah multikolinieritas dan merupakan cara yang sangat ampuh
adalah dengan regresi komponen utama.
Haris (2008) dalam penelitiannya mengenai multikolinieritas pada data produk
domestik regional bruto (PDRB) seluruh wilayah propinsi di Indonesia, mengatakan
analisis dengan regresi komponen utama cukup efektif dalam mengatasi
1.5Tujuan penelitian
Tujuan dari penelitian ini adalah menggunakan analisis regresi komponen utama
untuk mengatasi masalah multikolinieritas pada analisis regresi linier berganda,
sehingga diperoleh model persamaan regresi yang lebih baik.
1.6Manfaat penelitian
Penelitian ini diharapkan dapat memberikan manfaat bagi pembaca untuk lebih
mengetahui mengenai masalah mutikolinieritas dan cara mengatasinya.
Serta memberikan suatu solusi untuk mengatasi masalah multikolinieritas bagi peneliti
yang menggunakan analisis regresi linier berganda untuk menganalisis penelitian pada
berbagai bidang ilmu, seperti penelitian-penelitian di bidang sosial, ekonomi,
pertanian dll.
1.7Metodologi Penelitian
Penelitian ini dibuat berdasarkan studi literatur dan kepustakaan dan mengikuti
langkah-langkah sebagai berikut :
1. Terlebih dahulu menjelaskan konsep dasar matriks, analisis regresi linier
berganda, multikolinieritas, serta analisis komponen utama.
2. Mendeteksi keberadaan multikolinieritas.
3. Menguraikan penyelesaian masalah multikolinieritas menggunakan analisis
regresi komponen utama. Dengan langkah sebagai berikut :
a. Melakukan tahap analisis komponen utama untuk menghilangkan gejala
multikolinieritas.
b. Menentukan komponen utama yang masuk dalam model
c. Menduga parameter analisis regresi komponen utama
d. Melakukan transformasi menjadi model regresi linier berganda.
4. Menyelesaikan contoh kasus yang mengandung multikolinieritas. Dalam hal
Bab 2
LANDASAN TEORI
2.1Aljabar Matriks 2.1.1 Definisi
Matriks
Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen
yang disusun secara teratur menurut baris dan kolom sehingga berbentuk persegi
panjang, dimana panjang dan lebarnya ditunjukkan oleh banyaknya kolom dan baris
serta dibatasi tanda “[ ]” atau “( )”.
Sebuah matriks dinotasikan dengan simbol huruf besar seperti A, X, atau Z dan
sebagainya. Sebuah matriks A yang berukuran m baris dan n kolom dapat ditulis
sebagai berikut :
[
]
Atau juga dapat ditulis :
A = [ ] i= 1, 2,…, m ; j= 1, 2,…, n
Contoh :
Disebut matriks A dengan 2 baris dan 3 kolom. Jika A sebuah matriks, maka
digunakan untuk menyatakan elemen yang terdapat di dalam baris i dan kolom j
[ ] i = 1, 2 j = 1, 2, 3
Skalar
Suatu skalar adalah besaran yang hannya memiliki nilai, tetapi tidak memiliki arah.
Vektor Baris
Suatu matriks yang hannya terdiri dari satu baris dan n kolom disebut vektor baris.
[ ] disebut vektor baris
Vektor Kolom
Suatu matriks yang hannya terdiri dari m baris dan satu kolom disebut vektor kolom.
[ ] disebut vektor kolom
Kombinasi Linier
Vektor w merupakan kombinasi linier dari vektor – vektor jika terdapat
skalar sehingga berlaku :
, (2.1)
Jika vektor maka disebut persamaan homogen dan disebut
vektor yang bebas linier, yang mengakibatkan tetapi jika
ada bilangan yang tidak semuanya sama dengan nol, maka
disebut vektor yang bergantung linier.
2.1.2 Jenis-jenis Matriks
Matriks kuadrat adalah matriks yang memiliki baris dan kolom yang sama banyak.
dibawah diagonal utama merupakan cermin dari elemen diatas diagonal utama.
Matriks simetris jika artinya .
Matriks A disebut matriks identitas dan biasa diberi simbol I.
Matriks Nol
Matriks nol adalah suatu matriks dengan semua elemennya mempunyai nilai nol.
Biasanya diberi simbol , dibaca matriks nol.
Matriks Elementer
sama dengan nol. Untuk melihat kesingularan suatu matriks adalah dengan
menghitung determinan matriks tersebut. Apabila determinannya sama dengan nol
maka matriks tersebut singular.
Matriks Ortogonal
Matriks kuadrat [ ] dikatakan dapat didiagonalisasi secara orthogonal jika
didefinisikan sebagai matriks kuadrat yang inversnya sama dengan transposenya,
sehingga :
Maka P adalah matriks orthogonal
2.1.3 Operasi Matriks
Perkalian Matriks dengan Skalar
Jika [ ] adalah matriks mxn dan k adalah suatu skalar, maka hasil kali A dengan
k adalah [ ] matriks mxn dengan (1 )
Perkalian Matriks dengan Matriks
Jika adalah matriks mxp dan adalah matriks pxn maka hasil kali
dari matriks A dan matriks B yang ditulis dengan AB adalah C matriks mxn. Secara
matematik dapat ditulis sebagai berikut :
∑ (1 ) (2.2)
Penjumlahan Matriks
Jika adalah matriks mxn dan adalah matriks mxn maka
penjumlahan matriks dari matriks A dan matriks B yang ditulis dengan
dengan :
(i= 1, 2, …, m; j= 1, 2, …, n).
Pengurangan Matriks
Jika adalah matriks mxn dan adalah matriks mxn maka
pengurangan matriks dari matriks A dan matriks B yang ditulis dengan
dengan : (i= 1, 2, …, m; j= 1, 2, …, n).
Transpose Suatu Matriks
Jika adalah matriks mxn maka matriks nxm dengan dan
Matriks mxn yang umum dapat ditulis :
(A) atau |A|. Secara matematiknya ditulis :
Jika A adalah sebarang matriks kuadrat, maka det(A) = det(AT). Anton (2004, hal: 97)
Teorema
Jika A dan B adalah matriks kuadrat yang ordonya sama, maka det(AB) = det(A)(B).
Anton (2004, hal: 108)
Secara umum invers matriks A adalah :
Adjoint matriks A adalah suatu matriks yang elemen-elemennya terdiri dari
semua elemen-elemen kofaktor matriks A, dengan adalah kofaktor elemen-elemen
c. Jika A adalah matriks non singular maka
2.2Nilai Eigen dan Vektor Eigen
Jika A adalah matriks nxn, maka vektor tak nol X di dalam Rn dinamakan vektor eigen (eigenvector) dari A jika AX adalah kelipatan skalar dari X yakni :
AX = (2.3)
Untuk suatu skalar . Skalar dinamakan nilai eigen (eigen value) dari A dan X
dikatakan vektor eigen yang bersesuaian dengan .
Untuk mencari nilai eigen matriks A yang berukuran nxn, dari persamaan (2.3)
dapat ditulis kembali sebagai suatu persamaan homogen :
(2.4)
Dengan I adalah matriks identitas yang berordo sama dengan matriks A, dalam catatan
n buah akar
Jika nilai eigen disubstitusi pada persamaan maka solusi dari
vektor eigen adalah (2.6)
Jadi apabila matriks mempunyai akar karakteristik dan ada
kemungkinan bahwa diantaranya mempunyai nilai yang sama, bersesuaian dengan
akar-akar karakteristik ini adalah himpunan vektor–vektor karakteristik yang
orthogonal (artinya masing-masing nilai akar karakteristik akan memberikan vektor
karakteristik) sedemikian sehingga :
Tanpa menghilangkan sifat umum, vektor-vektor tersebut bisa dibuat normal
(standar) sedemikian rupa sehingga untuk semua i, suatu himpunan
vektor-vektor orthogonal yang telah dibuat normal (standar) disebut orthogonal set.
Apabila X merupakan matriks nxn, dimana kolom – kolomnya terdiri dari
vektor-vektor dan kemudian bisa ditulis dengan dua syarat sebagai berikut :
1. jika
jika
2. sehingga
Matriks yang mempunyai sifat demikian dinamakan matriks orthogonal.
Definisi :
Misalkan matriks nxn.
Determinan [
]
Dikatakan karakteristik polinom dari A.
Dikatakan persamaan karakteristik dari A.
2.3Matriks korelasi
Matriks korelasi adalah matriks yang didalamnya terdapat korelasi-korelasi. Andaikan
X adalah matriks data, ̅ adalah matriks rata-rata dan ∑ adalah matriks ragam
̅ dihitung dari matriks data yang dikalikan dengan vektor 1 dan konstanta
Selanjutnya, persamaan (2.7) dikalikan dengan vektor , sehingga dihasilkan
matriks ̅
Kurangkan matriks X dengan persamaan matriks (2.8) yang menghasilkan matriks
Persamaan (2.10) menunjukan dengan jelas hubungan operasi perkalian
matriks data X dengan ( ) dan transpose matriks data. Jika S telah diketahui
dari persamaan (2.10), maka S dapat dihubungkan ke matriks korelasi dengan cara :
̅
Dalam perkembangannya terdapat dua jenis regresi yang sangat terkenal, yaitu regresi
linier sederhana dan regresi linier berganda. Regresi linier sederhana digunakan untuk
menggambarkan hubungan antara suatu variabel bebas (X) dengan satu variabel tak
bebas (Y) dalam bentuk persamaan linier sederhana.
(2.12)
Regresi linier berganda merupakan perluasan dari regresi linier sederhana.
Perluasannya terlihat dari banyaknya variabel bebas pada model regresi tersebut.
Bentuk umum regresi linier berganda dapat dinyatakan secara statistik sebagai berikut:
Dalam model regresi linier berganda ada beberapa asumsi yang harus dipenuhi,
asumsi tersebut adalah :
1. Nilai rata-rata kesalahan pengganggu nol, yaitu untuk I = 1, 2, …, n
2. Varian sama untuk semua kesalahan pengganggu (asumsi
homokedastisitas)
3. Tidak ada otokorelasi antara kesalahan pengganggu, berarti kovarian
4. Variabel bebas , konstan dalam sampling yang terulang dan bebas
terhadap kesalahan pengganggu .
5. Tidak ada multikolinieritas diantara variabel bebas X.
6. artinya kesalahan pengganggu mengikuti distribusi normal
dengan rata-rata 0 dan varian
2.4.2 Metode Kuadrat Terkecil (MKT)
Metode kuadrat terkecil merupakan suatu metode yang paling banyak digunakan
untuk menduga parameter-parameter regresi. Pada model regresi linier berganda juga
digunakan metode kuadrat terkecil untuk menduga parameter. Biasanya penduga
kuadrat terkecil ini diperoleh dengan meminimumkan jumlah kuadrat galat. Misalkan
model yang akan diestimasi adalah parameter dari persamaan dengan n pengamatan,
maka diperoleh :
= + + + … + +
= + + + … + +
= + + + … + +
Persaman-persamaan diatas dapat ditulis dalam bentuk matriks :
Y = X + (2.14)
[ ] [
Untuk mendapatkan penaksir-penaksir MKT bagi , maka dengan asumsi
klasik ditentukan dua vektor ̂ ̂ sebagai :
Persamaan hasil estimasi dari persamaan (2.14) dapat ditulis sebagai :
Y = X ̂ +
atau
̂ (2.15)
Karena tujuan MKT adalah meminimumkan jumlah kuadrat dari kesalahan,
yaitu ∑ minimum
Oleh karena ̂ adalah skalar, maka matriks transposenya adalah :
( ̂ ) ̂
jadi,
Untuk menaksir parameter ̂ maka harus diminimumkan terhadap ̂ maka :
Menurut Sembiring (2003) metode kuadrat terkecil memiliki beberapa sifat yang baik.
Untuk menyelidiki sifatnya, pandang kembali model umum regresi linier pada
persamaan (2.14). disini dianggap bahwa bebas satu sama lain dan
Dengan demikian maka dan .
Jadi sifat penduga kuadrat terkecil adalah :
2. Varian Minimum
Jika maka matriks kovarian untuk ̂ diberikan oleh
Jika dan maka penduga kuadrat terkecil ̂
mempunyai varian minimum diantara semua penduga tak bias linier.
Bukti :
( ̂) [( ̂ ( ̂) ̂ ( ̂) )]
=
(2.20)
2.5 Uji Regresi Linier
Pengujian nyata regresi adalah sebuah pengujian untuk menentukan apakah ada
hubungan linier antara variabel tidak bebas Y dan variabel bebas
Uji yang digunakan adalah uji menggunakan statistik F berbentuk :
(2.21)
dengan :
JKR = Jumlah Kuadrat Regresi
JKS = Jumlah Kuadrat Sisa
= derajat kebebasan JKR
= Derajat kebebasan JKS
Dalam uji hipotesis, digunakan daerah kritis :
ditolak jika
dengan :
Selanjutnya, jika model regresi layak digunakan akan dilakukan lagi uji
terhadap koefisien-koefisien regresi secara terpisah untuk mengetahui apakah
koefisien tersebut layak dipakai dalam persamaan atau tidak.
Rumusan hipotesis untuk menguji parameter regresi secara parsial adalah
sebagai berikut :
artinya koefisien regresi ke–j tidak signifikan atau variabel bebas ke-j
tidak berpengaruh nyata terhadap Y.
artinya koefisien regresi ke-j signifikan atau variabel bebas ke-j
berpengaruh nyata terhadap Y.
Statistik uji yang digunakan untuk menguji parameter regresi secara parsial
adalah:
( ̂) ̂
√ ̂ (2.23)
Jika | ( ̂ )| > maka ditolak yang artinya variabel bebas ke- j
berpengaruh nyata terhadap Y.
2.6 Koefisien Determinasi ( )
Koefisien determinasi adalah nilai yang menunjukkan seberapa besar nilai variabel Y
dijelaskan oleh variable X. Koefisien determinasi merupakan salah satu patokan yang
biasa digunakan untuk melihat apakah suatu model regresi yang dicocokkan belum
atau sudah memadai, yang dinotasikan dengan R2. Koefisien determinasi ini hannya menunjukkan ukuran proporsi variansi total dalam respon Y yang diterangkan oleh
model yang dicocokkan (Walpole dan Myers, 1995)
Nilai koefisien determinasi ( ) dapat diperoleh dengan rumus :
Nilai R2 yang mendekati 0 (nol) menunjukkan bahwa data sangat tidak cocok dengan model regresi yang ada. Sebaliknya, jika nilai R2 mendekati 1 (satu) menunjukkan bahwa data cocok terhadap model regresi. Dapat disimpulkan bahwa
nilai R2 yang diperoleh sesuai dengan yang dijelaskan masing-masing faktor yang tinggal di dalam regresi. Hal ini mengakibatkan bahwa yang dijelaskan hannyalah
disebabkan faktor yang mempengaruhinya saja. Besarnya variansi yang dijelaskan
penduga sering dinyatakan dalam persen. Persentase variansi penduga tersebut adalah
2.7 Multikolinieritas
Istilah multikolinieritas pertama kali diperkenalkan oleh Ragnar Frisch pada tahun
1934, yang menyatakan bahwa multikolinieritas terjadi jika adanya hubungan linier
yang sempurna (perfect) atau pasti (exact) diantara beberapa atau semua variabel
bebas dari model regresi berganda (Rahardiantoro 2008).
Maksud dari adanya hubungan linier antar sesama variable adalah :
Misalkan terdapat k variable bebas . Hubungan linier yang
sempurna/pasti terjadi jika berlaku hubungan berikut :
(2.25)
Dimana merupakan bilangan konstan dan tidak seluruhnya nol atau
paling tidak ada satu yang tidak sama dengan nol, yaitu
Jika terdapat korelasi sempurna diantara sesama variabel bebas, sehingga nilai
koefisien korelasi diantara sesama variabel ini sama dengan satu, maka
konsekuensinya adalah koefisien-koefisien regresi menjadi tidak dapat ditaksir, nilai
standar eror setiap koefisien regresi menjadi tak hingga.
Pada analisis regresi, multikolinieritas dikatakan ada apabila beberapa kondisi
berikut dipenuhi :
1. Dua variable berkorelasi sempurna (oleh karena itu vektor–vektor yang
2. Dua variabel bebas hampir berkorelasi sempurna yaitu koefisien korelasinya
mendekati .
3. Kombinasi linier dari beberapa variabel bebas berkorelasi sempurna atau
mendekati sempurna dengan variable bebas yang lain.
4. Kombinasi linier dari satu sub-himpunan variabel bebas berkorelasi sempurna
dengan suatu kombinasi linier dari sub-himpunan variabel bebas yang lain.
2.7.1 Pendeteksian Multikolinieritas
Ada beberapa cara untuk mengetahui ada tidaknya multikolinieritas, yaitu :
1. Nilai korelasi (korelasi antar peubah bebas).
Prosedur ini merupakan pendeteksian yang paling sederhana dan paling
mudah. Jika nilai korelasi antar peubah ( ) melebihi 0,75 diduga terdapat
2. Faktor Variansi Inflasi (Variance Inflation Factor, VIF).
VIF adalah elemen-elemen diagonal utama dari invers matriks korelasi. VIF
digunakan sebagai kriteria untuk mendeksi multikolinieritas pada regresi linier
berganda yang melibatkan lebih dari dua variabel bebas. Nilai VIF lebih besar
dari 10 mengindikasikan adanya masalah multikolinieritas yang serius.
VIF untuk koefisien regresi –j didefinisikan sebagai berikut :
(2.27)
dengan :
= Koefisien determinasi antar dengan variabel bebas lainnya
2.7.2 Pengaruh Multikolinieritas
Koefisien regresi penduga ̂ yang diperoleh dengan metode kuadrat terkecil
mempunyai banyak kelemahan apabila terjadi multikolinieritas diantara variabel
bebas, yaitu :
1. Variansi ̂ Besar
Apabila determinan dari matriks , akibatnya variansi akan semakin
besar sehingga penduga kuadrat terkecil tidak efisien karena memiliki ragam
dan peragam yang besar. Dalam kasus multikolinieritas penduga kuadrat
tekecil tetap tak bias karena sifat ketakbiasan tidak ditentukan oleh asumsi
tidak adanya multikolinieritas, hannya akibat multikolinieritas penduga
memiliki ragam yang besar dan tidak dapat lagi disebut sebagai penduga yang
memiliki sifat linier, tak bias, dan mempunyai varian minimum atau yang
disebut BLUE (best linier unbiased estimator).
2. Selang Kepercayaan Penduga Lebih Lebar
Dalam situasi multikolinieritas antara variabel-variabel bebas dalam model
regresi linier mengakibatkan variansi penduga kuadrat terkecil menjadi besar
sehingga menghasilkan galat baku yang lebih besar, akibatnya selang
kepercayaan bagi parameter model regresi menjadi lebih besar.
3. Nilai Statistik-t yang Tidak Nyata
Multikolinieritas yang mengakibatkan galat baku penduga kuadrat terkecil
menjadi lebih besar, maka statistik t yang didefinisikan sebagai rasio antara
koefisien penduga dan galat baku koefisien penduga menjadi lebih kecil.
Akibatnya meningkatkan besarnya peluang menerima hipotesis yang salah
(kesalahan akan meningkat), karena suatu hipotesis yang seharusnya ditolak
tetapi berdasarkan pengujian hipotesis diputuskan untuk diterima, sebagai
4. Nilai Koefisien Determinasi (R2) yang Tinggi Tetapi Beberapa Nilai Statistik-t
Tidak Nyata
Dalam kasus adanya multikolinieritas, maka akan ditemukan beberapa
koefisien regresi yang secara individual tidak nyata berdasarkan uji statistik
t-student. Namun, koefisien determinasi (R2) dalam situasi yang demikian mungkin tinggi sekali serta berdasarkan uji koefisien regresi keseluruhan
berdasarkan uji F akan ditolak hipotesis nol, bahwa
2.8 Analisis Komponen Utama
Analisis komponen utama merupakan teknik statistik yang dapat digunakan untuk
mereduksi sejumlah variabel asal menjadi beberapa variabel baru yang bersifat
orthogonal dan tetap mempertahankan total keragaman dari variabel asalnya.
Analisis komponen utama bertujuan untuk mengubah dari sebagian besar
variabel asli yang digunakan yang saling berkorelasi satu dengan yang lainnya,
menjadi satu set variabel baru yang lebih kecil dan saling bebas (tidak berkorelasi
lagi), dan merupakan kombinasi linier dari variabel asal. Selanjutnya variabel baru ini
dinamakan komponen utama (principal component). secara umum tujuan dari analisis
komponen utama adalah mereduksi dimensi data sehingga lebih mudah untuk
menginterpretasikan data-data tersebut.
Analisis komponen utama bertujuan untuk menyederhanakan variabel yang
diamati dengan cara menyusutkan dimensinya. Hal ini dilakukan dengan
menghilangkan korelasi variabel melalui transformasi variabel asal ke variabel baru
yang tidak berkorelasi.
Variabel baru ( ) disebut sebagai komponen utama yang merupakan hasil
transformasi dari variable asal yang modelnya dalam bentuk catatan matriks adalah:
dengan :
A adalah matriks yang melakukan transformasi terhadap variabel asal
sehingga diperoleh vektor komponen .
Penjabarannya adalah sebagai berikut :
komponen utama apabila semua variabel yang diamati mempunyai satuan pengukuran
yang sama. Sedangkan, matriks Korelasi digunakan apabila variabel yang diamati
tidak mempunyai satuan pengukuran yang sama. Variabel tersebut perlu dibakukan,
sehingga komponen utama berdasarkan matriks korelasi ditentukan dari variabel baku.
2.8.1.1Komponen Utama Berdasarkan Matriks Kovarian (∑)
Dipunyai matriks kovarian ∑ dari p buah variable Total varian dari
variabel–variabel tersebut didefinisikan sebagai ∑ ∑ yaitu penjumlahan
dari unsur diagonal matriks ∑. Melalui matriks kovarian ∑ bisa diturunkan akar
ciri-akar cirinya yaitu dan vektor ciri–vektor cirinya
Komponen utama pertama dari vektor berukuran px1,
Komponen utama pertama dapat dituliskan sebagai :
(2.29)
dengan :
dan
Varian dari komponen utama pertama adalah :
∑ ∑
terhadap sama dengan nol.
Komponen utama kedua adalah kombinasi linier terbobot variabel asal yang
tidak berkorelasi dengan komponen utama pertama, serta memaksimumkan sisa
kovarian data setelah diterangkan oleh komponen utama pertama. Komponen utama
kedua dapat dituliskan sebagai :
dengan :
dan
Vektor pembobot adalah vektor normal yang dipilih sehingga keragaman
komponen utama kedua maksimum, serta orthogonal terhadap vektor pembobot
dari komponen utama pertama. Agar varian dari komponen utama kedua maksimum,
serta antara komponen utama kedua tidak berkorelasi dengan komponen utama
pertama, maka vektor pembobot dipilih sedemikian sehingga tidak
berkorelasi dengan varian komponen utama kedua ( ) adalah :
∑ ∑
∑ (2.33)
Varian tersebut akan dimaksimumkan dengan kendala dan cov
∑ Karena adalah vektor ciri dari ∑ dan ∑ adalah matriks simetrik, maka :
∑ ∑ ∑
Kendala ∑ dapat dituliskan sebagai Jadi fungsi
Lagrange yang dimaksimumkan adalah :
∑ (2.34)
Fungsi ini mencapai maksimum jika turunan parsial pertama
terhadap sama dengan nol, diperoleh
∑ ∑ (2.35)
Jika persamaan (2.35) dikalikan dengan maka diperoleh
∑ ∑ ∑
∑
∑
Oleh karena ∑ maka Dengan demikian persamaan (2.35) setelah
∑
∑ (2.36)
Jadi dan merupakan pasangan akar ciri dan vektor ciri dari matriks
varian kovarian ∑ Seperti halnya penurunan pada pencarian , akan diperoleh bahwa
adalah vektor ciri yang bersesuaian dengan akar ciri terbesar kedua dari matriks ∑
Secara umum komponen utama ke-j dapat dituliskan sebagai :
(2.37)
dengan :
dan
vektor pembobot diperoleh dengan memaksimumkan keragaman komponen utama
ke-j, yaitu :
∑ (2.38)
dengan kendala :
serta untuk .
Dengan kendala ini, maka akar ciri dapat diinterpretasikan sebagai ragam
komponen utama ke- j serta sesama komponen utama tidak berkorelasi.
Vektor pembobot yang merupakan koefisien pembobot variabel asal bagi
komponen utama ke-j diperoleh dari matriks peragam ∑ yang diduga dengan matriks
S berikut :
2.8.1.2Komponen Utama Berdasarkan Matriks Korelasi ( )
Jika variabel yang diamati tidak mempunyai satuan pengukuran yang sama, maka
variabel tersebut perlu dibakukan sehingga komponen utama ditentukan dari variabel
baku (Vincent gasperz, 1991). Variabel asal perlu ditransformasi ke dalam variabel
baku Z, dalam catatan matriks adalah :
(2.40)
dengan :
Z = variabel baku
= matriks simpangan baku dengan unsur diagonal utama
= variabel pengamatan
= nilai rata-rata pengamatan
Dengan, Nilai harapan , dan ragamnya ∑
Dengan demikian, komponen–komponen utama dari Z dapat ditentukan dari
vektor ciri yang diperoleh melalui matriks korelasi yang diduga dengan matriks ,
dimana vektor pembobot diperoleh dengan memaksimumkan keragaman
komponen utama ke-j dengan kendala :
serta untuk .
Semua formula yang telah diturunkan berdasarkan variabel-variabel
dengan matriks ∑ akan berlaku untuk peubah-peubah dengan matriks
Sehingga diperoleh komponen utama ke-j dengan menggunakan variable baku
Ragam komponen utama ke-j adalah sama dengan akar ciri ke-j, serta antara
komponen utama ke-i dan komponen utama ke- j tidak berkorelasi untuk .
Untuk meregresikan komponen utama dengan variabel bebas, maka perlu
dihitung skor komponen dari setiap pengamatan. Untuk komponen utama yang
diturunkan dari matriks korelasi , maka skor komponen utama dari unit pengamatan
ke-i ditentukan sebagai berikut :
(2.42)
dengan :
= vektor pembobot komponen utama ke-r
= vektor skor baku dari variabel yang diamati pada pengamatan ke-i
2.8.2 Kriteria Pemilihan Komponen Utama
Salah satu tujuan dari analisis komponen utama adalah mereduksi dimensi data asal
yang semula, terdapat p variable bebas menjadi k komponen utama .
Kriteria pemilihan k yaitu :
1. Didasarkan pada akar ciri yang lebih besar dari satu, dengan kata lain
hannya komponen utama yang memiliki akar ciri lebih besar dari satu yang
dilibatkan dalam analisis regresi komponen utama.
2. Proporsi kumulatif keragaman data asal yang dijelaskan oleh k komponen
utama minimal 80%, dan proporsi total variansi populasi bernilai cukup
2.8.3 Kontribusi Komponen Utama
Kontribusi komponen utama yang diturunkan dari matriks kovarian dan matriks
korelasi adalah sebagai berikut:
Proporsi total variansi populasi yang dijelaskan oleh komponen utama ke-j
berdasarkan matriks kovarian adalah :
∑ dengan (2.43)
Jadi kontribusi (dalam persentase) masing–masing komponen utama ke-j
terhadap total varian x adalah :
∑ x 100% (2.44)
Sedangkan, proporsi total variansi populasi yang dijelaskan oleh komponen
utama ke-j berdasarkan matriks korelasi, yaitu komponen yang dihasilkan berdasarkan
variable-variabel yang telah dibakukan (Z) adalah :
(2.45)
dengan :
= Akar ciri terbesar ke-j dari matriks korelasi R
= Trace matriks R yang merupakan jumlah diagonal utama matriks R, yang tidak lain sama dengan banyaknya variabel yang diamati, atau
sama dengan jumlah semua akar ciri yang diperoleh dari matriks R.
Jadi kontribusi (dalam persentase) masing–masing komponen utama ke-j
terhadap total varian x adalah :
Bab 3
PEMBAHASAN
3.1Regresi Komponen Utama
Regresi komponen utama adalah teknik yang digunakan untuk meregresikan
komponen utama dengan variabel tak bebas melalui metode kuadrat terkecil. Tahap
pertama pada prosedur regresi komponen utama yaitu menentukan komponen utama
yang merupakan kombinasi linier dari beberapa variabel X, dan tahap kedua adalah
variabel tak bebas diregresikan pada komponen utama dalam sebuah model regresi
linier.
Persamaan regresi komponen utama berdasarkan matriks kovarian pada
dasarnya hampir sama dengan persamaan regresi komponen utama berdasarkan
matriks korelasi yaitu variabel diganti dengan variabel baku
. Kedua persamaan tersebut digunakan sesuai dengan pengukuran variabel-variabel yang diamati.
Apabila diberikan notasi sebagai banyaknya komponen utama
yang dilibatkan dalam analisis regresi komponen utama, di mana k lebih kecil
daripada banyaknya variabel penjelas asli X, yaitu sejumlah p ( )
Maka Bentuk umum persamaan regresi komponen utama adalah :
(3.1)
dengan :
= variabel tak bebas
= variabel komponen utama
Komponen utama merupakan kombinasi linier dari variabel Z ;
(3.2)
dengan :
= komponen utama
= koefisien komponen utama = variabel baku
Komponen utama dalam persamaan (3.2) disubstitusikan ke
dalam persamaan regresi komponen utama (3.1), maka diperoleh :
̂ (3.3)
dengan :
= ̅
= (3.4)
3.2Uji Koefisien Regresi Komponen Utama
Pengujian koefisien regresi adalah sebuah pengujian untuk menentukan apakah
variabel bebas berpengaruh nyata terhadap variabel terikat. Pengujian Akan dilakukan
terhadap koefisien-koefisien regresi secara terpisah untuk mengetahui apakah
koefisien tersebut layak dipakai dalam persamaan atau tidak.
Rumusan hipotesis untuk menguji parameter regresi secara parsial adalah
sebagai berikut :
artinya koefisien regresi ke–j tidak signifikan atau variabel bebas ke-j
artinya koefisien regresi ke-j signifikan atau variabel bebas ke-j
berpengaruh nyata terhadap Y.
Untuk menguji signifikansi koefisien regresi dilakukan dengan
menggunakan uji t-student dengan statistik uji :
√ (3.5)
= ragam galat regresi komponen utama
= koefisien komponen utama
= nilai eigen ke-i
Jika | ( ̂)| > maka ditolak yang artinya variabel bebas ke- j
berpengaruh nyata terhadap Y.
Setelah koefisien diuji keberartiannya, persamaan regresi linier berganda (3.3)
yang terdapat variable baku Z ditransformasi menjadi variabel X sebagai variabel
bebasnya, maka model regresinya adalah :
̂ (3.8)
dengan :
̂ = variabel bebas
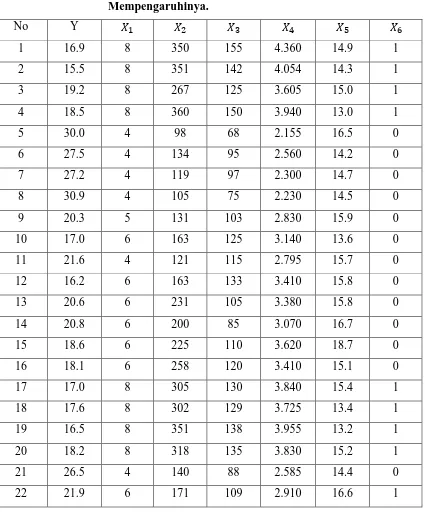
3.3Ilustrasi Regresi Komponen Utama Mengatasi Multikolinieritas
Sebagai teladan penggunaan analisis regresi komponen utama untuk mengatasi
masalah multikolinieritas, berikut ini akan dibahas suatu contoh kasus yang memiliki
multikolinieritas diantara variabel–variabel bebasnya. Data yang akan dibahas adalah
data yang tertera dalam tabel berikut :
23 34.1 4 86 65 1.975 15.2 0
24 35.1 4 98 80 1.915 14.4 0
25 27.4 4 121 80 2.670 15.0 0
26 31.5 4 89 71 1.990 14.9 0
27 29.5 4 98 68 2.135 16.6 0
28 28.4 4 151 90 2.670 16.0 0
29 28.8 6 173 115 2.595 11.3 1
30 26.8 6 173 115 2.700 12.9 1
Sumber : Bovas Abraham dan Johannes Ledolter 1983
Keterangan :
Y = Gas Mileage mil per galon
= Jumlah silinder
= pertukaran mesin dalam inch3
= Daya kuda
= Berat dalam 1000 pon
= Percepatan dalam detik
= Tipe/jenis mesin (straight [1]; V [0])
3.3.1 Analisis Dengan Regresi Linier Berganda
Analisa regresi dengan metode kuadrat terkecil persamaan (2.18) menghasilkan
persaman regresi sebagai berikut : (perhitungan pada lampiran A)
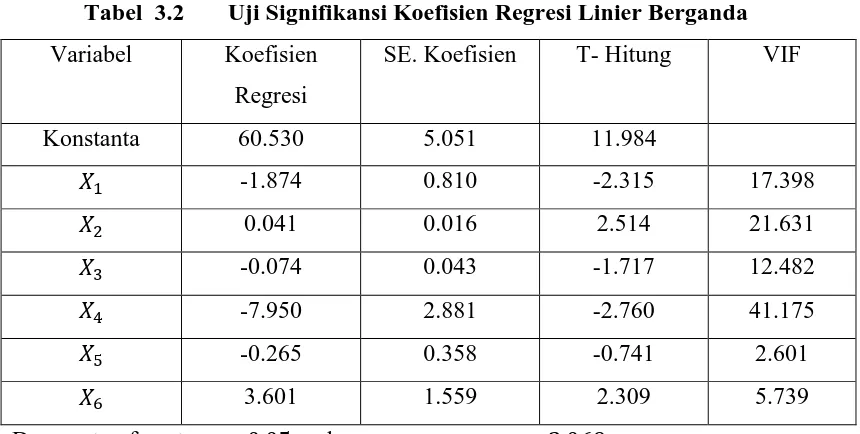
Tabel 3.2 Uji Signifikansi Koefisien Regresi Linier Berganda
Variabel Koefisien
Regresi
SE. Koefisien T- Hitung VIF
Konstanta 60.530 5.051 11.984
-1.874 0.810 -2.315 17.398
0.041 0.016 2.514 21.631
-0.074 0.043 -1.717 12.482
-7.950 2.881 -2.760 41.175
-0.265 0.358 -0.741 2.601
3.601 1.559 2.309 5.739
Dengan taraf nyata maka
( pada lampiran E)
Berdasarkan uji signifikansi koefisien regresi secara parsial dimana terdapat
variabel yang | ( ̂ )| < yaitu variabel bebas dan . Hal ini
menyebabkan bahwa diterima yang berarti terdapat variabel bebas ( dan )
yang tidak berpengaruh nyata terhadap variabel terikat (Y).
3.3.2 Pendeteksian Multikolinieritas
Untuk pendeteksian adanya multikolinieritas ada beberapa cara yang dapat digunakan
antara lain :
1. Nilai Korelasi
Dengan menggunakan persamaan (2.26) maka didapatkan nilai korelasi
Tabel 3.3 Nilai Korelasi Data Gas Mileage Antar Variabel Bebas
Variabel
1.000 0.944 0.872 0.914 -0.243 0.826
0.944 1.000 0.862 0.945 -0.219 0.750
0.872 0.862 1.000 0.905 -0.321 0.710
0.914 0.945 0.905 1.000 -0.60 0.632
-0.243 -0.219 -0.321 -0.60 1.000 -0.460
0.826 0.750 0.710 0.632 -0.460 1.000
(perhitungan pada lampiran B)
Berdasarkan nilai korelasi diatas terdapat korelasi antar variabel yang melebihi
0.75. Hal ini mengindikasikan bahwa terdapat multikolinieritas.
2. Faktor Variansi Inflasi (VIF)
Dengan menggunakan persamaan (2.27) maka didapatkan nilai VIF masing-masing
variabel bebas yang dijelaskan pada tabel berikut.
Tabel 3.4 Nilai Faktor Variansi Inflasi (VIF)
Variabel VIF
17.398
21.631
12.482
41.175
2.601
5.739
(perhitungan pada lampiran B)
3.3.3 Analisis Dengan Regresi Komponen Utama
Setelah dideteksi bahwa data gas mileage pada tabel (3.1) mengalami masalah
multikolinieritas pada variabel bebasnya maka data tersebut akan dianalisis
menggunakan analisis regresi komponen utama.
Karena skala pengukuran dari setiap variabel yang diamati tidak sama, maka
variabel tersebut ditransformasikan ke dalam variabel baku Z (persamaan 2.40).
Kemudian akan dianalisis dengan analisis Komponen utama yang ditentukan
berdasarkan pada matriks korelasi.
Correlation Matrix
Z1 Z2 Z3 Z4 Z5 Z6
Correlation Z1 1.000
Z2 .944 1.000
Z3 .872 .862 1.000
Z4 .914 .945 .905 1.000
Z5 -.243 -.219 -.321 -.060 1.000
Z6 .826 .750 .710 .632 -.460 1.000
(lampiran B)
Untuk menegetahui variabel komponen utama berdasarkan matriks korelasi,
terlebih dahulu dihitung nilai eigen dan vektor eigen yang bersesuaian, dengan
menggunakan persamaan (2.5) dan (2.46) maka diperoleh nilai eigen, serta proporsi
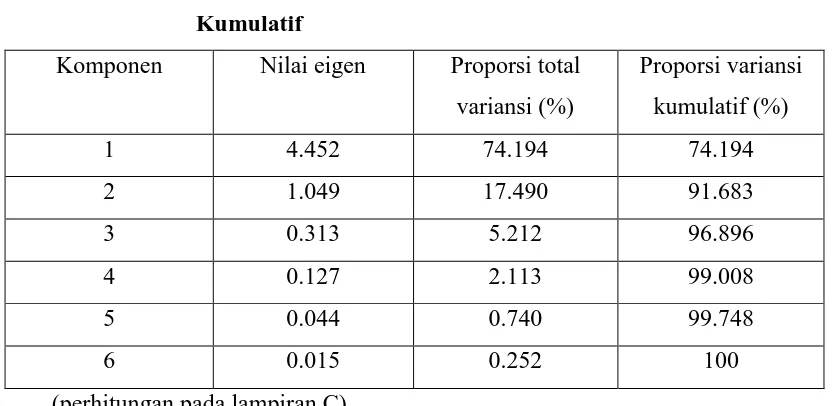
Tabel 3.5 Nilai Eigen, Proporsi Total Variansi dan Proporsi Variansi Kumulatif
Komponen Nilai eigen Proporsi total
variansi (%)
Berdasarkan kriteria pemilihan komponen utama maka komponen yang
terpilih adalah komponen utama pertama dan kedua karena memiliki nilai eigen lebih
besar dari 1 serta proporsi keragaman oleh kedua komponen utama tersebut telah
mampu menjelaskan 91.683 % keragaman dari variabel asal.
Setelah nilai eigen diketahui maka dengan menggunakan persamaan (2.6)
dapat dihitung nilai vektor eigen yang bersesuaian dengan nilai eigen, dimana vektor
eigen merupakan koefisien komponen utama. Hasil perhitungan diperoleh seperti pada
tabel berikut.
Tabel 3.6 Koefisien Komponen Utama (Vektor Eigen)
Berdasarkan persamaan (3.2) maka persamaan komponen utama adalah :
(3.9)
Untuk meregresikan komponen utama dengan variabel bebas, maka dihitung
skor komponen dari setiap pengamatan. Untuk komponen utama yang diturunkan dari
matriks korelasi , berdasarkan persamaan (2.42) maka didapatkan skor komponen
utama dari unit pengamatan ke-i seperti pada tabel berikut :
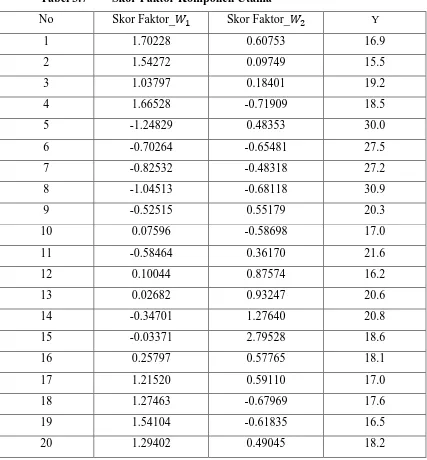
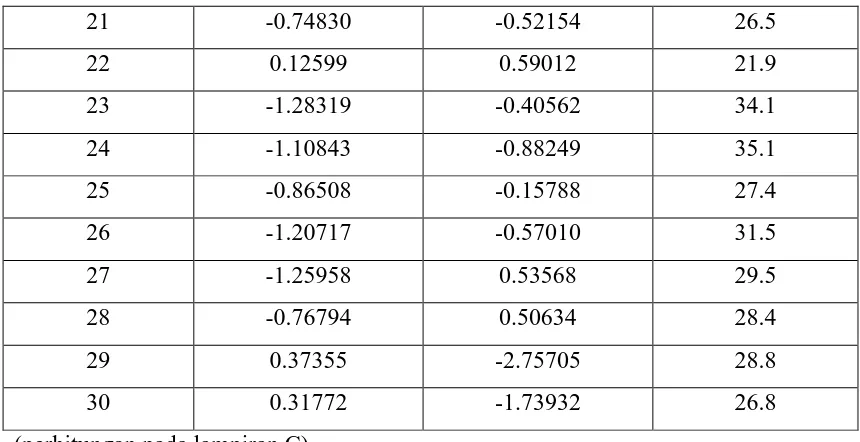
Tabel 3.7 Skor Faktor Komponen Utama
No Skor Faktor_ Skor Faktor_ Y
21 -0.74830 -0.52154 26.5
Skor komponen utama tersebut kemudian diregresikan dengan variabel bebas
Y dengan metode kuadrat terkecil. Adapun model regresi komponen utama dengan
dua komponen adalah : (perhitungan pada lampiran E)
̂ (3.10)
dengan :
̅
Tabel 3.8 Uji Signifikansi Koefisien Regresi Komponen Utama
Komponen
Koefisien Komponen utama dan sudah signifikan serta nilai VIF adalah 1, ini
menunjukkan bahwa sudah tidak ada lagi masalah multikolinieritas.
Dengan mensubstitusikan persamaan (3.9) ke persamaan (3.10) maka didapat
Model regresi linier berganda yang melibatkan variabel Z yang merupakan hasil
transformasi dari variabel W sebagai variabel bebas. Hasil transformasi ditunjukkan
̂ 3.3.4 Uji Signifikansi Koefisien Regresi Komponen Utama Variabel Baku
Koefisien regresi pada persamaan (3.11) akan diuji secara parsial. Berdasarkan
persamaan (3.6) dan (3.7) maka didapatkan nilai varian dan T-Hitung masing–masing
variabel bebas Z seperti pada tabel berikut.
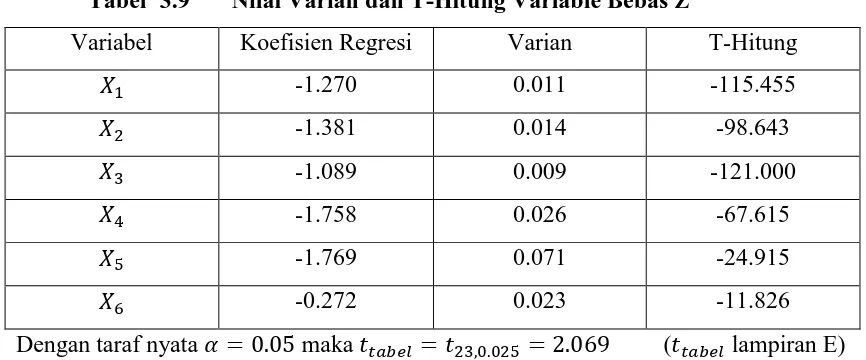
Tabel 3.9 Nilai Varian dan T-Hitung Variable Bebas Z
Variabel Koefisien Regresi Varian T-Hitung
-1.270 0.011 -115.455
-1.381 0.014 -98.643
-1.089 0.009 -121.000
-1.758 0.026 -67.615
-1.769 0.071 -24.915
-0.272 0.023 -11.826
Dengan taraf nyata maka ( lampiran E)
Berdasarkan uji signifikansi koefisien regresi secara parsial, didapatkan bahwa
semua | ( ̂ )| > Hal ini menyebabkan ditolak sehingga dapat
disimpulkan bahwa semua variabel bebas Z berpengaruh secara nyata terhadap
variabel terikat (Y).
Maka dengan menggunakan persamaan (2.40), persamaan (3.11) akan diubah
kebentuk semula. Persamaan yang terdapat variable Z ditransformasi menjadi variabel
X sebagai variabel bebasnya dengan
.
Sehingga diperoleh model regresi dengan variabel bebas X yaitu :
Bab 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
1. Analisis regresi komponen utama merupakan suatu metode yang dapat
mengatasi masalah multikolinieritas pada analisis regresi berganda. Pada
analisis regresi komponen utama semua variabel bebas masuk kedalam model,
tetapi sudah tidak terjadi multikolinieritas karena sudah dihilangkan pada tahap
analisis komponen utama.
2. Pada tahap analisis komponen utama berdasarkan matriks korelasi dihasilkan
dua buah komponen utama yang saling bebas (tidak ada korelasi) yang
menjelaskan 91.683% keragaman dari total keragaman variabel asal dengan
nilai akar ciri masing-masing 4.452 dan 1.049.
3. Nilai T-hitung masing-masing variable baku Z lebih besar dari T-tabel,
sehingga berdasarkan uji signifikan koefisien secara parsial semua variabel
pada regresi komponen utama berpengaruh nyata terhadap variable terikat (Y),
hal ini menjadi ukuran bahwa model regresi komponen utama merupakan
model yang tepat untuk analisis data.
4. Melalui analisis regresi komponen utama diperoleh persamaan regresi yang
sudah tepat untuk analisis data yaitu :
̂
4.2 Saran
Multikolinieritas merupakan masalah yang dapat menimbulkan model yang diperoleh
kurang baik untuk analisis, untuk itu multikolinieritas harus terlebih dulu diatasi.
Salah satu cara adalah dengan menggunakan analisis komponen utama. Agar masalah
multikolinieritas ini dapat teratasi dengan lebih tepat maka perlu dilakukan kajian
terhadap metode–metode lain yang juga dapat mengatasi masalah multikolinieritas.
Oleh karena itu, disarankan kepada peneliti selanjutnya agar menggunakan metode
yang lain untuk mengatasi masalah multikolinieritas serta membandingkannya dengan
DAFTAR PUSTAKA
Abraham, Bovas and Ledolter Johannes. 1983. Statistical Methods for Forecasting.
New York : John Wiley and Son Inc.
Anton, Howard. 1987. Aljabar Linier Elementer. Edisi Kelima. Jakarta : Erlangga.
Bakti, Haris.2008. Analisis Regresi Komponen Utama Untuk Mengatasi Masalah Multikolinieritas Dalam Analisis Regresi Linier Berganda. Diakses tanggal 8 april 2011
Chatterjee, Samprit and Price, Bertram. 1977. Regression Analysis by Example.
Second Edition. New York : University New York.
Drapper. N.R. and Smith. 1981. Applied Regression Analysis. Second Edition. New York : John Wiley and Son Inc.
Gasperz, Vincent. 1991. Ekonometrika Terapan. Jilid 2. Bandung : Tarsito.
Gujarati, Damodar. 1995. Ekonometrika Dasar. Terjemahan Sumarno. Jakarta : Erlangga
Naftali, Y. 2007. Regresi dan Multikolinieritas Dalam Regresi.
http://yohanli.wordpress.com/category/science/ Diakses tanggal 15 Februari, 2011.
Sembiring, R.K. 2003. Analisis Regresi. Bandung : ITB Bandung
Sigit, Nugroho. Regresi Ridge Untuk Mengatasi Multikolinieritas. e-Jurnal Statistika. Diakses tanggal 15 Februari, 2011
Supranto, J. 1984. Ekonometrik. Jilid 2. Jakarta : LPFE Universitas Indonesia.
Supranto, J. 2004. Analisis Multivariat. Jakarta : Rineka Cipta.