Analisis Tekuk pada Kolom Baja Tampang IWF akibat Gaya Tekan Aksial

(1)

ANALISA TEKUK PADA KOLOM BAJA TAMPANG

IWF AKIBAT GAYA TEKAN AKSIAL

TUGAS AKHIR

Diajukan Untuk Melengkapi Tugas-Tugas dan

Memenuhi Syarat Untuk Menempuh Ujian

Sarjana Teknik Sipil

Disusun Oleh :

050404120

RISKA LUMBANRAJA

BIDANG STUDI STRUKTUR

DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA

(2)

ANALISA TEKUK PADA KOLOM BAJA TAMPANG

IWF AKIBAT GAYA TEKAN AKSIAL

TUGAS AKHIR

Diajukan Untuk Melengkapi Tugas-Tugas dan

Memenuhi Syarat Untuk Menempuh Ujian

Sarjana Teknik Sipil

Disusun Oleh :

05 0404 120

RISKA LUMBANRAJA

Disahkan Oleh :

Pembimbing

NIP. 19520901 198112 1 001 Ir. Sanci Barus, MT

Ketua Departemen

NIP. 195612241981031002 Prof. Dr. Ing. Johannes Tarigan

BIDANG STUDI STRUKTUR

DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA

(3)

KATA PENGANTAR

Puji dan syukur kepada Tuhan Yang Maha Pengasih, yang telah

memberikan berkat dan kasih-Nya sehingga penulis dapat menyelesaikan Tugas

Akhir ini yang merupakan syarat utama yang harus dipenuhi untuk memperoleh

gelar sarjana Teknik dari Universitas Sumatera Utara dengan judul ”Analisis

Tekuk pada Kolom Baja Tampang Iwf akibat Gaya Tekan Aksial”.

Penulis menyadari bahwa selesainya tugas akhir ini tidak terlepas dari

bimbingan, dukungan dan bantuan dari semua pihak baik moril maupun materil.

Untuk itu, pada kesempatan ini penulis ingin menyampaikan rasa hormat dan

terima kasih yang setulusnya kepada :

1. Bapak Prof. Dr. Ing. Johannes Tarigan, selaku Ketua Departemen Teknik Sipil

Universitas Sumatera Utara.

2. Bapak Ir.Teruna Jaya, M.Sc., selaku Sekretaris Departemen Teknik Sipil

Universitas Sumatera Utara.

3. Bapak Ir. Sanci Barus, MT selaku pembimbing yang telah banyak meluangkan

waktu, tenaga dan pikiran dalam memberikan bimbingan yang tiada hentinya

kepada penulis dalam menyelesaikan Tugas Akhir ini.

4. Kedua Orang Tuaku tercinta ( A. Lumbanraja dan T. Siallagan ) yang selalu

memberi dukungan dan kasih sayangnya dan juga doa yang selalu menyertai

penulis. Buat kedua kakakku ( Ka’Retno dan Ka’Erna ) dan kedua adikku (

Loren dan Suparto ) yang kusayangi, terima kasih kuucapkan kepada kalian

(4)

5. Bapak/Ibu Dosen Staf Pengajar Jurusan Teknik Sipil Universitas Sumatera

Utara.

6. Semua teman-teman stambuk 2005, mulai NIM 001 – 149 yang selalu

menemani disaat susah dan senang walaupun kebanyakan main-mainya,

terutama pada Ronald A Marthin, Lady n Kenk2, Ganda Kurus, Albert, Alkes,

Elli gong2, Andreas, Dame, Nensi, Ari, dan juga teman2 yang sering main di

Pondasi. Saat-saat bersama kalian sangatlah menyenangkan.

7. Abang dan kakak stambuk 2002, 2003, 2004, dan adik-adik stambuk 2006,

2007 dan 2008 terima kasih atas support yang telah diberikan.

8. Teman satu Kampungku dan juga Winta yang juga turut memberi support.

9. Abang, kakak, teman2, dan juga adik2 dari GMKI yang selalu memberi

dukungan dan doanya.

10. Semua pihak yang tidak dapat disebutkan satu-persatu yang telah membantu

penulis baik secara langsung maupun tidak langsung dalam menyelesaikan

tugas akhir ini.

Penulis menyadari sepenuhnya bahwa tugas akhir ini masih jauh dari

sempurna, dikarenakan keterbatasan pengetahuan dan kemampuan dari penulis,

untuk itu penulis mengharapkan kritik dan saran agar penulis dapat meningkatkan

kemampuan menulis pada masa akan datang. Akhir kata, semoga tugas akhir ini

dapat bermanfaat dan memberikan sumbangan pengetahuan bagi yang

membacanya.

Medan, Agustus 2010

(5)

ABSTRAK

Pada konstruksi baja permasalahan stabilitas adalah merupakan hal yang

sangat penting, dikarenakan komponen struktur baja rentan terhadap tekuk akibat

pembebanan yang melebihi kapasitasnya sehingga terjadi ketidakstabilan pada

struktur baja. Terjadinya fenomena tekuk pada struktur baja disebabkan karena

elemen baja pada umumnya sangat tipis, sehingga mudah mengalami tekuk yang

akan mengurangi kapasitas dari struktur itu sendiri.

Pada permasalahan ini penulis mencoba menganalisa profil Iwf yang

mengalami pembebanan gaya aksial. Pada kenyataan struktur baja akan

mengalami tekuk dan terjadi ketidakstabilan akibat pembebanan gaya axial

dengan tiga cara, yaitu tekuk lentur, tekuk torsi, dan tekuk lentur dan tekuk torsi

sekaligus.

Oleh karena itu dibutuhkan penyelidikan stabilitas terhadap profil Iwf

yang mengalami pembebanan gaya aksial pada saat kapan mengalami hanya tekuk

lentur saja, tekuk torsi saja, dan kapan mengalami tekuk lentur dan tekuk torsi

sekaligus.

Dari hasil penyelidikan stabilitas terhasap profil Iwf yang mengalami

pembebanan gaya aksial hingga mencapai batas kritisnya, ternyata profil Iwf akan

(6)

DAFTAR ISI

KATA PENGANTAR ... i

ABSTRAK ... iii

DAFTAR ISI ... iv

DAFTAR NOTASI ... vi

BAB I. PENDAHULUAN ... 1

1.1. Umum dan Latar Belakang………….. ... 1

1.2. Permasalahan ... 3

1.3. Tujuan Penulisan ... 3

1.4. Pembatasan Masalah ... 4

1.5. Metode Pembahasan ... 4

BAB II. TINJAUAN PUSTAKA ... 5

2.1. Teori Tekuk……….. ... 5

2.1.1 Umum dan Latar Belakang...5

2.1.2 Stabilitas dari Struktur Kolom...9

2.1.3 Jenis-jenis Kegagalan Batang Tekan...11

2.2. Analisa Kolom ... 12

2.2.1 Kolom Euler ... 16

2.2.2 Rumus Kolom Euler ... 21

2.2.2.1 Kolom dengan Satu Ujung Terjepit dan Yang Lainnya Bebas ... 21

(7)

2.2.2.3 Kolom dengan Kedua Ujungnya

Terjepit...25

2.2.2.4 Kolom dengan Kedua Ujungnya Terjepit tetapi Salah satu dapat Bergeser Arah Lateral...27

2.2.2.5 Kolom dengan Ujung-ujungnya Terjepit dan Sendi...27

2.3. Panjang Efektif...32

2.4 Tekuk Torsi...34

2.4.1 Energi Regangan akibat Torsi Saint-Venant...37

2.4.2 Energi Regangan akibat Torsi Warping...39

2.4.3 Kombinasi Tekuk Lentur dan Tekuk Torsi...43

BAB III. ANALISA……….55

3.1. Umum………… ... 55

3.2. Kejadian akibat Tekuk Lentur ... 57

3.3. Kejadian akibat Tekuk Torsi...59

3.4 Analisa Panjang Kolom yang akan ditinjau...60

BAB IV. APLIKASI DAN PERENCANAAN ... 62

BAB V. KESIMPULAN DAN SARAN ... 90

5.1. Kesimpulan ... 90

5.2. Saran ... 92

(8)

DAFTAR NOTASI

L = panjang kolom

A = luas tampang

t = tebal tampang

γ = regangan geser

v = tegangan geser

G = modulus geser

E = modulus elastic

μ = poison rasio

J = konstanta torsi

Cw = konstanta warping

Ix, Iy = momen Inersia terhadap sumbu x dan sumbu y

Iy’Ix’ = momen inersia terhadap sumbu minimum dan maksimum

Ip = Ix + Iy = momen inersia polar

U, V = deformasi aksial pada arah x dan y

u = energi regangan total

u1 = energi regangan lentur

ua = energi regangan lentur akibat gaya tekan aksial

ub = energi regangan lentur akibat kurva lentur

ut = energi regangan torsi

v = energy potensial

va = energi potensial akibat gaya tekan aksial

(9)

λ = parameter kelangsingan

= rasio kelangsingan

r = jari – jari inersia

Ms = momen torsi murni

Mw = momen torsi terpilin

Mz = momen torsi total

Mf = momen lentur lateral pada satu sayap

If = momen inersia untuk satu sayap terhadap sumbu y

Vf = gaya geser sayap

uf = lendutan lateral salah satu sayap pada penampang sejarak z dari ujung

batang

Ѳ = sudut puntir per satuan panjang

R0 = jari – jari girasi polar terhadap pusat geser

Px,Py = beban kritis pada sumbu x dan y yang mengakibatkan kolom

mengalami tekuk lentur

Px’, Py’ = beban kritis pada sumbu maksimum dan minimum yang mengakibatkan

kolom mengalami tekuk lentur

PѲ = beban kritis yangmengakibatkan kolom mengalami tekuk torsi

Pkomb = beban kritis yang mengakibatkan kolom mengalami tekuk lentur dan

(10)

ABSTRAK

Pada konstruksi baja permasalahan stabilitas adalah merupakan hal yang

sangat penting, dikarenakan komponen struktur baja rentan terhadap tekuk akibat

pembebanan yang melebihi kapasitasnya sehingga terjadi ketidakstabilan pada

struktur baja. Terjadinya fenomena tekuk pada struktur baja disebabkan karena

elemen baja pada umumnya sangat tipis, sehingga mudah mengalami tekuk yang

akan mengurangi kapasitas dari struktur itu sendiri.

Pada permasalahan ini penulis mencoba menganalisa profil Iwf yang

mengalami pembebanan gaya aksial. Pada kenyataan struktur baja akan

mengalami tekuk dan terjadi ketidakstabilan akibat pembebanan gaya axial

dengan tiga cara, yaitu tekuk lentur, tekuk torsi, dan tekuk lentur dan tekuk torsi

sekaligus.

Oleh karena itu dibutuhkan penyelidikan stabilitas terhadap profil Iwf

yang mengalami pembebanan gaya aksial pada saat kapan mengalami hanya tekuk

lentur saja, tekuk torsi saja, dan kapan mengalami tekuk lentur dan tekuk torsi

sekaligus.

Dari hasil penyelidikan stabilitas terhasap profil Iwf yang mengalami

pembebanan gaya aksial hingga mencapai batas kritisnya, ternyata profil Iwf akan

(11)

BAB I

PENDAHULUAN

1.1Umum dan Latar Belakang

Baja adalah salah satu bahan kontruksi yang paling penting, sifat-sifatnya

yang terutama dalam penggunaan konstruksi adalah kekuatannya yang tinggi dan

sifat yang keliatannya. Keliatan ( ductility ) adalah kemampuan untuk

berdeformasi secara nyata baik dalam tegangan maupun dalam kompresi sebelum

terjadi kegagalan { Joseph E.Bowles, 1985 }.

Baja berdeformasi secara nyata dapat dilihat pada batang polos maupun

konstruksi portal sederhana. Portal terdiri dari elemen-elemen pelat, kolom, dan

balok kolom dimana sambungan balok dan kolom tidak dapat dikatakan mololit

seperti beton maka digunakan asumsi-asumsi dalam memudahkan didalam

menganalisa. Dalam perencanaan faktor yang harus mendapat perhatian utama

adalah masalah kekuatan atau keamanan, masalah keekonomisan dan masalah

estetika dari struktur yang direncanakan.

Suatu struktur dikatakan kuat atau aman apabila struktur tersebut mampu

memikul segala gaya, tegangan dan juga lendutan yang mungkin timbul akibat

dari pembebana yang bersifat sementara. Oleh karena itu seorang perencana harus

memperhatikan hal-hal tersebut diatas dengan sebaik-baiknya dalam

(12)

Dalam tugas akhir ini yang ditinjau adalah kolom baja. Apabila sebuah

batang lurus dibebani gaya tekan aksial dengan pemberian beban semakin lama

semakin tinggi, maka pada batang tersebut akan mengalami perubahan. Perubahan

dari keadaan sumbu batang lurus menjadi sumbu batang melengkung dinamakan

Tekuk.

Buckling (tekuk) terjadi akibat penekanan pada suatu batang dimana yang

mengalami gaya tekan aksial. Dalam hal ini, tekuk dapat terjadi sebelum atau

sesudah tegangan idiil dicapai terlebih dahulu, tentu tidak menjadi masalah dalam

perhitungan kekuatan baja. Namun apabila tekuk terjadi sebelum tegangan idiil

dicapai, tentu akan sangat berbahaya karena peristiwa tekuk terjadi secara

tiba-tiba tanpa memberi tanda-tanda misalnya terjadinya deformasi secara

perlahan-lahan yang semakin lama semakin besar.

(13)

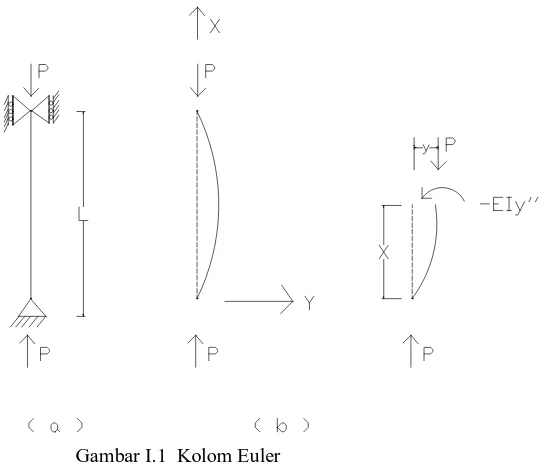
Bahwa batang yang ditekan akan mengalami bentuk yang sedikit

melengkung seperti pada gambar diatas. Jika sumbu koordinat diambil seperti

dalam gambar, momen dalam yang terjadi pada penampang sejauh x dari sumbu

asal adalah :

Mx = -EIy”

Dengan menyamakan momen lentur luar P.y, maka diperoleh persamaan :

EIy” + P.y = 0

1.2Permasalahan

Seperti yang kita ketahui bersama, gaya aksial secara individu dapat

menyebabkan peristiwa tekuk, dimana tekuk yang terjadi dapat berupa tekuk

lentur, tekuk torsi dan penggabungan antara tekuk lentur dan tekuk torsi. Ketiga

tekuk ini dapat menyebabkan ketidakstabilan kolom yang ditinjau.

1.3Tujuan Penelitian

Adapun maksud dan tujuan penulisan tugas akhir ini adalah untuk

menentukan berapa nilai Pkritis yang dapat diterima oleh kolom baja yang

bertampang Iwf sehingga pendimensian dapat seefisien mungkin dan untuk

mendapatkan suatu persamaan yang mengandung variable gaya normal ( P ),

(14)

1.4Pembahasan Masalah

Dalam analisa ini banyak permasalahan yang akan ditinjau maka untuk

memudahkan analisa pada penulisan ini diadakan pembatasan-pembatasan dan

penyederhanaan sebagai berikut :

1. Aplikasi terhadap profil IWF

2. Struktur adalah dengan tumpuan sendi-sendi

3. Bahan baja bersifat elastis linier sesuai dengan hukum Hooke

4. Akibat berat sendiri diabaikan

5. Perputaran tampang yang terjadi sangat kecil

6. Tekuk yang terjadi adalah tekuk elastic

1.5Metode Penelitian

Adapun metode yang akan digunakan dalam penulisan tugas akhir ini

adalah menggunakan aplikasi rumus-rumus yang sudah ada dan juga metode

(15)

BAB II

TINJAUAN PUSTAKA

II.1 Teori Tekuk

II.1.1 Umum dan Latar Belakang

Kolom merupakan batang tekan tegak yang bekerja untuk menahan

balok-balok loteng, rangka atap, lintasan crane dalam bangunan pabrik dan sebagainya

yang untuk seterusnya akan melimpahkan semua beban tersebut ke pondasi.

Dengan berbagai macam sebutan, seperti kolom, tiang, tonggak, dan

batang desak, batang ini pada hakekatnya jarang sekali mengalami tekanan aksial

saja.Apabila sebuah batang lurus dibebani gaya tekan aksial dengan pemberian

beban semakin lama semakin tinggi, maka pada batang tersebut akan mengalami

perubahan. Perubahan dari keadaan sumbu batang lurus menjadi sumbu batang

melengkung dinamakan Tekuk.

Pada hakekatnya batang yang hanya memikul tekan aksial saja jarang

dijumpai dalam struktur namun bila pembebanan diatur sedemikian rupa hingga

pengekangan ( restrain ) rotasi ujung dapat diabaikan atau beban dari

batang-batang yang bertemu diujung kolom bersifat simetris dan pengaruh lentur sangat

kecil dibandingkan dengan tekanan langsung maka batang tekan dapat

direncanakan dengan aman sebagai kolom yang dibebani secara konsentris.

Dari mekanika bahan diketahui bahwa hanya kolom yang sangat pendek

dapat dibebani hingga mencapi tegangan lelehnya, sedangkan keadaan yang

(16)

bahan batang sepenuhnya tercapai. Keadaan demikian yang kita sebut dengan

tekuk ( buckling ). Jadi pengetahuan tentang kestabilan batang tekan perlu bagi

pembaca yang merencanakan struktur baja.

Gambar II.1.1 Batang yang tertekuk akibat gaya aksial ( sumber : Salmon, 1992 )

Latar belakang tekuk kolom pertama kali dikemukakan oleh Leondharrt

Euler pada tahun 1759. Batang dengan beban konsentris yang semula lurus dan

semua seratnya tetap elastis hingga tekuk terjadi akan mengalami lengkungan

yang kecil pada gambar II.1.1. Walaupun Euler hanya menyelidiki batang yang

dijepit disalah satu ujung dan bertumpu sederhana ( simply supported ) di ujung

yang lainnya, logika yang sama dapat diterapkan pada kolom yang berperletakan

sendi, yang tidak memiliki pengekangan rotasi dan merupakan batang dengan

kekuatan tekuk terkecil. Kita akan mendapatkan rumus-rumus gaya kritis yang

dapat diterima oleh suatu batang sebelum tekuk terjadi.

Pendekatan Euler pada umumnya tidak digunakan untuk perencanaan

karena tidak sesuai dengan percobaan, dalam praktek kolom dengan panjang

umum tidak sekuat seperti yang dinyatakan oleh rumus-rumus Euler.

Considere dan Esengger pada tahun 1889 secara terpisah menemukan

bahwa sebagian dari kolom dengan panjang yang umum menjadi inelastic

sebelum tekuk terjadi dan harga E yang dipakai harus memperhitungkan adanya

(17)

mereka menyadari bahwa sesungguhnya kolom dengan panjang yang umum akan

hancur akibat tekuk inelastic dan bukan akibat tekuk elastic.

Akan tetapi pengertian yang menyeluruh tentang kolom dengan beban

konsentris baru dicapai pada tahun 1946 ketika Shanley menjabarkan teori yang

sekarang ternyata benar. Ia mengemukakan bahwa hakekatnya kolom masih

mampu memikul beban aksial yang lebih besar walaupun telah melentur, tetapi

kolom mulai melentur pada saat mencapai beban yang disebut beban tekuk, yang

menyertakan pengaruh inelastisitas pada sejumlah atau semua serat penampang

lintang.

Untuk menentukan kekuatan kolom dasar, kondisi kolom perlu didealisir

dengan beberapa anggapan. Mengenai bahan, kita dapat menganggap :

1. sifat tegangan-regangan tekan sama diseluruh titik pada penampang

2. tidak ada tegangan internal seperti akibat pendinginan setelah

penggilingan (rolling)

3. kolom lurus sempurna dan prismatis

4. resultante beban bekerja melalui sumbu pusat batang sampai batang mulai

melentur

5. kondisi ujung harus statis tertentu sehingga panjang antara sendi-sendi

ekivalen dapat ditentukan.

6. teori lendutan yang kecil seperti pada lenturan yang umum berlaku dan

gaya geser dapat diabaikan.

7. puntiran atau distorsi pada penampang lintang tidak terjadi selama

(18)

Setelah anggapan-anggapan diatas dibuat, sekarang disetujui bahwa kekuatan

suatu kolom dapat dinyatakan sebagai:

Dimana : tegangan rata-rata pada penampang

E t = modulus tangent pada P/A

KL/r = angka kelangsingan effektif (ujung sendi ekivalen)

Tekuk murni akibat beban aksial sesungguhnya hanya terjadi apabila

anggapan dari(1) sampai (7) diatas berlaku.Kolom biasanya merupakan satu

kesatuan dengan struktur,dan pada hakekatnya tidak dapat berlaku secara

independent. Kolom dapat dibedakan menjadi dua kelompok :

a. Kolom panjang, biasanya akan rusak akibat tekukan yang terjadi atau

kelebihan lentur melintang.

b. Kolom sedang, biasanya akan rusak akibat gabungan terjadinya

kehancuran material dan tekukan.

Tekuk dapat dibedakan atas tekuk elastis dan tekuk inelastis ( inelastic

Buckling ). Kolom dengan panjang yang umum akan hancur akibat tekuk

inelastic dan bukan akibat tekuk elastis. Pada kolom yang mengalami tekuk

inelastis, modulus elastisnya pada saat terjadi tekuk lebih kecil dari harga

awalnya. Dalam praktek, tekuk diartikan sebagai perbatasan antara lendutan stabil

dan tak stabil pada batang tekan jadi bukan kondisi sesaat yang terjadi pada

batang langsing elastic yang diisolir. Sering dikatakan bahwa beban tekuk praktis

(19)

II.1.2 Stabilitas dari Struktur Kolom

Analisa stabilitas suatu struktur batang berkaitan erat dengan masalah

kesetimbangan. Oleh karena itu pemahaman terhadap masalah kesetimbangan

merupakan suatu hal yang penting.

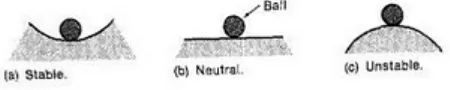
Konsep dari stabilitas sering diterangkan dengan menganggap

kesetimbangan dari bola pejal dalam beberapa posisi seperti gambar 2.1.3.

Gambar II.1.2a Stabilitas

Sumber : Alexander Chajes, “ Principles of Stability Theory ”

Walaupun bola dalam keadaan setimbang pada posisinya masing-masing,

dalam pengamatan memperlihatkan adanya perbedaan dari ketiga keadaan

tersebut.

- Posisi a

Bola berada pada permukaan yang cekung maka bila diberikan gangguan kecil dx,

bola akan kembali keposisi semula setelah berisolasi beberapa kali.

Keadaan kesetimbangan ini disebut dengan kesetimbangan stabil.

- Posisi b

Apabila bola berada pada permukaan yang datar, bila diberikan gangguan kecil dx

maka gangguan kecil ini tidak akan merubah gaya-gaya kesetimbangan maupun

energy potensial bola. Keadaan kesetimbangan ini disebut dengan kesetimbangan

(20)

- Posisi c

Bila bola berada pada permukaan yang cembung, diberikan gangguan kecil dx

maka akan terjadi pergeseran mendadak ( progressive movement ). Kese

timbangan ini disebut dengan kesetimbangan tidak stabil.

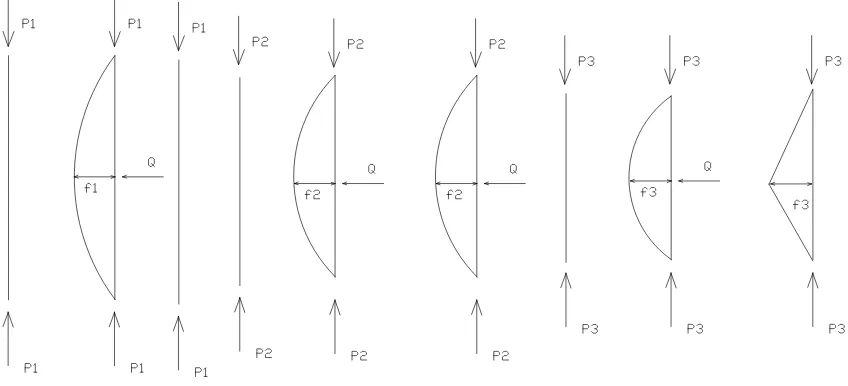
Gambar II.1.2b Tekuk

- Batang a, diberi muatan kecil, dari samping dimuati Q yang menekan batang maka akan terjaid lenturan . Bila gaya Q dihilangkan,

lenturan hilang dan batang lurus kembali. Peristiwa ini disebut dengan

bola dalam tempat yang cekung.

- Batang b, ditekan dengan , dimana > . Dari samping ditekan Q maka terjadi lenturan , Q dihilangkan tetapi masih tetap ada. Keadaan

ini disebut “indifferent”. Gaya disebut gaya , sedangkan tegangan

(ss ) yang timbul dalam luas tampang disebut tegangan kritis (

(21)

- Batang c, ditekan dengan , dimana > tetapi masih dalam batas batang belum patah. Dari samping ditekan Q bahkan lebih kecil dari pada

Q pada keadaan a. lengkung yang timbul akan menjalar terus sampai

batang itu patah. Peristiwa ini disebut “Labil”

II.1.3 Jenis-jenis Kegagalan Batang Tekan

Dari mekanika bahan telah diketahui bahwa batang tekan yang pendek

dapat dibebani sampai batang meleleh sedang batang tekan yang panjang akan

runtuh akibat tekuk. Pada keadaan yang umum keruntuhan akibat tekan terjadi

antara keruntuhan akibat kelelehan bahan dan akibat tekuk elastis, setelah bagian

penampang lintang meleleh, keadaan ini disebut tekuk inelastis ( inelastic

buckling ).

Ada tiga macam keruntuhan batang yaitu :

1. Keruntuhan akibat tegangan yang terjadi pada penampang yang telah

melampaui kekuatan materialnya.

2. Keruntuhan akibat batang tertekuk elastis ( elastic buckling ), ini terjadi

pada bagian konstruksi yang langsing. Disini Hukum Hooke masih berlaku

bagi serat penampang dan tegangan yang terjadi tidak melebihi batas

proporsional.

3. Keruntuhan akibat melelehnya sebagian serat yang disebut tekuk tak

(22)

dimana pada saat menekuk sejumlah serat menjadi inelastis maka modulus

elastis ketika tertekuk lebih kecil dari harga awalnya.

II.2 Analisa Kolom

Gambar II.2a Batang lurus yang dibebani gaya aksial

Sebuah batang lurus dengan panjang L yang dibebani oleh gay aksial P

seperti yang diperhatikan pada gambar II.2a uraian gaya-gaya yang bekerja pada

potongan sejauh x dari tumpuan, diperlihatkan pada gambar II.2b dimana N dan Q

adalah komponen gaya longitudinal dan transversal pada potongan itu, dan M

adalah momen lentur.

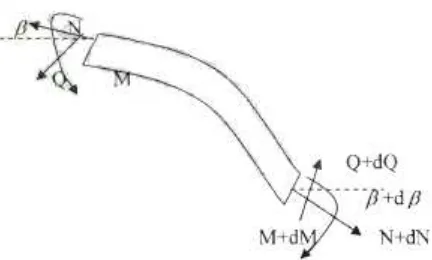
Gambar II.2b Potongan batang sejauh x dari tumpuan

Pengaruh dari adanya rotasi struktur, persamaan kesetimbangan dari

(23)

Gambar II.2c Kolom Terdeformasi

Untuk deformasi yang kecil, maka dapat diasumsikan bahwa sudut putar β

adalahkecil. Dengan demikian sin β dan cos β secara berurutan dapat dianggap β

dan l.

Persamaan kesetimbangan gaya dapat diperoleh dengan menguraikan

masing-masing gaya yang bekerja sesuai dengan subu x dan y. Dari uraian gaya

pafa sumbu x diperoleh :

-N + ( N + dN ) – Q β + ( Q + dQ ) ( β + dβ ) = 0

+ Q + β = 0

Dimana :

= dN/dx

= dQ/dx

= dβ /dx

dari uraian gaya pada sumbu y diperoleh :

-Q + ( Q+dQ ) – Nβ – ( N + dN )( β + dβ ) = 0

-N + β + = 0

Uraian Momen :

M – ( M + dM ) + Qdx = 0

Q =

(24)

M = dM/dx

Untuk batang yang ramping dapat dianggap bahwa tegangan dan gaya

geser melintang sangat kecil. Kita biasanya mengambil asumsi bahwa bentuk

kuadratik yang menggambarkan interaksi nonlinear antara gaya geser yang kecil

dan putaran dapat diabaikan. Dari asumsi yang diambil maka tiga persamaan

kesetimbangan disederhanakan menjadi bentuk berikut :

= 0 ( II.2a )

- β = 0 ( II.2b )

Q = 0 ( II.2c )

Bentuk dari β tidak terdapat ada persamaan II.2b karena telah hilang

akibat persamaan II.2a dengan mengeliminasi Q dari persamaan II.2c sehingga

menghasilkan.

= 0

= - ( II.2d )

Dimana I adalah momen Inersia dari penampang dan E adalah modulus

elastis bahan. Persamaan II.2d kita subtitusikan kedalam persamaan II.2c

diperoleh :

= 0

– N = 0

Untuk harga EI yang konstan, persamaan menjadi :

= 0

– N = 0

Persamaan II.2b merupakan bentuk kuadrik dalam variabel-variabel N dan

(25)

II.2a terlibat bahwa N konstan sepanjang X dan dari kondisi batas x=0 dan x=1,

kita lihat bahwa N = -P. Dengan demikian persamaann II.2b dapat disederhanakan

menjadi bentuk lazim dikenal :

– P = 0 ( II.2e )

Atau

EI + P = 0 ( II.2f )

Persamaan diatas adalah differensial dari kolom ramping yang mengalami

tekukan. Dari persamaan dapat ditentukan besarnya pada saat struktur akan

runtuh. Misalnya = dan subtitusikan kedalam persamaan sehingga

diperoleh :

+ K = 0 ( II.2g )

Persamaan umum dari persamaan differensial adalah :

Y = A sin kx + B cos kx + Cx + D ( II.2h )

Dimana : A, B, C, D adalah tetapan tertentu yang dapat ditentukan dengan

menggunakan syarat-syarat batas yaitu kondisi batas ujung-ujung batang (

boundary condition ).

II.2.1 Kolom Euler

Rumus kolom Euler diturunkan dengan membuat berbagai anggaan sebagai

berikut :

- Bahan elastic sehingga memenuhi Hukum Hooke

- Material homogen sempurna dan isotropis

(26)

- Penampang batang tidak terpuntir, elemennya tidak dipengaruhi tekuk setempat dan distorsi lainnya selama melentur

- Batang bebas dari tegangan residu

- Ujung-ujung batang ditumpu sederhana. Ujung bawah ditumpu pada sendi yang tidak dapat berpindah, ujung atas ditumpu pada tumpuan yang dapat

berotasu dengan bebas dan bergerak vertical tetapi tidak dapat bergerak

horizontal.

- Deformasi dari batang cukup kecil sehingga bentuk ( y’ )² dari persamaan kurva dapat diabaikan. Dari sini kurva dapat didekati

dengan y”.

Gambar II.2.1a Kolom Euler

Bahwa batang yang ditekan akan mengalami bentuk yang sedikit

melengkung seperti pada gambar II.2.1a. Jika sumbu koordinat diambil seperti

dalam gambar, momen dalam yang terjadi pada penampang sejauh x dari sumbu

asal adalah :

Mx = -EIy” ( II.2.1.a)

Dengan menyamakan momen lentur luar P.y, maka diperoleh persamaan :

(27)

Persamaan ( II.2.1.a) adalah persamaan differential linear dengan koefisien

konstan dan dapat dirubah menjadi :

y” + k².y = 0 (II.2.1.b)

dimana, k² = (II.2.1.c)

Penyelesaian umum persamaan (II.2.1.b)

y = A sin kx + B cos kx (II.2.1.d)

Untuk menentukan besaran konstanta A dan B, maka menggunakan syarat

batas :

y = 0 dan x = 0

y = 0 dan x = 1

Dengan memasukkan syarat batas pertama kedalam persamaan (II.2.1.d)

maka diperoleh :

B = 0

Sehingga diperoleh :

y = A sin kx (II.2.1.e)

Dari syarat batas kedua diperoleh :

A sin kl = 0 (II.2.1.f)

Persamaan (II.2.1.f) dapat dipenuhi oleh tiga keadaan yaitu :

a. Konstanta A = 0, yaitu tidak ada lendutan (II.2.1.g1)

b. kl = 0, yaitu tidak ada beban luar (II.2.1.g2)

(28)

Subtitusi persamaan (II.2.1.g3) kedalam persamaan (II.2.1.c) dan

persamaan (II.2.1.e) diperoleh :

(II.2.1.h)

(II.2.1.i)

Pada beban yang diberikan oleh persamaan (II.2.1.h) kolom berada dalam

keadaan kesetimbangan dalam bentuk yang agak bengkok, dimana bentuk

deformasinya diberikan oleh persamaan (II.2.1.i).

Ragam (mode) tekuk dasar yaitu lendutan dengan lengkungan tunggal

akan diperoleh jika nilai n diambil sama dengan 1, dengan demikian beban kritis

Euler untuk kolom adalah :

= (II.2.1.j)

Dan persamaan lendutan menjadi :

Y = A sin (II.2.1.k)

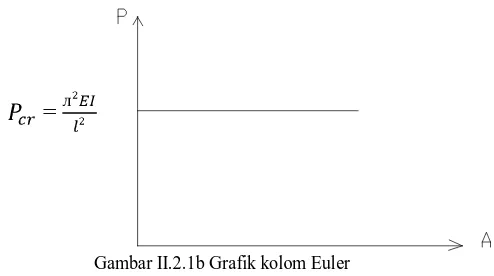
Kelakuan kolom Euler dapat digambarkan secara grafik seperti pada

gambar:

=

Gambar II.2.1b Grafik kolom Euler

Dari grafik dapat dilihat bahwa sampai beban Euler dicapai, kolom harus

(29)

a b c d

d

Gambar II.2.2.1

tetap lurus atau dapat dianggap berubah bentuk dengan amplitude tidak tentu.

Kelakuan ini menunjukkan bahwa keadaan kesetimbangan pada saat beban Euler

merupakan transisi dari kesetimbangan stabil dan tidak stabil.

II.2.2 Rumus Kolom Euler

II.2.2.1 Kolom dengan Satu Ujung Terjepit dan yang lainnya Bebas

Tinjau suatu sumbu-sumbu koordinat seperti ditunjukkan pada gambar,

dimana kolom dalam kedudukan yang agak melengkung, menghasilkan momen

lentur pada suatu penampang melintang sebesar :

M = - P ( δ – y ) ( II.2.2.1a)

Dan persamaan differensial M=-EI menjadi :

EI = P (δ – y ) ( II.2.2.1b)

Karena ujung atas kolom adalah bebas, maka jelaslah bahwa tekuk pada

kolom akan terjadi pada bidang dengan kekakuan lengkungan terkecil, yang

dianggap merupakan bidang simetris.

Nilai EI yang terkecil ini digunakan dalam persamaan ( II.2.2.1b ) diatas

(30)

k² =

Kita dapat menuliskan persamaan dalam bentuk :

+ k²y = k² δ

Penyelesaian umum dari persamaan ini adalah :

Y = A cos kx + B sin kx + δ

Dimana A dan B adalah konstanta integrasi, yang ditentukan dari

syarat-syarat ujung jepit kolom yaitu :

Y = = 0 pada x = 0

Syarat-syarat ini dipenuhi jika :

A = - δ B = 0

Dan persamaan b menjadi :

Y = δ ( 1 – cos kx ) ( II.2.2.1c)

Sedang syaraat pada ujung bebas kolom menghendaki bahwa

Y = δ pada x = 1

Yang memenuhi jika

δ cos kl = 0

Persamaan c menghendaki bahwa salah satu δ dan cos kl harus nol. Bila δ

= 0, maka lengkungan tidak ada. Bila cos kl = 0, kita akan memperoleh hubungan

Kl = ( 2n – 1 ) /2 ( II.2.2.1d)

Dimana n = 1, 2, 3,…… persamaan ini untuk menentukan nilai-nilai k

sehubungan dengan bentuk tekukan yang terjadi.

Nilai kl terkecil yang memenuhi persamaan ( II.2.2.1d) diperoleh dengan

(31)

Kl = l =

Atau = ( II.2.2.1e)

Besaran kx dalam persamaan ( II.2.2.1c) untuk kasus ini berubah-ubah

dari 0 s/d /2, dan bentuk lengkungan seperti ditunjukkan pada gambar diatas.

Dengan mensubtitusikan n = 2, 3, . . . . kedalam persamaan ( II.2.2.1d),

kita peroleh hubungannya dengan nilai-nilai beban kritis sebagai berikut :

= =

Besaran kx menurut persamaan (II.2.2.1c) dalam hal ini berubah dari 0 s/d

3 /2, dari 0 s/d 5 /2, . . . , dan hubungannya dengan kurva lengkungan pada

gambar (II.2.2.1c) dan gambar (II.2.2.1d). Untuk bentuk kurva lengkungan pada

gambar (II.2.2.1c) diperlukan suatu gaya sebesar sembilan kali beban kritis

terkecil, dan keadaan pada gambar (II.2.2.1d), diperlukan gaya sebesar dua puluh

lima kali beban kritis terkecil.

Bentuk-bentuk tekukan seperti itu hanya dapat terjadi pada batang yang

sangat ramping, dan dengan memasang penyokong pada titik peralihan untuk

mencegah lengkungan lateral. Sebaliknya bentuk tekukan ini adalah tidak stabil,

dan mempunyai arti praktis yang kecil, sebab struktur telah mengalami suatu

lengkungan yang besar pada saat beban mendekati nilai-nilai yang diberikan oleh

(32)

[image:32.595.261.347.106.347.2]

d

Gambar II.2.2.2

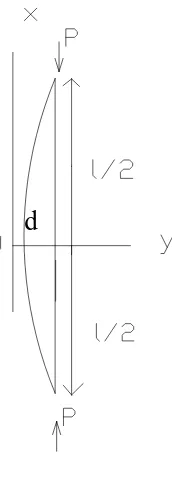
II.2.2.2 Kolom dengan Kedua Ujungnya berupa Sendi

Pada suatu kasus kolom dengan kedua ujungnya berupa sendi (gambar

II.2.2.2), tampak dari kesimetrisannya bahwa tiap setengah panjang batang adalah

mirip dengan batang pada gambar II.2.2.2. Karena itu beban kritis pada kasus ini

diperoleh dengan mensubtitusikan l/2 untuk besaran l dalam persamaan, yang

memberikan

= = = ( II.2.2.2a)

Kasus suatu batang dengan kedua ujung berupa sendi, mungkin dianggap

lebih sering dalam prakteknya dari yang lain. Kasus ini disebut “kasus dasar” (

(33)

[image:33.595.237.324.143.345.2]

Gambar II.2.2.3

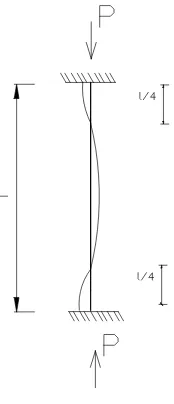
II.2.2.3 Kolom dengan Kedua Ujungnya Terjepit

Bila kedua ujung kolom berupa jepitan ( gambar II.2.2.3), maka ada

momen-momen reaksi yang mencegah ujung-ujung kolom dari perputaran selama

tekukan terjadi. Momen-momen ujung dan gaya-gaya tekan aksial adalah ekivalen

dengan gaya-gaya P yang bekerja eksentris seperti ditunjukkan pada gambar.

Titik-titik peralihan ditempatkan dimana garis kerja gaya P memotong kurva

lengkungan, sebab pada titik-titik ini momen lentur adalah nol.

Titik-titik peralihan dan titik tengah bentang membagi batang atas empat

bagian yang sama, yang masing-masing mirip dengan batang pada gambar . oleh

karena itu beban kritis dalam kasus ini diperoleh dengan mensubtitusikan l/4

untuk besaran l, yaitu:

( II.2.2.3a)

(34)

( a ) ( b ) dimana,

Penyelesaian dari persamaan ini adalah :

( II.2.2.3c)

Dari syarat batas :

y = 0 pada x = 0

y = 0 pada x = 0 didapat ;

, dan

Sehingga :

( II.2.2.3d)

( II.2.2.3e)

Maka didapat :

= ( II.2.2.3f)

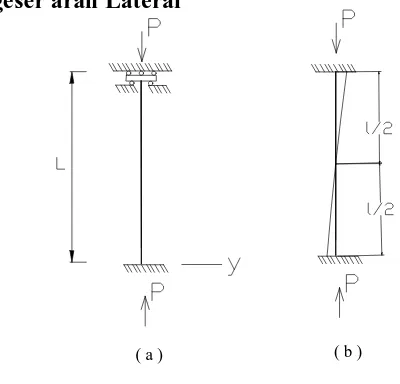
[image:34.595.177.377.575.767.2]

(35)

[image:35.595.235.359.320.488.2]

Gambar II.2.2.5

Pada gambar II.2.2.4a tampak bahwa kolom bebas gerak arah lateral pada

ujung atas tetapi dikendalikan sedemikian rupa, sehingga garis singgung pada

kurva elastic tetap tegak. Dengan adanya titik peralihan pada pertengahan bentang

(gambar II.2.2.4b), beban kritis didapatkan dengan mensubtitusikan l/2 untuk l

dalam persamaan ( II.2.2.1e), dan dengan demikian dalam kasus ini juga berlaku

rumus (II.2.2.2a).

II.2.2.5 Kolom dengan ujung-ujung Terjepit dan Sendi

Kita tinjau suatu penampang mn sejauh x dari sendi, dan dengan

lengkungan sebesar y ( gambar ), memberikan momen lentur sebesar :

Mx = P.y + H0.x ( II.2.2.5a)

Dengan demikian persamaan menjadi :

EI = -P.y – H0.x ( II.2.2.5b)

Dan dengan bantuan notasi k² = P/EI, persamaan b dapat dituliskan dalam

bentuk :

(36)

º

Penyelesaian umum dari persamaan ini adalah :

Y = A cos kx + B sin kx - x ( II.2.2.5d)

Dimana A dan B adalah konstanta integrasi, yang ditentukan dari

syarat-syarat ujung kolom yaitu :

Y = 0 pada x = 0 dan x = l

dy/dx = 0 pada x = l

Dari syarat ujung y = 0 pada x = 0 diperoleh A = 0. Untuk y = 0 pada x = l

memerlukan :

B = ( II.2.2.5e)

Sedang untuk dy/dx = 0 pada x = l memberikan :

Tg kl =kl ( II.2.2.5f)

Untuk memecahkan persamaan dipakai metoda grafis. Kurva-kurva pada

\gambar menyatakan tg kl sebagai fungsi kl. Kurva-kurva ini menyinggung garis

tegak kl = /2, 3 /2,. . . . pada titik jauh tak terhingga ( secara asimtotis ).

[image:36.595.232.508.521.672.2]

_{/2 3 /2 2} 5 _/2

(37)

Akar-akar persamaan ditunjukkan oleh titik perpotongan kurva dengan

garis lurus y = kl. Akar terkecil adalah absis dari koordinat titik A yaitu sebesar :

Kl = 4,493 radian

Yang memberikan nilai beban kritis sebesar

= = ( II.2.2.5g)

Dalam setiap kasus yang telah diterangkan diatas, dianggap bahwa kolom

bebas tertekuk dalam suatu arah, maka jelaslah bahwa besaran EI menyatakan

kekakuan lengkung terkecil. Jika kolom dikekang sedemikian rupa, sehingga

tekukan hanya mungkin dalam satu bidang utama saja, maka EI menyatakan

kekakuan lengkung dalam bidang itu.

Dalam pembicaraan sebelumnya juga dianggap bahwa batang sangat

langsing, sehingga tegangan tekan terbesar yang terjadi selama tekukan masih

dibawah batas proporsional bahan. Hanya dibawah persyaratan-persyaratan inilah

rumus-rumus beban kritis diatas dapat berlaku. Untuk menentukan batas

pemakaian rumus-rumus (Gambar III.5) ini, mari kita tinjau kasus dasar seperti

yang telah disebutkan sebelumnya. Dengan membagi beban kritis dari pers.

Dengan luas penampang melintang A, dan mengambil

r = ( II.2.2.5h)

Dimana r menyatakan jari-jari putaran, besar tegangan tekan kritis adalah

= ( II.2.2.5i)

Tegangan ini hanya tergantung pada besaran E dan rasio kelangsingan l/r.

Sebagai contoh, pada suatu struktur baja, batas proporsional 2100kg/cm² dan E =

(38)

[image:38.595.119.388.498.702.2]

Gambar II.2.2.7

100. Karenanya, beban kritis pada kolom dari bahan ini, yang bersendi pada

kedua ujungnya, dapat dihitung dengan pers. ,bila diinginkan rasio l/r lebih besar

dari 100. Jika l/r lebih kecil dari 100, tegangan tekan sudah mencapai batas

proporsional sebelum terjadi tekukan, sehungga pers ( II.2.2.5) tidak berlaku.

Pers. ( II.2.2.5a) dapat dinyatakan secara grafis oleh kurva ACB pada

gambar (II.2.7), dimana tegangan kritis digambarkan sebagai fungsi l/r. kurva

mendekati sumbu mendatar secara asimtot, dan tegangan kritis mendekati nol

dengan bertambahnya rasio kelangsingan. Kurva juga mendekati sumbu tegak

secara asimtor tetapi yang berlaku hanya sepanjang tegangan yang masih

dibawah batas proportiona bahan. Kurva pada gbr digambarkan untuk struktur

baja seperti yang disebut diatas, dan titik C berhubungan dengan batas proportiona

sebesar 2100kg/cm². jadi hanya bagian BC dari kurva yang memenuhi.

Sekarang bandingkan kasus-kasus lain yang dinyatakan pada gambar

II.2.2.1a, II.2.2.3, II.2.2.5 , analog didapat rumus tegangan-tegangan kritis sebagai

(39)

Tampak bahwa ketiga persamaan analog dengan pers.( II.2.2.5i), dimana

panjang l sebenarnya digantikan dengan panjang reduksi L. Dengan demikian

dapat dituliskan secara umum rumus tegangan sebagai berikut :

( II.2.2.5i)

Dimana besaran L = 2l, l/2, atau 0,6991.

II.3 Panjang Efektif

Sejauh ini pembahasan mengenai kekuatan kolom mengasumsikan sendi

dimana tidak ada kekangan rotasional momen. Kekangan momen nol pada ujung

merupakan situasi paling lemah untuk batang tekan yang salah-satu ujungnya

tidak dapat bergerak transversal relative terhadap ujung yang lainya. Untuk kolom

berujung sendi semacam ini, panjang ekivalen ujung sedu kL merupakan panjang

L sebenarnya, dengan demikian k = 1,0 seperti pada Gambar II.3. Panjang L

ekivalen berujung sendi disebut panjang efektif.

Untuk kebanyakan situasi nyata,kekangan momen pada ujung-ujung yang

ditahan seperti pada Gamabr II.3.Dimana panjang efektif tereduksi. Dalam banyak

situasi, sangat sulit, atau bahkan tidak mungkin, untuk menilai secara tepat derajat

kekangan momen yang disumbangkan oleh batang-batang berdekatan yang

mengikat ke kolom, oleh pondasi setempat dan lapisan tanah daibawahnya dan

interaksi penuh semua batang dalam struktur rangka baja.

Baik apakah derajat ujung ditentukan dengan tepat atau tidak,desainer

harus memahami konsep tentang braced frame (goyangan dicegah dengan sabuk

penyokong ) dan unbraced frame ( tanpa sabuk penyokong,goyangan tidak

(40)

Panjang efektif batang kolom pada suatu portal, bergantung pada jenis

portal yang ditinjau, yaitu portal bergoyang dan portal tidak bergoyang. Portal tak

bergoyang (yang disokong) adalah portal yang kestabilan lateralnya diberikan

oleh penyambung yang memadai ke penopang diagonal ke dinding geser, ke

struktur di dekatnya yang memiliki stabilitas lateral yang memadai, atau ke plat

lantai atau penutup atap yang diikat secara horizontal terhadap dinding atau

dengan system penopang yang sejajar dengan bidang portal. Atau dengan kaya

lain portal tak bergoyang didefenisikan sebagai portal yang tekuk bergoyangnya

dicegah oleh elemen penopang yang tidak termasuk rangka struktural itu sendiri.

Faktor K untuk portal bergoyang adalah 0<K<1.

Sedangkan portal tidak bergoyang (yang tidak disokong) adalah portal

yang kestabilan lateralnya bergantung pada kekakuan lentur balok dan kolom

yang disambung secara kaku. Faktor K untuk portal bergoyang adalah K>1.

[image:40.595.125.511.501.789.2]

Untuk kolom ideal dengan perletakan yang berbeda dapat dilihat pada

(41)

Gambar II.3 Tekuk dengan nilai untuk kolom ideaL

II.4 Tekuk Torsi

Dalam merencanakan struktur, tegangan torsi atau sering juga disebut

tegangan puntir, kadang-kadang merupakan tegangan yang sangat berpengaruh

sehingga beberapa persyaratan harus ditetapkan. Profil yang paling efisien untuk

memikul torsi ( puntir ) adalah profil bundar berongga cincin. Torsi adalah puntir

yang terjadi pada batang lurus aabila batang tersebut dibebani momen yang

cenderung menghasilkan rotasi terhadap sumbu longitudinal batang sehingga

tegangan geser yang terjadi pada penampang akibat torsi akan mempengaruhi

perencanaan struktur baja.

Pengaruh puntir umumnya bersifat sekunder, walaupun tidak selalu

merupakan pengaruh minor yang harus ditinjau secara gabungan dengan jenis

pengaruh lainnya. Profil yang baik bagi kolom dan balok, yaitu profil yang

bahannya jauh tersebar dari titik berat penampang, tetapi tidak efisien untuk

menahan torsi. Penampang lingkaran berdinding tipis dan boks lebih kuat untuk

memikul torsi daripada penampang dengan luas sama yang berbentuk kanal, I, T,

siku, atau Z.

Torsi timbul karena adanya gaya-gaya yang membentuk Koppel yang

cenderung memuntir batang terhadap sumbu longitudinalnya. Seperti yang

diketahui dari statika, momen kopel merupakan hasil dari gaya dan jarak tegak

lurus antara garis kerja gaya. Satuan untuk momen pada USCS adalah ( lb-ft ) dan

( lb-in ), sedangkan untuk satuan SI adalah ( Nm ).

Pemberian beban pada bidang yang tidak melalui pusat geser akan

mengakibatkan batang terpuntir jika tidak dicegah oleh pengekang eksternal.

(42)

maka hanya mengalami lentur ditambah dengan geser tanpa adanya torsi. Pusat

geser tidak selalu berimpit dengan titik berat penampang. Pada profil I simetris

pusat geser berada pada titik berat penampangnya.

Tegangan puntir akibat torsi terdiridari tegangan geser dan lentur.

Tegangan harus digabungkan dengan tegangan geser dan lentur yang bukan akibat

torsi. Tegangan puntir dapat dibedakan atas dua jenis yaitu puntir murni atau

istilah umumnya puntir Saint-Venant dan puntir terpilin ( warping torsion ).

Puntir murni terjadi bila penampang lintang yang datar sebelum torsi

bekerja tetap datar dan elemen penampang hanya mengalami rotasi selama

terpuntir. Batang bulat yang memikul torsi adalah satu-satunya keadaan puntir

murni. Puntir terpilin adalah pengaruh keluar bidang yang timbul bila sayap-sayap

berpindah secara lateral selama terpuntir, yang analog dengan lentur akibat beban

luar lateral.

1. Puntir murni ( Torsi Saint- Venant ).

Seperti lengkungan lentur ( perubahan kemiringan per satuan luas panjang

) yang dapat dinyatakan sebagai M/EI = d y/ dx² ( yakni momen dibagi

kekakuan lentur samadengan lengkungan lentur ). Pada puntir murni

momen torsi dibagi kekakuan puntir GJ sama dengan lengkungan puntir (

perubahan sudut per satuan panjang ).

Dimana :

= GJ

= Momen puntir murni ( Puntir Saint-Venant )

= Modulus elastis geser = E/ [2(1+µ)], yang merupakan fungsi dari

(43)

= Konstanta puntir

Dari persamaan diatas, tegangan akibat sebanding dengan jarak dari

pusat puntir.

2. Puntir terpilin ( Warping Torsion ).

Jika suatu balok memikul torsi seperti pada gambar maka sayap tekan

balok akan melengkung ke salah satu arah lateral dan sayap tariknya

melengkung ke arah lateral lainnya.

Bila penampang lintang berbentuk sedemikian rupa hingga dapat terpilin (

penampang menjadi tidak datar lagi ) jika tidak dikekang, maka system

yang dikekang akan mengalami tegangan. Keadaan terpuntir menunjukkan

balok yang puntirannya dicegah diujung-ujung tetapi sayap atasnya

melendut kea rah samping( lateral ) sebesar . Lenturan sayap ke

samping ini menimbulkan tegangan normal lentur ( tarik dan tekan ) serta

tegangan geser sepanjang lebar sayap.

Dengan demikian energy regangan akibat torsi juga terdiri dari dua bagian

dan dapat ditulis sebagai :

UT = UTSV + UTW

Dimana indeks TSV dan TW masing-masing menunjukkan kedua bagian

tersebut diatas.

(44)

Ø+dØ Ø

dØ

Gambar II.4.1 Torsi pada batang prismatik

[image:44.595.138.501.140.322.2]

Tinjaulah momen torsi yang bekerja pada tampang bulat tertutup dalam

gambar III.2.1 dibawah ini.

Kita anggap pemilinan keluar bidang tidak terjadi atau dapat diabaikan

pengaruhnya pada sudut puntir . Anggapan ini mendekati kenyataan bila ukuran

penampang lintang sangat kecil dibanding panjang batang dan sudut lekukan

penampang tidak besar. Juga, pada saat terpuntir penampang lintang dianggap

tidak mengalami distorsi. Jadi, laju punter ( punter persatuan panjang ) dapat

dinyatakan sebagai :

(II.4.1a)

Yang dapat dipandang sebagai lengkungan torsi ( laju perubahan sudut

punter). Karena regangan diakibatkan oleh relative antara penampang lintang di z

dan ( z + dz ), maka besarnya perpindahan di suatu titik sebangding dengan

Sudut regangan perpindahan di suatu titik sebanding dengan jarak r dari

pusat punter. Sudut regangan ( regangan geser ) disuatu elemen sejarak r dari

pusat adalah :

(45)

(II.4.1b)

Bila G adalah modulus geser, maka berdasarkan hokum Hooke tegangan

geser v menjadi :

(II.4.1c)

Jadi seperti yang ditunjukkan pada gambar II.1.6b, torsi elementer adalah :

(II.4.1d)

Momen penahan keseimbangan total adalah ;

(II.4.1e)

Serta karena dan G konstan disebatang penampang, maka :

(II.4.1f)

Dengan :

Persamaan ini dianggap sebagai analog dengan tekukan yakni momen

lentur M sama dengan kekakuan EI kali lengkungan .

Disini momen torsi ( ) sama dengan kekakuan punter GJ kali

lengkungan punter ( laju perubahan sudut punter ).

Energy regangan torsi :

dimana

(46)

[image:46.595.186.408.371.447.2] [image:46.595.111.380.548.630.2]

Gambar II.4.2a Torsi terpilin pada profil I

Irisan A-A Ø Puntir dicegah di ujung ini

Puntir dicegah di ujung ini

Puntir sayap atas setelah terpuntir

Gambar II.4.2b Puntiran pada penampang berprofil I

Sehingga energy regangan total ( torsi murni ) untuk sepanjang bentang

yang ditinjau adalah:

(II.4.1f)

Dengan :

II.4.2 Energi Regangan akibat Torsi Warping

Apabila sebuah balok I memikul momen torsi maka sayap tekan balok

akan melengkung kesalah satu arah lateralnya dan sayap tariknya melengkung

kearah lateral lainnya.

(47)

Jadi puntir terpilin ( warping ) terdiri atas dua bagian :

a. Rotasi elemen ( Ø ), yakni akibat punitr murni

b. Translasi yang balok melentur secara lateral, yakni akibat

pemilinan.

Untuk sudut Ø yang kecil maka berlaku :

(II.4.2a)

(II.4.2b)

Untuk satu sayap :

(II.4.2c)

Dimana :

= Momen lentur lateral pada satu sayap

= Momen inersia sayap terhadap sumbu y

Sehingga persamaan (II.4.2c) menjadi :

(48)

Maka : _(II.4.2e)

Dari persamaan (II.4.2b) didapat :

(II.4.2f)

(II.4.2g)

Dimana :

yang disebut dengan konstanta warping.

Jadi momen punter total merupakan jumlah dari bagian rotasi dan

bagian lentur latar . Sehingga momen punter total ( ) :

(II.4.2h)

Untuk selanjutnya persamaan ini analog dengan persamaan lentur, yakni

momen lentur M sama dengan kekakuan EI kali lengkungan . Disini momen

torsi akibat warping sama dengan kekakuan punter ECw kali lengkungan punter

pada sayap.

Dimana persamaan variasi energy lentur adalah :

(II.4.2i)

Subtitusikan persamaan (II.4.2a) ke persamaan (II.4.2i) didapat :

(49)

Subtitusikan dengan konstanta warping menjadi :

(II.4.2k)

Maka persamaan energy regangan warping sepanjang bentang yang

ditinjau adalah :

(II.4.2l)

Dengan demikian energy regangan total pada balok berpenampang I yang

mengalami tekuk torsi diperoleh dengan menjumlahkan persamaan

(II.4.2m)

Dari persamaan regangan akibat lentur dan energy regangan akibat torsi

sehingga didapat persamaan energy regangan total yang merupakan penjumlahan

dari kedua energy regangan tersebut. Karena energy regangan akibat lentur pada

saat terjadinya tekuk lentur dan tekuk torsi sekaligus sehingga dalam hal ini

penampang berpindah sejauh U dan V yang menyebabkan energy regangan lentur

menjadi dua, yaitu terhadap sumbu x dan sumbu y.

(50)

Gambar II.4.3 Defleksi dan Rotasi akibat Tekuk Lentur dan Tekuk Torsi

v

x'

C'

O

y

u

x

o

C

o

y

o

Pada kombinasi yang titik beratnya tidak berimpit dengan titik pusat geser,

maka tekuk yang terjadi dapat berupa kmbinasi tekuk lentur dan tekuk torsi.

Akibat tekuk lentur dan tekuk torsi pusat geser berpindah sejauh U dan V

dan berotasi dengan sudut

Dari syarat batas yang ada maka

U = V = 0 pada saat z = 0 dan l.

pada saat z = 0 dan l.

Persamaan U, V, dan yang memenuhi syarat-syarat batas yang ada :

( II.4.3a )

( II.4.3b )

( II.4.3c )

Dari persamaan energy regangan akibat lentur dan energy regangan akibat

torsi sehingga didapat persamaan energy regangan total yang merupakan

(51)

lentur pada saat terjadinya lentur dan tekuk torsi sekaligus sehingga dalam hal ini

penampang berpindah sejauh U dan V yang menyebabkan energy regangan lentur

menjadi dua, yaitu terhadap sumbu x dan sumbu y.

Energy regangan total ( U ) = Energi Regangan Lentur + Energi Regangan

Torsi.

( II.4.3d )

Persamaan :

Dimasukkan kedalam persamaan energy regangan total sehingga

persamaannya menjadi :

(

II.4.3e )

Dari identitas trigonometri didapat :

(52)

Dari persamaan di atas dicari nilai integral dari :

Persamaan energy regangan total menjadi :

( II.4.3f )

Dalam penyelesaian dengan metode energy didasarkan pada konsep

kesamaan antara energy regangan dengan kerja gaya luar untuk seluruh struktur

yang ditinjau. Oleh karena itu didalam penyelesaian persoalan, dibutuhkan

penyamaan antara energy regangan dengan kerja luar maka perlu diperhatikan

apakah struktur tersebut konservatif atau tidak.

Suatu system dikatakan konservatif apabila system berdeformasi akibat

pembebanan ditiadakan, system akan kembali ke posisi semula. Suatu system

dikatakan non-konservatif bila terdapat kehilangan energy misalnya dalam bentuk

gesekan, deformasi inelastic, dan lain-lain.

Sehingga suatu system yang non-konservatif memiliki energy potensial

system yang didefinisikan sebagai kemampuan gaya-gaya luar untuk melakukan

kerja yang direpresentasikan sebagai pengurangan energy dari system.

Besar energy potensial ( v ) terdiri dari 2 komponen yaitu gaya tekan

(53)

[image:53.595.135.531.249.681.2]

Gambar II.4.3a Akibat Lenturan

L b

S

x y

Gambar II.4.3b Deformasi Lateral selama Lenturan

v + dv u + du

B A

dz _ds

u v

y x

x z

y

( II.4.3g ) Akibat gaya tekan aksial ( ∆a ) :

Karena harganya kecil sehingga dapat diabaikan. Jadi pengaruh energy

potensial ( v ) yang diperhitungkan hanya akibat lenturan saja.

Akibat lenturan (∆b ) :

( II.4.3h )

Dari teori phytagoras :

( II.4.3i )

Dari teori binomial

Dengan anggapan deformasi kecil maka persamaan diatas menjadi :

( II.4.3j )

(54)

Gambar II.4.3c Perpindahan Akhir akibat Defleksi dan Rotasi

P'

P

r

b

a

0

X

Y

x

y

shear

center

Sehingga didapat besar :

( II.4.3l )

Perpindahan u dan v pada koordinat x dan y terjadi dari translasi pada

[image:54.595.204.445.220.412.2]

pusat geser sebesar u dan v perpindahan rotasi Ѳ dari pusat geser seperti pada

gambar dibawah ini :

Dari gambar didapat :

Karena

Sehingga :

(55)

Sehingga persamaan ∆b menjadi :

( II.4.3m )

Dari persamaan energy potensial sebelumnya,

sehingga persamaan energy potensial menjadi :

( II.4.3n )

Dari ekspresi di bawah ini didapat hubungan :

Dari hubungan diatas maka :

(56)

Maka

( II.4.3o )

Jumlah energy regangan ditambah energy potensial menjadi :

( II.4.3p )

Dari ekspressi yang sudah begitu familiar bagi kita:

Persamaan energy total menjadi :

( II.4.3q )

dimana

( II.4.3r )

(57)

Nilai determinan persamaan diatas adalah

Rumus diatas didapat dari Principles of Structural Stability Theory oleh

Alexander Chajes, yang juga digunakan pada buku peraturan baja Indonesia

metode Load and Resistance Factor Design ( LRFD ) dengan mengadopsi

persamaan diatas dengan tegangan kritis.

Jika penampang memiliki dua sumbu simetris dimana pusat geser dan titik

beratnya berhimpitan dan

( II.4.3s)

Sehingga akar persamaan diatas menjadi :

Persamaan diatas menunjukkan bahwa akibat pembebanan akan

menghasilkan tekuk lentur atau tekuk torsi

Seandainya penampang hanya memiliki satu sumbu simetris katakanlah

terhadap sumbu x sehingga

(58)

Didapat

dan

Ekspresi menyatakan tekuk lentur terhadap sumbu y sedangkan

persamaan kedua jika diselesaikan menyatakan kombinasi tekuk lentur dan tekuk

torsi.

Penyelesainnya adalah :

( II.4.3u )

Dimana

Dari penjelasan diatas terlihat pada persamaan

Jika penampang memiliki dua sumbu simetris dimana pusat geser dan titik

beratnya berimpitan maka penampang akan mengalami tekuk lentur atau tekuk

torsi.

Jika penampang memiliki satu sumbu simetris maka penampang akan

mengalami tekuk lentur atau kombinasi tekuk lentur dan tekuk torsi.

Jika penampang tidak memiliki sumbu simetris maka penampang akan

mengalami tekuk dimana pembebanannya persamaan pangkat tiga yang

pemecahannya dapat diselesaikan dengan kerja numeric. Bagaimanapun

penampang yang tidak memiliki sumbu simetris jarang digunakan sehingga bukan

merupakan masalah yang cukup serius.

(59)

Tidak dapat disederhanakan lagi. Persamaan diatas jika diselesaikan

menjadi

(60)

BAB III

ANALISA

III.1 Umum

Suatu kolom yang mengalami pembebanan gaya tekan aksial di titik

beratnya akan mengalami tekuk dengan tiga kejadian yang berbeda yaitu tekuk

lentur, tekuk torsi dan kombinasi tekuk lentur dan tekuk torsi sekaligus sehingga

dibutuhkan suatu analisa untuk memperhatikan kejadian mana yang akan terjadi

terlebih dahulu.

Dalam pembahasan ini penulis hanya akan menganalisa profil iwf ketika

mencapai beban kritisnya profil akan mengalami tekuk lentur atau mengalami

kombinasi ntekuk lentur dan tekuk torsi. Kejadian tersebut dapat diperhatikan

dengan menghitung besarnya beban kritis tekuk lentur ( Pcr ) dan beban kritis

tekuk lentur dan tekuk torsi ( Pkomb ). Jika beban Pcr lebih kecil dari beban

Pkomb maka penampang akan mengalami tekuk lentur.

( III.1a

)

Dimana : I = inertia minimum atau inertia pada sumbu lemahnya

Jika beban Pcr lebih besar dari beban Pkomb maka penampang akan

mengalami lentur dan berotasi dengan sudut yang lebih kecil sebesar ѳ.

( III.1b

(61)

Gambar III.1 Profil IWF

h

b Y X

Dari teori bab II didapat persamaan :

( III.1c )

( III.1d

)

Karena penampang memiliki dua sumbu simetris yaitu pada sumbu x’ dan

sumbu y’.

( III.1e

)

(62)

z z

u v

x _y x y

Py

Py Px

[image:62.595.139.466.137.615.2]

Px

Gambar III.2a Tekuk Lentur pada Kolom

M

int

Gambar III.2b Tekuk Lentur Kolom pada kondisi Ujung Sendi-sendi III.2 Kejadian akibat tekuk lentur

( III.2a

)

Dari hubungan momen dengan kelengkungan didapat :

( III.2b

(63)

( III.2c

)

; dimisalkan

( III.2d

)

Jawaban umum persamaan differensial diatas :

( III.2e

)

Dari syarat batas yang ada, y = 0 pada saat x = 0 dan x = L

Untuk x = 0 ; y = B = 0

Untuk x = L ; y = A sin kl = 0

Karena maka sin kl = 0

( III.2f

)

Untuk n = 1 ;

( III.2g

)

Dimana I = inersia pada sumbu lemahnya.

(64)

( III.3a

)

Dimana: G = modulus geser

E = modulus elastic

Dari teori elastisitas pada bidang yang mengalami geser didapat hubungan

G dan E.

( III.3b

)

= poison rasio, untuk baja = 0,3

E = 2,1 x 106 kg/cm2 Dari besaran diatas

Untuk penyederhanaan

J = konstanta torsi =

Cw = konstanta warping, dari table didapat harga Cw untuk profil IWF.

( III.3c

)

Dalam hal ini panjang ukuran profil yang ditinjau dibatasi sesuai dengan

menggunakan metode Load and Resistance Factor Design ( LRFD ), dimana

(65)

kl/r s

N/mm2

Gambar III.4a Grafik Tegangan-Rasio Kelangsingan

( III.3d

)

Sehingga panjang profil yang akan ditinjau :

( III.3e

)

Dengan catatan pada suatu saat panjang yang akan ditinjau tidak lagi

berada dalam batas elastic, sehingga persamaan pada beban kritis euler tidak

berlaku lagi.

III.4 Analisa Panjang Kolom yang akan ditinjau

Dari sebuah penelitian pada suatu batang yang terbuat dari baja lunak

seperti gambar diatas dapat diambil kesimpulan pada saat tegangan luluhnya

(66)

Gambar III.4b Kurva Modulus Tangen pada Kolom Euler Curve Tangen Modulus Curve Yield Plateu

?c

?p 1.5 2.0

0.5 1.0 0

1.0

0.5

PT/Py

Artinya pada saat rasio kelangsingan maka persamaan Euler tidak

dapat digunakan lagi karena pada saat itu tekuk yang terjadi adalah tekuk

inelastic.

Bila didefinisikan parameter kelangsingan :

( III.4a )

maka kolom berada dalam batas elastic ( III.4b )

(67)

X h = 912mm Y

b = 302mm t1 = 18mm

[image:67.595.128.509.259.570.2]

t2 = 34mm

Gambar IVb pot. a-a

Gambar IVa kolom dengan tumpuan sendi-sendi

BAB IV

APLIKASI DAN PERENCANAAN

Suatu profil IWF dengan ukuran 900 x 300, akan dianalisa besarnya beban

P yang akan terjadi. Panjang profil yang digunakan yaitu panjang profil dalam

batas elastic.

Dari bab III didapat persamaan :

penampang berada dalam batas elastic sehingga untuk kondisi

ujung sendi-sendi didapat , dimana nilai K = 1.

Batas maksimum panjang profil :

(68)

Sehingga didapat batas elastic panjang profil yang akan digunakan yaitu :

Dimana r = jari-jari inersia minimum.

Dari penampang dengan ukuran 900 x 300 pada profil IWF,

maka didapat rmin = 6,56cm

E = 2100000 kg/cm2 = 2400 kg/cm2

Sehingga panjang profil yang digunakan adalah :

Dari persamaan sebelumnya untuk suatu penampang yang memiliki dua

sumbu simetris yang mengalami pembebanan sehingga mencapai beban kritisnya

maka hanya aka nada dua kemungkinan beban kritis yang terjadi.

1.

2.

3.

Panjang profil yang ditinjau yaitu :

L =732cm, L = 800cm, L = 900cm, L = 1000cm, L = 1100cm, L = 1200cm,L =

(69)



Untuk menghitung besarnya tekuk lentur yang terjadi maka inersia yang

digunakan adalah inersia minimum tau menekuk pada sumbu lemahnya. Untuk L =732cm

- dimana

Karena maka

- dimana

Karena maka

-

, dimana : A = 364 cm2, dan

J =

(70)

Dari perhitungan diatas dapat kita lihat hasil perhitungan nya, yaitu :

o



digunakan adalah inersia minimum tau menekuk pada sumbu lemahnya. Untuk L = 800cm

dimana

maka

dimana

(71)

o



dimana

maka

dimana

(72)

o



dimana

maka

dimana

(73)

o



dimana

maka

dimana

(74)

o



digunakan adalah inersia minimum atau menekuk pada sumbu lemahnya. Untuk L =1200cm

dimana

maka

dimana

(75)

o



dimana

maka

dimana

(76)

o



dimana

maka

dimana

(77)

o

Berdasarkan peraturan baja AISC-LRFD 2005 ( lampiran ) didapat nilai KL

dengan batas yang berbeda dengan perhitungan diatas ( SNI 03-1729-2000 ) yaitu

:

Maka nilai Pkr pada peraturan ini dapat dihitung dengan panjang kolom

maksimum adalah 913,96cm.

Panjang profil yang ditinjau yaitu :

L =732cm, L = 800cm, L = 900cm, L = 913cm,



(78)

maka

dimana

maka

o

(79)

Y t2 = 30mm

Sehingga dari persamaan diatas didapat grafik hubungan beban dengan panjang

profil :

Profil IWF 800 x 300

-5.000.000,00 10.000.000,00 15.000.000,00 20.000.000,00 25.000.000,00

732 800 900 1000 1100 1200 1300 1311

P

(

k

g

)

[image:79.595.113.524.282.538.2]

L ( cm )

Grafik VI.a Grafik Beban Kritis dengan Panjang Kolom pada Kondisi Elastis

Px = P'x ( kg )

Py = P'y ( kg )

PѲ ( kg )

L Px = Px' Py = Py' PѲ

( cm ) ( kg ) ( kg ) ( kg )

732 800 900

(80)

X

Y

h = 708mm t2 = 28mm

t1 = 15mm

Data sebagai berikut :

-2.000.000,00 4.000.000,00 6.000.000,00 8.000.000,00 10.000.000,00 12.000.000,00 14.000.000,00 16.000.000,00

748 800 900 1000 1100 1200 1300 1339

P

(

k

g

)

L ( cm )

Px = P'x ( kg )

PѲ ( kg )

Py = P'y ( kg )

L Px = Px' Py = Py' PѲ

( cm ) ( kg ) ( kg ) ( kg )

748 12557857,27 511204,81 1182256,27

800 10978392,77 446908,02 1090933,26

900 8674285,64 353112,51 957712,16

1000 7026171,37 286021,14 862419,89

1100 5806753,20 236381,10 791914,38

1200 4879285,68 198625,79 738289,17

1300 4157497,85 169243,28 696556,14

(81)

b = 302mm X

Y

h = 594mm t2 = 23mm

t1 = 14mm

L Px = Px' Py = Py' PѲ

( cm ) ( kg ) ( kg ) ( kg )

732 8,393,527.46 456,862.89 1,081,597.54

800 7,675,159.55 417,761.85 1,028,135.34

900 6,064,323.59 330,083.44 908,254.10

1000 4,912,102.11 267,367.58 822,503.75

1100 4,059,588.52 220,964.94 759,058.19

1200 3,411,182.02 185,671.93 710,802.64

1300 2,906,569.30 158,205.67 673,248.48

1311 2,613,319.30 142,243.96 651,424.30

663,6691 299,293 9313444,12 -2.000.000,00 4.000.000,00 6.000.000,00 8.000.000,00 10.000.000,00 12.000.000,00

765 800 900 1000 1100 1200 1300 1371

P

(

k

g

)

L ( cm )

Px = P'x ( kg )

PѲ ( kg )

Py = P'y ( kg )

L Px = Px' Py = Py' PѲ

(82)

X

Y

h = 612mm

b = 202mm t2 = 23mm

t1 = 13mm

663,6691 299,293 9313444,12

L Px = Px' Py = Py' PѲ

( cm ) ( kg ) ( kg )