B a gia n 7
Ko o rd in a t Ku tu b
Bagian 7 Koordinat Kutub mempelajari bagaimana teknik integrasi yang telah Anda pelajari dalam bagian sebelumnya dapat digunakan untuk menyelesaikan soal yang berhubungan dengan koordinat kutub, yaitu sistem koordinat yang terdiri dari nilai x dan nilai sudut. Pengetahuan teknik integrasi dan teknik differensial yang telah Anda pelajari pada bagian sebelumnya, sangat bermanfaat untuk digunakan pada bagian tujuh ini. Untuk itu kuasai teknik integrasi dan differensial agar Anda tidak mempunyai masalah dalam penyelesaian soal koordinat kutub.
Kompetensi yang diharapkan setelah Anda menyelesaikan bagian 7 Koordinat Kutub adalah Anda akan mampu:
1. Membuat gambar grafik yang berasal dari persamaan kutub.
2. Menentukan koordinat kartesius yang berasal dari koordinat kutub, dan sebaliknya.
3. Menentukan persamaan ellips untuk koordinat kutub. 4. Menentukan titik potong untuk dua grafik koordinat kutub.
5. Menghitung garis singgung dan menghitung luas grafik koordinat kutub.
7.1
S is te m Ko o rd in a t Ku tu b
Dua orang Perancis yaitu Pierre Fermat dan Rene Descartes, telah memperkenalkan system koordinat yang sekarang kita kenal dengan sebutan system koordinat Cartesius atau siku-siku. Dasar pemikiran mereka ialah untuk menunjukkan kedudukan titik P pada bidang dengan dua bilangan yang ditulis dengan lambang (x,y) setiap bilangan menggambarkan jarak berarah dari dua sumbu yang tegak lurus sesamanya (Gambar 7.1). Sistem koordinat ini adalah dasar dari geometri analitik, dan sangat membantu pengembangan kalkulus diferensial dan kalkulus integral yang kita capai hingga saat ini.
Dengan memberikan jarak berarah dari dua sumbu yang tegak lurus bukanlah satu-satumya jalan untuk menunjukkan kedudukan suatu titik pada bidang. Cara lain adalah menggunakan apa yang disebut koordinat kutub.
Gambar 7.1 Gambar 7.2
7.1.1 Ko o rd in a t Ku tu b
Kita mulai dengan menggambar sebuah setengah-garis tetap yang dinamakan
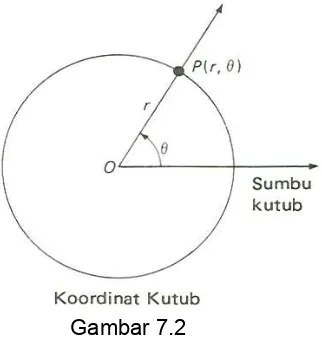
sumbu kutub yang berpangkal pada sebuah titik 0. Titik ini disebut kutub atau titik asal. Biasanya sumbu kutub ini kita gambar mendatar dan mengarah ke kanan dan oleh sebab itu sumbu ini dapat disamakan dengan sumbu x positif pada sebuah system koordinat siku-siku. Setiap titik P (selain dari kutub) adalah perpotongan antara sebuah lingkaran tunggal yang berpusat di 0 dan sebuah sinar tunggal yang memancar dari 0. Jika r adalah jari-jari lingkaran dan θ adalah salah satu sudut antara sinar dan sumbu kutub, maka (r, θ) dinamakan sepasang koordinat kutub
dari titik P (Gambar 7.2).
Titik-titik yang dilukiskan oleh koordinat kutub paling mudah digambar apabila kita menggunakan kertas grafik kutub. Pada kertas demikian telah tergambar lingkaran-lingkaran yang sepusat dan sinar-sinar yang memancar dari pusat itu. Kita dapat melihatnya pada Gambar 4.3, pada gambar ini telah terlukis beberapa titik.
Gambar 7.3 Gambar 7.4
Perhatikan sebuah sifat berikut yang tidak ada pada sebuah system koordinat Cartesius. Tiap titik memiliki banyak koordinat kutub. Ini adalah akibat sifat bahwa sudut-sudut θ + 2πn, n = 0, ±1, ±2,…memiliki kaki-kaki yang sama. Misalnya, titik dengan koordinat kutub (4, π/2) juga memiliki koordinat (4, 5π/2), (4, 9π/2), (-4, 3π/2), dan seterusnya. Bahkan hal ini berlaku juga jika r diperbolehkan memiliki nilai yang negatif. Dalam hal ini (r, θ) terletak pada sinar yang berlawanan arah dengan sinar yang dibentuk oleh θ dan yang terletak r satuan dari titik asal. Dengan demikian, titik dengan koordinat kutub (-3, π/6) dapat kita lihat pada Gambar 4.4, sedangkan (-4, 3π/2) adalah koordinat lain untuk (4, π/2). Titik asal mempunyai koordinat (0, θ), di mana θ sudut sembarang.
7.1.2 . P e rs a m a a n Ku tu b
Contoh persamaan kutub adalah:
r = 8 sin θ dan r =
θ
cos
-1
2
Seperti halnya dengan system koordinat siku-siku, kita juga dapat menggambarkan grafik sebuah persamaan kutub. Grafik persamaan kutub adalah himpunan titik-titik yang mempunyai paling sedikit sepasang koordinat kutub yang memenuhi persamaan yang bersangkutan. Salah satu cara untuk menggambar grafik itu adalah dengan menyusun daftar nilai-nilai koordinat, kemudian menggambar titik dengan koordinat-koordinat yang bersangkutan dan akhirnya menghubungkan titik itu dengan sebuah kurva yang mulus.
Contoh 7.1. : Gambar grafik persamaan kutub r = 8 sin θ
Penyelesaian :
Kita ganti kelipatan π/6 untuk θ dan menghitung nilai r yang bersangkutan. Apabila
θ naik dari 0 hingga 2π, grafik dilintasi dua kali (Gambar 4.5).
Contoh 7.2
Gambarlah grafik dari r =
θ
cos
-1
2
Penyelesaian :
Lihat Gambar 4.6. Perhatikan gejala yang tidak akan terjadi dengan system koordinat siku-siku. Koordinat (-2, 3π/2) tidak memenuhi persamaan. Walaupun demikian titik P (-2, 3π/2) terletak pada grafik, sebab (2, π/2) merupakan koordinat P dan memang memenuhi persamaan tersebut. Kita dapat menarik kesimpulan bahwa dalam system koordinat kutub, walaupun ada sepasang koordinat tertentu yang tidak memenuhi suatu persamaan, tetapi ini tidak perlu mengakibatkan bahwa titik yang bersangkutan tidak terletak pada grafik persamaan itu. Kenyataan ini mengakibatkan banyak kesulitan; kita harus belajar terbiasa dengan kenyataan tersebut.
Gambar 7.6
7.1.3 . H u b u n ga n d e n ga n Ko o rd in a t Ca rte s iu s
Andaikan sumbu kutub berimpit dengan sumbu x positif system koordinat Cartesius. Maka koordinat kutub (r, θ) sebuah titik P dan koordinat Cartesius (x, y) titik itu dihubungkan oleh persamaan :
x = r cos θ r2 = x2 + y2
y = r sin θ tan θ =
x
y
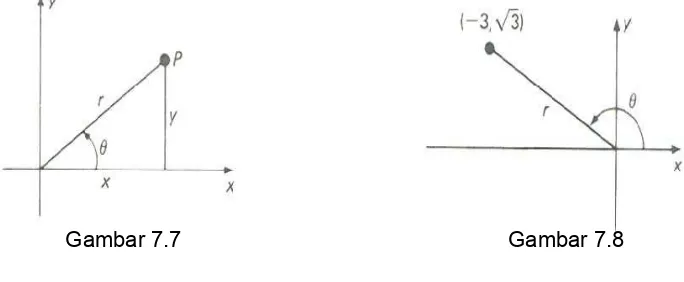
Hubungan tersebut jelas berlaku untuk sebuah titik P yang berada di dalam kuadran pertama, yang dapat kita lihat pada Gambar 4.7. mudah dibuktikan untuk titik-titik dalam kuadran lain.
Gambar 7.7 Gambar 7.8
Contoh 7.3
Tentukan koordinat Cartesius dari titik yang koordinat kutubnya adalah (4, π/6).
Tentukan juga koordinat kutub titik yang koordinat Cartesiusnya adalah (-3,
3
).Penyelesaian :
Jika (r, θ) = (4, π/6), maka
x = 4 cos
6
π
= 4 .
2
3
= 2
3
y = 4 sin
6
π
= 4 .
2
1
= 2
Jika, (x, y) = (-3,
3
), maka (lihat Gambar 8)r2 = (-3)2 + (
3
)2 = 12tan θ =
3
3
−
Salah satu nilai (r, θ) adalah (2
3
, 5π/6). Nilai lainnya adalah (-23
, -π/6).Ada kalanya grafik persamaan kutub dapat kita lukis dengan mencari persamaannya dalam system Cartesius. Sebagai contoh kita sajikan kasus di bawah ini.
Contoh 7.4
Buktikan bahwa grafik persamaan r = 8 sin θ (Contoh 1) adalah sebuah lingkaran dan bahwa grafik persamaan r = 2 / (1- cos θ) (Contoh 2) adalah sebuah parabol dengan jalan menulis persamaan Cartesius kurva tersebut.
Penyelesaian :
Kalikan ruas kiri dan kanan persamaan r = 8 sin θ dengan r, kita peroleh r2 = 8r sin θ
dalam bentuk Cartesius persamaan tersebut, menjadi : x2 + y2 = 8y
dan persamaan ini dapat diubah sebagai berikut : x2 + y2 - 8y = 0
x2 + y2 - 8y + 16 = 16 x2 + (y - 4)2 = 16
Persamaan terakhir ini adalah persamaan lingkaran yang berpusat di (0, 4) dan berjari-jari 4.
PERHATIKAN
Karena r bisa bernilai 0, ada kesalahan yang mungkin terjadi dalam mengalikan kedua sisi pada suatu persamaan kutub dengan r atau dalam membagi kedua bagian tersebut dengan r. Pada kasus yang pertama, kita dapat menambahkan kutub pada grafik; pada kasus kedua, kita dapat menghilangkan kutub dari grafik. Dalam Contoh di atas, kita kalikan kedua sisi dari r = 8 sin θ dengan r tanpa menimbulkan kesalahan karena kutubnya telah terdapat pada grafik sebagaimana titik dengan koordinat-θ 0.
Persamaan kedua kita ubah berturut-turut sebagai berikut :
r =
θ
cos
-1
2
r – r cos θ = 2 r - x = 2
r = x + 2 r2 = x2 + 4x + 4 x2 + y2 = x2 + 4x + 4 y2 = 4(x + 1)
Kita lihat bahwa persamaan terakhir ini adalah persamaan parabol dengan puncak di (-1, 0) dan dengan fokus di (0, 0)
7.1.4 . P e rs a m a a n Ku tu b u n tu k Ga ris , Lin gka ra n d a n Ko n ik
Jika sebuah garis melalui kutub, persamaannya adalah θ = θ0. Apabila garis tidak
melalui kutub, maka garistersebut berjarak misalnya d dari kutub (d>0). Andaikan θ0
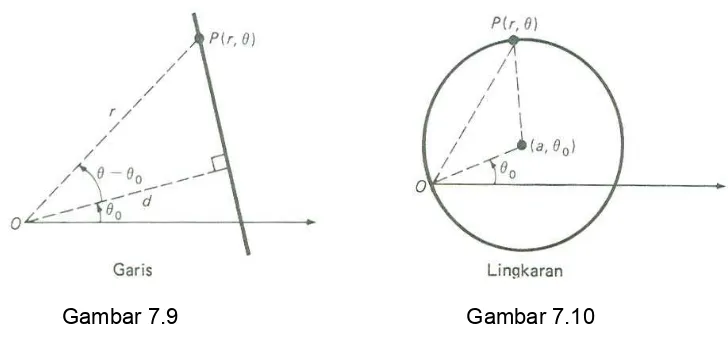
sudut antara sumbu kutub dan garis tegak lurus dari kutub pada garis itu (Gambar 7.9). Apabila P (r, θ) sebuah titik pada garis, maka cos (θ - θ0) = d/r, atau
Garis : r =
)
-(
cos
d
0
θ
θ
Apabila sebuah lingkaran dengan jari-jari a berpusat di kutub, pesamaannya adalah r = a. Apabila pusatnya di (r0, θ0), persamaannya agak rumit, kecuali kalau kita pilih
r0 = a (Gambar 7.10). Maka menurut hukum kosinus, a2 = r2 + a2 – 2ra cos (θ - θ0)
yang dapat disederhanakan menjadi :
Lingkaran : r = 2a cos (θ - θ0)
Gambar 7.9 Gambar 7.10
Suatu hal yang menarik jika θ0 = 0 dan θ0 = π/2. Yang pertama menghasilkan
persamaan r = 2a cos θ; yang kedua menghasilkan r = 2a cos (θ – π/2) atau r = 2a sin θ. Persamaan terakhir hendaknya dibandingkan dengan Contoh 1.
Akhirnya kalau sebuah konik (elips, parabol atau hiperbol) diletakkan sedemikian hingga fokusnya berada di kutub, garis arahnya berjarak d satuan dari kutub (Gambar 7.11), maka dengan menggunakan definisi konik, yaitu PF =ePL kita akan memperoleh
r = e
[
d
-
r
cos(
θ
-
θ
0)
]
atau secara setara : Konik : r =
)
-cos(
e
1
ed
0
θ
θ
+
Gambar 7.11
Ada lagi kasus yang menarik, yaitu untuk θ0 = 0 dan θ0 = π/2. Perhatikan bahwa
apabila e = 1 dan θ0 = 0 kita memperoleh persamaan dalam Contoh 7.2.
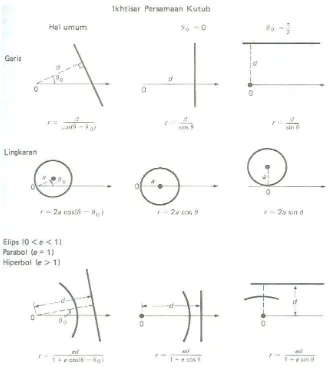
Hasil di atas kita ikhtisarkan dalam diagram berikut:
Contoh 7.5
Tentukan persamaan elips mendatar dengan keeksentrikan 21, berfokus di kutub
dan dengan garis arah tegak yang jaraknya 10 satuan disebelah kanan kutub.
Penyelesaian :
r =
θ
cos 1
10 .
2 1 2 1
+ =
2
cos
θ
10
+
Contoh 7.6
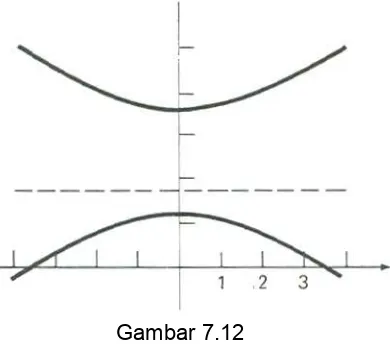
Tentukan jenis konik dan gambarlah grafik yang persamaannya r =
θ
sin
4
2
7
+
Penyelesaian
Kita tulis persamaan itu dalam bentuk baku sebagai berikut.
r =
θ
sin
4
2
7
+
= 1 2sinθ
2 7
+ = 1 2sin
θ
) ( 2 72 +
yang kita kenal sebagai koordinat kutub menggambar sebuah hiperbol dengan e = 2, berfokus di kutub dan dengan garis arah yang mendatar, sejauh 47 satuan di atas
sumbu polar (Gambar 7.12).
Gambar 7.12
7.1.5
Gra fik P e rs a m a a n Ku tu b
Grafik persamaan kutub yang telah dibahas sebelumnya terdiri atas garis, lingkaran dan konik. Sekarang kita akan membahas grafik-grafik yang lebih rumit bentuknya, yaitu kardioid, limason, mawar dan spiral. Walaupun bentuk grafiknya rumit, namun persamaannya tetap sederhana kalu digunakan persamaan kutub. Dituangkan dengan koordinat siku-siku, persamaannya tidak lagi sederhana. Jadi kita dapat melihat keuntungan adanya system koordinat ini. Ada kurva-kurva yang persamaannya sederhana dalam suatu system dan ada kurva yang persamaannya sederhana dalam system lain. Sifat demikian akan kita gunakan kelak untuk memecahkan suatu persoalan dengan memilih suatu system koordinat yang tepat.
Sifat simetri dapat membantu kita menggambar sebuah grafik. Di bawah ini ada beberapa pengujian kesimetrian yang cukup dalam koordinat kutub. Kebenarannya dapat dilihat pada gambar yang bersangkutan.
1. Grafik persamaan kutub simetri terhadap sumbu x (yaitu sumbu kutub dan perpanjangannya ke kiri) apabila θ diganti dengan –θ menghasilkan persamaan yang sama (Gambar 7.13).
2. Grafik persamaan kutub simetri terhadap sumbu y (yaitu garis θ = π/2) apabila θ diganti dengan π-θ menghasilkan persamaan yang sama (Gambar 7.14).
3. Grafik persamaan kutub simetri terhadap titik asal, apabila r diganti –r menghasilkan persamaan yang sama (Gambar 7.15).
Karena penggambaran banyak titik di dalam koordinat kutub, maka kemungkinan adanya simetri tidak teridentifikasi oleh ketiga tes ini.
Gambar 7.13 Gambar 7.14 Gambar 7.15
7.2 Ka rd io d d a n Lim a s o n
Kita perhatikan persamaan yang berbentuk
r = a ± b cos θ r = a ± b sin θ
a, b konstanta yang positif. Grafiknya dinamakan limason, di mana dalam hal khusus yaitu untuk a = b disebut kardiod. Grafiknya untuk tiap-tiap kasus dapat dilihat pada Gambar 7.16.
Gambar 7.16
Contoh 7.7
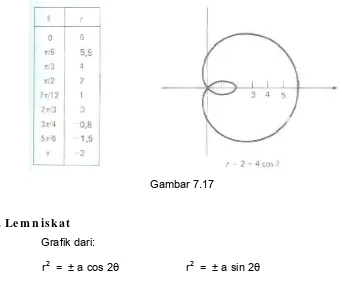
Selidiki persamaan r = 2 + 4 cos θ mengenai kesimetrian dan gambarlah grafiknya.
Penyelesaian
Oleh karena kosinus adalah fungsi genap (artinya cos(-θ) = cos θ, untuk semua θ), grafiknya simetrik terhadap sumbu x. Pengujian kesimetrian yang lain tidak berhasil. Daftar nilai dan grafiknya dapat dilihat pada Gambar 7.17.
Gambar 7.17
7.2 .1. Le m n is ka t
Grafik dari:
r2 = ± a cos 2θ r2 = ± a sin 2θ
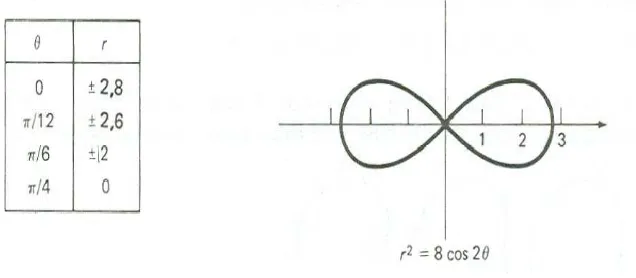
dinamakan lemniskat, dan berbentuk angka delapan.
Contoh 7.8
Selidiki persamaan r2 = 8 cos 2θ tentang kesimetrian dan gambarlah grafiknya.
Penyelesaian
Oleh karena cos (-2θ) = cos 2θ dan cos (2(π-θ)) = cos (2π - 2θ) = cos (-2θ) = cos 2θ
Maka grafiknya adalah simetrik terhadap sumbu x dan sumbu y (garis θ = 21 π). Jadi
simetrik juga terhadap titik asal. Daftar nilai dan grafik diperlihatkan pada Gambar 4.18.
Gambar 7.18
7.2 .2 . Ma w a r
Grafik persamaan kutub yang berbentuk
r = a cos nθ r = a sin nθ
adalah kurva-kurva berbentuk bunga yang dinamakan mawar. Banyaknya daun mawar itu adalah n apabila n ganjil dan 2n apabila n genap.
Contoh 7.9
Selidiki r = 4 sin 2θ mengenai kesimetrian dan kemudian gambarlah grafiknya.
Penyelesaian
Persamaan tersebut tidak memenuhi pengujian kesimetrian yang pertama dan yang ketiga. Sedangkan yang kedua menghasilkan :
sin 2(θ - π) = sin (2π - 2θ) = sin 2θ
Akan tetapi, grafiknya mempunyai ketiga jenis kesimetrian yang segera akan kita temukan. Ingat bahwa pengujian kita di atas adalah cukup, bukannya perlu.
Untuk menggambar grafik yang benar, kita menyusun sebuah daftar nilai yang agak lengkap untuk 0 ≤θ ≤π/2 dan yang agak ringkas untuk π/2 ≤ θ≤ 2π. Daftar ini dan grafiknya dapat dilihat pada Gambar 7.19. Anak panah pada grafik menggambarkan arah gerak titik P(r, θ) sepanjang grafik apabila θ naik dari 0 hingga 2π.
Gambar 7.19
7.2 .3 . S p ira l
Grafik persamaan r = aθ disebut spiral Archimedes; grafik persamaan r = aebθ dinamakan spiral logaritma.
Contoh 7.10
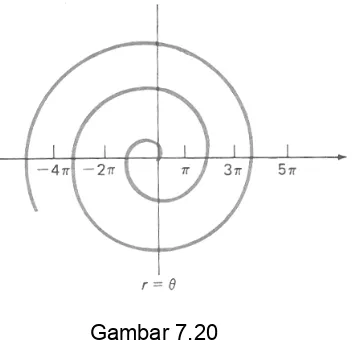
Gambarlah grafik r = θ untuk θ≥ 0.
Penyelesaian
Kita hilangkan daftar nilai, tetapi perhatikan bahwa grafik memotong sumbu kutub di (0, 0), (2π, 2π), (4π, 4π),…dan memotong perpanjangannya yang ke kiri di (π, π), (3π, 3π), (5π, 5π),…seperti dapat dilihat pada Gambar 4.20.
7.3 P e rp o to n ga n Ku rva -ku rva D e n ga n Ko o rd in a t Ku tu b
Dalam koordinat Cartesius, semua titik potong dua kurva dapat dicari dengan jalan menyelesaikan persamaan kurva bersama-sama. Hal ini tidak selalu mungkin jika kita menggunakan koordinat kutub. Ini disebabkan sebuah titik P memiliki banyak koordinat kutub, dan
Gambar 7.20
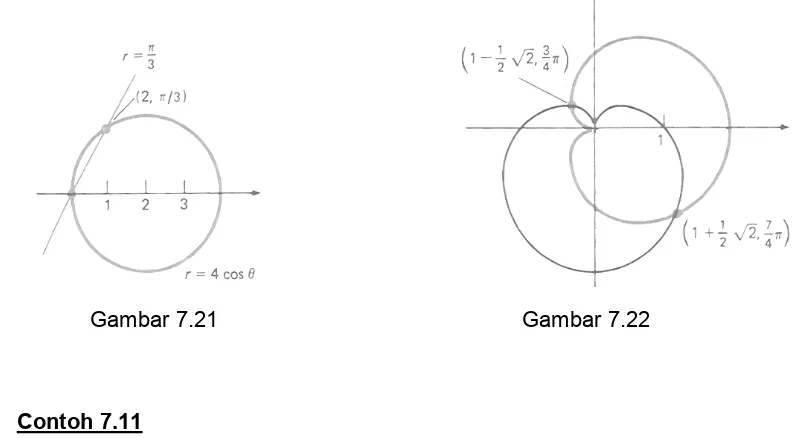
Satu pasang dapat memenuhi persamaan polar dari kurva yang lain. Misalnya (lihat Gambar 4.21), lingkaran r = 4 cosπ memotong garis θ = π/3 di dua titik, yaitu kutub dan (2, π/3). Tetapi harga pasangan terakhir inilah yang memenuhi kedua
persamaan tersebut. Ini disebabkan koordinat kutub yang memenuhi persamaan garis adalah (0, π/3) dan yang memenuhi persamaan lingkaran adalah (0, π/2).
Kesimpulan kita adalah sebagai berikut: Untuk dapat memperoleh semua perpotongan dua kurva dengan koordinat kutub, selesaikanlah persamaan-persamaan bersama-sama; kemudian gambarlah grafiknya secara seksama untuk memperoleh titik potong lain yang masih mungkin.
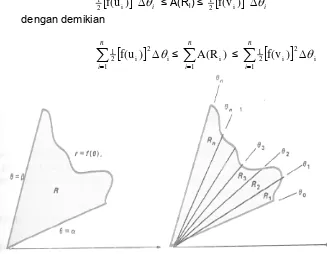
Gambar 7.21 Gambar 7.22
Contoh 7.11
Tentukan titik potong kardioid r = 1 + cos θ dan r = 1 - sin θ.
Penyelesaian
Apabila r dihilangkan dari dua persamaan tersebut, kita peroleh 1 + cos θ = 1 - sin
θ. Jadi cos θ = - sin θ, atau tan θ = -1. Kita simpulkan bahwa θ = 43 π dan θ = 4 7 π,
yang menghasilkan dua titik potong (1-21 2 ,
π
4
3 ) dan (1+ 2 2
1 ,
π
4
3 ). Grafik pada
Gambar 7.22, memperlihatkan, adanya titik potong yang ketiga, yaitu kutub. Ini disebabkan r = 0 dalam persamaan r = 1 + cos θ menghasilkan θ = π, tetapi r = 0 dalam persamaan r = 1- sin θ kita peroleh θ = π/2.
7.4
Ka lku lu s D e n ga n Ko o rd in a t Ku tu b
Dua persoalan paling mendasar dalam kalkulus adalah menentukan kemiringan garis singgung kurva dan menentukan luas suatu daerah yang dibatasi oleh sebuah kurva. Dalam sub bab ini, kita akan membahas kedua persoalan itu dengan menggunakan koordinat kutub. Dengan koordinat Cartesius, unsure luas dasar adalah luas persegi panjang. Dengan koordinat kutub unsure luas dasar ini adalah luas suatu juring (sektor) lingkaran (Gambar 7.23). Oleh karena luas lingkaran dengan jari-jari r adalah πr2 , kita dapat menarik kesimpulan bahwa luas sektor lingkaran dengan sudut pusat θ radian adalah (θ/2π)πr2 . Sehingga :
Gambar 7.23
7.4 .1. Lu a s d a la m Ko o rd in a t Ku tu b
Andaikan r = f(θ) menentukan sebuah kurva pada bidang dengan f kontinu dan tak negatif untuk α ≤ θ ≤ β dan β-α ≤ 2π. Maka kurva r = f(θ), θ = α’ dan θ = β membatasi sebuah daerah R (Gambar 7.24 kiri); kita hendak menentukan luas A(R).
Kita bagi selang
[
α
,β
]
menjadi n bagian selang oleh bilangan-bilangan θi, I = 0, 1,2, …n dengan α = θ0 < θ1 < θ2 < …< θn = β dengan demikian daerah R terbagi
menjadi daerah yang lebih kecil, yaitu R1, R2,…, Rn (Gambar 7.24 kanan). Maka
A(R) = A(R1) + A(R2) + … + A(Rn).
Kita aproksimasi luas A(Ri) dengan dua jalan. Pada selang ke-I,
[
θ
i-1,θ
i]
, fmencapai nilai minimum di ui dan mencapai nilai maksimumnya di vi (Gambar 4.25).
Jadi, apabila Δθi = θi - θi-1, kita peroleh
2
[
f(ui)]
21
i
θ
Δ ≤ A(Ri) ≤
[
f(v )]
2 i 2 1
i
θ
Δ
dengan demikian
≤
∑
≤=
n
i 1 i
)
A(R
∑
[
]
=
Δ
ni 1
i 2 i 2
1
f(v
)
θ
[
]
∑
=
Δ
ni 1
i 2 i 2
1
f(u
)
θ
Gambar 7.24
ambar 7.25
Ruas pertama dan ruas ketiga pertidaksamaan tersebut adalah jumlah Riemann
dan integral yang sama, yaitu, G
∫
β
1 2
α
2[f(θ)] dθ. Apabila norm partisi kita buat menuju
nol, kita peroleh (Prinsip Apit) rumus untuk luas, yaitu:
A =
∫
β
α
2
1[f(θ)]2dθ
entu saja rumus ini dapat dihafalkan. Akan tetapi yang lebih penting ialah
Contoh 7.12
T
mengingat cara bagaimana rumus ini kita peroleh. Juga dalam koordinat kutub, tiga kata kunci yang diperlukan ialah, potongan, aproksimasi, dan integralkan. Di bawah ini diberikan contoh-contoh tentang apa yang kita maksud.
daerah yang dibatasi oleh limason r = 2 + cos θ.
enyelesaian
ada di Gambar 7.26; θ bergerak dari 0 hingga 2π. Kita potong,
.4.2. Titik-titik Ekikordial
ama dengan lingkaran memiliki suatu titik ekikordial (yaitu suatu titik Tentukan luas
P
Gambar grafik
aproksimasi dan kemudian integralkan.
7
Limason bers
yang dilalui oleh talibusur-talibusur yang panjangnya sama). Untuk limason r = 2 + cos θ pada Contoh 7.12.
Gambar 7.26
Semua talibusur yang melalui kutub memiliki panjang 4. Perhatikan bahwa limason ini mempunyai luas 9π/2, sedangkan lingkaran berdiameter 4 yang bersesuaian dengannya mempunyai luas 4π. Jadi, memiliki talibusur yang panjangnya sama dalam semua arah melalui suatu titik belum cukup untuk menghitung luas.
Di sini diberikan satu soal terkenal yang tidak terpecahkan yang pertama kali diajukan pada tahun 1916. Dapatkah sebuah daerah pada bidang memiliki dua titik ekikordal ? Jawaban yang benar untuk pertanyaan ini (dengan buktinya) akan membuat Anda menjadi terkenal. Tetapi kami sarankan agar Anda menjawab soal ini pada bagian akhir pasal ini sebelum mencoba menjawab tantangan ini.
Karena kesimetrian, integral kita peroleh dengan batas antara 0 dan π dan kemudian mengalikannya dengan 2. Jadi,
A =
∫
+ +π
θ
θ
θ
0 2 d ) cos cos 4 4 ( =∫
+∫
+∫
+ π π πθ
θ
θ
θ
θ
0 0 0
d ) 2 cos 1 ( 2 1 d cos 4 4d =
∫
+∫
+∫
π π πθ
θ
θ
θ
θ
0 0 0
d 2 . 2 cos 4 1 d cos 4 2 9 d = π
θ
0 2 9 ⎥⎦ ⎤ ⎢⎣ ⎡+
[
4
sin
θ
]
π0 +π
θ
0 2 sin 4 1 ⎥⎦ ⎤ ⎢⎣ ⎡ =2
9
π
Contoh 7.13Tentukan luas satu daun dari mawar berdaun-empat r = 4 sin 2θ.
Penyelesaian
Mawar lengkap telah digambar pada Contoh 7.13, subbab sebelumnya. Di sini kita perlihatkan daun yang ada dalam kuadran pertama (Gambar 7.27).
Δ
≈
[ ]
f(
θ
)
2Δ
θ
2
1
A
A =
∫
2 / 0 2 d ) 2 sin 4 ( 2
1π
θ
θ
A =
∫
2 / 0 2 d 2 sin 16 2
1π
θ
θ
=
θ
θ
π d 2 4 cos -1 8 /2 0∫
A =
∫
∫
/2 0 2 / 0 d 4 . 4 cos d 4 π π
θ
θ
θ
A =
[ ]
4
θ
0π/2-[
sin
4
θ
]
π0/2 = 2πGambar 7.27
Contoh 7.14
Tentukan luas daerah yang ada di luar kardioid r = 1 + cos θ dan di dalam lingkaran
r =
3
sin θ.Penyelesaian
Grafik kurva yang diketahui digambarkan pada Gambar 7.28. Kita perlukan koordinat θ titik-titik potong; nilai θ kita tentukan dengan mencoba menyelesaikan kedua persamaan secara serentak.
1 + cos θ =
3
sin θ 1 + 2 cos θ + cos2 θ = 3 sin2θ 1 + 2 cos θ + cos2 θ = 3(1 - cos2θ) 4 cos2θ + 2 cos θ - 2 = 02 cos2θ + cos θ - 1 = 0 (2 cos θ – 1)(cos θ + 1) = 0
Δ
≈
[
3
sin
2θ
-
(1
+
cos
θ
)
2]
Δ
θ
2
1
A
A =
[
θ
θ
]
θ
π π d ) cos (1 -sin 3 2 1 /3 2 2∫
+cos θ =
2
1
, -1 → θ =
3
π
, π
A =
[
θ
θ
θ
]
θ
π π d cos -cos 2 -1 -sin 3 2 1 /3 2 2
∫
=θ
θ
θ
θ
π π d ) cos2 (1 2 1 -cos 2 -1 -) 2 cos -(1 2 3 2 1 /3∫
⎢⎣⎡ + ⎥⎦⎤ =[
θ
θ
]
θ
π π d 2 cos 2 cos 2 -2 1 /3∫
=
[
-
2
sin
θ
-
sin
2
θ
]
ππ/32
1
=⎥
⎦
⎤
⎢
⎣
⎡
+
2
3
2
3
2
2
1
=
1.299
4
3
3
≈
Gambar 7.28
7.4 .3 . Ga ris S in ggu n g d a la m Ko o rd in a t Ku tu b
Dengan koordinat Cartesius, kemiringan (slope) m dari garis singgung pada sebuah kurva adalah m = dy/dx. Dengan koordinat kutub kemiringan ini bukanlah dr/dθ. Apabila r = f(θ) menentukan persamaan kurva, kita tulis
y = r sin θ = f(θ)sin θ x = r cos θ = f(θ)cos θ Jadi,
θ
θ
θ
θ
θdx/d
dy/d
x/
y/
lim
x
y
lim
dx
dy
0 0x
Δ
Δ
=
Δ
Δ
=
Δ
Δ
=
→ Δ → Δkarena itulah,
θ
θ
θ
θ
θ
θ
θ
θ
)cos
(
f'
)sin
f(
)sin
(
f'
)cos
f(
m
+
−
+
=
Rumus di atas menjadi sederhana apabila grafik r = f(θ) melalui kutub. Andaikan, sebagai contoh, untuk suatu sudut α, r = f(α) = 0 dan f’(α) ≠ 0. Maka di kutub tersebut kita peroleh
α
α
α
α
α
tan
)cos
(
f'
)sin
(
f'
m
=
=
Oleh karena garis θ = α memiliki kemiringan tan α juga, maka kita dapat mengatakan bahwa garis tersebut menyinggung kurva di kutub.Jadi dapat ditarik kesimpulan bahwa garis singgung kurva di kutub dapat ditemukan dengan menyelesaikan persamaan f(θ) = 0. Kita beri contoh sebagai berikut.
Contoh 7.15
Perhatikan persamaan kutub r = 4 sin 3θ.
a. Tentukan kemiringan garis singgung di θ = π/6 dan θ = π/4. b. Tentukan garis singgung di kutub.
c. Gambar grafik.
d. Tentukan luas satu daun kurva.
Penyelesaian a.
θ
θ
θ
θ
θ
θ
θ
θ
)cos
(
f'
)sin
f(
)sin
(
f'
)cos
f(
m
+
−
+
=
=θ
θ
θ
θ
θ
θ
θ
θ
cos
3
cos
12
sin
3
sin
4
sin
3
cos
12
cos
3
sin
4
+
−
+
Di θ = π/6,
m =
-
3
2
3
.
0
.
12
2
1
.
1
.
4
-2
1
.
0
.
12
2
3
1.
.
4
=
+
+
Di θ = π/4,
m =
2
1
6
-2
-6
-2
2
2
.
2
2
.
12
-2
2
.
2
2
.
4
-2
2
.
2
2
.
12
2
2
.
2
2
.
4
=
=
+
b. Kita misalkan f(θ) = 4 sin 3θ = 0. Setelah iselesaikan diperoleh θ = 0, θ = π/3,
θ = 2π/3, θ = π, θ = 4π/3, dan θ = 5π/3.
c. Berhubung
sin 3(π-θ) = sin (3π-3θ) = sin 3π cos 3θ - cos 3π sin 3θ = sin 3θ
Maka dapat ditarik kesimpulan bahwa grafik simetri terhadap sumbu y, kita susun daftar nilai fungsi dan kemudian kita gambar grafik fungsi. Grafik ini diperlihatkan pada Gambar 7.29.
Gambar 7.29
d. A =
∫
=∫
3 /
0
/3
0 2 2
d 3 sin 8 d ) 3 sin 4 ( 2
1π
θ
θ
πθ
θ
=
∫
=∫
∫
3 /
0
/3
0
/3
0
d 6 . 6 cos 6 4 -d 4 d ) 6 cos -1 ( 4
π π π
θ
θ
θ
θ
θ
=
3 4 6 sin 3 2 -4
3 /
0
π
θ
θ
⎥⎦⎤π = ⎢⎣⎡