PENGOPTIMUMAN PADA MASALAH PEMROGRAMAN LINEAR
DENGAN KOEFISIEN INTER VAL
ANA FARIDA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PEN GETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
ANA FARIDA. Pengoptimu man pada Masalah Pemrogra man Linear dengan Koefisien Interval. Dib imbing o leh PRAPTO TRI SUPRIYO dan NUR A LIATININGTYA S.
Pada beberapa masalah aplikasi pe mrogra man linear (PL), koefisien pada model seringka li tidak bisa ditentukan secara tepat. Salah satu metode dalam menyelesaikan masalah PL in i adalah dengan menggunakan pendekatan interval, dimana koe fisien tak tentu tersebut diubah menjadi bentuk interval. Bentuk PL in i dina ma kan Linear Programming with Interval Coefficient (LPIC). Koefisien berbentuk interval menandakan perluasan toleransi (atau daerah) dimana para meter konstanta bisa diterima dan me menuhi model LPIC. Pada karya ilmiah in i akan dibahas salah satu metode dala m menyelesaikan LPIC yang telah dike mbangkan oleh JW Chinneck dan K Ra madan (2000). Masalah LPIC me miliki fungsi objektif dan kendala persamaan atau pertidaksamaan yang berkoefisien interval. Solusi optimu m dibagi menjad i dua, yaitu best optimum dan worst optimum. Dala m kasus minimisasi, best optimum adalah solusi yang me miliki nilai fungsi objektif terkec il, sedangkan worst optimum adalah solusi yang me miliki n ila i fungsi objektif te rbesar. Solusi optimu m pada LPIC didapatkan dengan mencari versi khusus dari fungsi objektif dan kendala yang mengoptimu mkan model, ya itu dipilih suatu nilai spesifik (nilai ekstrim) pada koefisien interval yang me mbuat model LPIC tersebut optimu m, sehingga pemecahan masalah LPIC diperoleh dengan menyelesaikan PL yang mengoptimu mkan model LPIC.
ii
ABSTRACT
ANA FARIDA. Optimization in Linear Progra mming with Interval Coefficients Proble ms. Supervised by PRAPTO TRI SUPRIYO and NUR A LIATININGTYA S.
On some applications of linear programming proble ms (LP), the coefficient on the model often can not be determined precisely. One method to solve this LP proble m is to use an interval approach, where uncertain coefficients are transformed into the form of intervals. LP form is called Linear Progra mming with Interval Coeffic ient (LPIC). Interval coeffic ient indicates shaped e xpansion of tolerance (or regions) where the constant parameters can be accepted and fulfilled the LPIC model. One of the methods in solving LPIC has been developed by JW Chinneck and K Ra madan (2000). LPIC prob le ms have objective functions and equations or inequalities constraints which their coeffic ients are intervals. The optimu m solutions are divided into two solutions , best optimu m solution and worst optimu m solution. In the case of minimizat ion, best optimu m is the solution that has the smallest objective function value, wh ile the worst optimu m is the solution that has the largest objective function value. The optimu m solution to the LPIC obtained by seeking a special version of the objective function and constraints that optimize model, which is selected a specific value (e xtre me value) on the interval coefficients that make LPIC model is optimu m. Therefore, solution is obtained by solving LP that optimize LPIC model.
iii
PENGOPTIMUMAN PADA MASALAH PEMROGRAMAN LINEAR
DENGAN KOEFISIEN INTER VAL
ANA FARIDA
Skripsi
sabagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PEN GETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
iv
Judul Skripsi
:
Pengoptimuman pada Masalah Pemrograman Linear dengan
Koefisien Interval
Nama
:
Ana Farida
NIM
:
G54053213
Menyetujui,
Pembimbing I
Pembimbing II
Drs.Prapto Tri Supriyo, M.Kom.
Dra. Nur Aliatiningtyas, MS.
NIP. 19630715 199002 1 002
NIP. 19610104 198803 2 002
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP 19650505 198903 2 004
v
KATA PENGAN TAR
Puji dan syukur penulis panjatkan kehadirat Allah Subhanallahu ta’ala atas segala nikmat, petunjuk, dan pertolongan-Nya sehingga penulisan skripsi in i berhasil diselesaikan.
Tema yang dipilih penulis adalah Riset Operasi dengan judul Pengoptimu man pada Masalah Pe mrogra man Linear dengan Koefisien Interval. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Mate matika, Fa kultas Matematika dan Ilmu Pengetahuan Ala m, Institut Pertanian Bogor. Penulis mengucapkan terima kasih kepada:
1. Bapak Drs.Prapto Tri Supriyo, M.Ko m. dan Ibu Dra. Nur Aliatin ingtyas, MS selaku dosen pembimb ing skripsi atas bimbingan, arahan, waktu, kesabaran dan ilmu pengetahuan yang telah diberikan sela ma penyusunan skrips i in i.
2. Bapak Dr.Ir. A mril Aman, Msc. selaku dosen penguji skripsi atas saran dan masukan yang diberikan kepada penulis.
3. Keluarga ku tercinta: bapak, Ibu, kaka k, adik dan seluruh keluarga besar yang telah me mbe rikan doa, dukungan dan kasih sayangnya.
4. Seluruh dosen Matematika FM IPA IPB yang telah me mberikan ilmu yang bermanfaat bagi penulis.
5. Staf TU Mate matika, Pak Yono, Bu Ade, Mas Heri, Bu Susi yang telah mengurusi segala administrasi.
6. Rizky, Nurus dan Fani selaku pembahas yang telah me mberikan bantuan, saran dan kritik kepada penulis.
7. Salma , Fitri, Manda dan Lia atas persahabatan, doa, nasihat, semangat dan dukungannya selama ini.
6. Penghuni Nexu z House: Fety, Kak Sirri, Lusi, Devi, Sa rah, Indah, Widy, Saly, Citra, Tyas dan Mutia atas kebersamaan, dukungan dan semangat yang diberikan.
7. Teman-te man Math 42: Novi, M ira, Lina, Yun i, Zil, Lela dan seluruh teman -te man la innya yang tidak bisa disebutkan satu-persatu.
8. Adik-adik Math 43 dan 44 atas segala kebersamaan dan bantuannya.
9. Kak Sri, Sofi, Weni, Era, Mia dan Novy yang telah me mberi semangat dan dukungan kepada penulis.
Penulis menyadari bahwa dala m tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan. Oleh karena itu, dibutuhkan krit ik dan saran yang me mbangun dari pe mb aca. Se moga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya mate matika dan menjad i inspirasi bagi penelit ian-penelit ian selanjutnya.
Bogor, Oktober 2011
vi
RIWAYAT HIDUP
Penulis merupakan anak kee mpat dari lima bersaudara, puteri dari pasangan Bapak Abdul Ghofa r dan Ibu Mahmudah. Penulis dilahirkan di Malang pada tanggal 19 Juli 1987. Pendidikan TK dite mpuh pada tahun 1991 di TK Sa lafiyah Gondanglegi. Pada tahun1993 penulis me lanjutkan sekolah di SDI Sala fiyah Gondanglegi dan menyelesaikannya pada tahun 1999. Setelah menyelesaikan pendidikan sekolah dasar, penulis melan jutkan pendidikan d i MTsN 3 Ma lang pada tahun 1999 sampai 2002. Pada tahun 2002 penulis me lanjutkan pendidikan menengah atas di MAN 3 Ma lang.
Pada tahun 2005, penulis melan jutkan pendidikan di Institut Pertanian Bogor. Penulis diterima d i Tingkat Persiapan Bersa ma (TPB) Institut Pertanian Bogor me lalu i ja lur Se le ksi Penerimaan Mahasiswa Baru (SPM B). Pada tahun 2006 penulis diterima di Departemen Geofisika dan Meteorologi, setahun kemudian pindah jurusan ke Departemen Matematika, Fa kultas Ilmu Pengetahuan Alam dan Mate matika.
vii
DAFTAR ISI
Halaman
DAFTAR TABEL ………. viii
DAFTAR GAM BAR ……… viii
DAFTAR LAMPIRAN ………... viii
I PENDAHULUAN ……… 1
1.1 Latar Be la kang ……… 1
1.2 Tu juan ………. 1
II LANDASAN TEORI ……… 1
III PEMBA HASAN ………... 5
3.1 LPIC dengan kendala pertida ksamaan interval ……… 7
3.2 LPIC dengan kendala persamaan interval ……… 13
IV STUDI KASUS DA N PENYELESA IANNYA ……… 18
V SIMPULAN DAN SA RAN ……… 23
5.1 Simpu lan ……… 23
5.2 Sa ran ……… 23
DAFTAR PUSTA KA ……….. 24
viii
DAFTAR TABEL
Halaman
1 Susunan Zat Gizi pada Pakan Aya m dan Kadar Min imu m Zat Gizi ……… 19
2 Batasan Pakan dala m Ransum dan Harga Pakan Aya m ... 19
3 Pe mecahan Masalah Pembe lian Pakan Te rnak Aya m ... 23
DAFTAR GAMBAR
Halaman 1 Ilustrasi himpunan konveks dan bukan himpunan konveks ... 32 SI pada Contoh 3 ... 5
3 SII pada Contoh 3 ... 6
4 Daerah fisibel C pada Contoh 3 ... 6
5 SI pada Contoh 4 ... 6
6 SII pada Contoh 4 ... 6
7 Daerah fisibel SI SII pada Contoh 4 ... 6
8 SI dan SII pada Contoh 5 ... 7
9 Ilustrasi irisan himpunan solusi dua pertidaksamaan (S) ... 8
10 Ilustrasi gabungan himpunan solusi dua pertidaksamaan (S) ... 8
11 S pada Contoh 6 ... 8
12 S pada Contoh 6 ... 8
13 Daerah fisibel solusi best optimum pada Contoh 7 ... 11
14 Daerah fisibel solusi worst optimum pada Contoh 7 ... 11
15 Daerah fisibel LPIC pada Contoh 7 ... 12
16 Daerah fisibel pada Contoh 10 ... 13
17 Daerah fisibel pada Contoh 11 ... 13
18 Daerah fisibel solusi best optimum pada Contoh 12 ... 16
19 Daerah fisibel solusi worst optimum pada Contoh 12 ... 18
20 Daerah fisibel LPIC pada Contoh 12 ... 18
DAFTAR LAMPIRAN
Halaman 1 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah LPIC dengan Kendala berbentuk Pertidaksa maan Interval ……… 262 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah LPIC dengan Kendala berbentuk Persamaan interva l ……… 28
I PENDAHULUAN
1.1 Latar Belakang
Pada beberapa masalah aplikasi pemrogra man linear (PL), koefisien pada model seringkali t idak bisa ditentukan secara tepat sehingga biasanya dibuat dalam perkiraan. Sa lah satu metode dalam menyelesaikan masalah PL in i adalah dengan menggunakan pendekatan interval, dimana koefisien tak tentu tersebut diubah menjadi bentuk interval. Bentuk PL ini dina ma kan Linear Programming with Interval Coefficient (LPIC). Koe fisien berbentuk interval menandakan perluasan toleransi (atau daerah) dimana para meter konstanta bisa diterima dan me menuhi model LPIC.
Pada awalnya, LPIC tidak banyak dibahas, penelitian sebelumnya lebih me musatkan pada kasus khusus tertentu, misalkan variabel 0-1 atau kasus PL dengan koefisien interval pada fungsi objektif saja. Topik LPIC ini d iperkena lkan secara luas pada tahun 1960-1980, dimu la i dari model kendala berbentuk upper-bound dan lower-bound (c1 a1x1 a2x2 ... anxn cu). Meskipun tidak berhubungan dengan LPIC, model in i me miliki kesamaan yaitu model kendala tersebut dibatasi titik e kstrim.
Shaocheng (1994) mentransformasikan LPIC menjad i dua PL yang me miliki kara kteristik khusus. Salah satu PL me miliki daerah fisibel terbesar (largest possible
feasible region) dan versi terbaik pada fungsi objektif (most favourable version of objective function ) untuk mene mukan solusi optimu m terbaik yang mungkin (best possible optimum solution). Sedangkan PL la innya me miliki daerah fisibel terkecil (smallest possible feasible region) dan versi baik yang terendah pada fungsi objektif (least favourable version of objective function) untuk mene mu kan solusi optimu m terburuk yang mungkin (worst possible optimum solution). Metode Shaocheng ini mengatasi masalah LPIC dengan syarat: (1) dibatasi variabel tak negatif saja, dan (2) hanya mengatasi kendala pertidaksamaan saja.
Pada karya ilmiah in i akan dibahas salah satu metode dala m menyelesaikan LPIC yang telah dike mbangkan oleh JW Ch inneck dan K Ra madan (2000). Metode in i me rupakan generalisasi dari metode Shaocheng, yaitu dengan menambahkan kendala persa maan interval dan serta variabel tak positif pada model LPIC.
1.2 Tujuan
Tujuan dari karya ilmiah in i adalah mengka ji metode pemecahan masalah LPIC secara teoritis dan mengimple mentasikannya dala m kasus nyata.
II LANDASAN TEORI
Definisi 1 (Fungsi Line ar)
Misalkan f(x1,x2,....,xn) adalah fungsi
dala m variabe l-variabel x1,x2,....,xn. Fungsi
) ,...., , (x1 x2 xn
f dinama kan fungsi linear jika dan hanya jika ada konstanta c1,c2,...,cn,
n n
n c x c x c x
x x x
f( 1, 2,...., ) 1 1 2 2 .... .
(Winston, 1995)
Sebagai contoh, f(x1,x2) x1 2x2
adalah fungsi linear, sedangkan
2 2 1 2 1, )
(x x xx
f bukan fungsi linear.
Definisi 2 (Persamaan dan Perti daksamaan Line ar)
Untuk sembarang fungsi linear )
,...., , (x1 x2 xn
f dan sembarang bilangan b, suatu persamaan f(x1,x2,....,xn) b disebut
persamaan linear dan f(x1,x2,....,xn) b atau
b x x x
f( 1, 2,...., n) disebut pertidaksamaan linear.
(Winston, 1995)
Pemr ograman Li near
Pe mrogra man linear (PL) adalah masalah optimisasi yang me miliki kara kteristik sebagai berikut:
1. Tujuan masalah tersebut adalah me maksimu mkan atau me min imu mkan fungsi linear dari seju mlah variabel keputusan. Fungsi tersebut dinamakan fungsi objektif.
3. Ada batasan tanda pada tiap variabel. Untuk sembarang variabel xi, pembatasan tanda menentukan xi harus tak negatif xi 0 atau tidak dibatasi tandanya (unrestricted in sign).
(Winston, 1995)
Definisi 3 (Bentuk Standar PL)
Suatu PL me miliki bentuk standar sebagai berikut:
min z cTx
terhadap kendala Ax b (1 )
0
b dan x 0
dimana x dan c adalah vektor beru kuran n, vektor b beru kuran m dan A berupa matriks berukuran m x n yang disebut juga matriks kendala dengan m n.
(Nash dan Sofer, 1996)
Contoh 1
Misalkan diberikan PL standar sebagai berikut:
Min z x1 2x2
terhadap kendala:
10 2
8 2
3 2
5 1
4 2 1
3 2 1
x x
x x x
x x x
(2)
dengan x1,x2,x3,x4,x5 0 Fungsi objektif ada lah z x1 2x2
Variabel keputusan adalah x1,x2,x3,x4,x5
10 8 3 , 1 0 0 0 2
0 1 0 2 1
0 0 1 2 1
0 0 0 2 1
,
5 4 3 2 1
b A
c x
x x x x x
Solusi Pemrograman Line ar
Suatu masalah PL dapat diselesaikan dala m berbagai tekn ik, salah satunya adalah metode simp leks. Metode ini dapat menghasilkan suatu solusi optimu m bagi masalah PL dan telah dike mbangkan Dantzig sejak tahun 1947, dan dalam perke mbangannya merupakan metode yang paling u mu m digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.
Pada masalah PL (1), ve ktor x yang me menuhi kendala Ax bdisebut solusi PL (1). Misalkan matriks A dapat dinyatakan
sebagai A B N , dengan B adalah matriks taksingular berukuran m x m yang ele mennya berupa koefisien variabel basis dan N adalah matriks berukuran m x (n-m) yang ele mennya berupa koefisien variabe l nonbasis pada matriks kendala. Matriks B disebut matriks basis untuk PL (1).
Misalkan x d inyatakan dengan vektor
N B
x x
x , dengan xB adalah vektor variabel
basis dan xN adalah vektor variabel nonbasis, ma ka Ax bdapat dinyatakan sebagai
b Nx Bx
x x N B Ax
N B
N B
(3 )
Karena matriks B adalah matriks taksingular, ma ka B me miliki invers, sehingga xB dapat dinyatakan sebagai:
N 1 1
B B b B Nx
x
(4)
Ke mudian, fungsi objektifnya berubah men jadi:
min N
T N B T
B x c x
c z
Definisi 4 (Solusi Basis)
Solusi dimana (n-m) variabel bern ilai nol disebut solusi basis. Variabel yang tidak bernila i nol disebut variabel basis dan variabel
yang bernilai nol disebut variabel nonbasis.
(Rao,1984)
Solusi dari suatu PL disebut solusi basis jika me menuhi syarat berikut:
i. solusi tersebut me menuhi kendala PL; ii. kolo m-ko lo m dari matriks kendala yang
berpadanan dengan komponen tak nol dari solusi tersebut adalah bebas linear.
(Nash dan Sofer, 1996)
Definisi 5 (Solusi Fisibel)
Se mbarang solusi yang me menuhi kendala Ax bdan x 0 disebut solusi fisibel.
(Rao,1984)
Definisi 6 (Solusi Fisibel B asis)
Vektor x disebut solusi fisibel basis jika x me rupakan solusi basis dan x 0.
(Nash dan Sofer, 1996)
Contoh 2
Misalkan diberi PL berikut: Min z x1 x2
terhadap kendala:
10 8 3
3 2
5 1
4 2 1
3 2 1
x x
x x x
x x x
(5 )
dengan x1,x2,x3,x4,x5 0, ma ka d iperoleh:
10 8 3 , 1 0 0 0 1
0 1 0 3 1
0 0 1 2 1
b A
Misalkan dip ilih xB x3 x4 x5 T dan T
2 1 x
x N
x , maka matriks basisnya
adalah
1 0 0
0 1 0
0 0 1 B
0 3 2
1 1 1 N
T T
0 1 1 B
c ,cNT 0 0T
Dengan menggunakan mat riks basis di atas, ma ka d iperoleh
T
0 0 N x
T
10 8 3 b B
xB 1 (6 )
11 b B cBT 1 z
Solusi (6) me rupakan solusi basis, karena me menuhi kendala pada PL (5) dan kolo m-kolo m pada matriks kendala yang berpadanan dengan komponen tak nol dari (6) yaitu B, bebas linear (kolo m yang satu bukan me rupakan kelipatan dari kolo m yang lain). Solusi (6) juga merupakan solusi fisibel basis, karena nilai-nilai variabelnya leb ih dari atau sama dengan nol.
Definisi 7( Daerah Fisibel)
Daerah fisibel suatu PL adalah himpunan semua titik yang me menuhi seluruh kendala PL dan batasan tanda PL .
(Winston, 1995)
Definisi 8 (Solusi Opti mum)
Solusi optimu m suatu PL adalah solusi fisibel yang mengoptimu mkan fungsi objektif. (Rao,1984)
Definisi 9 ( Hi mpunan Konveks)
Misalkan S adalah himpunan titik. Himpunan S disebut himpunan konveks jika segmen garis yang menghubungkan
sembarang titik-t itik dala m S seluruhnya termuat dala m S. Dengan kata la in, himpunan
n
R
S disebut himpunan konveks, jika untuk tiap x1,x2 S berla ku
S x
x1 (1 ) 2 dengan 0,1 . (Winston, 1995)
Ilustrasi himpunan konveks dan bukan himpunan konveks diberikan pada gambar dibawah in i.
(i) (ii)
(iii) (i v)
Ga mbar 1. Ilustrasi himpunan konveks dan bukan himpunan konveks.
Pada Ga mbar 1, lingka ran (i) dan persegi (ii) merupakan himpunan konveks, sedangkan bidang (iii) dan cincin (iv) bukan himpunan konveks.
Teore ma 1
Daerah fisibel dari PL ada lah konveks. (Rao,1984)
Bukt i:
Daerah fisibel S dari PL standar didefinisikan sebagai S {x|Ax b,x 0}.
Misalkan t itik x1dan x2 termasuk dala m himpunan S, ma ka
0 , 1
1 b x
Ax (1)
0 , 2
2 b x
Ax (2)
Jika persamaan (1) dika likan dengan dan persamaan (2) dika likan dengan 1 ,
1
0 dan ke mudian keduanya
diju mlahkan, maka didapat:
(3) ]
) 1 ( [
)) 1 ( ( ] ) 1 ( [
) 1 ( ] )[ 1 ( ] [
) 1 ( ] )[ 1 (
] [
2 1
2 1
2 1
2 1
b x x
A
b x
x A
b b
Ax Ax
b Ax
b Ax
[image:12.596.341.503.224.356.2]Persamaan (3) dapat ditulis sebagai Ax b.
Berdasarkan defin isi, ma ka x S atau
S x
x1 (1 ) 2 .
Jadi S {x|Ax b,x 0}adalah konveks.
Teorema 1 terbukti.
Definisi 10 (Titik Ekstrim)
Titik dari himpunan konveks yang tidak berada di dalam segmen garis yang menghubungkan dua titik la in di dala m himpunan tersebut dinamakan t itik e kstrim. Jika x S adalah titik ekstrim, ma ka tidak ada x1,x2 S sehingga x1 (1 )x2 S
untuk (0,1). Dengan kata lain, jika x titik e kstrim dan x1 (1 )x2 S untuk
) 1 , 0
( maka x x1 x2.
(Rao, 1984)
Teore ma 2
Se mua solusi fisibel basis adalah titik e kstrim dari himpunan konveks dari solusi fisibel.
(Rao, 1984) Bukt i:
Misalkanx [b1,b2,....,bm,bm1,0,..,0] adalah suatu solusi fisibel basis untuk PL. Dari Teore ma 1 diketahui bahwa daerah fisibel adalah himpunan konveks.
Misalkan x S bukan tit ik ekstrim, maka ada y,z S dimana y zsedemikian
sehingga x y (1 )z, 0 1 (4) Diketahui bahwa
] 0 ,.., 0 , , ,...., ,
[b1 b2 bm bm1 x
] ,.., , ,...., ,
[y1 y2 ym ym 1 yn y
] ,.., , ,...., ,
[z1 z2 zm zm1 zn z
untuk j m 1 diketahui xj 0 dan dari
persamaan (4)
j j
j y z
x (1 )
dimana λ 0,yj 0,zj 0. Hal ini hanya
akan terjadi jika yj 0dan zj 0. Selain itu karena x, ydan z fisibel ma ka
b Ax
b
Ay (5)
b Az
Misalkan aj kolo m ke-j dari matriks A
ma ka persa maan (5) dapat ditulis sebagai berikut:
b aj j n
j
x
1
b aj j n
j
y
1
(6)
b aj j n
j
z
1
karena untuk j m 1, ele men xj 0,
0
j
y dan zj 0 ma ka persa maan (6)
secara individu dapat ditulis
b aj j m
j
x
1
(7.a )
b aj j m
j
y
1
(7.b )
b aj j m
j
z
1
(7.c )
Jika persamaan (7.b) dikurangi oleh persamaan (7.c) menghasilkan
0 ) (
0
1
1 1
j j m
j
j m
j j m
j
z y
z y
j
j j
a
a a
Karena untuk j m, aj adalah kolo m
dari matriks A yang bersesuaian dengan variabel basis maka aj (j 1,...,m) saling
bebas linear (De finisi 4).
Karena aj saling bebas linear, maka
0 ) (
1
j j m
j
z y
j
a menyebabkanyj zj 0
untuk j,j 1,...,m. Akibatnya yj zj ,
m j
1
.
Seperti telah diketahui sebelumnya 0
j j z
y untuk m 1 j n, maka
z
Definisi 11 (Bilangan Inter val)
Bilangan interval pada garis bilangan adalah himpunan seluruh titik (bilangan) di antara dua titik u jung tertentu pada garis bilangan .
(Jeffrey, 2005)
Definisi 12 (Inter val tertutup)
Misalkan (a,b) dan a b. Interval tertutup [a,b] dari a ke b adalah
} |
{x a x b .
(Fra leigh,1969)
III PEMBAHASAN
Masalah LPIC me miliki koefisien interval, baik pada fungsi objektif maupun kendala. Salah satu cara untuk menyelesaikan masalah LPIC ini adalah dengan menggunakan metode yang dike mbangkan oleh JW Chinneck dan K Ra madan (2000). Metode ini merupakan generalisasi dari metode Shaocheng (1994), yaitu diperluas dengan: (i) me masukkan variabel yang tidak me miliki batasan tanda atau variabel urs (unrestricted in sign) pada x0 (variabel yang tidak terka it koefisien interval); (ii) me masukkan variabel tak positif, baik yang terkait da la m interval atau tida k; dan (iii) me masukkan kendala berbentuk persamaan.
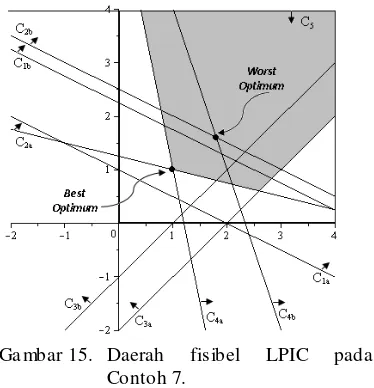
Tujuan LPIC adalah menentukan solusi best optimum dan worst optimum. Permasalahan LPIC yang akan dibahas hanya masalah min imisasi. Jika model berupa kasus ma ksimisasi, ma ka model tersebut diubah men jadi kasus min imisasi dengan cara mengalikan fungsi objektif dengan (-1). Pada kasus min imisasi, best optimum adalah solusi optimu m dengan nilai fungsi objektif terkec il dan worst optimum adalah solusi optimu m dengan nilai fungsi objekt if terbesar.
Solusi optimu m pada LPIC didapatkan dengan mencari versi khusus dari fungsi objektif dan kendala yang mengoptimu mkan model, yaitu dipilih suatu nilai spesifik (nilai ekstrim) pada koefisien interval yang me mbuat model LPIC tersebut optimu m. Suatu kendala berkoefisien interval a kan me miliki kendala spesifik (kendala dengan koefisien tentu) berjumlah tak hingga. Jadi untuk me mperoleh solusi optimu m, dipilih versi ekstrim kendala yang koefisiennya berupa kombinasi batas bawah dan batas atas koefisien interval.
Metode LPIC menyandarkan hubungan antar daerah fisibel dari kendala-kendala spesifik. Misalkan C adalah himpunan kendala dengan koefisien interval, CI dan
II
C adalah dua himpunan kendala berbeda yang dibangkitkan dari C dengan menggunakan versi ekstrim C. Daerah fisibel
yang memenuhi kendala CI disebut SI, sedangkan daerah fisibel yang me menuhi kendala CII disebut SII. Daerah fisibel tersebut me miliki hubungan sebagai berikut: 1. SI SII atau SII SI, yaitu suatu
daerah fisibel seluruhnya termuat dala m daerah fisibel la innya.
2. SI SII dan SI SII , yaitu suatu daerah fisibel me motong sebagian daerah fisibel la innya.
3. SI SII , yaitu tidak ada tumpang tindih (overlap) pada daerah-daerah fisibel.
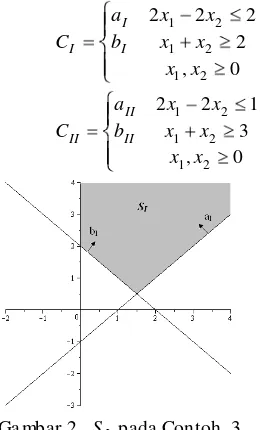
Contoh 3:
Misalkan
C
adalah himpunan kendala sebagai berikut:0 ,
] 3 , 2 [
] 2 , 1 [ 2 2
2 1
2 1
2 1
x x
x x b
x x a
C .
Jadi dapat dia mbil kendala spesifikCI dan
II
C sebagai berikut:
0 ,
2 2 2 2
2 1
2 1
2 1
x x
x x b
x x a
C I
I I
0 ,
3 1 2 2
2 1
2 1
2 1
x x
x x b
x x a
C II
II II
[image:14.596.325.455.499.714.2]Ga mbar 3. SII pada Contoh 3.
ma ka SII SI, sebagaimana diilustrasikan oleh Ga mbar 4.
Ga mbar 4. Dae rah fisibel C pada Contoh 3.
Contoh 4:
Misalkan C adalah himpunan kendala sebagai berikut:
0 ,
4 ] 4 , 3 [
2 ]
2 , 1 [
2 1
2 1
2 1
x x
x x
b
x x a
C .
Jadi dapat dia mbil kendala spesifikCI dan
II
C sebagai berikut:
0 ,
4 3
2 2
2 1
2 1
2 1
x x
x x b
x x a
C I
I I
0
,
4
4
2
2 1
2 1
2 1
x
x
x
x
b
x
x
a
C
IIII
II
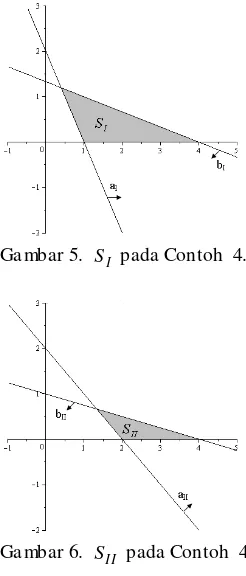
Ga mbar 5. SI pada Contoh 4.
Ga mbar 6. SII pada Contoh 4.
ma kaSI SII dan SI SII sebagaimana diilustrasikan oleh Ga mbar 7.
Ga mbar 7. Daerah fisibel SI SII pada Contoh 4.
Contoh 5:
Misalkan himpunan kendala C sebagai berikut:
2 2
1 ] 1 , 1 [ ] 1 , 1 [
2 1
2 1
x c
x b
x x
a
C .
Jadi dapat dia mbil kendala spesifikCI dan
II
C sebagai berikut:
2 2 1
2 1
2 1
x c
x b
x x a C
I
[image:15.596.106.519.73.766.2] [image:15.596.115.235.84.212.2] [image:15.596.324.447.86.374.2] [image:15.596.118.282.237.417.2]2 2
1
2 1
2 1
x c
x b
x x a C
II
II
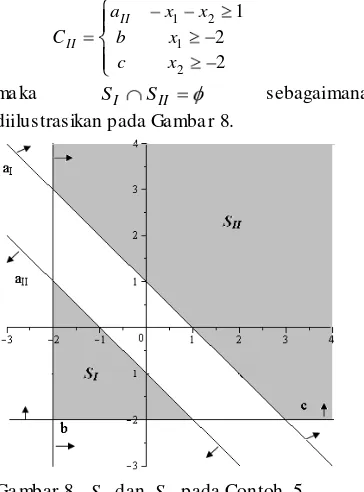
ma ka SI SII sebagaimana
diilustrasikan pada Ga mba r 8.
Ga mbar 8. SI dan SIIpada Contoh 5.
Permasalahan model LPIC dibagi men jadi dua, yaitu menyelesaikan LPIC dengan kendala berupa pertidaksamaan interval dan menyelesaikan LPIC dengan kendala persamaan interval.
3.1 LPIC deng an kendala perti daksamaan inter val
Bentuk u mu m model LPIC dengan kendala berupa pertidaksamaan interval adalah sebagai berikut:
Min
n
j
j j j c x
c Z
1
,
terhadap:
n
j
i i j ij
ij a x b b
a
1
,
, , (1)
untuk i 1,...,m
,
j
si 0
x
x
j
x dan xj 0 untuk
si
x
j
x . cj,cj ,aij,aij ,bi,bi I( ) dimana I( ) adalah himpunan seluruh bilangan interval pada .
Keterangan:
x = (x1,x2,x3,....,xn), dimanaxj adalah variabel ke-j.
x0 = variabel-variabel yang yang tidak terkait dengan koefisien interval, baik variabel tak negatif (xj 0)
atau variabel tak positif (xj 0)
maupun variabel urs (unrestricted in sign).
xsi = variabel-variabel yang terkait dengan koefisien interval, berupa variabel tak negatif atau variabe l tak positif.
ij
a = batas atas koefisien interval dari variabel ke-j pada kendala ke -i.
ij
a = batas bawah koefisien interval dari
variabel ke-j pada kendala ke-i.
i
b = batas bawah koefisien interval dari nila i ruas kanan/RHS (Right Hand Side)
pada kendala ke-i.
i
b = batas bawah koefisien interval dari nila i ruas kanan/RHS pada kendala ke-i.
j
c = batas atas koefisien interval variabel ke-j pada fungsi objektif.
j
c = batas bawah koefisien interval
variabel ke-j pada fungsi objekt if.
Tiap pertida ksamaan i pada (1) yang me miliki p koefisien interval dapat ditransformasikan menjadi 2p pertidaksamaan ekstrim yang berbeda. Pertidaksa maan tersebut diperoleh dengan cara mengo mbinasikan nila i batas atas dan batas bawah koefisien. Solusi optimu m diperoleh dengan me milih satu versi
pertidaksamaan ekstrim da ri 2p
pertidaksamaan ekstrim yang
mengoptimu mkan fungsi objektif. Formula pertidaksamaan khusus yang diperoleh dari pengaturan tiap batas bawah atau batas atas koefisien interval dina ma kan formula kara kteristik.
Pandang satu pertidaksamaan ke-i pada (1) dan Sk adalah himpunan solusi
pertidaksamaan e kstrim ke-k diantara 2p pertidaksamaan ekstrim yang berbeda dari i.
Misalkan
p
k Sk
S
2
1 adalah gabungan dari
seluruh himpunan solusi pertidaksamaan
ekstrim dan
pk Sk
S 2
1 adalah irisan dari
seluruh himpunan solusi pertidaksamaan ekstrim. Ilustrasi dari pengertian tersebut pada dua
[image:16.596.116.298.88.334.2]Ga mbar 9. Ilustrasi irisan himpunan solusi dua pertidaksamaan (S).
Ga mbar10. Ilustrasi gabungan himpunan
solusi dua pertidaksamaan (S).
Definisi 1
Untuk setiap pertidaksamaan kendala pada (1), jika ada suatu versi ekstrim pada formula kara kteristik sedemikiran rupa sehingga himpunan solusinya sama dengan S, maka versi in i disebut dengan pertidaksamaan range nila i ma ksimu m. Sedangkan jika suatu versi ekstrim pada formu la ka rakteristik sedemikiran rupa sehingga himpunan solusinya sama dengan S, maka versi ini disebut dengan disebut pertidaksamaan range nila i min imu m.
Contoh 6:
] 6 , 4 [ ] 5 , 2 [ 3 ,
1 x1 x2 , dimana x1,x2 0.
Pertidaksa maan interval ini me miliki 3 koefisien interval sehingga dapat dipecah men jadi 23 8pertidaksamaan e kstrim : (a) x1 2x2 4 (e) 3x1 2x2 4 (b) x1 2x2 6 (f) 3x1 2x2 6 (c) x1 5x2 4 (g) 3x1 5x2 4
(d) x1 5x2 6 (h) 3x1 5x2 6
Ga mbar 11. S pada Contoh 6.
Ga mbar 12. S pada Contoh 6.
Dapat dilihat dari Ga mbar 11 dan Ga mbar 12 bahwa S x 2|3x1 5x2 4 , sehingga
pertidaksamaan 3x1 5x2 4 (g) disebut
pertidaksamaan range nila i ma ksimu m. Sedangkan S x 2|x1 2x2 6 sehingga pertidaksamaan x1 2x2 6 (b) disebut pertidaksamaan range nilai minimu m.
Teore ma 1
Jika ada pertidaksa maan interval
b b x a
a j
n
j j
j, ,
1
dimana xj x0 xsi,
0
j
x untuk xj
x
si, maka a xj b nj j 1
adalah pertidaksamaan range nila i ma ksimu m
dan
n
j j jx b
a
1
adalah pertidaksa maan
[image:17.596.324.481.83.452.2] [image:17.596.116.302.88.332.2] [image:17.596.321.512.550.703.2]Bukt i:
Misalkan
n
j j jx b
a
1
adalah sembarang
versi khusus pertidaksamaan interval. Maka untuk sembarang solusi khusus xj 0
dimana xj
x
si, kita me mpunyain
j
n
j j j j
jx a x
a
1 1
. Misalkan x me menuhi
n
j j jx b
a
1
, ma ka x me menuhi
n
j j jx b b
a
1
. Akibatnya x juga
me menuhi
n
j j jx b
a
1
,untuk b,b b b.
Jadi terdapat sebuah titik x yang harus me menuhi seluruh versi pertidaksamaan interval la in secara bersamaan. Akibatnya,
berdasarkan Defin isi 1,
n
j j jx b
a
1
adalah
pertidaksamaan range nilai minimu m. Untuk sembarang solusi khusus xj 0
dimana xj
x
si, kita juga me miliki nj
n
j j j j
jx a x b b
a
1 1
. Misalkan x
me menuhi
n
j j jx b
a
1
, ma ka x juga
me menuhi
n
j j jx b
a
1
. Akibatnya x
me menuhi
n
j j jx b
a
1
, untuk
b b b
b, . Oleh karena itu, solusi x yang me menuhi sembarang versi pertidaksa maan interval juga akan dipenuhi oleh
n
j j jx b
a
1
. Jadi berdasarkan Defin isi 1,
n
j j jx b
a
1
adalah pertidaksamaan range
nila i ma ksimu m.
Akibat 1
Untuk xj 0 dimana
si
x
j
x , maka
b x
a j
n
j j 1
adalah pertidaksamaan range
nila i ma ksimu m dan
n
j j jx b
a
1
adalah
pertidaksamaan range nilai minimu m.
Bukt i:
Misalkan
n
j j jx b
a
1
adalah sembarang
versi khusus pertidaksamaan interval. Maka untuk sembarang solusi khusus xj 0
dimana xj
x
si, kita me mpunyain
j
n
j j j j
jx a x
a
1 1
. Misalkan x me menuhi
n
j j jx b
a
1
, maka x juga me menuhi
n
j j jx b b
a
1
. Akibatnya x juga
me menuhi
n
j j jx b
a
1
,untuk b,b b b.
Jadi terdapat sebuah titik x yang harus me menuhi seluruh versi pertidaksamaan interval la in secara bersamaan. Akibatnya,
berdasarkan Defin isi 1,
n
j j jx b
a
1
adalah
pertidaksamaan range nilai minimu m. Untuk sembarang solusi khusus xj 0
dimana xj
x
si, kita juga me miliki nj
n
j j j j
jx a x b b
a
1 1
. Misalkan x
me menuhi
n
j j jx b
a
1
, ma ka x juga
me menuhi
n
j j jx b
a
1
. Akibatnya x
me menuhi
n
j j jx b
a
1
, untuk
b b b
n
j j jx b
a
1
. Jadi berdasarkan Defin isi 1,
n
j j jx b
a
1
adalah pertidaksamaan range
nila i ma ksimu m.
Teore ma 2
Jika j
n
j j j c x
c Z
1
, adalah fungsi objektif
untuk xj 0 dimana xj
x
si, makan j n j j j j
jx c x
c
1 1
untuk solusi x yang
diberikan.
Bukt i:
Diketahuti c c dan xj 0dimana
si
x
j
x , maka cxj cxj. Untuk
n
j 1,2,..., dapat ditulis:
n j n j j j j j n n x c x c x c x c x c x c x c x c 1 1 2 2 1 1 .... .... Jadi n j n j j j j
jx c x
c
1 1
berlaku untuk solusi
x yang diberikan.
Akibat 2
Untuk xj 0, dimana xj
x
si, makan j n j j j j
jx c x
c
1 1
Bukt i:
Diketahuti c c dan xj 0dimana
si
x
j
x , maka cxj cxj. Untuk
n
j 1,2,..., dapat ditulis:
n j n j j j j j n n x c x c x c x c x c x c x c x c 1 1 2 2 1 1 .... .... Jadi n j n j j j j
jx c x
c
1 1
berlaku untuk solusi
x yang diberikan.
Definisi 2
Untuk masalah min imisasi dengan xj 0
dimana xj
x
si ,n j j jx c 1
dina ma kan
fungsi objektif terbaik (most favourable
objective function) dan
n j j jx c 1 dina makan
fungsi objektif terburuk (least favourable objective function) .
Teorema 1 dan Teore ma 2 menyediakan perhitungan dalam mencari solusi best optimum dan worst optimum LPIC, yaitu dengan mengubah masalah LPIC asli menjadi dua PL. Pe mecahan masalah LPIC adalah dengan menggunakan fungsi objektif terba ik dan pertidaksamaan range nilai ma ksimu m untuk menentukan solusi best optimum. Sedangkan untuk menentukan solusi worst optimum, digunakan fungsi objektif terburuk dan pertidaksamaan range nila i min imu m
Algoritma 1: Pe nyelesaian LPIC de ngan kendala berupa perti daksamaan inter val. Diberikan : min n
j cj cj xj
Z
1 , dengan
kendala n
j 1aij,aij xj bi,bi , dimana
m
i 1,..., dan xj, xj (x0 xsi). 1. Bentuk LPIC men jadi PL:
Min n j j jx c z 1 '
, dimana xj
x
siBerdasarkan Teore ma 2 cukup dipilih:
n
j
i i j ijx b
a
1 '
, , dimana xj
x
siBerdasarkan Teore ma 1 cukup dipilih:
0 , 0 , ' j ij j ij ij x a x a a
Dica ri best optimum dengan menyelesaikan PL diatas.
2. Bentuk LPIC men jadi PL:
Min n j j jx c z 1
" , dimana
x
si jx
Berdasarkan Teore ma 2 cukup dipilih:
0 , 0 ,
"
j j j j j x c x c c terhadap: n j i i j ijx ba
1
,
" , dimana xj
x
siBerdasarkan Teore ma 1 cukup dipilih:
0 , 0 , " j ij j ij ij x a x a a
Dica ri worst optimum dengan menyelesaikan PL diatas.
Algorit ma 1 menggambarkan metode umu m untuk mengatasi kasus min imisasi pada LPIC dengan kendala yang me miliki batasan saja. Jika kendala me miliki batasan ma ka kendala tersebut dikalikan dengan (-1).
Contoh 7:
Selesaikan LPIC dengan kendala pertidaksamaan interval berikut:
Min Z [1,3]x1 [2,4]x2
terhadap: 0 , 4 : ] 7 , 6 [ ] 5 , 3 [ : ] 1 , 2 [ : 5 ] 4 , 2 [ : ] 9 , 6 [ ] 6 , 4 [ ] 3 , 2 [ : 2 1 2 5 2 1 4 2 1 3 2 1 2 2 1 1 x x x C x x C x x C x x C x x C
Dengan menggunakan Algoritma 1, maka akan didapatkan solusi best optimum dari PL sebagai berikut:
Min z x1 2x2
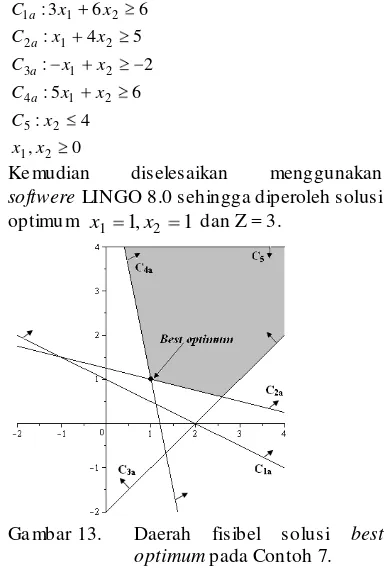
terhadap: 0 , 4 : 6 5 : 2 : 5 4 : 6 6 3 : 2 1 2 5 2 1 4 2 1 3 2 1 2 2 1 1 x x x C x x C x x C x x C x x C a a a a
Ke mudian diselesaikan menggunakan softwere LINGO 8.0 sehingga diperoleh solusi optimu m x1 1,x2 1 dan Z = 3.
Ga mbar 13. Daerah fisibel solusi best optimum pada Contoh 7.
Sedangkan untuk solusi worst optimum, LPIC tersebut diubah menjadi PL sebagai berikut:
Min z 3x1 4x2
terhadap: 0 , 4 : 7 3 : 1 : 5 2 : 9 4 2 : 2 1 2 5 2 1 4 2 1 3 2 1 2 2 1 1 x x x C x x C x x C x x C x x C b b b b
Ke mudian diselesaikan menggunakan softwere LINGO 8.0 sehingga diperoleh solusi optimu m x1 1.8,x2 1.6 dan Z = 11.8.
Ga mbar 14. Daerah fisibel solusi worst optimum pada Contoh 7.
[image:20.596.118.513.82.730.2] [image:20.596.320.514.87.376.2]Ga mbar 15. Daerah fisibel LPIC pada Contoh 7.
Sebagaimana PL b iasa, PL pada Algorit ma 1 me miliki 3 hasil yang mungkin, yaitu: (i) t itik optimu m finite bounded; (ii) unboundedness; atau (iii) infeasibility, akibatnya LPIC me miliki beberapa ke mungkinan berikut :
Jika solusi best optimum infeasible, maka seluruh LPIC infeasible.
Contoh 8:
Min Z x1 1,3x2 terhadap: 0 , ] 7 , 5 [ ] 2 , 1 [ : ] 1 , 2 [ : 2 1 2 1 2 2 1 1 x x x x C x x C
Solusi best optimum pada masalah LPIC d i atas adalah sebagai berikut:
Min Z x1 x2 terhadap: 0 , 5 2 : 2 : 2 1 2 1 2 2 1 1 x x x x C x x C a a
Dengan menggunakan softwere LINGO 8.0, solusi PL tersebut adalah infeasible, ma ka seluruh PL dari masalah LPIC di atas juga akan menghasilkan solusi infeasible.
Jika solusi worst optimu m unbounded, ma ka seluruh LPIC unbounded.
Contoh 9:
Min Z [1,2]x1 x2 terhadap: 0 , ] 8 , 5 [ ] 3 , 1 [ : 1 ] 4 , 2 [ : 2 1 2 1 2 2 1 1 x x x x C x x C
Solusi worst optimum pada masalah LPIC d i atas adalah sebagai berikut:
Min Z 2x1 x2 terhadap: 0 , 8 : 1 2 : 2 1 2 1 2 2 1 1 x x x x C x x C b b
Dengan menggunakan softwere LINGO 8.0, solusi PL tersebut adalah unbounded, maka seluruh PL dari masalah LPIC di atas juga akan menghasilkan solusi unbounded.
Jika solusi best optimum feasible dengan nila i
z
dan worst optimum infeasible, ma ka LPIC yang optimu m me miliki range antaraz
dan infeasibility.Contoh 10:
Min Z x1 1,3x2 terhadap: 0 , ] 7 , 2 [ ] 2 , 1 [ : ] 1 , 3 [ ] 2 , 1 [ : 2 1 2 1 2 2 1 1 x x x x C x x C
Pada kendala C1, koefisien interval padax2bertanda negatif. Oleh ka rena itu, kendala in i diubah terlebih dahulu men jadi: ] 1 , 3 [ ] 1 , 2 [
: 1 2
1 x x
C
Solusi best optimum pada masalah LPIC d i atas adalah sebagai berikut:
Min Z x1 x2 terhadap: 0 , 2 2 : 3 : 2 1 2 1 2 2 1 1 x x x x C x x C a a
Dengan menggunakan softwere LINGO 8.0, solusi dari PL tersebut adalah
0 , 1 2 1 x
x dan z 1.
Sedangkan solusi worst optimum pada masalah LPIC di atas adalah sebagai berikut:
[image:21.596.114.301.86.280.2]Dengan menggunakan softwere LINGO 8.0, solusi dari PL tersebut adalah infeasible.
Jadi masalah LPIC tersebut me miliki nila i optimu m yang berada antara z 1 dan infeasibility. Daerah fisibel pada solusi best optimum digambarkan sebagai berikut:
Ga mbar 16. Daerah fisibe l pada Contoh 10.
Jika solusi worst optimum feasible dengan nilai z dan best optimum unbounded, maka LPIC yang optimu m me miliki range antara dan z.
Contoh 11:
Min Z [1,3]x1 x2 terhadap:
0 ,
] 7 , 5 [ ] 1 , 1 [ 3 :
1 4 ] 1 , 2 [ :
2 1
2 1
2
2 1 1
x x
x x
C
x x C
Solusi best optimum pada masalah LPIC d i atas adalah sebagai berikut:
Min Z x1 x2 terhadap:
0 ,
5 3
:
1 4 :
2 1
2 1 2
2 1 1
x x
x x C
x x C
a a
Dengan menggunakan softwere LINGO 8.0, solusi dari PL tersebut adalah unbounded. Sedangkan solusi worst optimum pada masalah LPIC d i atas adalah sebagai berikut:
Min Z 3x1 x2 terhadap:
0 ,
7 3
:
1 4 2 :
2 1
2 1 2
2 1 1
x x
x x C
x x C
b b
Dengan menggunakan softwere LINGO 8.0, solusi dari PL tersebut adalah
1 . 1 , 7 .
2 2
1 x
x dan z 7.
Jadi masalah LPIC tersebut me miliki nila i optimu m yang berada antara
dan z 7. Daerah fisibel pada solusi worst optimum digambarkan sebagai berikut:
Ga mbar 17. Daerah fisibe l pada Contoh 11.
3.2 LPIC deng an kendal a persamaan inter val
Bentuk u mu m model ini ada lah sebagai berikut:
Min
n
j
j j j c x
c Z
1
,
Dengan kendala
n
j
i i j ij
ij
a
x
b
b
a
1
,
,
,(1) untuk i 1,...,m
,
j
si 0
x
x
j
x dan xj 0 untuk
si
x
j
x . cj,cj ,aij,aij ,bi,bi I( ) dimana I( ) adalah himpunan seluruh bilangan interval pada .
[image:22.596.343.506.179.369.2] [image:22.596.326.511.440.614.2]Teore ma 3
Pada kendala persa maan berbentuk interval
n
j
j j
j a x bb
a
1
,
, (2)
ma ka sepasang kendala pertidaksamaan berikut:
n
j j jx b
a
1
' , xj
x
si0 , 0 , ' j j j j
j a x
x a
a (3)
.
n
j j jx b
a
1
" , xj
x
si0 , 0 , " j j j j j x a x a
a (4)
mendefinisikan daerah konveks dimana tiap titiknya me menuhi sembarang versi khusus kendala persamaan interval.
Bukt i:
Misalkan x adalah suatu titik yang me menuhi sembarang versi khusus persamaan interval
n
j j jx b
a
1
.
Untuk xj 0 dimana xj
x
si, makan j n j n j j j j j j
jx a x b a x
a
1 1 1
)
( dan
b b
b .
Oleh karena itu,
n j n j j j j
jx a x b b
a
1 1
)
( , maka x juga
me menuhi
n
j j jx b
a
1
. Sela in itu,
n j n j j j j
jx b a x
a b
1 1
)
( , maka x juga
me menuhi n j j jx a b 1 atau n j j jx b
a
1
.
Jadi x me menuhi pertidaksa maan
n
j j jx b
a 1 dan n j j jx b
a
1
.
Misalkan { | , 0}
1
1 j
n
j j jx b x
a
S x dan
S
2 1,x
x dimana x1 (x1',x2',...,x'n),
) ,..., ,
(x1" x"2 x"n
2
x , ma ka:
n
j j jx b
a
1
' , dimana ' 0 j
x
(a)
n
j j jx b
a
1
" , dimana " 0 j
x
(b) Jika persamaan (a) dikalikan dengan dan persamaan (b) dikalikan dengan 1 ,
1
0 dan kemudian keduanya
diju mlahkan, maka didapat:
) ) 1 ( ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( 1 " ' 1 1 " ' 1 " 1 ' b x x a b b x a x a b x a b x a n j j j j n j n j j j j j n j j j n j j j 1 " ' " 1 '
1 (1 ) ,...., (1 ) )
( x x xn xn S
1 " " 1 ' '
1,...., ) (1 )( ,...., )
(x xn x xn S
1
) 1
( 2 S
1 x
x
Jadi { | , 0}
1
1 j
n
j j jx b x
a
S x adalah
daerah konveks.
Misalkan { | , 0}
1
2 j
n
j j jx b x
a
S x dan
S
2 1,x
x dimana x1 (x1',x2',...,x'n),
) ,..., ,
(x1" x"2 x"n
2
x , ma ka:
n
j j jx b
a
1
' , dimana ' 0 j
x
(d)
n
j j jx b
a
1
" , dimana " 0 j
x
(e) Jika persamaan (d) dikalikan dengan dan persamaan (e) d ika likan dengan 1 ,
1
0 dan kemudian keduanya
) ) 1 ( ( ) 1 ( ) 1 ( ) 1 ( ) 1 ( 1 " ' 1 1 " ' 1 " 1 ' b x x a b b x a x a b x a b x a n j j j j n j n j j j j j n j j j n j j j 1 " ' " 1 '
1 (1 ) ,...., (1 ) )
( x x xn xn S
1 " " 1 ' '
1,...., ) (1 )( ,...., )
(x xn x xn S
1
) 1
( 2 S
1 x
x
Jadi { | , 0}
1
2 j
n
j j jx bx
a
S x adalah
daerah konveks.
Jadi pertida ksamaan (3) dan (4) me rupakan daerah konveks dimana tiap titiknya me menuhi sembarang versi khusus kendala persamaan interval.
Pe mbuktian in i analog untuk xj 0 dimana
si
x
j
x .
Berdasarkan Teore ma 3, jika model LPIC me miliki kendala persa maan interval maka kendala persamaan tersebut diubah menjadi bentuk pertidaksamaan (3) dan (4). So lusi pada model PL ini menghasilkan nila i fungsi objektif terbaik.
Algoritma 2 : mene ntuk an setting koefisien best optimum untuk kendala persamaan inter val.
Diberikan k kendala persamaan interval dari
bentuk
n
j
j j
j a x bb
a
1
,
, dan titik best
optimum x* yang telah diperoleh mela lui Tore ma 3. Dicari aij dan bi yang
mengoptimu mkan mode l.
Selesaikan Phase I dari PL untuk himpunan kendala berikut: Maks k i n j k i i ij b a
1 1 1
terhadap :
n
j
i ij ja b
x
1
0 , untuk
k i 1,....,
i i i ij ij ij b b b a a a ,
untuk i 1,....,k,j 1,...,n.
Pe mecahan Algoritma 2 menghasilkan versi khusus kendala persamaan interval yang me miliki solusi best optimum.
Teore ma 4
Pada saat kendala persamaan interval dari bentuk (2) dimasukkan pada model, maka solusi worst optimum akan terjadi pada salah satu kendala berikut :
n
j
i j ij
x
b
a
1
'
, dimana0 , 0 , ' j ij j ij
ij a x
x a
a (5)
atau
n
j
i j ij
x
b
a
1
"
, dimana0 , 0 , " j ij j ij ij x a x a
a (6)
Bukt i:
Andaikan titik worst optimum x me menuhi sembarang versi khusus kendala persamaan
interval
n
j j jx b
a
1
dan me miliki nila i
fungsi objektif z. Berdasarkan Teore ma 3, titik ini a kan berada pada daerah konveks dari solusi yang mungkin, didefinisikan oleh (3) dan (4). Pe rsamaan (5) dan (6) me rupakan versi persamaan ekstrim dari (3) dan (4). Misalkan z' adalah nilai fungsi objektif yang ditentukan saat PL yang sama dipecahkan
dengan cara mengganti
n
j j jx b
a
1
dengan
(5), dan z" adalah fungsi objektif yang ditentukan saat PL yang sama dipecahkan
dengan cara mengganti
n
j j jx b
a
1
dengan
(6). Berdasarkan asumsi bahwa tit ik worst optimum x me miliki nilai fungsi objektif z, ma ka z z' dan z z". Na mun, dikarenakan konveksitas dari daerah (3) dan (4), d imana (5) dan (6) merupakan versi persa maan ekstrim dari (3) dan (4), maka
]
[
', " maks z zz . Ha l ini menimbu lkan
worst optimum terjadi ketika sembarang versi
khusus kendala persamaan
n
j j jx b
a
1
dimasukkan pada PL t idak terbukt i. Oleh karena itu, tit ik worst optimum dite mu kan hanya pada saat kendala yang bersesuaian dengan (5) atau (6) d imasukkan pada PL.
Teorema 4 menje laskan bahwa solusi worst optimum akan terjad i pada persamaan (5) atau (6). Sayangnya, diantara kedua persamaan tersebut tidak diketahui mana yang akan menghasilkan worst optimum pada nila i fungsi objektif. Jadi solusi algorit manya adalah me masukkan masing-masing persamaan (5) dan (6) kedala m model sehingga menghasilkan dua model PL yang berbeda, selanjutnya dipilih nila i yang terburuk pada fungsi objektif tersebut. Secara umu m, jika ada k kendala persamaan interval, ma ka ada 2k PL yang harus dipecahkan untuk mene mu kan solusi worst optimum.
Contoh 12:
Selesaikan LPIC dengan kendala berkoefisien interval berikut :
Min Z x1 x2
terhadap: 0 , 3 : ] 2 , 1 [ : ] 3 , 1 [ ] 2 , 1 [ : ] 4 , 3 [ ] 3 , 2 [ : 2 1 2 4 2 1 3 2 1 2 2 1 1 x x x C x x C x x C x x C
Dengan menggunakan Teorema 3, maka masing-masing kendala persamaan interval
1
C dan C2 diubah menjadi sepasang kendala
pertidaksamaan interval, ya itu:
3 : 1 2 : 4 2 : 3 3 : 2 1 2 2 1 2 2 1 1 2 1 1 x x C x x C x x C x x C b a b a
Berdasarkan langkah 1 Algorit ma 1, kendala pertidaksamaan interval C3 diubah men jadi:
1
: 1 2
3 x x
Ca
Jadi model best optimum pada LPIC d iatas adalah:
Min Z x1 x2
terhadap: 0 , 3 : 1 : 3 : 1 2 : 4 2 : 3 3 : 2 1 2 4 2 1 3 2 1 2 2 1 2 2 1 1 2 1 1 x x x C x x C x x C x x C x x C x x C a b a b a
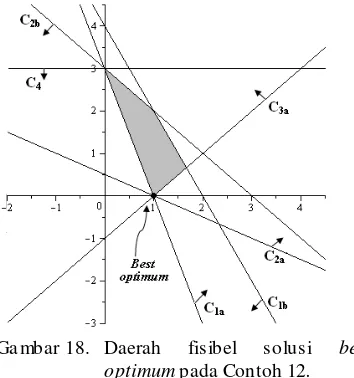
Ke mudian diselesaikan menggunakan softwere LINGO 8.0 sehingga diperoleh solusi optimu m x1 1,x2 0 dan Z = 1.
Ga mbar 18. Daerah fisibel solusi best optimum pada Contoh 12.
Dengan menggunakan Algoritma 2, maka akan didapatkan bentuk umum dari best optimum persamaan interval te rsebut, yaitu:
Maks a11 a22 b1 b2 terhadap: 2 2 2 1 1 1 22 22 22 11 11 11 2 22 2 21 1 1 12 2 11 1 0 0 b b b b b b a a a a a a b a x a x b a x a x Keterangan: 11
a = koefisien interval dari variabel x1
pada kendala C1
12
a = koefisien dari variabel x2 pada kendala C1
21
a = koefisien dari variabel x1 pada kendala C2
22
a = koefisien interval dari variabel x2
pada kendala C2
1
b = RHS berbentuk interval pada kendala
1
[image:25.596.326.503.233.422.2]2
b = RHS berbentuk interval pada kendala
2
C
11
a = batas bawah koefisien int