SISTEM INFORMASI GEOGRAFIS UNTUK MENENTUKAN RUTE TERPENDEK MENGGUNAKAN ALGORITMA DIJKSTRA
BERBASIS WEB (STUDI KASUS PADA SALAH SATU BIMBINGAN BELAJAR DI KOTA MEDAN)
SKRIPSI
DEBI SULARMAN HUTABALIAN 101421041
PROGRAM STUDI S1 EKSTENSI ILMU KOMPUTER FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA MEDAN
2014
SISTEM INFORMASI GEOGRAFIS UNTUK MENENTUKAN RUTE TERPENDEK MENGGUNAKAN ALGORITMA DIJKSTRA
BERBASIS WEB (STUDI KASUS PADA SALAH SATU BIMBINGAN BELAJAR DI KOTA MEDAN)
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Komputer
DEBI SULARMAN HUTABALIAN 101421041
PROGRAM STUDI S1 EKSTENSI ILMU KOMPUTER FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA MEDAN
2014
Judul SISTEM INFORMASI GEOGRAFIS UNTUK MENENTUKAN RUTE TERPENDEK MENGGUNAKAN ALGORITMA DIJKSTRA BERBASIS WEB (STUDI KASUS PADA SALAH SATU BIMBINGAN BELAJAR DI KOTA MEDAN)
Kategori SKRIPSI
Nama DEBI SULARMAN HUTABALIAN Nomor Induk Mahasiswa 101421041
Program Studi S1 EKSTENSI ILMU KOMPUTER Departemen ILMU KOMPUTER
Fakultas ILMU KOMPUTER DAN TEKNOLOGI INFORMASI (FASILKOM-TI)
Diluluskan di
Medan, 11 Februari 2014
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Marihat Situmorang, M. Kom Dr. Poltak Sihombing, M.Kom NIP 19631214 1989031 001 NIP 19620317 199103 1 001
Diketahui/Disetujui oleh
Departemen Ilmu Komputer Fasilkom-TI USU Ketua,
Dr. Poltak Sihombing, M.Kom NIP 19620317 199103 1 001
:
: : : : : :
PERNYATAAN
SISTEM INFORMASI GEOGRAFIS UNTUK MENENTUKAN RUTE TERPENDEK MENGGUNAKAN ALGORITMA DIJKSTRA
BERBASIS WEB (STUDI KASUS PADA SALAH SATU BIMBINGAN BELAJAR DI KOTA MEDAN)
SKRIPSI
Penulis mengakui bahwa skripsi ini adalah hasil kerja penulis sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, 11 Februari 2014
Debi Sularman Hutabalian 101421041
Segala puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus, atas berkat karunia, hikmat dan kebijaksanaan yang diberikan, sehingga penulis dapat menyelesaikan skripsi ini dengan baik.
Dengan segala kerendahan hati, pada kesempatan ini penulis menyampaikan terima kasih kepada semua pihak yang telah membantu penyelesaian skripsi ini. Penulis mengucapkan terima kasih kepada:
1. Bapak Prof. Dr. Syahril Pasaribu, DTMH, M.Sc(CTM), SpA(K) sebagai Rektor Universitas Sumatera Utara,
2. Bapak Prof. Muhammad Zarlis, M.Kom sebagai Dekan Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara,
3. Bapak Dr. Poltak Sihombing, M. Kom sebagai Ketua Jurusan Ilmu Komputer sekaligus sebagai Pembimbing I,
4. Ibu Maya Silvi Lydia, BSc. MSc sebagai Sekretaris Program Studi S1 Ilmu Komputer,
5. Bapak Drs.Marihat Situmorang, M.Kom selaku Pembimbing II dan sekaligus sebagai Dosen di Program Studi S1 Ilmu Komputer,
6. Bapak Drs. Agus Salim Harahap, M.Si sebagai Dosen Pembanding I dan sekaligus sebagai Dosen di Program Studi S1 Ilmu Komputer,
7. Bapak Ade Candra, S.T,. M.Kom sebagai Dosen Pembanding II dan sekaligus sebagai Dosen di Program Studi S1 Ilmu Komputer,
8. Seluruh Dosen dan Staff Pegawai di Program Studi S-1 Ilmu Komputer Universitas Sumatera Utara,
9. Dan teristimewa untuk kedua orang tua terkasih, Ayahanda Ringkot Hutabalian, S.Pd dan Ibunda Drs. Lindawati Siringo-ringo yang telah memberikan dukungan moril dan materil serta doa yang tidak ternilai kepada penulis sehingga dapat menyelesaikan skripsi ini.
10. Kak Rutdina Rusliani Hutabalian, Kak Togi Marito Hutabalian, A.Md dan Adik Putri Ningsih Astuti Hutabalian, A.Md, serta Bere-bere ku yang lucu, yang selalu memberikan dukungan dan semangat kepada penulis.
11. Terimakasih kepada teman-teman kuliah Program Ekstensi S1 Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara yang memberikan masukan, semangat kepada penulis.
12. Kepada Bapak dan Ibu Gembala GPdI Elshaddai, Youth Pastor El’s Generation Pdm. Moody Tambuwun, S.Si dan seluruh teman-teman sepelayanan di GPdI Elshaddai atas doa yang tulus, dorongan, semangat, dan motivasi kepada penulis.
13. Kepada Seluruh teman-teman Komsel 3G, yang sudah banyak memberikan semnagat bahkan doa selama ini.
14. Kepada Dytha_Pianist, makasih nyuk buat motivasinya, doa, dukungan yang tak pernah pudar untuk membakar kobaran api semangat agar dapat memperjuangkan skripsi ini sampai tuntas.
15. Dan tidak lupa kepada seluruh rekan-rekan seperjuangan S1 Ekstensi stambuk 2010 Kom A dan Kom B, serta abang-abang dan kakak-kakak senior yang ada di Program Studi S1 Ilmu Komputer yang telah memberikan dukungan moril kepada penulis dalam penyelesaian skripsi ini.
Sekali lagi penulis mengucapkan terima kasih kepada semua pihak yang membantu dalam penyelesaian skripsi ini yang tidak dapat disebutkan satu persatu, terima kasih atas ide, saran, dan motivasi yang diberikan.
Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan. Oleh karena itu penulis menerima kritik dan saran dari semua pihak yang bersifat membangun dan menyempurnakan skripsi ini. Penulis berharap semoga skripsi ini bermanfaat bagi penulis sendiri pada khususnya dan pembaca pada umumnya.
Terima kasih, Tuhan Yesus Memberkati.
Medan, 11 Februari 2014
Debi Sularman Hutabalian
Kota Medan merupakan wilayah Kota yang sedang berkembang dan juga menjadi pusat daerah perdagangan, perindustrian, perkantoran, pariwisata, pendidikan dan lain-lain. Sebagai kota yang sedang berkembang, maka perlu dibangun s e b u a h l a y a n a n i n f o r m a s i m e n g e n a i f a s i l i t a s u m u m d i K o t a M e d a n Penulis membuat sebuah aplikasi Sistem Informasi Geografis untuk menetukan jarak terpendek suatu Bimbingan Belajar. Google maps digunakan untuk menampilkan peta online dan lintasan terpendek yang akan dilalui, serta jarak yang akan di tempuh. Metode yang digunakan untuk mencari lintasan terpendek ini adalah algoritma Dijkstra. Algoritma Dijkstra adalah sebuah algoritma rakus (greedy algorithm) yang dipakai dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah (direct graph) dengan bobot sisi yang bernilai positif dan terlebih dahulu menentukan node awal dan node tujuan dengan jumlah bobot terkecil.
Kata Kunci: Sistem Informasi Geografis, Pencarian Lintasan Terpendek, Algoritma Dijkstra
Web Based Geographic Information System To Determine Shortest Path Using Dijkstra Algorthm (Case Study One Of
Education Center In Medan City)
ABSTRACT
Medan is a developing city and center of commerce, industry, offices, government, t o u r i s m , e d u c a t i o n a n d e t c . A s t h e d e v e l o p i n g c i t y , s o n e e d b e b u i l t w i t h i n f o r m a t i o n s e r v i c e l i k e p u b l i c f a c i l i t y i n t h e M e d a n C i t y . After did research, writer make an application of Geographical Information System to determines shortest distance of Education Center. Google maps is used to show online map and shortest path will be traveled and then distance will be taken on. Method is used to search this shorter path is Algorithm of Dijkstra. Algorithm of Di j ks t r a i s a gr e e dy a l gor i t h m us e d t o s ol ve s hor t e s t pa t h p r obl e m fo r a direct graph with positive weight and before that determined the first node a n d t h e p u r p o s e n o d e w i t h t h e s u m o f s m a l l w e i g h t .
Keyword : Geographic Information System, Determing a Shortest Path, Dijkstra’s Algoritm
Halaman
Judul i
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak vi
1.2 Perumusan Masalah 4
1.3 Batasan Masalah 4
1.4 Tujuan Penelitian 5
1.5 Manfaat Penelitian 5
1.6 Metode Penelitian 5
1.7 Sistematika Penulisan 6
Bab 2 Landasan Teori 7
2.1 Pengertian Sistem Informasi Geografis 7
2.1.1 Data Spasial 9
2.4 Pencarian Rute Terpendek Dengan Algoritma Dijkstra 16
2.5 Geografis Kota Medan 17
Bab 3 Analisis dan Perancangan Sistem 19
3.1 Analisis Sistem 19
3.1.1 Analisis Masalah 19
3.1.2 Analisis Kebutuhan Sistem 20
3.1.2.1 Kebutuhan Fungsional Sistem 20 3.1.2.2 Kebutuhan Nonfungsional Sistem 21
3.1.3 Pemodelan 21
3.1.3.1 Diagram Konteks 22
3.1.3.2 Data Flow Diagram (DFD) 22 3.1.3.2.1 Data Flow Diagram (DFD) Level 0 23 3.1.3.2.2 Data Flow Diagram (DFD) Level 1 23
3.1.3.2.3 Data Flow Diagram (DFD) Level 2 24 3.1.3.3 Model Data (Entity Relationship Diagram) 25
3.1.3.4 Desain Database 25 3.2 Perancangan Sistem Antar Muka (Interface) 33
3.2.1 Perancangan Input 33
3.2.1.1 Perancangan Input Berita 33
3.2.1.2 Perancangan Ubah Password 34 3.2.1.3 Perancangan Input Admin 35 3.2.1.4 Perancangan Input Jarak Terpendek 36
3.2.2 Perancangan Output 37
3.2.2.1 Perancangan Olah Data Berita 37 3.2.2.2 Perancangan Olah Data Lokasi 38 3.2.2.3 Perancangan Olah Data Admin 39 3.2.2.4 Perancangan Hasil Pencarian Rute Terpendek 40
3.3 Perhitungan Rute Terpendek 40
Bab 4 Implementasi dan Pengujian Sistem 49
4.1 Implementasi Sistem 49
4.2 Tampilan Program 57
4.2.1 Halaman index 57
4.2.2 Halaman Buku Tamu 57
4.2.3 Halaman Tentang Algoritma Dijkstra 58
4.2.4 Halaman About Us 59
4.2.5 Halaman Pencarian Rute Terpendek 59
4.3 Pengujian 61
4.3.1 Pengujian Black Box (Black Box Testing) 61
4.3.2 Kasus dan hasil pengujian 62
4.3.2.1 Pengujian login 62
4.3.2.2 Pengujian pengolahan data admin 63 4.3.2.3 Pengujian pengolahan data cabang 65 4.3.2.4 Pengujian pengolahan data cabang 67 4.3.2.5 Pengujian pengolahan data berita 70 4.3.2.6 Pengubahan Data Password admin 72 4.3.2.7 Penginputan data komentar 73
4.3.2.8 Pencarian rute terpendek 73
Bab 5 Kesimpulan dan Saran 75
5.1 Kesimpulan 75
5.2 Saran 75
Daftar Pustaka 76
LAMPIRAN A : Listing Program A
DAFTAR TABEL
No. Tabel Nama Tabel Halaman
3.1 Tabel Admin 25
3.2 Tabel Lokasi 26
3.3 Tabel Berita 26
3.4 Tabel Buku Tamu 26
3.5 Data Objek Peta 42
4.1 Rencana Pengujian 61
4.2 Pengujian Login 62
4.3 Pengujian Input Data Admin 63
4.4 Pengujian Ubah Data Admin 64
4.5 Pengujian Hapus Data Admin 65
4.6 Pengujian Input Data Cabang 65
4.7 Pengujian Ubah Data Cabang 66
4.8 Pengujian Hapus Data Cabang 67
4.9 Pengujian Input Data Cabang 68
4.10 Pengujian Ubah Data Cabang 68
4.11 Pengujian Hapus Data Cabang 69
4.12 Pengujian Input Data Berita 70
4.13 Pengujian Ubah Data Berita 71
4.14 Pengujian Hapus Data Berita 71
4.15 Pengujian Ubah Data Password 72
4.16 Penginputan Data komentar 73
4.17 Pencarian rute terpendek 73
DAFTAR GAMBAR
No. Gambar Nama Gambar Halaman
2.1 Sub-Sistem SIG 8
2.2 Ilustrasi Urian Sub-Sistem SIG 9
2.3 Model data vector 10
2.4 Model Data Raster 11
2.5 Perbedaan Proyeksi (a) Cylindrical, (b)Planar dan (c) Conical
13
2.6 Contoh Graph Berarah dan Berbobot 14
2.7 Contoh Graph tidak berarah dan berbobot 15 2.8 Contoh Graph berarah dan tidak berbobot 15 2.9 Contoh Graph tidak berarah dan tidak berbobot 15
3.1 Diagram Ishikawa 20
3.8 Flowchart Ubah Password 29
3.9 Flowchart Olah Data Berita 30
3.10 Flowchart Olah Data Lokasi 31
3.11 Flowchart Olah Data Admin 32
3.12 User Interface Perancangan Input Berita 33 3.13 User Interface Perancangan Ubah Password 34 3.14 User Interface Perancangan Input Admin 35 3.15 User Interface Perancangan Input Jarak Terpendek 36 3.16 Interface Perancangan Olah Olah Data Berita 37 3.17 User Interface Perancangan Olah Data Lokasi 38 3.18 User Interface Perancangan Olah Data Admin 38 3.19 User Interface Perancangan Hasil Pencarian Jarak 40
4.1 Contoh Graf Untuk Mencari Rute Terpendek 50 4.2 Contoh Algoritma Dijkstra Langkah Pertama 50
4.3 Penjelasan Fungsi Label Pada Graf 50
4.4 Contoh Algoritma Dijkstra Langkah Kedua 51 4.5 Contoh Algoritma Dijkstra Langkah Ketiga 52 4.6 Contoh Algoritma Dijkstra Langkah Keempat 52 4.7 Contoh Algoritma Dijkstra Langkah Kelima 53 4.8 Contoh Algoritma Dijkstra Langkah Keenam 53 4.9 Contoh Algoritma Dijkstra Langkah Ketujuh 54 4.10 Contoh Algoritma Dijkstra Langkah Kedelapan 54 4.11 Contoh Algoritma Dijkstra Langkah Kesembilan 55 4.12 Contoh Algoritma Dijkstra Langkah Kesepuluh 55 4.13 Contoh Algoritma Dijkstra Langkah Kesebelas 56 4.14 Graf Hasil Pencarian Rute Terpendek Dengan Algoritma
Dijkstra
56
4.15 Tampilan Menu Utama 57
4.16 Tampilan Buku Tamu 58
4.17 Tampilan Tentang Algoritma Dijkstra 58
4.18 Halaman about Us 59
4.19 Halaman Pencarian Rute Terpendek 60
4.20 Tampilan Hasil Pencarian Rute Terpendek 60
ABSTRAK
Kota Medan merupakan wilayah Kota yang sedang berkembang dan juga menjadi pusat daerah perdagangan, perindustrian, perkantoran, pariwisata, pendidikan dan lain-lain. Sebagai kota yang sedang berkembang, maka perlu dibangun s e b u a h l a y a n a n i n f o r m a s i m e n g e n a i f a s i l i t a s u m u m d i K o t a M e d a n Penulis membuat sebuah aplikasi Sistem Informasi Geografis untuk menetukan jarak terpendek suatu Bimbingan Belajar. Google maps digunakan untuk menampilkan peta online dan lintasan terpendek yang akan dilalui, serta jarak yang akan di tempuh. Metode yang digunakan untuk mencari lintasan terpendek ini adalah algoritma Dijkstra. Algoritma Dijkstra adalah sebuah algoritma rakus (greedy algorithm) yang dipakai dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah (direct graph) dengan bobot sisi yang bernilai positif dan terlebih dahulu menentukan node awal dan node tujuan dengan jumlah bobot terkecil.
Web Based Geographic Information System To Determine Shortest Path Using Dijkstra Algorthm (Case Study One Of
Education Center In Medan City)
ABSTRACT
Medan is a developing city and center of commerce, industry, offices, government, t o u r i s m , e d u c a t i o n a n d e t c . A s t h e d e v e l o p i n g c i t y , s o n e e d b e b u i l t w i t h i n f o r m a t i o n s e r v i c e l i k e p u b l i c f a c i l i t y i n t h e M e d a n C i t y . After did research, writer make an application of Geographical Information System to determines shortest distance of Education Center. Google maps is used to show online map and shortest path will be traveled and then distance will be taken on. Method is used to search this shorter path is Algorithm of Dijkstra. Algorithm of Di j ks t r a i s a gr e e dy a l gor i t h m us e d t o s ol ve s hor t e s t pa t h p r obl e m fo r a direct graph with positive weight and before that determined the first node a n d t h e p u r p o s e n o d e w i t h t h e s u m o f s m a l l w e i g h t .
1 BAB 1 PENDAHULUAN
1.1Latar Belakang
Kota Medan merupakan Ibukota Sumatera Utara, yang secara geografis terletak pada posisi antara 03°. 30' - 03°. 48' LU dan 98°. 35' - 98° . 44' BT dengan ketinggian 30 meter diatas permukaan laut. Kota Medan mempunyai temperature rata-rata 27° C. Kota Medan adalah salah satu daerah yang akan menuju kearah kota Metropolitan. Selain itu, kota Medan merupakan pusat daerah perdagangan, perindustrian, perhubungan, pariwisata, dan juga pendidikan [17].
Dalam memasuki era industrialisasi dan globalisasi, bangsa Indonesia membutuhkan Sumber Daya Manusia yang berkualitas, memiliki pengetahuan, keterampilan dan keahlian sesuai dengan kemajuan teknologi dalam menunjang pembangunan di segala bidang. Untuk memenuhi hal tersebut, pendidikan luar sekolah seperti bimbingan belajar diharapkan meningkatkan kualitas sumber daya manusia.
Lembaga bimbingan belajar sebagai tempat pelayanan pendidikan siswa yang dilakukan di luar jam sekolah sangat memperhatikan kebutuhan dari masyarakat. Bimbingan belajar melayani masalah pendidikan, pengembangan kreatifitas anak, dan sebagainya. Khusus di Kota Medan terdapat banyak bimbingan belajar yang mempunyai segmentasi berbeda. Banyaknya lembaga bimbingan belajar yang berada dalam masyarakat menyebabkan konsumen selektif dalam memilih, serta banyaknya lembaga bimbingan belajar yang bermunculan saat ini, menjadikan persaingan yang semakin ketat.
Namun, keberadaan lokasi lembaga bimbingan belajar ini juga menjadi salah satu pilihan dan daya tarik tersendiri bagi masyarakat. Aksesibilitas dan transportasi yang sulit menjadi kendala, akan berdampak negatif dalam proses kegiatan belajar. Informasi tentang keberadaan lembaga Bimbingan belajar ini sangatlah penting, agar masyarakat mengetahui Lembaga Bimbingan belajar mana yang terdekat dengan lingkungan tempat tinggal mereka dan mencegah kemacetan. Untuk menghemat jarak dan waktu dalam perjalanan menuju Lokasi Bimbingan belajar tersebut dibutuhkan jalur terpendek.
Pencarian jarak terpendek merupakan suatu permasalahan yang sering timbul pada pengguna transportasi, karena pengguna transportasi dalam melakukan perjalanan membutuhkan solusi bagaimana rute yang akan dilalui adalah rute atau jarak yang paling minimum (terkecil), sehingga efisiensi waktu dapat terpenuhi. Dalam penghitungan jalur terpendek yang akan ditempuh tersebut biasanya orang menggunakan cara manual.
Dengan adanya aplikasi penentuan rute terpendek dengan menggunakan algoritma Dijkstra ini, berperan untuk memudahkan kita dalam penghitungan jarak tersebut dimana kita hanya memasukkan data yang dibutuhkan dan penghitungan dilakukan secara otomatis. Metode Dijkstra adalah salah satu metode yang digunakan untuk menyelesaikan masalah dalam pencarian rute terpendek. Oleh karena itu melalui perancangan dan pembuatan website ini diharapkan dapat menampilkan gambaran peta lokasi lembaga bimbingan yang terkemuka sehingga lebih menarik dan dapat dinikmati oleh masyarakat luas.
Pada penelitian sebelumnya telah dilakukan beberapa penelitian tentang pencarian lintasan terpendek dengan algoritma dijkstra yaitu :
jalan terpendek antara kota yang satu dengan kota yang lainnya di Jawa Timur. Sedangkan informasi lainnya yang dapat diperoleh antara lain informasi mengenai pemerintahan, jumlah penduduk, tempat wisata, nama gunung, makanan khas, kerajinan, dan kesenian tradisional yang berasal dari suatu daerah. Program ini dirancang tanpa menggunakan satelit namun hanya menggunakan database, sehingga penggunaannya lebih murah dibandingkan dengan menggunakan satelit [4].
2. Sistem ini dibangun menggunakan metode dijkstra, yakni metode pencarian rute terpendek menuju pusat kesehatan dengan menentukan titik awal dan titik tujuan kemudian membandingkan semua kemungkinan hasil pencarian sehingga mendapatkan rute yang paling terpendek dengan tampilan web geographic information system. Dengan adanya Penentuan Rute Terpendek Menuju Pusat Kesehatan Menggunakan Metode Dijkstra Berbasis Web Geographic Information System ini, diharapkan pengguna dapat dengan mudah mendapatkan informasi mengenai pusat kesehatan yang terdekat untuk memperkecil resiko yang tidak diinginkan [14].
Atas dasar latar belakang masalah di atas, di Tugas Akhir ini penulis mengambil judul ”Implementasi Algoritma Dijkstra Untuk Menentukan Rute Terpendek Berbasis Web (Studi Kasus : Salah Satu Lembaga Bimbingan Belajar di Kota Medan)”.
1.2Perumusan Masalah
Setelah melihat latar belakang masalah yang telah diuraikan di atas maka timbul rumusan masalah dalam skripsi ini yaitu :
1. Membuat aplikasi sistem informasi geografis berbasis web dalam menampilkan lokasi salah satu Bimbingan Belajar di kota Medan.
2. Mengimplementasikan algoritma djikstra di dalam peta.
1.3 Batasan masalah
Adapun batasan pada penelitian ini sebagai berikut :
1. Jalan yang digunakan adalah jalan protokol dan tidak termasuk gang atau lorong,
2. Untuk mencari dan menentukan lintasan terpendek digunakan Algoritma Dijkstra,
3. Graf yang digunakan adalah graf berarah dan berbobot,
4. Adapun Perangkat lunak yang digunakan adalah MySQL, menggunakan bahasa pemrograman PHP dan perangkat lunak yang mendukung pembuatan aplikasi ini,
5. Objek yang digunakan untuk pencarian rute jalur terpendek adalah salah satu Lembaga Bimbingan Belajar di Kota Medan,
6. Dalam proses pencarian jalur terpendek ditentukan terlebih dahulu data asal dan data tujuan, sehingga proses pencarian dan penentuan jarak terjadi pada sistem. 7. Data hasil menampilkan rute(jalan) yang dilalui untuk jarak terdekat,
1.4 Tujuan penelitian
Tujuan dari penelitian ini adalah
1. Merancang aplikasi sistem informasi geografis lokasi Bimbingan Belajar di Kota Medan berbasis web.
2. Mempermudah masyarakat (pelajar) yang berada di Kota Medan maupun dari luar Kota Medan untuk mengetahui lokasi Bimbingan Belajar yang terdapat di Kota Medan.
1.5Manfaat penelitian
Manfaat yang dapat diperoleh dari penulisan skripsi ini adalah sebagai berikut untuk memberikan informasi dalam menentukan jarak terpendek Lembaga Bimbingan belajar dan diharapkan dapat digunakan dalam aplikasi kehidupan sehari-hari oleh masyarakat agar nantinya dapat mengefisiensikan waktu dan biaya.
1.6Metodologi Penelitian
Metodologi penelitian yang digunakan dalam penulisan tugas akhir ini adalah sebagai berikut :
1. Studi Literatur
Melakukan studi kepustakaan melalui hasil penelitian berupa buku, jurnal, dan artikel-artikel yang relevan, serta mempelajari lebih dalam teori-teori tentang pencarian rute terpendek dan Algoritma Dijkstra
2. Pengumpulan Data
Tahapan selanjutnya yaitu pengumpulan data yang berhubungan dengan penelitian.
3. Analisis dan Perancangan Sistem
Melakukan analisis terhadap masalah yang ada untuk mendapatkan solusi dari masalah tersebut dan membuat perancangan aplikasi pencarian rute terpendek berbasis web.
4. Pengkodean
5. Pengujian dan Pemeliharaan
Melakukan pengujian terhadap aplikasi SIG yang dihasilkan dan melakukan pemeliharaan sistem
6. Dokumentasi
Membuat dokumentasi dalam bentuk laporan penelitian dalam hal ini tugas akhir.
1.7Sistematika Penulisan
Agar penulisan menjadi lebih terstruktur, maka penulisan ini dibagi menjadi lima bab sebagai berikut:
BAB 1 : PENDAHULUAN
Bab ini berisi mengenai latar belakang masalah, perumusan masalah, batasan masalah, tujuan penulisan dan sistematika penulisan.
BAB 2 : LANDASAN TEORI
Pada bab ini dibahas mengenai teori Sistem Informasi Geografis, Data Spasial SIG, graf, Pencrian Rute Terpendek Dengan Algoritma Dijkstra, serta teori lainnya yang mendukung.
BAB 3 : ANALISIS DAN DESAIN SISTEM
Bab ini berisi analisis permasalahan & kebutuhan dalam merancang sistem informasi geografis serta proses digitasi peta yang akan ditampilkan pada antarmuka.
BAB 4 : IMPLEMENTASI DAN PENGUJIAN SISTEM
Bab ini berisi tentang implementasi dan pengujian sistem informasi geografis yang telah dirancang.
BAB 5 : KESIMPULAN DAN SARAN
7 BAB 2
LANDASAN TEORI
2.1 Pengertian Sistem Informasi Geografis
Sistem Informasi Geografis adalah bahagian dari pada sistem informasi yang diaplikasikan untuk data geografi atau alat database untuk analisis dan pemetaan sesuatu yang terdapat dan terjadi di bumi. Menurut ESRI (Environmental System Research Institute) mendefinisikan, SIG adalah kumpulan yang terorganisir dari perangkat keras komputer, perangkat lunak, data geografis dan personil yang dirancang secara efisien untuk memperoleh, menyimpan, mengupdate, memanipulasi, menganalisis, dan menampilkan semua bentuk informasi yang bereferensi geografi[13].
SIG akan selalu diasosiasikan dengan sistem yang berbasis komputer, walaupun pada dasarnya SIG dapat dikerjakan secara manual, SIG yang berbasis komputer akan sangat membantu ketika data geografis merupakan data yang besar (dalam jumlah dan ukuran) dan terdiri dari banyak tema yang saling berkaitan.
SIG mempunyai kemampuan untuk menghubungkan berbagai data pada suatu titik tertentu di bumi, menggabungkannya, menganalisa dan akhirnya memetakan hasilnya. Data yang akan diolah pada SIG merupakan data spasial yaitu sebuah data yang berorientasi geografis dan merupakan lokasi yang memiliki sistem koordinat tertentu, sebagai dasar referensinya. Sehingga aplikasi SIG dapat menjawab beberapa pertanyaan seperti; lokasi, kondisi, trend, pola dan pemodelan. Kemampuan inilah yang membedakan SIG dari sistem informasi lainnya. Berikut beberapa keuntungan menggunakan SIG :
1. SIG mempunyai kemampuan untuk memilih dan mencari detail yang
3. SIG dengan mudah menghasilkan peta-peta tematik yang dapat digunakan untuk menampilkan informasi-informasi tertentu. Peta-peta tematik tersebut dapat dibuat dari peta-peta yang sudah ada sebelumnya, hanya drngan memanipulasi atribut-atributnya,
4. SIG memiliki kemampuan untuk menguraikan unsur-unsur yang terdapat dipermukaan bumi menjadi beberapa layer data spasial.
Sistem informasi geografis terbagi menjadi beberapa komponen sistem (subsistem), sebagai berikut:
1. Data Input
Subsistem ini bertugas untuk mengumpulkan dan mempersiapkan data spasial dan atribut dari berbagai sumbernya.
2. Data Output
Subsistem ini menampilkan atau menghasilkan keluaran seluruh atau sebagian basis data baik dalam bentuk softcopy maupun hardcopy.
3. Data Management
Subsistem ini mengorganisasikan baik data spasial maupun atribut ke dalam sebuah basisdata sedemikian rupa sehingga mudah dipanggil, diupdate dan diedit.
4. Data Manipulation & Analysis
Subsistem ini menentukan informasi-informasi yang dapat dihasilkan oleh SIG.
Jika subsistem SIG tersebut diperjelas berdasarkan uraian jenis masukan, proses, dan jenis keluaran yang ada didalamnya, maka subsistem SIG dapat juga digambarkan sebagai berikut :
Gambar 2.2 Ilustrasi Urian Sub-Sistem SIG [7]
2.1.1 Data Spasial
Sebagian besar data yang akan ditangani dalam SIG merupakan data spasial yaitu sebuah data yang berorientasi geografis, memiliki sistem koordinat tertentu sebagai dasar referensinya dan mempunyai dua bagian penting yang membuatnya berbeda dari data lain, yaitu informasi lokasi (spasial) dan informasi deskriptif (attribute) yang dijelaskan berikut ini :
1. Informasi lokasi (spasial), berkaitan dengan suatu koordinat baik koordinat geografi (lintang dan bujur) dan koordinat XYZ, termasuk diantaranya informasi datum dan proyeksi.
2.1.2 Format Data Spasial
Secara sederhana format dalam bahasa komputer berarti bentuk dan kode penyimpanan data yang berbeda antara file satu dengan lainnya. Dalam SIG, data spasial dapat direpresentasikan dalam dua format, yaitu:
2.1.2.1 Model Data Vektor
Model data vektor diwakili oleh symbol-simbol atau yang selanjutnya dalam SIG dikenal dengan feature, seperti feature titik (point), feature garis (line), feature area (surface).
Gambar 2.3 Model data vector [14]
Keuntungan utama dari format data vektor adalah ketepatan dalam merepresentasikan fitur titik,batasan dan garis lurus. Hal ini sangat berguna untuk analisa yang membutuhkan ketepatan posisi, misalnya pada basisdata batas-batas kadaster. Contoh penggunaan lainnya adalah untuk mendefinisikan hubungan spasial dari beberapa fitur. Kelemahan data vektor yang utama adalah ketidakmampuannya dalam mengakomodasi perubahan gradual.
2.1.2.2. Model Data Raster
pixel dinyatakan dengan baris ke –m dak kolom ke –n. Data yang disimpan dalam format ini data hasil scanning, seperti gambar digital (citra dengan format BMP, JPG, dan lain-lain), citra satelit digital (landsat, SPOT, dan lain-lain).
Gambar 2.4 Model Data Raster [7]
Data raster sangat baik untuk merepresentasikan batas-batas yang berubah secara gradual, seperti jenis tanah, kelembaban tanah, vegetasi, suhu tanah dan sebagainya. Keterbatasan utama dari data raster adalah besarnya ukuran file, semakin tinggi resolusi grid-nya semakin besar pula ukuran filenya dan sangat tergantung pada kapasistas perangkat keras yang tersedia. Data vektor relatif lebih ekonomis dalam hal ukuran file dan presisi dalam lokasi, tetapi sangat sulit untuk digunakan dalam komputasi matematik. Sedangkan data raster biasanya membutuhkan ruang penyimpanan file yang lebih besar dan presisi lokasinya lebih rendah, tetapi lebih mudah digunakan secara matematis.
2.1.3 Sumber Data Spasial
Salah satu syarat SIG adalah data spasial, yang dapat diperoleh dari beberapa sumber antara lain:
1. Peta Analog
2.2 Peta
Peta merupakan penyajian grafis dari permukaan bumi dalam skala tertentu dan digambarkan pada bidang datar melalui poyeksi peta dengan menggunakan simbol-simbol tertentu sebagai perwakilan dari objek-objek spasial di permukaan bumi [9].
Pada masa sekarang, peta tidak hanya berfungsi sebagai penunjuk lokasi, peta juga dapat digunakan untuk dasar perancangan pembangunan, pengambilan keputusan, dan lain-lain. Secara umum, fungsi peta adalah sebagai penunjuk posisi atau lokasi relatif ( letak suatu tempat dalam hubunganya dengan tempat lain di permukaan bumi), memperlihatkan ukuran ( dapat dilihat luas dan jarak suatu daerah di atas permukaan bumi), memperlihatkan bentuk ( misalnya bentuk dari benua, Negara dan lain-lain) danmengumpulkan menyeleksi data-data dari suatu daerah dan menyajikan di atas peta.
2.2.1 Proyeksi Peta
Proyeksi peta merupakan teknik-teknik yang digunakan untuk menggambarkan sebagian atau keseluruhan permukaan tiga dimensi yang secara kasar berbentuk bola ke permukaan datar dua dimensi dengan distorsi seminimal mungkin. Distorsi dapat dikurangi dengan membagi daerah membagi daerah yang dipetakan menjadi bagian yang tidak terlalu luas dan menggunakan bidang datar [9].
Secara sederhana proyeksi peta dapat didefinisikan sebagai usaha mengubah bentuk bola (bidang lengkung) kebentuk datar, dengan persyaratan sebagai berikut:
1. Bentuk ( sudut dan arah) yang diubah itu harus tetap sama (proyeksi conform),
2. Luas permukaan yang diubah harus tetap dengan memperhitungkan faktor skala (proyeksi ekuivalen),
Proyeksi-proyeksi yang sudah ada dapat dikelompokkan dalam beberapa bidang, yaitu:
1. Proyeksi silinder (cylindrical), menggunakan silinder sebagai bidang proyeksi.
2. Proyeksi azimunthal, menggunakan bidang datar sebagai bidang proyeksi (planar),
3. Proyeksi kerucut (conical), menggunakan kerucut sebagai bidang proyeksi,
Gambar 2.5 Perbedaan Proyeksi (a) Cylindrical, (b)Planar dan (c)Conical [7] Proyeksi UTM merupakan proyeksi Peta yang banyak di pilih dan di gunakan dalam kegiatan pemetaan di Indonesia karena di nilai memenuhi syarat-syarat ideal yang sesuai dengan bentuk, letak dan luas Indonesia. Spesifikasi UTM antara lain adalah
1. Menggunakan bidang silender yang memotong bola bumi pada dua meridian standart yang mempunyai faktor skala k=1,
2. Lebar zone 6° dihitung dari 180° BB dengan nomor zone 1 hingga ke 180° BT dengan nomor zone 60. Tiap zone mempunyai meridian tengah sendiri,
3. Setiap zone memiliki meridian tengah sendiri dengan faktor perbesaran = 0.9996,
2.3 Graph
Graph adalah suatu diagram yang memuat informasi tertentu jika diinpretasikan secara tepat. Gaph digunakan untuk menggambarkan berbagai macam struktur yang ada. Tujuannya adalah sebagai visualisasi objek-objek agar lebih mudah dimengerti [10].
Graph G didefinisikan sebagai pasangan himpunan (V, E), ditulis dengan notasi G= (V, E), yang dalam hal ini V adalah himpunan tidak kosong dari simpul-simpul (vartices atau node) dan E adalah himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul [6]. Menurut arah dan bobotnya, graph dibagi menjadi empat bagian yaitu:
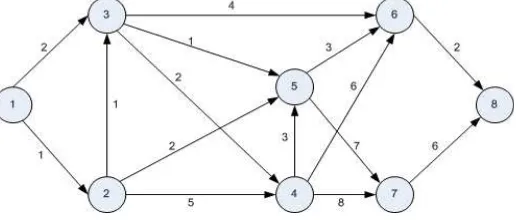
1. Graph berarah dan berbobot adalah graf yang tiap verteks (titiknya) diwakili oleh sebuah anak panah yaitu sebuah kurva berarah dan setiap sisinya memiliki bobot. Sebagai contoh pada gambar ditunjukkan:
V (G) = { 1,2,3,4,5,6,7,8}
E (G) = { [1,2], [1,3], [2,3], [2,4], [2,5], [3,4], [3,5], [3,6], [4,5], [4,6], [4,7], [5,6], [5,7], [6,8], [7,8]}
Setiap sisi pada titik graph memiliki bobot yang berbeda-beda.
Gambar 2.6 Contoh Graph Berarah dan Berbobot
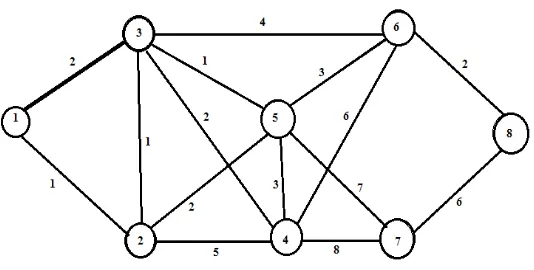
Gambar 2.7 Contoh Graph tidak berarah dan berbobot
3. Graph berarah dan tidak berbobot adalah graph yang setiap verteksnya diwakili sebuah anak panah yang menunjukkan sebuah arah, tapi setiap sisinya tidak memiliki bobot atau nilai.
Gambar 2.8 Contoh Graph berarah dan tidak berbobot
4. Graph tidak berarah dan tidak berbobot adalah gaph yang setiap verteks tidak diwakili sebuah anak panah dan setiap sisinya tidak memiliki bobot atau nilai.
2.4 Pencarian Rute Terpendek Dengan Algoritma Dijkstra
Algoritma dijkstra merupakan salah satu jenis algoritma yang cukup terkenal dipakai untuk memecahkan permasalahan yang terkait dengan optimasi yang bersifat sederhana dan sebagai penyelesaian permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah dengan bobot-bobot sisi (edge weights) yang bernilai positif. Algoritma ini pertama kali ditemukan dan diterapkan oleh Edger W. Dijkstra. Algoritma ini mencari lintasan terpendek dalam sejumlah langkah berdasarkan bobot terkecil dari titik ke titik lain.
Lintasan dari simpul asal haruslah merupakan lintasan terpendek diantara semua lintasannya ke simpul-simpul yang belum terpilih. Dengan kata lain strategi dari algoritma ini adalah ambillah lintasan yang memiliki bobot minimum yang menghubungkan sebuah simpul yang sudah terpilih dengan simpul yang belum terpilih. Lintasan dari simpul asal ke simpul yang baru haruslah merupakan lintasan terpendek diantara semua lintasannya ke semua simpul-simpul yang belum terpilih.
Input algoritma ini adalah sebuah graf yang berarah dan berbobot (weighted directed graph) G dan sebuah sumber vertices s dan dalam G dan V adalah himpunan ssemua vertices dalam graph G.
G = ( V , E )
Dimana : G= Graph
V= Vertices (titik)
E= Edge (jarak)
Secara garis besar, pseudo-code algoritma dijkstra yaitu [1]:
function Dijkstra (input M : matriks, a : simpul awal) tabel
{ Mencari lintasan terpendek dari impul awal a ke semua simpul lainnya
Masukan: matriks ketetanggaan (M) dari graf berbobot G dan simpul awal a
Keluaran: tabel D yang berisi panjang lintasan terpendek
17
{Langkah 0 inisialisasi} for i 1 to n do
S[i] 0 D[i] m[a,i] endfor
{Langkah 1}
S[a] 1 {karena simpul a adalah simpul asal lintasan terpendek, jadi simpul a sudah pasti terpilih dalam lintasan terpendek}
D[a] ∞ {tidak ada lintasan terpendek dari simpul a ke a} {Langkah 2, 3, ..., n-1}
for i 2 to n-1 do
Cari j sedemikian hingga S[j] = 0 dan D[j] = Minimum{D[1], D[2], ..., D[n]}
S[j] 1 {Simpul j sudah terpilih ke dalam lintasan terpendek}
Hitung D[i] yang baru dari a ke simpul i ∉ S dengan cara sebagai berikut:
D[i] Minimum{D[i], (D[j] + M[j,i])} endfor
return
2.5Geografis Kota Medan
Kota Medan merupakan Ibukota Propinsi Sumatera Utara, yang secara geografis terletak pada posisi antara 03° 30' LU – 03° 48' LU dan 98° 39' BT - 98° 47', 36'' BT dengan ketinggian antara 3-30 meter diatas permukaan laut. Kota Medan mempunyai temperature rata-rata 27°C. Kota Medan merupakan pusat daerah perdagangan, perindustrian, pendidikan, perhubungan, serta pariwisata. Banyak tempat bersejarah yang bisa kita kunjungi dan kita apresiasi di Kota Medan.
Secara administrative, Kota Medan memiliki wilayah seluas 265,10Km2 yang terdiri dari 21 Kecamatan dan 151 Kelurahan dengan batas-batas Kotanya sebagai berikut:
Sebelah Utara : Berbatasan dengan Selat Malaka
Sebelah Selatan : Berbatasan dengan Kabupaten Deli Serdang Sebelah Barat : Berbatasan dengan Kabupaten Deli Serdang Berdasarkan informasi dari kantor BPS Kota Medan melalui buku Medan Dalam Angka Tahun 2004 jumlah penduduk di Kota Medan tercatat sebanyak 2.053.778 jiwa, jumlah itu tercatat lebih besar dibanding jumlah penduduk dari tahun-tahun sebelumnya. Tahun 2000 misalnya, penduduk Kota Medan hanya mencapai 1.898.013 jiwa.
19 BAB 3
ANALISIS DAN PERANCANGAN SISTEM
3.1 Analisis Sistem
Dalam perancangan sebuah sistem diperlukan analisis untuk keperluan sistem. Dengan adanya analisis sistem, sistem yang dirancang diharapkan akan lebih baik dan memudahkan dalam pengembangan sistem selanjutnya. Tujuan dari analisa sistem ini sendiri adalah agar sistem yang dirancang menjadi tepat guna dann ketahanan dari sitem tersebut akan lebih terjaga.
Sistem ini akan dapat digunakan oleh masyarakat untuk mencari rute terpendek menuju salah satu Bimbingan Belajar yang ada di Kota Medan. Sistem ini dirancang menggunakan Algoritma Dijkstra untuk mencari rete terpendeknya.
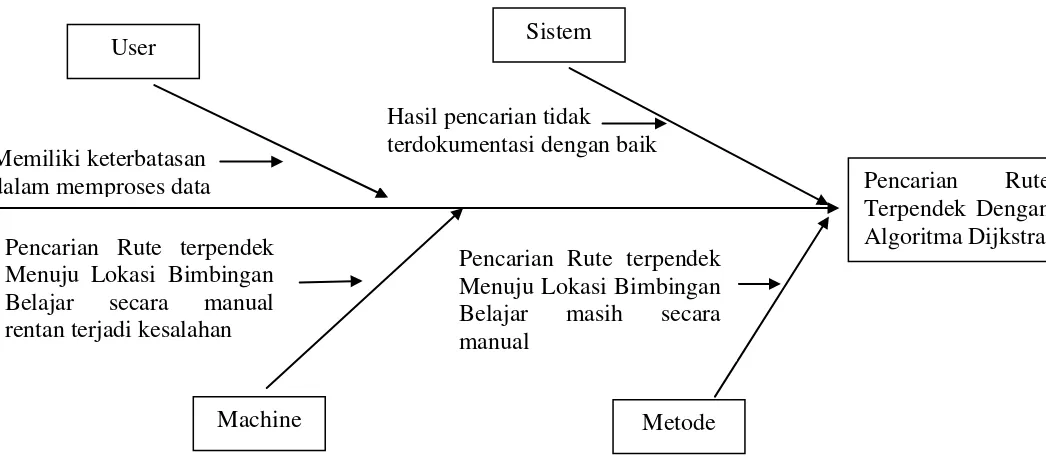
3.1.1 Analisis Masalah
Gambar 3.1 Diagram Ishikawa 3.1.2 Analisis Kebutuhan Sistem
Untuk mempermudah menganalisis sebuah sistem dibutuhkan dua jenis kebutuhan. Kebutuhan fungsional dan kebutuhan nonfungsional. Kebutuhan fungsional adalah kebutuhan yang berisi proses-proses apa saja yang nantinya dilakukan oleh sistem. Sedangkan kebutuhan nonfungsional adalah kebutuhan yang menitik beratkan pada properti prilaku yang dimiliki oleh sistem.
3.1.2.1 Kebutuhan Fungsional Sistem
Menggunakan analisis diharapkan suatu sistem dapat diuraikan secara utuh menjadi komponen-komponen dasar dengan tujuan identifikasi, mengevaluasi permasalahan dan kebutuhan yang diharapkan, dan analisis ini juga dilakukan untuk menjamin bahwa sistem yang dibangun sesuai dengan kebutuhan penelitian.
Hasil analisis kebutuhan sistem adalah :
1. Sistem dapat memberikan rute terpendek untuk menuju lokasi Bimbingan Belajar dengan menggunakan algoritma Dijkstra,
2. Sistem dapat digunakan setiap orang sebagai media untuk memberikan informasi serta lokasi Bimbingan Belajar kepada masyarakat luas,,
3. Sistem dapat memberikan informasi lokasi Bimbingan Belajar secara geografis.
User Sistem
Machine Metode
Memiliki keterbatasan dalam memproses data
Hasil pencarian tidak terdokumentasi dengan baik
Pencarian Rute terpendek Menuju Lokasi Bimbingan Belajar secara manual rentan terjadi kesalahan
Pencarian Rute terpendek Menuju Lokasi Bimbingan Belajar masih secara manual
21
3.1.2.2 Kebutuhan Nonfungsional Sistem
Analisis non fungsional menunjukkan kesuliatan saat pengembangan sistem sehingga sistem tidak terlalu berjalan optimal namun sistem tersebut dapat dijalankan. Adapun kebutuhan non fungsional dari sistem yang dirancang mencakup:
1. Dari segi performance, sistem ini dirancang: - Tampilan/interface yang menarik
- Dilengkapi dengan informasi berupa Help dan About dan tampilan data berita dari sistem.
- Dari segi delay, sistem ini dirancang dengan waktu tunda yang sesuai dengan waktu tunda dikarenakan proses ini membutuhkan sebuah koneksi internet sehingga waktu loading tergantung dari koneksi internet tersebut seperti untuk menampilkan peta dari hasil pencarian rute terpendek dikarenakan peta yang ditampilkan berasal dari API Google
2. Dari segi Informasi, sistem ini dirancang :
- Digunakan untuk menginformasikan bagaimana cara menambahkan data lokasi.
- Digunakan untuk menginformasikan apabila password yang telah dimasukan pengguna salah.
3. Dari segi keamanan/security, sistem ini dirancang dengan proses login untuk hak akses halaman admin pada web server.
3.1.3. Pemodelan
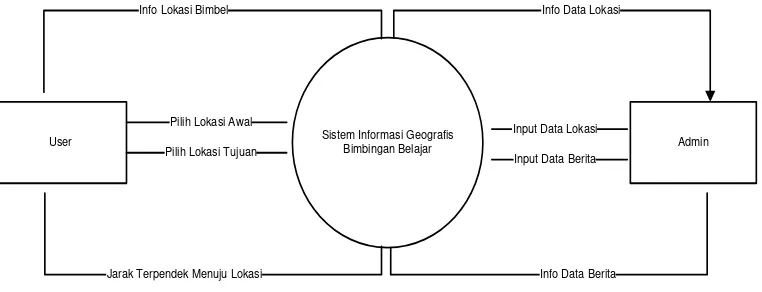
3.1.3.1 Diagram Konteks
Diagram konteks merupakan aliran yang memodelkan hubungan antara sistem dengan entitas. Selain itu diagram konteks merupakan diagram yang paling awal yang terdiri dari suatu proses data dan menggambarkan ruang lingkup suatu sistem secara garis besarnya. Aliran dalam diagram konteks memodelkan masukan ke sistem dan keluaran dari sistem.
User Sistem Informasi Geografis Admin Bimbingan Belajar
Info Data Lokasi
Info Data Berita Input Data Berita Input Data Lokasi Pilih Lokasi Tujuan
Pilih Lokasi Awal Info Lokasi Bimbel
Jarak Terpendek Menuju Lokasi
Gambar 3.2 Diagram Konteks
Diagram konteks diatas menggambarkan hubungan antara entitas-entitas yang terdapat diluar sistem dengan sistem dan masukan serta keluaran dari sistem. Dalam sistem aplikasi kamus ini, terdapat 3 entitas yaitu :
1. User
User adalah siapa saja yang mengakses website yang sudah dirancang dan dibangun.
2. Admin
Admin adalah user yang memiliki hak akses penuh atas sistem pada web server dapat melakukan update data.
3.1.3.2 Data Flow Diagram (DFD)
23
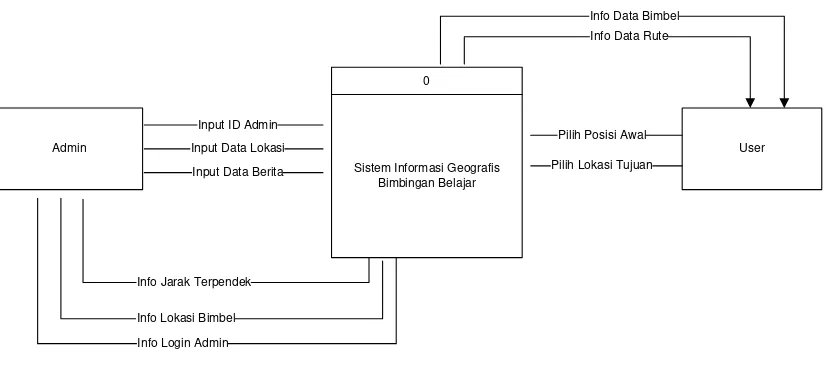
3.1.3.2.1 Data Flow Diagram (DFD) Level 0
Admin User
Info Data Bimbel
Pilih Lokasi Tujuan
Info Data Rute
Input Data Berita
Info Lokasi Bimbel Info Login Admin
Gambar 3.3 DFD Level 0
Penjelasan DFD level 0 pencarian rute terpendek menuju Bimbingan Belajar di kota Medan diatas adalah sebagai berikut:
1. Admin
Admin login ke sistem dengan memasukkan username dan password lalu sistem akan menapilkan halaman admin untuk menginput data. Admin menginputkan data-data jarak jalan yang akan melewati setiap Bimbingan Belajar yang ada di kota Medan.
2. User
User dapat memilih posisi awal keberangkatan menuju salah satu Bimbingan Belajar yang ada di kota Medan, kemudian user memilih posisi tujuan yang diinginkan dan sistem akan menampilkan rute jalan yang akan dilewati beserta rute terpendek yang akan dilaluinya.
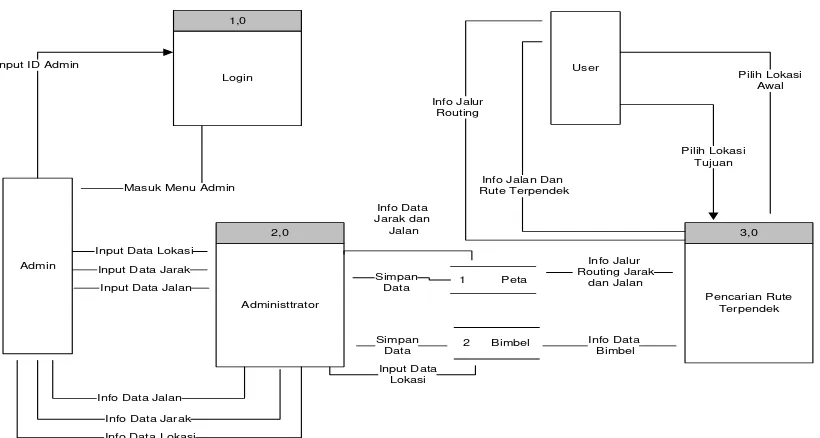
3.1.3.2.2 Data Flow Diagram (DFD) Level 1
1,0
Input Data Lokasi Input Data Jarak Input Data Jalan
Info Data Jalan Info Data Jarak Info Data Lokasi
User
DFD level 1 proses simpan data dan proses pencarian data jalur terpendek menuju Bimbingan Belajar di kota Medan diatas adalah admin melakukan proses penyimpanan data, dan User melakukan pencarian data jalan jalur terpendek.
3.1.3.2.3 Data Flow Diagram (DFD) Level 2
Data flow diagram level 2 proses laporan pencarian pada gambar 3.4 memuat proses laporan jalur rute terpendek
25
Pada DFD level 2 ini adalah proses hasil pencarian rute terpendek menuju Bimbingan Belajar di kota Medan diatas adalah user melakukan proses pencarian data jalur jalan terpendek untuk menuju Bimbingan Belajar di kota Medan.
3.1.3.3 Model Data (Entity Relationship Diagram)
Entity Relationship Diagram (ERD) akan menjelaskan hubungan antar entitas dalam sebuah sistem. Rancangan sistem informasi geografis terdiri dari banyak aspek yang saling terkait. Maka sebelum merancang basisdata, disusun terlebih dahulu model ERD dari Sistem Informasi Geografis ini.
3.1.3.4 Desain Database
Database adalah representasi kumpulan fakta yang saling berhubungan disimpan secara bersama sedemikian rupa dan tanpa pengulangan (redudansi) yang tidak perlu, untuk memenuhi berbagai kebutuhan. Menurut Bambang Hariyanto (2004), database adalah kumpulan data (elementer) yang secara logik berkaitan dalam merepresentasikan fenomena/fakta secara terstruktur dalam domain tertentu untuk mendukung aplikasi pada sistem tertentu.
Tujuan dari perancangan database server pada aplikasi ini adalah untuk mengatasi ketebatasan memori pada perangkat mobile. Disamping itu database yang diletakkan pada web server ditujukan untuk pengembangan/penambahan kata oleh admin. Database yang dirancang pada web server menggunakan MYSQL.
Berikut ini nama-nama tabel yang digunakan beserta field-field yang terdapat pada masing-masing table. Pada setiap tabel dibawah hanya admin yang dapat melakukan update(menambah, mengedit dan menghapus record).
3.1.3.4.1 Tabel admin
Tabel 3.1 Tabel Admin
Nama Field Tipe Panjang Keterangan
Username Varchar 30 username admin
Password Varchar 30 password admin
3.1.3.4.2 Tabel Lokasi
Tabel 3.2 Tabel Lokasi
Nama Field Tipe Panjang Keterangan
Id_lokasi Int 10 Primary
nama_lokai Varchar 30 nama lokasi
Lat Varchar 30 latititude lokasi
Lng Varchar 30 longitude lokasi
Kategori Varchar 30 kategori lokasi
3.1.3.4.3 Tabel Berita
Tabel 3.3 Tabel Berita
Field Type Panjang Keterangan
id_berita* Int 10 Primary
judul_berita Varchar 30 judul berita
isi_berita Text isi berita
tanggal_berita Datetime tanggal berita diterbitkan
3.1.3.4.4 Tabel Komentar
Tabel 3.4 Tabel Buku Tamu
Nama Field Tipe Panjang Keterangan
id_komentar Int 10 Primary
nama_komentar Varchar 30 nama pengomentar
Email Varchar 60 Email pengomentar
Komentar Text - isi komentar
27
3.1.3.5 Flowchart
Flowchart (Bagan Alir Program) adalah suatu bagan yang menggambarkan arus logika dari data yang akan diproses dalam suatu program dari awal sampai akhir.
Dengan kata lain flowchart (bagan alir program) dapat didefinisikan sebagai sebuah bagan yang menunjukkan aliran di dalam program atau prosedur sistem secara logika. Flowchart biasanya digunakan sebagai alat bantu komunikasi dan untuk dokumentasi. Bagan alir sistem merupakan bagan yang menunjukkan arus kegiatan dari keseluruhan sistem. Bagan ini menjelaskan urutan–urutan dari prosedur–prosedur yang ada dalam sistem. Bagan alir sistem menunjukkan apa yang dikerjakan di sistem.
3.1.3.5.1 Flowchart Login Admin
Start
Masukkan Username Dan Password
Pengecekan Username Dan Password
Jika Username dan Passwort tidak valid?
Tampil Halaman
Akun A1
Y
Flowchart diatas merupakan alur untuk login admin, admin harus memasukkan username dan password untuk masuk ke halaman administrator. Proses pengecekan pun terjadi. Jika username dan password tidak valid maka username dan password salah sebaliknya jika username dan password valid maka akan terus ke halaman akun.
3.1.3.5.2 Flowchart Menu Admin
Start
Gambar 3.7 Menu Admin
29
3.1.3.5.3 Flowchart Ubah Password
A.1.1
Masukkan Password lama. Password baru, konfirmasi
Password Baru
Proses Perubahan Password
Jika Password Lama == False && Password= Konfirmasi password?
Password BERUBAH
Proses Perubahan Password
A.1 F
T
Gambar 3.8 Flowchart Ubah Password
3.1.3.5.4 Flowchart Olah Data Berita
Gambar 3.9 Flowchat Olah Data Berita
31
3.1.3.5.5 Flowchart Olah Data Lokasi
Gambar 3.10 Flowchart Olah Data Lokasi
3.1.3.5.6 Flowchart Olah Data Admin
Gambar 3.11 Flowchart Olah Data Admin
33
3.2 Perancangan Sistem Antarmuka (Interface)
Pada bagian perancangan interface ini dibuat desain yang sederhana sehingga dapat dikembangkan lagi. Desain interface aplikasi terdiri dari dua bagian, yaitu perancangan Input dan Output.
3.2.1 Perancangan Input
3.2.1.1 Perancangan Input Berita
Gambar 3.12 User Interface Perancangan Input Berita
untuk menginput data yang akan mau diinput serta 2 inputan text yang terdapat di halaman ini, yaitu inputan text untuk judul berita dan isi berita.
3.2.1.2 Perancangan Ubah Password
Gambar 3.13 User Interface Perancangan Ubah Password
35
konfirmasi password baru. Apabila ketiga item ini terisi dengan valid maka proses pengubahan password berhasil
3.2.1.3 Perancangan Input Admin
Gambar 3.14 User Interface Perancangan Input Admin
halaman ini, yaitu inputan text untuk input username dan inputan text untuk input password.
3.2.1.4 Perancangan Input Jarak Terpendek
Gambar 3.15 User Interface Perancangan Input Jarak Terpendek
37
3.2.2 Perancangan Output
3.2.2.1 Perancangan Olah Data Berita
Gambar 3.16 User Interface Perancangan Olah Data Berita
3.2.2.2 Perancangan Olah Data Lokasi
Gambar 3.17 User Interface Perancangan Olah Data Lokasi
39
3.2.2.3 Perancangan Olah Data Admin
Gambar 3.18 User Interface Perancangan Olah Data Admin
3.2.2.4 Perancangan Hasil Pencarian Jarak Terpendek
Gambar 3.19 User Interface Perancangan Hasil Pencarian Jarak Terpendek
Halaman ini adalah halaman untuk menampilkan hasil pencarian rute terpendek yang berasal dari form untuk mencari rute terpendek yang sudah diinput oleh user. Di dalam halaman ini akan ditampilkan total rute yang ditempuh dan dengan rute-rute mana saja yang akan dipilih. Selain itu user juga dapat memilih untuk melihat peta rute manasaja yang akan lebih cepat dilewati.
3.3 Perhitungan Jarak
41
Gambar 3.20 berikut ini menunjukkan graph yang akan dipakai dalam algoritma dijkstra untuk pencarian rute tercepat. Graph ini didapatkan dari gambar peta Kota Medan yang sudah ada sebelumnya.
Pada graf yang terdapat dalam tabel 3.5, nama persimpangan diwakili oleh nama node, sedangkan nama jalur diwakili dengan penomoran pada tiap simpul. Adapun pembuatan huruf A, B, C pada nama node adalah untuk mempermudah dalam mengelompokkan letak persimpangan. Data-data inilah yang nantinya akan menjadi tolak ukur untuk melihat panjang rute sehingga akan didapatkan rute terpendek dari setiap lokasi lembaga bimbingan belajar yang ada.
Tabel 3.5 Data Objek Peta
Simbol Nama Objek Kategori
A Jalan Setia Budi No.129A Cabang Medica B Jalan Gatot Subroto Jalan Besar C Jalan T Amir Hamzah Jalan Besar D Jalan Yos Sudarso No.175B Cabang Medica
E Jalan Merdeka No.2 Cabang Medica
F Jalan Sei Batang Hari Jalan Besar G Jalan Jamin Ginting No.241 Cabang Medica H Universitas Sumatera Utara Tempat Umum
I Rumah Makan Wong Solo Tempat Umum
J Jalan Krakatau Jalan Besar
K Jalan Gajah Mada Jalan Besar
L Jalan Nusantara Jalan Besar
M Jalan Iskandar Muda No.19 A/B/C Cabang Medica N Plaza Medan Polonia Jalan Besar
43
P Bandara Polonia Tempat Umum
Q Jalan Jenderal A.H Nasution Jalan Besar R Jalan Brigjen Zein Hamid No.24-D Cabang Medica S Jalan Sisingamaraja No.348 Cabang Medica T Jalan Sisingamaraja No.251/252 Cabang Medica U Jalan Sisingamaraja Jalan Besar
V Jalan Dipoenogoro Jalan Besar
W Jalan Profesor Muhammad Yamin Jalan Besar
X Jalan Garuda II Jalan Besar
Y Jalan Sentosa Baru No.17A Cabang Medica
Z Jalan Cemara Jalan Besar
A1 Jalan William Iskandar Jalan Besar
Gambar graph/titik utuk objek peta BT/BS Medica yang digambarkan dengan menggunakan metode djikstra. Berikut ini akan diberikan suatu contoh perhitungan djikstra yang merupakan perhitugan jarak terpendek dari graph yang ditunjukkan di atas :
Contoh Studi Kasus : Tentukan Rute Terpendek dengan menggunakan algoritma Djikstra dari node awal B menuju node akhir yaitu M.
B – F = 0.87 KM F – I = 0.70 KM I – M = 0.91 KM
I F
0.70 B
0.87
Jarak Total : 0.87 + 0.70 + 0.91 = 2.48 KM
Gambar graph/titik utuk objek peta bimbingan belajar Medica yang digambarkan dengan menggunakan metode djikstra. Berikut ini akan diberikan suatu contoh perhitungan djikstra yang merupakan perhitugan jarak terpendek dari graph yang ditunjukkan di atas :
Adapun coding PHP yang dignakan untuk mencari perhitungan ini adalah sebagai berikut :
<?php
$neighbors['Jalan Jamin Ginting No.241'] = array('Jalan
Jenderal A.H Nasution' => 2.19, 'Jalan Setia Budi No.129A' =>
2.99
,'Universitas Sumatera Utara' => 1.93, 'Bandara Polonia' =>
1.94);
$neighbors['Jalan Setia Budi No.129A'] = array('Jalan Jamin
Ginting No.241' => 2.99, 'Universitas Sumatera Utara' => 1.36,
'Rumah Makan Wong Solo' => 1.80, 'Jalan Sei Batang Hari' =>
1.46, 'Jalan Gatot Subroto' => 2.32);
$neighbors['Jalan Gatot Subroto'] = array('Jalan Setia Budi
No.129A' => 2.32, 'Jalan Sei Batang Hari' => 0.88, 'Rumah Makan
Wong Solo' => 1.15,
'Jalan Gajah Mada' => 1.61, 'Jalan Profesor Muhammad Yamin' =>
4.87, 'Jalan T Amir Hamzah' => 2.40);
$neighbors['Jalan Sei Batang Hari'] = array('Jalan Setia Budi
No.129A' => 1.46, 'Jalan Jamin Ginting No.241' => 1.93
, 'Rumah Makan Wong Solo' => 0.98, 'Jalan Gatot Subroto' =>
0.88,);
$neighbors['Universitas Sumatera Utara'] = array('Jalan Setia
Budi No.129A' => 1.36, 'Jalan Jamin Ginting No.241' => 1.93,
'Rumah Makan Wong Solo' => 1.83, 'Jalan Iskandar Muda No.19
A/B/C' => 1.55, 'Jalan Patimura' => 1.37, 'Bandara Polonia' =>
2.41);
$neighbors['Jalan Jenderal A.H Nasution'] = array('Jalan Jamin
45
'Jalan Brigjen Zein Hamid No.24-D' => 1.34, 'Jalan
Sisingamaraja No.348' => 2.40);
$neighbors['Jalan Brigjen Zein Hamid No.24-D'] = array('Jalan
Jenderal A.H Nasution' => 1.34,
'Jalan Sisingamaraja No.348' => 2.47);
$neighbors['Rumah Makan Wong Solo'] = array('Jalan Setia Budi
No.129A' => 1.80, 'Jalan Gatot Subroto' => 1.15, 'Jalan Sei
Batang Hari' => 0.98,
'Universitas Sumatera Utara' => 1.83, 'Jalan Gajah Mada' =>
0.73, 'Jalan Nusantara' => 0.90, 'Jalan Iskandar Muda No.19
A/B/C' => 0.96);
$neighbors['Jalan Gajah Mada'] = array('Jalan Gatot Subroto' =>
1.61, 'Rumah Makan Wong Solo' => 0.73, 'Jalan Nusantara' =>
0.37,
'Plaza Medan Polonia' => 0.50);
$neighbors['Jalan Nusantara'] = array('Jalan Gajah Mada' =>
0.37, 'Rumah Makan Wong Solo' => 0.90,
'Jalan Iskandar Muda No.19 A/B/C' => 0.15, 'Plaza Medan
Polonia' => 0.39, 'Jalan Patimura' => 0.86);
$neighbors['Jalan Iskandar Muda No.19 A/B/C'] = array('Jalan
Nusantara' => 0.15, 'Rumah Makan Wong Solo' => 0.96,
'Universitas Sumatera Utara' => 1.55, 'Jalan Patimura' =>
0.74);
$neighbors['Jalan Patimura'] = array('Jalan Iskandar Muda No.19
A/B/C' => 0.74, 'Jalan Nusantara' => 0.86,
'Plaza Medan Polonia' => 1.03, 'Universitas Sumatera Utara' =>
1.37, 'Jalan Dipoenogoro' => 1.17,'Bandara Polonia' => 1.93);
$neighbors['Bandara Polonia'] = array('Jalan Patimura' => 1.93,
'Universitas Sumatera Utara' => 2.41,
'Jalan Jenderal A.H Nasution' => 2.05, 'Jalan Jamin Ginting
No.241' => 1.94, 'Jalan Sisingamaraja No.348' => 2.47,
'Jalan Sisingamaraja No.251/252' => 2.13, 'Jalan Sisingamaraja'
$neighbors['Jalan Profesor Muhammad Yamin'] = array('Bandara
Polonia' => 2.31, 'Plaza Medan Polonia' => 0.95 , 'Jalan
Patimura' => 1.93,
'Jalan Gatot Subroto' => 4.87, 'Jalan Garuda II' => 1.80,'Jalan
Sisingamaraja' => 3.95, 'Jalan Sentosa Baru No.17A' => 1.16
,'Jalan T Amir Hamzah' => 3.80, 'Jalan Krakatau' => 2.47,
'Jalan Dipoenogoro' => 3.95);
$neighbors['Jalan Sisingamaraja'] = array('Jalan Profesor
Muhammad Yamin' => 3.95, 'Jalan Sisingamaraja No.251/252' =>
0.57,
'Jalan Dipoenogoro' => 3.08, 'Bandara Polonia' => 2.01, 'Jalan
Garuda II' => 3.40);
$neighbors['Jalan Sisingamaraja No.251/252'] = array('Jalan
Sisingamaraja' => 0.57, 'Bandara Polonia' => 2.13,
'Jalan Sisingamaraja No.348' => 0.61, 'Jalan Garuda II' =>
3.90);
$neighbors['Jalan Sisingamaraja No.348'] = array('Jalan
Sisingamaraja No.251/252' => 0.61, 'Jalan Brigjen Zein Hamid
No.24-D' => 2.47,
'Jalan Jenderal A.H Nasution' => 2.40, 'Bandara Polonia' =>
2.47, 'Jalan Garuda II' => 4.33);
$neighbors['Jalan Sentosa Baru No.17A'] = array('Jalan Profesor
Muhammad Yamin' => 1.16, 'Jalan Garuda II' => 1.00,
'Jalan Jenderal A.H Nasution' => 2.4, 'Bandara Polonia' =>
2.47, 'Jalan Krakatau' => 3.19, 'Jalan Cemara' => 3.52,
'Jalan William Iskandar' => 3.35);
$neighbors['Jalan Garuda II'] = array('Jalan Sentosa Baru
No.17A' => 1.00, 'Jalan Sisingamaraja No.348' => 4.33,
'Jalan Sisingamaraja No.251/252' => 3.9, 'Jalan Sisingamaraja'
=> 3.40, 'Jalan Profesor Muhammad Yamin' => 1.80, 'Jalan
William Iskandar' => 4.16);
$neighbors['Jalan Dipoenogoro'] = array('Plaza Medan Polonia'
47
'Bandara Polonia' => 2.31, 'Jalan Sisingamaraja' => 3.08,
'Jalan Profesor Muhammad Yamin' => 2.75);
$neighbors['Plaza Medan Polonia'] = array('Jalan Dipoenogoro'
=> 0.95, 'Jalan Gajah Mada' => 0.50,
'Jalan Nusantara' => 0.39, 'Jalan Patimura' => 1.03, 'Jalan
Profesor Muhammad Yamin' => 3.37);
$neighbors['Jalan T Amir Hamzah'] = array('Jalan Profesor
Muhammad Yamin' => 3.80, 'Jalan Gatot Subroto' => 2.40,
'Jalan Krakatau' => 2.56, 'Jalan Merdeka No.2' => 2.27, 'Jalan
Yos Sudarso No.175B' => 3.56);
$neighbors['Jalan Krakatau'] = array('Jalan T Amir Hamzah' =>
2.56, 'Jalan Sentosa Baru No.17A' => 3.19,
'Jalan Profesor Muhammad Yamin' => 3.80, 'Jalan Cemara' =>
2.68, 'Jalan Yos Sudarso No.175B' => 2.08);
$neighbors['Jalan William Iskandar'] = array('Jalan Cemara' =>
1.23, 'Jalan Sentosa Baru No.17A' => 3.35,
'Jalan Garuda II' => 4.16);
$neighbors['Jalan Cemara'] = array('Jalan William Iskandar' =>
1.23, 'Jalan Merdeka No.2' => 2.68,
'Jalan Yos Sudarso No.175B' => 3.73, 'Jalan Sentosa Baru
No.17A' => 3.52, 'Jalan Krakatau' => 2.68);
$neighbors['Jalan Merdeka No.2'] = array('Jalan Cemara' =>
2.68,
'Jalan T Amir Hamzah' => 2.27, 'Jalan Krakatau' => 1.27, 'Jalan
Yos Sudarso No.175B' => 2.08);
function dijkstra($neighbors, $start) {
$closest = $start;
while (isset($closest)) {
$marked[$closest] = 1;
foreach ($neighbors[$closest] as $vertex => $distance) {
if (isset($marked[$vertex]))
continue;
$dist = (isset($paths[$closest][0]) ? $paths[$closest][0]
if (!isset($paths[$vertex]) || ($dist <
$paths[$vertex][0])) {
if (isset($paths[$closest])) {
$paths[$vertex]= $paths[$closest];
}
$paths[$vertex][] = $closest;
$paths[$vertex][0] = $dist;
}
}
unset($closest);
foreach ($paths as $vertex => $path) {
if (isset($marked[$vertex]))
continue;
$distance = $path[0];
if ((!isset($min) || $distance < $min) ||
!isset($closest)) {
$min = $distance;
$closest = $vertex;
}
}
}
return $paths;
}
49 BAB 4
IMPLEMENTASI DAN PENGUJIAN SISTEM
4.1 Implementasi Sistem
Pada bab ini akan dilakukan implementasi dan pengujian terhadap aplikasi yang dibangun. Tahapan ini dilakukan setelah analisis dan perancangan selesai dilakukan dan selanjutnya akan diimplementasikan kedalam bahasa pemograman. Setelah implementasi maka dilakukan pengujian terhadap aplikasi. Aplikasi yang telah dibangun akan diimplementasikan untuk mengetahui apakah sistem tersebut dapat berjalan sesuai dengan tujuannya atau tidak.
Tujuan implementasi adalah untuk menerapkan perancangan yang telah dilakukan terhadap sistem sehingga user dapat mengetahui sistem yang telah dibangun sebagai simulasi dari aplikasi penerapan algoritma Dijkstra untuk menentukan rute terpendek pada salah satu lembaga bimbingan belajar di Kota Medan.
Agar sistem perancangan yang telah dikerjakan dapat berjalan baik atau tidak, maka perlu kiranya dilakukan pengujian terhadap sistem yang telah dikerjakan. Oleh karena itu, dibutuhkan beberapa komponen untuk mencakup perangkat keras (Hardware) dan perangkat lunak (software).
Untuk bisa menerapkan algoritma ini dibutuhkan beberapa data yang harus disiapkan, yaitu :
1. Beberapa Titik/simpul/daerah, titik/simpul/daerah yang bisa dijangkau secara langsung, dan juga jarak antara mereka.
Jika dicontohkan dengan salah satu graf akan seperti ini :
Gambar 4.1 Contoh Graf Untuk Mencari Rute Terpendek
Titik A adalah titik awal/keberangkatan, titik F adalah titik akhir/tujuan. Kemudian kita akan mencari rute manakah yang harus dilewati dan memilik total jarak yang paling dekat. Untuk bisa mendapatkan rute itu, maka grafik diatas ditambahkan beberapa kotak untuk mengisi beberapa label. Seperti ini :
Gambar 4.2 Contoh Algoritma Dijkstra Langkah Pertama
Penjelasannya adalah:
51
Setelah itu ada beberapa langkah yang harus dilakukan, yaitu :
1. Mengisi kotak label pada titik awal dengan label urutan 1 dan label jarak 0. 2. Menetapkan label jarak sementara untuk semua titik yang dapat dihubungi
langsung dari awal.
3. Pilih titik dengan label jarak sementara terkecil dan menuliskan nilainya di label jarak, serta tambahkan label urutan-nya.
4. Masukan label jarak sementara pada setiap titik yang belum memiliki label urutan dan label jarak dan dapat dihubungi langsung dari titik yang baru saja ditulis label jarak dan label urutan-nya. nilainya diisi dengan total dari label jarak dari titik sebelumnya dan jarak dari titik tersebut. Jika label jarak sementara di titik tersebut sudah memiliki nilai, maka harus diganti hanya jika nilai yang baru lebih kecil.
5. Pilih titik dengan label jarak sementara terkecil dan menggunakan label jarak sementara-nya sebagai label jarak dari titik tersebut, serta tambahkan label urutan-nya.
6. Ulangi langkah 4 dan 5 hingga titik tujuan memiliki label jarak dan label urutan.
Maka pada langkah pertama adalah Mengisi kotak label pada titik awal dengan label urutan 1 dan label jarak 0.
Kemudian mengisi label jarak sementara titik yang dapat dihubungi langsung dari titik A yakni titik B, C, dan D .
Gambar 4.5 Contoh Algoritma Dijkstra Langkah Ketiga
Maka yang terpilih adalah titik B karena memiliki label jarak sementara terkecil, dan mengisi nilai label jarak-nya sama dengan label jarak sementara serta memberikan label urutan-nya.
Gambar 4.6 Contoh Algoritma Dijkstra Langkah Keempat
53
sudah ada dan lebih kecil (6), jadi label jarak sementara-nya tidak diganti dan tetap bernilai 6.
Langkah selanjutnya adalah memilih label jarak sementara terkecil. Karena titik D dan titik C memiliki label jarak sementara yang sama yakni 6, maka bisa memilih salah satu dari kedua titik tersebut. Misalkan titik C yang dipilih, maka berikan label jarak dan label urutan-nya.
Gambar 4.7 Contoh Algoritma Dijkstra Langkah Kelima
Kemudian titik yang dapat dihubungi secara langsung dari titik C dan belum memilik label jarak adalah titik D dan E. Titik D => 6 + 2 = 8, lebih besar jika dibandingkan dengan nilai label jarak sementara yang dimiliki oleh titik E sebelumnya (6), maka nilai 8 diabaikan dan tetap diisi 6. Titik E => 6 + 3 = 9, maka langsung saja label jarak sementara titik D diisi dengan 9.
Selanjutnya titik E terpilih karena memiliki label jarak sementara terkecil. Berikan label jarak dan label urutan-nya.
Gambar 4.9 Contoh Algoritma Dijkstra Langkah Ketujuh
Dan titik F dan E adalah titik yang dapat dihubungi secara langsung dari titik D dan belum memilik label jarak. Titik F => 6 + 4 = 10 dan langsung diisikan kedalam label jarak sementara-nya. sedangkan titik E => 6 + 2 = 8 dan lebih kecil dari pada nilai sebelumnya yaitu 9, maka nilai label jarak sementara-nya diganti dengan 8.
Gambar 4.10 Contoh Algoritma Dijkstra Langkah Kedelapan
55
Gambar 4.11 Contoh Algoritma Dijkstra Langkah Kesembilan
Titik F adalah titik terakhir yang dapat dihubungi secara langsung dari titik E dan belum memilik label jarak serta merupakan titik tujuan. Titik F => 8 + 2 = 10 dan lebih kecil dari pada nilai sebelumnya yaitu 11, maka nilai label jarak sementara-nya diganti dengan 10.
Karena titik F adalah stu-satunya titik terakhir yang belum mempunyai label jarak dan label urutan. maka lansung saja berikan nilai label jarak dan label urutan-nya. Dengan begitu titik tujuan sudah memiliki label jarak dan label jarak sementara.
Gambar 4.13 Contoh Algoritma Dijkstra Langkah Kesebelas
Dengan begitu diketahui rute yang harus dilewati dan memiliki jarak terpendek dari titik A menuju titik F adalah A -> E -> D -> F 0 + 6 + 2 + 2 = 10
57
4.2 Tampilan Program
Subbab ini akan menunjukkan tampilan program dan desain program website dari hasil perancangan yang telah dibangun pada bab sebelumnya sebelumnya.
4.2.1 Halaman index
Halaman home adalah halaman awal pada sistem ini. Pada halaman home, berisi informasi mengenai profil website, buku tamu, contact us,algoritma djikstra, dan menu rute terpendek, dan menampilkan foto galeri website. Berikut adalah tampilan home :
Gambar 4.15 Tampilan Menu Utama 4.2.2 Halaman Buku Tamu
Gambar 4.16 Tampilan Buku Tamu 4.2.3 Halaman Tentang Algoritma Dijkstra
Halaman ini adalah halaman yang menampilkan tentang algoritma dijkstra dimana terdapat pengertian dan cara kerja algoritma djikstra. Algoritma djikstra sendiri adalah algoritma yang digunakan dalam pencarian rute terpendek yang dirancang dalam website ini. halaman ini dapat dilihat pada gambar di bawah ini.
![Gambar 2.1 Sub-Sistem SIG [7]](https://thumb-ap.123doks.com/thumbv2/123dok/102814.8652/23.595.183.453.595.741/gambar-sub-sistem-sig.webp)
![Gambar 2.2 Ilustrasi Urian Sub-Sistem SIG [7]](https://thumb-ap.123doks.com/thumbv2/123dok/102814.8652/24.595.110.546.145.368/gambar-ilustrasi-urian-sub-sistem-sig.webp)
![Gambar 2.5 Perbedaan Proyeksi (a) Cylindrical, (b)Planar dan (c) Conical [7]](https://thumb-ap.123doks.com/thumbv2/123dok/102814.8652/28.595.145.552.272.433/gambar-perbedaan-proyeksi-a-cylindrical-planar-dan-conical.webp)