Penyelesaian Permainan Flow Colors dengan Meminimumkan Deviasi Panjang Tiap Jalur

(1)

PENYELESAIAN PERMAINAN

FLOW COLORS

DENGAN

MEMINIMUMKAN DEVIASI PANJANG TIAP JALUR

IRFAN CHAHYADI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Permainan

Flow Colors dengan Meminimumkan Deviasi Panjang Tiap Jalur adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juni 2014

Irfan Chahyadi

(4)

ABSTRAK

IRFAN CHAHYADI. Penyelesaian Permainan Flow Colors dengan Meminimumkan Deviasi Panjang Tiap Jalur. Dibimbing oleh AMRIL AMAN dan FARIDA HANUM.

Flow Colors adalah permainan puzzle asah otak. Tugas pemain adalah menghubungkan setiap pasangan titik berwarna sama dengan pipa sehingga memenuhi area permainan dengan warna. Pipa-pipa yang berbeda warna tidak boleh bersilangan/overlapping. Permasalahan permainan ini dapat dimodelkan sebagai masalah pembuatan rute pada graf yang merupakan modifikasi dan pengembangan dari model Traveling Salesman Problem (TSP). Dalam karya ilmiah ini akan dibahas bagaimana memformulasikan Puzzle Flow Colors dengan meminimumkan deviasi panjang semua jalur menggunakan integer linear programming serta menyelesaikannya dengan software LINGO 11.0.

Kata kunci: integer linear programming, puzzle Flow Colors, Traveling Salesman Problem

ABSTRACT

IRFAN CHAHYADI. Solving Flow Colors Game to Minimize Length Deviation of Each Line. Supervised by AMRIL AMAN and FARIDA HANUM.

Flow Colors is a puzzle game, where players must connect every pair of points of the same color with a pipe so that the pipes cover all the game areas with colors. Pipes with different colors should not be intersected/ overlapped. This problem can be modelled as a problem of making routes on a graph which is a modification of Traveling Salesman Problem (TSP). This study presents how to formulate puzzle of Flow Colors to minimize length deviation of the lines represented by the pipes by applying method of integer linear programming and solving it by using LINGO 11.0 computer software.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENYELESAIAN PERMAINAN

FLOW COLORS

DENGAN

MEMINIMUMKAN DEVIASI PANJANG TIAP JALUR

NAMA PENULIS

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

BOGOR 2014

(6)

(7)

Judul Skripsi : Penyelesaian Permainan Flow Colors dengan Meminimumkan Deviasi Panjang Tiap Jalur

Nama : Irfan Chahyadi NIM : G54100057

Disetujui oleh

Dr. Ir. Amril Aman, M.Sc. Pembimbing I

Dra. Farida Hanum, M.Si. Pembimbing II

Diketahui oleh

Dr. Toni Bakhtiar, M.Sc. Ketua Departemen

(8)

PRAKATA

Puji dan syukur penulis ucapkan kepada Allah SWT. atas segala nikmat, rahmat, karunia dan pertolongan yang telah diberikan sehingga karya ilmiah ini berhasil diselesaikan. Judul karya ilmiah ini adalah Penyelesaian Permainan Flow Colors dengan Meminimumkan Deviasi Panjang Tiap Jalur. Penyusunan karya ilmiah ini tidak lepas dari bantuan beberapa pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada:

1 Allah SWT atas segala rahmat dan karunia-Nya,

2 Nabi besar Muhammad SAW sebagai nabi akhir zaman,

3 Keluarga tercinta: Ayah dan Mamah yang selalu memberi nasihat, motivasi dan doa,

4 Dr. Ir. Amril Aman, M.Sc. selaku Pembimbing I atas kesabaran dalam membimbing penulis serta saran dan ilmunya yang bermanfaat,

5 Dra. Farida Hanum, M.Si. selaku Pembimbing II yang telah membimbing dan memotivasi penulis dalam menulis karya ilmiah ini,

6 Drs. Prapto Tri Supriyo, M.Kom. selaku Dosen Penguji yang telah memberikan ilmu, saran, serta dukungan,

7 seluruh dosen Departemen Matematika IPB yang telah membimbing dan memberikan ilmunya selama ini,

8 para staf Departemen Matematika IPB yang telah membantu dalam berbagai hal

9 teman seperjuangan bimbingan: Kak Razon, Kak Fardan, Kak Dina, Kak Gita, Kak Elisa, Kak Suzie, Kak Agung, Eric, Pupu, Alin,

10 Kamil, Danang, Ayun, Vina, Imad, Fikri, Fajar, Syafi’i, Rendi, Komti, Adi, Tri, Nyoman, Irfan N, Bonno, Tuty, Susi, Abi, Irma, Aul, Dedi, Syika dan seluruh teman-teman seperjuangan di Gumatika,

11 Kak Rio, Kak Dayat, Kak Mirna, Kak Galih dan semua Kakak kelas Matematika 46 sebagai contoh yang baik,

12 semua sahabat Matematika 47 sebagai keluarga yang ceria, 13 semua adik-adik Matematika 48 dan 49 yang selalu mendukung,

14 dan semua pihak yang telah membantu penulis dalam menyelesaikan karya ilmiah ini.

Penulis menyadari bahwa dalam karya ilmiah ini masih terdapat banyak kekurangan dan masih jauh dari kesempurnaan. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun agar karya ilmiah ini dapat terus menambah wawasan pembaca sekalian. Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan, khususnya bidang matematika.

Bogor, Juni 2014

(9)

DAFTAR ISI

DAFTAR TABEL viii

DAFTAR GAMBAR viii

DAFTAR LAMPIRAN viii

PENDAHULUAN 1

Latar Belakang 1

Perumusan Masalah 2

Tujuan Penelitian 2

Ruang Lingkup Penelitian 2

LANDASAN TEORI 2

Linear Programming 2

Ekuivalensi Formulasi 3

Integer Programming 4

Traveling Salesman Problem 4

DESKRIPSI DAN FORMULASI MASALAH 5

Deskripsi Masalah 5

Pemodelan 6

STUDI KASUS 9

Skenario 1 9

Skenario 2 12

Skenario 3 12

Skenario 4 13

HASIL DAN PEMBAHASAN 14

SIMPULAN DAN SARAN 17

Simpulan 17

Saran 18

DAFTAR PUSTAKA 18

LAMPIRAN 19

(10)

DAFTAR TABEL

1 Matriks kemungkinan pembuatan ruas jalur × 9

2 Sel given pada Flow Colors berukuran × dengan 6 warna 12 3 Sel given pada Flow Colors berukuran × dengan warna 13 4 Sel given pada Flow Colors berukuran × 13

5 Panjang tiap jalur hasil solusi Skenario 1 14

DAFTAR GAMBAR

1 Flow Colors × 1

2 Ilustrasi permainan Flow Colors × dengan 5 warna dan solusinya 5 3 Perbedaan dengan kendala eliminasi subtur (kiri) dan tanpa kendala

eliminasi subtur (kanan) 8

4 Kasus Flow Colors berukuran × 9

10 Hasil solusi Skenario 3 15

11 Hasil solusi Skenario 4 15

12 Solusi optimal yang tak tunggal 16

13 Karakteristik kasus yang tidak memiliki solusi 17

DAFTAR LAMPIRAN

1 Script komputasi MATLAB untuk membangkitkan matriks � , 19 2 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 1 20 3 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 2 21 4 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 3 22 5 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 4 23

6 Hasil komputasi LINGO 11.0 untuk Skenario 1 24

(11)

PENDAHULUAN

Latar Belakang

Dalam perkembangannya matematika memiliki peranan penting dalam memecahkan masalah kehidupan sehari-hari. Tidak hanya permasalahan dalam dunia nyata, matematika juga dapat menyelesaikan beberapa permasalahan yang ditemukan dalam sebuah permainan. Beberapa permainan dapat diselesaikan dengan matematika seperti Sudoku, Challenger puzzle, N-Queens problem, dan masih banyak lagi. Dalam karya ilmiah ini akan dibahas pemecahan masalah permainan Flow Colors dengan pendekatan matematika. Flow Colors adalah permainan puzzle asah otak yang dikembangkan oleh Mohammed Nafiz Almadhoun. Selain di website-nya, permainan ini dapat ditemui di beberapa

platfom seperti Android sebagai sebuah aplikasi.

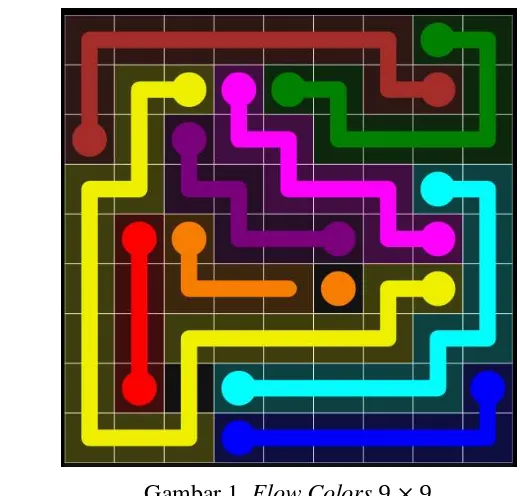
Dalam permainan Flow Colors, tugas pemain adalah menghubungkan setiap pasangan titik berwarna sama dengan pipa sehingga memenuhi area permainan dengan warna. Namun pipa-pipa tersebut tidak boleh bersilangan/overlapping.

Contoh kasus dapat dilihat pada Gambar 1. Area permainan merupakan persegi dengan banyak sel. Tingkat kesulitan puzzle ini ditentukan oleh besarnya area permainan dan banyaknya warna. Permasalahan permainan ini dapat dimodelkan sebagai masalah pembuatan rute pada graf yang merupakan modifikasi dan pengembangan dari model Traveling Salesman Problem (TSP) sehingga dapat diselesaikan dengan metode Integer Linear Programming (ILP). Dalam karya ilmiah ini akan dibahas bagaimana memformulasikan permainan puzzle Flow Colors dengan metode integer linear programming, serta menyelesaikannya menggunakan software LINGO 11.0.

(12)

2

Perumusan Masalah

Permainan ini mengundang beberapa pertanyaan menarik untuk bidang ilmu matematika:

1. Dapatkah permainan ini dipecahkan dengan konsep matematika?

2. Teknik matematika apa yang dapat digunakan untuk menyelesaikan permasalahan ini?

Tujuan Penelitian

Tujuan penelitian ini ialah memodelkan puzzle Flow Colors menggunakan

Integer Linear Programming dengan meminimumkan deviasi panjang tiap jalur dan menyelesaikannya dengan software LINGO 11.0.

Ruang Lingkup Penelitian

Puzzle yang akan dibahas dalam karya ilmiah ini adalah Flow Colors dengan ukuran × . Puzzle ini dapat dikembangkan sampai ukuran berapapun. Dalam karya ilmiah ini, penulis membatasi pembahasan hanya sampai Flow Colors

berukuran × .

LANDASAN TEORI

Untuk dapat memodelkan puzzle Flow Colors, diperlukan beberapa pemahaman teori tentang linear programming, Ekuivalensi Formulasi, integer programming, dan Traveling Salesman Problem.

Linear Programming

Fungsi linear dan pertidaksamaan linear merupakan konsep-konsep dasar yang harus dipahami terkait dengan linear programming. Sebuah fungsi � � , � , … , � dari variabel � , � , … , � adalah fungsi linear jika dan hanya jika untuk suatu himpunan konstanta , , … , , fungsi � berbentuk

� � , � , … , � = � + � + ⋯ + � , sedangkan untuk suatu fungsi linear

� � , � , … , � dan sembarang bilangan , pertidaksamaan � � , � , … , �

dan � � , � , … , � disebut pertidaksamaan linear (Winston 2004).

Dalam Winston (2004), masalah linear programming (LP) adalah masalah pengoptimuman yang memenuhi ketentuan-ketentuan berikut ini:

1. Tujuan masalah tersebut adalah memaksimumkan (atau meminimumkan) fungsi linear dari variabel keputusan. Fungsi yang ingin dimaksimumkan atau diminimumkan disebut fungsi objektif.

2. Nilai dari variabel keputusan harus memenuhi sekumpulan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

(13)

3

Ekuivalensi Formulasi

Dalam memformulasikan permasalahan dunia nyata banyak terdapat model yang kompleks. Untuk beberapa kasus, formulasi tersebut dapat diekspresikan secara matematik dengan lebih dari satu cara. Ekspresi yang berbeda tersebut mungkin tidak ekuivalen secara matematik namun secara komputasi lebih mudah untuk diselesaikan (Dantzig dan Thapa 1997). Misalkan dalam suatu model matematik terdapat fungsi nilai mutlak yang didefinisikan sebagai fungsi terhadap � dengan:

|�| = { �,_−�, �_{� < .}

Permasalahan tersebut bukan LP karena terdapat fungsi nilai mutlak yang merupakan fungsi taklinear. Menurut Dantzig dan Thapa (1997), jika fungsi nilai mutlak muncul dalam persamaan umum, maka tidak mungkin memformulasikan ulang fungsi tersebut menjadi persamaan linear. Namun jika fungsi tersebut hanya terdapat pada fungsi objektif, maka model tersebut dapat diformulasikan ulang menjadi pemrograman linear.

Misalkan diberikan fungsi objektif untuk meminimumkan jumlah bobot dari nilai mutlak dengan taknegatif terhadap sekumpulan kendala linear, yaitu: Minimumkan � = ∑ |� |

Dari definisi nilai mutlak:

|�+− �−| = { �

+_{− �}−_, _�+ _�−

(14)

4

Dari 3 kemungkinan tersebut diperoleh:

(i) Jika �+ > �−, maka �+ > dan �− = sehingga menjadi fungsi linear dalam fungsi objektifnya.

Integer Programming

Pemrograman integer atau integer programming (IP) adalah LP dengan sebagian atau seluruh variabel diharuskan bilangan bulat taknegatif. Jika seluruh variabel diharuskan bilangan bulat (integer) maka masalah tersebut disebut pure integer programming. Jika hanya sebagian variabel diharuskan integer maka disebut mixed integer programming. Integer programming dengan variabel harus bernilai 0 atau 1 disebut 0-1 IP (Winston 2004).

Traveling Salesman Problem

Menurut Fournier (2009), Traveling Salesman Problem (TSP) dapat dipandang sebagai permasalahan penentuan cycle Hamilton pada suatu graf yaitu

cycle yang melewati semua verteks dari graf tersebut tepat satu kali. TSP merupakan permasalahan seorang penjual yang harus melakukan tur ke sejumlah kota, berangkat dari sembarang kota awal, melewati setiap kota tepat sekali, dan terakhir kembali ke kota di mana ia berangkat. Penentuan rute ditetapkan berdasarkan jarak minimum yang akan ditempuh.

Persamaan permasalahan TSP dengan Flow Colors adalah setiap sel harus terlewati tepat satu kali, dan tidak diperbolehkan adanya subtur; sedangkan perbedaannya, pada Flow Colors rute tidak kembali ke titik awal (bukan cycle

Hamilton), dan rute tidak tunggal. Misalkan sebuah permasalahan TSP terdiri dari

N kota dan adalah jarak dari kota ke kota untuk ≠ dan = dengan adalah bilangan yang relatif besar. Didefinisikan variabel keputusan:

(15)

5 Solusi permasalahan TSP tersebut didapatkan dengan menyelesaikan formulasi berikut: Kendala terakhir disebut kendala penghilang subtur atau Subtour Eliminating Constraint (SEC) yaitu kendala yang mencegah terjadinya cycle Hamilton yang tidak memuat semua verteks. Kendala ini selanjutnya akan dimodifikasi sesuai dengan permasalahan Flow Colors.

DESKRIPSI DAN FORMULASI MASALAH

Deskripsi Masalah

Pada puzzleFlow Colors, area permainan merupakan sel-sel persegi dengan ukuran × sehingga total sel dalam satu permainan adalah . Contoh puzzle Flow Colors dapat dilihat pada Gambar 2. Terdapat titik given, yaitu pasang

titik berbeda warna yang telah diberikan di awal permainan dan diletakkan di sel-sel yang berbeda dengan 2. Tugas pemain ialah menghubungkan kedua titik given yang warnanya sama hanya dengan sebuah jalur sehingga solusi yang diharapkan adalah buah jalur dengan warna sesuai given-nya. Ruas jalur antara dua sel yang berdekatan hanya dapat dibuat dengan arah kanan, kiri, atas, bawah,

(16)

6

dan tidak boleh diagonal. Jadi, jalur merupakan sekumpulan ruas jalur yang saling terhubung dan berlanjut. Permasalahan lain yang harus dihadapi pemain adalah setiap jalur tidak boleh saling bersilangan atau overlapping dan setiap sel harus terlewati oleh tepat satu jalur (Madhoun 2014). Dalam karya ilmiah ini akan dicari solusi terbaik dengan kriteria deviasi dari panjang tiap jalur adalah minimum.

Pemodelan

Berdasarkan analisis masalah, maka dapat dibuat formulasi masalah tersebut ke dalam bentuk integer linear programming (ILP). Bentuk formulasi masalah

puzzle Flow Colors berukuran × dengan buah warna diberikan sebagai = jumlah total warna,

� = rata-rata ideal panjang tiap jalur �− .

Variabel keputusan

, , = { ; jika sel dan terhubung dengan ruas jalur berwarna _{; selainnya,}

, = { ; jika sel terisi warna _{; selainnya,}

panjang jalur berwarna :

= ∑ ∑ , ,

Fungsi objektif dari masalah ini ialah meminimumkan deviasi panjang tiap jalur. Hal ini dapat diperoleh dengan meminimumkan jumlah selisih panjang tiap jalur berwarna dengan rata-ratanya:

Minimumkan ∑|� − |

(17)

7 Dengan fungsi nilai mutlak sebagai fungsi objektif, maka permasalahan ini menjadi pemrograman taklinear. Dalam komputasinya, LINGO 11.0 tidak dapat menjamin diperolehnya solusi optimum global jika model tersebut adalah pemrograman taklinear. Oleh sebab itu perlu adanya ekuivalensi formulasi fungsi nilai mutlak menjadi fungsi linear. Model tersebut dapat diformulasikan ulang menjadi pemrograman linear dengan mengganti nilai mutlaknya dengan bagian positif dan negatifnya, yaitu dan .

; = , , … , ; = , , … , sehingga

� − = − ; ∀

dengan fungsi nilai mutlaknya

|� − | = + ; ∀

maka fungsi objektif dapat diubah menjadi:

Minimumkan ∑( + )

∀ Kendala

Kendala dalam permasalahan ini ialah:

1. Kemungkinan pembuatan ruas jalur dibatasi oleh parameter �.

� , − , , ; ∀ , , .

2. Semua sel terisi tepat satu warna.

∑ , =

∀

; ∀ .

3. Semua sel given sudah terisi satu warna.

, = ; ∀ , �.

4. Semua sel given terhubung dengan tepat satu ruas jalur.

∑ , ,

∀

+ ∑ , ,

∀

= ; ∀ , �.

5. Untuk setiap sel nongiven, terdapat tepat satu ruas jalur yang menghubungkan sel tersebut menuju ke sembarang sel.

∑ , , − ,

∀

= ; ∀ , = { | , �}.

6. Untuk setiap sel nongiven, terdapat tepat satu ruas jalur yang menghubungkan sembarang sel menuju sel tersebut.

∑ , , − ,

∀

= ; ∀ , = { | , �}.

7. Untuk setiap ruas jalur, dua sel yang dihubungkannya berwarna sama dengan ruas jalur tersebut.

, + , − ∙ , , ; ∀ , , .

8. Setiap ruas jalur tidak diperbolehkan bolak-balik.

(18)

8

9. Tidak diperbolehkan adanya suatu subtur.

Dalam pembuatan solusi, terdapat kemungkinan terjadinya subtur seperti pada Gambar 3 sehingga perlu dibuat kendala eliminasi subtur.

Gambar 3 Perbedaan dengan kendala eliminasi subtur (kiri) dan tanpa kendala eliminasi subtur (kanan)

Tanpa kendala eliminasi subtur, akan terdapat subtur sehingga terdapat lebih dari buah jalur (dengan adalah banyaknya warna, = ). Hal ini melanggar aturan permainan yaitu hanya terdapat buah jalur. Kendala tersebut dituliskan sebagai berikut:

, − , + ∙ , , − ; ∀ , , .

Subtur yang terjadi pada Gambar 3 yaitu subtur 16-17-23-29-28-22-16 yang berwarna biru muda. Misalkan = untuk warna biru muda, sehingga

, , = , , = ⋯ = , , = dengan = . Subtur

ini menghasilkan 6 pertidaksamaan berikut:

, − , +

Jika semua pertidaksamaan ini dijumlahkan maka hasilnya:

∙ ∙

,

sehingga subtur tersebut (dan semua subtur lain yang mungkin) dihilangkan oleh kendala eliminasi subtur.

10.Persamaan tambahan untuk pelinearan fungsi nilai mutlak.

� − = − ; ∀

11.Kendala ketaknegatifan variabel

(19)

9

STUDI KASUS

Permasalahan Flow Colors yang akan dibahas pada karya ilmiah ini diperoleh dari website Mohammed Almadhoun yang beralamat di Madhoun (2014). Selanjutnya akan dibahas empat skenario dengan tingkat kesulitan yang berbeda. Perlu diperhatikan bahwa di website tersebut hanya disajikan soal-soal Flow Colors

berukuran × hingga × . Skenario pertama dan ketiga tidak diperoleh dari

website tersebut.

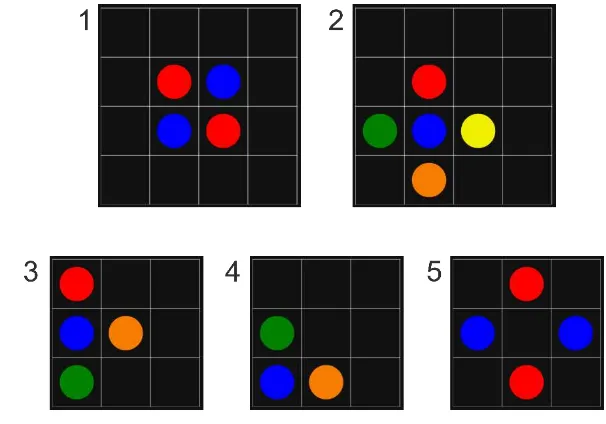
Skenario 1

Skenario pertama menguji model dengan soal Flow Colors berukuran × dan warna. Misalkan diberikan 4 titik given, yaitu 2 titik berwarna merah pada sel 1 dan 6 serta berwarna biru pada sel 3 dan 5. Sebelum memformulasikan masalah tersebut, perlu dibuat model tiruan dari Flow Colors. Sel-sel dalam area permainan direpresentasikan sebagai berikut:

Gambar 4 Kasus Flow Colors berukuran ×

Pada skenario ini area permainan berukuran × sehingga diperoleh matriks kemungkinan pembuatan ruas jalur:

Tabel 1 Matriks kemungkinan pembuatan ruas jalur ×

Sel 1 2 3 4 5 6 7 8 9

(20)

10

Matriks � dapat dibangkitkan dengan cara sebagai berikut:

� , = { , | − | = [| − | = (

[ > mod , ≠ ]

[ < mod , ≠ ])]

, selainnya

Matriks � dapat juga dibangkitkan dengan software MATLAB dengan script pada Lampiran 1 dengan = .

panjang jalur berwarna :

= ∑ ∑ , ,

Fungsi objektif dari masalah ini ialah meminimumkan jumlah selisih panjang tiap jalur berwarna dengan rata-ratanya. Hasil pelinearan fungsi objektifnya sebagai berikut:

Minimumkan ∑( + )

=

(21)

11

Kendala

Kendala dalam permasalahan ini ialah:

1. Kemungkinan pembuatan ruas jalur dibatasi oleh parameter �.

� , − , , ; ∀ = , , … , ; = , , … , ; = ,

2. Semua sel terisi tepat satu warna.

∑ ,

=

= ; ∀ = , , … ,

3. Semua sel given sudah terisi satu warna.

, = ; ∀ , { , , , , , , , }

4. Semua sel given terhubung dengan tepat satu ruas jalur.

∑ , ,

5. Untuk setiap sel nongiven, terdapat tepat satu ruas jalur yang menghubungkan sel tersebut menuju ke sembarang sel.

∑ , ,

9

=

− , = ; ∀ { , , , }; = ,

6. Untuk setiap sel nongiven, terdapat tepat satu ruas jalur yang menghubungkan sembarang sel menuju sel tersebut.

∑ , ,

9

=

− , = ; ∀ { , , , }; = ,

7. Untuk setiap ruas jalur, dua sel yang dihubungkannya berwarna sama dengan ruas jalur tersebut.

, + , − ∙ , , ; ∀ = , , … , ; = , , … , ; = ,

8. Setiap ruas jalur tidak diperbolehkan bolak-balik.

, , + , , ; ∀ = , , … , ; = , , … , ; = ,

9. Tidak diperbolehkan adanya suatu subtur.

, − , + ∙ , ,

∀ = , , … , ; = , , … , ; = ,

10.Persamaan tambahan untuk pelinearan fungsi nilai mutlak.

. − = − ; ∀ = ,

11.Kendala ketaknegatifan variabel

, , { , } ; ∀ = , , … , ; = , , … , ; = ,

, { , } ; ∀ = , , … , ; = ,

, ; ∀ = , , … , ; = ,

; ∀ = ,

(22)

12

Skenario 2

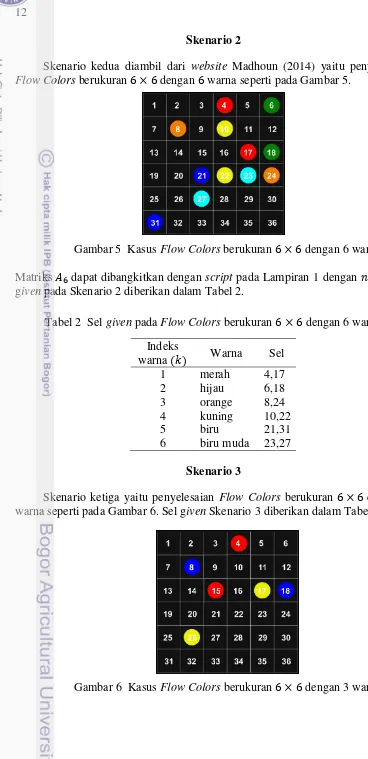
Skenario kedua diambil dari website Madhoun (2014) yaitu penyelesaian

Flow Colors berukuran × dengan warna seperti pada Gambar 5.

Gambar 5 Kasus Flow Colors berukuran × dengan 6 warna Matriks �₆ dapat dibangkitkan dengan script pada Lampiran 1 dengan = . Sel given pada Skenario 2 diberikan dalam Tabel 2.

Tabel 2 Sel given pada Flow Colors berukuran × dengan 6 warna Indeks

warna Warna Sel

1 merah 4,17

2 hijau 6,18

3 orange 8,24

4 kuning 10,22

5 biru 21,31

6 biru muda 23,27

Skenario 3

Skenario ketiga yaitu penyelesaian Flow Colors berukuran × dengan 3 warna seperti pada Gambar 6. Sel given Skenario 3 diberikan dalam Tabel 3.

(23)

13 Tabel 3 Sel given pada Flow Colors berukuran × dengan warna

Indeks

warna Warna Sel

1 merah 4,15

2 biru 8,18

3 kuning 17,26

Skenario 4

Skenario keempat diambil dari website Madhoun (2014) yaitu penyelesaian

Flow Colors berukuran × dengan warna seperti pada Gambar 7.

Gambar 7 Kasus Flow Colors berukuran ×

Matriks �₉ dapat dibangkitkan dengan script pada Lampiran 1 dengan = . Sel

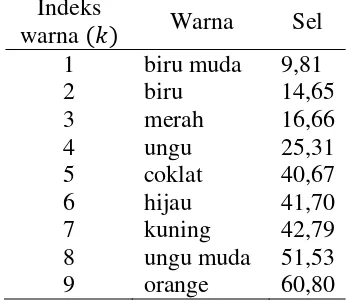
given Skenario 4 diberikan dalam Tabel 4.

Tabel 4 Sel given pada Flow Colors berukuran × Indeks

warna Warna Sel

1 biru muda 9,81

2 biru 14,65

3 merah 16,66

4 ungu 25,31

5 coklat 40,67

6 hijau 41,70

7 kuning 42,79

8 ungu muda 51,53

(24)

14

HASIL DAN PEMBAHASAN

Data dan formulasi yang telah dipaparkan pada Skenario 1, 2, ,3 dan 4 dimasukkan ke dalam proses komputasi menggunakan software LINGO 11.0.

Script setiap skenario disajikan pada Lampiran 2, 3, 4 dan 5. Solusi Flow Colors

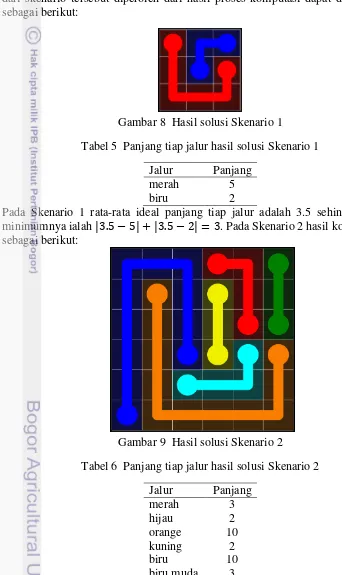
dari skenario tersebut diperoleh dari hasil proses komputasi dapat digambarkan sebagai berikut:

Gambar 8 Hasil solusi Skenario 1

Tabel 5 Panjang tiap jalur hasil solusi Skenario 1 Jalur Panjang

merah 5

biru 2

Pada Skenario 1 rata-rata ideal panjang tiap jalur adalah 3.5 sehingga deviasi minimumnya ialah | . − | + | . − | = . Pada Skenario 2 hasil komputasinya sebagai berikut:

merah 3

hijau 2

orange 10

kuning 2

biru 10

(25)

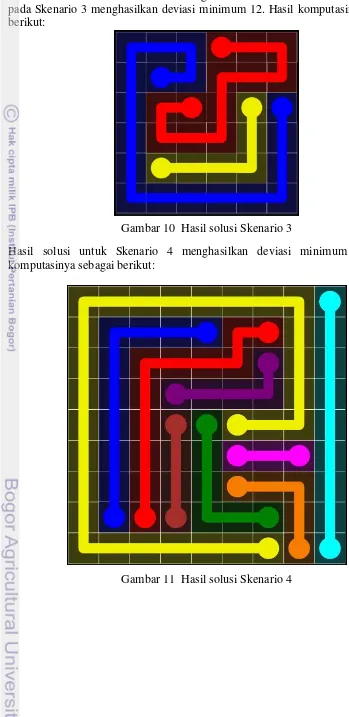
15 Hasil solusi untuk Skenario 2 menghasilkan deviasi minimum 20, sedangkan pada Skenario 3 menghasilkan deviasi minimum 12. Hasil komputasinya sebagai berikut:

Hasil solusi untuk Skenario 4 menghasilkan deviasi minimum 44. Hasil komputasinya sebagai berikut:

(26)

16

Panjang tiap jalur hasil solusi Skenario 3 dan 4 dapat dilihat pada Tabel 7 dan 8. Tabel 7 Panjang tiap jalur hasil solusi Skenario 3

Jalur Panjang

merah 11

biru 17

kuning 5

Untuk suatu kasus tertentu, solusi optimal Flow Colors dapat tidak tunggal. Hal ini dicontohkan pada kasus berikut:

Hasil solusi kasus tersebut selalu menghasilkan panjang jalur masing-masing 5, 5, dan 3 namun dengan kombinasi yang berbeda. Nilai optimum yang dihasilkan selalu sama yaitu 2.6667.

Selain kasus-kasus di atas, terdapat beberapa kasus yang tidak memiliki solusi. Beberapa karakteristik yang menyebabkan suatu kasus tidak memiliki solusi ialah sebagai berikut:

1 Terdapat titik given yang berhimpit dan bersilangan antara dua warna given, karena untuk setiap pembuatan jalur dari satu warna akan memotong jalur warna lainnya.

2 Terdapat titik given yang terapit di tengah dengan empat given lain.

Karena setiap titik given harus terhubung dengan tepat satu ruas jalur, maka terdapat 4 kemungkinan pembuatan ruas jalur (kanan, kiri, atas, dan bawah)

(27)

17 dan setiap dua sel yang dihubungkan satu ruas jalur harus berwarna sama dengan ruas jalur tersebut. Dalam kasus ini, sel given tersebut dikelilingi oleh

given berwarna berbeda sehingga tidak ada solusi yang memenuhi. 3 Terdapat titik given yang terapit di sisi dengan tiga given lain.

Sama dengan kasus sebelumnya namun hanya terdapat 3 kemungkinan pembuatan ruas jalur karena 1 kemungkinan lainnya dibatasi oleh 1 sisi area permainan.

4 Terdapat titik given yang terapit di sudut dengan dua given lain.

Sama dengan kasus sebelumnya namun hanya terdapat 2 kemungkinan pembuatan ruas jalur karena 2 kemungkinan lainnya dibatasi oleh 2 sisi area permainan.

5 Terdapat titik given yang berseberangan dan bersilangan di sisi antara dua warna given.

Setiap titik given dengan warna tertentu harus saling terhubung. Jika keempat

given tersebut berada pada sisi area permainan dan saling bersilangan, maka akan ada satu sel yang terlewati oleh kedua jalur berbeda warna tersebut. Namun setiap sel hanya boleh terisi tepat satu warna sehingga tidak ada solusi yang memenuhi.

SIMPULAN DAN SARAN

Simpulan

Dalam karya ilmiah ini diperlihatkan bahwa permainan Flow Colors dapat dipandang sebagai permasalahan riset operasi yang diformulasikan menggunakan

integer linear programming dan dapat diselesaikan menggunakan software LINGO 11.0. Dari keempat skenario, terlihat bahwa model yang dibuat mampu menyelesaikan permasalahan Flow Colors dengan tingkat kesulitan yang cukup tinggi hingga ukuran × dengan 9 warna. Deviasi panjang tiap warna bervariasi

(28)

18

bergantung pada banyaknya sel, banyaknya warna dan posisi given. Ada pula kasus

Flow Colors yang menghasilkan solusi optimum yang tidak tunggal. Serta, tidak semua kombinasi posisi given dalam sebuah kasus Flow Colors memiliki solusi. Beberapa karakteristik khusus dapat menyebabkan satu kasus tidak memiliki solusi.

Saran

Pada karya ilmiah ini hanya dibahas tentang penyelesaian Puzzle Flow Colors

dengan meminimumkan deviasi panjang tiap warna. Saran untuk penulisan selanjutnya adalah dengan mencari penyelesaian dari Puzzle Flow Colors jenis lain yang lebih rumit seperti Bridge Colors dll. Dapat pula dicari pola variasi solusi dan menentukan posisi given yang diberikan agar variasi solusi Flow Colors tunggal. Selain itu, perbaikan model dan formulasi masalah masih mungkin dilakukan agar efektif dalam menyelesaikan puzzle Flow Colors dengan tingkat kesulitan yang lebih tinggi.

DAFTAR PUSTAKA

Fournier JC. 2009. Graph Theory and Applications. New Jersey (US): John Wiley & Sons.

Dantzig GB, Thapa MN. 1997. Linear Programming 1: Introduction. California (US): Springer.

Madhoun, MN. 2014. Flow Colors [Internet]. [diunduh 2014 Mar 17]. Tersedia pada: http://moh97.us/flow/.

(29)

19 Lampiran 1 Script komputasi MATLAB untuk membangkitkan matriks � ,

function F=Aij(n)

%Matriks kemungkinan pembuatan ruas jalur

A=zeros(n^2)+triu(ones(n^2),1)-triu(ones(n^2),2)+tril(ones(n^2),-

1)-tril(ones(n^2),-2)+triu(ones(n^2),n)-triu(ones(n^2),n+1)+tril(ones(n^2),-n)-tril(ones(n^2),-n-1);

for i=1:n-1

A(i*n,i*n+1)=0; A(i*n+1,i*n)=0;

end

disp(A)

end

(30)

20

Lampiran 2 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 1

MODEL:

@FOR(WARNA(K):W(K)=@SUM(JALUR(I,J):X(I,J,K)));

!FUNGSI OBJEKTIF;

MIN=@SUM(WARNA(K):T1(K)+T2(K));

!KENDALA 1;

@FOR(JALURW(I,J,K):A(I,J)-X(I,J,K)>=0);

!KENDALA 2;

@FOR(SEL(I):@SUM(WARNA(K):Y(I,K))=1);

!KENDALA 3;

@FOR(GIVEN(I):WG(I)=@FLOOR((@INDEX(GIVEN,I)+1)*0.5));

@FOR(GIVEN(I):Y(I,WG(I))=1);

!KENDALA 4;

@FOR(GIVEN(I):@SUM(SEL(J):X(I,J,WG(I)))+@SUM(SEL(J):X(J,I,WG(I)))=

1);

!KENDALA 5;

@FOR(WARNA(K):@FOR(NONGIVEN(I):@SUM(SEL(J):X(I,J,K))-Y(I,K)=0));

!KENDALA 6;

@FOR(WARNA(K):@FOR(NONGIVEN(I):@SUM(SEL(J):X(J,I,K))-Y(I,K)=0));

!KENDALA 7;

@FOR(JALURW(I,J,K):Y(I,K)+Y(J,K)-2*X(I,J,K)>=0);

!KENDALA 8;

@FOR(JALURW(I,J,K):X(I,J,K)+X(J,I,K)<=1);

!KENDALA 9;

@FOR(WARNA(K):@FOR(SEL(I):@FOR

(31)

21 Lampiran 3 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 2

MODEL:

!FUNGSI OBJEKTIF;

!KENDALA 1;

!KENDALA 2;

!KENDALA 3;

!KENDALA 4;

1);

!KENDALA 5;

!KENDALA 6;

!KENDALA 7;

!KENDALA 8;

!KENDALA 9;

(32)

22

Lampiran 4 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 3

MODEL:

!FUNGSI OBJEKTIF;

!KENDALA 1;

!KENDALA 2;

!KENDALA 3;

!KENDALA 4;

1);

!KENDALA 5;

!KENDALA 6;

!KENDALA 7;

!KENDALA 8;

!KENDALA 9;

(33)

23 Lampiran 5 Script komputasi LINGO 11.0 untuk menyelesaikan Skenario 4

MODEL:

!FUNGSI OBJEKTIF;

!KENDALA 1;

!KENDALA 2;

!KENDALA 3;

!KENDALA 4;

1);

!KENDALA 5;

!KENDALA 6;

!KENDALA 7;

!KENDALA 8;

!KENDALA 9;

(34)

24

Lampiran 6 Hasil komputasi LINGO 11.0 untuk Skenario 1 Sel

(35)

25 Lampiran 8 Hasil komputasi LINGO 11.0 untuk Skenario 3

(36)

26

(37)

27

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 4 Desember 1992 sebagai anak tunggal dari pasangan Bapak Sunardi dan Ibu Siti Asiyah. Tahun 2010 Penulis lulus dari SMA Negeri 3 Bogor dan diterima di Institut Pertanian Bogor di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam melalui jalur Undangan Seleksi Masuk IPB dengan memperoleh Beasiswa BidikMisi.

Selama mengikuti perkuliahan penulis menjadi asisten matakuliah Kalkulus II tahun ajaran 2011/2012 dan 2012/2013. Penulis juga aktif mengajar matakuliah Pengantar Matematika, Landasan Matematika, dan Kalkulus di Bimbingan Belajar Mafia Clubs.