Analisis Sensitivitas Pada Optimalisasi Assignment Problem Dengan Metode Hungarian

(1)

i

ANALISIS SENSITIVITAS PADA OPTIMALISASI

ASSIGNMENT

PROBLEM

DENGAN METODE HUNGARIAN

SKRIPSI

NIXON FRITCH M SIBURIAN

050803022

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

ANALISIS SENSITIVITAS PADA OPTIMALISASIASSIGNMENT PROBLEM

DENGAN METODE HUNGARIAN

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

NIXON FRITCH M SIBURIAN 050803022

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(3)

iii

PERSETUJUAN

Judul : ANALISIS SENSITIVITAS PADA OPTIMALISASI

ASSIGNMENT PROBLEM DENGAN METODE

HUNGARIAN

Kategori : SKRIPSI

Nama : NIXON FRITCH M SIBURIAN

Nomor Induk Mahasiswa : 050803022

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, April 2010

Komisi Pembimbing :

Pembimbing II Pembimbing I

Dra. Elly Rosmaini, M.Si Drs. Faigiziduhu Bu’ulolo, M.Si NIP. 19600520 198503 2 002 NIP. 19531218 198003 1 003

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

(4)

PERNYATAAN

ANALISIS SENSITIVITAS PADA OPTIMALISASIASSIGNMENT PROBLEM

DENGAN METODE HUNGARIAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, April 2010

(5)

v

PENGHARGAAN

Segala puji dan syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa atas kasih

serta segala berkat dan anugrah-Nya yang senantiasa dilimpahkanNya hingga skripsi

ini dapat terselesaikan dengan baik.

Demikian, penulis juga menyadari keterlibatan berbagai pihak yang telah

membantu demi terselesaikannya skripsi ini. Oleh karena itu terima kasih penulis

ucapkan kepada:

1. Ibu Dra. Elly Rosmaini, M.Si, dan Bapak Drs. Faigiziduhu Bu’ulolo, M.Si

selaku dosen pembimbing I dan II yang telah memberikan bimbingan dalam

penulisan skripsi ini.

2. Bapak Prof. Dr. Herman Mawengkang dan Drs. H. Haludin Panjaitan selaku

komisi penguji atas segala masukan yang telah diberikan.

3. Bapak Dr. Saib Suwilo, M.Sc selaku Ketua Departemen Matematika FMIPA

USU

4. Bapak Prof. Dr. Eddy Marlyanto, M.Sc selaku Dekan FMIPA USU

5. Ayahanda, OT. Siburian, dan Ibunda, R. Lumban Gaol, yang saya kasihi atas

doa dan segala dukungan moril dan materiil yang telah diberikan.

6. Saudara-saudara saya, Marina Lucia M. Siburian, Felix Julius F. Siburian,

Richson Christ J. Siburian, K’ Ita, K’ Tina, atas doa dan dukungannya.

7. Trisnawati Sitompul, atas bantuan, semangat, dan doa dalam mengerjakan

skripsi ini.

8. Teman-teman Matematika st’05 yang peduli atas bantuan dan perhatiannya.

9. Teman-teman cyber saya, M. Reza Hermansyah, Yudi AXL Aritonang, Putri

Tika CS, Monang Matondang, M. Reza Fahlevi, dan teman-teman sma yang

lain atas bantuan password jurnalnya.

Penulis juga menyadari masih banyak kekurangan dalam skripsi ini, baik dalam

teori maupun penulisannya, karena itu penulis mengharapkan saran dari pembaca

(6)

Akhir kata, kiranya skripsi ini dapat bermanfaat bagi pihak pembaca.

Hormat saya,

(7)

vii

ABSTRAK

(8)

ABSTRACT

(9)

viii

Bab 1 Pendahuluan 1

1.1 Latar Belakang 1

Bab 2 Landasan Teori 7

2.1 Matriks 7

2.1.1 Pengertian Matriks 7

2.1.2 Penjumlahan Matriks 7

2.1.3 Perkalian Matriks 8

2.1.4 Perkalian Matriks dengan Bilangan 8

2.2 Persoalan Optimasi dan Program Linear 9

2.3 Masalah Transportasi 10

2.4 Metode Hungarian 14

2.5 Analisis Sensitivitas 17

2.6 Analisis Sensitivitas pada Metode Hungarian 20 2.6.1 Analisis Sensitivitas pada Variabel Non Basis 22 2.6.2 Analisis Sensitivitas pada Variabel Basis 23 2.7 Perbedaan Analisis Sensitivitas Dengan Metode Simpleks dan Metode Hungarian 24 2.7.1 Perubahan Koefisien Fungsi Tujuan Utuk Variabel Nonbasis 26 2.7.2 Perubahan Koefisien Fungsi Tujuan Utuk Variabel Basis 27

Bab 3 Pembahasan 29

3.1 Assigment Problem 29

3.2 Contoh Kasus dan Penyelesaiannya 29

3.3 Penerapan Analisis Sensitivitas Pada Metode Hungarian 34 3.3.1 Perubahan Koefisien Fungsi Tujuan Variabel Non Basis 35 3.3.2 Perubahan Koefisien Fungsi Tujuan Variabel Basis 36 Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan 37

4.2 Saran 37

(10)

LAMPIRAN A RANGE VARIABEL BASIS 39

(11)

x

DAFTAR TABEL

Halaman

Tabel 3.2.1 Jarak berbagai tempat produksi ke tempat pemasaran 26

Tabel 3.2.2 Penetapan standar 26

Tabel 3.2.3 Biaya opportunity baris 1 27

Tabel 3.2.7 Biaya opportunity kolom 1 28

Tabel 3.2.11 Penyelesaian optimal 30

Tabel 3.3.1.1 Range variabel koefisien non basis 32

Tabel 3.3.2.1 Range variable koefisien basis 33

(12)

ABSTRAK

(13)

vii

ABSTRACT

(14)

BAB 1

PENDAHULUAN

1.1 Latar belakang

Assignment problem yang biasa dibentuk dengan matriks berbobot merupakan salah satu

masalah dalam dunia teknik informatika, di mana masalah ini merupakan masalah yang

metode penyelesaiannya cukup kompleks. Assignment problem adalah suatu masalah

mengenai pengaturan pada individu (objek) untuk melaksanakan tugas (kegiatan), sehingga

dengan demikian biaya yang dikeluarkan untuk pelaksanaan penugasan tersebut dapat

diminimalkan.

Salah satu dalam menyelesaikan persoalan ini adalah algoritma Brute Force, di mana

dalam algoritma ini seluruh kemungkinan solusi diperhitungkan sebagai kandidat solusi. Dan

algoritma penyelesaiannya menggunakan kompleksitas faktorial. Tentu saja hal ini sangat

menggunakan resource yang besar dan penyelesaian dengan metode ini menjadi tidak efisien.

Alternatif lain dalam menyelesaikan masalah assignment ini adalah dengan

menggunakan algoritma Hungarian. Algoritma Hungarian adalah salah satu algoritma yang

digunakan untuk menyelesaikan persoalan masalahassignment. Versi awalnya, yang dikenal

dengan metode Hungarian, ditemukan dan dipublikasikan oleh Harold Kuhn pada tahun

1955. Algoritma ini kemudian diperbaiki oleh James Munkres pada tahun 1957. Oleh karena

itu, algoritma ini kemudian dikenal juga dengan nama algoritma Kuhn-Munkres. Algoritma

yang dikembangkan oleh Kuhn ini didasarkan pada hasil kerja dua orang matematikawan asal

Hungaria lainnya, yaitu Denes Konig dan Jeno Egervary. Keberhasilan Kuhn

menggabungkan dua buah penemuan matematis dari Jeno Egervary menjadi satu bagian

merupakan hal utama yang menginspirasikan lahirnya Algoritma Hungarian. Dengan

menggunakan algoritma ini, solusi optimum sudah pasti akan ditemukan. Namun untuk hal

ini, kasusnya dibatasi, yaitu bila ingin menemukan solusi terbaik dengan nilai minimum

(least cost search). Keuntungan terbesar penggunaan algoritma Hungarian adalah

kompleksitas algoritmanya yang polinomial. Metode yang digunakan dalam algoritma

(15)

xii

Analisis sensitivitas merupakan analisis yang dilakukan pada solusi optimal suatu

persoalan program linear karena adanya perubahan diskrit parameter untuk melihat berapa

besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan optimalitasnya.

Program linear merupakan suatu metode penyelesaian untuk memperoleh solusi optimal

(maksimum/minimum) dari suatu persoalan.

Analisisis sensitivitas dapat dipakai untuk memprediksi keadaan apabila terjadi

perubahan yang cukup besar, misalnya terjadi perubahan pembagian atau alokasi tugas

karena adanya perubahan nilai optimal yang sudah dicapai. Berubahnya alokasi tugas ini

menyebabkan berubahnya urutan prioritas yang baru dan tindakan apa yang perlu dilakukan.

1.2 Perumusan Masalah

Yang menjadi permasalahan dalam penelitian ini adalah menganalisis perubahan nilai

optimal yang telah didapat dan pengaruhnya terhadap pembagian atau alokasi tugas

(penugasan) yang optimal.

1.3. Tinjauan Pustaka

(Paul R Thie, 1983). Andaikan sebuah penempatan manager mempunyai 8 pekerjaan

yang berbeda yang dilaksanakan bulan depan dan 8 buah mesin yang berbeda untuk

mengerjakan pekerjaan ini. Andaikan bahwa untuk setiap mesin dan pekerjaan yang berbeda,

ada nilai yang dikeluarkan jika mesin yang diberikan ditempatkan untuk mengerjakan sebuah

pekerjaan. Faktor nilai ini mencakup biaya manajemen waktu, biaya produksi, dan lain-lain.

Disini jelas bahwa manager mencari penugasan dari mesin ke pekerjaan yang akan

meminimumkan total biaya setiap bulannya. Salah satu cara untuk menyelesaikan

permasalahan ini secara sederhana untuk membuat penugasan yang mungkin, menghitung

nilai keseluruhan, dan memilih penugasan yang menghasilkan biaya minimum. Tetapi untuk

setiap masalah sederhana seperti pendekatan tidak semuanya efisien, karena ada 8! = 40.320

(16)

masalah transportasi sehingga algoritma yang akan diperkenalkan dapat digunakan sebagai

alat yang efektif untuk meminimalkan nilai penugasan.

Untuk masalah penugasan secara umum, andaikan ada m individu atau mesin I1, I2,

I3,…,Im yang akan ditugaskan untuk n pekerjaan J1, J2, J3,…,Jn, dan untuk setiap Ii dan Jj, ada

nilai keseluruhan Cij yang dikeluarkan jika Ii ditugaskan kepada Jj. Dapat diasumsikan m = n ;

jika kasusnya tidak seperti ini, dapat memasukkan variabel tambahan untuk individu atau

mesin kepermasalahan sehingga angkanya menjadi sama, seluruh nilai variabel tambahan

adalah 0.

Solusi optimal untuk masalah yang dimodifikasi ini akan diubah langsung kepada

solusi awal. Dengan asumsi ini, permasalahan adalah menghitung penugasan untuk semua m

individual ke n pekerjaan sedemikian sehingga keseluruhan total biaya adalah minimum.

Masalah ini dapat dengan mudah diformulasikan sebagai permasalahan program integer.

Anggaplah :

0 , jika pekerjaan tidak ditugaskan ke mesin

1, jika pekerjaan ditugaskan ke mesin

ij

Kemudian masalah penugasan dapat dibuat menjadi :

(17)

xiv

(Hamdy A Taha. 1996). Pemecahan optimal dan penugasan tetap sama jika sebuah

konstanta ditambahkan ke atau dikurangkan dari setiap baris atau kolom di matrik biaya ini.

Struktur khusus dari model penugasan ini memungkinkan pengembangan sebuah teknik

pemecahan yang efisien yang disebut metode Hungarian.

(S.S Rao, 1987). Dalam banyak permasalahan yang praktis, pengambil keputusan

sangat tertarik bukan hanya untuk mendapatkan solusi optimal dalam masalah linear

programming, tetapi juga ingin mengetahui bagaimana solusi optimum diganti dengan

berbagai parameter dalam masalah transportasi, yang mana digunakan post-optimality

analysis untuk mengetahui perubahannya.

(Zulkifli Alamsyah, 2008). Analisis sensitivitas adalah suatu analisis yang

mempelajari dampak perubahan – perubahan yang terjadi baik pada parameter (koefisien

fungsi tujuan) maupun pada ketersediaan sumber daya (nilai sebelah kanan), terhadap solusi

dan nilai harga bayangan dari sumber daya. Kegunaannya adalah agar pengambil keputusan

dapat memberikan respon lebih cepat terhadap perubahan – perubahan yang terjadi.

Analisis sensitivitas didasarkan atas informasi pada solusi optimal yang memberikan

kisaran nilai – nilai parameter dan nilai sebelah kanan. Perubahan atau variasi dalam suatu

persoalan program linear yang biasanya dipelajari melalui post optimality analysis dapat

dipisahkan ke dalam tiga kelompok umum yaitu :

1. Analisis yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa

besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan

optimalitasnya. Jika suatu perubahan kecil dalam parameter menyebabkan perubahan

drastis dalam solusi, dikatakan bahwa solusi adalah sangat sensitive terhadap nilai

parameter itu. Sebaliknya, jika perubahan parameter tidak mempunyai pengaruh besar

terhadap solusi dikatakan solusi relative insensitive terhadap nilai parameter tersebut.

2. Analisa yang berkaitan dengan perubahan structural. Masalah ini muncul bila

persoalan program linear dirumuskan kembali dengan menambahkan atau

menghilangkan kendala dan atau variabel untuk menunjukkan operasi model

(18)

3. Analisa yang berkaitan dengan perubahan kontinu parameter untuk menentukan

urutan solusi dasar yang menjadi optimal jika perubahan ditambah lebih jauh, ini

dinamakan Parametric – Programming

1.4 Tujuan Penelitian

Secara umum tujuan dari penelitian ini untuk menyelesaikan promblema analisis sensitivitas

terhadap perubahan pembagian atau alokasi tugas serta pengaruhnya pada pembagian atau

alokasi tugas (penugasan) yang optimal.

1.5 Kontribusi Penelitian

Dengan mengadakan penulisan ini, penulis berharap dapat menambah referensi, menambah

pengetahuan dan pemahaman bagi penulis, pembaca dan pengambil keputusan baik

pemerintah maupun perusahaan swasta atau instansi yang lain yang menggunakan metode

Hungarian dalam memecahkan masalah pembagian atau alokasi tugas untuk para pekerjanya.

1.6 Metode Penelitian

Secara umum, penelitian dilakukan dengan beberapa langkah sebagai berikut :

1. Menguraikan masalah metode hungarian dan tahapan – tahapan dalam pengambilan

keputusan.

2. Menjelaskan analisis sensitivitas pada metode hungarian dan pengaruhnya terhadap alokasi

tugas.

3. Menyelesaikan contoh permasalahan metode hungarian dan melakukan analisis sensitivitas

pada nilai optimal.

(19)

xvi

BAB II

LANDASAN TEORI

2.1 Matriks

2.1.1 Pengertian Matriks

Matriks adalah susunan elemen-elemen yang berbentuk persegi panjang yang terdiri dari

baris dan kolom dan dibatasi dengan tanda [ ] atau ( ). Bilangan-bilangan dalam susunan

tersebut dinamakan entri dalam matriks. Jika adalah sebuah matriks, maka akan

menggunakan untuk menyatakan entri yang terdapat di dalam baris dan kolom dari

matriks . Secara umum matriks dituliskan sebagai berikut:

=

Matriks di atas disebut matriks berukuran kali (ditulis × ) karena memiliki baris

dan kolom.

2.1.2 Penjumlahan Matriks

Jika dan adalah sebarang dua matriks yang ukurannya sama, maka jumlah + adalah

matriks yang diperoleh dengan menambahkan bersama-sama entri yang bersesuaian dalam

kedua matriks tersebut. Matriks-matriks yang ukurannya berbeda tidak dapat dijumlahkan

(20)

2.1.3 Perkalian Matriks

Jika adalah matriks × dan adalah matriks × , maka hasil kali adalah matriks

× yang entri-entrinya ditentukan sebagai berikut. Untuk mencari entri dalam baris- dan

kolom- dari , pilihlah baris- dari matriks dan kolom- dari matriks . Kalikanlah

entri-entri yang bersesuaian dari baris dan kolom tersebut bersama-sama dan kemudian

tambahkanlah hasil kali yang dihasilkan (Anton, 1988 :25).

Contoh :

Tinjaulah perkalian matriks dan . Karena adalah matriks berukuran2 × 3 dan adalah

matriks berukuran 3 × 2 maka hasil kali adalah matriks 2 × 2. Perhitungan-perhitungan

untuk hasil kali adalah:

2.1.4 Perkalian Matriks Dengan Bilangan

Jika adalah suatu matriks dan adalah suatu bilangan, maka hasil kali (product) adalah

matriks yang diperoleh dengan mengalikan masing-masing entri dari oleh . Dalam hal ini

ditulis = ( ). Khususnya dengan yang disebut negatif dari , diartikan matriks

yang diperoleh dari dengan cara mengalikan setiap elemennya dengan 1 atau cukup

dengan mengubah tanda semua elemennya.

(21)

xviii

Richard Bronson (1996 : 1) menyatakan bahwa masalah optimasi merupakan masalah

memaksimumkan atau meminimumkan sebuah besaran tertentu yang disebut tujuan objektif

(objective) yang bergantung pada sejumlah berhingga variabel masukan (input variabels).

Variabel-variabel ini dapat tidak saling bergantung, atau saling bergantung melalui satu atau

lebih kendala (constrains). Persoalan optimasi merupakan persoalan mencari nilai numerik

terbesar (maksimasi) atau nilai numerik terkecil (minimasi) yang mungkin dari sebuah fungsi

pada sejumlah variabel tertentu.

Dalam sebuah persoalan optimasi, dicari nilai untuk variabel- variabel yang tidak

melanggar (bertentangan) dengan kendala-kendala yang menyangkut variabel-variabel

tersebut dan yang memberikan nilai optimum (maksimum atau minimum) pada fungsi yang

hendak dioptimumkan. Dalam tulisan ini akan diperhatikan cara optimasi yang telah

dipergunakan dalam memodel persoalan fisik, ekonomi, tehnik, dan segala macam persoalan

bisnis yang sesuai. Cara ini disebut Program Linear.

Program linear yang diterjemahkan dari Linear Programming (LP) adalah suatu cara

untuk menyelesaikan persoalan pengalokasian sumber-sumber yang terbatas di antara

beberapa aktivitas yang bersaing, dengan cara yang terbaik yang mungkin dilakukan.

Persoalan pengalokasian ini akan muncul manakala seseorang harus memilih tingkat

aktivitas-aktivitas tertentu yang bersaing dalam hal penggunaan sumber daya langka yang

dibutuhkan untuk melaksanakan aktivitas-aktivitas tersebut. Beberapa contoh situasi dari

uraian di atas antara lain adalah pengalokasian fasilitas produksi, persoalan pengalokasian

sumber daya nasional untuk kebutuhan domestic, penjadwalan produksi, solusi permainan

(game), dan pemilihan pola pengiriman (shipping). Program Linear (PL) atau Linear

Programming adalah suatu model dari penelitian operasional untuk memecahkan masalah

optimasi. Program linier merupakan salah satu metode Penelitian Operasional yang banyak

digunakan di bidang industri, transportasi, perdagangan, perkebunan, perikanan, tehnik, dan

lain sebagainya.

Program linear merupakan matematika terapan dari aljabar linear dimana dalam

memecahkan persoalan dunia nyata melalui tahap-tahap sebagai berikut:

1. Memahami masalah di bidang yang bersangkutan

2. Menyusun model matematika

(22)

4. Menafsirkan jawaban model menjadi jawaban atas masalah yang nyata.

Masalah optimasi tidak semuanya dapat diselesaikan dengan metode Program Linear.

Prinsip-prinsip utama yang mendasari penggunaan metode Program Linear adalah:

1. Adanya sasaran. Sasaran dalam model matematika masalah program linear berupa

fungsi tujuan (fungsi objektif) yang akan dicari nilai optimalnya (maksimum /

minimum).

2. Ada tindakan alternatif, artinya nilai fungsi tujuan dapat diperoleh dengan berbagai

cara dan diantaranya alternatif itu memberikan nilai.

3. Adanya keterbatasan sumber daya. Sumber daya atau input dapat berupa waktu,

tenaga, biaya, bahan, dan sebagainya. Pembatasan sumberdaya disebut kendala

(constrains ) pembatas.

4. Masalah harus dapat dituangkan dalam bahasa matematika yang disebut model

matematika. Model matematika dalam program linear memuat fungsi tujuan dan

kendala. Fungsi tujuan harus berupa fungsi linear dan kendala berupa pertidaksamaan

atau persamaan linear.

5. Antar variabel yang membentuk fungsi tujuan dan kendala ada keterikatan, artinya

perubahan pada satu peubah akan mempengaruhi nilai peubah yang lain.

2.3 Masalah Transportasi

Model transportasi merupakan kasus khusus dari persoalan program linear dengan tujuan

untuk “mengangkut” barang tunggal dari berbagai asal ke berbagai tujuan dengan biaya

angkut serendah mungkin.

Adanya informasi tentang besar kapasitas tiap-tiap asal, permintaan total

masing-masing tempat tujuan, dan biaya pengiriman per-unit barang untuk lintasan yang

dimungkinkan, maka model transportasi digunakan untuk menentukan program pengiriman

optimal yang melibatkan biaya pengiriman total yang minimum. Model transportasi adalah

suatu kasus khusus dari persoalan program linear, berarti model transportasi memiliki ciri

khas yang dimiliki pula oleh masalah program linear, yaitu :

(23)

xx

2. Kuantitas komoditas atau barang dan yang didistribusikan dari setiap sumber dan yang

diminta oleh setiap tujuan, besarnya tertentu.

3. Komoditas yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai

dengan permintaan dan atau kapasitas sumber.

4. Ongkos pengangkutan komoditas dari suatu sumber ke suatu tujuan, besarnya tertentu.

5. Jumlah variabel dasar m + n - 1, dimana m adalah jumlah baris dan n adalah jumlah kolom.

Apabila jumlah variabel dasar kurang dari m + n – 1 yang disebut dengan degenerasi,

maka harus ditambahkan variabel dasar dengan nilai nol.

Dalam menggambarkan masalah transportasi, perlu digunakan istilah istilah yang

tidak khusus karena masalah transportasi adalah masalah yang umum, yaitu pendistribusian

berbagai komoditi dari berbagai kelompok pusat penerima yang disebut tujuan, sedemikian

rupa sehingga meminimalisasi biaya distribusi total. Secara umum, sumberi (i = 1, 2, ..., m)

mempunyai supply si unit yang akan didistribusikan ke tujuan-tujuan dan tujuan (j = 1, 2,

...,n) mempunyai permintaan di unit yang dikirim dari sumber-sumber.

Asumsi dasar metode transportasi ini adalah biaya mendistribusikan unit-unit dari sumber i

ke tujuan j berbanding langsung dengan jumlah yang akan didistribusikan, dimana c_ij

menyatakan biaya per unit yang didistribusikan.

Apabila Z merupakan biaya distribusi total dan x_ij (i =1, 2, ..., m ; j = 1, 2, ..., n) adalah jumlah unit yang harus didistribusikan dari sumber i ke tujuan j, maka formulasi

pemrograman linier masalah transportasi. Dari penjelasan di atas, maka rumus metode

transportasi dapat diformulasikan sebagai berikut :

Meminimumkan :

(24)

Dalam arti sederhana, model transportasi berusaha menentukan rencana transportasi

sebuah barang dari sejumlah sumber ke sejumlah tujuan. Data dalam model ini mencakup:

a) Tingkat penawaran di setiap sumber dan jumlah permintaan di setiap tujuan.

b) Biaya transportasi per unit barang dari setiap sumber ke setiap tujuan.

Karena hanya terdapat suatu barang, sebuah tujuan dapat menerima permintaannya

dari suatu sumber atau lebih. Tujuan dari model ini adalah menentukan jumlah yang harus

dikirim dari setia sumber ke setiap tujuan sedemikian rupa sehingga biaya transportasi total

diminimumkan. Asumsi dasar dari model ini adalah bahwa biaya transportasi di sebuah rute

tertentu adalah proporsional secara langsung dengan jumlah unit yang dikirimkan. Defenisi

“unit transportasi” akan bervariasi bergantung pada jenis “barang” yang dikirimkan.

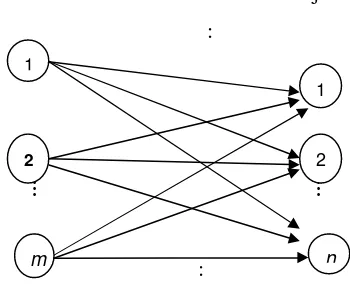
Gambar dibawah ini memperlihatkan sebuah model transportasi dari sebuah jaringan

dengan sumber dan tujuan. Sebuah sumber dan tujuan diwakili dengan sebuah node.

Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman

barang tersebut. Jumlah penawaran di sumber adalah dan permintaan di tujuan

adalah . Biaya unit transportasi antara sumber dan adalah .

Anggap mewakili jumlah barang yang dikirimkan dari sumber ke tujuan , maka model

LP yang mewakili masalah transportasi ini diketahui secara umum sebagai berikut:

(25)

xxii

Kelompok batasan pertama menetapkan bahwa jumlah pengiriman dari sebuah

sumber tidak dapat melebihi penawarannya. Demikian pula kelompok batasan kedua

mengharuskan bahwa jumlah pengiriman ke sebuah tujuan harus memenuhi permintaannya.

Model yang baru digambarkan diatas menyiratkan bahwa jumlah penawaran harus

setidaknya sama dengan jumlah permintaan . Apabila jumlah penawaran sama dengan

jumlah permintaan ( = ), formulasi yang dihasilkan disebut Model Transportasi

Berimbang (balanced transportation model). Model ini berbeda dengan model di atas hanya

dalam fakta bahwa semua batasan adalah persamaan yaitu:

Masalah penetapan (assignment problem) adalah suatu masalah mengenai pengaturan pada

individu (objek) untuk melaksanakan tugas (kegiatan), sehingga dengan demikian biaya yang

dikeluarkan untuk pelaksanaan tugas tersebut dapat diminimalkan (N. Soemartojo, 1994 :

(26)

Masalah ini merupakan salah satu kasus khusus dari masalah transportasi yang

penyelesaiannya menggunakan metode Hungarian. Metode Hungarian dikembangkan atas

dasar pendekatan VAM ( Vogel’s Approximation Method), yaitu dengan cara meminimalkan

biaya penalti( opportunity cost ) yang tidak memanfaatkan biaya sel termurah. Pendekatan

VAM merupakan suatu metode yang menggunakan pendekatan dengan cara meminimalkan

biaya penalti akibat gagal memilih pengisian sel yang memiliki alternatif terbaik.

Howard Anton (1988 : 59) menyatakan bahwa masalah penetapan tugas mensyaratkan

bahwa fasilitas sama banyaknya dengan tugas, katakanlah sama dengan n. Dalam hal ini

maka ada n! cara yang berlainan untuk menetapkan tugas kepada fasilitas berdasarkan

penetapan satu-satu (one-to-one basic). Banyaknya penetapan ini adalah n! karena terdapat n

cara untuk menetapkan tugas pertama, n-1 cara untuk menetapkan tugas kedua, n-2 cara

untuk menetapkan tugas ketiga, dan seterusnya yang jumlah seluruhnya adalah:

n.(n-1).(n-2)…3.2.1 = n! penetapan yang mungkin.Diantara ke n! penetapan-penetapan yang mungkin

ini kita harus mencari satu penetapan yang optimal.

Untuk mendefinisikan penetapan yang optimal secara tepat, maka kita akan

memperkenalkan kuantitas – kuantitas berikut ini misalkan :

cij = biaya untuk menetapkan tugas ke – j kepada fasilitas ke – i, untuk i, j = 1, 2,…, n.

Satuan dari cij dapat berbentuk rupiah, dollar, mil, jam, dan lain-lain, satuan apapun yang

sesuai dengan masalahnya.Kita mendefiinisikan matriks biaya (cost matrix) sebagai matriks n

x n :

C =

Pernyataan bahwa sebuah tugas yang unik harus ditetapkan kepada setiap fasilitas

berdasarkan satu – satu adalah ekuivalen dengan syarat bahwa tidak ada dua cij yang

bersangkutan berasal dari baris yang sama atau kolom yang sama.

Definisi 1

Jika diketahui sebuah matriks biaya C yang berdimensi n x n maka penetapan

(27)

xxiv

entrinya yang berasal dari baris yang sama atau kolom yang sama (Howard Anton,

1988 : 60)

Maka sebuah penetapan optimal akan didefenisikan sebagai berikut:

Definisi 2

n entri dari sebuah penetapan dinamakan biaya (cost) penetapan tersebut. Penetapan

biaya yang paling kecil dinamakan penetapan optimal (optimal assignment) (Howard

Anton, 1988 : 60).

Masalah penetapan adalah untuk mencari penetapan optimal dalam sebuah matriks

biaya. Misalnya dalam menetapkan n peralatan kepada n tempat konstruksi, maka cij dapat

merupakan jarak diantara peralatan ke-i dan tempat konstruksi ke-j. Sebuah penetapan

optimal adalah penetapan untuk mana jarak seluruhnya yang ditempuh untuk memindahkan n

peralatan tersebut adalah minimum (Howard Anton, 1988 : 60).

Secara mendetail model untuk masalah penetapan dapat ditulis dalam suatu bentuk

program linear sebagai berikut:

(28)

m = jumlah objek (individu atau sumber daya)

n = jumlah tugas yang akan diselesaikan

xij = 1, apabila objek i ditugaskan untuk tugas j

xij = 0, apabila objek i tidak ditugaskan untuk tugas j

Andi Trio Sungkowo (2004: 31) mengatakan langkah – langkah dalam menjalankan metode

Hungariannn adalah sebagai berikut:

1. Menyusun matriks biaya.

2. Mengurangkan elemen-elemen pada setiap baris dengan elemen terkecil pada baris

yang sama.

3. Mengurangkan elemen-elemen pada setiap kolom dengan elemen terkecil pada kolom

yang sama. Langkah ini akan menghasilkan Total Opportunity Cost (TOC).

4. Tutup elemen-elemen bernilai nol pada TOC dengan garis-garis mendatar atau tegak.

Misalkan n adalah banyaknya baris atau kolom dan banyaknya garis penutup elemen

nol sekurang-kurangnya k, maka:

Jika k = n, berarti sudah diperoleh program optimal. Proses dihentikan dan susun

penugasan

Jika k< n, maka proses dilanjutkan dengan mengikuti langkah 5.

5. Cari bilangan terkecil dari bilangan-bilangan yang tak tertutup garis, misalkan e.

Selanjutnya:

a. Semua elemen yang tak tertutup garis dikurangi e.

b. Semua elemen yang yang tertutup oleh satu garis tidak diubah.

c. Semua elemen yang tertutup oleh dua garis ditambah dengan e.

Setelah diperoleh tabel baru kembali ke langkah – 4.

2.5 Analisis Sensitivitas

Para analis jarang dapat menentukan parameter model Program Linier seperti (m, n, Cj, aij, bi)

dengan pasti karena nilai parameter ini adalah fungsi dari beberapa uncontrolable variabel.

Sementara itu solusi optimal model Program Linier didasarkan pada

(29)

xxvi

tersebut terhadap solusi optimal. Analisa perubahan parameter dan pengaruhnya terhadap

solusi Program Linier disebut Post Optimality Analisis.

Istilah post optimality menunjukkan bahwa analisa ini terjadi setelah diperoleh solusi

optimal, dengan mengasumsikan seperangkat nilai parameter yang digunakan dalam model.

Atau Analisis Postoptimal (disebut juga analisis pasca optimal atau analisis setelah

optimal, atau analisis kepekaan dalam suasana ketidaktahuan) merupakan suatu

usaha untuk mempelajari nilai-nilai dari peubah-peubah pengambilan keputusan

dalam suatu model matematika jika satu atau beberapa atau semua parameter model

tersebut berubah atau menjelaskan pengaruh perubahan data terhadap penyelesaian optimal

yang sudah ada.

Dapat diketahui bahwa dunia nyata yang diabstraksikan dan disimplifikasikan ke

dalam model PL, tidak sederhana seperti rumusan Program Linier. Oleh karena itu

dalam dan kehidupan dunia nyata, selalu dihadapkan pada pertanyaan- pertanyaan

keragu-raguaan seperti “apa yang akan terjadi, jika” ini dan itu berubah?

Persoalan peluang dan ketidakpastiaan pertanyaan-pertanyaan tersebut harus dapat dijawab

dalam rangka meyakinkan pendirian terhadap sesuatu yang akan diputuskan kelak. Dengan

demikian hasil yang diharapkan tersebut adalah hasil yang memang ”paling mungkin“

dan ”paling mendekati”, atau “perkiraan yang paling tepat”. Uji kepekaan hasil dan pasca

optimal (sebut saja selanjutnya analisis postoptimal) yang dapat memberikan jawaban

terhadap persoalan-persoalan tersebut diatas. Analisis postoptimal sangat berhubungan

erat dengan atau mendekati apa yang disebut Program Parametrikal atau Analisis

Parametrisasi.

Perubahan atau variasi dalam suatu persoalan Program Linier yang bisaanya dipelajari

melalui Post Optimality analysis dapat dipisahkan ke dalam tiga kelompok umum, yaitu :

1. Analisa yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa

besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan

optimalitasnya, ini dinamakanAnalisa Sensitivitas. Jika suatu perubahan kecil dalam

parameter menyebabkan perubahan drastis dalam solusi, dikatakan bahwa solusi

adalah sangat sensitif terhadap nilai parameter itu. Sebaliknya, jika perubahan

parameter tidak mempunyai pengaruh besar terhadap solusi dikatakan solusi relatif

(30)

2. Analisa yang berkaitan dengan perubahan struktural. Masalah ini muncul bila

persoalan Program Linier dirumuskan kembali dengan menambahkan atau

menghilangkan kendala dan atau variabel untuk menunjukkan operasi model

alternatif. Perubahan struktural ini dapat dimasukkan dalam analisa sensitivitas.

3. Analisa yang berkaitan dengan perubahan kontinu parameter untuk menentukan

urutan solusi dasar yang menjadi optimal jika perubahan ditambah lebih jauh, ini

dinamakanParametric-Programming.

Diketahui Model Matematika Persoalan Program Linear adalah sebagai berikut:

Menentukan nilai dari X1, X2, X3, …, Xn sedemikian rupa sehingga:

Z = C1X1+C2X2+…+CjXj+…+CnXn = ( Optimal [maksimum/minimum] )

Yang kemudian disebut sebagai Fungsi Tujuan ( Objektive Function ) dengan pembatasan (

fungsi kendala/syarat ikatan):

Berdasarkan Model Matematika Persoalan Program Linier di atas analisis sensitivitas

dapat dikelompokkan berdasarkan perubahan-perubahan parameter:

1) Perubahan koefisien fungsi tujuan untuk variabel non basis.

2) Perubahan koefisien fungsi tujuan untuk variabel basis.

3) Perubahan Koefisien teknologi (koefisien input-output).

4) Perubahan Nilai-Sebelah-Kanan (NSK) fungsi kendala.

(31)

xxviii

6) Adanya tambahan perubahan (variabel) pengambilan keputusan (Xj) (perubahan

nilai n).

2.6 Analisis Sensitivitas pada Metode Hungarian

Dalam persoalan assignment problem tidak semua parameter-parameter di atas dapat

diterapkan. Seperti yang diketahui bahwaassignment problem memiliki ciri khusus yaitu:

1. Semua fungsi kendala bertanda ‘=’

2. Semua nilai aij bernilai 1 atau 0

3. Semua nilai sebelah kanan (NSK) fungsi kendala adalah 1.

Telah dijelaskan sebelumnya bahwa ada 6 jenis analisis sensitivitas pada masalah

program linier. Setiap permasalahan yang dapat dibentuk dalam program linier memiliki

masalah analisis yang berbeda. Untuk itu, harus diteliti terlebih dahulu jenis analisis

sensitivitas yang sesuai denganAssignment problem.

Untuk mengetahui bagian mana pada Assignment problem yang harus dianalisis,

harus diteliti dari bentuk umum Assignment problem itu sendiri. Dari bentuk umum

Assignment problem dapat dilihat bahwa fungsi kendala diformulasikan dalam bentuk sebagai

berikut:

Ini berarti nilai sebelah kanan untuk persamaan kendala telah ditetapkan adalah 1. Ciri ini lah

yang membedakan antara masalah transportasi dengan assignment problem. Kalau pada

masalah transportasi dikenal adanya permintaan dan persediaan dengan nilai yang berbeda,

(32)

Jadi, sangat tidak mungkin kalau dianalisis nilai sebelah kanan, yang biasa dianalisis pada

masalah transportasi.

Pada bagian fungsi objektif, bentuk umumnya adalah:

=

(2.7) Sebagai contoh 35X₁₁ artinya untuk pekerja pertama mengerjakan job pertama dengan biaya

35. Dalam dunia nyata biaya pengerjaan suatu job bisa berubah, baik naik ataupun turun.

Selain finansial, biaya dalam hal ini bisa berarti lama waktu pengerjaan dan resiko dalam

pengerjaan.

Misalnya suatu perusahan dengan 4 jenis job telah memiliki formula tertentu dalam

memilih 4 pekerjanya sehingga semua pekerja dapat bekerja dengan optimal dan tentu saja

dengan biaya minimal. Namun seiring berjalan nya waktu dan semakin ahlinya suatu pekerja

dalam mengerjakan pekerjaannya, bisa saja pekerja meminta kenaikan upah nya. Akibatnya

ada kenaikan biaya disini. Tidak efisien apabila harus merubah formula optimal sebelumnya.

Tentu saja perusahaan harus menganalisis hal ini, sampai seberapa jauh perusahaan bisa

menaikkan upah pekerja agar hasil tetap optimal dan tidak mengubah formula optimal

sebelumnya. Jadi yang memungkinkan untuk melakukan analisis sensitivitas adalah pada

parameter perubahan koefisien fungsi tujuan.

Perubahan kofisien fungsi tujuan dapat terjadi karena perubahan keuntungan atau

ongkos suatu kegiatan. Misal, diinginkan untuk menentukan pegaruh perubahan keuntungan

per unit produk 1 (C1). Pada suatu kasus dimana produk 1 menguntungkan untuk diproduksi,

jika C1 turun di bawah nilai tertentu, maka dapat menyebabkan produk 1 yang akan

diproduksi menjadi berkurang atau bahkan tidak menguntungkan untuk diproduksi.

Sebaliknya jika C1 naik di atas nilai tertentu, dapat menyebabkan kenaikan jumlah produk 1

yang akan diproduksi.

Pada kasus lain lain bisa jadi produk 1 tidak menguntungkan untuk diproduksi karena

keuntungan per unit (C1 nya) rendah. Jika C1 turun dapat dipastikan tidak akan berpengaruh

(33)

xxx

menjadi menguntungkan untuk diproduksi. Dari uraian di atas, dapat disimpulkan bahwa

terdapat suatu batas atas dan batas bawah (range) perubahan C1 dimana keputusan optimal

tidak berpengaruh.

Tabel optimal yang telah didapat dengan metode Hungariannn menunjukkan

variabel yang menjadi basis dan variabel non basis. Variabel yang koefisien pada tabel

optimal adalah 0 merupakan variabel basis. Sebaliknya variabel yang koefisien pada tabel

optimal bukan 0 merupakan variabel non basis.

2.6.1 Analisis Sensitivitas pada Variabel Non Basis

Cara yang lazim digunakan untuk menganalisis sensitivitas adalah dengan metode simpleks.

Seiring berkembangnya ilmu pengetahuan ada beberapa cara yang dapat digunakan, salah

satunya metode Arsham-Khan. Namun dasarnya masih menggunakan metode simpleks.

Sama halnya dengan metode yang akan digunakan oleh penulis dalam menganalisis

sensitivitas padaassignment problem ini, penulis akan mencoba dengan metode yang sedikit

berbeda dan dengan formulasi yang berbeda pula.

Range koefisien dari variabel non basis adalah seberapa besar nilai koefisien variabel

non basis dapat diturunkan atau pun dinaikkan sehingga hasil optimal sebelumnya tidak

terganggu. Ini berarti ada 2 batasan yang akan dicari yaitu batas bawah dan batas atas range.

Ada beberapa notasi yang akan muncul pada pembahasan berikutnya, antara lain:

ij

C = koefisien/ besar biaya karyawan ke-i untuk job ke-j pada tabel awal,

^

ij

C = koefisien/ besar biaya karyawan ke-i untuk job ke-j pada tabel optimal,

Batas bawah koefisien variabel non basis adalah hasil pengurangan koefisien variabel

non basis pada tabel awal dengan koefisien pada tabel akhir. Artinya setiap koefisien non

basis hanya bisa diturunkan sebesar koefisien pada tabel optimalnya. Hal ini dimaksudkan

agar tabel optimal tidak terganggu. Apabila nilai koefisien diturunkan lebih besar dari

koefisien tabel optimalnya maka kemungkinan variabel basis akan berubah yang berdampak

berubah pula nilai optimalnya. Maka batas bawah range koefisien non basis dapat

(34)

Xij = Cij –

^

ij

C

(2.8)

Sedangkan yang menjadi batas atas variabel non basis untuk kasus minimasi adalah

adalah M atau bilangan yang sangat besar atau ∞. Hal ini terjadi karena untuk kasus

meminimasi biaya, variabel yang masuk non basis menunjukkan bahwa koefisiennya terlalu

besar sehingga tidak ekonomis untuk dipakai. Sehingga andaikan koefisien dari variabel non

basis dinaikkan seberapapun, tetap tidak akan mengganggu hasil optimal sebelumnya.

2.6.2 Analisis Sensitivitas pada Variabel Basis

Dalam mencari range untuk variabel basis ada beberapa langkah yang harus diperhatikan:

1. Perhatikan tabel optimal, cari nilai ambang batas yang menyebabkan tabel optimal

tidak terganggu. Nilai ambang batas tersebut adalah nilai koefisien variabel non

basis terkecil. Notasikan nilai ambang batas tersebut dengan .

2. Cari range variabel basis.

Nilai batas bawah range variabel basis adalah:

Xij = CijXij –

(2.9)

Dan nilai batas atas range variabel basis adalah:

Xij = CijXij +

(2.10)

Sehingga didapat range koefisien variabel basis:

(CijXij – ) Cij Xij (CijXij + )

(2.11)

3. Periksa hubungan suatu variabel basis dengan variabel lain yang satu kolom atau satu

baris dengan variabel tersebut. Apakah penambahan pada langkah sebelumnya telah

layak atau apakah mengganggu tabel optimal yang telah didapat. Ganti range apabila

(35)

xxxii

2.7 Perbedaan Analisis Sensitivitas dengan Metode Simplex dan Metode Hungarian

Di dalam metode Simplex, analisis sensitivitas selain digunakan dalam

pengecekan/pengujian, analisis ini lebih bermanfaat untuk menghindari pengulangan

perhitungan dari awal, apabila terjadi perubahan-perubahan pada masalah Linear

Programmning Simplex.

Dalam Assignment problem, metode Simplex jarang digunakan dalam mencari nilai

optimalitas, karena Assignment problem memiliki keistimewaan dari persoalan-persoalan

Linear Programming lainnya. Untuk menemukan perbedaan analisis sensitivitas dengan

metode Simplex dan metode Hungarian, akan dibahas sebuah kasus Linear Programming

dengan metode Simplex beserta analisis sensitivitasnya, setelah itu akan dibandingkan

dengan metode Hungarian.

Jadi yang dibahas dalam kasus ini adalah analisis sensitivitas terhadap koefisien

fungsi tujuan meliputi penempatan kisaran pada nilai koefisien secara khusus pada koefisien

variabel kontinu. Selama nilai aktual koefisien fungsi tujuan berada dalam kisaran

optimalitas, solusi dasar layak sekarang akan tetap optimal. Jadi untuk variabel nonbasis,

kisaran optimalitas menyatakan nilai koefisien untuk variabel yang akan tetap menjadi

variabel nonbasis. Sebaliknya, kisaran optimalitas untuk variabel basis menyatakan nilai

koefisen fungsi tujuan untuk variabel yang akan tetap menjadi bagian dari solusi layak dasar

(36)

Iterasi 0

Kolom Kunci adalah kolom yang mempunyai nilai pada baris Z yang bernilai negatif

dengan angka terbesar.

2. Memilih baris kunci

Baris Kunci adalah baris yang mempunyai indeks terkecil.

Indeks = Nilai Kanan : Nilai Kolom Kunci.

3. Mengubah nilai-nilai baris kunci

Baris Baru Kunci = Baris Kunci : Angka Kunci.

4. Mengubah nilai-nilai selain baris kunci sehingga nilai-nilai kolom kunci

(selain baris kunci) = 0

Baris baru = baris lama – (koefisien angka kolom kunci x nilai baris

baru kunci)

Iterasi 2 ( Tabel Optimal )

BV C 60 30 20 0 02 03 b

Dari tabel ini dapat didefinisikan beberapa hal sebagai berikut:

(37)

xxxiv

=

1 2 8

0 2 4

0,5 1,5

2.7.1 Perubahan Koefisien Fungsi Tujuan Untuk Variabel Nonbasis

Kasus ini terjadi karena adanya perubahan, baik pada kontribusi keuntungan maupun pada

kontribusi ongkos dari kegiatan yang direpresentasikan oleh variabel nonbasis. Pada contoh

kasus di atas, satu-satunya variabel keputusan nonbasis adalah x2.Saat ini koefisien fungsi

tujuan x2 adalah c2 = 30.

Jika c2 berubah dari 30 menjadi ( 30 + ) tidak mengubah harga dan b. Karena itu

ruas kanan untuk variabel basis (VB), yaitu b, tidak akan berubah sehingga variabel basis

tetap fisibel. Karena c2 adalah variabel nonbasis, maka CBV juga tidak akan berubah.

Satu-satunya yang koefisien baris ( zj-cj)nya akan berubah karena perubahan c2 ini adalah x2.

Dengan demikian, BV akan tetap optimal jika 0, dan BV akan menjadi

suboptimal jika 0. Dalam hal terakhir ini, harga z mungkin dapat diperbaiki dengan

memasukkan x2 ke dalam basis.

Dari contoh kasus diketahui bahwa:

. = [0 20 60]

0 jika > 5 sehingga BV tidak lagi optimal. Artinya, jika harga c2 naik atau turun sebesar 5

atau kurang, maka BV akan tetap optimal, tetapi jika naik atau turunnya lebih besar dari 5,

maka BV tidak lagi optimal.Misalnya jika c2 = 40, solusi basis saat ini akan menjadi

(38)

2.7.2 Perubahan Koefisien Fungsi Tujuan Untuk Variabel Basis

Mengubah koefisien fungsi tujuan variabel basis (BV) artinya mengubah cBV sehingga

beberapa koefisien pada baris 0 (baris zj – cj) dari tabel optimal akan berubah. Misalkan c1

(39)

xxxvi

= 10 + 0,5

Karena 0, maka 10 + 0,5 0

Dari hasil di atas menunjukkan bahwa penyelesaian basis saat ini akan tetap optimal

sepanjang -4, 20, . Dengan kata lain penyelesaian basis saat ini akan tetap

optimal jika -4 20. Artinya, jika c1 turun sebesar 4 atau kurang, atau c1 naik hingga 20,

maka penyelesaian basis saat ini akan tetap optimal.

Dari contoh kasus diatas dapat kita ambil kesimpulan bahwa:

1. Pengerjaan analisis sensitivitas dengan metode Simplex lebih memakan waktu yang

lama dibandingkan dengan analisis sensitivitas dengan metode Hungarian.

2. Analisis sensitivitas dengan metode Hungarian hanya dapat dipakai untuk

penyelesaian kasus penugasan saja dan hanya terbatas pada analisis koefisien fungsi

tujuan, sedangkan metode simplex dapat digunakan untuk masalah program linier

selain assignment problem dan dapat menganalisis parameter – parameter dalam

(40)

BAB III

PEMBAHASAN

3.1 Assigment Problem

Pada umumnya assignment problem memiliki karakreistik atau kriteria bahwa cacah baris

sama dengan cacah kolom pada tabel assignment (m = n),karena assignment problem

mensyaratkan bahwa banyaknya fasilitas sama dengan banyaknya tugas. Penetapan

pekerjaan dilakukan dengan tujuan agar penyelesaian semua pekerjaan minimum atau

maksimumkan profit dari pekerjaan-pekerjaan tersebut.

Telah diketahui bahwa matriks assignment harus berbentuk bujur sangkar yaitu cacah

pekerja sama dengan cacah pekerjaannya. Adapun bentuk menyelesaikan masalah tersebut

adalah dengan menggunakan langkah-langkah atau prosedur metode Hungarian. Untuk

memudahkan pemahaman penyelesaian assignment problem dibawah ini diberikan contoh

kasus padaassignment problem.

3.2 Contoh kasus dan Penyelesaiannya

Sebuah perusahaan ban ‘Blackstone’ mempunyai 4 tempat produksi ban yang berlainan

lokasinya. Perusahaan tersebut harus mengirimkan satu container ban untuk masing-masing

tempat produksi keempat tempat pemasaran yang berlainan sehingga terjadi pemerataan

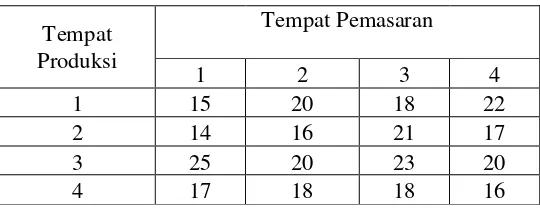
pemasaran untuk masing-masing tempat produksi. Jarak dalam mil diantara berbagai tempat

produksi dan tempat pemasaran diberikan dalam tabel berikut:

(41)

xxxviii

Bagaimanakah seharusnya perusahaan tersebut mengirimkan ban dari keempat tempat

produksi ketempat pemasaran untuk meminimumkan jarak yang ditempuh?

Penyelesaian:

a) Model Matematika Program Linear

Untuk membuat model matematika program linear masalah ini, disusun dahulu tabel

penetapan standar sebagai berikut:

Dengan demikian, model matematika program linear untuk masalah diatas adalah:

(42)

X13 + X23 + X33 + X43 = 1

X14 + X24 + X34 + X44 = 1

Xij = 0 atau Xij = 1

b) Penyelesaian Optimal Dengan Metode Hungarian

Matriks biaya untuk masalah di atas adalah:

15 20 18 22

14 16 21 17

25 20 23 20

17 18 18 16

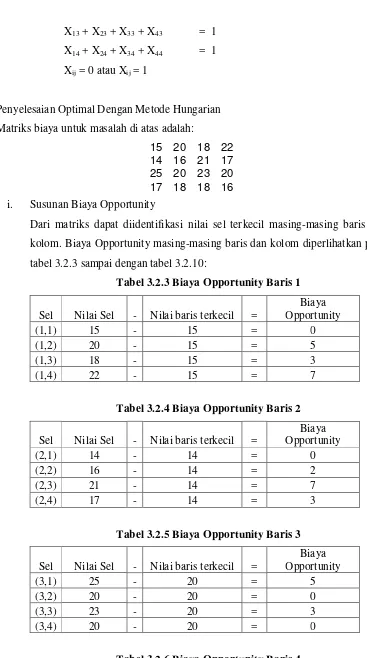
i. Susunan Biaya Opportunity

Dari matriks dapat diidentifikasi nilai sel terkecil masing-masing baris dan

kolom. Biaya Opportunity masing-masing baris dan kolom diperlihatkan pada

tabel 3.2.3 sampai dengan tabel 3.2.10:

Tabel 3.2.3 Biaya Opportunity Baris 1

Sel Nilai Sel - Nilai baris terkecil =

Biaya

(43)

xl

Biaya

Dengan demikian susunan biaya opportunity barisnya adalah:

0 5 3 7

0 2 7 3

5 0 3 0

1 2 2 0

Tabel 3.2.7 Biaya Opportunity Kolom 1

Biaya

(44)

Sel Nilai Sel - Nilai baris terkecil = Biaya

Dengan demikian susunan biaya opportunity baris dan kolom adalah:

0 5 1 7

0 2 5 3

5 0 1 0

1 2 0 0

ii. Analisis Kelayakan Biaya Opportunity Keseluruhan

Dari matriks dapat ditarik garis horizontal pada baris tiga dan baris empat,

serta garis vertical pada kolom satu (karena memiliki sel dengan biaya

opportunity = 0)

0 5 1 7

0 2 5 3

5 0 1 0

1 2 0 0

Ternyata pada matriks cacah garis yang dapat ditarik minimal ada tiga buah.

Ini berarti penyelesaian optimal belum tercapai. Dengan demikian, proses

selanjutnya adalah mengidentifikasi sel yang terletak pada titik potong kedua

garis dan nilai sel terkecil yang terletak di luar garis tersebut.

iii. Penyusunan Matriks Biaya Opportunity Baru

Berdasarkan matriks diatas tampak bahwa sel (3,1) = 5 dan sel (4,1) = 1

merupakan titik potong kedua garis tersebut dan sel (1,3) = 1 merupakan nilai

sel terkecil yang terletak di luar ketiga garis tersebut. Selanjutnya nilai sel

(1,3) = 1 ditambah kedalam sel (3,1) dan (4,1) serta dikurangkan terhadap

sel-sel lain yang terletak di luar garis-garis tersebut yaitu sel-sel (1,2), sel-sel (1,3), sel-sel

(1,4), sel (2,2), sel (2,3), dan sel (2,4). Ini berarti sel (1,3) menjadi nol. Dengan

demikian susunan biaya opportunnity yang baru adalah:

0 4 0 6

0 1 4 2

6 0 1 0

(45)

xlii

iv. Analisis Kelayakan Matriks Biaya Opportunity Keseluruhan

0 4 0 6

0 1 4 2

6 0 1 0

2 2 0 0

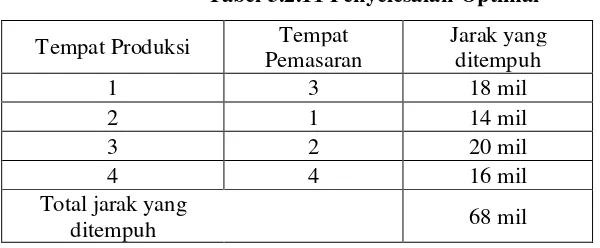
Dari matriks tampak bahwa cacah garis yang dapat ditarik ada empat buah.

Dengan demikian penyelesaian optimal telah tercapai dengan susunan

penetapan sebagai berikut:

3.3 Penerapan Analisis Sensitivitas pada Metode Hungarian

Untuk menggambarkan perubahan ini akan dianalisis matriks biaya opportunity

optimal dari contoh kasus di atas:

0 4 0 6

0 1 4 2

6 0 1 0

2 2 0 0

pada matriks biaya opportunity optimal, dapat ditunjukkan bahwa variabel yang

memiliki koefisien 0 merupakan variabel basis. Sedangkan koefisien yang tidak

bernilai 0 merupakan variabel non basis. Berdasarkan matriks opportunity optimal

diketahui bahwa variabel basisnya adalah: X11, X13,X21, X32, X34, X43, X44. Varibel

non basisnya adalah: X12, X14, X22, X23, X24, X31, X33, X41, X42.

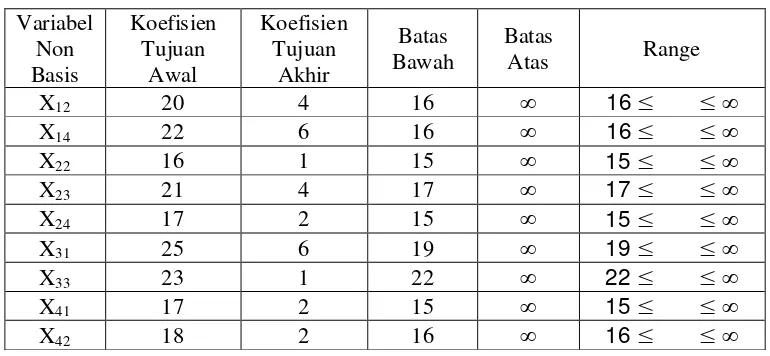
3.3.1 Perubahan Koefisien Fungsi Tujuan Variabel Non Basis

Variabel non basis dalam pengertian assignment problem adalah semua variabel yang

(46)

Misalkan untuk variabel non basis X12 yang memiliki nilai sebesar 20 yakni pekerja 1

mengerjakan pekerjaan 2. Apabila koefisien X12 dinaikkan berapapun, X12 tetap tidak

ekonomis untuk dikerjakan, yang berarti bahwa batas atas dari X12 adalah . Sebaliknya jika

X12 diturunkan sampai jumlah tertentu, ada kemungkinan X12 cukup ekonomis untuk

dikerjakan.

Batas bawah X12 adalah:

X12 = X12(tabel awal) – X12(tabel akhir)

= 20 – 4

= 16

Syarat matriks opportunity optimal tetap optimal jika X12(tabel akhir) 16. Jadi range nilai X12

optimal adalah16 .

Dapat disimpulkan bahwa selama 16 , X12tidak ekonomis untuk diproduksi dan

karenanya tidak akan merubah solusi optimal. Sebaliknya jika X12 diturunkan kurang dari 16,

akan menguntungkan untuk diproduksi, yang berarti solusi tidak optimal lagi.

Hal ini berlaku untuk mencari range koefisien variabel non basis yang lainnya.

Tabel 3.3.1.1 Range Variabel Koefisien Non Basis

Variabel

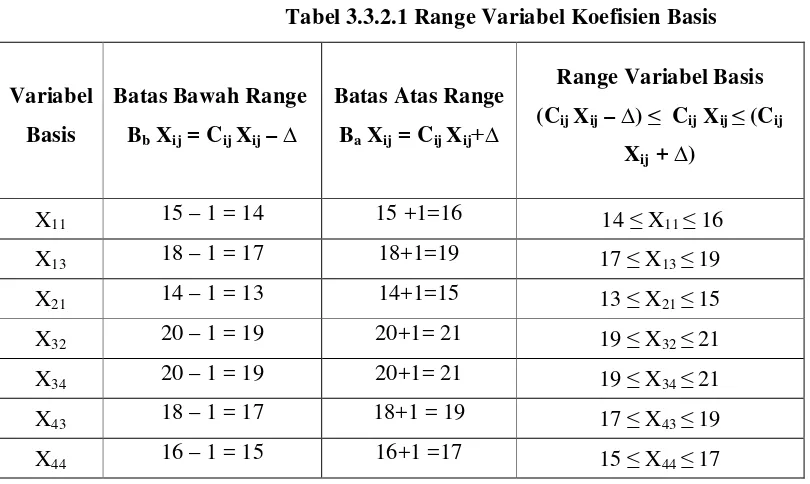
3.3.2 Perubahan Koefisien Fungsi Tujuan Variabel Basis

Variabel-variabel basis adalah X11, X13,X21, X32, X34, X43, X44 dengan koefisien fungsi tujuan

masing-masing adalah 15, 18, 14, 20, 20, 17, 18, 16.

(47)

xliv

0 4 0 6

0 1 4 2

6 0 1 0

2 2 0 0

Nilai terkecil dari koefisien non basis pada matriks optimal adalah 1. Sehingga didapat = 1.

Langkah 2: Menentukan range dari penambahan .

Tabel 3.3.2.1 Range Variabel Koefisien Basis

Variabel

Langkah 3: Periksa kelayakan range basis pada langkah ke 2.

Setiap range yang telah diperoleh pada langkah ke 2 sebenarnya telah memenuhi tabel

optimal sebelumnya. Artinya apabila terjadi perubahan koefisien fungsi tujuan sebesar range

yang telah didapat pada langkah ke 2 hal tersebut tidak mengubah solusi optimal sebelumnya.

Namun ada beberapa perubahan range yang masih tetap layak dan tidak mengubah formula

optimal sebelumnya.

a. Variabel X11

Setelah membandingkan nilai-nilai koefisien fungsi tujuan pada variabel yang sebaris

dan sekolom dengan variabel X11, ternyata batas atas range X11 masih bisa dinaikkan

sampai 17. Hal ini tidak akan mengubah nilai optimal karena koefisien terbesar

(48)

X11akan tetap menjadi variabel basis dan tidak mengganggu formula solusi optimal

sebelumnya.

Range X11berubah menjadi 14 X11 17.

b. Variabel X13

dan sekolom dengan variabel X13, ternyata batas bawah range X13 masih bisa

diturunkan sampai 16. Hal ini tidak akan mengubah nilai optimal karena koefisien

terkecil setelah variabel X13 pada baris pertama adalah 15 dan pada kolom ketiga

adalah 18. Jadi X13akan tetap menjadi variabel basis dan tidak mengganggu formula

solusi optimal sebelumnya.

c. Variabel X21

diturunkan sampai . Hal ini tidak akan mengubah nilai optimal karena koefisien

terkecil pada baris kedua dan kolom pertama adalah variabel X21sendiri. Jadi apabila

nilai koefisien X21 diturunkan sampai , X21tetap akan jadi variabel basis bahkan

besar biaya pada solusi optimal bisa ditekan.

d. Variabel X32

Setelah membandingkan variabel X32 dengan variabel yang sebaris dengan nya tidak

ada variabel lain yang nilai koefisien nya lebih kecil dari X32. Dan bila dibandingkan

dengan variabel yang sekolom dengan X32 maka akan didapat variabel X22yang nilai

koefisien nya lebih kecil yaitu sebesar 16. Namun karena variabel X22 tidak

merupakan variabel basis tetap saja X32 yang dipilih. Sehingga apabila nilai koefisien

X32 diturunkan sampai , X32tetap akan jadi variabel basis bahkan besar biaya pada

solusi optimal bisa ditekan.

e. Variabel X44

diturunkan sampai . Hal ini tidak akan mengubah nilai optimal karena koefisien

(49)

xlvi

apabila niali koefisien X44 diturunkan sampai , X44tetap akan jadi variabel basis

bahkan besar biaya pada solusi optimal bisa ditekan.

Dari langkah 3 didapat range variabel basis yang baru yaitu:

Tabel 3.3.2.2 Range Variabel Koefisien Basis Baru

Range Variabel Basis

(CijXij – ) Cij Xij (Cij

Xij + )

14 X11 17

16 X13 19

X21 15

X32 21

19 X34 21

17 X43 19

(50)

BAB IV

KESIMPULAN

4.1 Kesimpulan

Berdasarkan dari hasil pembahasan yang dilakukan maka dapat diambil kesimpulan yaitu:

1. Untuk menyelesaikan assignment problem dengan menggunakan prosedur metode

Hungarian terdiri dari tiga tahap, yaitu penyusunan matriks biaya opportunity, analisis

kelayakanassignment problem,dan penyusunan ulang matriks biaya opportunity.

2. Setelah didapat hasil range sementara perlu dilakukan pengecekan kelayakan pada

variabel basis.

3. Pengerjaan analisis sensitivitas dengan menggunakan metode Hungarian lebih

sederhana dibandingkan dengan metode Simpleks yang memiliki prosedur pengerjaan

dengan tabel yang masih terlalu panjang.

4. Dalam pengerjaan dengan metode Hungarian didapat kelemahan yaitu masih kurang

akuratnya hasil range yang diperoleh sehingga masih dilakukan pengecekan dengan

software QM sedangkan dalam pengerjaan dengan metode Simpleks tidak demikian.

4.2 Saran

1. Untuk memakaisoftware Program Linier seperti QM dan QS sebagai alat bantu dalam

menyelesaikan masalah analisis sensitivitas pada optimalisasi assignment problem

dengan metode Hungarian.

2. Adanya kelemahan analisis sensitivitas pada metode Hungarian yang hanya dapat

menganalisis koefisien fungsi tujuan sehingga penulis berharap agar dikemudian hari

(51)

xlviii

DAFTAR PUSTAKA

Alamsyah. Zulkifli. 2008.Pemodelan dalam Riset Operasi. Bandung: Institut Teknologi Bandung.

Anton, Howard. 1987.Aljabar Linier Elementer.Jakarta: Erlangga.

Rao, S.S. 1987.Optimization Theory and Application. San Diego, USA: Dept. of Mechanical Engg.

Taha, Hamdy A. 1996.Operation Research. Fayetteville: University of Arkansas.

Thie, Paul R.1983. An Introduction to Linear Programming and Game Theory. Canada : Department of Mathematics Boston College.

(52)

(53)

l