Perbandingan Analisis Sensitivitas Menggunakan Partisi Optimal dan Basis Optimal pada Optimasi Linear

(1)

PERBANDINGAN ANALISIS SENSITIVITAS MENGGUNAKAN

PARTISI OPTIMAL DAN BASIS OPTIMAL PADA OPTIMASI

LINEAR

MIRNA SARI DEWI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Perbandingan Analisis Sensitivitas Menggunakan Partisi Optimal dan Basis Optimal pada Optimasi Linear adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Desember 2013

(4)

ABSTRAK

MIRNA SARI DEWI. Perbandingan Analisis Sensitivitas Menggunakan Partisi Optimal dan Basis Optimal pada Optimasi Linear. Dibimbing oleh BIB PARUHUM SILALAHI dan PRAPTO TRI SUPRIYO.

Analisis sensitivitas menjelaskan sampai sejauh mana pengaruh perubahan parameter-parameter model optimasi linear, yaitu koefisien fungsi tujuan dan nilai ruas kanan kendala, terhadap penyelesaian optimal. Analisis sensitivitas yang biasa digunakan adalah dengan pendekatan basis optimal berdasarkan metode simpleks. Pada karya ilmiah ini dibahas analisis sensitivitas dengan pendekatan lain yaitu analisis menggunakan partisi optimal yang unik berdasarkan metode interior point untuk menentukan range dan shadow price. Tujuan penelitian ini adalah memaparkan analisis sensitivitas menggunakan partisi optimal berdasarkan buku acuan yang berjudul Interior Point Methods for Linear Optimization pada subbab Sensitivity Analysis yang disusun oleh C. Roos, T. Terlaky, dan J. PH. Vial sehingga dapat ditentukan nilai shadow price dan range serta membandingkan hasil yang diperoleh dengan yang dihasilkan oleh metode simpleks dengan bantuan perangkat lunak LINDO 6.1. Hasil analisis sensitivitas yang diperoleh dengan pendekatan partisi optimal juga lebih akurat dari pada menggunakan pendekatan basis optimal (metode simpleks) terutama untuk kasus yang memiliki solusi optimal primal atau dual yang tidak unik. Namun saat masalah primal dan masalah dual memiliki solusi optimal yang unik, metode simpleks dan pendekatan partisi optimal menghasilkan informasi yang persis sama.

Kata kunci: analisis sensitivitas, partisi optimal, range, shadow price

ABSTRACT

MIRNA SARI DEWI. Comparing Optimal Partitions and Optimal Bases of Sensitivity Analysis on Linear Optimizations. Supervised by BIB PARUHUM SILALAHI and PRAPTO TRI SUPRIYO.

Sensitivity analysis is studying the effect of parameters of the linear optimization model, i.e. the coefficients of objective function and right-hand side value constraints to the optimal solution. Sensitivity analysis used in the classical approach (the simplex method) is based on the optimal basis. This paper presents briefly sensitivity analysis by using the unique optimal partition based on the interior point method to determine the range and shadow price. The purpose of this study is to present the sensitivity analysis of the optimal partition based on a reference book entitled Interior Point Methods for Linear Optimization in Section Sensitivity Analysis prepared by C. Roos, T. Terlaky, and J. PH. Vial so that can be determined the shadow price and range value and compare the obtained results with those produced by the simplex method with the help of software LINDO 6.1. Sensitivity analysis obtained results with the optimal partition approach is also more accurate than using the optimal bases approach (simplex method), especially for cases that have a primal or dual optimal solution is not unique. But when the primal and the dual has a unique optimal solution, simplex method and optimal partition approach produces the same information

(5)

PERBANDINGAN ANALISIS SENSITIVITAS MENGGUNAKAN

PARTISI OPTIMAL DAN BASIS OPTIMAL PADA OPTIMASI

LINEAR

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

MIRNA SARI DEWI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Perbandingan Analisis Sensitivitas Menggunakan Partisi Optimal dan Basis Optimal pada Optimasi Linear

Nama : Mirna Sari Dewi NIM : G54090042

Disetujui oleh

Dr Ir Bib Paruhum Silalahi, MKom Pembimbing I

Drs Prapto Tri Supriyo, MKom Pembimbing II

Diketahui oleh

Dr Toni Bakhtiar, MSc Ketua Departemen

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Januari 2013 ini ialah analisis sensitivitas, dengan judul Perbandingan Analisis Sensitivitas Menggunakan Partisi Optimal dan Basis Optimal pada Optimasi Linear.

Terima kasih penulis ucapkan kepada Bapak Dr Ir Bib Paruhum Silalahi, MKom dan Drs Prapto Tri Supriyo, MKom selaku pembimbing, serta Ibu Dra Farida Hanum, MSi selaku dosen penguji yang telah banyak memberi saran, motivasi dan bimbingan dalam penulisan karya ilmiah ini. Ucapan terima kasih juga penulis berikan kepada seluruh mahasiswa Matematika angkatan 44, 45, 46, 47, 48, dan 49 serta teman-teman di luar Departemen Matematika baik di dalam Institut Pertanian Bogor maupun di luar Institut Pertanian Bogor atas kritik, saran dan doanya selama pembuatan karya ilmiah ini. Terima kasih juga penulis berikan kepada seluruh staf Departemen Matematika dan staf Fakultas Matematika dan Ilmu Pengetahuan Alam. Ungkapan terima kasih juga tak lupa penulis sampaikan kepada ayah, ibu, serta seluruh keluarga, atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Desember 2013

(9)

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

I PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Tujuan Penelitian 1

1.3 Metode Penelitian 1

II TINJAUAN PUSTAKA 2

2.1 Masalah Optimasi Linear 2

2.2 Analisis Sensitivitas 3

2.3 Makna Simbol 3

2.4 Bentuk Khusus 4

III PEMBAHASAN 4

3.1 Primal Dual 4

3.2 Primal-Dual dengan Pendekatan Partisi Optimal 5

3.3 Ranges dan Shadow Prices 6

3.4 Analisis Sensitivitas dengan Pendekatan Klasik 7

IV STUDI KASUS 8

V SIMPULAN 15

DAFTAR PUSTAKA 15

LAMPIRAN 16

(10)

DAFTAR TABEL

1 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus I) 11 2 Range dan shadow price yang diperoleh dari LINDO (Kasus I) 11 3 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus II) 12 4 Range dan shadow price yang diperoleh dari LINDO (Kasus II) 13 5 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus III) 14 6 Range dan shadow price yang diperoleh dari LINDO (Kasus III) 14

DAFTAR GAMBAR

1 Contoh daerah fisibel 2

2 Fungsi nilai optimal untuk 6

3 Daerah fisibel (D) kasus I 8

4 Daerah fisibel (D) kasus II 12

5 Daerah fisibel (D) kasus III 13

DAFTAR LAMPIRAN

(11)

1

I PENDAHULUAN

1.1 Latar Belakang

Saat ini manfaat optimasi sangat terasa dan diterima secara luas sebagai alat yang berguna dalam berbagai masalah kehidupan. Sebagian besar perusahaan menggunakan pemodelan untuk memecahkan berbagai masalah praktis; sebagai contoh masalah transportasi, perencanaan produksi, masalah keputusan investasi, masalah pencampuran, masalah lokasi dan alokasi, dan masih banyak lagi. Salah satu jenis optimasi adalah optimasi linear.

Secara matematis penyelesaian optimal sebuah kasus optimasi linear selalu berhubungan dengan penyelesaian optimal sebuah kasus optimasi linear yang lain. Bentuk hubungan ini dikenal sebagai dualitas di dalam optimasi linear. Penyelesaian optimal kasus optimasi linear dengan algoritme simpleks pada dasarnya mengandung informasi yang sangat berharga berkaitan dengan perubahan parameter-paremeter dan variabel-variabel yang digunakan. Sejauh mana perubahan itu berperan terhadap penyelesaian optimal adalah informasi yang sangat berharga guna menurunkan alternatif-alternatif keputusan selain keputusan optimal. Informasi ini dapat diperoleh dengan cara analisis sensitivitas.

Analisis sensitivitas menjelaskan sampai sejauh mana pengaruh perubahan parameter-parameter model optimasi linear, yaitu koefisien fungsi tujuan dan nilai ruas kanan kendala, terhadap penyelesaian optimal. Analisis sensitivitas yang biasa digunakan adalah dengan pendekatan klasik (metode simpleks) berdasarkan basis optimal. Pada karya ilmiah ini dibahas analisis sensitivitas dengan pendekatan lain yaitu analisis menggunakan partisi optimal yang unik berdasarkan metode interior point.

1.2 Tujuan

Karya ilmiah ini bertujuan:

1 memaparkan analisis sensitivitas dengan partisi optimal berdasarkan buku acuan yang berjudul Interior Point Methods for Linear Optimization pada subbab Sensitivity Analysis yang disusun oleh C. Roos, T. Terlaky dan J. PH. Vial, kemudian menentukan nilai shadow price dan range,

2 untuk masalah yang sama dilakukan juga analisis sensitivitas menggunakan metode simpleks dengan bantuan perangkat lunak LINDO 6.1,

3 membandingkan hasil yang diperoleh dengan kedua pendekatan.

1.3 Metode Penelitian

Metode yang digunakan dalam penulisan karya ilmiah ini adalah dengan dua pendekatan:

1 studi literatur,

(12)

2

II TINJAUAN PUSTAKA

2.1 Masalah Optimasi Linear

Model optimasi linear meliputi tiga unsur utama yaitu: 1 fungsi tujuan

2 variabel keputusan 3 kendala

Optimasi linear merupakan sebuah model untuk menemukan suatu nilai variabel keputusan yang optimal dengan cara memaksimumkan atau meminimumkan fungsi tujuan terhadap kendala-kendala (Winston 2004).

Dalam model optimasi linear, tujuan yang hendak dicapai harus diwujudkan ke dalam sebuah fungsi linear. Selanjutnya fungsi itu dimaksimumkan atau diminimumkan terhadap kendala-kendala yang ada sehingga fungsi linear tersebut dapat dikatakan sebagai fungsi tujuan. Variabel keputusan adalah variabel persoalan yang akan memengaruhi nilai tujuan yang hendak dicapai. Cara untuk menentukan variabel-variabel keputusan ini adalah dengan mengajukan pertanyaan: keputusan apa yang harus dibuat agar nilai fungsi tujuan menjadi maksimum atau minimum. Misalkan, adalah jumlah bangku yang harus diproduksi, maka adalah variabel keputusan (Siswanto 2007). Pembatasan terhadap nilai-nilai variabel keputusan disebut kendala. Misalkan, harus berada antara 1 dan 5, maka kendalanya dapat dituliskan menjadi 1 dan 5 (Winston 2004).

Untuk masalah maksimisasi, solusi optimal pada optimasi linear adalah suatu titik pada daerah fisibel dengan nilai fungsi tujuan paling besar sedangkan untuk masalah minimisasi, solusi optimal pada optimasi linear adalah suatu titik pada daerah fisibel dengan nilai fungsi tujuan paling kecil. Daerah fisibel adalah himpunan titik-titik yang memenuhi semua kendala dan pembatasan tanda pada optimasi linear tersebut (Winston 2004).

Contoh:

maksimumkan = 2 + 2 dengan kendala + 2 4

3 + 2 6

, 0.

Daerah fisibel dari masalah optimasi linear tersebut dapat dilihat pada Gambar 1.

(13)

3

Dalam menentukan solusi optimal pada optimasi linear, kendala pada model optimasi linear haruslah berbentuk standar, yaitu dengan menambahkan variabel slack dan variabel surplus. Variabel slack adalah variabel yang berfungsi untuk menampung sisa kapasitas pada kendala yang berupa pembatas. Misalkan, kendala suatu masalah optimasi linear adalah 2 + 2. Bentuk standarnya yaitu 2 + +� = 2, dengan � adalah variabel slack. Variabel surplus adalah variabel yang berfungsi untuk menampung kelebihan nilai ruas kiri pada kendala yang berupa syarat. Misalkan, kendala suatu masalah optimasi linear adalah

2 + 2. Bentuk standarnya yaitu 2 + − �= 2, dengan � adalah variabel

surplus (Siswanto 2007).

Metode simpleks menghasilkan solusi basis pada optimasi linear. Solusi basis untuk = (dengan persamaan linear dan variabel ) diperoleh dengan menetapkan − variabel (variabel nonbasis) sama dengan nol dan memecahkan nilai-nilai dari variabel (variabel basis) yang tersisa. Jika − variabel sama dengan nol maka akan menghasilkan nilai yang unik untuk

variabel yang tersisa, dengan kata lain, kolom-kolom untuk variabel yang

tersisa adalah bebas linear. Solusi basis yang semua variabelnya taknegatif disebut basic feasiblesolution (Winston 2004).

Dua buah vektor taknegatif dan � dalam ℝ dikatakan complementary vector jika ��= 0. Jika berlaku juga +� > 0, maka dan � disebut strictly complementary vector (Roos et al. 2006).

2.2 Analisis Sensitivitas

Analisis sensitivitas menjelaskan sampai sejauh mana pengaruh perubahan parameter-parameter model optimasi linear, yaitu koefisien fungsi tujuan dan nilai ruas kanan kendala, terhadap penyelesaian optimal. Analisis sensitivitas parameter koefisien fungsi tujuan adalah persoalan penentuan batas atas dan batas bawah nilai koefisien fungsi tujuan dimana pada interval itu solusi optimal variabel keputusan tidak berubah. Analisis sensitivitas parameter nilai ruas kanan kendala adalah persoalan penentuan batas atas dan batas bawah nilai ruas kanan kendala dimana pada interval itu nilai dual price atau shadow price tidak berubah.

Shadow price, disebut juga dual price, merupakan tambahan nilai fungsi tujuan yang terjadi karena tambahan satu unit nilai ruas kanan kendala (Siswanto 2007). Hubungan kenaikan suatu nilai fungsi tujuan dan suatu nilai shadow price ini bersifat linear dan hanya valid dalam interval (range) tertentu.

2.3 Makna Simbol

(14)

4

Vektor baris adalah suatu matriks berukuran 1 × , dengan n adalah bilangan-bilangan real, sedangkan vektor kolom adalah suatu matriks berukuran

× 1, dengan n adalah bilangan-bilangan real (Leon 1998). Misalkan =

1

2 ⋮ ,

maka adalah vektor kolom.

2.4 Bentuk Khusus

Penyelesaian kasus optimasi linear dapat menyimpang dari perilaku umum. Hasil penyelesaian yang menyimpang ini dikelompokkan ke dalam kasus-kasus khusus optimasi linear. Kasus-kasus tersebut ialah degenerasi, solusi optimal jamak, tidak fisibel (infeasible), dan tidak terbatas.

Sebuah optimasi linear (OL) dikatakan degenerasi jika memiliki setidaknya satu basic feasible solution dengan satu variabel basis yang bernilai nol (Winston 2004). Solusi optimal jamak adalah penyelesaian sebuah kasus optimasi linear di mana titik sudut ekstrem yang menghasilkan nilai optimal fungsi tujuan terdapat lebih dari satu titik (Siswanto 2007).

Kendala pada kasus OL pada umummya membentuk suatu daerah fisibel, namun jika kendala pada kasus OL tidak membentuk suatu daerah fisibel atau daerah fisibelnya adalah himpunan kosong maka kasus tersebut dikatakan tidak fisibel (infeasible). Kasus nilai fungsi tujuan tidak terbatas terjadi bila susunan kendala membentuk sebuah daerah fisibel terbuka yang memiliki luas tidak terbatas. Untuk masalah maksimisasi, kasus nilai fungsi tujuan tidak terbatas terjadi jika daerah fisibel terbuka ke atas dan fungsi tujuan dimaksimumkan terhadap daerah fisibel ini. Sedangkan untuk masalah minimisasi, kasus nilai fungsi tujuan tidak terbatas terjadi jika daerah fisibel terbuka ke bawah dan fungsi tujuan diminimumkan terhadap daerah fisibel ini (Winston 2004).

III PEMBAHASAN

3.1 Primal-Dual

Setiap masalah OL dapat dimodelkan secara matematis ke suatu bentuk yang disebut bentuk primal dan bentuk dual.

Format standar bentuk masalah primal (P) dan masalah dual (D) dari suatu OL adalah sebagai berikut:

(P) min { � ∶ = , 0 }, (D) max { � ∶ � +� = ,� 0 },

dengan persamaan linear dan variabel, c, x, s ∈ ℝn dan b, y ∈ ℝm, A adalah matriks di ℝ × dengan pangkat m.

Misalkan nilai optimal (P) dan (D) berturut-turut dilambangkan dengan

� = min { � ∶ = , 0 },

(15)

5

Misalkan daerah fisibel masalah (P) dan masalah (D) dilambangkan dengan

P ≔{ ∈ ℝ ∶ = , 0 },

D ≔{( , �) ∈ ℝ ∶ � +� = ,� 0 }.

Jika (P) dan (D) keduanya fisibel maka solusi optimal dari (P) dan (D) dapat dilambangkan oleh �∗ dan �∗, dengan

�∗_{≔ ∈ � ∶} � ₌_�_,

�∗_≔_{ _, _{� ∈ � ∶} � ₌ _�_}_.

3.2 Primal-Dual dengan Pendekatan Partisi Optimal

Berikut adalah teorema yang mendasari pembentukan partisi optimal.

Teorema 1 (Teorema Dualitas) Jika (P) dan (D) fisibel maka kedua masalah memiliki solusi optimal. Kemudian, ∈ � dan ( , �) ∈ �, ini adalah solusi yang optimal jika dan hanya jika �� = 0. Jika tak satu pun dari dua masalah memiliki solusi yang optimal, maka keduanya (P) dan (D) tidak fisibel atau salah satu dari dua masalah adalah tidak fisibel dan yang lain tak terbatas (Roos et al. 2006).

Teorema 2 (Teorema Goldman-Tucker) Jika (P) dan (D) fisibel maka terdapat strictly complementary optimal solution, yaitu suatu pasangan solusi optimal ( , �) dengan +� > 0 (Roos et al. 2006).

Berdasarkan teorema tersebut, maka dapat didefinisikan partisi optimal dari (P) dan (D), yakni

∶= { ∶ > 0 untuk suatu ∈ �∗},

� ∶= { ∶ � > 0 untuk suatu ( ,�) ∈ �∗}.

Teorema Dualitas (Teorema 1) berimplikasi bahwa � =∅, dan teorema Goldman-Tucker (Teorema 2) berimplikasi � = {1, 2,…, }.

Berikut adalah lema tentang partisi optimal. Notasi dan _� mengacu pada pembatasan vektor ∈ ℝ dengan indeks masing-masing adalah anggota himpunan dan �. melambangkan pembatasan terhadap kolom dengan indeks anggota himpunan , dan _� pembatasan terhadap kolom dengan indeks anggota himpunan �.

Lema 1

Misalkan ∗∈ �∗ dan ( ∗, �∗) ∈ �∗. Diperoleh

�∗ _{= {} _{∶ ∈ �}_, �_�∗_{= 0},}

�∗ ₌ _, _�_: _, _{� ∈ �}_,_�� ∗ _{= 0} _(Roos_{et al.}_2006).

Lema 2

Diberikan partisi optimal ( ,�) dari (P) dan (D), himpunan solusi optimal dari kedua masalah tersebut adalah

�∗ _{= {} _{∶ ∈ �}_,

� = 0},

(16)

6

Berdasarkan Lema 2 maka sekarang �∗ dan �∗, dapat dinyatakan dengan syarat-syarat partisi optimal menjadi,

�∗ _{= {} _∶ _{= ,} _0,

� = 0},

�∗ ₌ _, _�_: � ₊_� _{= ,}_� _{= 0,}_�

� 0 .

3.3 Ranges dan Shadow Prices

Analisis sensitivitas ialah suatu analisis untuk menentukan shadow price dan range dari semua koefisien (nilai dari ruas kanan kendala primal) dan

(nilai dari ruas kanan kendala dual). Pada suatu kasus, nilai koefisien atau

mungkin saja merupakan break point (titik patahan). Jika koefisien tersebut

adalah break point, maka koefisien tersebut memiliki dua shadow price: shadow price kiri dan shadow price kanan. Namun jika koefisien tersebut bukan suatu break point, maka terdapat sebuah shadow price yang berada pada suatu interval linearitas terbuka dan range dari koefisien berada pada interval linearitas tersebut. Gambar 2 berikut memperlihatkan suatu contoh perubahan nilai optimal untuk perubahan nilai .

Gambar 2 Fungsi nilai optimal untuk cj

Dari Gambar 2 jika bernilai 1 atau 2 maka merupakan suatu break point terhadap nilai optimalnya sehingga memiliki dua nilai shadow price, sedangkan jika bukan suatu break point terhadap nilai optimalnya maka memiliki satu nilai shadow price (Jansen et al. 1997).

Misalkan ∗ adalah solusi optimal dari (P) dan ( ∗, �∗) adalah solusi optimal dari (D). Berdasarkan pendekatan partisi optimal range didapat dengan meminimumkan dan memaksimumkan (Roos et al.2006) dengan

{ ∶ = , 0, ��∗ = 0}. (1)

Shadow price kiri dan kanan dari ditentukan dengan meminimumkan dan memaksimumkan dengan

∶ � ₊_�_{= ,}_� _0,_�� ∗ _{= 0} _. ₍₂₎

Untuk range diperoleh dengan meminimumkan dan memaksimumkan nilai dengan

(17)

7

Shadow price kiri dan kanan dari ditentukan dengan meminimumkan dan memaksimumkan dengan

{ ∶ = , 0, ��∗ = 0}. (4)

Jika (P) dan (D) fisibel maka formula untuk range dan shadow price koefisien dan dapat disederhanakan sebagai berikut.

Formula (1) dapat dirumuskan menjadi

{ ∶ = , 0, _� = 0} (5)

dan (2) menjadi

∶ � ₊_� _{= ,}_� _{= 0,}_�

� 0 . (6) Hal yang sama berlaku untuk (3) yang dapat dirumuskan menjadi

∶ � ₊_� _{= ,}_� _{= 0,}_�

� 0 , (7) dan (4) menjadi

{ ∶ = , 0, _� = 0}. (8)

3.4 Analisis Sensitivitas dengan Pendekatan Klasik

Analisis sensitivitas dengan pendekatan klasik menggunakan metode simpleks dalam menyelesaikan masalah optimasi linear. Metode simpleks menghasilkan solusi basis dari masalah optimasi linear, sehingga solusi dengan pendekatan klasik ini ditentukan dengan sebuah basis optimal.

Diasumsikan bahwa matriks berukuran × dan pangkat ( ) = , indeks variabel basis dari yang berjumlah dinotasikan dengan ’, sehingga ’ adalah submatriks _′ berukuran × yang nonsingular dari dengan

′ ′ = , �′ = 0 dengan �’ adalah indeks variabel nonbasis dari . Solusi

basis primal dapat ditentukan dengan

= ′

�′ ∶=

′ −1

0 (9)

dan solusi basis dual dapat ditentukan dengan = −�_′ _�′ , � = _�� ′ basis dikatakan optimal primal jika solusi basis primal tersebut optimal di (P), dan sebuah basis dikatakan optimal dual jika solusi basis dual tersebut optimal di (D).

(18)

8

IV STUDI KASUS

Pada bagian ini akan disajikan studi kasus analisis sensitivitas masalah optimasi linear. Hasil analisis sensitivitas yang diperoleh dengan menggunakan partisi optimal akan dibandingkan dengan hasil yang diperoleh dengan bantuan perangkat lunak LINDO. Kasus yang diamati adalah sebagai berikut :

1 solusi optimal masalah primal unik, dan solusi optimal masalah dual tidak unik,

2 solusi optimal masalah primal unik, dan solusi optimal masalah dual unik, 3 solusi optimal masalah primal tidak unik, dan solusi optimal masalah dual

unik.

4.1 Kasus I

Misalkan masalah primal (P) didefinisikan sebagai berikut

min 4 1−5 2+ 11 3

terhadap − ₂+ 3 ₃ = 0 ₁− ₂− ₃ = 1 ₁, ₂, ₃ 0.

Masalah dualnya (D) adalah max ₂

terhadap ₂ 4

− ₁ − ₂ −5

3 ₁ − ₂ 11.

Masalah dual (D) dapat diselesaikan secara grafik, dan daerah fisibelnya yang dapat dilihat di Gambar 3.

Gambar 3 Daerah fisibel (D) Kasus I

Dari Gambar 3 dapat ditentukan himpunan solusi optimalnya adalah

�∗_{= {(}

1, 2): 1 1 5, 2 = 4} dan nilai optimalnya adalah 4. Variabel

(19)

9 meminimumkan dan memaksimumkan ₂. Dari perkalian matriks =

0 −1

(20)

10

Range dan Shadow Price untuk =

Dengan menggunakan formula (7) range ₁ dapat ditentukan dengan meminimumkan dan memaksimumkan ₁.

∶ � ₊_� _{= ,}_� _{= 0,}_�

Range dan Shadow Price untuk = −

Dengan menggunakan formula (7) range ₂ dapat ditentukan dengan meminimumkan dan memaksimumkan ₂. Perkalian matriks � +� = :

0 1

Dengan menggunakan formula (8), shadow price untuk ₂dapat ditentukan dengan meminimumkan dan memaksimumkan ₂. Karena ₂ = 0, maka shadow price untuk ₂ adalah 0.

Range dan Shadow Price untuk =

(21)

11

Tabel 1 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus I) Koefisien Range Shadow price

1 = 0 Koefisien Range Shadow price

1 = 0

Dari Tabel 1 dan Tabel 2 dapat dilihat bahwa terdapat perbedaan hasil range dan shadow price pada koefisien ₁ = 0. Analisis sensitivitas dengan metode simpleks (LINDO) tidak mendeteksi bahwa ₁ = 0 merupakan break point. Sedangkan analisis sensitivitas dengan pendekatan partisi optimal mendeteksi bahwa ₁ = 0 merupakan break point, sehingga koefisien ₁ memiliki dua nilai shadow price, yaitu shadow price kiri yang bernilai 1 dan shadow price kanan yang bernilai 5. Shadow price kiri digunakan ketika nilai koefisien ₁ diturunkan dari nilai awalnya, sedangkan Shadow price kanan digunakan ketika nilai koefisien ₁ dinaikkan dari nilai awalnya. Misalkan jika nilai koefisien ₁ diturunkan satu satuan dari nilai awalnya menjadi ₁ = −1 maka nilai optimalnya menjadi 3, dan jika nilai koefisien ₁ dinaikkan satu satuan dari nilai awalnya menjadi ₁ = 1 maka nilai optimalnya menjadi 9.

4.2 Kasus II

min 31 ₁−5 ₂+ 11 ₃

terhadap 3 1− 2+ 3 3 = 0

7 1− 2− 3 = 1

(22)

12

Masalah dual (D) dapat diselesaikan secara grafik, dan daerah fisibelnya dapat dilihat di Gambar 4.

Gambar 4 Daerah fisibel (D) Kasus II

�∗ _{= {(}

1, 2): 1 = 1, 2 = 4} dan nilai optimalnya adalah 4. Variabel slack

dari setiap kendala dual masing-masing ialah

3 1+ 7 2+�1= 31  �1 = 31−3 1−7 2

− 1 − 2+�2 = −5  �2 =−5 + 1+ 2

3 1− 2+�3 = 11  �3= 11−3 1+ 2

Dengan memasukkan nilai ₁ = 1 dan 2 = 4 maka akan diperoleh nilai

untuk setiap variabel slack dan dapat disimpulkan bahwa semua variabel slack dapat menjadi positif pada solusi optimal kecuali variabel slack pada konstrain

3 ₁+ 7 ₂ 31 dan − ₁− ₂ −5 yaitu �₁ =�₂ = 0. Karena di dual �₁ = shadow price dengan menggunakan partisi optimal pada Tabel 3.

Tabel 3 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus II) Koefisien Range Shadow price

(23)

13

Tabel 4 Range dan shadow price yang diperoleh dari LINDO (Kasus II) Koefisien Range Shadow price

1 = 0 price yang sama antara perhitungan dengan pendekatan partisi optimal dan metode simpleks.

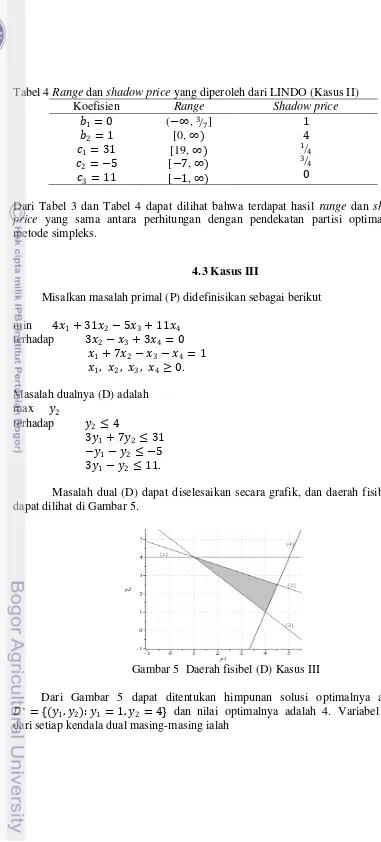
4.3 Kasus III

min 4 1+ 31 2−5 3+ 11 4

Masalah dual (D) dapat diselesaikan secara grafik, dan daerah fisibelnya dapat dilihat di Gambar 5.

Gambar 5 Daerah fisibel (D) Kasus III

�∗ _{= {(}

1, 2): 1 = 1, 2 = 4} dan nilai optimalnya adalah 4. Variabel slack

(24)

14

hanya variabel ₁, ₂ dan ₃ yang dapat menjadi positif. Oleh karena itu diperoleh partisi optimal ( , �), dengan � = {4} dan = {1, 2, 3}.

Dari Lema 2 diperoleh:

�∗ _{= {} _{∈ �}_:

4 = 0} dan (P) memiliki solusi yang tidak unik: {( 1, 2,

3): , ¼ − ¼ , 3 ¼ − ¼ ; 0 1}. Kemudian hasil perhitungan

range dan shadow price disajikan pada Tabel 5.

Tabel 5 Range dan shadow price yang diperoleh dari hasil perhitungan (Kasus III) Koefisien Range Shadow price

1 = 0

Tabel 6 Range dan shadow price yang diperoleh dari LINDO (Kasus III) Koefisien Range Shadow price

1 = 0

Pada Tabel 5 dan Tabel 6 dapat dilihat bahwa terdapat perbedaan range dan shadow price yang diperoleh dengan menggunakan partisi optimal dan metode simpleks. Pada koefisien ₁ = 0, untuk shadow price yang sama, pendekatan partisi optimal mendeteksi range yang lebih besar. Kemudian pada koefisien

1 = 4, 2 = 31 dan 3 = −5 analisis dengan menggunakan metode simpleks

tidak mendeteksi adanya break point, sehingga shadow price yang diperoleh dengan metode simpleks merupakan subset dari shadow price dengan pendekatan partisi optimal. Karena koefisien ₁, ₂ dan ₃ adalah break point maka koefisien

1, 2 dan 3 memiliki dua nilai shadow price berturut-turut, yaitu shadow price

kiri yang bernilai 1, 1

(25)

15

V SIMPULAN

Analisis sensitivitas dengan metode simpleks (menggunakan pendekatan basis optimal) untuk kasus yang memiliki solusi optimal primal atau dual yang tidak unik, hasilnya akan mengalami ketaksempurnaan informasi. Sedangkan analisis sensitivitas dengan pendekatan partisi optimal untuk kasus yang memiliki solusi optimal primal atau dual yang tidak unik, menghasilkan informasi yang lebih akurat. Namun saat masalah primal dan masalah dual memiliki solusi optimal yang unik, metode simpleks dan pendekatan partisi optimal menghasilkan informasi yang persis sama.

DAFTAR PUSTAKA

Jansen B, de Jong J.J, Roos C, Terlaky T. 1997. Sensitivity analysis in linear programming: just be careful!. European Journal of Operations Research. 101: 15-28.doi: 10.1016/S0377-2217(96)00172-5.

Leon SJ. 1998. Linear Algebra with Applications. Ed ke-5. New Jersey (US): Prentice Hall.

Roos C, Terlaky T, Vial J-Ph. 2006. Interior Point Methods for Linear Optimization. New York (US): Springer.

Siswanto. 2007. Operations Research. Jilid 1. Jakarta (ID): Erlangga. Winston WL. 2004. Operations Research Applications and Algorithms. 4th

(26)

16

Lampiran 1 Studi kasus I dengan menggunakan LINDO

Input Primal :

min 4x1-5x2+11x3 subject to -x2+3x3=0 x1-x2-x3=1

end

Output Primal :

LP OPTIMUM FOUND AT STEP 0

OBJECTIVE FUNCTION VALUE

1) 4.000000

VARIABLE VALUE REDUCED COST X1 1.000000 0.000000 X2 0.000000 0.000000 X3 0.000000 12.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -1.000000 3) 0.000000 -4.000000

NO. ITERATIONS= 0

RANGES IN WHICH THE BASIS IS UNCHANGED:

OBJ COEFFICIENT RANGES

VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE X1 4.000000 INFINITY 3.000000 X2 -5.000000 INFINITY 4.000000 X3 11.000000 INFINITY 12.000000

RIGHTHAND SIDE RANGES

ROW CURRENT ALLOWABLE ALLOWABLE RHS INCREASE DECREASE 2 0.000000 0.000000 INFINITY 3 1.000000 INFINITY 1.000000

Input Dual : max y2

subject to y2<=4 -y1-y2<=-5

(27)

17

Output Dual :

1) 4.000000

VARIABLE VALUE REDUCED COST Y2 4.000000 0.000000 Y1 1.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 1.000000 3) 0.000000 0.000000 4) 12.000000 0.000000

NO. ITERATIONS= 2

VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE Y2 1.000000 INFINITY 1.000000 Y1 0.000000 0.000000 INFINITY

ROW CURRENT ALLOWABLE ALLOWABLE RHS INCREASE DECREASE 2 4.000000 1.000000 3.000000 3 -5.000000 1.000000 4.000000 4 11.000000 INFINITY 12.000000

Lampiran 2 Studi kasus II dengan menggunakan LINDO

Input Primal :

min 31x1-5x2+11x3

subject to 3x1-x2+3x3=0 7x1-x2-x3=1

end

Output Primal :

1) 4.000000

(28)

18

X2 0.750000 0.000000 X3 0.000000 12.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -1.000000 3) 0.000000 -4.000000

NO. ITERATIONS= 0

VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE X1 31.000000 INFINITY 12.000000 X2 -5.000000 INFINITY 2.000000 X3 11.000000 INFINITY 12.000000

subject to 3y1+7y2<=31 -y1-y2<=-5

3y1-y2<=11 end

Output Dual :

1) 4.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 0.250000 3) 0.000000 0.750000 4) 12.000000 0.000000

(29)

19

Lampiran 3 Studi kasus III dengan menggunakan LINDO

Input Primal :

(30)

20

subject to y2<=4 3y1+7y2<=31 -y1-y2<=-5 3y1-y2<=11 end

Output Dual :

1) 4.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 1.000000 3) 0.000000 0.000000 4) 0.000000 0.000000 5) 12.000000 0.000000

NO. ITERATIONS= 2

VARIABLE CURRENT ALLOWABLE ALLOWABLE COEF INCREASE DECREASE Y2 1.000000 INFINITY 1.000000 Y1 0.000000 0.000000 INFINITY

(31)

21

RIWAYAT HIDUP

Penulis lahir di Manado pada tanggal 11 Juni 1991 dari ayah Amir Kara dan ibu Siti Aminah. Penulis adalah putri ketiga dari tiga bersaudara. Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 2003 di SD Negeri Bekasi Jaya XI dan Sekolah Menengah Pertama pada tahun 2006 di SMP Negeri 1 Bekasi. Tahun 2009 penulis lulus dari SMA KORPRI Bekasi dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.