ANALISIS SENSITIVITAS MASALAH TRANSPORTASI DALAM BILANGAN FUZZY SEGITIGA KARYA ILMIAH OLEH LEONORA PONCODINI NIM

ANALISIS SENSITIVITAS MASALAH TRANSPORTASI DALAM BILANGAN FUZZY SEGITIGA

KARYA ILMIAH

OLEH

LEONORA PONCODINI NIM. 1603123180

PROGRAM STUDI S1 MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS RIAU

PEKANBARU 2020

ANALISIS SENSITIVITAS MASALAH TRANSPORTASI DALAM BILANGAN FUZZY SEGITIGA

Leonora Poncodini

Mahasiswa Program Studi S1 Matematika Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus Bina Widya, Pekanbaru 28293

leonora.poncodini@gmail.com

ABSTRACT

This article discusses the sensitivity analysis of transportation problems in triangular fuzzy numbers. The optimal solution of the transportation problem is obtained after converting the triangular fuzzy number in the transportation problem into a crisp number. When the optimal solution obtained remains the same for a long time, a sensitivity analysis is carried out to determine changes in the optimal solution by changing parameters on the right side, eliminating variables and adding new constraints to transportation problems.

Keywords: Triangular fuzzy number, ranking function, transportation problem ABSTRAK

Artikel ini membahas analisis sensitivitas masalah transportasi dalam bilangan fuzzy segitiga. Solusi optimal dari masalah transportasi didapat setelah mengubah bilangan fuzzy segitiga pada masalah transportasi menjadi bentuk bilangan tegas.

Ketika solusi optimal yang diperoleh tetap sama untuk waktu yang lama dilakukan analisis sensitivitas untuk mengetahui perubahan solusi optimal dengan melakukan perubahan parameter pada ruas kanan, penghapusan variabel dan penambahan kendala baru pada masalah transportasi.

Kata kunci: Bilangan fuzzy segitiga, fungsi rangking, masalah transportasi 1. PENDAHULUAN

Riset operasi merupakan penerapan beberapa metode ilmiah yang membantu memecahkan persoalan yang muncul dalam kehidupan sehari-hari, kemudian diinteprestasikan dalam pemodelan matematika untuk mendapatkan solusi yang optimal. Teknik untuk menyelesaikan riset operasi terkait masalah optimisasi adalah pemrograman linear [10, h. 49].

Pemrograman linear pertama kali diperkenalkan oleh George Dantzig pada tahun 1947 yang melibatkan fungsi obyektif dan fungsi kendala [5]. Salah satu pemrograman linear yang dapat diterapkan untuk masalah optimisasi adalah masalah aliran jaringan, biasanya terkait dengan aplikasi yang melibatkan masalah transportasi, penugasan dan transshipment [4, h. 213]. Masalah transportasi muncul dalam perencanaan distribusi barang dan jasa dari berbagai lokasi asal (supply) ke beberapa lokasi tujuan (demand ) [9, h. 193]. Menurut Hillier [4, h.

213] tujuan masalah transportasi adalah untuk meminimalkan biaya pengiriman barang dari asal ke tujuan.

Pada pemrograman linear untuk memberikan fleksibilitas dalam nilai yang tidak pasti dapat diatasi dengan mengganti bilangan crisp (tegas) menjadi bilangan fuzzy (samar) [3]. Kemudian untuk mendapatkan penyelesaian terbaik diperlukan suatu analisis, yaitu analisis sensitivitas.

Analisis sensitivitas adalah alat dasar untuk mempelajari gangguan dalam masalah optimisasi [7] dan dilakukan untuk mengetahui pengaruh perubahan yang terjadi pada parameter-parameter persoalan program linear terhadap solusi optimal yang telah diperoleh.

Penelitian ini merupakan review sebagian dari artikel Hashem [3]. Penulis tertarik untuk melakukan analisis sensitivitas perubahan parameter pada solusi optimal dari masalah transportasi, yaitu pada ruas kanan, penghapusan variabel dan penambahan kendala. Untuk pembahasan ini, pada bagian 2 didiskusikan masalah transportasi. Kemudian dilanjutkan dibagian 3 dengan analisis sensitivitas pada masalah transportasi, dan diakhiri dibagian 4 dengan contoh analisis sensitivitas pada masalah transportasi.

2. MASALAH TRANSPORTASI

Masalah transportasi dengan persediaan dan permintaan dalam bilangan fuzzy segitiga dirumuskan sebagai berikut.

min Z = c₁₁x₁₁+· · · + c1nx_1n+ . . . + c_m1x_m1+· · · + cmnx_mn. }

(1) kendala

x11 + x12 + · · · + x1n ≤ (r1, s1, t1), ... ≤ ... x_m1 + x_m2 + · · · + xmn ≤ (rm, s_m, t_m),

x11 + x21 + · · · + xm1 = (r1, s1, t1), ... = ... x_1n + x_2n + · · · + xmn = (r_n, s_n, t_n),

























(2)

xij ≥ 0, i = 1, 2, 3, . . . , m, j = 1, 2, 3, . . . , n. (3) Selanjutnya untuk menyelesaikan masalah transportasi pada persamaan (1), (2), dan pertidaksamaan (3) terlebih dahulu persediaan dan permintaan fuzzy

pada masalah transportasi disusun dalam bentuk bilangan tegas dengan menggunakan robust ranking (ℜ) [2], yaitu

ℜ(rij, s_ij, t_ij) = r_ij + 2s_ij+ t_ij

4 .

Setelah bilangan tegas dari masalah transportasi diperoleh, selanjutnya dapat dicari solusi optimal masalah transportasi dengan langkah-langkah sebagai berikut:

Langkah 1. Menentukan solusi variabel basis awal dengan metode sudut barat laut (Northwest Corner Method) [1]. Menurut Murthy [8, h. 156]

jika x_ij adalah variabel basis, maka diperoleh u_i+ v_j = c_ij,

dengan cij adalah koefisien fungsi obyektif, nilai ui dan vj adalah variabel dual.

Langkah 2. Menguji apakah koefisien fungsi obyektif variabel nonbasis baru

˜

c_ij = u_i+ v_j− cij ≤ 0,

dengan c_ij adalah koefisien fungsi obyektif variabel nonbasis. Jika setiap variabel nonbasis sudah negatif, maka variabel basis adalah solusi optimal. Sebaliknya, jika terdapat variabel nonbasis yang positif, maka solusi belum optimal dan dilanjutkan ke langkah 3.

Langkah 3. Memilih koefisien fungsi obyektif variabel nonbasis ˜cij positif tertinggi. Oleh karena itu dipilih x_ij sebagai variabel basis baru dan mengeluarkan variabel basis menjadi variabel nonbasis.

Jika masih terdapat ˜cij = ui+vj−cij > 0, maka solusi belum optimal dan kembali ke langkah 1.

Selanjutnya solusi optimal yang sudah diperoleh disusun dalam bentuk tabel optimal yang didasarkan pada pemrograman linear. Berdasarkan Winston [10, h.

272] rumus untuk baris pertama pada tabel optimal yaitu

Z + (C_BB⁻¹N − CN)X_N = C_BB⁻¹b, (4) dengan:

X_B := Vektor variabel basis.

X_N := Vektor variabel nonbasis.

C_B := Vektor koefisien fungsi obyektif untuk variabel basis.

C_N := Vektor koefisien fungsi obyektif untuk variabel nonbasis.

B := Matriks kolom koefisien kendala variabel basis.

B⁻¹ := Matriks kolom koefisien kendala variabel nonbasis.

aj := Vektor koefisien variabel ke-j.

c_j := Koefisien fungsi tujuan untuk variabel ke-j.

b := Vektor ruas kanan kendala.

X˜_j := Koefisien kendala kolom ke-j.

Z := Nilai optimal.

C˜j := Koefisien fungsi obyektif variabel xj. Berdasarkan persamaan (4) diperoleh:

(i) Koefisien kendala kolom ke-j

X˜_j = B⁻¹a_j, j = 1, 2, . . . , n. (5) (ii) Nilai ruas kanan

X_B = B⁻¹b. (6)

(iii) Nilai optimal

Z = C_BB⁻¹b. (7)

(iv) Koefisien fungsi obyektif variabel x_j

C˜j = CBB⁻¹aj − cj, j = 1, 2, . . . , n. (8) Rumus pada persamaan (5), (6), (7), dan (8) dapat disajikan pada Tabel 1.

Tabel 1: Tabel Optimal

Variabel basis Koefisien variabel fungsi obyektif Ruas kanan

Z C_BB⁻¹a_j− cj C_BB⁻¹b

X_B B⁻¹a_j B⁻¹b

Setelah tabel optimal diperoleh selanjutnya dapat dilakukan analisis sensitivitas pada masalah transportasi.

3. ANALISIS SENSITIVITAS PADA MASALAH TRANSPORTASI Analisis sensitivitas dioperasikan setelah diperoleh tabel optimal dari masalah transportasi. Melalui analisis sensitivitas dapat dilihat pengaruh solusi optimal setelah dilakukan perubahan parameter. Perubahan parameter yang dibahas yaitu:

(i) Perubahan nilai ruas kanan.

Nilai ruas kanan mengalami perubahan jika pada saat proses produksi terjadi perubahan permintaan atau ketersediaan. Analisis ini menunjukkan selang perubahan jumlah ketersediaan sumberdaya yang tidak menyebabkan perubahan nilai dual price kendala yang bersangkutan.

Jika nilai ruas kanan yaitu b = [ b₁ b₂ . . . b_n ]^T berubah menjadi b^′ = [ b₁ b₂ . . . b^′_k . . . b_n) ]^T maka diperoleh

b^′ = [ b₁ b₂ . . . (b_k+ λ∆b_k) . . . b_n]^T,

dengan b_k adalah nilai ruas kanan ke-k untuk λ parameter positif.

Selanjutya diperoleh nilai ruas kanan yang baru setelah dilakukan perubahan sebagai berikut:

X_B^′ = B⁻¹b^′,

= B⁻¹[ b1 b2 . . . (bk+ λ∆bk) . . . bn]^T, X_B^′ = B⁻¹b + λ∆b_k∑n

i=1β_ik, β_ik ≥ 0.

(ii) Penghapusan variabel.

Suatu variabel pada masalah transportasi dihapus apabila terjadi pemeliharaan jalan, pemotongan jalan ataupun permasalahan yang menyebabkan variabel harus dihapus. Penghapusan pada variabel nonbasis tidak mempengaruhi solusi optimal. Sebaliknya, bila penghapusan dilakukan pada variabel basis maka mempengaruhi solusi optimal. Adapun langkah-langkah penghapusan pada variabel basis [7] sebagai berikut:

1. Menghilangkan kolom dari variabel basis yang dihapus pada tabel optimal.

2. Mengalikan baris dari variabel basis yang dihapus dengan (-1).

3. Mereduksikan tabel untuk mendapatkan solusi optimal yang baru.

(iii) Penambahan kendala baru.

Jika terjadi suatu kondisi baru pada proses produksi, maka kendala baru harus ditambahkan pada fungsi kendala permasalahan transportasi. Misal ditambah kendala baru Am+1X ≤ bm+1 atau dapat ditulis

((A_m+1)_N − (Am+1)_BB⁻¹N )X_N + X_n+1 = b_m+1− (Am+1)_BB⁻¹b, (9) dengan (A_m+1) adalah dekomposisi ((A_m+1)_B(A_m+1)_N) dan X_n+1 adalah variabel slack [6].

Dari persamaan (9) didapat solusi optimal baru jika bm+1 − (Am+1)BB⁻¹b ≥ 0, sebaliknya jika bm+1 −(Am+1)BB⁻¹b < 0 maka solusi belum optimal, kemudian melalui reduksi dapat ditentukan solusi optimalnya.

4. CONTOH ANALISIS SENSITIVITAS PADA MASALAH TRANSPORTASI

Pada bagian ini, dilakukan analisis sensitivitas pada masalah transportasi. Pertama, dicari solusi optimal dari masalah transportasi yang diberikan. Kedua, solusi yang diperoleh dibentuk menjadi tabel optimal. Ketiga, dilakukan analisis sensitivitas pada tabel optimal.

Misal diberikan masalah transportasi dengan persediaan dan permintaan dalam bilangan fuzzy segitiga sebagai berikut:

min Z = 5x₁₁+ 3x₁₂+ 2x₁₃+ 7x₁₄+ 9x₁₅+ 4x₂₁+ 10x₂₂+ 5x₂₃ +3x₂₄+ 11x₂₅+ 8x₃₁+ 14x₃₂+ 6x₃₃+ 13x₃₄+ 2x₃₅ +16x₄₁+ 8x₄₂+ 15x₄₃+ 12x₄₄+ 4x₄₅.

(10)

kendala

x11+ x12+ x13+ x14+ x15 ≤ (19, 25, 31).

x21+ x22+ x23+ x24+ x25 ≤ (59, 65, 71).

x₃₁+ x₃₂+ x₃₃+ x₃₄+ x₃₅ ≤ (56, 60, 64).

x₄₁+ x₄₂+ x₄₃+ x₄₄+ x₄₅ ≤ (72, 80, 88).

x₁₁+ x₂₁+ x₃₁+ x₄₁ = (49, 55, 61).

x₁₂+ x₂₂+ x₃₂+ x₄₂ = (23, 30, 37).

x₁₃+ x₂₃+ x₃₃+ x₄₃ = (27, 35, 43).

x₁₄+ x₂₄+ x₃₄+ x₄₄ = (44, 45, 46).

x₁₅+ x₂₅+ x₃₅+ x₄₅ = (63, 65, 67).





































(11)

x_ij ≥ 0, (i = 1, 2, 3, 4, j = 1, 2, 3, 4, 5). (12) Masalah transportasi pada persamaan (10), (11), dan pertidaksamaan (12) dapat disusun dalam bentuk matriks sebagai berikut:

min Z = [5 3 2 7 9 4 10 5 3 11 8 14 6 13 2 16 8 15 12 4] X. (13) kendala





















1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1

1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0

0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0

0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0

0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0

0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1



















 X =





















(19, 25, 31) (59, 65, 71) (56, 60, 64) (72, 80, 88) (49, 55, 61) (23, 30, 37) (27, 35, 43) (44, 45, 46) (63, 65, 67)





















. (14)

X ≥ 0, (15)

dengan X = [x₁₁ x₁₂ x₁₃ x₁₄ x₁₅ x₂₁ x₂₂ x₂₃ x₂₄ x₂₅ x₃₁ x₃₂ x₃₃ x₃₄ x₃₅ x₄₁ x₄₂ x₄₃ x₄₄ x₄₅]^T.

Solusi optimal dari masalah transportasi pada persamaan (10), (11) dan pertidaksamaan (12) diperoleh dengan menggunakan metode sudut barat laut dan pengujian optimalitas, kemudian disajikan pada Tabel 2.

Tabel 2: Solusi Optimal Masalah Transportasi Fuzzy Segitiga

v1 v2 v3 v4 v5

u1

5 3 2

(19, 25, 31)

7 9

(19, 25, 31)

u2

4 (15, 20, 25)

10 5 3

(44, 45, 46)

11

(59, 65, 71)

u3

8 (34, 35, 36)

14 6

(8, 10, 12)

13 2

(14, 15, 16) (56, 60, 64)

u4

16 8

(23, 30, 37)

15 12 4

(49, 50, 51) (72, 80, 88) (49, 55, 61) (23, 30, 37) (27, 35, 43) (44, 45, 46) (63, 65, 67)

Berdasarkan persamaan (13), (14), pertidaksamaan (15) dan solusi optimal pada Tabel 2, diperoleh sebagai berikut:

1. Variabel basis (X_B)

X_B = (x₁₃, x₂₁, x₂₄, x₃₁, x₃₃, x₃₅, x₄₂, x₄₅).

2. Matriks B dan invers dari matriks B

B =

















1 0 0 0 0 0 0 0

0 1 1 0 0 0 0 0

0 0 0 1 1 1 0 0

0 0 0 0 0 0 1 1

0 1 0 1 0 0 0 0

0 0 0 0 0 0 1 0

1 0 0 0 1 0 0 0

0 0 1 0 0 0 0 0

















, B⁻¹=

















1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 −1

0 0 0 0 0 0 0 1

0 −1 0 0 1 0 0 1

−1 0 0 0 0 0 1 0

1 1 1 0 −1 0 −1 −1

0 0 0 0 0 1 0 0

0 0 0 1 0 −1 0 0















 .

3. Koefisien variabel basis fungsi obyektif (C_B) dan koefisien variabel nonbasis fungsi obyektif (C_N)

CB = [

2 4 3 8 6 2 8 4 ]

, CN = [

5 3 7 9 10 5 11 14 13 16 15 12 ]

.

4. Nilai ruas kanan (b)

b = [ (19, 25, 31) (59, 65, 71) (56, 60, 64) (72, 80, 88) (49, 55, 61) (23, 30, 37) (27, 35, 43) (44, 45, 46) ]^T.

Berdasarkan persamaan (8) diperoleh koefisien fungsi obyektif variabel x_j ( ˜C_ij) pada solusi optimal sebagai berikut:

C˜11 = CBB⁻¹a11− c11 = CBB⁻¹ [

1 0 0 0 1 0 0 0 ]T

− 5 = −1.

Dengan cara yang sama diperoleh nilai ˜C₁₂, ˜C₁₃, ˜C₁₄, . . ., ˜C₄₅.

Kemudian berdasarkan persamaan (5) diperoleh koefisien kendala kolom ke-j ( ˜X_ij) pada solusi optimal sebagai berikut:

X˜11= B⁻¹a11= B⁻¹ [

1 0 0 0 1 0 0 0 ]T

= [

1 0 0 1 −1 0 0 0 ]T

.

Dengan cara yang sama diperoleh nilai ˜X₁₂, ˜X₁₃, ˜X₁₄, . . ., ˜X₄₅.

Selanjutnya berdasarkan persamaan (6) diperoleh nilai ruas kanan pada solusi optimal sebagai berikut:

B⁻¹b = [ (19, 25, 31) (15, 20, 25) (44, 45, 46) (34, 35, 36) (8, 10, 12) (14, 15, 16) (23, 30, 37) (49, 50, 51)]^T

Kemudian berdasarkan persamaan (7) diperoleh nilai optimal (Z) pada solusi optimal sebagai berikut:

Z = C_BB⁻¹b = [

(958, 1057, 1192) ]

.

Dengan demikian nilai koefisien fungsi obyektif, koefisien kendala, nilai ruas kanan, dan nilai optimal masalah transportasi disajikan pada Tabel 3.

Tabel 3: Tabel Optimal Masalah Transportasi

x11x12x13x14x15x21x22x23x24x25x31x32x33x34x35x41x42x43x44x45 Ruas Kanan Baris Z -1 -1 0 -4 -11 0 -8 -3 0 -13 0 -8 0 -6 0 -6 0 -7 -3 0 (958, 1057, 1192)

Basis

x13 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (19, 25, 31)

x21 0 0 0 -1 0 1 1 1 0 1 0 0 0 -1 0 0 0 0 -1 0 (15, 20, 25)

x24 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 (44, 45, 46)

x31 1 0 0 1 0 0 -1 -1 0 -1 1 0 0 1 0 1 0 0 1 0 (34, 35, 36) x33 -1 -1 0 -1 -1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 (8, 10, 12) x35 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 -1 0 -1 -1 0 (14, 15, 16)

x42 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 (23, 30, 37)

x45 0 -1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 1 0 1 1 1 (49, 50, 51)

Kemudian setelah mendapatkan tabel optimal, dapat dilakukan analisis sensitivitas perubahan parameter pada masalah transportasi sebagai berikut:

(i) Perubahan nilai ruas kanan.

Misalkan masalah transportasi pada persamaan (10), (11), dan pertidaksamaan (12) dengan solusi optimal pada Tabel 3, ruas kanan ke-2 yaitu b₂ = (59, 65, 71) mengalami perubahan karena jumlah persediaan digudang menurun menjadi

b^′₂ = (59 + λ, 65 + 2λ, 71 + 3λ),

sehingga diperoleh nilai ruas kanan yang baru yaitu

X_B^′ = B⁻¹[ 25 65 + 2λ 60 80 55 30 35 45 ]^T , X_B^′ =

[

25 20 + 2λ 45 35− 2λ 10 15 + 2λ 30 50 ]T

. (16) Dari persamaan (16) diperoleh nilai λ sebagai berikut:

20 + 2λ≥ 0 atau λ ≥ −10 35− 2λ ≥ 0 atau λ ≤ 17.5 15 + 2λ≥ 0 atau λ ≥ −7.5





. (17)

Kemudian diperoleh irisan dari nilai λ pada pertidaksamaan (17) adalah

−7.5 ≤ λ ≤ 17.5. (18)

Misal pada rentang pertidaksamaan (18) dipilih λ = 7.5, sehingga ruas kanan pada persamaan (16) menjadi

B⁻¹b^′ = [

25 35 45 20 10 30 30 50 ]T

. (19)

Selanjutnya, karena nilai ruas kanan pada persamaan (19) bernilai positif, maka nilai yang dihasilkan sudah optimal. Oleh karena perubahan ruas kanan kendala juga mempengaruhi nilai optimal, kemudian dengan menggunakan nilai ruas kanan yang baru pada persamaan (19), diperoleh nilai optimal yang baru yaitu

Z = C_BB⁻¹b^′ = 1045.

Dengan demikian nilai ruas kanan dan nilai optimal yang baru disajikan pada Tabel 4.

Tabel 4: Tabel Optimal Perubahan Ruas Kanan Kendala (b^′₂)

x11x12x13x14x15x21x22x23x24x25x31x32x33x34x35x41x42x43x44x45 Ruas Kanan Baris W -1 -1 0 -4 -11 0 -8 -3 0 -13 0 -8 0 -6 0 -6 0 -7 -3 0 1045

Basis

x13 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 25 x21 0 0 0 -1 0 1 1 1 0 1 0 0 0 -1 0 0 0 0 -1 0 35 x24 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 45 x31 1 0 0 1 0 0 -1 -1 0 -1 1 0 0 1 0 1 0 0 1 0 20 x33 -1 -1 0 -1 -1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 10 x35 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 -1 0 -1 -1 0 30 x42 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 30 x45 0 -1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 1 0 1 1 1 50

(ii) Penghapusan variabel.

(a.) Penghapusan variabel basis.

Misal pada masalah transportasi persamaan (10), (11), dan pertidaksamaan (12) dengan solusi optimal Tabel 3 dihapus variabel basis x₃₃, yaitu pengiriman barang asal 3 ke tujuan 3 karena terjadi pemeliharaan jalan. Kemudian kolom variabel basis x₃₃ pada Tabel 3 dihapus dan mengalikan baris variabel basis x₃₃ pada Tabel 3 dengan (-1). Selanjutnya dengan memasukkan variabel x₂₃ menjadi variabel basis menggantikan x₃₃, sehingga melalui reduksi diperoleh solusi optimal dari penghapusan variabel basis x₃₃ yaitu pada Tabel 5.

Tabel 5: Tabel Optimal Penghapusan Variabel Basis x₃₃

x11x12x13x14x15x21x22x23x24x25x31x32x34x35x41x42x43x44x45 Ruas Kanan Baris W -4 -4 0 -7 -14 0 -8 0 0 -13 0 -8 -6 0 -6 0 -4 -3 0 (982, 1087, 1228)

Basis

x13 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (19, 25, 31)

x21 1 1 0 0 1 1 1 0 0 1 0 0 -1 0 0 0 -1 -1 0 (7, 10, 13)

x24 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 (44, 45, 46)

x31 0 -1 0 0 -1 0 -1 0 0 -1 1 0 1 0 1 0 1 1 0 (42, 45, 48) x23 -1 -1 0 -1 -1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 (8, 10, 12) x35 0 1 0 0 1 0 1 0 0 1 0 1 0 1 -1 0 -1 -1 0 (14, 15, 16)

x42 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 (23, 30, 37)

x45 0 -1 0 0 0 0 -1 0 0 0 0 -1 0 0 1 0 1 1 1 (49, 50, 51)

(b.) Penghapusan variabel nonbasis.

Jika tabel optimal pada Tabel 3 dihapus variabel nonbasis x₁₁, maka tidak mempengaruhi solusi optimal.

(iii) Penambahan kendala baru.

Misal masalah transportasi pada persamaan (10), (11), dan pertidaksamaan (12) mengalami kondisi baru pada proses produksi, sehingga terjadi penambahan kendala baru yaitu

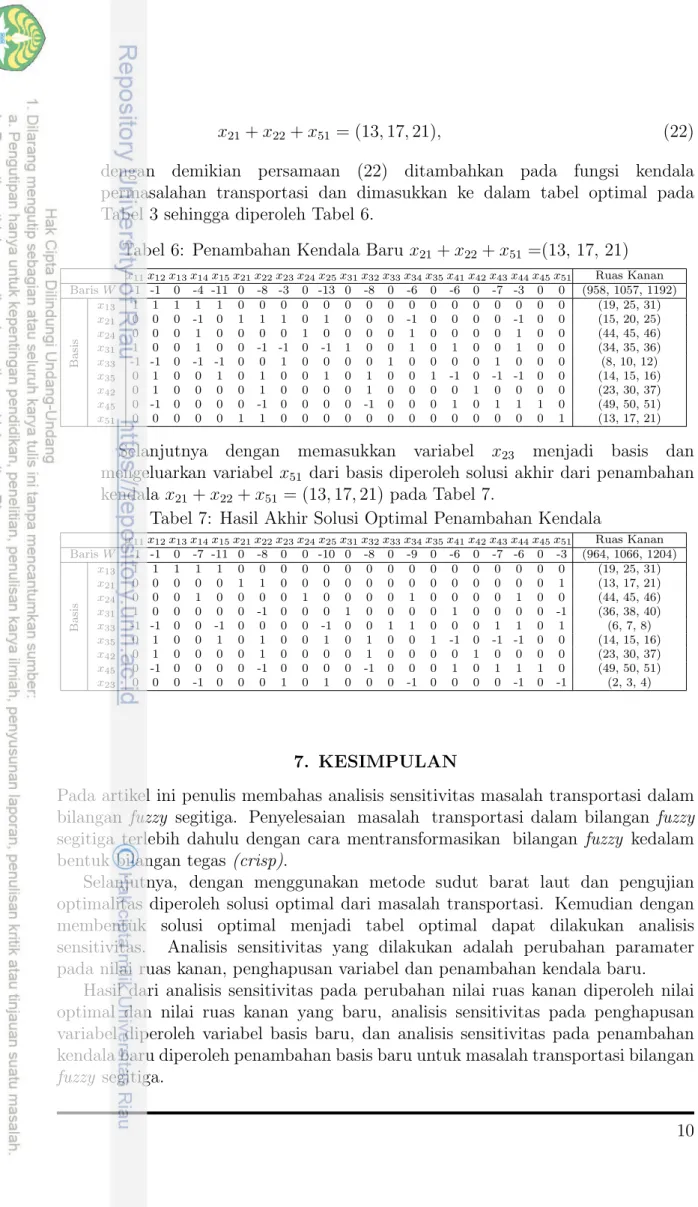
x₂₁+ x₂₂≤ (13, 17, 21). (20)

Selanjutnya dilakukan uji terhadap kendala baru, yaitu dengan mensubstitusikan koefisien variabel basis fungsi obyektif terhadap pertidaksamaan (20) sehingga diperoleh

(15, 20, 25) + 0≤ (13, 17, 21), (21)

karena pertidaksamaan (21) tidak terpenuhi, maka kendala baru tersebut berpengaruh pada nilai optimal.

Kemudian pertidaksamaan (20) diubah menjadi bentuk standar yaitu