Optimasi Program Linier Pecahan Dengan Fungsi Tujuan Berkoefisien Interval

(1)

OPTIMASI PROGRAM LINIER PECAHAN DENGAN FUNGSI

TUJUAN BERKOEFISIEN INTERVAL

SKRIPSI

M KHAHFI ZUHANDA

090803064

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

OPTIMASI PROGRAM LINIER PECAHAN DENGAN FUNGSI TUJUAN BERKOEFISIEN INTERVAL

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

M KHAHFI ZUHANDA 090803064

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : OPTIMASI PROGRAM LINIER PECAHAN

DENGAN FUNGSI TUJUAN BERKOEFISIEN INTERVAL

Kategori : SKRIPSI

Nama : M KHAHFI ZUHANDA

Nomor Induk Mahasiswa : 090803064

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, September 2013

Komisi Pembimbing :

Pembimbing 2, Pembimbing 1,

Dr. Esther Sorta M Nababan, M.Sc Drs.Sawaluddin,M.I.T

NIP. 19610318 198711 2 001 NIP. 19591231 199802 1 001

Diketahui/ Disetujui oleh:

Departemen Matematika FMIPA USU Ketua,

(4)

PERNYATAAN

OPTIMASI PROGRAM LINIER PECAHAN DENGAN FUNGSI TUJUAN BERKOEFISIEN INTERVAL

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, September 2013

(5)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT yang senantiasa

memberikan segala rahmat dan hidayah-Nya, dan yang telah memberi kekuatan

akal dan fikiran sehingga penulis dapat menyelesaikan skripsi ini dalam waktu

yang ditetapkan.

Ucapan terima kasih penulis sampaikan kepada Bapak Drs. Sawaluddin,

M.I.T selaku pembimbing I dan Ibu Dr. Esther Sorta M Nababan, M.Sc selaku

pembimbing II yang telah menyediakan waktunya untuk membimbing dan

memberikan pengarahan kepada saya sehingga penyusunan skripsi ini dapat

diselesaikan.

Penulis juga mengucapkan terima kasih kepada Bapak Drs. Agus Salim

Harahap, M.Si dan Bapak Drs. Suwarno Ariswoyo, M.Si selaku dosen penguji

saya, Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si selaku Ketua

dan Sekretaris Departemen Matematika FMIPA USU Medan, Dekan dan

Pembantu Dekan FMIPA USU, seluruh staff pengajar Matematika di FMIPA

USU, beserta pegawai Administrasi.

Penulis juga mengucapkan terima kasih kepada orang tua tercinta Zunaidi,

SE yang telah memberikan dukungan, doa, dan semua bantuan yang diperlukan

penulis, Adik-adik penulis yang penulis sayangi Novi Dara Utami, Arbie Saldi

Zusri dan Pri Zuri Hartadi yang selalu menghibur di saat penulis senang ataupun

susah. Akhirnya penulis juga mengucapkan terima kasih kepada seluruh

teman-teman dekat penulis, khususnya kepada Hani Syahida Harahap, Johannes

Antonius Manurung, Rahmat Ramadhan Siregar, Andri Sinaga, Muhammad

Syukran, Nur Zakiya Harahap, Aswin Bahar Lubis dan teman-teman yang tidak

dapat saya sebutkan satu persatu yang telah memberikan dorongan semangat serta

(6)

ABSTRAK

Beberapa tahun belakangan, telah ditemukan beberapa cara untuk menyelesaikan kasus program linier. Salah satunya adalah progam linier pecahan (PLP). Pada beberapa masalah aplikasi program linier (PL), koefisien pada model seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam menyelesaikan masalah ini adalah dengan menggunakan pendekatan interval, dimana koefisien tak tentu tersebut diubah menjadi bentuk interval. Program linier pecahan dengan fungsi tujuan berkoefisien interval dapat diselesaikan dengan transformasi yang diperkenalkan oleh Charnes dan Cooper. Metode ini menggunakan kombinasi titik awal dan akhir dari interval yang digunakan sebagai pengganti koefisien selang interval. Hasil kajian ini menunjukkan bahwa persoalan optimasi program linier pecahan dengan koefisien interval dapat ditransformasikan ke dalam bentuk linier dengan menggunakan transformasi Charnes dan Cooper.

(7)

ABSTRACT

In the recent years, was found some approaches to solve linear programming problem. One of them is linear fractional programming problem (LFP). On some applications of linear programming problems (LP), the coefficient on the model often can not be determined precisely. One method to solve this LP problem is to use an interval approach, where uncertain coefficients are transformed into the form of intervals. The linear fractional programming problem with interval coefficients in objective function is solved by the variable transformation. The transformation was introduced by Charnes and Cooper. In this method a combination of the first and the last points of the intervals are used in place of the intervals. This research showed that optimization linear fractional programming with interval coefficient in objective function can be transformed with Charnes

and Chooper’s transformation.

(8)

DAFTAR ISI

Daftar Tabel viii

Datar Lampiran ix

Bab 1 Pendahuluan

1.1 Latar Belakang 1

1.2 Rumusan Masalah 3

1.3 Batasan Masalah 3

1.4 Tinjauan Pustaka 3

1.5 Tujuan Penelitian 5

1.6 Kontribusi Penelitian 5

1.7 Metodologi Penelitian 6

Bab 2 Landasan Teori

2.1 Interval 7

2.2 Linear Programming Interval Coefficient (LPIC) 8

2.3 Program Linier Pecahan (PLP) 9

2.4 Program Linier 10

Bab 3 Pembahasan

3.1 Hubungan Program Linier Pecahan dengan Program Linier 20

3.2 Transformasi Charnes-Cooper 21

3.3 Program Linier Pecahan Dengan Fungsi Tujuan Berkoefisien

Interval 22

Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan 37

4.2 Saran 37

Daftar Pustaka 48

(9)

DAFTAR TABEL

Halaman

Tabel 2.1 Bentuk Tabel Simpleks 15

(10)

DAFTAR LAMPIRAN

Halaman Lampiran 1. Tampilan Data Input dan Output QM for Windows untuk

Penyelesaian Maksimasi Program Linier Kasus 1 39

Lampiran 2. Tampilan Data Input dan Output QM for Windows untuk

(11)

ABSTRAK

Beberapa tahun belakangan, telah ditemukan beberapa cara untuk menyelesaikan kasus program linier. Salah satunya adalah progam linier pecahan (PLP). Pada beberapa masalah aplikasi program linier (PL), koefisien pada model seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam menyelesaikan masalah ini adalah dengan menggunakan pendekatan interval, dimana koefisien tak tentu tersebut diubah menjadi bentuk interval. Program linier pecahan dengan fungsi tujuan berkoefisien interval dapat diselesaikan dengan transformasi yang diperkenalkan oleh Charnes dan Cooper. Metode ini menggunakan kombinasi titik awal dan akhir dari interval yang digunakan sebagai pengganti koefisien selang interval. Hasil kajian ini menunjukkan bahwa persoalan optimasi program linier pecahan dengan koefisien interval dapat ditransformasikan ke dalam bentuk linier dengan menggunakan transformasi Charnes dan Cooper.

(12)

ABSTRACT

In the recent years, was found some approaches to solve linear programming problem. One of them is linear fractional programming problem (LFP). On some applications of linear programming problems (LP), the coefficient on the model often can not be determined precisely. One method to solve this LP problem is to use an interval approach, where uncertain coefficients are transformed into the form of intervals. The linear fractional programming problem with interval coefficients in objective function is solved by the variable transformation. The transformation was introduced by Charnes and Cooper. In this method a combination of the first and the last points of the intervals are used in place of the intervals. This research showed that optimization linear fractional programming with interval coefficient in objective function can be transformed with Charnes

and Chooper’s transformation.

(13)

BAB 1

PENDAHULUAN

1.1Latar Belakang

Dalam beberapa tahun terakhir, para pakar matematika telah banyak

mencoba melakukan pendekatan untuk memecahkan permasalahan Program

Linier Pecahan (PLP). Dalam tulisan ini akan menjelaskan Program Linier

Pecahan merupakan salah satu kasus khusus dari pemrograman non linier, yang

umumnya digunakan untuk masalah-masalah kehidupan nyata dengan pemodelan

satu atau lebih tujuan seperti keuntungan /biaya, aktual pendapatan / standarisasi,

input / karyawan, dan lain-lain. Dan itu diterapkan untuk berbagai disiplin ilmu

seperti sebagai teknik, bisnis, keuangan, ekonomi, dan lain-lain.

Pemrograman Linier Pecahan (PLP) adalah kelas khusus dari

pemrograman non linier yang dapat ditransformasikan menjadi masalah

pemrograman linier dengan metode Charnes dan Cooper. (Stancu-Minansian,

1997)

Program Linear adalah suatu cara untuk menyelesaikan persoalan

pengalokasian sumber-sumber yang terbatas di antara beberapa aktivitas yang

bersaing dengan cara terbaik yang mungkin dilakukan. Misalnya pengalokasian

fasilitas produksi, sumber daya nasional untuk kebutuhan domestik, penjadwalan

(14)

Program Linier memiliki beberapa sifat yaitu proporsionalitas, addivitas,

divisibilitas dan kepastian. Sifat linearitas suatu kasus dapat ditentukan dengan

menggunakan beberapa cara. Secara statistik, kita dapat memeriksa kelinearan

menggunakan grafik (diagram pencar) ataupun menggunakan uji hipotesa. Secara

teknis, linearitas ditunjukkan oleh adanya sifat proporsionalitas, additivitas,

divisibilitas dan kepastian fungsi tujuan dan pembatas.

Pada beberapa masalah aplikasi pemrograman linier (PL), koefisien pada

model seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam

menyelesaikan masalah PL ini adalah dengan menggunakan pendekatan interval,

dimana koefisien tak tentu tersebut diubah menjadi bentuk interval. Bentuk PL ini

dinamakan Linear Programming with Interval Coefficient (LPIC). Koefisien

berbentuk interval menandakan perluasan toleransi (atau daerah) dimana

parameter konstanta bisa diterima dan memenuhi model LPIC.

Pada tulisan ini akan dibahas salah satu metode dalam menyelesaikan

LPIC yang telah dikembangkan oleh JW Chinneck dan K Ramadan (2000).

Masalah LPIC memiliki fungsi objektif dan kendala persamaan atau

pertidaksamaan yang berkoefisien interval. Solusi optimum dibagi menjadi dua,

yaitu best optimum dan worst optimum. Dalam kasus minimisasi, best optimum

adalah solusi yang memiliki nilai fungsi objektif terkecil, sedangkan worst

optimum adalah solusi yang memiliki nilai fungsi objektif terbesar. Solusi

optimum pada LPIC didapatkan dengan mencari versi khusus dari fungsi objektif

dan kendala yang mengoptimumkan model, yaitu dipilih suatu nilai spesifik (nilai

ekstrim) pada koefisien interval yang membuat model LPIC tersebut optimum,

sehingga pemecahan masalah LPIC diperoleh dengan menyelesaikan PL yang

mengoptimumkan model LPIC. (Farida, 2011)

Berdasarkan uraian ini, peneliti tertarik untuk memilih judul penelitian

(15)

1.2Rumusan Masalah

Rumusan masalah dalam penelitian ini adalah :

Maksimumkan Z = [ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1,]

Kendala

x_j  0 ( j = 1,2,…,m)

1. Menentukan Optimasi Program Linier Pecahan dengan koefisen fungsi

tujuan memiliki interval (interval).

2. Mentransformasikan permasalahan menjadi bentuk linier.

1.3Batasan Masalah

Batasan dalam penelitian ini adalah :

1. Mentransformasikan Optimasi Program Linier Pecahan.

2. Koefisien pada program linier pecahan berbentuk interval.

1.4Tinjauan Pustaka

Sebagai sumber pendukung teori dalam penulisan ini, maka penulis

mengggunakan beberapa pustaka antara lain :

Program Linier merupakan suatu teknik perencanaan yang menggunakan

model matematika dengan tujuan menemukan beberapa kombinasi alternatif dari

pemecahan masalah yang kemudian dipilih mana yang terbaik untuk menyusun

strategi dan langkah-langkah kebijakan tentang alokasi sumber daya yang ada

agar mencapai tujuan atau sasaran yang diinginkan secara optimal dengan

melibatkan variabel-variabel linear. Dalam model program linear dikenal dua

macam fungsi, yaitu fungsi objektif (objective function) dan fungsi kendala

(16)

Winston, W.L, 2003. Operations Research: Applications and Algorithms,

menyatakan bahwa bentuk umum model program linier adalah sebagai

berikut:

a = Koefisien teknologi dari variabel keputusan

ke-j pada kendala ke-i.

i

b = Koefisien ruas kanan pada kendala ke-i

Program Linier Pecahan (PLP) secara luas dikembangkan oleh seorang

matematisi Hungaria B.Martos dan asosiasinya di tahun 1960an dengan

memusatkan pada masalah optimisasi. Beberapa metode penyelesaian masalah ini

Charnes dan Cooper (1962) telah menyarankan metode mereka dengan

bergantung pada transformasi ini (PLP) kepada ekivalen program linier. Bentuk

(17)

Maksimumkan Z = �_� +

+

Kendala

0  x

dimana ∈ � , x merupakan vektor dari variabel keputusan, , ∈ �

dan b adalah koefisien vektor yang diketahui, ∈ � adalah matriks yang

diketahui dan , ∈ � adalah konstanta. Kendala permasalahan dibatasi wilayah

feasible | � + > 0 , yaitu wilayah yang penyebut adalah positif atau

penyebut dari fungsi tujuan harus negatif di daerah feasible secara keseluruhan.

(Charnes & Cooper ,1962)

Pada beberapa masalah aplikasi pemrograman linier (PL), koefisien pada

model seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam

1.5Tujuan Penelitian

Secara umum, tujuan penelitian ini adalah untuk mengkaji masalah optimasi

Program Linier Pecahan (PLP) dengan fungsi tujuan berkoefisien interval.

1.6Kontribusi Penelitian

Hasil kajian ini diharapkan dapat menambah referensi bagi pembaca dan

pengambil keputusan dalam menyelesaikan optimasi Program Linier Pecahan

(18)

1.7Metodologi Penelitian

Penelitian ini bersifat studi literatur yang disusun berdasarkan rujukan pustaka

dengan langkah-langkah sebagai berikut:

Langkah-1: Melakukan studi keperpustakaan dengan mengumpulkan bahan

yang merujuk pada tulisan ini.

Langkah-2: Menjelaskan prosedur untuk mereduksi program linier pecahan

dengan fungsi tujuan berkoefisien interval.

Langkah-3: Menyelesaikan contoh numerik permasalahan dalam program

(19)

BAB 2

LANDASAN TEORI

2.1 Interval

Interval adalah himpunan bilangan real yang berada di antara dua bilangan

tertentu sebagai batas

Sifat-sifat Interval :

Jika = , dan = , dengan 0 B, maka:

- + = + , + (Penjumlahan)

- − = − , − (Pengurangan)

- ∗ = min , , , , { , , , } (Perkalian)

- / = , ∗[1,1] (Pembagian)

Jika 0∈ , maka A / B tidak terdefinisi.

Jika A, B, dan C∈ �( ) maka:

- + = + , ∗ = ∗ (Komutatif)

- + + = + + , ∗ ∗ = ∗( ∗ ) (Assosiatif)

- 0,0 1,1 , adalah elemen netral pada sifat penjumlahan dan pembagian

- Interval bilangan Riil tidak memiliki pembagi 0

- Bilangan Riil = , , ≠ tidak memiliki invers pada sifat

penjumlahan dan perkalian, namun,0∈ − 1∈( / )\

- ∗ +  ∗ + ∗ (Subdistributif)

- + = + , ∈ �

(20)

2.2 Linear Programming Interval Coefficient (LPIC)

Pada beberapa masalah aplikasi pemrograman linier (PL), koefisien pada model

seringkali tidak bisa ditentukan secara tepat. Salah satu metode dalam

Salah satu metode dalam menyelesaikan LPIC yang telah dikembangkan

oleh JW Chinneck dan K Ramadan (2000). Masalah LPIC memiliki fungsi

objektif dan kendala persamaan atau pertidaksamaan yang berkoefisien interval.

Solusi optimum dibagi menjadi dua, yaitu best optimum dan worst optimum.

Dalam kasus minimisasi, best optimum adalah solusi yang memiliki nilai fungsi

objektif terkecil, sedangkan worst optimum adalah solusi yang memiliki nilai

fungsi objektif terbesar. Solusi optimum pada LPIC didapatkan dengan mencari

versi khusus dari fungsi objektif dan kendala yang mengoptimumkan model, yaitu

dipilih suatu nilai spesifik (nilai ekstrim) pada koefisien interval yang membuat

model LPIC tersebut optimum, sehingga pemecahan masalah LPIC diperoleh

(21)

Bentuk linier dari persamaan LPIC adalah :

Maka Best Optimum dan Worst Optimum

(22)

2.3 Program Linier Pecahan (PLP)

Bidang dari Program Linier Pecahan (PLP) secara luas dikembangkan oleh

seorang matematisi Hungaria B.Martos dan asosiasinya di tahun 1960an dengan

memusatkan pada masalah optimisasi. Beberapa metode penyelesaian masalah ini

Charnes dan Cooper (1962) telah menyarankan metode mereka dengan

bergantung pada transformasi ini (PLP) kepada ekivalen program linier. Bentuk

umum dari masalah PLP dapat dibuat sbb :

Maksimumkan Z = �_� +

diketahui dan , ∈ � adalah konstanta. Kendala permasalahan dibatasi wilayah

feasible | � + > 0 , yaitu wilayah yang penyebut adalah positif. Atau,

penyebut dari fungsi tujuan harus negatif di daerah feasible secara keseluruhan.

(Charnes & Cooper ,1962)

2.3 Program linier

Optimasi.

Optimasi adalah sarana untuk mengekspresikan model matematika yang

bertujuan memecahkan masalah dengan cara terbaik. Untuk tujuan bisnis, hal ini

berarti memaksimalkan keuntungan dan efisiensi serta meminimalkan kerugian,

biaya atau resiko. Hal ini juga berarti merancang sesuatu untuk meminimalisasi

bahan baku atau memaksimalisasi keuntungan. Adapun keinginan untuk

memecahkan masalah dengan model optimasi secara umum sudah digunakan pada

(23)

Program Linier.

Program linier merupakan model umum yang dapat digunakan dalam

pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal.

Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau

menentukan tingkat setiap kegiatan yang akan dilakukannya, di mana

masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas.

Secara sederhana, dapat diambil contoh bagian produksi suatu perusahaan yang

dihadapkan pada masalah penentuan tingkat produksi masing-masing jenis produk

dengan memperhatikan batasan faktor-faktor produksi: mesin, tenaga kerja, bahan

mentah, dan sebagainya untuk memperoleh tingkat keuntungan maksimal atau

biaya yang minimal.

Pada masa modern sekarang, program linier masih menjadi pilihan dalam

upaya untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal.

Dalam memecahkan masalah di atas, Program linier menggunakan model

matematis. Sebutan “linier” berarti bahwa semua fungsi matematis yang disajikan

dalam model ini haruslah fungsi-fungsi linier. Dalam Program linier dikenal dua

macam fungsi, yaitu fungsi tujuan (objective function) dan fungsi-fungsi batasan

(constraint function). Fungsi tujuan adalah fungsi yang menggambarkan

tujuan/sasaran di dalam permasalahan program linier yang berkaitan dengan

pengaturan secara optimal sumber daya-sumber daya, untuk memperoleh

keuntungan maksimal atau biaya minimal. Pada umumnya nilai yang akan

dioptimalkan dinyatakan sebagai Z. Fungsi batasan merupakan bentuk penyajian

secara matematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan

secara optimal ke berbagai kegiatan.

Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahan

yang dihadapi ke dalam model program linier, maka ada lima syarat yang harus

(24)

1. Tujuan

Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin

dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang

disebut fungsi tujuan.

2. Alternatif perbandingan

Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan;

misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu

terlambat dan biaya terendah.

3. Sumber daya

Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas

4. Perumusan kuantitatif

Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif

dalam apa yang disebut model matematika.

5. Keterkaitan peubah

Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus

memiliki hubungan fungsional atau hubungan keterkaitan.

Model Dasar

Model dasar program linier dapat dirumuskan sebagai berikut:

Carilah nilai-nilai x1,x2, ,xj yang dapat menghasilkan berbagai

(25)

)

Dengan syarat bahwa fungsi tujuan tersebut memenuhi kendala-kendala

atau syarat-syarat ikatan sebagai berikut:

1

c Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah

pengambilan keputusan dalam fungsi tujuan.



j

x Peubah pengambilan keputusan atau kegiatan (yang ingin dicari;

yang tidak diketahui).



ij

a Koefisien teknologi peubah pengambilan keputusan (kegiatan yang

bersangkutan) dalam kendala ke-i.



(26)

Asumsi – asumsi program linier

1. Linieritas

Asumsi ini menginginkan agar perbandingan antara input yang satu

dengan input lainnya, atau untuk suatu input dengan output besarnya tetap dan

terlepas (tidak tergantung) pada tingkat produksi.

2. Proposionalitas

Asumsi ini menyatakan bahwa jika peubah pengambilan keputusan, xj

berubah maka dampak perubahannya akan menyebar dalm proposi yang sama

terhadap fungsi tujuan, cjxj, dan juga pada kendalanya, aijxj.

3. Aditivitas

Asumsi ini menyatakan bahwa nilai parameter suatu kriteria optimisasi

(koefisien peubah pengambilan keputusan dalam fungsi tujuan) merupakan

jumlah dari nilai individu-individu c j dalam model PL tersebut.

4. Divisibilitas

Asumsi ini menyatakan bahwa peubah-peubah pengambilan keputusan

j

X , jika diperlukan dapat dibagi ke dalam pecahan-pecahan.

5. Deterministik

Asumsi ini menghendaki agar semua parameter dalam PL (yaitu nilai –

nilai cj, aij , dan bi) tetap dan dikehendaki atau ditentukan secara pasti.

Metode Simpleks

Apabila suatu masalah Linier Programming hanya mengandung dua kegiatan

(variabel-variabel keputusan) saja, maka dapat diselesaikan dengan metode grafik.

(27)

lagi, sehingga diperlukan metode simpleks. Metode ini lazim dipakai untuk

menentukan kombinasi dari tiga variabel atau lebih.

Masalah Program linier yang melibatkan banyak variabel keputusan dapat

dengan cepat dipecahkan dengan bantuan komputer. Bila variabel keputusan yang

dikandung tidak terlalu banyak, masalah tersebut dapat diselesaikan dengan suatu

algoritma yang biasanya sering disebut metode tabel simpleks. Disebut demikian

karena kombinasi variabel keputusan yang optimal dicari dengan menggunakan

tabel-tabel.

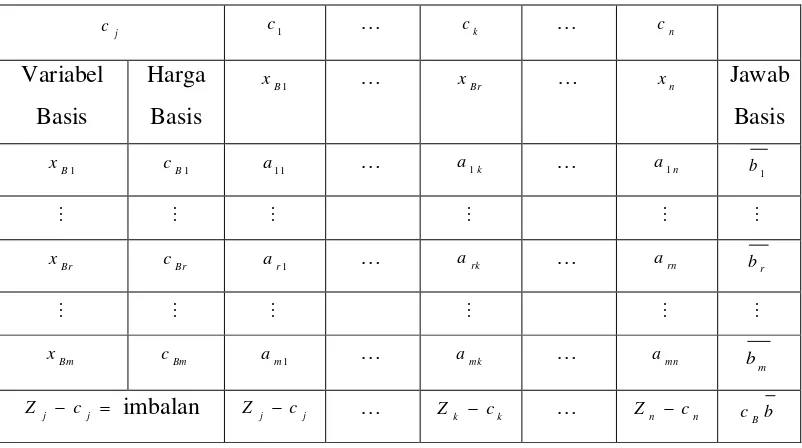
Tabel 2.1 Bentuk tabel simpleks

j

Sebelum menyelesaikan suatu tabel simpleks terlebih dahulu menginisialisasikan

dan merumuskan suatu persoalan keputusan kedalam model matematik persamaan

linier, caranya sebagai berikut:

1. Konversikan semua ketidaksamaan menjadi persamaan.

Agar persamaan garis batasan memenuhi persyaratan penyelesaian pada daerah

kelayakan (feasible) maka model program linier diubah menjadi suatu model yang

sama dengan menambahkan variabel slack, surplus dan variabel buatan (artificial

(28)

variabel) pada tiap batasan (constraint) serta memberi harga nol kepada setiap

koefisien C nya. Batasan dapat di modifikasi sebagai berikut:

a. Untuk batasan bernotasi   dapat dimodifikasikan kepada bentuk persamaan dengan menambahkan variabel slack ke dalam nya.

b. Untuk batasan bernotasi  atau   diselesaikan dengan menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel

buatan ini akan merusak sistem batasan, hal ini dapat diatasi dengan

membuat suatu bilangan besar M sebagai harga dari variabel buatan

tersebut dalam fungsi tujuan. Jika persoalan maksimal maka dibuat –M

sebagai harga, dan jika persoalan minimal dibuat +M sebagai harga dari

variabel buatan. Cara pendekatan ini dikenal dengan metode M besar

(Big M method).

Penambahan variabel slack dan variabel buatan (artificial variabel) pada tiap

batasan (constrain) untuk persoalan maksimal dapat dirumuskan sebagai berikut:

(29)

n j

x_j  0,  1, , ; x_i  b_i,i 1,,m ; B_i b_i,i  m₁ 1,,m

2. Menyusun persamaan – persamaan di dalam tabel awal simpleks.

Tabel 2.2 Bentuk tabel awal simpleks sebelum pivoting

j

simpleks adalah sebagai berikut:

Langkah 1 : Mengecek nilai optimal imbalan.

Untuk persoalan maksimal : zk  ck = minimal {zj  cj : j R}.

Jika zk  ck  0 maka selesai, berarti jawab atau solusi sudah optimal.

Untuk persoalan minimal : zk  ck = maksimal {zj  cj : j R}.

Jika z_k  c_k  0 maka selesai, berarti jawab atau solusi sudah optimal.

(30)

j

a Koefisien dari semua variabel dalam sistem batasan.



Bi

c Harga dari variabel.

Langkah 2 : Menentukan variabel yang akan masuk dalam basis.

Untuk persoalan maksimal jika terdapat beberapa z_j  c_j  0

maka kolom yang menjadi kolom pivot adalah kolom dengan zj  cj terkecil, dan

variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk

kedalam basis. Untuk persoalan minimal jika terdapat beberapa z_j  c_j  0 maka

kolom yang menjadi kolom pivot adalah kolom dengan zj  cj terbesar, dan

variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke

dalam basis.

Langkah 3 : Menentukan variabel yang akan keluar dari basis.

Menetapkan variabel yang keluar dari basis yaitu :

pivot yang demikian adalah variabel yang keluar dari basis.

Langkah 4 : Menyusun tabel simpleks baru.

Untuk menyusun tabel simpleks yang baru, maka harus mencari

koefisien elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot

dapat dicari dengan menghubungkan kolom pivot dengan baris pivot sedemikian

(31)

elemen pivot, Koefisien – koefisien baris pivot baru dapat dicari dengan

menggunakan rumus sebagai berikut :

rk rj

a a

(2.9)

Untuk menghitung nilai baris baru lainnya dilakukan dengan menggunakan rumus

sebagai berikut :

Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru.

Jika imbalan sudah optimal maka tafsirkan hasil penyelesaian, jika

belum optimal maka kembali kepada langkah 2.

Tabel 2.3 Bentuk tabel simpleks sesudah pivoting

(32)

BAB 3

PEMBAHASAN

3.1 Hubungan Program Linier Pecahan dengan Program Linier

Program Linier Pecahan (PLP) adalah generalisasi dari Program Linier

(PL). Fungsi tujuan dari program linier berbentuk fungsi linier, sedangkan fungsi

tujuan dalam program linier pecahan merupakan rasio dari dua fungsi linier.

Program linier pecahan merupakan menjadi kelas khusus dari program linier.

Dikatakan kelas khusus karena program linier pecahan dapat ditransformasikan

kedalam bentuk linier dimana fungsi penyebut pada fungsi tujuan program linier

pecahan bernilai 1 dan persamaan penyebut dalam fungsi tujuan dimasukkan

kedalam persamaan fungsi kendala.

Program linier dan program linier pecahan merupakan masalah optimasi

yang menggunakan persamaan dan pertidaksamaan linier dan masing-masing

persoalannya memiliki daerah feasible. Pada umumnya, program linier

menghitung kebijakan untuk mencari laba maksimum atau biaya minimum.

Sedangkan pada program linier pecahan digunakan untuk menghitung rasio

efisiensi optimal seperti keuntungan/biaya. Program linier pecahan bertujuan

mencari rasio dari 2 buah fungsi tujuan dalam program linier untuk mendapatkan

hasil yang optimal. Sebagai contoh dalam konteks program linier adalah

memaksimalkan keuntungan pada fungsi tujuan yaitu, keuntungan = pendapatan

– biaya. Apabila pada program linier keuntungan maksimum yang didapat adalah Rp 100.000 (= Rp 1.100.000 pendapatan – Rp. 1000.000 biaya). Dengan

demikian, pada program linier memiliki efisiensi sebesar Rp 100.000 / Rp

1000.000 = 0,1. Apabila menggunakan PLP mungkin bisa meningkatkan efisiensi

sebesar Rp 10.000 / Rp. 50.000 = 0,2 dengan keuntungan hanya Rp 10.000, yang

(33)

3.2 Transformasi Charnes-Cooper

Program Linier Pecahan merupakan kelas khusus dari progam non linier. Charnes

dan Cooper memperkenalkan transformasinya untuk mengubah bentuk non linier

program linier pecahan kebentuk program linier. Dimana fungsi penyebutnya

adalah bernilai 1. Setelah di transformasikan maka fungsi penyebutnya

dimasukkan kedalam fungsi kendala.

Bentuk umum masalah program linier pecahan adalah sebagai berikut:

Maksimumkan = a1 1+a2 2+⋯+ak +ak +1

c1 1+c2 2+⋯+ck +ck +1

Kendala _{1 1}+⋯+ …. (1)

1 0,…, 0

dimana adalah matriks 1 x m, untuki=1,…,k dan b adalah m-dimensi konstanta

vektor kolom.

Maka itu, diasumsikan bahwa:

1 1+ 2 2+⋯+ + +1> 0 untuk semua � = ( 1,…, ) ∈ �, Dimana X

hasil daerah feasible dari persamaan (1).

Untuk menyelesaikan persamaan (1). Transformasi Charnes-Chooper menetapkan

untuk:

= 1

1 1+ 2 2+⋯+ + +1

1 1 + 2 2 +⋯+ + +1 = 1

(34)

Sehingga, persamaan (1) ditransformasikan kedalam permasalahan program linier:

Maksimumkan = _{1 1} + _{2 2} +⋯+ + ₊₁

Kendala _{1 1} +⋯+

1 1 + 2 2 +⋯+ + +1 = 1

1 0,…, 0, 0

…. (2)

Dengan diasumsikan variabel = 1

1 1+ 2 2+⋯+ + +1 =

untuk i=1,…,k,

persamaan (2) dapat di reduksi menjadi:

Maksimumkan = 1 1 + 2 2 +⋯+ + +1

Kendala _{1 1}+⋯+

1 1+ 2 2 +⋯+ + +1 = 1

1 0,…, 0, 0…. (3)

(Borza, 2012)

3.3 Program Linier Pecahan Dengan Fungsi Tujuan Berkoefisien Interval

Pada beberapa masalah aplikasi program linier, koefisien pada model

seringkali tidak bisa ditentukan secara tepat. Jadi dalam kasus seperti itu, jauh

lebih baik untuk memilih koefisien sebagai interval bukan merupakan angka tetap.

Sebagai contoh salah satu dari situasi ini terjadi ketika koefisien bilangan fuzzy.

Dalam kasus ini jika pengambil keputusan menetapkan α-tingkat kepuasan, maka bilangan fuzzy diubah menjadi interval. Oleh karena itu, dalam berbagai situasi

seperti itu untuk menyelesaikan permasalahan dalam bentuk pemrograman

matematika dengan koefisien interval. Salah satu metode dalam menyelesaikan

masalah PL ini adalah dengan menggunakan pendekatan interval, dimana

(35)

dinamakan Linier Programming with Interval Coefficient (LPIC). Koefisien

berbentuk interval menandakan perluasan toleransi (atau daerah) dimana

parameter konstanta bisa diterima dan memenuhi model LPIC. (Farida, 2011)

Sehingga permasalahan optimasi program linier pecahan dengan fungsi

tujuan berkoefisien interval merupakan kombinasi persoalan program linier

pecahan dengan program linier dengan koefisen interval. Sehingga persamaan

persoalan tersebut dapat dituliskan menjadi:

Maksimumkan Z = [ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

(k= 1,2,3,…m ) dan ( j= 1,2,3,…n)

Kendala _{1 1}+⋯+

1 0,…, 0

… (4)

Untuk menyelesaikan permasalahan ini diasumsikan bahwa [ 1, 1] 1+

[ 2, 2] 2+⋯+ [ , ] + [ +1, +1] > 0 untuk semua � = 1,…, ∈

�, dimana X adalah daerah feasible kompak,

Untuk menyelesaikan persamaan (4), diasumsikan variabel

t = 1

[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

sehingga diperoleh:

Maksimumkan = [ 1, 1] 1 + [ 2, 2] 2 +⋯+ [ , ] + [ +1, +1]

Kendala _{1 1} +⋯+ t

[c_1,d₁] ₁ + [c₂, d₂] ₂ +⋯+ [c_k,d_k] + [c_k+1,d_k+1] = 1

1 0,…, 0, 0

(36)

Dengan diasumsikan variabel = 1

[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]=

untuk i=1,…,k, persamaan (5) dapat di reduksi menjadi:

Maksimumkan = [ _{1, 1}] ₁+ [ _{2, 2}] ₂+⋯+ [ _, ] +

[ +1, +1]

Kendala _{1 1}+⋯+ t

[ _{1, 1}] ₁+ [ ₂, ₂] ₂+. . . +[ _, ] + [ _+1, ₊₁] = 1

₁ 0,…, 0, 0

… (6)

Kombinasi linier dari masing-masing daerah interval mengikuti persamaan:

Maksimum = [ 1 1+ (1− 1) 1] 1+ [ 2 2 + (1− 2) 2] 2+⋯+

[ + (1− ₁) ] + [ ₊₁ ₊₁+ (1− ₊₁) ₊₁]

Kendala _{1 1}+⋯+ − 0

[ _{1 1}+ (1− ₁) ₁] ₁+ [ _{2 2}+ (1− ₂) ₂] ₂+⋯+ [ +

(1− ) ] + [ +1 +1+ (1− +1) +1] = 1

1 0,…, 0, 0, 0 1 ,… , 0 1, untuk

i=1,…,k+1

…(7)

Dari persamaan (7). Pada fungsi kendala dapat di reduksi menjadi:

[ _{1 1}+ (1− ₁) ₁] ₁+⋯+ [ + (1− ) ] + [ ₊₁ ₊₁ + (1 − +1) +1] = 1

[ 1 1 1 + 1 1− 1 1 1+⋯+ 1+ − + +1 +1

(37)

[ 1 1 1 − 1 1 1]+…+ [ 1− ] + [ +1 +1 − +1 +1 ] +

1 1+⋯+ + +1 = 1

[ _{1 1} ₁− ₁ +⋯+ − + ₊₁ ₊₁ − ₊₁ ] + _{1 1}+⋯

+ + +1 = 1

… (8)

Karena,

0 untuk = 1,…, , 0, 0 β_i 1, − 0 untuk = 1,…, +

1

Oleh karena itu persamaan (8) dapat ditulis:

1 1 + [ 1 1 1− 1 +⋯+ − + +1 +1− +1 ]

1 + ₁ ₁− ₁ +⋯+ − + ₊₁− ₊₁ ]

…(9)

Dengan mengkombinasikan persamaan (8) dan (9) menghasilkan:

1 1 1 +⋯+ + +1

1 + 1 1− 1 +⋯+ − + +1− +1

… (10)

Yang selanjutnya direduksi menjadi:

1 1+⋯+ + +1 1

…(11)

Dan

1 1+⋯+ + +1 1

(38)

Oleh karena itu, dengan menggunakan persamaan (11) dan (12), persamaan (7)

ditransformasikan kedalam persamaan berikut:

Maksimumkan = [ 1 1+ (1− 1) 1] 1+ [ 2 2 + (1− 2) 2] 2+⋯+

[ + (1− 1) ] + [ +1 +1+ (1−

+1) +1]

Kendala c1 1+⋯+ ck + ck+1 1

d_{1 1}+⋯+ d_k + d_k+1 1

_{1 1}+⋯+ − 0

₁ 0,…, 0, 0, 0 αi 1 untuki=1,…,k+1

… (13)

Jika ( ₁,…, , ) menjadi titik daerah feasible dari persamaan (13),

dengan 0 1, − 0 untuk i=1,…,k+1, maka fungsi objektif dalam

persamaan (13) dapat ditulis sebagai:

1 1 1− 1 +⋯+ − + +1 +1− +1 ] +b1 1+⋯+

bk + bk+1 1 1− 1 +⋯+ − + +1− +1 ] +b1 1+

⋯+ bk + bk+1 = a1 1+⋯+ ak + ak+1

Persamaan diatas membuktikan bahwa ₁, 2,…, +1 merupakan batas

bawah dari koefisien interval pada fungsi tujuan. Maka worst optimum pada

persamaan fungsi tujuan adalah Z= a_{1 1}+⋯+ a_k + a_k+1

Sehingga bentuk transformasi optimasi program linier pecahan dengan fungsi

tujuan berkoefisien interval adalah

Maksimumkan Z= _{1 1} +⋯+ + ₊₁

Kendala _{1 1}+⋯+ + +1 1

1 1+⋯+ + +1 1

(39)

₁ 0,…, 0, 0, untukk=1,…,m

Sedangkan untuk memperoleh best optimum maka diambil batas atas dari

koefisien interval pada fungsi tujuan. Sehingga bentuk transformasi optimasi

program linier pecahan dengan fungsi tujuan berkoefisien interval adalah

Maksimumkan Z= _{1 1}+⋯+ + ₊₁

Kendala _{1 1}+⋯+ + +1 1

1 1+⋯+ + +1 1

1 1+⋯+ − 0

₁ 0,…, 0, 0, untukk=1,…,m

Berikut akan dibuktikan bahwa Program linier pecahan dengan fungsi tujuan

berkoefisien interval dibawah ini sama dengan metode Charnes-Cooper.

Maksimumkan Z=[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

[ 1, 1] 1+[ 2, 2] 2+⋯+[ , ] +[ +1, +1]

Kendala _{1 1}+⋯+

1 0,…, 0

(k= 1,2,…,m ) dan( j= 1,2,…,n)

Bukti:

Karena koefisien interval pada pembilang fungsi tujuan memiliki nilai yang sama.

Nilai koefisien fungsi tujuan pada best optimum dan worst optimum adalah sama.

Maka persoalan optimasi program linier pecahan dengan fungsi tujuan

berkoefisien interval diatas dapat ditransformasikan menjadi:

Maksimumkan Z= _{1 1} +⋯+ + +1

(40)

1 1+⋯+ + +1 1

1 1+⋯+ − 0

₁ 0,…, 0, 0, untukk=1,…m

Karena koefisien ruas kiri persamaan pertama dan kedua pada fungsi kendala

sama, Maka persamaan pertama dan kedua dikombinasikan, sehingga diperoleh

persamaan program liniernya menjadi:

Maksimumkan Z= _{1 1}+⋯+ + +1

Kendala _{1 1}+⋯+ + +1 = 1

_{1 1}+⋯+ − 0

₁ 0,…, 0, 0, untuk = 1,…,

Sehingga terbukti bahwa optimasi program linier pecahan dengan fungsi tujuan

berkoefisien interval sesuai dengan bentuk transformasi yang diperkenalkan oleh

Charnes dan Cooper. (Borza, 2012)

Kasus 1

PT Sayang Anak memproduksi dua jenis mainan yang terbuat dari kayu

yang berupa boneka dan kereta api. Boneka dijual dengan harga Rp 27.000 -

35.000/ lusin yang setiap lusinnya memerlukan biaya material sebesar Rp

10.000-14.000 serta biaya tenaga kerja sebesar Rp 10.000-14.000-16.000. Kereta api yang dijual

seharga Rp 21.000 -30.000/ lusin memerlukan biaya material sebesar Rp

9.000-12.000 dan biaya tenaga kerja Rp 10.000-13.000. Apabila perusahan dikenai pajak

pembuatan sekitar Rp 5000-8000. Untuk membuat boneka dan kereta api ini

diperlukan dua kelompok tenaga kerja, yaitu tukang kayu dan tukang poles. Setiap

lusin boneka memerlukan 2 jam pemolesan dan 1 jam pekerjaan kayu, sedangkan

setiap lusin kereta api memerlukan 1 jam pemolesan dan 1 jam pekerjaan kayu.

Meskipun pada setiap minggunya perusahaan ini dapat memenuhi seluruh

(41)

dan 80 jam untuk pekerjaan kayu. Dari pengamatan pasar selama ini dapat

dikatakan bahwa kebutuhan akan kereta api tidak terbatas, tetapi untuk boneka

tidak lebih dari 40 lusin yang terjual setiap minggunya. Bagaimanakah formulasi

dari persoalan di atas untuk mengetahui berapa lusin jenis mainan masing-masing

yang harus dibuat setiap minggu dengan mengoptimalkan efisiensi

keuntungan/pendapatan ?

(dikutip dari Bu’ulolo, 2005; dengan modifikasi)

Solusi:

Fungsi Tujuan

Fungsi tujuan merupakan fungsi dari variabel keputusan yang akan

dimaksimumkan (untuk pendapatan atau keuntungan) atau diminimumkan (untuk

ongkos). Pada persoalan ini akan dimaksimumkan (pendapatan/minggu) –

(ongkos material/minggu) – (ongkos tenaga kerja/minggu).

Pendapatan dan ongkos-ongkos ini dapat diekspresikan dengan menggunakan

variabel keputusan x1 dan x2 sebagai berikut :

Pendapatan /minggu = [27, 35] x1 + [21, 30] x2

Ongkos material/minggu = [10, 14] x1 + [9, 12] x2

Ongkos tenaga kerja/minggu = [14,16] x1 + [10,13] x2

Pajak = [5, 8]

Sehingga yang akan dimaksimumkan adalah :

Pendapatan = [27, 35] x1 + [21, 30] x2

Biaya = [10+14, 14+16] x1 + [9+10, 12+13] x2 + [5, 8]

=[24, 30] x1 + [19, 25] x2 + [5, 8]

Fungsi biaya dapat disimbolkan dengan g(x). Sehingga untuk menyatakan

(42)

g(x) = [24, 30] x1 + [19, 25] x2 + [5, 8]

Keuntungan = Pendapatan – Biaya

= [3, 5] x1 + [2, 5] x2 + [-8, -5]

dimana fungsi keuntungan disimbolkan dengan fungsi f(x). Sehingga untuk

menyatakan persamaan fungsi tujuan dari keuntungan dapat ditulis:

Untuk menyatakan nilai fungsi tujuan akan digunakan variabel Z dan dapat

ditulis:

Maksimumkan f(x) = Z = [3, 5] x1 + [2, 5] x2 + [-8, -5]

Sehingga persamaan fungsi tujuan diatas merupakan bentuk fungsi tujuan model

LPIC

Pembatas

Pembatas merupakan kendala yang dihadapi sehingga kita tidak bisa menentukan

harga-harga variabel keputusan secara sembarang. Pada persoalan di atas ada 3

pembatas yang dihadapi yaitu :

Pembatas 1 : Setiap minggu tidak lebih dari 100 jam waktu pemolesan yang

dapat digunakan.

Pembatas 2 : Setiap minggu tidak lebih dari 80 jam waktu pengerjaan kayu yang

dapat digunakan.

Pembatas 3 : Karena permintaan yang tebatas, maka tidak lebih dari 40 lusin

boneka yang dapat dibuat setiap minggu. Jumlah material yang dapat digunakan

diasumsikan tidak terbatas sehingga tidak ada pembatas untuk hal ini.

Dengan menggunakan simbol matematik dapat ditulis :

Pembatas 1 : 2x1 + x2 100

Pembatas 2 : x1 + x2 80

(43)

Pembatas Tanda

Pembatas tanda adalah yang menjelaskan apakah variabel keputusannya

diasumsikan hanya berharga nonnegatif atau variabel keputusan boleh berharga

positif, boleh juga negatif. Pada contoh diatas kedua variabel keputusan harus

berharga nonnegatif sehingga harus dinyatakan bahwa : x1 0 dan x2 0

Dengan demikian, formulasi lengkap dari persoalan PT Sayang Anak adalah :

Maksimumkan Z = [3, 5] x1 + [2, 5] x2 + [-8, -5]

Kendala

2 x1 + x2 100

x1 + x2 80

x1  40

x1 0 , x2 0

Setelah dicapai solusi optimum untuk x1= 20, dan x2= 60 dan Z= [172, 395].

Sehingga keuntungan maksimum yang diperoleh PT Sayang Anak diantara Rp

172.000 hingga Rp 395.000 dengan modal investasi sebesar 1.625.000 hingga Rp

2.108.000. Sehingga efisiensi dari keuntungan dan biaya PT Sayang Anak adalah

172.000/1.625.000= 0.1058 pada worst optimum. Sedangkan efisiensi pada best

optimum diperoleh sebesar 395.000/2.108.000= 0.1873.

Dengan menggunakan optimasi program linier pecahan dengan fungsi tujuan

berkoefisien interval dapat meningkatkan rasio dari efisiensi keuntungan dan

(44)

Maka bentuk persamaan optimasi program linier pecahan dengan fungsi tujuan

berkoefisien interval adalah

Maksimumkan Z= ( )

( ) =

[3, 5] 1 + [2,5] 2 + [−5, −8]

[24,30] 1 + [19,25] 2 +[5, 8]

Kendala

2 x1 + x2 100

x1 + x2 80

x1  40

x1 0 , x2 0

Transformasi optimasi program linier pecahan dengan fungsi tujuan berkoefisien

interval-nya menjadi:

Maksimumkan Z= [3, 5] 1 + [2, 5] 2 + [−8,−5]

Kendala 24 ₁+ 19 ₂+ 5 1

34 ₁+ 25 ₂+ 8 1

2 1+ 2−100  0

1+ 2−80  0

1 −40  0

(45)

Sehingga bentuk persamaan program linier untuk memperoleh efisiensi best

optimum-nya adalah

Maksimumkan Z= 5 ₁ + 5 ₂ -5t

Kendala 24 1+ 19 2+ 5 1

34 ₁+ 25 ₂+ 8 1

2 1+ 2−100  0

1+ 2−80  0

1−40  0

1 0, 2 0, 0

Dari perhitungan program linier diatas maka diperoleh nilai rasio efisiensi best

optimum dari keuntungan dan biaya dengan solusi ₁ = 0, 2 = 0.0525, =

0.0007 dan = 0.259. Efisiensinya meningkat dari 0.1873 menjadi 0.259.

Dengan memproduksi mainan kereta api sebanyak x2= 2=

0.0525

0.0007 = 75

biaya modal sebesar Rp 1.883.000 dan keuntungan sebesar Rp 367.000.

Sedangkan untuk worst optimum-nya maka bentuk transformasi optimasi program

linier pecahan dengan fungsi tujuan berkoefisien interval adalah

Maksimumkan Z= 3 ₁ + 2 ₂ + -8t

Kendala 24 1+ 19 2+ 5 1

34 ₁ + 25 ₂+ 8 1

2 ₁ + ₂−100  0

1+ 2−80  0

1−40  0

(46)

Dari persamaan program linier diatas maka diperoleh rasio tertinggi worst

optimum untuk efisiensi keuntungan dan biaya dengan solusi ₁ = 0.0415, 2 =

0, = 0.001 dan = 0.1161. Meningkat dari 0.1058 menjadi 0.1161. Dengan

memproduksi mainan boneka sebanyak x1= 1 =

0.0415

0.001 = 41 , dengan biaya

modal sebesar Rp 992.000 dan keuntungan sebesar Rp 115.000.

Kasus 2

Tentukan solusi dar optimasi program linier pecahan dibawah ini!

Maksimumkan Z = ( )

( ) =

[1.5,3] 1+3,4 2+[5, 6]

0.5,2.5 1+1.5,3 2+[2,4]

Kendala −2 1+ 2 3

2 1+ 3 2 10

1− 2 4

₁ 0, ₂ 0

Ditransformasikan kedalam bentuk transformasi optimasi program linier pecahan

dengan fungsi tujuan berkoefisien interval menjadi:

Maksimumkan Z= [1.5, 3] u1 + [3, 4] u2 + [5, 6]t

Kendala: 0.5 ₁+ 1.5 ₂+ 2 1

2.5 ₁+ 3 ₂+ 4 1

−2 ₁+ ₂ −3  0

2 1+ 3 2−10  0

1− 1−4  0

(47)

Untuk memperoleh best optimum dari program linier yang memiliki fungsi tujuan

yang berbentuk LPIC. Maka diambil batas atas dari koefisien interval pada fungsi

tujuan sehingga persamaan program liniernya menjadi:

Maksimumkan Z= 3 1 + 4 2 + 6

Kendala 0.5 1+ 1.5 2+ 2 1

2.5 ₁+ 3 ₂+ 4 1

−2 ₁+ ₂−3  0

2 ₁+ 3 ₂−10  0

1− 1−4  0

₁ 0, ₂ 0, 0

Dari persamaan program linier diatas maka diperoleh solusi ₁ = 1, 2 = 0, =

0.25 dan = 4.5. Nilai optimal dari fungsi tujuan adalah 4.5 dengan nilai pada

titik x1= 1=

1

0.25= 4 sedangakan pada titik x2 adalah 0.

Sedangkan untuk menentukan nilai worst optimum diambil nilai batas bawah dari

koefisien interval. Sehingga persamaan program liniernya menjadi:

Maksimukan Z= 3 1 + 4 2 + 6

Kendala 0.5 1+ 1.5 2+ 2 1

2.5 1+ 3 2+ 4 1

−2 1+ 2 −3  0

2 ₁+ 3 ₂−10  0

1− 1−4  0

(48)

Dari persamaan diatas maka diperoleh untuk nilai worst optimum pada fungsi

tujuan adalah dengan solusi ₁ = 1, 2 = 0, = 0.25 dan = 2.75. Nilai

optimal dari fungsi tujuan adalah 2.75 dengan nilai pada titik x1= 1 =

1

0.25 = 4

sedangakan pada titik x2 adalah 0.

Dari contoh kasus diatas dapat dilihat bahwa optimasi program linier pecahan

dengan fungsi tujuan berkoefisien interval menghasilkan nilai optimal yang lebih

baik dibandingkan penyelesaian dengan metode optimasi program linier biasa.

Hal ini disebabkankan oleh faktor koefisien yang berada dalam interval, sehingga

pemilihan nilai terbaik lebih fleksibel.

Dengan demikian nilai optimum yang dihasilkan dari suatu nilai dalam interval

dapat memberikan hasil yang lebih baik daripada nilai optimum yang dihasilkan

dari satu koefisien tertentu. Hal ini meningkatkan efisiensi biaya pada masalah

(49)

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Kesimpulan yang dapat diperoleh dari uraian di atas adalah sebagai berikut:

1. Optimasi program linier pecahan dengan fungsi tujuan berkoefisien

interval menghasilkan nilai optimal yang lebih baik dibandingkan

penyelesaian dengan metode optimasi program linier biasa.

2. Interval dapat digunakan sebagai pengganti koefisien yang sulit

ditentukan.

4.2 Saran

1. Optimasi Program linier pecahan dengan fungsi tujuan berkoefisien

interval lebih baik digunakan dari program linier dan LPIC dalam

(50)

DAFTAR PUSTAKA

Borza, M. 2012. Solving Linear Fractional Programming Problems with Interval Coefficients in the Objective Function.Applied Mathematical Sciences. 6(69): 3443 – 3452

Bu’ulolo, F. 2005. “ Analysis Sensitivitas pada Program Integer Campuran”.

Jurnal Sistem Teknik Industri (Nomor 4 tahun 2005). Hlm. 78-84.

Charnes, A. and Cooper, W.W. 1962. Programming with linear fractional functions, Naval Research Logistics Quaterly. 9: 181-186.

Chinneck, J.W. dan Ramadan, K. 2000. Linear Programming with Interval Coeﬃcients. Journal of the Operational Research Society. 51: 209–220.

Farida, A. 2011. “Pengoptimuman pada Masalah Pemrograman Linear dengan Koefisien Interval ”. Sekolah Pascasarjana-IPB.

Khaled, R. 1996. Linear Programming with Interval Coeﬃcients. Thesis, Carleton University

Saprida, M. 2009. “Analisis Sensitivitas dan Ketidakpastian dalam Program

Linear”.Tesis. Sekolah Pascasarjana-USU.

Stancu-Minasian, I.M. 1997. Fractional Programming: Theory, Methods and Applications. Dordrecht: Kluwer Academic Publishers.

Winston, W.L,. 2003. Operations Research: Applications and Algorithms, edisi-4,

(51)

LAMPIRAN A. Tampilan Data Input dan Output QM for Windows untuk Penyelesaian Maksimasi Program Linier Contoh 1

Module/Submodule: Linear Programming

Problem title: Best Optimum Kasus 1

Data and Summary --- Data

(52)

Problem title: Worst Optimum Kasus 1

(53)

LAMPIRAN B. Tampilan Data Input dan Output QM for Windows untuk Penyelesaian Maksimasi Program Linier Kasus 2

Problem title: Best Optimum Kasus 2

(54)

Problem title: Worst Optimum Contoh 2