matematika LIMIT TRIGONOMETRI K e l a s Kurikulum 2006/2013 Tujuan Pembelajaran

(1)

LIMIT TRIGONOMETRI

Tujuan Pembelajaran

Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Dapat menghitung limit fungsi trigonometri di suatu titik.

2. Dapat menghitung limit fungsi trigonometri dengan menggunakan sifat-sifat limit fungsi.

3. Dapat menyelesaikan masalah yang berkaitan dengan limit fungsi trigonometri.

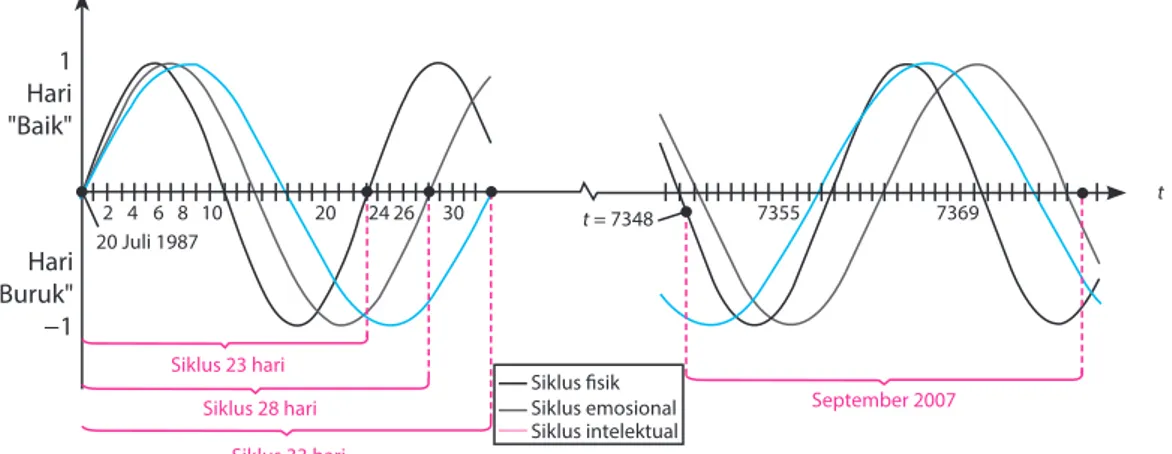
Pernahkah kamu berada pada kondisi emosional seperti optimis, senang, atau gembira pada suatu hari, kemudian pada hari berikutnya merasa kurang bersemangat atau sedih? Tidak hanya kondisi emosional, kondisi fi sik dan intelektual seseorang juga selalu mengalami siklus layaknya roda yang berputar sejak ia dilahirkan. Para ahli merumuskan keteraturan siklus emosional, fi sik, dan intelektual seseorang dalam model bioritme yang dinyatakan dalam fungsi sinus berikut. Fisik (siklus 23 hari): P=sin2 t,t≥

23 0

π

Emosional (siklus 28 hari): E=sin2 t,t≥

28 0

π

Intelektual (siklus 33 hari): I=sin2 t,t≥

33 0

π

dengan t = banyak hari sejak seseorang dilahirkan.

matematika

XI

K

e

l

a

s

Kurikulum 2006/2013

(2)

2

1 Hari "Baik" Hari "Buruk" −1 2 4 6 8 10 20 26 30 _{t = 7348} 7355 20 Juli 1987 7369 t Siklus fi sik Siklus emosional Siklus intelektual September 2007 Siklus 33 hari Siklus 28 hari Siklus 23 hari 24

Gambar 1. Bioritme seseorang selama bulan September 2007

Model tersebut dapat membantu kamu mengetahui baik buruknya kondisi emosional, fi sik, dan intelektual seseorang, misalnya saat mendekati tanggal 1 September 2007 (hari ke-7.348 sejak kelahirannya). Contoh perhitungan untuk pendekatan kondisi emosional ini dapat dituliskan sebagai berikut.

lim lim sin

. . t E t t →7 348 = →7 348 2 28 π

Agar kamu dapat menyelesaikan perhitungan tersebut dan mengetahui fakta-fakta menarik lainnya, mari pelajari tentang limit fungsi trigonometri berikut.

A. Defi nisi Limit Trigonometri

Pada sesi sebelumnya, kamu telah mempelajari bahwa limit fungsi f(x) untuk x mendekati

c adalah lim

x c→ f x

( )

, dengan f(x) merupakan fungsi aljabar dan c → R. Jika f(x) memuat

perbandingan trigonometri, bentuk lim

x c→ f x

( )

disebut sebagai limit trigonometri. Contoh

limit trigonometri adalah sebagai berikut. 1. lim sin x→0 x 2. lim cos x x x → − π 4 2 1 2 3. lim cos tan x x x → + + 0 1 2 3

Teorema pada limit aljabar juga berlaku pada limit trigonometri. Agar kamu ingat kembali, perhatikan teorema limit berikut.

(3)

3

Teorema Limit

Jika lim

x c→ f x

( )

dan limx c→ g x

( )

ada, k sembarang konstanta real, serta n ∈ bilangan bulat

positif, berlaku: 1. lim x c→ k k= 2. lim x c→ x c= 3. lim lim x c→ k f x⋅

( )

=kx c→ f x

( )

4. lim lim lim

x c→ f x

( )

±g x

( )

 =x c→ f x

( )

±x c→ g x

( )

5. lim lim lim

x c→ f x g x

( )

⋅

( )

 =x c→ f x

( )

⋅x c→ g x

( )

6. lim lim lim , lim x c x c x c x c f x g x f x g x g x → → → →

( )

=

( )

dengan

( )

≠0 7. lim x c n n x c → = 8. lim lim x c n x c n f x f x →

(

( )

)

=

(

→

( )

)

9. lim_{x c}_→ n x=nc, dengan c≥0 untuk genapn

10. lim lim , lim

x c n x c n x c f x f x f x n

→

( )

= →

( )

dengan →

( )

≥0 untuk genap

Sama halnya dengan limit aljabar, secara umum ada dua cara yang dapat digunakan untuk menyelesaikan limit trigonometri, yaitu dengan substitusi langsung dan cara alternatif (memodifi kasi bentuk fungsi dan menggunakan rumus limit trigonometri).

B. Menyelesaikan Limit Fungsi Trigonometri dengan Substitusi Langsung

Bentuk umum substitusi langsung pada limit fungsi trigonometri sama dengan limit aljabar, yaitu sebagai berikut.

1. lim x c→ f x

( )

=f c

( )

2. lim x c f x g x f c g c →

( )

=

( )

Cara ini wajib dicoba terlebih dahulu dalam perhitungan limit fungsi. Jika substitusi langsung menghasilkan bentuk tak tentu misalnya 0

0, gunakan cara alternatif agar diperoleh bentuk tertentu, misalnya suatu bilangan real, ∞, dan –∞. Agar kamu lebih mudah dalam menyelesaikan persoalan limit trigonometri, mari ingat kembali nilai perbandingan trigonometri sudut-sudut istimewa berikut ini.

(4)

4

Sudut Istimewa Perbandingan Trigonometri 0° 30° 45° 60° 90° 0 π₆ π₄ π₃ π₂ sin 1 2 0 0= 1 2 1 1 2 = 1 2 2 1 2 3 1 2 4 1= cos 1 2 4 1= 1 2 3 1 2 2 1 2 1 1 2 = 1 2 0 0= tan 0 1 3 3 1 3 Tak terdefi nisi

Contoh Soal 1

Tentukan hasil dari limit-limit fungsi trigonometri berikut. a. lim cos x x → π 6 2 b. lim sin tan

x x x →π

(

+

)

4 2 c. lim cos cos x x x → + + 0 2 5 3 4 Pembahasan:

a. lim cos cos cos

x x → =    = = π π π 6 2 2 6 3 1 2

b. lim sin tan sin tan sin tan

x x x →

(

+

)

=    + = + = + = π π π π π 4 2 2 4 4 2 4 1 1 2 c. lim cos cos cos cos x x x → + + = + +

( )

=

( )

+ + = = 0 2 5 3 0 2 5 3 0 1 2 5 1 6 6 1 4 4 4

C. Menyelesaikan Limit Fungsi Trigonometri dengan Cara Alternatif

1. Memodifi kasi Bentuk Fungsi

Jika substitusi langsung menghasilkan bentuk tak tentu, salah satu cara yang dapat digunakan untuk menyelesaikan limit trigonometri adalah dengan memodifi kasi bentuk fungsi. Modifi kasi dapat dilakukan dengan menggunakan rumus-rumus trigonometri yang sudah dipelajari sebelumnya, yaitu sebagai berikut.

(5)

5

a. Identitas perbandingan tan sin cos cotan cos sin nx nx nx nx nx nx

( )

=

( )

atau

( )

=

( )

b. Identitas Pythagoras sin2

( )

_nx ₊cos2

( )

_nx ₌₁

c. Sinus sudut rangkap sin

( )

nx = sinnx nx        2 2 cos 2

d. Kosinus sudut rangkap

_cos _sin cos nx nx n_x

( )

= −    _ =    _ − 1 2 2 2 2 1 2 2 =    _ − _ _ cos2 sin2 2 2 n_x n_x

Contoh Soal 2

Tentukan nilai dari lim cos sin x x x →π₄ − 2₂ 1 2 . Pembahasan:

Mula-mula, gunakan cara substitusi langsung. lim cos sin lim cos sin x x x x → − = →     −     = π π π π 4 2 4 2 2 1 2 2 4 1 2 4 ccos sin π π 2 1 2 0 1 1 0 0 2 2     − = − =

Oleh karena substitusi langsung menghasilkan bentuk tak tentu 0

0, maka cara alternatifnya adalah memodifi kasi bentuk fungsi.

(6)

6

Dengan menggunakan rumus identitas Pythagoras dan pemfaktoran, diperoleh: lim cos sin lim sin sin lim si x x x x x x x → → → − = − − = − π π π 4 2 4 2 4 2 1 2 1 2 1 2 1 nn sin sin sin sin 2 1 2 1 2 1 2 4 1 2 1 1 2 x x x

(

)

(

+

)

− = +     = + = + = π π

Jadi, nilai dari lim cos sin x x x →π − 4 2₂ 1 2 adalah 2.

Contoh Soal 3

Tentukan nilai dari lim cos cos sin x x x x →π₄ − 2 _. Pembahasan:

Mula-mula, gunakan cara substitusi langsung.

lim cos

cos sin lim

cos cos sin cos x x x x x → − = →     − = π π π π π 4 4 2 2 4 4 4 ππ π 2 π 4 4 0 1 2 2 1 2 2 0 0     − = − = cos sin

(7)

7

Dengan menggunakan rumus kosinus sudut rangkap dan pemfaktoran, diperoleh:

lim cos

cos sin lim

cos sin cos sin lim x x x x x x x x x x → → → − = − − = π π π 4 4 2 2 2 44 4 4 1 2 2 1 2 2 2

cos sin cos sin

cos sin cos sin x x x x x x +

(

)

(

−

)

− = + = + = π π

Jadi, nilai dari lim cos cos sin x x x x →π − 4 2 _{adalah 2 .}

Contoh Soal 4

Tentukan nilai dari lim sin sin sin .cos sin

x x x x x x → − − 0 3 3 2 1 2 2 . Pembahasan:

lim sin sin

sin .cos sin

sin sin sin x x x x x x → − − = −

(

)

(

0 3 3 3 2 1 2 2 0 2 0 1 2

(

2 0

))

)

(

)

−

(

)

= cos0 sin0 0 0 3

Dengan menggunakan rumus sinus sudut rangkap dan pemfaktoran, diperoleh:

lim sin sin

sin .cos sin

lim sin sin

x x x x x x x x x → → − − = −

(

)

0 3 3 0 2 2 1 2 2 1 2 11 2 2 1 2 3 0 2 2

.sin .cos .cos sin

lim sin sin

sin .cos x x x x x x x x

(

)

− = _→

(

−

)

xx x x x x x x x − =

(

−

)

−

(

)

= − = → sin

lim sin sin

sin cos sin

3 0 2 2 2 1 2 1 1 0 1 Jadi, nilai dari lim sin sin

sin .cos sin

x x x x x x → − − 0 3 3 2 1 2 2 adalah 1.

(8)

8 2. Menggunakan Rumus Limit Trigonometri

Adakalanya modifi kasi fungsi masih menghasilkan bentuk tak tentu. Oleh karena itu, perlu digunakan rumus limit trigonometri. Untuk memperoleh rumus limit trigonometri, kamu dapat menganalisis grafi k f x x

x

( )

=sin dan menghitung nilai dari lim_x sinx

x →0 . Perhatikan grafi k fungsi f x x x

( )

=sin berikut. 1 −3 −2 −1 0 1 (3,14, 0) = (π , 0) Y (−3,14, 0) = (−π , 0) 2 3 X (radian) f x x x

( )

=sin

Dari grafi k tersebut, terlihat bahwa jika x bergerak semakin dekat dengan 0, baik dari kiri (x < 0) maupun dari kanan (x > 0), f(x) bergerak semakin dekat dengan 1. Hal ini juga didukung dengan tabel hubungan antara x dengan −1 ≤ x < 1 dan f x x

x

( )

=sin berikut. x ±1 ±0,5 ±0,2 ±0,1 ±0,01 ±0,001 ... → 0 f x x x

( )

=sin 0,84147 0,95885 0,99335 0,99833 0,99998 0,99999 ... → 1 Dari grafi k dan tabel tersebut, diperoleh kesimpulan bahwa untuk x → 0, nilai

f x x

x

( )

=sin semakin mendekati 1. Secara matematis, dapat ditulis sebagai berikut. limsin

x x x

→0 =1

Dengan cara yang sama, kamu dapat memperoleh rumus berikut. limtan

x x x

(9)

9

Dari kedua rumus tersebut, dapat dikembangkan rumus-rumus limit trigonometri berikut.

No. Rumus Limit Trigonometri No. Rumus Limit Trigonometri

1.

limsin lim sin limtan lim

tan x x x x x x x x x x x x → → → → = =       = 0 0 0 0 1 3. lim sin tan lim tan sin lim sin x x x a bx c dx a bx c dx ax bx cx → → → ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ 0 0 0 ttan lim tan sin . . dx ax bx cx dx a b c d x = ⋅ ⋅       = →0 2.

limsin lim sin limtan lim

tan x x x x ax bx ax bx ax bx ax bx → → → → = =    0 0 0 0  =a b 4.

limsin lim

sin limtan x p x p x p a x p b x p a x p b x p a x p → → → −

(

)

−

(

)

=

(

−−

)

−

(

)

bb x p a x p b x p a b x p −

(

)

=

(

−−

)

       = → lim tan

Selain rumus-rumus tersebut, cara pemfaktoran dan perkalian akar sekawan seperti pada limit aljabar juga dapat digunakan dalam penyelesaian limit trigonometri.

Contoh Soal 5

Tentukan hasil dari limit-limit fungsi trigonometri berikut. a. limsin x x x →0 4 b. limsin tan x x x →0 3 6 c. _lim tan x x x x x x → − +

(

)

(

−

)

− +

(

)

1 2 2 2 4 3 1 5 4 Pembahasan: a. limsin sin

x x x → =

( )

₌ 0 4 4 0 0 0 0

0, maka dengan menggunakan rumus trigonometri nomor 2, diperoleh:

limsin x x x →0 = = 4 4 1 4

Cara lain yang dapat digunakan adalah sebagai berikut.

limsin lim sin limsin

x x x x x x x x x → = → × →    = =

( )

= 0 0 0 4 4 4 4 4 4 4 4 1 4

(10)

10

Jadi, lim sin .

x x x →0 = 4 ₄ b. limsin tan sin tan x x x → =

( )

= 0 3 6 3 0 6 0 0 0

0, maka dengan menggunakan rumus trigonometri nomor 3, diperoleh:

limsin tan x x x →0 = = 3 6 3 6 1 2

Cara lain yang dapat digunakan adalah sebagai berikut. limsin tan lim sin tan lim x x x x x x x x x → → → = ⋅

( )

   _ = 0 0 3 6 3 6 3 6 3 6 00 3 3 6 6 3 6 1 1 3 6 1 2 sin tan x x x x ⋅ ⋅    _ = ⋅ ⋅ = Jadi, limsin

tan . x x x →0 = 3 6 1 2

c. lim tan tan

x x x x x x → − +

(

)

(

−

)

− +

(

)

= −

( )

+

(

)

( )

− − 1 2 2 2 2 2 4 3 1 5 4 1 4 1 3 1 1 1 5 1

(( )

+

(

)

= ⋅ ₌ 4 0 0 0 0 0 2 2 tan

0, maka dengan menggunakan rumus limit trigonometri nomor 4, diperoleh:

lim tan lim tan

x x x x x x x x x x → → − +

(

)

(

−

)

− +

(

)

= −

(

)

(

−

)

(

−

)

1 2 2 2 1 4 3 1 5 4 1 3 1 xx x x x x x x −

(

)

(

−

)

=

(

−

)

−

(

)

⋅ −

(

)

−

(

)

= − −

(

)

⋅ = − → 1 4 3 4 1 1 2 1 4 1 2 2 1 2 2 lim tan 22 9

Jadi, lim tan .

x x x x x x → − +

(

)

(

−

)

− +

(

)

= − 1 2 2 2 4 3 1 5 4 2 9

(11)

11 Contoh Soal 6

lim sin .... x x x x →0 + = 2 3 2 (SMUP 2010) A. 0 B. 1 C. −1 D. 2 E. −2 Jawaban: B Pembahasan:

lim sin sin

x x x x →0 + = + = 2 3 2 2 3 2 0 0 0 0 0

0, maka dengan menggunakan rumus trigonometri nomor 1 dan pemfaktoran, diperoleh:

lim sin lim sin

lim x x x x x x x x x x → → → + =  +         = +  0 2 3 2 ₀ 2 2 0 1 1 1 1        = +    

( )

= sinx x 2 2 1 0 1 1 1

Jadi, lim sin .

x x x x →0 + = 2 3 2 1

Contoh Soal 7

Tentukan nilai dari lim sin tan x x x x → + 0 2 2 2 8 2 2 ! Pembahasan:

(12)

12

lim sin tan sin tan x x x x → + ₌

( )

+

( )

= 0 2 2 2 2 2 2 8 2 2 8 0 2 0 2 0 0 0

0, maka dengan menguraikan bentuknya menjadi penjumlahan pecahan, serta menggunakan rumus 1 dan 2, diperoleh:

lim sin

tan lim tan

sin tan x x x x x x x x x → → + ₌  ₊      = 0 2 2 2 ₀ 2 2 2 2 8 2 2 8 2 2 2 llim tan sin tan lim tan sin x x x x x x x x x x → → + ×       = + 0 2 2 2 2 2 2 0 2 2 4 2 2 4 22 2 4 1 1 5 2 2 2 2 x x x x ×       =

( )

+ = tan

Jadi, lim sin tan x x x x → + ₌ 0 2 2 2 8 2 2 5 .

D. Menyelesaikan Limit Fungsi Trigonometri dengan Memadukan Cara

Alternatif

Dua cara alternatif yaitu memodifi kasi bentuk fungsi dan menggunakan rumus limit trigonometri dapat dipadukan penggunaannya tergantung bentuk soal. Biasanya, fungsi dimodifi kasi terlebih dahulu hingga memuat bentuk yang dapat diselesaikan dengan rumus limit trigonometri. Mari pahami bentuk soal dan langkah-langkah penyelesaiannya melalui contoh-contoh soal berikut.

Contoh Soal 8

Nilai dari lim cos tan x x x → − 0 2 1 2 adalah .... (UN 2016) A. 1 8 D. 1 B. 1 4 E. 2 C. 1 2 Jawaban:A

(13)

13

Pembahasan:

Mula-mula, gunakan cara substitusi langsung. lim cos tan cos tan x x x → − _{= −}

( )

= − = 0 2 2 2 1 2 1 0 2 0 1 1 0 0 0

0, maka gunakan rumus kosinus sudut rangkap berikut.

cos

( )

nx = − sin nx cos nx sin nx

  ⇔ −

( )

=     1 2 2 1 2 2 2 2 _{, dengan n = 1}

Berdasarkan rumus tersebut dan rumus 2, diperoleh: lim cos tan lim sin tan lim sin x x x x x x x x → → → − ₌ =     0 2 0 2 2 0 1 2 2 1 2 2 2 1 2 

(

)

          =     → 2 2 2 0 2 2 1 2 2 1 2 2 2 1 2 1 tan . . . . . .lim sin x x x x x 22 2 2 1 2 2 2 1 1 1 4 1 2 2 2 2 2 x x x    

( )

(

)

          =

( )( )

    = . tan . 88 Jadi, lim cos

tan . x x x → − ₌ 0 2 1 2 1 8

Contoh Soal 9

Nilai lim cos

sin .tan .... x x x x → − ₌ 0 1 8 2 2 (UN 2014) A. 16 B. 12 C. 8 D. 4 E. 2 Jawaban: C

(14)

14

Pembahasan:

lim cos sin tan cos sin tan x x x x → − ⋅ = −

( )

⋅

( )

= −

( )

= 0 1 8 2 2 1 8 0 2 0 2 0 1 1 0 0 00 0

0, maka gunakan rumus kosinus sudut rangkap berikut.

cos

( )

nx = − sin nx cos nx sin nx

  ⇔ −

( )

=     1 2 2 1 2 2 2 2 _{, dengan n = 8}

Berdasarkan rumus tersebut dan rumus 2, diperoleh:

lim cos

sin tan lim

sin sin tan lim x x x x x x x x x → → → − ⋅ = ⋅ = ⋅ 0 0 2 0 1 8 2 2 2 4 2 2 2 ssin sin sin tan limsin sin

4 4 2 2 4 4 4 4 2 4 4 4 4 0 x x x x x x x x x x x x x ⋅ ⋅ ⋅ ⋅ ⋅ = ⋅ ⋅ → ⋅⋅ ⋅ ⋅ ⋅ =

( )( )( )( )( )( )

= 2 2 2 2 2 2 2 1 1 2 1 2 1 8 x x x x sin tan

Jadi, lim cos

sin tan . x x x x → − ⋅ = 0 1 8 2 2 8

SUPER "Solusi Quipper"

Trik-trik menghitung limit trigonometri adalah sebagai berikut.

1. Sinus dan tangen dapat diabaikan (dihilangkan) dengan ketentuan berikut. a. sinm_{nx = (nx)}m

b. tanm_{nx = (nx)}m

2. Bentuk kosinus dapat diubah dengan menggunakan rumus berikut. a b c d . cos ( ) . cos ( ) . cos ( ) . cos 1 1 2 1 1 2 1 2 2 2 2 2 − − − − nx nx nx nx nx nx n = = = xx nx nx −1 − 1 2 = = ( ) . cos e

Syarat: setelah penyederhanaan (misalnya pemfaktoran), bentuk sinm_{nx dan tan}m_nx

(15)

15

Sekarang, mari selesaikan contoh soal 8 dan 9 dengan SUPER "Solusi Quipper".

Penyelesaian contoh soal 8 dengan SUPER "Solusi Quipper"

lim cos tan . x x x x x → −

(

)

(

)

=

_{( )}

0 2 2 2 1 2 1 2 2 SUPER no. 2a SUPER no. 1b == = 1 2 4 1 8

Penyelesaian contoh soal 9 dengan SUPER "Solusi Quipper"

lim cos sin tan . x x x x x → − ⋅

(

)

(

)

= 0 1 8 2 2 1 2 8 SUPER no. 2a SUPER no. 1

(( )

( )

= = 2 2 2 32 4 8 x. x

Contoh Soal 10

Nilai lim sin cos sin

tan sin cos

x x x x x x x x x x → ⋅ ⋅ − ⋅ ⋅ ⋅

(

)

(

−

)

= 0 3 3 2 2 2 2 2 2 4 2 8 1 2 ... Pembahasan:

Dengan memfaktorkan terlebih dahulu, kemudian menggunakan SUPER "Solusi Quipper", diperoleh:

lim sin cos sin

tan sin cos

x x x x x x x x x x → ⋅ ⋅ − ⋅ ⋅ ⋅

(

)

(

−

)

0 3 3 2 2 2 2 2 2 4 2 8 1 2 Faaktorkan pembilang

(

)

= − ⋅

(

−

)

⋅ ⋅ →

lim sin cos

tan s x x x x x x 0 3 2 2 2 1 2 4 2 iin cos lim 8 1 2 2 2 0 x x x x x

(

)

(

−

)

(

)

(

)

= − ⋅

(

→ SUPER no. 1a SUPER no. 1

))

⋅ ⋅

(

)

= − ⋅ ⋅ ⋅ ⋅ ⋅ = − → 3 2 0 4 4 4 2 8 2 8 4 2 8 1 4 x x x x x x lim

Jadi, lim sin cos sin

tan sin cos

x x x x x x x x x x → ⋅ ⋅ − ⋅ ⋅ ⋅

(

)

(

−

)

= 0 3 3 2 2 2 2 2 2 4 2 8 1 2 −− 1 4.

E. Aplikasi Limit Trigonometri

Pada umumnya, aplikasi limit trigonometri disajikan dalam bentuk soal cerita terkait disiplin ilmu seperti Fisika, Biologi, Ekonomi, dan sebagainya. Langkah-langkah menyelesaikan soal cerita terkait limit trigonometri adalah sebagai berikut.

(16)

16

1. Tentukan nilai yang didekati oleh x untuk melengkapi notasi limit fungsinya.

2. Selesaikan limit fungsi yang diperoleh dengan cara substitusi langsung terlebih dahulu.

3. Jika substitusi langsung menghasilkan bentuk tak tentu, gunakan cara alternatif yang sesuai dengan bentuk fungsinya.

Contoh Soal 11

Sebuah partikel bergerak dalam bidang datar dengan fungsi jarak (dalam meter) terhadap waktu (dalam detik) dinyatakan sebagais t

( )

=sint+4 . Jika kecepatan v saat t dirumuskan t

dengan v t s t h s t h h

( )

=

(

+

)

−

( )

→ lim

0 (dalam meter/detik), tentukan kecepatan partikel saat t

= 2π detik. Pembahasan:

Mula-mula, tentukan v(t) dengan mensubstitusikan s(t) = sin t + t ke v(t).

v t s t h s t h t h t h t t h h h

( )

=

(

+

)

−

( )

=

(

+

)

+

(

+

)

−

[

+

]

→ → lim

lim sin sin

0

4 4

G

Gunakan: lim lim lim

lim x c→ f x

( )

+g x

( )

 =x c→ f x

( )

+x c→ g x

( )

(

)

=_hh t h t _h h t h t h A B → → +

(

)

− +

(

+

)

− − = 0 0 4 4 2 sin sin lim sin sin co Gunakan: ss sin

lim cos sin

1 2 1 2 2 1 2 1 2 0 A B A B t h t t h t h +

(

)

⋅

(

−

)

    =

(

+ +

)

⋅

(

+ − →

))

+ + − = +    ⋅ ₊ → → → h t h t h t h h h h h h lim lim cos sin lim 0 0 0 4 4 4 2 1 2 1 2 44 2 1 2 1 2 ₄ 2 1 2 0 0 h h t h h h t h h =  +    + =

(

)

    → →

lim cos .limsin

cos ++

= +

4 4 cost

(17)

17

Selanjutnya, tentukan kecepatan v saat t = 2 π detik atau v(2 π ).

v 2

( )

π =cos2π+ = + =4 1 4 5