Soal Soal dan Pembahasan UN Matematika SMA IPA 2012

(1)

w w w .pur w antow ahyudi.com Page 1

SOAL-SOAL dan PEM BAHASAN UN

M ATEM ATIKA SM A/ M A IPA

TAHUN PELAJARAN 2011/ 2012

1. Akar-akar persamaan kuadrat x2 +ax - 4=0 adalah p dan q. Jika p2 - 2pq + q2 =8a, maka nilai a = ....

A. -8 B. -4 C. 4 D. 6 E. 8

Jaw ab:

BAB III Persamaan dan Fungsi Kuadrat

x2 +ax – 4 = 0



a =1 ; b = a ; c = -4

p + q = - = - = - a ; p . q = = = - 4

p2 - 2pq + q2 =8a

(p + q)2 – 2pq – 2pq = 8a



( p2 + q2 = (p + q)2 – 2pq ) (p + q)2 – 4pq = 8a

(-a)2 – 4.(-4) = 8a a2 + 16 = 8a a2 – 8a + 16 = 0 (a - 4 ) ( a – 4) = 0 a – 4 = 0

a = 4

Jaw abannya C

2. Persamaan kuadrat x2 + (m-2)x + 2m - 4=0 mempunyai akar-akar real, maka bat as nilai m yang memenuhi adalah....

A. m

≤ 2 atau m ≥ 10 C. m < 2 atau m > 10

E. -10

≤ m ≤

-2 B. m

≤

-10 at au m

≥

-2 D. 2 < m < 10

Jaw ab:

(2)

w w w .pur w antow ahyudi.com Page 2 mempunyai akar-akar real maka D

≥ 0

D = b2 – 4 ac

(m-2)2 – 4 . 1. (2m - 4)

≥ 0

m2 – 4m + 4 – (8m – 16)

≥ 0

m2 – 4m + 4 – 8m + 16

≥ 0

m2 – 12m + 20

≥ 0

(m -10)(m-2)

≥ 0

nilai bat as m = 10 dan m = 2

(m-10 = 0



m = 10 ; m -2 = 0



m = 2) + + + + - - - + + + + + 2 10

didapat nilai m

≥ 10 atau m ≤ 2

Jaw abannya A

3. Umur pak Andi 28 t ahun lebih t ua dari umur Amira. Umur bu Andi 6 t ahun lebih muda dari umur pak Andi. Jika jum lah um ur pak Andi, bu Andi, dan Am ira 119 t ahun, maka jumlah um ur Amira dan bu Andi adalah ....

A. 86 t ahun C. 68 t ahun E. 58 t ahun B. 74 t ahun D. 64 t ahun

Jaw ab:

BAB IV Sist em Persamaan Linear dan Kuadrat

M isal : x = umur pak Andi y = umur bu Andi z = umur Amira

x + y + z = 119 ...(1) x = 28 + z ...(2)

y = x – 6 = (28 + z) - 6 = 22 + z ...(3)

(3)

w w w .pur w antow ahyudi.com Page 3 3z = 119 – 50

= 69

z = = 23



umur Amira

Umur bu Andi = y = 22 + z

= 22 + 23 = 45

jumlah um ur Amira dan bu Andi = z + x = 23 + 45 = 68 t ahun Jaw abannya C

4. Diketahui fungsi f(x) = 3x – 1 dan g(x) = 2x

2

– 3. Komposisi fungsi ( g

°

f) (x) = ....

A. 9x2 – 3x + 1 C. 9x2 – 6x + 6 E. 18x2 – 12x - 1

B. 9x2 – 6x + 3 D. 18x2 – 12x - 2 Jaw ab:

BAB XIII Fungsi Kom posisi dan Fungsi Invers

( g

°

f) (x) = g (f(x) )

= g (3x – 1)

= 2 (3x – 1)

2

- 3

= 2 (9x

2

– 6x + 1) – 3

= 18x

2

– 12x + 2 – 3

= 18x

2

– 12x - 1

Jawabannya E

5. Diket ahui vekt or

⃗

=

2

−

1

;

⃗

=

4

−

3

6

;

⃗

=

2

−

1

3

. Jika

⃗

t egak lurus

⃗

, maka hasil dari (

⃗

- 2

⃗

) . (3

⃗

) adalah....

A. 171 B. 63 C. -63 D. -111 E. -171

Jaw ab:

BAB XX Vekt or

⃗

t egak lurus

⃗

maka

⃗

.

⃗

= 0

2

−

1

.

4

−

3

6

(4)

w w w .pur w antow ahyudi.com Page 4 4p = 12

p = 3

(

⃗

- 2

⃗

) . (3

⃗

) =

3

2

−

1

–

2

4

−

3

6

.

3

2

−

1

3

=

3

2

−

1

–

8

−

6

12

.

6

−

3

9

=

−

5

8

−

13

.

6

−

3

9

= -30 + (-24) + (-117) = -30 – 24 – 117 = -171 Jaw abannya E

⃗

=

2

−

3

dan

⃗

=

3

−

2

−

4

. Sudut ant ara vekt or

⃗

dan

⃗

adalah...

A. 1350 B. 1200 C. 900 D. 600 E. 450

Jaw ab:

BAB XX Vekt or

a

.

b

= |

a

| |

b

| cos



cos



=

|

.

|

.

b

a

b

a

=

2 3 2 2 2 1 2 3 2 2 2 1 3 3 2 2 1 1

. b b b

a a a b a b a b a       = 2 2 2 2 2 2 ) 4 ( ) 2 ( 3 . 3 ) 3 ( 2 ) 4 ).( 3 ( ) 2 ).( 3 ( . 3 . 2            

=

2 2 2 2 2 2 ) 4 ( ) 2 ( 3 . 3 ) 3 ( 2 12 6 . 6          = 2 2 2 2 2 2 ) 4 ( ) 2 ( 3 . 3 ) 3 ( 2 0      

(5)

cos



= 0





= 90

0

Jaw abannya C

⃗

= 5

⃗

+ 6

⃗

+

⃗

dan

⃗

=

⃗

- 2

⃗

- 2

⃗

. Proyeksi ort hogonal vekt or

⃗

pada

⃗

adalah....

A.

⃗

+ 2

⃗

+ 2

⃗

C. .

⃗

- 2

⃗

+ 2

⃗

E. 2

⃗

+ 2

⃗

-

⃗

B.

⃗

+ 2

⃗

- 2

⃗

D. -

⃗

+ 2

⃗

+ 2

⃗

Jaw ab:

BAB XX Vekt or

Proyeksi vekt or ort ogonal

a

pada

b

adalah :

|

c

| =













2

|

.

b

a

.

b

=

2 2 2 2 ) ) 2 ( ) 2 ( 1 ( 2 2 1 1 6 5                          

.















2

1

=

9 2 12

5 















2

1

= -1















2

1

=













2

1













2

1

= -

i

+2

j

+2

k

Jaw abannya D

8. Diket ahui a = , b = 2 dan c = 1. Nilai dari . .

. . adalah...

A. 1 B. 4 C. 16 D. 64 E. 96

Jaw ab:

BAB I Perpangkaan dan Bent uk Akar

. .

. . =

(6)

w w w .pur w antow ahyudi.com Page 6 =

.

=

.

=

.

=

. = = 4

Jaw abannya B

9. Lingkaran L = ( x + 1 )2 + ( y – 3 )2 = 9 mem ot ong garis y = 3. Garis singgung lingkaran yang melalui t it ik pot ong ant ara lingkaran dan garis t ersebut adalah ....

A. x = 2 dan x = -4 C. x = -2 dan x = 4 E. x = 8 dan x = -10 B. x = 2 dan x = -2 D. x = -2 dan x = - 4

Jaw ab:

BAB XI Lingkaran

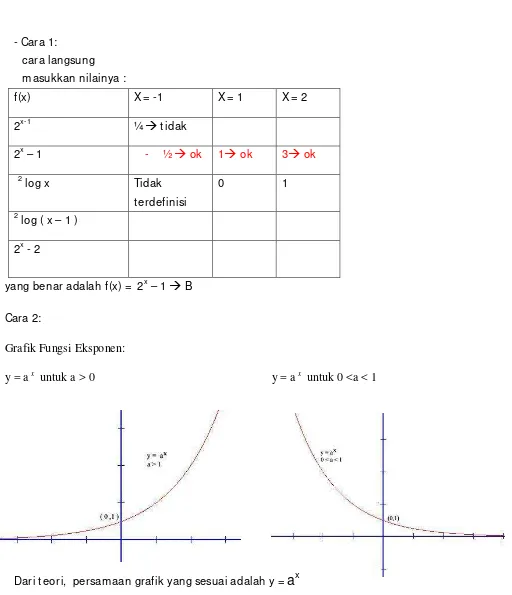
[image:6.612.71.375.405.688.2]

Lingkaran dengan pusat (a,b) dan jari-jari r adalah (x – a)2 + (y – b)2 = r2

gambar sket sa lingkaran :

Lingkaran L = ( x + 1 )2 + ( y – 3 )2 = 9

(7)

w w w .pur w antow ahyudi.com Page 7 Terlihat pada gambar bahw a garis singgung lingkaran yang melalui t it ik pot ong ant ara lingkaran dan garis t ersebut adalah x = -4 dan x = 2

Jaw abannya A

10. Bent uk √ √

√ √ dapat disederhanakan menjadi bent uk ....

A. -25 – 5

√

21

C. -5 + 5

√

21

E. -5 -

√

21

B. -25 + 5

√

21

D. -5 +

√

21

Jaw ab:

BAB I Perpangkaan dan Bent uk Akar

b

a



1

=

b

a



1

.

b

a

b

a



=

b a

  2

√ √

√ √ =

√ √

√ √ .

√ √ √ √

= √ . √

.

= √ = -5 -

√

21

Jaw abannya E

11. Diket ahui 5 log 3 = a dan 3 log 4 = b. Nilai 4 log 15 =...

A. C. E.

B. D.

Jaw ab:

BAB II Logarit ma

4

log 15 = 4 log 3.5

= 4 log 3 + 4 log 5

= 4 log 3 +



(

a

log

b =

a

b

x x

log

; x bisa berapa saja, x = 3 disesuaikan dengan soal)

(8)

w w w .pur w antow ahyudi.com Page 8 3

log 4 = b



4 log 3 = 5

log 3 = a



3 log 5 =

= +

=

+

= Jaw abannya A

12. Bayangan garis x – 2y = 5 bila dit ransformasi dengan mat riks t ransformasi

3

5

1

2

dilanjut kan dengan pencerm inan t erhadap sumbu X adalah...

A. 11x + 4y = 5 C. 4x + 11y = 5 E. 3x + 11 y = 5 B. 4x + 2y = 5 D. 3x + 5y = 5

Jaw ab:

BAB XXI Transformasi Geomet ri dan BAB XIX M at riks T1 =

3

5

1

2

; T2 =















1

0

1

T = T2 o T1













' '

y

x

=















1

0

1

3

5

1

2













y

x

=

1.3 + 0.1

1.5 + 0.2

0.3 + (

−

1) .1

0.5 + (

−

1) .2













y

x

=

3

5

−

1

−

2

y

C

A

B

x

.



















C = A . B



B = A-1 . C

Jika A.B = C maka

1. A = C .

B

1

2. B =

A

1

. C

(9)

w w w .pur w antow ahyudi.com Page 9 A-1 =

| .( ) ( . )|

−

2

−

5

1

3

=

−

2

−

5

1

3

B = A-1 . C













y

x

=

−

2

−

5

1

3

.













' '

y

x

x = -2 - 5 y = + 3

subst it usikan ke dalam persamaan x – 2y = 5

-2 - 5 - 2 ( + 3 ) = 5 -2 - 5 - 2 - 6 = 5

-4 - 11 = 5

⟺

| dikali - |



4 + 11 = - 5 Sehingga bayangannya adalah 4x + 11y = -5

Tidak ada jaw aban

13. Diket ahui mat riks A =

3

5

−

1

, B =

5

−

3

6

dan C =

−

3

−

1

9

Jika A + B – C =

8

5

−

4

, maka nilai x + 2xy + y adalah...

A. 8 B. 12 C. 18 D. 20 E. 22

Jaw ab:

BAB XIX M at riks

A + B – C =

3

5

−

1

+

5

−

3

6

-

−

3

−

1

9

=

8

5

−

4

3 + x – (-3) = 8

x = 8 – 3 -3 = 2 5 – 3 – y = -x

(10)

w w w .pur w antow ahyudi.com Page 10 M aka nilai x + 2xy + y = 2 + 2.2.4 + 4 = 2 + 16 + 4 = 22

Jaw abannya E

14. Nilai x yang memenuhi pert idaksamaan 92x – 10 . 9x + 9 > 0, x

∈

R adalah.... A. x < 1 at au x > 9 C. x < -1 at au x > 2 E. x < -1 at au x > 1 B. x < 0 at au x > 1 D. x < 1 at au x > 2

Jaw ab:

BAB I Perpangkat an dan Bent uk Akar

92x – 10 . 9x + 9 > 0

misal 9x = y, maka y2 – 10y + 9 > 0 (y – 9)(y-1) > 0

+ + + - - - + + + + 1 9 hasilnya y < 1 at au y > 9

9x < 1 at au 9x > 9 9x < 90 9x > 91 x < 0 at au x > 1 Jaw abannya B

15. Fungsi yang sesuai dengan grafik berikut adalah....

A. f(x) = 2x-1 B. f(x) = 2x – 1 C. f(x) = 2 log x

D. f(x) = 2 log ( x – 1 ) E. f(x) = 2x - 2

Jaw ab:

(11)

w w w .pur w antow ahyudi.com Page 11 - Cara 1:

cara langsung masukkan nilainya :

f(x) X = -1 X = 1 X = 2

2x-1 ¼



t idak

2x – 1 - ½



ok 1



ok 3



ok

2

log x Tidak

t erdefinisi

0 1

2

log ( x – 1 ) 2x - 2

[image:11.612.57.569.112.707.2]

yang benar adalah f(x) = 2x – 1



B Cara 2:

Grafik Fungsi Eksponen:

y = a

x

untuk a > 0 y = a

x

untuk 0 <a < 1

(12)

w w w .pur w antow ahyudi.com Page 12 kit a t ambahkan konst ant a menjadi y =

a

x

+ C

dari grafik soal dapat diambil nilai x nya : -1, 0, 1 dan 2 unt uk x = -1



a-1 + C = - ½



1/ a + C = - ½

unt uk x = 0



1 + C = 0



C = -1

karena C sudah didapat , maka a dapat dicari:

1/ a + C = - ½



1/ a – 1 = - ½

1/ a = 1 – ½

1/ a = ½ a = 2 maka y = f(x) = 2x – 1 Jaw abannya B

16. Jumlah n suku pert ama deret arit met ika dinyat akan dengan Sn = 2n 2

+ 4n. Suku ke-9 dari deret arit met ika t ersebut adalah ....

A. 30 B. 34 C. 38 D. 42 E. 46

Jaw ab:

BAB XVIII Not asi Sigma dan Barisan Deret

Hubungan Un dan Sn

Un = Sn - Sn1

suku ke 9:

U

9

= S

9

– S

8

Sn = 2n 2

+ 4n S9 = 2 . 9

2

+ 4. 9 = 162 + 36 = 198 S8 = 2. 8

2

+ 4 . 8 = 128 + 32 = 160

(13)

w w w .pur w antow ahyudi.com Page 13 17. Anak usia balit a dianjurkan dokt er unt uk mengkonsumsi kalsium dan zat besi sedikit nya

60 gr dan 30 gr. Sebuah kapsul mengandung 5 gr kalsium dan 2 gr zat besi, sedangkan sebuah t ablet mengandung 2 gr kalsium dan 2 gr zat besi. Jika harga sebuah kapsul Rp.1.000,00 dan harga sebuah t ablet Rp.800,00, maka biaya minimum yang harus dikeluarkan unt uk memenuhi kebut uhan anak balit a t ersebut adalah...

A. Rp 12.000,00 C. Rp 18.000,00 E. Rp36.000,00 B. Rp14.000,00 D. Rp24.000,00

Jaw ab:

BAB XVII Program Linear misal x =jumlah t ablet kalsium y = jum lah t ablet zat besi

5x + 2y

≤

60



jika x = 0 maka y = 30, jika y = 0 maka x = 12 didapat t it ik (0,30) dan (12,0) 2 x + 2y

≤

30



jika x = 0 maka y = 15, jika y = 0 maka x = 15 didapat t it ik (0,15) dan (15,0) 1000 x + 800 y



biaya m inimum ?

eliminasi y: 5x + 2y = 60 2 x + 2y = 30 - 3x = 30 x = 10 2x + 2y = 30 2y = 30 – 2x y = 15 – x = 15 – 10 = 5

t it ik pot ongnya (10,5)

ambil t it ik-t it k yang lain, karena

≤ , maka ambil titik yang mendekati sumbu masing

-masing:

dari sumbu y:

(14)

w w w .pur w antow ahyudi.com Page 14 dari sumbu x:

Dari t it ik (12,0) dan (15,0)



t it ik (12,0) yang belaku

(0,15) (12,0) (10,5) 1000 x + 800 y 12000 12000 12000

ket iganya nilainya sama sehingga nilai minimumnya adalah Rp. 12.000,00 Jaw abannya A

18. Suku banyak berderajat 3, jika dibagi (x2 – x - 6) bersisa 5x-2, jika dibagi (x2 - 2x - 3 ) bersisa ( 3x + 4 ). Suku banyak t ersebut adalah....

A. x3 – 2x2 + x + 4 C. x3 – 2x2 - x - 4 E. x3 + 2x2 - 4 B. x3 – 2x2 + x - 4 D. x3 – 2x2 + 4

Jaw ab:

BAB XII Suku Banyak

cara 1:

Suku banyak berderajat 3



f(x) = ax3 + bx2+ cx + d

f(x) = (x2 – x - 6) h(x) + 5x – 2 = (x – 3)(x + 2) h(x) + 5x – 2

f(3) = 27 a + 9b + 3 c + d = 5 . 3 – 2 = 13 f(-2) = -8 a + 4b - 2 c + d = 5 .(-2) – 2 = -12 -

35 a + 5b + 5c = 25



| : 5|



7a + b + c = 5 ....(1)

f(x) = (x2 - 2x - 3 ) h (x) + 3x + 4 = (x – 3)(x + 1) h(x) + 3x + 4

f(3) = 27 a + 9b + 3 c + d = 3 . 3 + 4 = 13 f(-1) = - a + b – c + d = 3. (-1) + 4 = 1 -

28 a + 8b + 4c = 12



| : 4|



7 a + 2 b + c = 3 ...(2)

(15)

w w w .pur w antow ahyudi.com Page 15 7 a + 2 b + c = 3 -

-b = 2 b = -2 masukkan nilai b:

7a + b + c = 5



7a – 2 + c =5 7a + c = 7

a adalah variabel pangkat t iga (

≠ 0), diasumsikan bahwa a bukan pecahan dan nilainya

≥1, nilai yang memungkinkan adalah a = 1 sehingga c = 7

– 7a = 7 – 7 = 0

nilai d :

27 a + 9b + 3 c + d = 13 27 . 1 + 9. (-2) + 3. 0 + d = 13 d = 13 – 27 + 18

= 4

M aka suku banyak t ersebut adalah :

f(x) = ax3 + bx2+ cx + d = x3 - x2+ 0. x + 4 = x3 - x2 + 4 Jaw abannya D

Cara 2:

f(x) = (x2 – x - 6) h(x) + 5x – 2 = (x – 3)(x + 2) h(x) + 5x – 2 f(3) = 5.3 – 2 = 13

f(-2) = 5 . (-2) – 2 = -12

masukkan nilai salah sat u f(3) at au f(-2) ke salah sat u jaw aban. Didapat D yang benar

19. Keunt ungan seorang pedagang bert ambah set iap bulan dengan jumlah yang sama. Jika keunt ungan pada bulan pert ama sebesar Rp46.000,00 dan pert ambahan keunt ungan set iap bulan Rp18.000,00 maka jum lah keunt ungan sampai bulan ke-12 adalah ....

A. Rp 1.740.000,00 C. Rp 1.840.000,00 E. Rp 2.000.000,00 B. Rp 1.750.000,00 D. Rp 1.950.000,00

(16)

w w w .pur w antow ahyudi.com Page 16 BAB XVIII Not asi Sigma dan Barisan Deret

Barisan soal adalah barisan arit met ika dengan: a = U1 = 46.000

U2 = 46.000 + 18.000 = 64.000

b = U2 – U1 = 64.000 – 46.000 = 18.000

S

n

=

2

n

(2a +(n-1) b)

S12 = 2 12

(2. 46000 +(12-1). 18000)

= 6 (92000 + 198000) = 6 . 290000

= Rp. 1.740.000,00 Jaw abannya A

20. Barisan geomet ri dengan dengan suku ke 5 adalah dan rasio = , maka suku ke-9 barisan geomet ri t ersebut adalah...

A. 27 B. 9 C. D. E.

Jaw ab:

Barisan geomet ri dengan: U5 = ; r =

U

n

= ar

1



n

cari nilai a dulu:

U5 = = a.( ) 4

(17)

w w w .pur w antow ahyudi.com Page 17 maka U9 = a .r

8

= 27. .( )8 = = = Jaw abannya E

21. Diket ahui premis-prem is sebagai berikut :

Premis 1 : Jika hari ini hujan deras, maka Bona t idak keluar rumah. Premis 2 : Bona keluar rumah.

Kesimpulan yang sah dari premis-premis t ersebut adalah ....

A. Hari ini hujan deras B. Hari ini hujan t idak deras

C. Hari ini hujan t idak deras at au bona t idak keluar rumah D. Hari ini t idak hujan dan Bona t idak keluar rumah

E. Hari ini hujan deras at au Bona t idak keluar rumah

Jaw ab:

BAB VI Logika M at emat ika

p = hari ini hujan deras q = Bona t idak keluar rumah ~q = Bona keluar rumah

p

⟺

q ~q

Kesimpulannya adalah ~p (Hari ini t idak hujan deras)



M odus Tollens

(18)

w w w .pur w antow ahyudi.com Page 18 22. Ingkaran pernyat aan “ Jika sem ua anggot a keluarga pergi, maka sem ua pint u rumah

dikunci rapat ” adalah ....

A. Jika ada anggot a rumah yang t idak pergi maka ada pint u rumah yang t idak dikunci rapat .

B. Jika ada pint u rumah yang t idak dikunci rapat maka ada anggot a keluarga yang t idak pergi.

C. Jika semua pint u rumah dit ut up rapat maka semua anggot a keluarga pergi. D. Semua anggot a keluarga pergi dan ada pint u rumah yang t idak dikunci rapat . E. Semua pint u rumah t idak dikunci rapat dan ada anggot a keluarga yang t idak pergi.

Jaw ab

BAB VI Logika M at emat ika

Negasi kalimat berkuant or :

~(semua p)



ada/ beberapa ~p ~(ada/ beberapa p)



semua ~p

p = sem ua anggot a keluarga pergi, maka ~ p = ada anggot a keluarga yg t idak pergi q = sem ua pint u rumah dikunci rapat , maka ~ q = ada pint u rumah yang t idak dikunci rapat

Jaw aban yang cocok adalah A

23. Suku ke-t iga dan suku ke-t ujuh suat u deret geomet ri bert urut -t urut 16 dan 256. Jum lah t ujuh suku pert ama deret t ersebut adalah ....

A. 500 B. 504 C. 508 D. 512 E. 516

Jaw ab:

Deret Geomet ri:

(19)

U

n

= ar

1



n

U3 = 16 = ar 2

U7 = 256 = ar 6

= = = r4 = 16 r =

√

16

= 2 16 = ar2

16 = a . 22 a = = 4

karena r > 1 , maka Sn =

1

)

1

(



r

a

n

S

7

=

1

2

)

1

2

(

4

7



=

1 ) 127 ( 4

= 508

Jawabannya C

24. Nilai

→

0

√ = ....

A. -30 B. -27 C. 15 D. 30 E. 36

Jaw ab:

BAB XIV Limit Fungsi

→

0

√ =

→

0

√

√ √

=

→

0

. ( √ )

(20)

w w w .pur w antow ahyudi.com Page 20 =

→

0

. ( √ )

=

→

0

- 5 .

(

3 +

√

9

+

)

= -5 . ( 3 +

√

9

) = -5 . 6 = -30 Jaw abannya A

25. Nilai

→

0

= ....

A. -2 B. -1 C. 0 D. 1 E. 2

Jaw ab:

BAB XIV Limit Fungsi

→

0

=

→

0

( )

=

→

0

=

→

0

.

=

→

0

2



= 1 ; =

= 2. 1 . = 1

Jaw abannya D

26. Suat u perusahaan mem produksi unit barang, dengan biaya (4x2 - 8x + 24) dalam ribu rupiah unt uk t iap unit . Jika barang t ersebut t erjual habis dengan harga

(21)

w w w .pur w antow ahyudi.com Page 21 A. Rp 16.000,00 C. Rp 48.000,00 E. Rp 64.000,00

B. Rp 32.000,00 D. Rp 52.000,00

Jaw ab:

BAB XV Differensial

Biaya Produksi dalam ribuan per unit adalah: B = 4x2 - 8x + 24

Keunt ungan = (Harga x barang) – (biaya produksi x barang)



dalam ribuan K = 40 x –(4x2 - 8x + 24). x

= 40x – 4x3 + 8x2 – 24 x = – 4x3 + 8x2 + 16 x Agar keunt ungan maksim um maka = 0 -12x2 + 16x + 16 = 0



-3x2 + 4x + 4 = 0 (-3x - 2 ) (x – 2) = 0

x = - at au x = 2

yangberlaku adalah nilai yang posit if yait u x = 2

M asukkan ke K : -4 . 23 + 8. 22 + 16. 2

-32 + 32 + 32 = 32



dalam ribuan menjadi 32 x Rp.1000 = Rp. 32.000 Jaw abannya B

27. Himpunan penyelesaian persamaan cos2x -2cos x = -1; 0 < x <

2π adalah ....

A. { 0,

π,

π, 2π } C. { 0,

π, π,

π }

E. { 0,

π, π }

B. { 0,

π,

π, 2π }

D. { 0,

π,

π }

Jaw ab:

BAB VII Trigonomet ri

cos2x = cos2x – sin2x = cos2x – (1 – cos2x) = 2 cos2x - 1

(22)

w w w .pur w antow ahyudi.com Page 22 cos2x -2cos x = -1

2 cos2x – 1 – 2 cos x + 1 = 0 2 cos2x – 2cos x = 0

cos2x – cos x = 0 cosx . (cosx – 1) = 0

cos x = 0 ; cos x = 1 cos x = cos cos x = cos 00

cos x = cos



, maka x₁_,₂=





+ k. 0

360

cos x = cos 1

x

= + 0. 2

π ;

x

₂=- + 1. 2

π

= =

cos x = cos 00 1

x

= 0 + 0. 2

π ;

x

₂= 0 + 1. 2

π

= 0 = 2

π

karena int ervalnya 0 < x <

2π

,

maka nilai yang memenuhi adalah dan

Tidak ada jaw aban

28. Diket ahui segienam berat uran. Jika jari-jari lingkaran luar segienam berat uran adalah 10 sat uan, maka luas segienam berat uran t ersebut adalah ....

A. 150 sat uan luas C. 150

√

3

sat uan luas E. 300

√

2

sat uan luas B. 150

√

2

sat uan luas D. 300 sat uan luas

Jaw ab:

Bangun Dat ar

Luassegi-n = r 2

sin

Type equation here.

(23)

w w w .pur w antow ahyudi.com Page 23 = 3 . 100. sin 600

= 300. ½

√

3

= 150.

√

3

sat uan luas Jaw abannya C

29. Nilai dari sin 75° - sin165° adalah ....

A.

√

2

B.

√

3

C.

√

6

D.

√

2

E.

√

6

Jaw ab:

BAB VII Trigonomet ri

Sin A - sin B = 2 cos

2 1

(A + B) sin

2 1

(A –B)

sin 75° - sin165 = 2 cos

2 1

(750 + 1650) sin

2 1

(750 –1650) = 2 cos

2 1

. 2400 sin

2 1

(-900) = 2 cos 1200 sin (-450)

sin – = - sin cos – = cos t an – = t an

Cos (180

0

-



) = - cos



= 2 cos (1800 – 600) . – sin 450 = - 2 cos 600. – sin 450

= 2. ½ . ½

√

2

= ½

√

2

Jaw abannya D

30.

Diketahui α

–

β =

dan sin α . sin β =

dengan α dan β merupakan sudut lancip. Nilai

cos (α + β) = ...

A. 1 B. C. D. E. 0

(24)

w w w .pur w antow ahyudi.com Page 24 BAB VII Trigonomet ri

cos (A + B) = cos A cos B – sin A Sin B

cos (A - B) = cos A cos B + sin A Sin B



cos A cos B = cos (A - B) - sin A Sin B

cos (α + β) =

cos α cos β

–

sin α sin β

= cos (α

-

β)

-

sin α sin β

-

sin α sin β

= cos – ¼ - ¼

= ½ - ½ = 0 Jaw abannya E

31. Luas daerah yang dibat asi oleh kurva y= x2 - 4x + 3 dan y = 3 – x adalah ....

A. sat uan luas C. sat uan luas E. sat uan luas

B. sat uan luas D. sat uan luas

Jaw ab:

BAB XVI Int egral

t anpa gambar :

kurva y= x2 - 4x + 3



ax2 – 4x + 3



a > 0 , kurva t erbuka ke at as sehingga garis y = 3 – x berada di at as.

Tit ik pot ong kurva dan garis yang merupakan bat asnya: masukkan persamaan garis ke dalam kurva:

3 – x = x2 - 4x + 3 x2 - 4x + 3 + x – 3 = 0 x2 - 3x = 0

x (x – 3) = 0

(25)

w w w .pur w antow ahyudi.com Page 25 L =





b

a

dx

y

)

(

₂ ₂ dx

=







3

0

2

))

3

4

(

3

(

x

dx

=









3

0

2

)

3

4

3

(

x

dx

=





3

0

2

)

3

(

x

dx

= x2 - x3

|

= - 9

= = sat uan luas Jaw abannya C

32. Volume benda put ar yang t erjadi bila daerah yang dibat asi oleh kurva y= x2 dan y = 4x -3 diput ar 360° mengelilingi sumbu X adalah ....

A. 13

π satuan volume

D. 12

π satuan volume

B. 13

π satuan volume

E. 12

π satuan volume

C. 12

π satuan volume

Jaw ab:

BAB XVI Int egral

Volume benda diput ar t erhadap sum bu x maka,

V=



y

dx

b

a



2

y= x2



a > 0 , kurva t erbuka ke at as garis y = 4x -3 berada di at as kurva

t it ik pot ong/ bat as:

subsit usikan persamaan y = 4x -3 ke dalam persamaan y= x2 : 4x -3 = x2

(26)

w w w .pur w antow ahyudi.com Page 26 (x – 3) (x- 1) = 0

x = 3 dan x = 1



bat as at as dan baw ah

V=



y

dx

b

a



2

=





x  x dx

3

1

2 2 2

) ) ( ) 3 4 ((

=





x  x x dx 3

1

4 2

) ) 9 24 16

((

=



( x

3

– 12x

2

+ 9x - x

5

)

|

=



( (3

3

– 1) – 12(3

2

– 1) + 9(3-1) - (3

5

-1) )

=



( . 26 – 12. 8 + 9. 2 - . 242 )

=



(

– 96 + 18 -

)

=



(

– 78 -

)

=



(

)

=



= 12



Jaw abannya E

33. Nilai

∫

( 2 sin 2

−

3 cos )

= ....

A. -5 B. -1 C. 0 D. 1 E. 2

Jaw ab:

BAB XVI Int egral dan BAB VII Trigonomet ri



sin(axb)dx = -

a

1

cos (ax+b) + c



cos(axb)dx =

a

1

sin (ax+b) + c

∫

( 2 sin 2

−

3 cos )

=

(

−

2. cos 2

−

3 sin

) |

(27)

w w w .pur w antow ahyudi.com Page 27 = 2 – 3 = -1

Jaw abannya B

34. Hasil dari

∫

( )

=

...

A.

( ) + C C. ( ) + C E. ( ) + C

B.

( ) + C D. ( ) + C

Jaw ab:

BAB XVI Int egral

misal : u =

3

−

2 + 7

du = (6x – 2) dx

= 2 (3x – 1) dx



(3x – 1) dx = du

∫

₍ ₎ =

∫

=

∫

= . u- 6 + C

=

+ C =

( )

+ C

Jaw abannya D

35. Nilai dari

∫

( 4

−

+ 5)

= ....

A. B. C. D. E.

Jaw ab:

BAB XVI Int egral

∫

( 4

−

+ 5)

= x3 - x2 + 5x

|

(28)

w w w .pur w antow ahyudi.com Page 28 = . 7 - . 3 + 5. 1

= - + 5

= =

Jaw abannya E

36. Bilangan t erdiri dari 4 angka disusun dari angka-angka 1, 2, 3, 5, 6, dan 7. Banyak susunan bilangan dengan angka-angka yang berlainan (angka-angkanya t idak boleh berulang) adalah....

A. 20 B. 40 C. 80 D. 120 E. 360

Jaw ab:

BAB X Peluang

Angka t erdiri dari 1, 2, 3, 5, 6, 7



6 angka

akan dibuat 4 digit angka t idak boleh berulang



XXXX digit pert ama : bisa sem ua angka



6

digit kedua : 6 -1 = 5 ( 1 angka sudah t erpakai dan set erusnya...) digit ket iga : 5 – 1 =4

digit keempat : 4 -1 = 3

M aka banyaknya susunan bilangan dengan angka-angka yg berlainan adalah: 6 x 5 x 4 x 3 = 360

Jaw abannya E

37. Dua buah dadu dilempar undi bersama-sama sat u kali. Peluang m uncul mat a dadu berjumlah 5 at au 7 adalah ....

A. B. C. D. E.

Jaw ab:

BAB X Peluang

P (A  B ) = P(A) + P(B) =

)

(

)

(

S

n

A

n

+

)

(

)

(

S

n

(29)

w w w .pur w antow ahyudi.com Page 29 n(S) = banyaknya kemungkinan kejadian sam ple = 6 x 6 = 36

P(A) = peluang kemungkinan jum lah dadu berjumlah 5 (1,4), (2,3), (3,2),(4,1)



4 kejadian

=

36 4

P(B) = peluang kemungkinan jum lah dadu berjumlah 7 (1,6), (2,5), (3,4),(4,3), (5,2), (6,1)



6 kejadian =

36 6

P (A  B ) =

36 4

+

36 6

=

36 10

=

18 5

Jaw abannya C

38. Dat a yang diberikan dalam t abel frekuensi sebagai berikut :

Nilai modus dari dat a pada t abel adalah ....

A. 49,5 - C. 49,5 + E. 49,5 + B. 49,5 - D. 49,5 +

Jaw ab:

BAB IX St at ist ika

Modus dari suatu data berkelompok adalah:

M₀ = L +



















2 1

1 _c

M ₀ = modus dat a berkelom pok



kelas 50 – 59 adalah kelas m odus karena mem punyai frekuensi yang t erbanyak (12)

L = t epi baw ah kelas m odus



50 – 0,5 = 49,5 Kelas Frekuensi

20 – 29 30 – 39 40 – 49 50 – 59 60 – 69 70 – 79 80 – 89

(30)

w w w .pur w antow ahyudi.com Page 30 c = panjang kelas (t epi at as – t epi baw ah kelas



59,5 – 49.5 = 10

modus)



₁ = selisih frekuensi kelas modus dengan frekuensi



12 – 8 = 4 kelas sebelum nya



2

= selisih frekuensi kelas modus dengan frekuensi



12 – 9 = 3

kelas sesudahnya

M₀ = L +



















2 1

1 _c

= 49,5 + 

    

3 4

4

. 10 = 49,5 +

Jaw abannya D

39. Panjang rusuk kubus ABCD.EFGH adalah 12 cm. Jika P t it ik t engah CG, maka jarak t it ik P dengan garis HB adalah ....

A. 8

√

5

cm B. 6

√

5

cm C. 6

√

3

cm D. 6

√

2

cm E. 6 cm Jaw ab:

BAB VIII Dimensi Tiga

H G E F P

O

D C

(31)

w w w .pur w antow ahyudi.com Page 31 P

H O B dit anya OP =...?

BH = 12

√

3

; GP = CP = ½ . 12 = 6 HP2 = GH2 + GP2

= 122 + 62= 144 + 36 = 180 HP =

√

180

= 6

√

5

= BP

∆

BHP adalah sama kaki HO = BO = ½ . 12

√

3

= 6

√

3

OP =

(

)

−

(

)

=

( 6

√

5)

−

( 6

√

3)

=

√

180

−

108

=

√

72

= 6

√

2

cm

Jaw abannya D

40. Diket ahui limas segi empat berat uran P.QRST. Dengan rusuk alas 3 cm dan rusuk t egak 3

√

2

cm. Tangen sudut ant ara garis PT dan alas QRST adalah ....

A.

√

3

B.

√

2

C.

√

3

D. 2

√

2

E. 2

√

3

Jaw ab:

BAB VIII Dimensi Tiga

(32)

w w w .pur w antow ahyudi.com Page 32 3

√

2

cm

T S O

Q 3 cm R Alas limas P T S

O

T α O

Q R

Tan α

= =



OP =

√

−

panjang diagonal RT = panjang diagonal QS = 3 x

√

2

= 3

√

2

PT = 3

√

2

; OT = ½ diagonal RT = ½ . 3

√

2

=

√

2

OP =

( 3

√

2

)

−

(

√

2

)

=

18

−

= = =

√

6

Tan α =

= = √

√ = √

√ = =

√

3