KELAS XI IPA
(Penelitian Quasi Eksperimen di SMA N 5 Kota Tangerang Selatan)
Skripsi
Diajukan dalam Rangka Penyelasaian Studi Strata-1 untuk Memperoleh Gelar Sarjana Pendidikan
Oleh:
DONI WIDIANTO
108017000047
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UIN SYARIF HIDAYATULLAH
JAKARTA
Adaptif Siswa Kelas XI
IPA"
diajukan kepada Fakultas Ilmu Tarbiyah danKeguruan Universitas Islam Negeri Syarif Hidayatullah Jakarta. dan telah dinyatakan lulus dalam Ujian Munaqasah pada tanggal27 Juni 2014 dihadapan dewan penguji. Karena itu, penulis berhak memperoleh gelar Sarjana 51 (S.Pd) dalam bidang Pendidikan matematika.
Jakarta, September 2014
Panitia Ujian Munaqasah
Ketua Panitia (Ketua Jurusan)
Dr. Kadir. M.Pd
Tanggal
l? -
0g
-
?&( (.1-
og
-10tq
NIP. 19670812 199402 1 001Sekertaris (Sekertaris Jurusan)
't6
Abdul Muin. S.Si. M.Pd
NIP. 19751201 200604
I
003Penguji I
Otong Suhyanto. M.Si
NrP. 19681104 199903
I
001Penguji
II
Dr. Tita Khalis M.. M.Kom
NIP. 19690924 199903 2 003
!*: ?9
*9
tYt9:
?q:
??!:l
Mengetahui
Dekan Fakultas Ilmu Tarbiyah dan Keguruan
NIM
Jurusan
Anekatan
Alamat
Nama
NIP
Dosen Jurusan
Nama
NIP
Dosen Jurusan
ME}IYATAKAN DENGAIY SESUNGGUHI{YA
Bahwa skripsi yang berjudul Pengaruh Metode Penemuan Terbimbing
(Guided Discovery
Method)
dalam Pembelajaran Matematika terhadap Kemampuan Penalaran Adaptif Siswa Kelas)il
IPA
adalahbenarhasilkaryasendiri di bawah bimbingan dosen: 10801?000047
Pendidikan Matematika
2008
Jl. Inpres Raya No. 8 Rt/Rw 01107 Larangan
Utara-C iledug-Tangerang-Banten
LiaKurniawati, M. Pd
1976A521 200801 2 008
Pendidikan Matematika
Maifalinda Fatra, M.Pd
19700528 199603 20A2
Pendidikan Matematika
1.
Demikian surat pernyataan ini saya buat dengan sesungguhnya dan saya siap
menerima segala konsekuensi apabila terbukti bahwa skripsi ini bukan hasil karya
sendiri.
i
Mathematics learning to The Students’ Adaptive Reasoning Skills". Thesis Department of Mathematics Education, Faculty of Tarbiyah and Teachers Training, Syarif Hidayatullah State Islamic University Jakarta, June 2014
The purpose of this research is to analyze the students’ adaptive reasoning skills. The research was conducted at SMA N 5 Kota Tangerang Selatan, in 2013/2014. The method of the research used experimental method with two group randomized subject post test only design. Subject for this research are 68 students consist of 34 students of experimental group and 34 students of control group which selected in cluster random sampling technique at student of science program 11th class. Data of adaptive reasoning skill collected with test. The results of research that the students’ adaptive reasoning skills who are taught by guided discovery method higher than students taught by traditional method. This matter visible from the mean score of the results test students’ adaptive reasoning skills who taught with guided discovery method is 65,24 and who taught with traditional method have mean score of the test students’ adaptive reasoning is 50,56. Results of hypothesis test with Mann-Whitney test get Zcount = 4,2, and Ztable = 2,00 with standard significant to 5%
(Zcount > Ztable). Thus, the conclusion of this research that the methematics learning by
using guided discovery method have a significant effect on students’ adaptive reasoning skills.
ii
(Guided Discovery Method) dalam Pembelajaran Matematika terhadap Kemampuan Penalaran Adaptif Siswa”. Skripsi Jurusan Pendidikan Matematika, Fakultas Ilmu
Tarbiyah dan Keguruan, Universitas Islam Negeri Syarif Hidayatullah Jakarta, Juni
2014
Tujuan penelitian ini adalah untuk menganalisis pengaruh metode penemuan terbimbing dalam pembelajaran matematika terhadap kemampuan penalaran adaptif siswa. Penelitian dilakukan di SMA N 5 Kota Tangerang Selatan, Tahun Pelajaran
2013/2014. Metode penelitian yang digunakan adalah quasi eksperimen dengan
desain Two Group Randomized Subject Post Test Only. Subyek penelitian ini adalah
68 siswa yang terdiri dari 34 siswa kelompok eksperimen dan 34 siswa kelompok
kontrol yang diperoleh dengan teknik cluster random sampling pada siswa kelas XI
IPA. Kemampuan penalaran adaptif siswa dikumpulkan dengan menggunakan tes. Hasil penelitian menunjukkan bahwa kemampuan penalaran adaptif siswa yang diajar dengan metode penemuan terbimbing lebih tinggi daripada siswa yang diajar dengan pembelajaran konvensional. Hal ini dapat dilihat dari nilai rata-rata hasil tes kemampuan penalaran adaptif siswa yang diajar dengan metode penemuan terbimbing adalah sebesar 65,24 dan nilai rata-rata hasil tes kemampuan penalaran adaptif siswa yang diajar dengan pembelajaran konvensional adalah sebesar 50,56. Berdasarkan hasil pengujian hipotesis dengan uji Mann-Whitney, diperoleh harga Zhitung = 4,22 dan Ztabel = 2,00 dengan taraf signifikansi 5 % (Zhitung > Ztabel). Dengan demikian, kesimpulan penelitian ini adalah pembelajaran matematika dengan menggunakan metode penemuan terbimbing mempunyai pengaruh yang signifikan terhadap kemampuan penalaran adaptif siswa.
iii
telah memberikan kemudahan dan kekuatan sehingga penulis dapat menyelesaikan skripsi ini dengan sebaik-baiknya. Shalawat dan salam semoga tetap tercurahkan kepada Nabi Muhammad SAW beserta seluruh keluarga, sahabat, dan para pengikutnya sampai akhir zaman.
Selama penulisan skripsi ini, penulis menyadari sepenuhnya bahwa tidak sedikit kesulitan yang dialami. Namun, berkat kesungguhan hati, perjuangan, doa, dan semangat dari berbagai pihak untuk penyelesaian skripsi ini, semua dapat teratasi. Oleh sebab itu penulis mengucapkan terimakasih kepada:
1. Ibu Nurlena Rifa’i, M.A.,Ph.D., Dekan Fakultas Ilmu Tarbiyah dan Keguruan UIN syarif Hidayatullah Jakarta.
2. Bapak Dr. Kadir, M.Pd., Ketua Jurusan Pendidikan Matematika Fakultas Ilmu
Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
3. Bapak Abdul Muin, M.Pd, Sekretaris Jurusan Pendidikan Matematika
Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta.
4. Ibu Dr. Tita Khalis Maryati, M. Kom, selaku Dosen Penasehat Akademik
yang penuh kesabaran, bimbingan, waktu, arahan dan semangat dalam membimbing penulis selama mengikuti perkuliahan.
5. Ibu Lia Kurniawati, M.Pd sebagai Dosen Pembimbing I dan Ibu Maifalinda
Fatra, M.Pd sebagai Dosen pembimbing II yang telah memberikan waktu, bimbingan, arahan, motivasi, dan semangat dalam membimbing penulis dalam menyelesaikan penulisan skripsi ini. Semoga Allah SWT membalas segala kebaikan ibu. Aamiin.
6. Seluruh Dosen Jurusan Pendidikan Matematika UIN Syarif Hidayatullah
iv
dibutuhkan.
8. Staff Fakultas Ilmu Tarbiyah dan Keguruan dan Staf Jurusan Pendidikan
Matematika UIN Syarif Hidayatullah Jakarta yang telah memberi kemudahan dalam pembuatan surat-surat serta sertifikat.
9. Kepala SMA N 5 Kota Tangerang Selatan yang telah memberikan izin kepada
penulis untuk melakukan penelitian.
10.Ibu Eka Rostika Sari, S.Pd selaku guru pamong tempat penulis mengadakan
penelitian, seluruh dewan guru dan staff SMA N 5 Kota Tangerang Selatan yang telah membantu penulis dalam melaksanakan penelitian ini, serta Siswa dan siswi SMA N 5 Kota Tangerang Selatan, khususnya kelas XI IPA 1 dan XI IPA 3.
11.Teristimewa untuk Almarhum Ayahanda Sarwi, yang selama hidupnya tak
henti-hentinya mendoakan, melimpahkan kasih sayang, memberikan dukungan moril dan materil kepada penulis. Semoga Allah SWT mengampuni segala dosa dan menerima segala amal kebaikan ayahanda, serta mudah-mudahan ini menjadi bakti penulis kepada almarhum. Aamiin.
12.Ibunda tercinta Muslikha, Kakakku tercinta Wahidin Widodo dan adikku
tercinta Mutmainah Wisesa serta semua keluarga yang selalu mendoakan dan mendorong penulis untuk tetap semangat dalam mengejar dan meraih cita-cita.
13.Sahabat tercinta Muhammad Faozan Afandi, Muhammad Aulia Sifa, Firman
Ramadhan, Arif Rahman Akbar, Saeful Anwar, Muhammad Ikmal Januar, Muhammad Shidik, Muliahadi Tumanggor, dan Tomi Novano. Terimakasih atas ketersediaannya dalam memberikan dukungan dan motivasinya.
14.Teman-teman seperjuangan Jurusan Pendidikan Matematika angkatan 2008,
v
semoga skripsi ini dapat berguna bagi penulis khususnya dan bagi para pembaca pada umumnya.
Jakarta, Juni 2014
vi
ABSTRAK ... ii
KATA PENGANTAR ... iii
DAFTAR ISI ... vi
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... x
DAFTAR LAMPIRAN ... xi
BAB I: PENDAHULUAN A. Latar Belakang Masalah ... 1
B. Identifikasi Masalah ... 6
C. Pembatasan Masalah ... 7
D. Rumusan Masalah ... 7
E. Tujuan Penelitian ... 8
F. Manfaat Penelitian ... 8
BAB II: DESKRIPSI TEORETIK, KERANGKA BERPIKIR DAN HIPOTESIS PENELITIAN A. Deskripsi Teoritik 1. Teori Belajar dan Pembelajaran Matematika ... 9
a. Teori Belajar yang Relevan dengan Metode Penemuan Terbimbing (Guided Discovery Method) ... 9
1) Teori Pembelajaran Konstruktivisme ... 9
2) Teori Jerome Bruner ... 10
b. Pembelajaran Matematika ... 11
2. Kemampuan Penalaran Adaptif (Adaptive Reasoning) ... 16
a. Pengertian Penalaran Adaptif ... 16
b. Indikator Kemampuan Penalaran Adaptif ... 19
3. Metode Penemuan Terbimbing ... 21
vii
D. Pengajuan Hipotesis ... 32
BAB III: METODOLOGI PENELITIAN A. Tempat dan Waktu Penelitian ... 33
B. Metode dan Desain Penelitian ... 33
C. Populasi dan Teknik Pengambilan Sampel ... 34
D. Teknik Pengumpulan Data ... 34
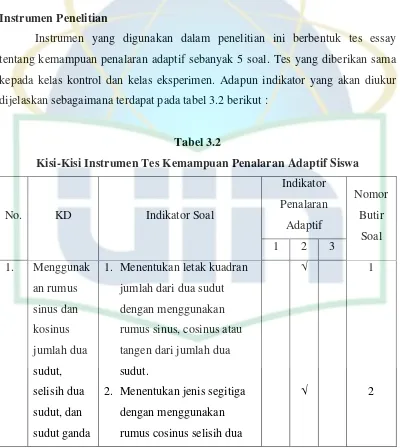
E. Instrumen Penelitian ... 35
1. Uji Validitas ... 38
2. Uji Reliabilitas ... 39
3. Uji Taraf Kesukaran Soal ... 40
4. Uji Daya Pembeda Soal ... 41
F. Teknik Analisis Data ... 42
G. Hipotesis Statistik ... 47
BAB IV: HASIL PENELITIAN DAN PEMBAHASAN A. Deskripsi Data ... 48
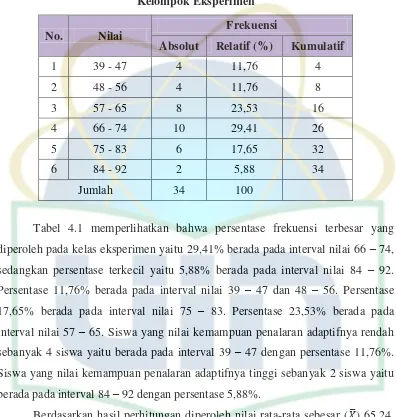
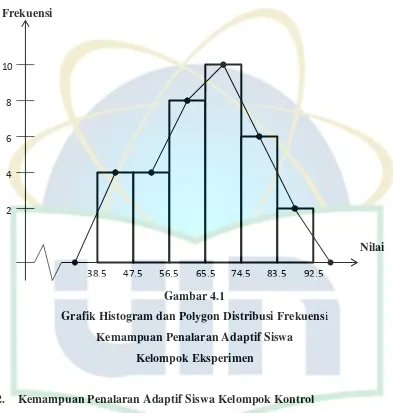
1. Kemampuan Penalaran Adaptif Siswa pada Kelompok Eksperimen ... 48
2. Kemampuan Penalaran Adaptif Siswa pada Kelompok Kontrol ... 50
3. Perbandingan Kemampuan Penalaran Adaptif Siswa pada Kelas Eksperimen dan Kelas Kontrol ... 52
4. Persentase Kemampuan Penalaran Adatif Siswa Pada Kelompok Eksperimen dan Kelompok Kontrol ... 55
B. Hasil Pengujian Persyaratan Analisis ... 57
1. Uji Normalitas Tes Kemampuan Penalaran Adaptif Siswa ... 57
viii BAB V: KESIMPULAN DAN SARAN
A. Kesimpulan ... 68
B. Saran ... 68
DAFTAR PUSTAKA ... 70
ix
Tabel 3.2 Kisi-Kisi Instrumen Tes Kemampuan Penalaran Adaptif Siswa .... 35
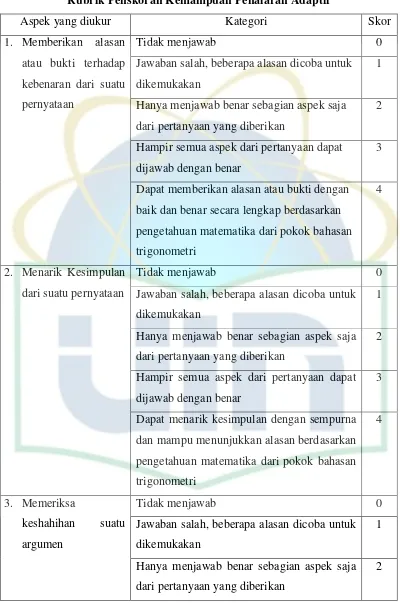
Tabel 3.3 Rubrik Penskoran Kemampuan Penalaran Adaptif ... 37
Tabel 3.4 Klasifikasi Nilai Koefisien Reliabilitas ... 40
Tabel 3.5 Klasifikasi Tingkat Kesukaran ... 41
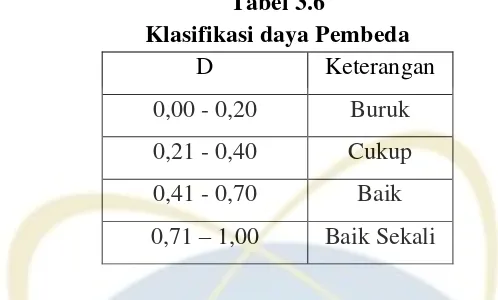
Tabel 3.6 Klasifikasi daya Pembeda ... 42
Tabel 4.1 Distribusi Frekuensi Kemampuan Penalaran Adaptif Siswa Kelompok Eksperimen ... 49
Tabel 4.2 Distribusi Frekuensi Kemampuan Penalaran Adaptif Siswa Kelompok Kontrol ... 51
Tabel 4.3 Perbandingan Kemampuan Penalaran Adaptif Siswa Kelompok Eksperimen dan Kelompok Kontrol ... 53
Tabel 4.4 Persentase Kemampuan Penalaran Adaptif Siswa Kelompok Eksperimen dan Kelompok Kontrol ... 55
Tabel 4.5 Hasil Perhitungan Uji Normalitas ... 57
[image:13.595.114.511.162.628.2]x
Gambar 4.2 Grafik Histogram dan Polygon Distribusi Frekuensi
Kemampuan Penalaran Adaptif Siswa Kelompok Kontrol ... 52 Gambar 4.3 Kurva Perbandingan Nilai Kemampuan Penalaran Adaptif Siswa pada Kelompok Eksperimen dan Kelompok Kontrol ... 54 Gambar 4.4 Persentase Kemampuan Penalaran Adaptif Siswa
Kelompok Eksperimen dan Kelompok Kontrol ... 56 Gambar 4.5 Kurva Uji Perbedaan Data Kelompok Eksperimen dan
[image:14.595.110.512.145.642.2]xi
Lampiran 3 LKS Eksperimen ... 91
Lampiran 4 Kisi-kisi Uji Coba Instrumen Penalaran Adaptif ... 121
Lampiran 5 Uji Coba Instrumen Tes Kemampuan Penalaran Adaptif Siswa Kelas XI IPA Pokok Bahasan Trigonometri ... 123
Lampiran 6 Kunci Jawaban Uji Coba Instumen Tes ... 125
Lampiran 7 Rubrik Penskoran Kemampuan Penalaran Adaptif ... 132
Lampiran 8 Hasil Uji Validitas Instrumen ... 134
Lampiran 9 Hasil Uji Reliabilitas Instrumen ... 135
Lampiran 10 Hasil Uji Taraf Kesukaran Instrumen ... 136
Lampiran 11 Hasil Uji Daya Beda Soal ... 137
Lampiran 12 Langkah-langkah Penghitungan Uji Validitas, Reliabilitas, Taraf Kesukaran, dan Daya Pembeda Soal ... 138
Lampiran 13 Rekapitulasi Hasil Uji Validitas, Reliabilitas, Taraf Kesukaran, dan Daya Pembeda ... 141
Lampiran 14 Kisi-kisi Instrumen Penalaran Adaptif ... 142
Lampiran 15 Instrumen Tes Kemampuan Penalaran Adaptif Siswa Kelas XI IPA Pokok Bahasan Trigonometri ... 144
Lampiran 16 Hasil Post Test Kelas Eksperimen ... 145
Lampiran 17 Hasil Post Test Kelas Kontrol ... 146
Lampiran 18 Distribusi Frekuensi Kelompok Eksperimen ... 147
Lampiran 19 Distribusi Frekuensi Kelompok Kontrol ... 151
Lampiran 20 Perhitungan Uji Normalitas Kelompok Eksperimen ... 155
Lampiran 21 Perhitungan Uji Normalitas Kelompok Eksperimen ... 157
Lampiran 22 Perhitungan Uji Hipotesis Statistik ... 159
Lampiran 23 Tabel Nilai r Product Moment ... 161
Lampiran 24 Luas Di Bawah Kurva Normal ... 162
xii
1
A. Latar Belakang Masalah
Perkembangan ilmu pengetahuan dan teknologi saat ini mengalami kemajuan yang sangat pesat. Kemajuan tersebut mengantarkan masyarakat pada suatu era global dimana setiap individu dituntut untuk mampu beradaptasi dan menyelesaikan setiap permasalahan yang muncul. Oleh karenanya, diperlukan suatu tindakan dalam upaya mempersiapkan sumber daya manusia yang unggul dalam rangka memenuhi akan kebutuhan menghadapi tantangan global tersebut.
Pendidikan merupakan salah satu upaya yang dapat dilakukan oleh pemerintah untuk mempersiapkan dan mengembangkan sumber daya manusia yang ada. Sumber daya manusia yang dimaksud adalah kemampuan peserta didik untuk mampu menghadapi berbagai permasalahan yang muncul dalam kehidupan sehari-hari. Selain itu, pendidikan juga memiliki peran dalam membentuk karakter baik terhadap peserta didik sebagai bagian terpenting dalam mewujudkan kemajuan suatu bangsa. Diharapkan dengan mempersiapkan sumber daya manusia berupa kemampuan peserta didik yang cakap dan berkarakter yang baik dapat memajukan suatu bangsa sebagaimana yang disebutkan dalam tujuan pendidikan nasional, yaitu sebagai berikut :
Tujuan pendidikan nasional adalah untuk mengembangkan kemampuan dan membentuk watak serta peradaban bangsa yang bermartabat dalam rangka mencerdaskan kehidupan bangsa, bertujuan untuk berkembangnya potensi peserta didik agar menjadi manusia yang beriman dan bertakwa pada Tuhan Yang Maha Esa, berakhlak mulia, sehat, berilmu, cakap, kreatif, mandiri, dan menjadi warga Negara yang demokratis serta
bertanggung jawab.1
Tujuan pendidikan dapat dicapai secara menyeluruh apabila proses pembelajaran yang dilakukan di sekolah terlaksana secara optimal. Proses pembelajaran dalam pelaksanaannya melibatkan guru sebagai fasilitator atau
1
pengajar dan siswa sebagai subjek belajar. Peristiwa belajar yang disertai dengan proses pembelajaran akan lebih terarah dan sistematis karena dalam proses pembelajaran terdapat peran guru, bahan belajar dan lingkungan kondusif yang sengaja diciptakan untuk mencapai tujuan yang diinginkan.
Pelaksanaan pembelajaran matematika di sekolah merupakan salah satu upaya yang dapat digunakan untuk mencapai tujuan pembelajaran dalam pendidikan. Pentingnya mempelajari matematika, tidak lain karena perannya dalam berbagai kehidupan, berbagai informasi dan gagasan yang banyak dikomunikasikan atau disampaikan dengan bahasa matematika. Selain itu, berbagai keterampilan atau kecakapan peserta didik juga dapat dikembangkan melalui belajar matematika. Oleh karena itu, mata pelajaran matematika bisa dikatakan sebagai bagian terpenting dalam pembelajaran di sekolah dalam hal ini perannya adalah untuk mempersiapkan dan mengembangkan kemampuan peserta didik.
Pembelajaran matematika pada dasarnya bertujuan untuk melatih pola pikir dan pola sikap siswa. Menurut Kilpatrick, dkk (2001) menyatakan bahwa tujuan pembelajaran matematika adalah membentuk pola pikir siswa yang dapat diukur dari kemampuan atau kecakapan yang dimilikinya, yang disebut dengan kecakapan matematika (mathematical proficiency) dimana terdapat lima jenis kompetensi matematika siswa yang perlu dikembangkan dalam pembelajaran matematika di sekolah, meliputi: pemahaman konsep (conceptual understanding), kelancaran berprosedural (procedural fluency), kompetensi strategis (strategic competency), penalaran adaptif (adaptif reasoning), dan berkarakter produktif
(produktive disposition).2
Pendapat lain mengenai tujuan pembelajaran matematika diungkapkan oleh Widdiharto (2004), yang menyatakan bahwa :
Tujuan pembelajaran matematika adalah terbentuknya kemampuan bernalar pada diri siswa yang tercermin melalui kemampuan berfikir kritis, logis, sistematis, dan memiliki sifat objektif, jujur, disiplin dalam
2
Jeremy Kilpatrick, Jane Swafford, and Bradford Findell (eds.), Adding It Up: Helping
memecahkan suatu permasalahan baik dalam bidang matematika, bidang
pelajaran lain, maupun dalam kehidupan sehari-hari.3
Berdasarkan tujuan pembelajaran yang telah diungkapkan diatas, dapat dikatakan bahwa pengembangan dan pemanfaatan kemampuan penalaran siswa menjadi salah satu tujuan penting dalam pembelajaran matematika di sekolah. Kemampuan penalaran yang dimaksud adalah kemampuan penalaran adaptif dimana kemampuan ini sebagai bagian dari salah satu kompetensi matematika yang harus dikuasai siswa untuk dipakai dalam menyelesaikan suatu permasalahan.
Kemampuan penalaran adaptif merupakan kemampuan siswa untuk
berpikir secara logis mengenai hubungan antara konsep dan situasi.4 Kemampuan
penalaran adaptif melibatkan proses berpikir atau bernalar secara mendalam ketika menghadapi persoalan matematika. Proses penalaran ini dinyatakan dengan benar atau valid apabila merupakan hasil dari pengamatan yang seksama dari berbagai alternatif dan menggunakan pengetahuan dalam memberikan penjelasan dan pembenaran suatu kesimpulan. Salah satu bentuk manifestasi dari penalaran adaptif adalah memberikan pembenaran terhadap proses dan hasil suatu pekerjaan. Pembenaran di sini dimaksudkan sebagai naluri dalam memberikan alasan-alasan yang cukup, misalnya dalam pembuktian matematika atau dalam memeriksa kebenaran dari suatu pernyataan matematika.
Banyak upaya yang telah dilakukan terhadap proses pembelajaran matematika di sekolah, namun masih terlihat belum mengacu pada pengembangan terhadap kompetensi matematika berupa kemampuan bernalar siswa. Hal tersebut bisa dilihat dari hasil penelitian yang ada dan prestasi belajar dalam bidang matematika yang didalamnya mengukur kemampuan penalaran sebagai bagian dari kompetensi matematika. Salah satunya adalah hasil penelitian PISA (Program for International Student Assessment) pada tahun 2009 melakukan assessment terhadap kemampuan literasi matematika untuk siswa berusia 15
3
Rachmadi Widdiharto, Model-model Pembelajaran Matematika SMP, (Yogyakarta : PPPG Matematika, 2004), h. 1
4
tahun, diperoleh hasil bahwa kemampuan siswa Indonesia masih tergolong rendah
yaitu mendapat peringkat ke- 61 dari 65 peserta.5
Penelitian lain dilakukan oleh TIMSS (Trend in International Mathematics and Science Study) pada tahun 2011 melakukan tes kemampuan matematika terhadap siswa kelas 8 terdiri atas kemampuan dalam pengetahuan (knowing), aplikasi (applying), dan penalaran (reasoning) menampilkan kemampuan siswa Indonesia menduduki peringkat ke-38 dari 42 negara dengan nilai rata-rata 386,
dibawah rata-rata internasional 500.6 Hasil penelitian tersebut menunjukkan
bahwa masih rendahnya kemampuan matematika siswa dilihat dari skor yang diperoleh sebagai pengukur terhadap kompetensi matematika yang didalamnya terdapat kemampuan penalaran siswa.
Berdasarkan hasil observasi di SMA N 5 Kota Tangerang Selatan melalui wawancara dengan guru matematika kelas XI IPA menunjukkan bahwa kemampuan penalaran adaptif siswa masih sangat rendah. Hal ini dapat terlihat dari siswa yang masih mengalami kesulitan ketika dihadapkan pada soal-soal matematika khususnya soal yang mengukur kemampuan penalaran adaptif dan guru kurang memperhatikan perkembangan kemampuan penalaran khususnya kemampuan penalaran adaptif siswa dalam kegiatan pembelajarannya. Hal ini yang menyebabkan lemahnya kemampuan penalaran adaptif siswa, akibatnya mereka tidak dapat menyelesaikan soal-soal matematika dengan baik sehingga hasil belajar matematika di sekolah tersebut rendah.
Rendahnya kemampuan penalaran adaptif siswa tidak lain karena dipengaruhi oleh beberapa faktor, diantaranya adalah masih sedikit nya pembelajaran yang terjadi di sekolah dengan menerapkan kemampuan berpikir siswa untuk menyelesaikan masalah selama proses pembelajaran berlangsung. Pada umum nya guru hanya memberikan latihan untuk menyelesaikan persoalan matematika sebatas di tingkat pemahaman siswa saja, akan tetapi jarang atau sedikit sekali memberikan persoalan matematika yang mengharuskan penggunaan
5
OECD, PISA 2009 Results : Executive Summary, 2010, tersedia di (http://www.oecd.org/pisa/pisaproducts/46619703.pdf), diakses tanggal 10 mei 2013 pukul 15.44
6
kemampuan seperti menganalisa, berpikir kritis dan kreatif sebagai alat untuk menyelesaikannya.
Penyebab lain kemampuan penalaran adaptif siswa masih rendah yaitu dikarenakan oleh metode pembelajaran matematika yang dipakai kebanyakan guru masih menggunakan pendekatan tradisional. Pembelajaran dengan pendekatan ini adalah pembelajaran dengan menggunakan metode konvensional dimana pelaksanaannya masih menerapkan kombinasi antara metode ceramah dan ekspositori selama proses pembelajaran berlangsung. Penggunaan metode tersebut menjadikan peran guru semakin dominan dan siswa hanya pasif menerima begitu saja apa yang diberikan oleh guru. Pembelajaran yang digunakan juga sedikit sekali menerapkan aktivitas siswa secara optimal sehingga yang terjadi adalah selain mengakibatkan daya berpikirnya lemah, siswa pun menjadi kurang memiliki kreativitas yang tinggi dan berpikir kritis terhadap penyelesaian persoalan matematika.
Berdasarkan dari beberapa persoalan tersebut, maka dapat dikatakan bahwa kemampuan penalaran adaptif menjadi bagian penting yang masih harus dikembangkan dan dimiliki oleh siswa. Oleh karen itu, diperlukan suatu proses pembelajaran matematika yang dapat mengembangkan dan mengaplikasikan kemampuan tersebut dalam setiap tahapan proses pembelajarannya. Salah satu alternatif yang mungkin dapat dimanfaatkan untuk mencapai tujuan ini adalah dengan menerapkan metode penemuan terbimbing (guided discovery method) dalam pembelajaran matematika.
Metode penemuan terbimbing adalah suatu metode pembelajaran yang menekankan proses berpikir secara kritis dan analitis untuk mencari dan menemukan sendiri jawaban berupa konsep atau prinsip umum terhadap suatu bahan atau data yang disediakan dengan bimbingan guru. Metode ini memberikan keleluasaan bagi siswa untuk melakukan penyelidikan dan menarik suatu
kesimpulan dengan menggunakan terkaan, intuisi, dan mencoba – coba (trial and
Pembelajaran dengan metode penemuan terbimbing menempatkan peran guru hanya sebagai pendamping yaitu memberikan bimbingan seperlunya kepada siswa dalam mencari dan menemukan suatu konsep atau pengetahuan. Dengan bimbingan guru ini diharapkan dapat menstimulasi siswa untuk mulai melakukan berpikir dengan kemampuan penalarannya. Kemudian dengan proses penemuan yang dilakukannya, akhirnya siswa juga dapat mengembangkan kemampuan penalaran adaptifnya sehingga dapat dimanfaatkan tidak hanya dalam proses pembelajaran, melainkan juga dalam kehidupan sehari-hari.
Berdasarkan permasalahan yang telah diuraikan, peneliti tertarik
melakukan penelitian eksperimen dengan mengambil judul : “Pengaruh Metode
Penemuan Terbimbing (Guided Discovery Method) dalam Pembelajaran Matematika terhadap Kemampuan Penalaran Adaptif siswa SMA Kelas XI IPA”
B. Identifikasi Masalah
Berdasarkan uraian latar belakang masalah di atas, maka dapat diidentifikasikan permasalahan sebagai berikut :
1. Hasil penelitian PISA dan TIMSS menunjukkan bahwa kemampuan
penalaran siswa masih rendah.
2. Masih sedikitnya guru yang menerapkan pembelajaran yang menekankan
pada proses berpikir siswa.
3. Pembelajaran matematika di sekolah masih banyak yang menggunakan
pendekatan tradisional.
4. Pembelajaran matematika di sekolah masih berpusat pada guru, sehingga
siswa kurang berpartisipasi dan hanya pasif selama pembelajaran.
5. Siswa belum mampu memberikan alasan atau bukti terhadap kebenaran suatu
pernyataan.
C. Pembatasan Masalah
Berdasarkan uraian yang telah disampaikan di atas, maka dalam penelitian ini perlu diadakan pembatasan masalah agar pengkajian masalah dalam penelitian ini lebih terfokus dan terarah.
Penelitian ini akan difokuskan dan diukur pada hal-hal sebagai berikut :
1. Metode penemuan yang dimaksud dalam penelitian ini adalah metode
penemuan terbimbing di mana dalam pembelajarannya siswa didorong untuk berpikir kritis dalam menganalisis suatu data sehingga dapat menemukan konsep atau prinsip umum berdasarkan bahan atau data yang telah disediakan oleh guru. Peran guru dalam pembelajaran ini adalah sebagai penunjuk jalan, membimbing siswa agar menggunakan ide, konsep, dan keterampilan yang sudah mereka pelajari sebelumnya untuk mendapatkan pengetahuan baru.
2. Kemampuan penalaran adaptif yang akan diteliti meliputi kemampuan dalam
memberikan alasan atau bukti terhadap kebenaran suatu pernyataan, menarik kesimpulan dari suatu pernyataan, dan memeriksa kesahihan dari suatu argumen.
3. Kemampuan siswa yang akan diteliti yaitu siswa kelas XI IPA SMA dengan
materi trigonometri.
D. Rumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, rumusan masalah dalam penelitian ini adalah :
1. Bagaimana kemampuan penalaran adaptif siswa yang diajarkan dengan
metode penemuan terbimbing (guided discovery method) ?
2. Bagaimana kemampuan penalaran adaptif siswa yang diajarkan dengan
pembelajaran konvensional ?
3. Apakah terdapat pengaruh metode penemuan terbimbing (guided discovery
method) terhadap kemampuan penalaran adaptif siswa dalam pembelajaran
E. Tujuan Penelitian
Berdasarkan rumusan masalah yang telah disebutkan, tujuan dalam penelitian ini adalah:
1. Mengetahui dan mendeskripsikan kemampuan penalaran adaptif siswa yang
mendapat pembelajaran dengan metode penemuan terbimbing.
2. Mengetahui dan mendeskripsikan kemampuan penalaran adaptif siswa yang
mendapat pembelajaran dengan pembelajaran konvensional.
3. Mengetahui dan menganalisis pengaruh metode penemuan terbimbing
terhadap kemampuan penalaran adaptif siswa.
F. Manfaat Penelitian
Penelitian ini diharapkan dapat memberikan manfaat, diantaranya adalah bagi :
1. Guru
Penggunaan metode penemuan terbimbing dalam pembelajaran matematika sebagai suatu alternatif meningkatkan kemampuan penalaran adaptif siswa.
2. Siswa
Setelah memperoleh penyajian materi dengan menggunakan metode penemuan terbimbing, diharapkan dapat meningkatkan kemampuan penalaran adaptif siswa.
3. Sekolah
Sebagai suatu sumbangan pemikiran dalam upaya peningkatan kualitas pembelajaran matematika
4. Bagi peneliti
Sebagai pengalaman langsung dalam pelaksanaan pembelajaran dengan metode penemuan terbimbing.
5. Bagi pembaca
9
A. Deskripsi Teoritik
1. Teori Belajar dan Pembelajaran Matematika
a. Teori Belajar yang Relevan dengan Metode Penemuan Terbimbing (Guided discovery method)
Berikut ini adalah beberapa teori belajar yang berkaitan dengan metode penemuan terbimbing.
1) Teori Pembelajaran Konstruktivisme
Teori pembelajaran konstruktivisme menyatakan bahwa perkembangan kognitif seseorang merupakan suatu proses individu secara aktif membangun sistem arti pemahaman dan realita melalui pengalaman dan interaksi baik antar
individu maupun dengan lingkungan.1 Hal terpenting dari teori konstruktivisme
berarti apabila siswa ingin mendapatkan informasi yang kompleks agar tertanam dalam benaknya, maka siswa itu sendiri yang harus aktif menemukan dan mentransformasikan informasi kompleks tersebut.
Tasker (1992) mengungkapkan bahwa terdapat tiga penekanan dalam teori belajar konstruktivisme meliputi : (1) peran aktif siswa dalam mengkonstruksi pengetahuan secara bermakna, (2) pentingnya membuat kaitan antara gagasan dalam pengkontruksian secara bermakna, dan (3) mengaitkan antara gagasan
dengan informasi baru yang diterima.2
Menurut Slavin (1994) terkait teori konstruktivisme, menyatakan bahwa : Satu prinsip penting dalam psikologi pendidikan adalah bahwa guru tidak dapat hanya sekedar memberikan pengetahuan pada siswa, tetapi siswa harus membangun sendiri pengetahuan dalam benaknya. Guru dapat memberikan kemudahan dalam proses ini dengan memberikan kesempatan siswa untuk menentukan atau menerapkan ide-ide mereka sendiri untuk belajar, dan membelajarkan siswa dengan secara sadar menggunakan strategi mereka sendiri untuk belajar. Guru dapat memberikan siswa anak
1
Trianto, Model Pembelajaran Terpadu dalam Teori dan Praktek, (Jakarta : Prestasi Pustaka Publisher, 2007), h. 27
2
tangga yang membawa siswa kepemahaman yang lebih tinggi, dengan
catatan siswa sendiri yang harus memanjatnya.3
Beberapa prinsip yang sering diambil dari konstruktivisme menurut
Suparno (1997), antara lain : 4
1. Pengetahuan dibangun oleh siswa secara aktif.
2. Tekanan dalam proses belajar terletak pada siswa.
3. Mengajar adalah membantu siswa belajar.
4. Tekanan dalam proses belajar lebih pada proses, bukan pada hasil akhir.
5. Kurikulum menekankan partisipasi siswa.
6. Guru sebagai fasilitator.
Berdasarkan uraian di atas, dapat dikatakan bahwa inti dari teori pembelajaran konstruktivisme adalah lebih menekankan pada siswa untuk aktif mengkonstruksi atau membangun pengetahuannya sendiri sedangkan peran guru hanya sebagai pembimbing dan fasilitator selama proses pembelajaran.
2) Teori Jerume Bruner
Teori belajar dari Bruner lebih dikenal dengan istilah pembelajaran penemuan (discovery learning). Teori belajar ini menindaklanjuti teori belajar konstruktivisme yang menyatakan bahwa siswa harus aktif di dalam kelas. Proses aktif tersebut dapat dilakukan dengan cara melalui suatu pembelajaran penemuan (discovery learning) yaitu di mana siswa mengorganisasi bahan yang dipelajari
dengan suatu bentuk akhir.5 Prosedur ini berbeda dengan jenis pembelajaran
penerimaan (reception learning), di mana guru menerangkan semua informasi dan
siswa harus mempelajari semua bahan atau informasi tersebut.6
Bruner menyatakan tentang pembelajaran yang seharusnya dilakukan di sekolah sebagai berikut :
Belajar akan lebih bermakna bagi siswa jika mereka memusatkan perhatiannya untuk memahami struktur materi yang dipelajari. Untuk memperoleh struktur informasi, siswa harus aktif di mana mereka harus
3
Trianto, loc. cit. 4
Ibid., h. 29
5
Dalyono, Psikologi Pendidikan, (Jakarta : Rineka Cipta, 2005), h. 41
6
mengidentifikasi sendiri prinsip-prinsip kunci daripada hanya sekedar menerima penjelasan dari guru. Oleh karena itu guru harus memunculkan
masalah yang mendorong siswa untuk melakukan kegiatan penemuan.7
Aplikasi ide-ide Bruner dalam pembelajaran, digambarkan oleh Woolfolk (1997) sebagai berikut : 8
1. Memberikan contoh dan bukan contoh dari konsep yang dipelajari.
2. Membantu siswa mencari hubungan antar konsep.
3. Mengajukan pertanyaan dan membiarkan siswa mencoba menemukan sendiri
jawabannya.
4. Medorong siswa untuk membuat dugaan yang bersifat intuitif.
Berdasarkan uraian di atas, maka dapat dikatakan bahwa pembelajaran yang terjadi di sekolah sudah seharusnya dapat dilakukan dengan menggunakan pembelajaran yang mendorong kepada siswa untuk menemukan sendiri konsep atau pengetahuan yang sedang dipelajari. Pembelajaran ini bisa dilakukan dengan cara guru menyediakan bahan yang didalamnya dimunculkan suatu masalah yang
dapat mendorong siswa untuk melakukan kegiatan-kegiatan seperti
mengidentifikasi, memahami sampai pada menemukan prinsip-prinsip umum yang ada dalam bahan atau materi yang telah disediakan.
b. Pembelajaran Matematika
Belajar merupakan aktivitas yang paling utama dalam keseluruhan proses di setiap jenjang pendidikan. Ini berarti berhasil atau tidaknya pencapaian tujuan pendidikan tergantung kepada bagaimana proses belajar yang dialami oleh siswa. Oleh karena itu, pemahaman tentang arti belajar dengan segala aspek dan bentuknya harus dapat dipahami agar tidak terjadi kekeliruan dalam proses belajar.
Belajar dapat diartikan sebagai suatu proses usaha yang dapat dilakukan seseorang untuk memperoleh suatu perubahan tingkah laku yang baru secara keseluruhan, sebagai hasil pengalamannya sendiri dalam interaksi dengan
7
Trianto, op. cit, h. 33
8
lingkungannya.9 Adanya perubahan dalam diri seseorang di sini berarti dapat dijadikan sebagai bukti bahwa seseorang tersebut telah melakukan kegiatan belajar.
Morgan, dalam buku Introduction to Psychology mengemukakan, “belajar
adalah setiap perubahan yang relatif menetap dalam tingkah laku yang terjadi sebagai suatu hasil dari latihan atau pengalaman”.10
Definisi ini menyatakan bahwa untuk dapat disebut belajar, maka perubahan yang terjadi harus lah relatif menetap, artinya tidak bersifat sementara. Perubahan itu sendiri merupakan hasil yang diperoleh dari proses belajar selama kurun waktu yang cukup panjang.
Pendapat lain tentang belajar disampaikan oleh Hamalik, belajar diartikan
sebagai modifikasi atau memperteguh kelakuan melalui pengalaman.11 Menurut
pengertian tersebut dapat dikatakan bahwa belajar merupakan suatu proses, suatu kegiatan dan bukan suatu hasil atau tujuan. Dalam hal ini berarti belajar bukan hanya sekedar mengingat, akan tetapi lebih luas daripada itu, yakni mengalami.
Good dan Bophy dalam bukunya Educational Psychology : A Realistic
Approach menjelaskan bahwa belajar merupakan suatu proses yang tidak dapat dilihat dengan nyata, proses itu terjadi di dalam diri seseorang yang sedang mengalami belajar dalam usahanya untuk memperoleh hubungan-hubungan
baru.12 Hubungan-hubungan baru itu sendiri dapat berupa : antara
perangsang-perangsang, antara reaksi-reaksi, atau antara perangsang dan reaksi. Oleh karena itu dapat dikatakan bahwa belajar itu bukan berupa tingkah laku yang nampak akan tetapi suatu proses yang terjadi secara internal dalam diri seseorang.
Berdasarkan beberapa pendapat dari para ahli, maka dapat disimpulkan bahwa pengertian belajar adalah suatu proses yang terjadi dalam diri seseorang melalui pengalaman atau interaksi dengan lingkungan sehingga hasilnya di dapat suatu perubahan tingkah laku yang bersifat relatif menetap pada diri seseorang.
9
Slameto, Belajar dan Faktor-faktor yang Mempengaruhinya, (Jakarta : Rineka Cipta, 2003), h. 2
10
M. Ngalim Purwanto, Psikologi Pendidikan, (Bandung : Remaja Rosdakarya, 2011), h. 84
11
Oemar Hamalik, Kurikulum dan Pembelajaran, (Jakarta : Bumi Aksara, 2009), h. 36
12
Adapun perubahan tingkah laku tersebut sebagai hasil belajar dapat berupa perubahan sikap, pengetahuan, keterampilan, dan sebagainya.
Pembelajaran menurut Corey (1986), adalah suatu proses dimana lingkungan seseorang secara disengaja dikelola untuk memungkinkan ia turut serta dalam tingkah laku tertentu dalam kondisi-kondisi khusus atau menghasilkan
respon terhadap situasi tetentu.13 Pendapat lain yang sejalan tentang pembelajaran
disampaikan oleh Fontana yaitu pembelajaran merupakan upaya penataan lingkungan yang memberi nuansa agar program belajar tumbuh dan berkembang
secara optimal.14 Dengan demikian dapat dikatakan bahwa proses pembelajaran
lebih kepada bersifat eksternal yang sengaja direncanakan dan dapat bersifat rekayasa perilaku.
Menurut UUSPN No. 20 tahun 2003 menyatakan bahwa pembelajaran adalah proses interaksi peserta didik dengan pendidik dan sumber belajar pada
suatu lingkungan belajar.15 Hamalik memberikan definisi pembelajaran, yaitu
sebagai suatu kombinasi yang tersusun meliputi unsur-unsur manusiawi, material, fasilitas, perlengkapan, dan prosedur yang saling mempengaruhi mencapai tujuan
pembelajaran.16 Salah satu bagian terpenting dalam proses pembelajaran adalah
terjadinya interaksi antara berbagai unsur yang terkait dalam pembelajaran. Oleh karena itu, dengan adanya interaksi maka akan terjadi kegiatan belajar didukung dengan ketersediaan berbagai unsur yang diperlukan sehingga diharapkan proses pembelajaran itu sendiri dapat terlaksana secara optimal.
Berdasarkan beberapa pengertian tentang pembelajaran yang diungkapkan oleh para ahli, maka dapat disimpulkan bahwa pembelajaran adalah suatu upaya untuk menciptakan kondisi agar suasana atau kegiatan belajar dapat terjadi dengan melibatkan interaksi berbagai unsur yang diperlukan sehingga proses belajar dapat berlangsung secara optimal.
13
Syaiful Sagala, Konsep dan Makna Pembelajaran untuk Membantu Memecahkan
Problematika Belajar dan Mengajar, (Bandung : Alfabeta, 2008), h. 61
14
Tim MKPBM, Common Text Book Strategi Pembelajaran Matematika Kontemporer, (Bandung : JICA-UPI, 2001), h. 8
15
Sagala, op. cit, h. 62
16
Matematika merupakan salah satu bidang studi yang dipelajari siswa dari tingkat dasar sampai perguruan tinggi. Pentingnya mempelajari matematika tidak lain dikarenakan memiliki banyak peran terhadap berbagai segi kehidupan, seperti yang diungkapkan oleh Cornelius (1982), belajar matematika diperlukan karena matematika merupakan (1) sarana berpikir yang jelas dan logis, (2) sarana untuk memecahkan masalah kehidupan sehari-hari, (3) sarana mengenal pola-pola hubungan dan generalisasi pengalaman, (4) sarana untuk mengembangkan kreativitas, dan (5) sarana untuk meningkatkan kesadaran terhadap perkembangan budaya.17
Menurut Cobb (1991), belajar matematika bukanlah suatu proses „pengepakan’ pengetahuan secara hati-hati, melainkan hal mengorganisir aktivitas, dimana kegiatan ini diinterpretasikan secara luas termasuk aktivitas dan
berpikir konseptual.18 Adanya aktivitas yang dilakukan oleh siswa menunjukkan
bahwa siswa tersebut sedang melakukan kegiatan belajar dalam hal ini yaitu belajar matematika. Oleh karena nya, belajar matematika itu sendiri dapat dilakukan oleh siswa dengan cara siswa melakukan berbagai aktivitas yang berkaitan dengan matematika seperti melakukan perhitungan, memanipulasi, mencari solusi dan menyelesikan permasalahan, serta melakukan penarikan kesimpulan, sehingga dengan berbagai aktivitas tersebut dapat meningkatkan kemampuan berpikir siswa.
Cobb juga mendefinisikan bahwa belajar matematika merupakan proses
dimana siswa secara aktif mengkonstruksi pengetahuan matematika.19
Berdasarkan definisi tersebut, jika dikaitkan dengan pembelajaran, maka dapat disimpulkan bahwa pembelajaran matematika adalah suatu upaya untuk menciptakan kondisi agar suasana atau kegiatan belajar dapat terjadi dengan melibatkan berbagai unsur dan peran aktif siswa guna memperoleh ilmu pengetahuan dan keterampilan matematika sehingga nantinya diharapkan dapat digunakan dalam kehidupan sehari-hari.
17
Mulyono Abdurrahman, Pendidikan bagi Anak Berkesulitan Belajar, (Jakarta : Rineka Cipta, 2003), h. 253
18
MKPBM, op. cit, h. 71
Secara umum pengetahuan dan keterampilan sebagai kompetensi yang harus dicapai dalam belajar matematika menurut Kilpatrick, dkk. (2001)
dirumuskan menjadi 5 bagian, yaitu :20
1. Pemahaman konsep (conceptual understanding), yaitu kemampuan dalam
memahami konsep, operasi, dan relasi dalam matematika.
2. Kelancaran berprosedur (prosedural fluency), yaitu kemampuan dalam
menerapkan prosedur secara fleksibel, akurat, efisiensi, dan benar.
3. Kompetensi strategis (strategic competence), yaitu kemampuan untuk
memformulasikan, merepresentasikan, dan menyelesaikan permasalahan matematika.
4. Penalaran adaptif (adaptive reasoning), yaitu kemampuan untuk berpikir
secara logis, melakukan refleksi (perenungan), memberikan penjelasan, dan mengajukan pembenaran.
5. Disposisi produktif (productive disposition), yaitu kemampuan untuk selalu
memandang matematika secara positif, menguntungkan, dan bermakna. Selain lima kompetensi di atas, menurut Suhendra, dkk. terdapat beberapa
kompetensi lain yang juga dapat dicapai dalam belajar matematika, yaitu : 21
1. Komunikasi ide atau gagasan yang didalamnya terdapat kegiatan menafsirkan
dan menyatakan ide atau gagasan secara tulisan, lisan, dan atau melalui perbuatan, serta kegiatan deminstrasi.
2. Koneksitas antar topik, satu topik matematika dihubungkan dengan topik
matematika lain atau mengaitkan sebuah topik matematika dengan bidang studi lain dalam kegiatan pembelajaran.
3. Pemecahan masalah yang meliputi bagaimana memahami masalah, memilih
strategi pemecahan masalah, dan menyelesaikan atau memecahkan masalah itu sendiri.
Berdasarkan uraian diatas, dapat dikatakan bahwa terdapat beberapa kompetensi yang harus dicapai dalam pembelajaran matematika, salah satunya adalah kemampuan penalaran adaptif.
20
Kilpatrick, op. cit., h. 116
21
2. Kemampuan Penalaran Adaptif (Adaptive Reasoning) a. Pengertian Penalaran Adaptif
Salah satu yang menjadi tujuan dan aspek kompetensi dasar dalam pembelajaran matematika adalah penalaran. Penalaran (reasoning) dapat didefinisikan sebagai “proses pencapaian kesimpulan logis berdasarkan fakta dan sumber yang relevan, pentransformasian yang diberikan dalam urutan tertentu untuk menjangkau kesimpulan”.22
Fadjar Shadiq (2004) memberikan definisi tentang penalaran yaitu “suatu kegiatan, suatu proses atau suatu aktivitas berpikir untuk menarik kesimpulan atau membuat suatu pernyataan baru yang benar berdasarkan pada beberapa pernyataan yang kebenarannya telah dibuktikan atau diasumsikan sebelumnya”.23 Lebih lanjut lagi, Depdiknas dalam Fadjar Shadiq menyebutkan bahwa “materi matematika dan penalaran matematika merupakan dua hal yang tidak dapat dipisahkan. Materi matematika dipahami melalui penalaran, dan penalaran dipahami dan dilatihkan melalui belajar materi matematika”.24
Kemampuan penalaran berperan penting untuk mengetahui dan mempelajari matematika. Kemampuan bernalar menjadikan siswa dapat memecahkan masalah dalam kehidupannya, di dalam dan di luar sekolah. Dengan menggunakan penalaran, maka siswa dapat memvalidasi cara berpikir mereka sehingga dapat meningkatkan rasa percaya diri dengan matematika dan berpikir secara matematik.
Penalaran dapat digolongkan menjadi dua jenis yaitu penalaran induktif dan penalaran deduktif.
Penalaran induktif adalah proses berpikir yang berusaha menghubungkan fakta-fakta atau kejadian-kejadian khusus yang sudah diketahui menuju kepada
22
Lia Kurniawati, ALGORITMA Jurnal Matematika dan Pendidikan Matematika, (Jakarta : CeMED, 2006), h. 81
23
Fadjar Shadiq, Penalaran, Pemecahan Masalah, dan Komunikasi dalam Pembelajaran
Matematika, (Yogyakarta : PPPG Matematika, 2004), h. 2
24
Sri Wardhani, Paket Fasilitasi Pemberdayaan KKG/MGMP Matematika “Analisis SI
suatu kesimpulan yang bersifat umum.25 Beberapa kegiatan atau proses yang tergolong dalam penalaran induktif diantaranya : (a) menarik kesimpulan dari satu kasus atau sifat khusus yang satu diterapkan pada kasus khusus yang lainnya (transduktif), (b) penarikan kesimpulan berdasarkan keserupaan data atau proses (analogi), (c) penarikan kesimpulan umum berdasarkan sejumlah data yang teramati (generalisasi), (d) memperkirakan jawaban, solusi atau kecenderungan : interpolasi dan ekstrapolasi, (e) memberi penjelasan terhadap model, fakta, sifat, hubungan, atau pola yang ada, dan (f) menggunakan pola hubungan untuk
menganalisis situasi, dan menyusun konjektur. 26
Penalaran deduktif adalah “the process of reaching a conclusion by
applying general assumptions, procedures, or principles”27, yakni proses mencapai kesimpulan dengan menerapkan asumsi umum, prosedur, atau prinsip-prinsip. Beberapa kegiatan atau proses yang tergolong dalam penalaran deduktif diantaranya : (a) melaksanakan perhitungan berdasarkan aturan atau rumus tertentu, (b) menarik kesimpulan logis berdasarkan aturan inferensi, memeriksa validitas argumen, membuktikan, dan menyusun argumen yang valid, dan (c) menyusun pembuktian langsung, pembuktian tak langsung dan pembuktian
dengan induksi matematika. 28
Kegiatan atau proses penalaran induktif dan deduktif sering kali dilihat sebagai suatu proses berpikir yang terpisah. Padahal, kedua proses ini merupakan suatu pemikiran yang berjalan seiringan. Kemampuan berpikir deduktif seseorang sering kali muncul setelah kemampuan berpikir induktif dikuasai. Hal tersebut sejalan dengan apa yang disampaikan oleh Depdiknas, yaitu :
Ciri utama matematika adalah penalaran deduktif, yaitu kebenaran suatu konsep atau pernyataan diperoleh sebagai akibat logis dari kebenaran sebelumnya. Sehingga kaitan antar konsep atau pernyataan dalam matematika bersifat konsisten. Namun demikian, dalam pembelajaran,
25
Ibid., h. 12
26
Utari Sumarmo, Berfikir dan Disposisi Matematik : Apa, Mengapa, dan Bagaimana
Dikembangkan pada Peserta Didik, (Bandung : FPMIPA UPI, 2010), h. 6
27
Aufmann, dkk., Mathematical Thingking and Quantitative Reasoning, (Boston : Houghton Mifflin Company, 2008), h. 6
28
pemahaman konsep sering diawali secara induktif melalui pengalaman peristiwa nyata atau intuisi.29
Pada tahun 2001, National Research Council (NRC) memperkenalkan satu penalaran yang menurut penelitinya mencakup kemampuan penalaran induktif dan deduktif, yang kemudian diperkenalkan dengan istilah penalarn adaptif. Dalam laporan penelitiannya, Kilpatrick, dkk. (2001), menyampaikan definisi penalaran adaptif, yaitu “adaptive reasoning – capacity for logical thought, reflection, explanation, and justification”.30 Pernyataan tersebut dapat diterjemahkan bahwa penalaran adaptif merupakan kemampuan siswa untuk menarik kesimpulan secara logis, memperkirakan jawaban, memberikan penjelasan mengenai konsep dan prosedur jawaban yang digunakan, serta menilai kebenarannya secara matematik.
Terkait dengan penalaran adaptif, Kilpatrick juga memberikan penjelasan lain, yaitu :
Adaptive reasoning refers to the capacity to think logically about the relationships among concepts and situations. Such reasoning is correct and valid, stems from careful consideration of alternatives, and includes knowledge of how to justify the conclusions.31
Pernyataan di atas menjelaskan bahwa penalaran adaptif merujuk pada kemampuan siswa untuk berpikir secara logis mengenai hubungan antara konsep dan situasi yang dihadapinya. Penalaran yang benar dan sah muncul dari kemampuan untuk menyajikan alternatif secara tepat, termasuk pengetahuan untuk menilai dan menyimpulkan.
Mengacu pada pembelajaran yang melibatkan kemampuan penalaran adaptif, maka suatu konsep tidak cukup dimiliki oleh siswa hanya melalui rangkaian cerita, melainkan harus mampu dirumuskannya dengan menggunakan pemikiran yang logis, sistematis, dan kritis. Kemudian memperkuat mentalnya melalui suatu representasi sehingga mampu mengaplikasikannya pada situasi yang
29
Fadjar Shadiq, Kemahiran Matematika, (Yogyakarta : Depdiknas, 2009), h. 2
30
Kilpatrick, loc. cit. 31
tepat, serta yakin terhadap setiap proses yang dilaluinya dan pengetahuan yang diperolehnya karena telah terbukti kebenarannya.
Kemampuan penalaran adaptif sangat dibutuhkan dalam mempelajari matematika seperti yang dinyatakan oleh Kilpatrick, yaitu
In mathematics, adaptive reasoning is the glue that holds everything together, the lodestar that guides learning. One uses it to navigate through the many facts, procedures, concepts, and solution methods and to see that they all fit together in some way, that they make sense32
yakni dalam matematika, penalaran adaptif merupakan perekat yang memegang segala kemampuan matematika secara bersama-sama, termasuk sebagai pedoman dalam memandu pembelajaran. Seseorang menggunakan penalaran adaptif untuk mencari dan mengatur berbagai fakta, prosedur, konsep, dan cara penyelesaian serta menganalisis bahwa itu semua terjalin dalam suatu langkah yang tepat.
Salah satu bentuk manifestasi dari penalaran adaptif adalah memberikan pembenaran terhadap proses dan hasil suatu pekerjaan. Pembenaran disini dimaksudkan sebagai naluri dalam memberikan alasan-alasan yang cukup, misalnya dalam pembuktian matematika atau dalam memeriksa kebenaran dari suatu pernyataan matematika.
Kemampuan penalaran adaptif dapat ditunjukkan oleh siswa ketika
menemui tiga kondisi, yaitu :33
1. Mengetahui pengetahuan dasar yang cukup. Dalam hal ini siswa mempunyai
pengetahuan prasyarat sebelum memasuki pengetahuan baru.
2. Tugas yang dapat dimengerti atau dipahami dan menyenangkan bagi siswa.
3. Konteks yang disajikan telah dikenal dan menyenangkan bagi siswa.
b. Indikator Kemampuan Penalaran Adaptif
Siswa dikatakan mampu melakukan penalaran bila ia mampu menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika
32 Ibid. 33
dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika. Dalam kaitan itu pada penjelasan teknis Peraturan Dirjen Dikdasmen Depdiknas Nomor 506/C/Kep/PP/2004 tanggal 11 November 2004 tentang rapor merah diuraikan bahwa indikator siswa memiliki kemampuan dalam
penalaran adalah mampu : 34
1. Mengajukan dugaan.
2. Melakukan manipulasi matematika.
3. Menarik kesimpulan, menyusun bukti, memberikan alasan atau bukti
terhadap kebenaran solusi.
4. Menarik kesimpulan dari pernyataan.
5. Memeriksa kesahihan suatu argumen.
6. Menemukan pola atau sifat dari gejala matematis untuk membuat
generalisasi.
Seseorang dikatakan mampu menggunakan penalarannya secara adaptif sesuai dengan kebutuhan, situasi, dan kondisi, bila ia telah dapat melakukan
beberapa hal di bawah ini, antara lain : 35
1. Berpikir, bersikap, dan bertindak berdasarkan kaidah-kaidah yang logis.
2. Memberikan alasan terjadi atau tidak terjadinya sesuatu, baik secara induktif
maupun deduktif.
3. Menggunakan ide atau gagasan disertai (jika perlu) dengan argumentasi yang
logis.
Menurut Nurjanah, dkk. dalam Research Article nya yang berjudul “Developing Coursware Of Mathematics For Secondary School Learning As Support For Education Unit Level Curriculum” disebutkan bahwa indikator
penalaran adaptif sebagai berikut :36
1. Competency on propose hypothesis or conjecture (kemampuan dalam mengajukan dugaan atau konjektur).
34
Sri Wardhani, op. cit., h. 14
35
Suhendra, op. cit., h. 7.21
36
Nurjanah, Developing Coursware Of Mathematics For Secondary School Learning As
2. Can give reason of the given answer (dapat memberikan alasan atau bukti terhadap kebenaran suatu pernyataan).
3. Can make conclussion from a statement (dapat membuat kesimpulan dari suatu pernyataan).
4. Can correct the thruth of an argument (dapat memeriksa kesahihan dari suatu argumen).
5. Can find pattern of a mathematics problem (dapat menemukan pola pada suatu gejala atau persoalan matematika).
Berdasarkan uraian diatas, maka indikator yang akan digunakan untuk kepentingan penelitian adalah kemampuan dalam memberikan alasan atau bukti terhadap kebenaran suatu pernyataan, menarik kesimpulan dari suatu pernyataan, dan memeriksa kesahihan dari suatu argumen.
3. Metode Penemuan Terbimbing (Guided Discovery Method) a. Pengertian Metode Penemuan Terbimbing
Metode penemuan (discovery learning) adalah “metode mengajar yang
mengatur pengajaran sedemikian rupa sehingga anak memperoleh pengetahuan yang sebelumnya belum diketahuinya itu tidak melalui pemberitahuan, sebagian
atau seluruhnya ditemukan sendiri”.37 Kegiatan penemuan dilakukan oleh siswa
itu sendiri selama proses pembelajaran untuk menemukan sesuatu hal yang baru bagi dirinya. Hal-hal baru tersebut dapat berupa konsep, teorema, rumus, pola, aturan dan sejenisnya.
Metode penemuan dapat diartikan juga sebagai “suatu prosedur mengajar
yang mementingkan pengajaran perseorangan, manipulasi objek dan lain-lain percobaan, sebelum sampai pada generalisasi”.38 Metode ini lebih menekankan pada pengalaman langsung siswa terlibat dalam pembelajaran sehingga dapat
37
E. T. Ruseffendi, Pengajaran Matematika Moderen untuk Orang Tua Murid dan SPG, (Bandung : Tarsito, 1979), h. 209
38
dikatakan proses dalam kegiatan pembelajaran lebih diutamakan daripada hasil belajarnya.39
Sund berpendapat bahwa “discovery adalah proses mental (misalnya : kegiatan mengamati, mencerna, mengerti, menggolong-golongkan, membuat dugaan, menjelaskan, mengukur, membuat kesimpulan dan sebagainya) dimana siswa mampu mengasimilasi sesuatu konsep atau prinsip”.40
Penggunaan metode ini dalam kelas dilakukan dengan cara siswa dibiarkan menemukan sendiri atau mengalami proses mental itu sendiri, sedangkan peran guru hanya membimbing dan memberikan instruksi.
Menurut Ruseffendi, metode penemuan sangat penting dalam
pembelajaran matematika, sebab : 41
1. Pada kenyataannya ilmu-ilmu itu ditemukan melalui penemuan.
2. Matematika adalah bahasa abstrak, konsep dan lain-lainnya itu akan lebih
baik melekat bila melalui penemuan dengan jalan memanipulasi dan berpengalaman dalam benda-benda kongkrit.
3. Generalisasi itu penting; melalui penemuan generalisasi yang diperoleh akan
lebih mantap.
4. Dapat meningkatkan kemampuan pemecahan masalah.
5. Setiap anak adalah makhluk kreatif.
6. Menemukan sesuatu oleh sendiri dapat menumbuhkan rasa percaya diri
terhadap dirinya sendiri, dapat meningkatkan motivasi (termasuk motivasi intrinsik), melakukan pengkajian lebih lanjut, dapat menumbuhkan sikap positif terhadap matematika.
Pendapat lain yang sejalan dengan Russefendi tentang pentingnya metode penemuan digunakan dalam pembelajaran di sekolah yaitu disampaikan oleh Suryosubroto, menyatakan bahwa metode penemuan merupakan salah satu
39
E. Mulyasa, Menjadi Guru Profesional menciptakan Pembelajaran Kreatif dan
Menyenangkan, (Bandung : Remaja Rosdakarya, 2005), h. 101
40
Roestiyah N.K., Strategi Belajar Mengajar, (Jakarta : Rineka Cipta, 2008), h. 20
41
metode mengajar yang banyak digunakan di sekolah-sekolah yang sudah maju.
Hal itu disebabkan karena : 42
1. Merupakan suatu cara untuk mengembangkan cara belajar siswa aktif.
2. Dengan menemukan sendiri, menyelidiki sendiri, maka hasil yangg diperoleh
akan setia dan tahan lama dalam ingatan, tak mudah dilupakan anak.
3. Pengertian yang ditemukan sendiri merupakan pengertian yang betul-betul
dikuasai dan mudah digunakan atau ditransfer dalam situasi lain.
4. Dengan menggunakan strategi penemuan anak belajar menguasai salah satu
metode ilmiah yang akan dikembangkannya sendiri.
5. Dengan metode penemuan itu juga, anak belajar berpikir analisis dan
mencoba memecahkan problema yang dihadapi sendiri; kebiasaan ini akan ditransfer dalam kehidupan bermasyarakat.
Berdasarkan pendapat yang telah disampaikan oleh beberapa ahli, maka dapat dikatakan bahwa metode penemuan adalah suatu metode mengajar yang menitikberatkan pada aktifitas siswa dalam belajar, mengarahkan siswa untuk melakukan proses kegiatan mental dimana siswa mengasimilasi sesuatu konsep atau prinsip, serta adanya sedikit peran guru dalam pembelajaran sehingga dapat memberikan dampak atau hal positif kepada siswa baik selama proses pembelajaran maupun ketika melakukan kegiatan dalam kehidupan sehari-hari.
Metode penemuan yang digunakan dalam pembelajaran pada awalnya berupa penemuan secara murni. Maier (1995) mengemukakan bahwa penemuan
secara murni disebut sebagai “heuristik”, yakni apa yang hendak ditemukan, jalan
atau proses semata-mata ditentukan oleh siswa itu sendiri.43 Pembelajaran dengan
metode ini dalam kegiatannya siswa diarahkan untuk menemukan sesuatu,
merumuskan suatu hipotesa, atau menarik suatu kesimpulan sendiri.44 Oleh karena
itu, bisa dikatakan pembelajaran seperti ini memerlukan waktu yang relatif lama bagi siswa untuk sampai pada menemukan suatu konsep atau menarik suatu kesimpulan itu sendiri.
42
Suryosubroto, op. cit, h. 191-192
43
Markaban, Model Pembelajaran Matematika dengan Pendekatan Penemuan
Terbimbing, (Yogyakarta : PPPG Matematika, 2006), h. 9
Pembelajaran dengan metode penemuan murni membutuhkan konsep dasar untuk menemukan konsep yang baru, sehingga tidak semua siswa dapat menemukan sendiri kesimpulan yang diharapkan. Mengingat masih adanya kekurangan dalam pembelajaran dengan metode penemuan murni, maka muncul metode penemuan yang dipandu oleh guru.
Metode penemuan yang dipandu oleh guru dikenal dengan metode penemuan terbimbing (guided discovery method). Metode ini melibatkan suatu dialog atau interaksi antara siswa dan guru dimana siswa mencari kesimpulan yang diinginkan melalui suatu urutan pertanyaan yang diatur oleh guru.45 Siswa didorong untuk berpikir sendiri, menganalisis sendiri, sehingga dapat menemukan prinsip umum berdasarkan bahan atau data yang telah disediakan guru. Peran guru dalam metode ini adalah sebagai fasilitator, guru membimbing siswa jika diperlukan. Adapun sampai seberapa jauh siswa dibimbing, tergantung pada kemampuannya dan materi yang sedang dipelajari.
Selain itu, pada pembelajaran yang menerapkan metode penemuan terbimbing, siswa diberikan situasi dimana siswa bebas menyelidiki dan menarik
kesimpulan. Oleh karena itu, aktivitas seperti terkaan, intuisi dan mencoba – coba
(trial and error) hendaknya dianjurkan dan guru sebagai penunjuk jalan dan membantu siswa agar mempergunakan ide, konsep dan keterampilan yang sudah
mereka pelajari untuk menemukan pengetahuan yang baru.46
Metode penemuan terbimbing sangat bermanfaat apabila diterapkan dalam pembelajaran matematika di sekolah. Hal ini sejalan dengan apa yang disampaikan Sobel, menyatakan bahwa “untuk kebanyakaan situasi di dalam kelas, paling baik diterapkan pendekatan penemuan terbimbing, dimana guru memimpin murid dengan tahapan-tahapan yang benar, mengijinkan adanya diskusi, menanyakan pertanyaan yang menuntun, dan memperkenalkan ide pokok bila dirasa perlu”.47
45
Ibid., h. 10
46
Ibid., h. 15.
47
Max A. Sobel dan Evan M. Maletsky, Mengajar Matematika : Sebuah Buku Sumber
Pembelajaran dengan metode penemuan terbimbing, melibatkan peran yang cukup besar dari siswa karena pembelajaran tidak lagi berpusat pada guru tetapi pada siswa. Guru memulai kegiatan belajar mengajar dengan menjelaskan kegiatan yang akan dilakukan siswa dan mengorganisir kelas untuk kegiatan seperti pemecahan masalah, investigasi atau aktivitas lain. Pemecahan masalah merupakan suatu tahap yang penting dan menentukan. Ini dapat dilakukan secara individu maupun kelompok. Dengan membiasakan siswa dalam kegiatan pemecahan masalah diharapkan dapat meningkatkan kemampuan siswa dalam mengerjakan soal matematika, karena siswa dilibatkan berpikir matematika pada saat manipulasi, eksperimen dan menyelesaikan masalah.
b. Langkah-langkah dalam Metode Penemuan Terbimbing (Guided discovery method)
Pembelajaran dengan metode penemuan tebimbing merupakan suatu pembelajaran dimana siswa ditekankan untuk aktif menemukan suatu konsep yang akan dipelajari dengan bimbingan guru sehingga konsep atau pengetahuan yang diperoleh tidak melenceng jauh dari tujuan yang sudah ditetapkan. oleh karena itu, diperlukan suatu langkah-langkah untuk merealisasikan proses pembelajaran tersebut.
Secara garis besar, Mulyasa mengemukakan cara mengajar dengan metode
penemuan menempuh langkah-langkah sebagai berikut: 48
1. Adanya masalah yang akan dipecahkan.
2. Sesuai dengan tingkat perkembangan kognitif peserta didik.
3. Konsep atau prinsip yang harus ditemukan oleh peserta didik melalui
kegiatan tersebut perlu dikemukakan dan ditulis secara jelas.
4. Harus tersedia alat dan bahan yang diperlukan.
5. Susunan kelas diatur sedemikian rupa sehingga memudahkan terlibatnya arus
bebas pikiran peserta didik dalam kegiatan belajar-mengajar.
6. Guru harus memberikan kesempatan kepada peserta didik untuk
mengumpulkan data.
48
7. Guru harus memberikan jawaban dengan tepat dan tepat dengan data dan informasi yang diperlukan peserta didik.
Richard Scuhman memberikan langkah-langkah yang lebih rinci dalam
metode penemuan, sebagai berikut : 49
1. Identifikasi kebutuhan siswa.
2. Seleksi pendahuluan terhadap prinsip-prinsip, pengetahuan konsep dan
generalisasi yang akan dipelajari.
3. Seleksi bahan, dan problema atau tugas-tugas.
4. Membantu memperjelas :
- Tugas atau problema yang akan dipelajari.
- Peranan masing-masing siswa.
5. Mempersiapkan setting kelas dan alat-alat yang diperlukan.
6. Mengecek pemahaman siswa terhadap masalah yang akan dipecahkan dan
tugas-tugas siswa.
7. Memberi kesempatan pada siswa untuk melakukan penemuan.
8. Membantu siswa dengan informasi atau data, jika diperlukan oleh siswa.
9. Memimpin analisis sendiri (self analysis) dengan pertanyaan yang
mengarahkan dan mengidentifikasi proses.
10.Merangsang terjadinya interaksi antar siswa dengan siswa.
11.Memuji dan membesarkan siswa yang bergiat dalam proses penemuan.
12.Membantu siswa merumuskan prinsip-prinsip dan generalisasi atas hasil
penemuannya.
Langkah-langkah yang telah dikemukakan oleh para ahli tersebut menjadi dasar dalam menentukan langkah-langkah pembelajaran dengan menggunakan metode penemuan terbimbing. Terkait pembelajaran menggunakan metode
penemuan terbimbing, Markaban memberikan langkah-langkah sebagai berikut :50
1. Merumuskan masalah yang akan diberikan kepada siswa dengan data
secukupnya, perumusannya harus jelas, hindari pernyataan yang
menimbulkan salah tafsir sehingga arah yang ditempuh siswa tidak salah.
49
Suryosubroto, op. cit, h. 199-200
50
2. Dari data yang diberikan guru, siswa menyusun, memproses, mengorganisir, dan menganalisis data tersebut. Dalam hal ini, bimbingan guru dapat diberikan sejauh yang diperlukan saja. Bimbingan ini sebaiknya mengarahkan siswa untuk melangkah ke arah yang hendak dituju, melalui pertanyaan-pertanyaan, atau LKS.
3. Siswa menyusun konjektur (prakiraan) dari hasil analisis yang dilakukannya.
4. Bila dipandang perlu, konjektur yang telah dibuat siswa tersebut diatas
diperiksa oleh guru. Hal ini penting dilakukan untuk meyakinkan kebenaran prakiraan siswa, sehingga akan menuju arah yang hendak dicapai.
5. Apabila telah diperoleh kepastian tentang kebenaran konjektur tersebut, maka
verbalisasi konjektur sebaiknya diserahkan juga kepada siswa untuk menyusunya. Di samping itu perlu diingat pula bahwa induksi tidak menjamin 100% kebenaran konjektur.
6. Sesudah siswa menemukan apa yang dicari, hendaknya guru menyediakan
soal latihan atau soal tambahan untuk memeriksa apakah hasil penemuan itu benar.
Berdasarkan uraian diatas, maka dalam penelitian ini langkah-langkah metode pembelajaran penemuan terbimbing yang akan dipakai disesuaikan dengan apa yang disampaikan oleh Markaban, yaitu :
1. Guru memberikan rumusan masalah kepada siswa dengan data secukupnya,
dan dengan perumusan yang jelas tidak menimbulkan salah tafsir.
2. Dari data yang diberikan, siswa melakukan kegiatan seperti menyusun,
memproses, mengorganisir, dan menganalisis data tersebut. Guru membimbing siswa agar melangkah ke arah yang tepat melalui pertanyaan-pertanyaan dalam LKS.
3. Siswa menyusun konjektur (perkiraan) dari hasil analisis yang dilakukannya.
4. Guru memeriksa kebenaran konjektur yang sudah dibuat, kemudian siswa
menyusun sendiri kesimpulan dari kegiatan yang telah dilakukan.
5. Setelah siswa menemukan apa yang dicari, guru memberikan soal latihan atau
c. Kelebihan dan Kelemahan
Kelebihan dari metode penemuan terbimbing : 51
1. Siswa dapat berpartisipasi aktif dalam pembelajaran yang disajikan.
2. Menumbuhkan sekaligus menanamkan sikap inquiry (mencari-temukan).
3. Mendukung kemampuan problem solving siswa.
4. Memberikan wahana interaksi antar siswa, maupun siswa dengan guru,
dengan demikian siswa juga terlatih untuk menggunakan bahasa Indonesia yang baik dan benar.
5. Materi yang dipelajari dapat mencapai tingkat kemampuan yang tinggi dan
lebih lama membekas karena siswa dilibatkan dalam proses menemukannya (Marzano, 1992)
Kekurangan dari metode penemuan terbimbing : 52
1. Untuk materi tertentu, waktu yang tersita lebih lama.
2. Tidak semua siswa dapat mengikuti pelajaran dengan cara ini. Di lapangan,
beberapa siswa masih terbiasa dan mudah mengerti dengan metode konvensional.
3. Tidak semua topik cocok disampaikan dengan metode ini. Umumnya
topik-topik yang berhubungan dengan prinsip dapat dikembangkan dengan metode penemuan terbimbing.
4. Pembelajaran Konvensional
Salah satu pendekatan pembelajaran yang masih berlaku dan sangat banyak digunakan oleh guru adalah pembelajaran konvensional. Pembelajaran
konvensional merupakan pembelajaran dimana pelaksanaannya masih
menerapkan kombinasi antara metode ceramah dan ekspositori selama proses pembelajaran berlangsung. Penggunaan metode tersebut menjadik