Bifurkasi pada Model Interaksi Tumbuhan dan Herbivora

(1)

BIFURKASI PADA MODEL INTERAKASI

TUMBUHAN DAN HERBIVORA

IRMA SAHARA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Bifurkasi pada Model Interaksi Tumbuhan dan Herbivora adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Desember 2013

Irma Sahara

(4)

ABSTRAK

IRMA SAHARA. Bifurkasi pada Model Interaksi Tumbuhan dan Herbivora. Dibimbing oleh ALI KUSNANTO dan PAIAN SIANTURI.

Saha dan Bandyopadhyay (2005) memodelkan sistem mangsa-pemangsa yang merepresentasikan interaksi tumbuhan dan herbivora. Pada karya ilmiah ini, dicari bifurkasi yang terjadi dengan terlebih dulu menganalisis kestabilan titik tetap. Ada tiga titik tetap yang diperoleh dengan jenis kestabilan titik tetap ditentukan oleh nilai eigen yang diperoleh dari ketiga titik tetap tersebut. Titik tetap pertama dan kedua bersifat sadel dan terdapat empat kasus pada titik tetap ketiga agar mencapai kestabilan. Dengan pemilihan parameter tertentu, diperoleh bifurkasi Hopf yakni terjadinya perubahan kestabilan dari spiral stabil menjadi spiral tak stabil dan terdapat limit cycle pada titik tetap ketiga.

Kata kunci: bifurkasi Hopf, limit cycle, model interaksi tumbuhan dan herbivora.

ABSTRACT

IRMA SAHARA. Bifurcation Existence in The Interaction Model of Plant and Herbivore. Supervised by ALI KUSNANTO and PAIAN SIANTURI.

Saha and Bandyopadhyay (2005) have modeled prey-predator systems that represent the interactions of plants and herbivores. In this paper, there are three fixed points obtained. The stability type of the fixed point is determined by the eigenvalues of each fixed point. Both first and second fixed points were found to be saddle points; and four cases were associated with the third fixed point. The Hopf bifurcation was obtained for the third fixed point, as the stability type was changed to be unstable spiraled previously stable spiraled. It was also found the existence of the cycle limit. Both of these were the indicators of existence of the Hopf bifurcation.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

BIFURKASI PADA MODEL INTERAKSI

TUMBUHAN DAN HERBIVORA

IRMA SAHARA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Bifurkasi pada Model Interaksi Tumbuhan dan Herbivora Nama : Irma Sahara

NIM : G54080082

Disetujui oleh

Drs Ali Kusnanto, MSi Dr Paian Sianturi

Pembimbing I Pembimbing II

Diketahui oleh

Dr Toni Bakhtiar, MSc Ketua Departemen

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Bifurkasi pada Model Interaksi Tumbuhan dan Herbivora berhasil diselesaikan.

Terima kasih penulis ucapkan kepada ayah, ibu, kakak, serta seluruh keluarga besar atas dukungan, motivasi, kasih sayang dan doa yang tiada henti-hentinya. Ungkapan terima kasih juga disampaikan kepada Bapak Drs Ali Kusnanto, MSi dan Bapak Dr Paian Sianturi selaku pembimbing atas arahan, bimbingan, dan motivasi dalam menyelesaikan tugas akhir ini, kepada Bapak Ir Ngakan Komang Kutha Ardana, MSc yang telah banyak memberi saran dan perbaikan, serta kepada seluruh dosen dan staf Departemen Matematika IPB atas segala ilmu yang diberikan dan bantuannya selama perkuliahan. Tak lupa juga ucapan terima kasih kepada sahabat satu perjuangan Saefrudin, Hadi, dan Herlan serta IKADA, BEM FMIPA 2010, ADKESMAH BEM FMIPA 2011, BEM KM 2012, sahabat POKJA SPP 2012, koordinator POKJA SPP BEM FEMA 2012, Yayasan Karya Salemba Empat, Poliklinik IPB, teman-teman kosan Bara N0. 31, teman-teman satu pengajian, dan sahabat Matematika 42, 43, 44, 45, 46, 47, dan 48 yang telah banyak membantu dalam proses penyusunan tugas akhir ini.

Semoga karya ilmiah ini bermanfaat.

Bogor, Desember 2013

(9)

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

PENDAHULUAN 1

Latar Belakang 1

Tujuan 2

LANDASAN TEORI 2

PEMODELAN 5

PEMBAHASAN 6

Penentuan Titik Tetap Model 6

Analisis Kestabilan Titik Tetap Model 6

Bifurkasi Hopf 9

SIMULASI 10

Dinamika Populasi Tumbuhan dan Herbivora Kasus 1 10 Dinamika Populasi Tumbuhan dan Herbivora Kasus 2 11 Dinamika Populasi Tumbuhan dan Herbivora Kasus 3 13 Dinamika Populasi Tumbuhan dan Herbivora Kasus 4 14

SIMPULAN 15

DAFTAR PUSTAKA 15

LAMPIRAN 16

(10)

DAFTAR TABEL

1 Kondisi kestabilan titik tetap � 9

2 Titik tetap, nilai eigen, dan kestabilan 10

DAFTAR GAMBAR

1 Bidang fase kasus 1 11

3 Bidang fase kasus 2 dengan arah orbit dari dalam ke luar 12

5 Bidang fase kasus 4 dengan arah orbit dari luar ke dalam 14 6 Bidang fase kasus 4 dengan arah orbit dari dalam ke luar 14

DAFTAR LAMPIRAN

1 Penondimensionalan model 16

2 Penentuan titik tetap model interaksi tumbuhan dan herbivora 17

3 Penentuan nilai eigen 19

(11)

PENDAHULUAN

Latar Belakang

Pada suatu ekosistem, salah satu fenomena alami kehidupan adalah peristiwa makan dan dimakan antara individu yang satu dengan yang lainnya. Ada yang menjadi mangsa dan ada yang menjadi pemangsa. Salah satunya adalah interaksi antara tumbuhan (mangsa) dan herbivora (pemangsa) yang mana perilaku dinamis tumbuhan dan herbivora dapat dianalogikan seperti sistem mangsa-pemangsa (prey-predator system).

Interaksi yang lainnya yaitu kompetisi dan simbiosis. Kompetisi tejadi karena memperebutkan makanan yang sama, memperebutkan habitat yang sama atau memperebutkan pasangan untuk berkembang biak. Sedangkan simbiosis terjadi karena adanya hubungan yang erat antara dua jenis makhluk hidup yang berbeda sehingga masing masing makhluk hidup tersebut memilki ketergantungan terhadap makhluk hidup yang lain.Setiap makhluk hidup pasti akan membutuhkan makhluk hidup lainnya. Seiring dengan interaksi tersebut terdapat rangkaian peristiwa makan dan dimakan yang menjadikan ekosistem tetap seimbang karena tidak ada makhluk hidup yang dapat hidup terisolasi atau hidup tersendiri.

Menurut teori interaksi antara pemangsa dan yang dimangsa, hubungan antara tanaman dan herbivora adalah siklus. Ketika tumbuhan (mangsa) dalam jumlah banyak maka herbivora (pemangsa) meningkatkan jumlahnya, sehingga mengurangi populasi mangsa, yang pada gilirannya menyebabkan jumlah dari tumbuhan berkurang. Hal ini menunjukkan bahwa populasi herbivora berfluktuasi di sekitar kapasitas sumber makanan, dalam hal ini tumbuhan (Fatik 2010).

Beberapa faktor berperan ke dalam populasi dan membantu menstabilkan interaksi antara pemangsa dan yang dimangsa. Sebagai contoh, heterogenitas spasial dipertahankan, yang berarti akan selalu ada tanaman yang tidak ditemukan oleh herbivora. Proses ini memainkan peran yang sangat penting bagi herbivora yang memakan satu spesies tanaman dan mencegah herbivora ini menghabiskan sumber makanan mereka. Pertahanan tanaman juga membantu menstabilkan interaksi antara pemangsa dan yang dimangsa. Sebagai contoh tumbuhan mengeluarkan senyawa beracun atau berbahaya yang akan berdampak negatif pada herbivora yang mengkonsumsinya sehingga herbivora tidak meyukainya.

Permasalahan dalam matematika dari model ekologi adalah penetapan syarat-syarat yang menjamin keunikan dari limit cycle model mangsa-pemangsa. Pada model dua dimensi diketahui bahwa bisa saja tidak ada limit cycle dari model kompetisi. Untuk jenis model mangsa-pemangsa, keberadaan dan stabilitas limit cycle terkait keberadaan dan stabilitas titik tetap positif. Jika titik tetap tidak ada maka populasi pemangsa cenderung mengalami kepunahan. Jika titik tetap positif ada dan tidak stabil maka harus muncul setidaknya satu limit cycle.

(12)

makanan dan ruang. Jumlah biomassa tumbuhan yang dirusak oleh herbivora mengikuti Holling tipe III.

Pada karya ilmiah ini akan dibahas tentang kestabilan, bifurkasi, dan perilaku model tumbuhan dan herbivora berdasarkan beberapa kasus yang diperoleh. Pertama melakukan penentuan titik tetap tetap, menetukan matriks Jacobi untuk dilakukan pelinieran, dan menentukan nilai eigen untuk menganalisis kestabilan titik tetap. Kemudian menunjukkan jenis bifurkasi yang terjadi, mengkaji limit cycle yang muncul dari bifurkasi Hopf, serta membahas perilaku dinamis yang diperoleh dari beberapa kasus.

Tujuan

1 Menganalisis kestabilan titik tetap pada model interaksi tumbuhan dan herbivora.

2 Menunjukkan jenis bifurkasi pada model interaksi tumbuhan dan herbivora. 3 Mengkaji perilaku dinamik pada model interaksi tumbuhan dan herbivora. 4 Mengkaji limit cycle yg muncul dari bifurkasi Hopf pada model interaksi

tumbuhan dan herbivora.

LANDASAN TEORI

Misalkan diberi sistem persamaan diferensial taklinear sebagai berikut:

̇ = . (1)

Persamaan (1) disebut sistem dimensi satu atau sistem orde satu dengan � adalah nilai real fungsi dari waktu � dan adalah nilai real fungsi dari . Persamaan (1) memunyai titik tetap = _∗ jika memenuhi _∗ = . Titik tetap disebut juga titik kritis atau titik kesetimbangan (Tu 1994).

Untuk suatu sistem persamaan diferensial taklinear, analisis kestabilannya dilakukan melalui pelinearan. Misalkan dilakukan pelinearan terhadap persamaan (1). Dengan menggunakan ekspansi Taylor di sekitar titik tetapnya diperoleh:

̇ = + � . (2)

Persamaan (2) merupakan sistem persamaan diferensial taklinear dengan matriks Jacobi,

dan � suku berorde tinggi yang bersifat lim

→∞� = . Menurut Tu (1994), pada persamaan (2) disebut pelinearan dari sistem taklinear persamaan (2) yang dituliskan dalam bentuk

(13)

Jika matriks berukuran × , maka suatu vektor tak nol di � disebut vektor eigen dari A jika untuk suatu skalar yang disebut nilai eigen dari berlaku

= . (3)

Vektor disebut vektor eigen yang bersesuaian dengan nilai eigen . Untuk mencari nilai eigen dari matriksyang berukuran × maka persamaan (3) dapat dituliskan kembali sebagai berikut:

− = , (4)

dengan adalah matriks identitas. Persamaan (4) memunyai solusi tak nol jika dan hanya jika

det − Ι = | − | = . (5)

Persamaan (5) disebut persamaan karakteristik dari matriks (Anton dan Rorres 2004).

Misalkan

= .

Dari persamaan (5), maka persamaan karakteristiknya menjadi

| − _{− | = ,}

Dengan demikian diperoleh nilai eigen dari matriks sebagai berikut:

, = � ± √� − Δ.

Menurut Strogatz (1994), untuk menentukan kestabilan dari suatu sistem dapat dilihat dari nilai Δ . Ada tiga kasus untuk nilai Δ, yaitu:

 _{Δ <} .

Jika kedua nilai eigen berbeda tanda maka titik tetap bersifat sadel.  _{Δ >} .

 _{� − Δ >} .

 Jika � > dan kedua nilai eigen real bernilai positif, maka titik tetap bersifat simpul tak stabil.

 Jika � < dan kedua nilai eigen real bernilai negatif, maka titik tetap bersifat simpul stabil.

 _{� − Δ <} .

(14)

 Jika � < dan kedua nilai eigen imajiner ± � , maka titik tetap bersifat spiral stabil.

 Jika � = dan kedua nilai eigen imajiner ± � , maka titik tetap bersifat center.

 _{� − Δ =} .

Parabola � − Δ = adalah garis batas antara simpul dan spiral.

Star nodes atau degenerate terletak pada parabola ini. Jika kedua nilai eigen bernilai sama mama titik tetap bersifat simpul sejati.  _{Δ =} .

Jika salah satu nilai eigen bernilai nol, maka titik asal bersifat titik tetap tak terisolasi.

Penondimensionalan adalah suatu metode untuk menyederhanakan suatu persamaan banyak parameter menjadi persamaan dengan sedikit parameter. Biasanya penondimensionalan mengelompokkan beberapa parameter dengan sebuah parameter tunggal (Strogatz 1994).

Contoh:

diberikan model mangsa pemangsa sebagai berikut:

� = ̇ = − ,

maka diperoleh model dengan satu parameter , yaitu:

̇ = − ,

̇ = − + .

Selanjutnya, Strogatz (1994) menjelaskan bahwa struktur kualitatif dari suatu sistem dinamika dapat berubah karena adanya perubahan dari parameter sistem dinamika tersebut. Hal inilah yang disebut bifurkasi. Bifurkasi adalah suatu kondisi terjadinya perubahan jumlah atau kestabilan titik tetap pada sistem dinamik. Titik yang mengalami kondisi ini disebut titik bifurkasi. Pada bifurkasi satu-dimensi ditemukan kasus-kasus untuk bifurkasi saddle-node, bifurkasi transcritical, dan bifurkasi pitchfork (supercritical dan subcritical). Sedangkan pada kasus dua-dimensi ditemukan kasus bifurkasi Hopf.

Bifurkasi saddle-node adalah bifurkasi yang terjadi jika salah satu dari nilai parameter tidak terdapat titik tetap dan pada sisi lain terdapat dua titik tetap, dimana yang satu stabil dan yang lainnya tidak stabil.

(15)

Bifurkasi dapat bersifat superkritis atau subkritis yang mengakibatkan limit cycle

menjadi stabil atau tidak stabil. Misalkan:

̇ = , , R , (7)

adalah sistem persamaan diferensial mandiri orde-2 yang bergantung pada parameter a ∈ R. Diasumsikan bahwa matriks Jacobi = , memiliki sepasang nilai eigen kompleks

, = ± � , (8)

yang menjadi imajiner murni saat = , yaitu = dan = > . Kemudian, ketika melewati = stabilitas kesetimbangan berubah.

PEMODELAN

Model yang akan dianalisis adalah model interaksi tumbuhan dan herbivora yang mana dinamika perilakunya analogi dengan model mangsa-pemangsa. Pada model diasumsikan bahwa tidak adanya herbivora, populasi tumbuhan tumbuh sesuai dengan hukum logistik pertumbuhan dengan daya dukung lingkungan dan tingkat kelahiran intrinsik �. Daya dukung lingkungan dan tingkat kelahiran interinsik � diasumsikan konstan dan positif. Asumsi-asumsi tersebut merupakan asumsi standar yang digunakan untuk sebuah kompetisi makanan dan ruang antar individu dari spesies yang sama serta pada kepadatan yang tinggi kematian meningkat karena peluang frekuensi pertemuan antarindividu tinggi pada setiap epidemi. Jumlah biomasa tumbuhan yang dihancurkan oleh herbivora diasumsikan mengikuti respon fungsional Holling jenis-III sebagai interaksi antara tumbuhan dan herbivora. Respon fungsional adalah tingkat yang mana setiap herbivora menangkap biomasa tumbuhan. Herbivora menghasilkan keturunan untuk setiap kematian biomasa tumbuhan dan tingkat kepadatan kematian independen . Model dua dimensi tumbuhan dan herbivora diatur oleh persamaan sebagai berikut:

(16)

Tingkat kematian independen.

Semua parameter �, , , , , dan yang terlibat dalam sistem model diasumsikan positif dan faktor konversi diasumsikan memenuhi kondisi < <

. Sistem model tumbuhan dan herbivora mengandung banyak parameter. Oleh karena itu untuk meminimumkan parameter maka sistem model ditransformasikan ke bentuk yang lebih sederhana dengan penondimensionalan model. Pada persamaan (9) didefinisikan � = √ , � = √ , � = ��

�√ , =

�

√ , =

�

√ �, =

, dan = �

√ �, sehingga diperoleh:

̇ = � = − _{− + ,}

(10)

̇ = � = + − ,

(Bukti sistem persamaan (10) dapat dilihat pada Lampiran 1)

PEMBAHASAN

Penentuan Titik Tetap Model

Titik tetap dari persamaan (10) akan diperoleh dengan menetapkan ̇ = ,

̇ = sehingga diperoleh tiga titik tetap, yaitu � , , � , , dan � _∗, _∗ dengan

∗ = √ − ,

∗ = − ∗ + ∗

∗ .

(Bukti dapat dilihat lihat pada lampiran 2) Karena titik tetap positif, akibatnya kondisi < _∗ < .

Analisis Kestabilan Titik Tetap Model

(17)

=

(

− − + +

+ + − ₎

.

(Bukti dapat dilihat pada lampiran 3) Kestabilan titik tetap dapat dilihat dari nilai eigen yang dihasilkan oleh matriks Jacobi persamaan (10) yang dievaluasi pada titik tetap tersebut. Selanjutnya, kestabilan di sekitar titik tetap diperiksa.

Titik tetap � , disubstitusikan ke matriks Jacobi sehingga diperoleh:

, = ( _{− ).}

Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik

det( , − ) = , sehingga akan diperoleh nilai eigen untuk matriks , , yaitu:

= , = − .

Karena parameter diasumsikan positif, maka > dan < . Kedua nilai eigen real dan berbeda tanda sehingga kestabilan titik tetapnya bersifat sadel.

Titik tetap � , disubstitusikan ke matriks Jacobi sehingga diperoleh:

, =

det( , − ) = , sehingga akan diperoleh nilai eigen matriks , , yaitu:

= − <

= + − .

(Bukti dapat dilihat pada lampiran 3) Kondisi _∗ < dan > menyebabkan > + sebagai syarat parameter dalam sistem model. Oleh karena itu > sehingga kestabilan titik tetapnya bersifat sadel.

Titik tetap � _∗, _∗ disubstitusikan ke matriks Jacobi sehingga diperoleh:

=

(18)

= − + √ − ,

(Bukti dapat dilihat pada lampiran 3) kemudian untuk penyederhanaan, kita simbolkan

= − dan = √ − .

Berdasarkan kondisi yang telah diperoleh maka sesuai dengan analisis kestabilan, kestabilan titik tetap yang diperoleh dipengaruhi oleh nilai parameter-parameter yang dipilih, yaitu parameter , , , dan sehingga harus diperiksa dari kondisi

, dan .

Oleh karena > maka kondisi dari positif > , sedangkan kondisi dari bisa < atau > dan kondisi dari bisa < atau >

. Kondisi > dapat diturunkan menjadi < ∗

− (Bukti dapat dlihat pada lampiran 4), sedangkan kondisi < dapat diturunkan menjadi > ∗

− (Bukti dapat dilihat pada lampiran 4). Dari sini terdapat empat kasus, yaitu:

1. < , < ∗

Untuk kasus pertama akan menghasilkan kedua nilai eigen imajiner _, = −�±��

(19)

Tabel Kondisi kestabilan titik tetap � Dari Tabel 1 dapat dilihat bahwa setiap kasus mempunyai titik tetap dengan jenis kestabilan ada yang stabil dan ada yang tidak stabil. Pada saat penondimensionalan = �

√ yang mana artinya bahwa nilai parameter berbanding terbalik dengan tingkat kejenuhan kepadatan tumbuhan ( ), = �

√ � yang mana artinya bahwa nilai parameter berbanding lurus dengan tingkat kematian independen herbivora ( ), dan = �

√ � artinya bahwa nilai parameter berbanding lurus dengan tingkat serapan maksimum herbivora yang mana berbanding lurus juga dengan parameter karena = . Diketahui > ∗

− ,

artinya kondisi tersebut dihadapkan pada saat tingkat kejenuhan kepadatan tumbuhan rendah. Sedangkan < ∗

− , artinya kondisi tersebut dihadapkan pada saat tingkat kejenuhan kepadatan tumbuhan tinggi.

Bifurkasi Hopf

Diketahui nilai eigen titik tetap � _∗, _∗ dari persamaan 2, yaitu:

, =− ± √ − .

Pada kondisi > dan = − < kestabilan � _∗, _∗ adalah spiral stabil, sedangkan pada kondisi < dan = − < kestabilan

� ∗, ∗ spiral tak stabil.

Fenomena perubahan kestabilan terjadi ketika melewati = . Pada kondisi

= dihasilkan sepasang nilai eigen yang bernilai imajiner murni. Dalam kasus ini fenomena perubahan kestabilan tersebut dikenal sebagai bifurkasi Hopf.

(20)

SIMULASI

Dinamika Populasi tumbuhan dan herbivora dapat ditunjukkan melalui kurva yang menggambarkan populasi populasi tumbuhan dan herbivora pada kurun waktu tertentu. Selanjutnya dilakukan simulasi numerik melalui proses komputasi. Pada proses komputasi, masing-masing variabel dan parameter membutuhkan suatu nilai awal.

Pada saat penondimensionalan model, diketahui bahwa parameter-parameter

=_√� , = �

√ � , = , dan = �

√ � sangat berpengaruh untuk melihat dinamika populasi tumbuhan dan herbivora. Tidak sembarangan dalam menetukan nilai awal parameter. Nilai awal yang ditentukan harus memenuhi kondisi-kondisi setelah dilakukan proses analisis model. Berikut kondisi umum parameter yang harus dipenuhi: ≤ ≤ dan > yang mana nilai parameter-parameter tersebut diasumsikan positif. Berdasarkan dari kasus-kasus yang diperoleh, pada proses simulasi akan diperlihatkan pengaruh dari tingkat kejenuhan kepadatan tumbuhan ( ), tingkat kematian independen ( ), dan tingkat serapan maksimum herbivora ( ) terhadap dinamika populasi tumbuhan dan herbivora.

Dinamika Populasi Tumbuhan dan Herbivora Kasus 1

Pada kasus pertama, kondisi < , < ∗ tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen ( > ). Titik tetap, nilai eigen, dan jenis kestabilan pada kasus pertama disajikan dalam tabel sebagai berikut.

Tabel 1 Titik tetap, nilai eigen, dan kestabilan

Titik Tetap � � Kestabilan

� , . = − . + . � = − . − . � Spiral stabil

Pada tabel 2 titik tetap yang diperoleh � , . dengan nilai eigen = − . +

(21)

Gambar 1 Bidang fase kasus 1

Pada Gambar 1 diberikan ilustrasi bidang fase di sekitar titik tetap dengan jenis kestabilan spiral stabil. Di awal waktu, populasi tumbuhan dan herbivora sama-sama mengalami pertumbuhan dengan perkembangan yang sangat pesat terjadi pada tumbuhan. Pertumbuhan populasi tumbuhan yang sangat pesat menyebabkan suplai makanan yang tersedia buat herbivora melimpah sehingga pertumbuhan populasi herbivora juga berkembang pesat. Namun seiring berjalannya waktu populasi tumbuhan berkurang. Kompetisi antar herbivora juga terjadi ketika populasi tumbuhan semakin berkurang sehingga populasi herbivora juga semakin berkurang sampai pada akhirnya kedua populasi mengalami osilasi dan mencapai kestabilan.

Pada kasus kedua, kondisi < , > ∗

− , dan > . Nilai parameter yang dipilih adalah = , = . , = . , dan = , serta nilai awal =

dan = . . Pada kasus kedua dihadapkan pada kondisi dengan tingkat kejenuhan kepadatan tumbuhan rendah ( > ∗

− ) dan pada kondisi dengan tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen ( > ). Titik tetap, nilai eigen, dan jenis kestabilan pada kasus kedua disajikan dalam tabel sebagai berikut.

� , = . + . � = . − . � Spiral tak stabil

Pada Tabel 3 titik tetap yang diperoleh � , dengan nilai eigen = . +

(22)

Pada Gambar 2 diberikan ilustrasi bidang fase di sekitar titik tetap dengan jenis kestabilan spiral tak stabil. Pada ilustrasi titik tetap � , muncul limit cycle. Diilustrasikan orbit bergerak berlawanan dengan arah jarum jam. Orbit masuk ke dalam titik sampai ada batas yang berbentuk siklus yang dikenal sebagai siklus limit atau limit cycle. Dengan ini fenomena yang terjadi pada kasus kedua, yaitu perubahan kestabilan titik tetap dan keberadaan limit cycle karena berubahnya nilai parameter sistem yang merupakan sifat bifurkasi Hopf. Keberadaan limit cycle

diperkuat oleh Gambar 3 yang merupakan kebalikan penggambaran dari Gambar 2. Pada gambar 3 orbit bergerak keluar dari titik tetap dengan arah yang sama sehingga orbit akan terus bergerak dan bertemu hingga ada batas yang berbentuk siklus yang dikenal sebagai limit cycle.

Gambar 3 Bidang fase kasus 2 dengan arah orbit dari dalam ke luar

(23)

tumbuhan dan antar herbivora juga terjadi sehingga seiring berjalannya waktu, pertumbuhan kedua populasi berfluktuasi dengan jenis kestabilan spiral tak stabil.

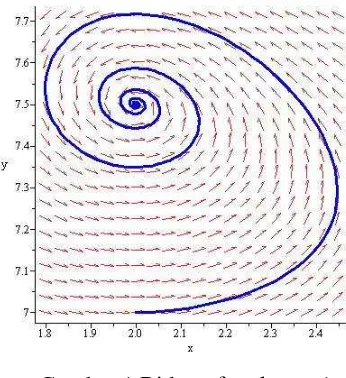
Pada kasus ketiga, kondisi > , < ∗

− , dan > . Nilai parameter yang dipilih adalah = , = . , = . , dan = . , serta nilai awal

= dan = . Pada kasus ketiga dihadapkan pada kondisi dengan tingkat kejenuhan kepadatan tumbuhan yang lebih tinggi ( < ∗

− ) dan pada kondisi dengan tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen ( > ). Titik tetap, nilai eigen, dan jenis kestabilan pada kasus ketiga disajikan dalam tabel sebagai berikut.

� , . = − . = − . Simpul stabil

Pada Tabel 4 titik tetap yang diperoleh adalah � , . dengan nilai eigen =

. dan = . sehingga kestabilannya bersifat simpul stabil (Gambar 4).

(24)

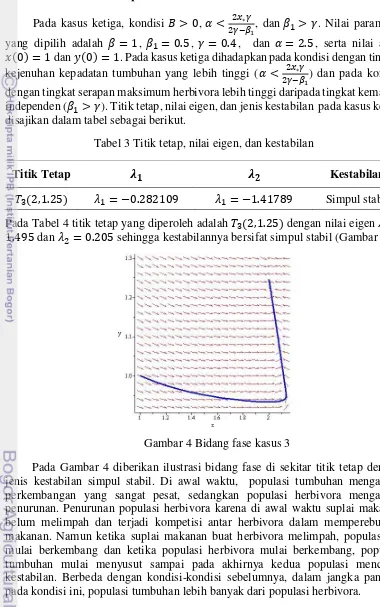
Pada kasus keempat, kondisi > , > ∗

− , dan > . Nilai parameter yang dipilih adalah = , = . , = . , dan = , serta nilai awal =

dan = . Pada kasus keempat dihadapkan pada kondisi dengan tingkat kejenuhan kepadatan tumbuhan rendah ( > ∗

− ) dan pada kondisi dengan tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen ( > ). Titik tetap, nilai eigen, dan jenis kestabilan pada kasus keempat disajikan dalam tabel sebagai berikut.

� , = . = . Simpultak stabil

Pada Tabel 5 titik tetap yang diperoleh adalah � , dengan nilai eigen =

. dan = . sehingga kestabilannya bersifat simpul tak stabil (Gambar 5).

Gambar 5 Bidang fase kasus 4 dengan arah orbit dari luar ke dalam

(25)

SIMPULAN

Pada model yang dibahas, diperoleh tiga titik tetap. Dari ketiga titik tetap, kestabilan titik tetap pertama dan kedua selalu sadel, sedangkan kestabilan titik tetap ketiga berbeda-beda bergantung nilai parameter yang diberikan. Dengan pemilihan nilai parameter tertentu, diperoleh bifurkasi Hopf yang memunculkan fenomena limit cycle. Hal ini terjadi pada saat perubahan kestabilan titik tetap ketiga dari spiral stabil berubah menjadi spiral tak stabil.

Dinamika populasi dipengaruhi oleh tingkat kejenuhan kepadatan tumbuhan, tingkat serapan maksimum herbivora, dan tingkat kematian independen. Pada kondisi dengan tingkat kejenuhan kepadatan tumbuhan tinggi dan tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen, populasi tumbuhan dan herbivora stabil. Pada kondisi dengan tingkat kejenuhan kepadatan tumbuhan rendah dan tingkat serapan maksimum herbivora lebih tinggi daripada tingkat kematian independen, populasi tumbuhan tidak stabil. Dalam jangka panjang, populasi herbivora cenderung lebih banyak dibandingkan dengan populasi tumbuhan, namun pada kondisi dengan tingkat kejenuhan tumbuhan yang lebih tinggi, populasi tumbuhan lebih banyak dibandingkan dengan populasi herbivora.

DAFTAR PUSTAKA

Anton H, Rorres C. 2004. Aljabar Linear Elementer. Ed ke-8. Indriasari R, Harmein I, Penerjemah. Jakarta (ID): Erlangga.

Fatik BM. 2010. Textbook of Animal Behaviour. New Delhi:PHI Learning Pvt. Ltd. Saha T dan Bandyopadhyay M. 2005. Dynamical Analysis of A Plant-Herbivore Model: Bifurcation and Global Stability. J. Appl. Math. And Computing 19: 327-344.

Strogatz SH. 1994. Nonlinear Dynamics and Chaos with Application to Physics, Biology, Chemistry, and Engineering. Massachusets (US): Addison-Wesley Publishing Company.

(26)

Lampiran 1 Penondimensionalan model

Diberikan model interaksi Tumbuhan dan Herbivora :

�

Persamaan di atas ditransformasikan menjadi sistem persamaan yang lebih sederhana dengan melakukan penondimensional sebagai berikut:

(27)

= �√ √

√

+ − √

=

�√ ∙ + − �√ ∙

= + − = + − ,

dengan = �

√ , =

�

√ �, = , dan = � √ �.

Lampiran 2 Penentuan titik tetap model interaksi tumbuhan dan herbivora Titik tetap akan diperoleh dengan menetapkan persamaan (10) sebagai berikut:

̇ = − _{− + = ,}

̇ = + − = .

 Dari persamaan pertama akan diperoleh nilai sebagai berikut:

̇ =

− _{− + =}

− _{= +}

− + =

+ − − =

+ − − − =

dari sini diperoleh:

= ∩ + − − − =

= ∩ = + − −

= ∩ = − + .

(28)

̇ = + − = + =

= +

− + =

dari sini diperoleh:

= ∩ − + =

= ∩ − =

= ∩ _{= −}

= ∩ = √ − .

 Substitusi = untuk mendapatkan nilai ke persamaan = dan = − ( + )

.

= , karena = maka =

= − ( + ), karena = maka

− +

=

− + =

− = ∩ + =

= ∩ + = ,

dengan + adalah definit positif.

Sehingga diperoleh titik tetap � , = , dan � , = , .  Substitusi = √

− untuk mendapatkan nilai ke persamaan = − ( + )

.

= − ( + ), karena = √

− maka ∗ =

− ∗ ( + ∗ )

(29)

Lampiran 3 Penentuan nilai eigen

Dengan melakukan pelinearan pada persamaan (10) diperleh Matriks Jacobi sebagai berikut:

 Pelinearan titik tetap � , akan diperoleh matriks Jacobi sebagai berikut:

, =

(

− ₊

+ − )

.

Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik

�( , − ) = sehingga diperoleh

Jadi nilai eigennya adalah sebagai berikut:

= − ,

= + − .

 Pelinearan titik tetap � ∗, ∗ diperoleh matriks Jacobi sebagai berikut:

(30)

∗, ∗ =

Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik

�( _∗, ∗ − ) = sehingga diperoleh

(31)

(32)

< ∗

− −

< ₋∗

−

< _{− ∙}∗ ₋−

(33)

RIWAYAT HIDUP

Penulis dilahirkan di Indramayu pada tanggal 23 Juli 1990 dari Bapak Agus dan Ibu Juenah. Penulis merupakan putra keempat dari empat bersaudara. Tahun 2002 penulis lulus dari SD Negeri Karanganyar, tahun 2005 penulis lulus dari SMP Negeri 1 Terisi, dan tahun 2008 penulis lulus dari SMA Negeri 1 Sindang. Penulis diterima sebagai mahasiswa Institut Pertanian Bogor pada tahun 2008 melalui jalur Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) Jurusan Matematika sebagai mayor. Pada tingkat kedua penulis memilih Statistika Terapan sebagai minor. Selama mengikuti perkuliahan, penulis pernah menjadi pengajar les Kalkulus TPB. Saat Tingkat Persiapan Bersama, penulis mendapatkan beasiswa pemerintah daerah Jawa Barat, pemerintah daerah Indramayu, dan LAZ Al-Hurriyyah. Pada tahun 2011-2013, penulis mendapat beasiswa Karya Salemba Empat.

Penulis aktif dalam organisasi kemahasiswaan seperti organisasi mahasiswa daerah dan organisasi intra kampus. Pada tahun 2009-2010, penulis menjadi sekretaris umum Ikatan Keluarga dan Mahasiswa dharma Ayu (IKADA) sebagai sekretasi umum. Pada tahun 2010, penulis menjadi anggota Departemen Internal Badan Eksekutif Mahasiswa (BEM) Fakultas Matematika dan Ilmu Pengetahuan Alam. Pada tahun 2011, penulis menjadi ketua Departemen Advokasi dan Kesejahteraan Mahasiswa Badan Eksekutif Mahasiswa (BEM) Fakultas Matematika dan Ilmu Pengetahuan Alam. Pada tahun 2012, penulis menjadi koordinator Kesejahteraan Mahasiswa se-IPB Badan Eksekutif Mahasiswa Keluarga Mahasiswa IPB.

Penulis juga aktif dalam berbagai kepanitiaan seperti kepanitiaan Masa Perkenalan Kampus Mahasiswa Baru 2009, Pesta Sains 2009 dan 2010, SPIRIT 2010, Masa Perkenalan Fakultas Matematika dan Ilmu Pengetahuan 2010 dan 2011, POKJA SPP dan POKJA Beasiswa 2012, dan kepanitiaan lainnya. Selain itu penulis juga pernah menjadi moderator seminar Lokakarya Kementerian Lingkungan Hidup, moderator Kajian Seputar Kampus Institut Pertanian Bogor 2012, master of ceremony, Dialog Rektor Institut Pertanian Bogor 2012, fasilitator