ANALISIS POLA KELAHIRAN MENURUT UMUR
STUDI KASUS DI INDONESIA TAHUN 1987 DAN TAHUN 1997
SUMIHAR MEINARTI
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis berjudul Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997 adalah karya saya sendiri dengan arahan dan bimbingan dari komisi pembimbing serta belum pernah diajukan dalam bentuk apapun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan oleh pihak lain telah penulis sebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2009
ABSTRACT
SUMIHAR MEINARTI. Analysis of Fertility Pattern based on Age Group: Case Study in Indonesia for Year 1987 and 1997. Supervised by HADI SUMARNO and SISWANDI.
One of the three demographic components that affects population is fertility, apart from death and migration. Age specific fertility rate is fertility indicator, which calculates birth according to age group. Generally, fertility pattern based on age group have the following pattern: increase in age of 15- 29, slowly decrease in age of 30 – 34 and sharply decrease in age of 35 – 49. Some mathematical functions which can be used to model the pattern of fertility are Hadwiger, Gamma, Beta, Gompertz and Coale-Trussell. The objectives of this research are to estimate parameter model and to find the best model. The data used in this research are Indonesian fertility data in 1987 and 1997. Parameters are estimated using maximum likelihood method and the criteria for choosing the best model are R2 and mean absolute percentage error. The result of this research shows that Coale-Trussell is the best model and Hadwiger function also performs well.
Keywords: fertility pattern, age group, maximum likelihood method.
RINGKASAN
SUMIHAR MEINARTI. Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997. Dibimbing oleh HADI SUMARNO dan SISWANDI.
Salah satu dari tiga komponen demografi yang dapat mempengaruhi perubahan penduduk adalah kelahiran (fertilitas), selain kematian (mortalitas) dan perpindahan (migrasi). Informasi tentang jumlah penduduk sangat penting bagi pemerintah dalam merencanakan pembangunan, demikian pula informasi tentang jumlah kelahiran diperlukan pemerintah dalam merencanakan pembangunan berbagai fasilitas yang dibutuhkan khususnya pengembangan fasilitas kesehatan bagi ibu dan anak.
Untuk mengukur kelahiran, dapat dilihat dari CBR (Crude Birth Rate), TFR (Total Fertility Rate) dan ASFR (Age Specific Fertility Rate). CBR merupakan indikator kelahiran yang dalam perhitungannya hanya memerlukan keterangan tentang jumlah anak yang dilahirkan dan jumlah penduduk tanpa membedakan penduduk laki-laki dan penduduk perempuan yang masih kanak-kanak. ASFR merupakan indikator kelahiran yang memperhitungkan perbedaan kelahiran menurut kelompok umur. TFR adalah jumlah dari ASFR. Corak perubahan kelahiran menurut umur, secara umum untuk semua masyarakat menunjukkan gambaran pola yang sama, yaitu menaik pada usia suburnya, kemudian sedikit menurun dan akhirnya menurun hingga usia suburnya. Keistimewaan ini memungkinkan pola tersebut dipadankan dengan fungsi matematika. Ada beberapa fungsi matematika yang biasa digunakan untuk memodelkan kelahiran menurut umur yaitu Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell.
Berdasarkan hal tersebut di atas, maka penelitian ini bertujuan untuk mempelajari metode pendugaan parameter model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell dan melakukan pendugaan parameter terhadap model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell berdasarkan data kelahiran Indonesia serta menentukan model terbaik dengan menggunakan uji koefisien determinasi (R2 ) dan Mean Absolut Percentage Error.
mendekati angka kelahiran total sebenarnya 3) Berdasarkan R2 (koefisien determinasi) dan Mean Absolut Percentage Error model yang terbaik adalah Coale-Trussell, sedangkan model kedua terbaik setelah Coale-Trussell adalah Hadwiger.
©Hak cipta milik Institut Pertanian Bogor, tahun 2009
Hak cipta dilindungi Undang-undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.
a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik dan tinjauan suatu masalah. b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian
Bogor.
ANALISIS POLA KELAHIRAN MENURUT UMUR
STUDI KASUS DI INDONESIA TAHUN 1987 DAN TAHUN 1997
SUMIHAR MEINARTI
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis : Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997
Nama : Sumihar Meinarti NRP : G551070061
Disetujui Komisi Pembimbing
Dr. Ir. Hadi Sumarno, M.S. Drs. Siswandi, M.Si Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil Anwar Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang telah melimpahkan berkat dan rahmat sehingga karya ilmiah ini berhasil diselesaikan.
Ungkapan terima kasih penulis sampaikan kepada orang tua dan seluruh keluarga yang telah memberikan dukungan, doa dan kasih sayangnya. Selanjutnya penulis sampaikan terima kasih kepada:
1. Dr. Ir. Hadi Sumarno, M.S. dan Drs. Siswandi, M.Si selaku pembimbing yang telah memberikan bimbingan dan motivasi dengan penuh kesabaran kepada penulis.
2. Ir. Retno Budiarti, M.S. selaku penguji luar komisi yang telah memberikan saran dan kritiknya.
3. Rekan-rekan mahasiswa S-2 Matematika Terapan IPB angkatan 2007 baik BUD maupun regular atas persahabatannya selama ini dan semoga tidak akan berakhir. 4. Semua pihak yang telah membantu penulis, yang tidak dapat penulis sebutkan
satu persatu.
Penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Semoga karya ilmiah ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain yang membutuhkan.
Bogor, Agustus 2009
ANALISIS POLA KELAHIRAN MENURUT UMUR
STUDI KASUS DI INDONESIA TAHUN 1987 DAN TAHUN 1997
SUMIHAR MEINARTI
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis berjudul Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997 adalah karya saya sendiri dengan arahan dan bimbingan dari komisi pembimbing serta belum pernah diajukan dalam bentuk apapun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan oleh pihak lain telah penulis sebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2009
ABSTRACT
SUMIHAR MEINARTI. Analysis of Fertility Pattern based on Age Group: Case Study in Indonesia for Year 1987 and 1997. Supervised by HADI SUMARNO and SISWANDI.
One of the three demographic components that affects population is fertility, apart from death and migration. Age specific fertility rate is fertility indicator, which calculates birth according to age group. Generally, fertility pattern based on age group have the following pattern: increase in age of 15- 29, slowly decrease in age of 30 – 34 and sharply decrease in age of 35 – 49. Some mathematical functions which can be used to model the pattern of fertility are Hadwiger, Gamma, Beta, Gompertz and Coale-Trussell. The objectives of this research are to estimate parameter model and to find the best model. The data used in this research are Indonesian fertility data in 1987 and 1997. Parameters are estimated using maximum likelihood method and the criteria for choosing the best model are R2 and mean absolute percentage error. The result of this research shows that Coale-Trussell is the best model and Hadwiger function also performs well.
Keywords: fertility pattern, age group, maximum likelihood method.
RINGKASAN
SUMIHAR MEINARTI. Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997. Dibimbing oleh HADI SUMARNO dan SISWANDI.
Salah satu dari tiga komponen demografi yang dapat mempengaruhi perubahan penduduk adalah kelahiran (fertilitas), selain kematian (mortalitas) dan perpindahan (migrasi). Informasi tentang jumlah penduduk sangat penting bagi pemerintah dalam merencanakan pembangunan, demikian pula informasi tentang jumlah kelahiran diperlukan pemerintah dalam merencanakan pembangunan berbagai fasilitas yang dibutuhkan khususnya pengembangan fasilitas kesehatan bagi ibu dan anak.
Untuk mengukur kelahiran, dapat dilihat dari CBR (Crude Birth Rate), TFR (Total Fertility Rate) dan ASFR (Age Specific Fertility Rate). CBR merupakan indikator kelahiran yang dalam perhitungannya hanya memerlukan keterangan tentang jumlah anak yang dilahirkan dan jumlah penduduk tanpa membedakan penduduk laki-laki dan penduduk perempuan yang masih kanak-kanak. ASFR merupakan indikator kelahiran yang memperhitungkan perbedaan kelahiran menurut kelompok umur. TFR adalah jumlah dari ASFR. Corak perubahan kelahiran menurut umur, secara umum untuk semua masyarakat menunjukkan gambaran pola yang sama, yaitu menaik pada usia suburnya, kemudian sedikit menurun dan akhirnya menurun hingga usia suburnya. Keistimewaan ini memungkinkan pola tersebut dipadankan dengan fungsi matematika. Ada beberapa fungsi matematika yang biasa digunakan untuk memodelkan kelahiran menurut umur yaitu Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell.
Berdasarkan hal tersebut di atas, maka penelitian ini bertujuan untuk mempelajari metode pendugaan parameter model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell dan melakukan pendugaan parameter terhadap model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell berdasarkan data kelahiran Indonesia serta menentukan model terbaik dengan menggunakan uji koefisien determinasi (R2 ) dan Mean Absolut Percentage Error.
mendekati angka kelahiran total sebenarnya 3) Berdasarkan R2 (koefisien determinasi) dan Mean Absolut Percentage Error model yang terbaik adalah Coale-Trussell, sedangkan model kedua terbaik setelah Coale-Trussell adalah Hadwiger.
©Hak cipta milik Institut Pertanian Bogor, tahun 2009
Hak cipta dilindungi Undang-undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.
a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik dan tinjauan suatu masalah. b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian
Bogor.
ANALISIS POLA KELAHIRAN MENURUT UMUR
STUDI KASUS DI INDONESIA TAHUN 1987 DAN TAHUN 1997
SUMIHAR MEINARTI
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis : Analisis Pola Kelahiran Menurut Umur Studi Kasus di Indonesia Tahun 1987 dan Tahun 1997
Nama : Sumihar Meinarti NRP : G551070061
Disetujui Komisi Pembimbing
Dr. Ir. Hadi Sumarno, M.S. Drs. Siswandi, M.Si Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil Anwar Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa yang telah melimpahkan berkat dan rahmat sehingga karya ilmiah ini berhasil diselesaikan.
Ungkapan terima kasih penulis sampaikan kepada orang tua dan seluruh keluarga yang telah memberikan dukungan, doa dan kasih sayangnya. Selanjutnya penulis sampaikan terima kasih kepada:
1. Dr. Ir. Hadi Sumarno, M.S. dan Drs. Siswandi, M.Si selaku pembimbing yang telah memberikan bimbingan dan motivasi dengan penuh kesabaran kepada penulis.
2. Ir. Retno Budiarti, M.S. selaku penguji luar komisi yang telah memberikan saran dan kritiknya.
3. Rekan-rekan mahasiswa S-2 Matematika Terapan IPB angkatan 2007 baik BUD maupun regular atas persahabatannya selama ini dan semoga tidak akan berakhir. 4. Semua pihak yang telah membantu penulis, yang tidak dapat penulis sebutkan
satu persatu.
Penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Semoga karya ilmiah ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain yang membutuhkan.
Bogor, Agustus 2009
RIWAYAT HIDUP
Penulis dilahirkan di Kotabumi, Lampung Utara pada tanggal 13 Mei 1967 dari ayah B.Sitompul dan Ibu D.Siregar. Penulis merupakan anak keempat dari lima bersaudara.
Tahun 1986 penulis lulus dari SMA Negeri 2 Tanjung Karang Bandar Lampung dan pada tahun yang sama penulis melanjutkan pendidikan sarjana pada jurusan Pendidikan Matematika Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas Lampung, lulus tahun 1990.
Tahun 1993 penulis masuk Pegawai Negeri Sipil di Departemen Pendidikan Nasional, sebagai staf pengajar di Sekolah Menengah Atas Teluk Naga Tangerang.
Sejak tahun 1995 hingga sekarang penulis sebagai staf pengajar di Sekolah Menengah Atas Negeri 7 Tangerang.
DAFTAR ISI
Halaman
DAFTAR TABEL ... xi DAFTAR GAMBAR ... xii DAFTAR LAMPIRAN ... xiii I PENDAHULUAN ... 1
1.1 Latar Belakang ………...……...…..…………...……. 1 1.2 Tujuan Penelitian ………...……….……...……. 1 II TINJAUAN PUSTAKA ... 2
2.1 Beberapa Pengertian Demografi ... 2 2.2 Beberapa Pengertian Teori Peluang ... 2 2.3 Beberapa Fungsi Penduga Bentuk Sebaran Kelahiran Umur Tertentu .. 4 2.4 Metode Kemungkinan Maksimum ... 7 2.5 Uji Kelayakan Model ... 7
III METODOLOGI PENELITIAN ... 9 3.1 Sumber Data ... 9
DAFTAR TABEL
Halaman
1. Tabel 1 Nilai dugaan TFR tahun 1987 dan 1997 ... 24 2. Tabel 2 Hasil R2 dan MAPE tahun 1987 ... 25 3. Tabel 3 Hasil R2 dan MAPE tahun 1997 ... 25
DAFTAR GAMBAR
Halaman
1.Data kelahiran Indonesia tahun 1987 ... 17 2.Data kelahiran Indonesia tahun 1997... 18 3.Kurva fungsi Hadwiger data Indonesia tahun 1987 dan tahun 1997 ... 18 4. Kurva fungsi Gamma data Indonesia tahun 1987 dan tahun 1997 ... . 19
5. Kurva fungsi Beta data Indonesia tahun 1987 dan tahun 1997... 20
6. Kurva fungsi Gompertz data Indonesia tahun 1987 dan tahun 1997... 21
7. Kurva fungsi Coale-Trussell data Indonesia tahun 1987 dan tahun 1997.. 23
DAFTAR LAMPIRAN
Halaman
1. Nilai harapan dari fungsi yang memodelkan angka kelahiran menurut umur ... 30 2. Program maximum likelihood fungsi Hadwiger untuk data tahun 1987 ………… 34 3. Program maximum likelihood fungsi Hadwiger untuk data tahun 1997 ... 35 4. Program maximum likelihood fungsi Gamma untuk data tahun 1987 …………... 36 5. Program maximum likelihood fungsi Gamma untuk data tahun 1997 …………... 37 6. Program maximum likelihood fungsi Beta untuk data tahun 1987 ……… 38 7. Program maximum likelihood fungsi Beta untuk data tahun 1997 ……….... 39 8. Program maximum likelihood fungsi Gompertz untuk data tahun 1987 ………… 40 9. Program maximum likelihood fungsi Gompertz untuk data tahun 1997 ………… 41 10.Program Coale-Trussell untuk data tahun 1987 ……….. 42 11.Program Coale-Trussell untuk data tahun 1997 ……….. 43
BAB I
PENDAHULUAN
1.1Latar Belakang
Salah satu dari tiga komponen demografi yang dapat mempengaruhi perubahan penduduk adalah kelahiran (fertilitas), selain kematian (mortalitas) dan perpindahan (migrasi). Informasi tentang jumlah penduduk sangat penting bagi pemerintah dalam merencanakan pembangunan.
Untuk mengukur kelahiran, dapat dilihat dari CBR (Crude Birth Rate), TFR (Total Fertility Rate) dan ASFR (Age Specific Fertility Rate). ASFR merupakan indikator kelahiran yang memperhitungkan perbedaan kelahiran menurut kelompok umur.
Corak perubahan kelahiran menurut umur, secara umum untuk semua masyarakat menunjukkan gambaran pola yang sama, yaitu menaik pada usia suburnya, kemudian sedikit menurun dan akhirnya menurun hingga akhir usia suburnya. Keistimewaan ini memungkinkan pola tersebut dipadankan dengan fungsi matematika. Ada beberapa fungsi matematika yang biasa digunakan untuk memodelkan kelahiran menurut umur yaitu Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell. Maksud dari penelitian ini adalah memilih model terbaik untuk memodelkan angka kelahiran menurut umur di Indonesia.
1.2Tujuan Penelitian
Dengan memperhatikan latar belakang masalah, penelitian ini bertujuan :
1. Mempelajari metode pendugaan parameter model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell.
2. Melakukan pendugaan parameter terhadap model Hadwiger, Beta, Gamma, Gompertz dan Coale-Trussell berdasarkan data kelahiran Indonesia .
BAB II
TINJAUAN PUSTAKA
2.1Beberapa Pengertian Demografi
Definisi 2.1.1 [ Angka Kelahiran Menurut Umur]
Angka Kelahiran Menurut Umur (Age Specific Fertility Rate/ASFR) adalah nilai yang menunjukkan banyaknya kelahiran per seribu perempuan pada kelompok umur tertentu.
(Lembaga Demografi FE UI, 2000)
Definisi 2.1.2 [ Angka Kelahiran Total ]
Angka Kelahiran Total (Total Fertility Rate/TF ) adalah rata-rata anak yang dilahirkan seorang perempuan selama masa usia suburnya.
(Lembaga Demografi FE UI, 2000)
2.2 Beberapa Pengertian Teori Peluang
Definisi 2.2.1 [ Ruang Contoh dan Kejadian ]
Himpunan semua kemungkinan dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan . Suatu kejadian A adalah himpunan bagian dari ruang contoh .
(Grimmet & Stirzaker, 1992)
Definisi 2.2.2 [Field F ]
Suatu himpunan F yang anggotanya terdiri atas himpunan bagian dari disebut field jika memenuhi syarat-syarat berikut:
1 Jika A, B∈F maka A ∪ B ∈F dan A ∩ B ∈ F 2 Jika A∈F maka c
A ∈ F 3 Ø ∈F
Definisi 2.2.3 [Medan-
σ
]Medan-
σ
adalah suatu himpunan F yang anggotanya terdiri atas himpunan bagian dari yang memenuhi syarat-syarat berikut:1 Ø ∈F
2 Jika A A1, 2, ... ∈ F , maka
1
i i
A
∞
=
∈ F
3 Jika A ∈ F maka c
A ∈ F
(Grimmet & Stirzaker, 1992)
Definisi 2.2.4 [ Peubah Acak ]
Suatu peubah acak X adalah suatu fungsi X :Ω →R dengan sifat
( )
{
ω
∈Ω:Xω
≤ x}
∈F untuk setiap x∈R.(Grimmet & Stirzaker, 1992)
Peubah acak dinotasikan dengan huruf kapital, misalnya X, Y, Z. Sedangkan nilai peubah acak dinotasikan dengan huruf kecil, seperti x, y, z.
Definisi 2.2.5 [Fungsi Sebaran]
Fungsi sebaran dari suatu peubah acak X adalah suatu fungsi F R: →[0,1] yang diberikan oleh FX( )x =P X( ≤x)
(Grimmet & Stirzaker,1992)
Definisi 2.2.6 [Fungsi Kepekatan Peluang]
Fungsi kepekatan peluang adalah limit dari peluang suatu individu mengalami
kejadian pada interval pendek t ke t+ ∆t persatuan panjang ∆t, dan dapat diekspresikan sebagai,
0
( )
( ) lim
t
P t T t t f t
t
∆ →
≤ < + ∆ =
∆
Definisi 2.2.7 [Peubah Acak Kontinu]
Peubah acak X dikatakan kontinu jika fungsi sebarannya dapat dinyatakan sebagai ( ) ( ) ,
x X
F x f u du x R
−∞
=
∫
∈dengan f R: →[0, )∞ adalah fungsi yang terintegralkan. Fungsi f dikatakan fungsi kepekatan peluang dari peubah acak.
(Grimmet & Stirzaker, 1992)
Definisi 2.2.8 [ Nilai Harapan ]
Jika X adalah peubah acak kontinu dengan fungsi kepekatan peluang f X (x) , maka nilai harapan dari X adalah : E[X] =
∫
∞
∞ −
x f X (x) dx
(Hogg dan Craig, 1995)
2.3Beberapa Fungsi Penduga Bentuk Sebaran Kelahiran Umur Tertentu
Fungsi angka kelahiran mempunyai dua bagian penting yaitu kelahiran total dan
intensitas kelahiran yang dinyatakan sebagai berikut :
h(u; θ) = θ1f(u; θ2,...., θr)
dengan u mewakili umur, f(u; θ2,...., θr) merupakan fungsi yang digunakan untuk mewakili kelahiran umur tertentu, θ1 mewakili angka kelahiran total.
Berikut akan dijelaskan lima fungsi yang biasa digunakan untuk menduga bentuk
sebaran kelahiran umur tertentu yaitu Hadwiger, Gamma, Beta, Gompetz, Coale-Trussell.
Kelima fungsi tersebut dipilih karena memenuhi sifat ASFR yaitu menaik kemudian sedikit menurun dan akhirnya menurun.
2.3.1Fungsi Hadwiger
Misalkan U peubah acak umur wanita yang melahirkan anak. Peubah acak U
menyebar Hadwiger dengan fungsi kepekatan peluang sebagai berikut :
f(u) = π β α u
β 3/2 − 2( + −2)
β β α u
u
e , dengan nilai tengah β .
2.3.2Fungsi Gamma
Misalkan U peubah acak umur wanita yang melahirkan anak. Peubah acak U
menyebar Gamma dengan fungsi kepekatan peluang sebagai berikut :
f(u) =
( ) (
)
− − − Γ −β
β
α
α α m u m u exp 1 1dengan u > m.
Nilai m sebagai umur paling muda menikah,untuk model ini m=14, dan
( )
u e−udu∞ −
∫
= Γ 0 1 αα
, dengan nilai tengah m+αβ
.
2.3.3Fungsi Beta
Misalkan U peubah acak umur wanita yang melahirkan anak. Peubah acak U
menyebar Beta dengan fungsi kepekatan peluang sebagai berikut :
( )
(
)
] , [ 1 1 1 1β
α
β α B a b a b a u a b a u u f − − − − − − − − −= dengan a < u < b .
Parameter adan b masing-masing menerangkan umur terendah dan tertinggi melahirkan anak. Model ini menggunakan a =15 , b = 50, dan
(
)
=∫
−(
−)
− 1 0 1 1 1, u u du
B
α
β
α β , dengan nilai tengahβ
α
α
+β
+a b2.3.4Fungsi Gompertz
Misalkan U peubah acak umur wanita yang melahirkan anak. Peubah acak U
menyebar Gompertz dengan fungsi kepekatan peluang sebagai berikut :
f(u) =
αβ exp
− − − − − α β α m u m u
exp dengan u > m.
Nilai m sebagai umur paling muda menikah, digunakan m=14, dengan nilai tengah
( )
1ln − Ψ
+
α
β
α
m
2.3.5Fungsi Coale-Trussell
Sesuai dengan norma agama dan norma sosial, kelahiran akan terjadi setelah
pernikahan, sehingga rata-rata kelahiran menurut umur pada wanita dapat dinyatakan
sebagai perkalian antara proporsi wanita telah menikah dengan ASMFR. ASMFR
menyatakan tingkat kelahiran bagi wanita yang telah menikah. Gambaran pola kelahiran
bagi wanita yang menikah telah diteliti oleh Coale dan Trussell pada tahun 1971. Beliau
menyatakan bahwa tingkat kelahiran bagi wanita telah menikah dapat diuraikan menjadi
r(u; M,β) = M n(u) exp [β v(u)] dengan M menyatakan koefisien tingkat kelahiran alami, β menyatakan koefisien tingkat perilaku hentian, n(u) menyatakan standar tingkat kelahiran alami umur u, dan v(u) menyatakan standar tingkat perilaku hentian bagi wanita kelompok umur u. Fungsi kontinu dari n(u) dan v(u) berdasarkan penelitian Hadi S. tahun 2003 dapat dinyatakan sebagai berikut :
( )
−
− −
= u u
u
n 0,02
77 , 14
88 , 29 exp
89 , 0
4
( )
−
− =
21 , 15
30 exp 30
439 , 0
4 , 7 4
, 6
u u
u v
Selain hal di atas Coale bersama McNeil menemukan model standar bagi pola sebaran
umur perkawinan yaitu
c(u) = α 19465 . 0
exp[-0.174( 0 6.06 ) exp( 0.2881( 0 6.06α))] α
α
α u−u − − − u−u −
Dari hal tersebut di atas maka fungsi kelahiran menurut umur adalah sebagai berikut:
f(u; β, M) = C(u) r(u; M,β)
dengan r(u; M,β) = Mn(u) exp [β v(u)] dan C(u) =
∫
uc x dx0 ( ) .
c(u) = α 19465 . 0
exp[-0.174( 0 6.06 ) exp( 0.2881( 0 6.06α))] α
α
α u−u − − − u−u −
PolyGamma[n,z] adalah turunan logaritma dari fungsi gamma dan PolyGamma[n,z]=
( )
( )
( )
n n n
dz z d
z = Ψ
Ψ dengan
( )
( )
zdz d
z = Γ
Ψ log .
2.4 Metode Kemungkinan Maksimum
Salah satu metode untuk melakukan pendugaan parameter adalah dengan metode
kemungkinan maksimum (maximum likelihood method). Misalkan X1, X2,...,Xn adalah peubah acak dari sebaran yang mempunyai fungsi kepekatan peluang f(X, β) dengan parameter β dimana β ∈ himpunan ruang parameter. Fungsi likehood adalah fungsi kepekatan peluang bersama f
(
X1,X2,...,Xn,β)
yang merupakan fungsi dari β yang dinotasikan denganL (β) = f
(
X1,X2,...,Xn,β)
=∏
ni=1 f (Xi, β)
Penduga β yang memaksimumkan fungsi likelihood dapat dicari dengan menentukan solusi dari persamaan
0 ) (
log =
∂ ∂
β β
L
0 ) , ( log
1
= ∂
∂
∑
=
n i
i
X f
β β
(Hogg & Craig, 1995)
2.5Uji Kelayakan Model
Untuk mengetahui model yang digunakan dapat menyesuaikan data dengan baik
maka dilakukan uji kelayakan model. Ada pun uji kelayakan model yang digunakan
adalah :
2.5.1 Koefisien Determinasi:
R2= 1
(
)
(
)
∑
∑
= =
− −
n i
i n i
i i
y y
y y
1
2 2
1 dengan y
i = aktual, yˆ = dugaan, dan y = rata-rata
Nilai R2 terletak pada [0,1]. Makin dekat nilai R2 dengan 1, semakin kecil kesalahan akibat penggunaan yˆ .
(Agresti & Finlay, 1999)
2.5.2 Persentase Rataan Galat Absolut ( Mean Absolute Percentage Error ) MAPE =
−
∑
=
∧
n i
i i y
y n 1
1
x 100%
MAPE (Mean Absolute Percentage Error) artinya presentase rataan absolut dari
perbedaan antara nilai sebenarnya dengan nilai dugaan.
BAB III
METODOLOGI PENELITIAN
3.1 Sumber Data
Data yang digunakan dalam penelitian ini adalah data kelahiran menurut umur untuk
Indonesia pada tahun 1987 dan tahun 1997 yang berdasarkan sensus penduduk 1990 dan
sensus penduduk 2000.
3.2 Langkah-langkah Penelitian
1. Mempelajari metode pendugaan parameter fungsi Hadwiger, Gamma, Beta,
Gompertz dan Coale-Trussell.
2. Melakukan pendugaan parameter dengan menggunakan metode maximum likelihood
terhadap model Hadwiger, Gamma, Beta dan Gompertz berdasarkan data kelahiran
Indonesia dengan menggunakan software Mathematica 6.0.
3. Menentukan model terbaik dengan menggunakan uji R2 (koefisien determinasi) dan
BAB IV
APLIKASI MODEL
4.1Pendugaan Parameter
Pendugaan parameter dilakukan terhadap fungsi Hadwiger, Gamma, Beta dan
Gompertz dengan menggunakan metode kemungkinan maksimum (Maximum Likelihood Method )
4.1.1 Metode Kemungkinan Maksimum Fungsi Hadwiger Fungsi Hadwiger memiliki fungsi kepekatan peluang
f(u) = π β α u
β 3/2 2( 2)
exp− +β− β α u
u
.
Berikut ini tahapan pendugaan parameter.
1) L(α,β ) =
∏
(
)
= n i i U f 1 ,β α = ∑ ∑ = = + − − =
∑
n i n i i i n U U n i i n e U 1 2 1 22 1 2
2 / 3 1 2 /
1 1 α
β α β α
π
αβ
2) logL(α,β) =
β α β α β α π α
∑
∑
∑
= = = − − − + + − n i i n i n i i i U U U n n n n 1 2 1 1 2 2 1 2 ] log[ 3 ] log[ ] log[ 2 ] log[ 4 2 1Untuk memperoleh nilai penduga bagi
α
danβ yang memaksimumkan fungsi log-likelihood maka turunan pertama dari logL(α,β) terhadapα
dan logL(α,β) terhadap3) = ∂ ∂ α β α, ) ( logL 0 2 1 4 8 2 2 1 1 1 = − − +
∑
∑
= =β
α
αβ
α
α
n i i n i i U U n nβ
α
αβ
α
α
∑
∑
= = = − + ⇔ n i i n i i U U n n 1 1 2 1 2 4∑
∑
= = = − + ⇔ n i i n i i U U n n 1 1 2 2 1 24
αβ
αβ
α
α
β
∑
∑
= = = − + ⇔ n i i n i i U U n n 1 1 2 2 2 1 24
β
β
α
β
∑
∑
= = + − = ⇔ n i i n i i U n U n 1 2 1 2 1 2 42
β
β
α
β
∑
∑
= = + − = ⇔ n i n i i i U n U n 1 1 2 2 1 2 42 β β
β α
Jadi α∧ =
∑
∑
= = + − ± n i i n i i U n U n 1 2 1 1 22 β β
β
4) =
∂ ∂ βα β ) , ( logL 0 1 2 2 1 2 1 2 1
2 − =
−
∑
∑
= = β α α β n i i n i i U U n 12 2 1 2 1 2 β α α β∑
∑
= = = − ⇔ n i i n i i U U n∑
∑
= = = − ⇔ n i i n i i U U n 1 2 1 2 2 12
α
β
α
β
0 2 1 1 2 1 22 + − =
∑
∑
∑
= = = − − ± − = ⇔ n i i n i n i i i U U U n n 1 2 1 1 4 2 1 2 ) 1 ( 4 4 2α
α
β
Jadi
β
∧ =∑
∑
∑
= = = − − ± − n i i n i n i i i U U U n n 1 2 1 1 4 2 1 4 ) 1 ( 16α
α
4.1.2 Metode Kemungkinan Maksimum Fungsi Gamma
Fungsi Gamma memiliki fungsi kepekatan peluang
f(u) = ( 14) exp[ 14] ] [ 1 1
β
β
α
α α − −− − u
u
Gamma .
Berikut ini tahapan pendugaan parameter.
1) L(
α
,β
)=∏
(
)
= n i i U f 1 ,
β
α
= α α β ββ
α
n n i i U n i i n U Gamma 14 1 1 1 exp ) 14 ( ] [ 1 + − = − ∑ − =∑
2) logL(
α
,β
)=β β αβ β α β β αβ
∑
∑
∑
= = = − + − − + − + + + − − n i i n i n i ii U U
U Log Gamma n n n 1 1 1 ] 14 log[ ] 14 [ ]] [ log[ ] log[ 14
Untuk memperoleh nilai penduga bagi
α
danβ
yang memaksimumkan fungsi log-likelihood, turunan pertama dari log L(α
,β
) terhadapα
dan log L(α
,β
) terhadapβ
harus sama dengan 0, sehingga :3) = ∂ ∂ β β α, ) ( logL + + − − + − + + + −
∑
=∑
= β α α β α α n i i n i i U U Gamma n n n 1 1 ] 14 log[ ] 14 log[ ]] [ log[ ] log[ 2 1 1 ] 14 log[ ] 14 log[ ]] [ log[ ] log[ 14 β αβ β α β β αβ∑
∑
= = + − − + − + + + − n i n i i i U U Gamma n n n+ 1 2
β
∑
= n i i U = 0[ ]
[
[ ]
]
[
]
[
]
2 1 2 1 2 2 2 14 log 14 log log log β αβ β β β α β β β αβ β αβ∑
=∑
= + − + + − − − − − ⇔ n i i n i i U U Gamma n n n[ ]
[
[ ]
]
log[
14]
log[
14]
0log log 14 2 1 2 1 2 1 2 2
2 + =
+ − − + − + + + −
∑
=∑
=∑
= β β αβ β β β α β β β αβ β n i i n i i n ii U U
U Gamma n n n 0 14 2 1 2
2 − + =
− ⇔
∑
=β
β
αβ
β
n i i U n nαβ
n U n n i i = + − ⇔∑
=1 14α
β
n U n n i i∑
= + − = ⇔ 1 14Jadi
β
∧ =4)
β
β
α
β
β
β
α
α
β
] 14 [ ] , 0 [ ] log[ ) , (log 1 i
n i U PolyGamma n n
L + − − +
− = ∂
∂
∑
== 0
Hasil turunan parsial log ( , ) =0 ∂ ∂
α
β
α
Ltidak dapat disajikan dalam bentuk analitik,
sehingga
α
∧ tidak dapat diperoleh secara eksplisit. Dengan bantuan software Mathematica 6.0 diperoleh hasil secara numerik.4.1.3 Metode Kemungkinan Maksimum Fungsi Beta Fungsi Beta mempunyai fungsi kepekatan peluang
f(u) =
(
)
] , [ 15 50 15 50 15 1 15 50 15 1 1 1β
α
β α Beta uu − − − −
− − − − − .
Berikut ini tahapan pendugaan parameter.
1) L(
α
,β
)=∏
(
)
= n i i U f 1 ,
β
α
=(
)
nn i n i n n i i Beta U U ] , [ ) 35 ( ) 35 15 1 ( 35 ) 15 ( 1 1 ) 1 ( 1 1
β
α
β α α∑
∑
= − − − − = − − −2) logL(
α
,β
)= + + − − − −
∑
= n i i U Beta n n 1 ) 15 ( 35 1 1 log ]] , [ log[ ] 35log[
α
β
α
∑
(
) (
)
∑
= = + − + − + + − n
i i n i i U U 1 1 ] 15 log[ 1 15 35 1 1 log
α
β
Untuk memperoleh nilai penduga bagi
α
danβ
yang memaksimumkan fungsi log-likelihood maka turunan pertama dari logL(α
,β
) terhadapα
dan logL(α
,β
) terhadapβ
harus sama dengan 0, sehingga :3) = ∂ ∂
α
α
β
) , (logL
(
)
+ + −
−
−nlog[35] n PolyGamma[0,
α
] PolyGamma[0,α
β
]
∑
= + − n i i U 1 ] 15log[ = 0
Hasil turunan parsial = ∂ ∂
α
β
α
, ) ( logL0 tidak dapat disajikan dalam bentuk
analitik, sehingga
α
∧ tidak dapat diperoleh secara eksplisit. Dengan bantuan software Mathematica 6.0 diperoleh hasil secara numerik.4) =
∂ ∂
β
β
α
, ) (logL
(
)
] , 0 [ ] , 0 [
β
−α
+β
−n PolyGamma PolyGamma +
∑
(
)
= + − n i i U Log 1 15 35 11 = 0
Hasil turunan parsial = ∂ ∂
β
α
β
) , ( logL0 tidak dapat disajikan dalam bentuk analitik,
sehingga
β
∧ tidak dapat diperoleh secara eksplisit. Dengan bantuan software Mathematica 6.0 diperoleh hasil secara numerik.4.1.4 Metode Kemungkinan Maksimum Fungsi Gompertz Fungsi Gompetz memiliki fungsi kepekatan peluang
f(u) =
α
β
exp(- ))14 exp( 14
α
β
α
− − − − u u .Berikut ini tahapan pendugaan parameter.
1) L(
α
,β
)= ( , )1 β α
∏
= n i i U f = − − − ∑
∑
= − − = n i U n i i n i e U 1 14 1 ) 14 (exp
β
αα
α
β
2) log L(
α
,β
)= - − + − + −∑
= − − − α αβ β α αα n α
i Ui e n n n 1 14 ] log[ ] log[ 14 α
∑
= n i i U 1Untuk memperoleh nilai penduga bagi
α
dan β yang memaksimumkan fungsi log-likelihood maka turunan pertama dari logL(α,β) terhadapα
dan logL(α,β) terhadapβ harus sama dengan 0, sehingga :
3) =
∂ ∂ βα β ) , ( logL -α α βα
∑
= α − − − + − n i Ui e n 1 14 = 0∑
= − − − = ⇔ n i Ui e n 1 14 α α β α∑
= − − − = ⇔ n i Ui e n 1 14 α βJadi β∧ =
∑
= − − − n i Ui e n 1 14 α4) =
∂ ∂ αα β ) , ( logL − + − + −
∑
= − − 2 1 14 ] log[ ] log[ 14α
αβ
β
α
α
α
n αi Ui e n n n + − − + + − +
∑
∑
= = − − − − − −α
α
αβ
β
β
α
n α αi n i i U U U e e n n n i i 1 1 2 14 14 ) 14 ( ] log[ ] log[ 2 2 1 α
∑
= n i i U = 0Hasil turunan parsial = ∂ ∂ αα β ) , ( logL
0 tidak dapat disajikan dalam bentuk analitik,
sehingga α∧ tidak dapat diperoleh secara eksplisit. Dengan bantuan software Mathematica 6.0 diperoleh hasil secara numerik.
4.2 Aplikasi Data Indonesia
Data angka kelahiran menurut umur untuk Indonesia digunakan data tahun 1987 dan
tahun 1997 . Dilihat dari data tahun 1987, ASFR tertinggi pada kelompok umur dua puluh sampai dua puluh empat tahun. Sedangkan data pada tahun1997, ASFR tertinggi pada kelompok umur dua puluh lima sampai dua puluh sembilan tahun. Menurutnya
tingkat kelahiran di semua kelompok umur dengan tingkat penurunan usia muda yang
lebih cepat menyebabkan pola kelahiran menurut umur di Indonesia berangsur-angsur
semakin landai yang mencerminkan terjadinya pergeseran median usia melahirkan
menuju usia yang lebih tua. Gambaran tersebut mengindikasikan kondisi yang lebih baik
karena meningkatnya usia melahirkan akan mengurangi resiko kematian si ibu mau pun
bayinya pada saat melahirkan. Penurunan ASFR ini menyebabkan TFR pada tahun 1997 turun jika dibandingkan tahun 1987 yaitu dari 3,33 menjadi 2,34. Adapun data kelahiran
Indonesia tahun 1987 dan tahun 1997 terlihat pada diagram batang dibawah ini.
-0.020 0.040 0.060 0.080 0.100 0.120 0.140 0.160 0.180
ASFR
15 - 19 20 - 24 25 - 29 30 - 34 35 - 39 40 - 44 45 - 49
UMUR Indone s ia 1987
Gambar 1 Data kelahiran Indonesia tahun 1987
Gambar 2 Data kelahiran Indonesia tahun 1997
4.2.1 Penduga Parameter Fungsi Hadwiger
Dengan menggunakan data Indonesia tahun 1987, menghasilkan nilai dugaan
parameter
α
= 2,80 dan β = 28,25 sehingga fungsi angka kelahiran menurut umur( )
28
28,25 2).
25 , 28 ( 84 , 7 2 /3 + −
−
=
u ue
u
u
h
Sedangkan dengan menggunakan data Indonesia tahun 1997, menghasilkan nilai dugaan
parameter
α
= 2,79 dan β = 29,20 sehingga fungsi angka kelahiran menurut umuradalah :
( )
) 2 20 , 29 20 , 29 ( 78 , 7 2 / 3
20 − + −
= u u e u u
h seperti terlihat pada Gambar 3 di bawah ini.
( )
) 2 25 , 28 25 , 28 ( 84 , 7 2 / 328 − + −
= u u e u u
h
( )
) 2 20 , 29 20 , 29 ( 78 , 7 2 / 3
20 − + −
= u u e u u h
a. Hadwiger tahun 1987 b. Hadwiger tahun 1997
Gambar 3 Kurva fungsi Hadwiger data Indonesai tahun 1987 dan tahun 1997
20 25 30 35 40 45 Umur u
0.05 0.10 0.15 0.20 h u
_ nilai dugaan ... nilaisebenarnya R2= 0,97
20 25 30 35 40 45 Umur u
0.02 0.04 0.06 0.08 0.10 0.12 0.14h u
_ nilai dugaan ... nilaisebenarnya R2= 0,97
-0.020 0.040 0.060 0.080 0.100 0.120 0.140 ASFR
15 - 19 20 - 24 25 - 29 30 - 34 35 - 39 40 - 44 45 - 49
UM UR Indone sia 1997
Hasil dari fungsi hadwiger, nilai dugaan untuk umur muda lebih tinggi dari nilai
sebenarnya, sedangkan untuk umur tua nilai dugaan di bawah nilai sebenarnya. Nilai
tengah umur melahirkan tahun 1987 adalah umur 28,3 tahun dan tahun 1997 pada umur
29,2 tahun. Dari kedua gambar di atas terlihat adanya penurunan tingkat kelahiran di
semua umur, hal ini menyebabkan angka kelahiran total turun dari 3,29 tahun 1987
menjadi 2,31 tahun 1997. Mean Absolute Percentage Error untuk hadwiger tahun 1987 sebesar 0,74% dan tahun 1997 sebesar 0,53%.
4.2.2 Penduga Parameter Fungsi Gamma
Dengan menggunakan data Indonesia tahun 1987, menghasilkan nilai dugaan
parameter
α
= 3,61 dan β = 3,94 sehingga fungsi angka kelahiran menurut umuradalah :
( )
(
)
− − −
=
94 , 3
14 exp
14 006
,
0 u 2,61 u
u
h .
Sedangkan dengan menggunakan data Indonesia tahun 1997, menghasilkan nilai dugaan
parameter
α
= 3,81 dan β = 3,99 sehingga fungsi angka kelahiran menurut umuradalah :
( )
(
)
−
− −
=
99 , 3
14 exp
14 003
,
0 u 2,81 u
u
h , seperti terlihat pada Gambar 4 di
bawah ini.
( )
(
)
− − −
=
94 , 3
14 exp
14 006 ,
0 u 2,61 u
u
h
( )
(
)
− − −
=
99 , 3
14 exp
14 003 ,
0 u 2,81 u
u h
a. Gamma tahun 1987 b. Gamma tahun 1997
Gambar 4 Kurva fungsi Gamma data Indonesia tahun 1987 dan tahun 1997
20 25 30 35 40 45 Umur u
0.05 0.10 0.15 0.20
h u _ nilai dugaan
... nilaisebenarnya R2= 0,97
20 25 30 35 40 45 Umur u
0.02 0.04 0.06 0.08 0.10 0.12
0.14h u _ nilai dugaan
... nilaisebenarnya R2= 0,97
Hasil dari fungsi gamma, nilai dugaan untuk umur muda lebih tinggi dari nilai
sebenarnya sedangkan untuk umur tua nilai dugaan di bawah nilai sebenarnya. Nilai
tengah umur melahirkan tahun 1987 adalah umur 28,2 tahun dan tahun 1997 pada umur
29,2 tahun. Dari kedua gambar di atas terlihat adanya penurunan tingkat kelahiran di
semua umur, hal ini menyebabkan angka kelahiran total turun dari 3,30 tahun 1987
menjadi 2,31 tahun 1997. Mean Absolute Percentage Error untuk gamma tahun 1987 sebesar 0,86% dan tahun 1997 sebesar 0,55%.
4.2.3 Penduga Parameter Fungsi Beta
Dengan menggunakan data Indonesia tahun1987, menghasilkan nilai dugaan parameter
α
= 1,85 dan β = 2,99 sehingga fungsi angka kelahiran menurut umuradalah :
( )
99 , 1 85 , 0 35 15 1 35 15 96 , 0 − − −
= u u
u h
Sedangkan dengan menggunakan data Indonesia tahun 1997, menghasilkan nilai dugaan
parameter
α
=1,88 dan β = 2,72 sehingga fungsi angka kelahiran menurut umur adalah :( )
0,88 1,7235 15 1 35 15 61 , 0 − − −
= u u
u
h , seperti terlihat pada Gambar 5 di bawah ini
( ) 0,85 1,99
35 15 1 35 15 96 , 0 − − −
= u u
u
h ( )
72 , 1 88 , 0 35 15 1 35 15 61 , 0 − − −
= u u
u h
a. Beta tahun 1987 b. Beta tahun 1997
Gambar 5 Kurva fungsi Beta data Indonesia tahun 1987 dan tahun 1997
20 25 30 35 40 45 Umur u
0.02 0.04 0.06 0.08 0.10 0.12 h u
_nilai dugaan ...nilaisebenarnya R2= 0,95
20 25 30 35 40 45 Umur u
0.05 0.10 0.15 h u
_nilai dugaan ...nilaisebenarnya R2= 0,97
Hasil dari fungsi beta, nilai dugaan untuk umur muda di bawah nilai sebenarnya
sedangkan untuk umur tua nilai dugaan ada yang lebih tinggi dari nilai sebenarnya dan
ada yang di bawah nilai sebenarnya. Nilai tengah umur melahirkan tahun 1987 adalah
umur 24,8 tahun dan tahun 1997 pada umur 26,4 tahun. Dari kedua gambar di atas
terlihat adanya penurunan tingkat kelahiran di semua umur, hal ini menyebabkan angka
kelahiran total turun dari 3,37 tahun 1987 menjadi 2,37 tahun 1997. Mean Absolute Percentage Error untuk beta tahun 1987 sebesar 0,92% dan tahun 1997 sebesar 0,85%.
4.2.4Penduga Parameter Fungsi Gompertz
Dengan menggunakan data Indonesia tahun1987, menghasilkan nilai dugaan parameter
α
= 5,94 dan β = 6,27 sehingga fungsi angka kelahiran menurut umuradalah :
( )
− − − − − = 94 , 5 14 exp 27 , 6 94 , 5 14 exp 52 ,
3 u u
u
h .
Sedangkan dengan menggunakan data Indonesia tahun1997, menghasilkan nilai dugaan
parameter
α
=6,23 dan β = 6,57 sehingga fungsi angka kelahiran menurut umur adalah :( )
− − − − − = 23 , 6 14 exp 57 , 6 23 , 6 14 exp 47 ,2 u u
u
h , seperti terlihat pada Gambar 6 di bawah ini.
( )
− − − − − = 94 , 5 14 exp 27 , 6 94 , 5 14 exp 52 ,3 u u
u
h
( )
− − − − − = 23 , 6 14 exp 57 , 6 23 , 6 14 exp 47 ,
2 u u
u h
a. Gompertz tahun 1987 b. Gompertz tahun 1997
Gambar 6 Kurva fungsi Gompertz data Indonesia tahun 1987 dan tahun 1997
20 25 30 35 40 45 Umur u
0.05 0.10 0.15 0.20 h u
_nilai dugaan ...nilaisebenarnya R2= 0,96
20 25 30 35 40 45 Umur u
0.02 0.04 0.06 0.08 0.10 0.12 0.14 h u
_nilai dugaan ...nilaisebenarnya R2= 0,97
Hasil dari fungsi Gompertz, nilai dugaan untuk umur muda lebih tinggi dari nilai
sebenarnya sedangkan untuk umur tua nilai dugaan di bawah nilai sebenarnya. Nilai
tengah umur melahirkan tahun 1987 adalah umur 27,3 tahun dan tahun 1997 pada umur
27,9 tahun. Dari kedua gambar di atas terlihat adanya penurunan tingkat kelahiran di
semua umur, hal ini menyebabkan angka kelahiran total turun dari 3,28 tahun 1987
menjadi 2,29 tahun 1997. Mean Absolute Percentage Error untuk Gompertz tahun 1987 sebesar 1% dan tahun 1997 sebesar 0,58%.
4.2.5 Penduga Parameter Coale danTrussell
Dengan menggunakan data Indonesia tahun 1987, menghasilkan nilai dugaan
parameter
α
=1,61, β=0,02, M =0,30 sehingga fungsi angka kelahiran menurut umur adalahh
( )
u
=
0
,
09
exp
[
−
0
,
08
(
u
−
19
,
6
−
exp
(
−
0
,
13
(
u
−
19
,
6
)
)
)
]
− − − − − 21 , 15 30 exp 30 439 , 0 02 , 0 exp 02 , 0 77 , 14 88 , 29 exp 89 , 0 30 , 0 4 , 7 4 , 6 4 u u u u
Sedangkan dengan menggunakan data Indonesia tahun 1997, menghasilkan nilai
dugaan parameter
α
= 2,14 , β = -0,26 , M = 0,26 sehingga fungsi angka kelahiran menurut umur adalahh
( )
u
=
0
,
07
exp
[
−
0
,
06
(
u
−
20
,
6
−
exp
(
−
0
,
10
(
u
−
20
,
6
)
)
)
]
− − − − − − 21 , 15 30 exp 30 439 , 0 26 , 0 exp 02 , 0 77 , 14 88 , 29 exp 89 , 0 26 , 0 4 , 7 4 , 6 4 u u u u
seperti terlihat pada Gambar 7 di bawah ini.
h
( )
u =0,09exp[
−0,08(
u−19,6−exp(
−0,13(
u−19,6)
)
)
]
h( )
u =0,07exp[
−0,06(
u−20,6−exp(
−0,10(
u−20,6)
)
)
]
− −
− u 0,02 u
77 , 14 88 , 29 exp 89 , 0 30 , 0 4 − −
− u 0,02u
77 , 14 88 , 29 exp 89 , 0 26 , 0 4 − − 21 , 15 30 exp 30 439 , 0 02 , 0 exp 4 , 7 4 , 6 u u − − − 21 , 15 30 exp 30 439 , 0 26 , 0 exp 4 , 7 4 , 6 u u
[image:48.612.92.512.76.355.2]a. Coale-Trussell tahun 1987 b. Coale-Trussell tahun 1997
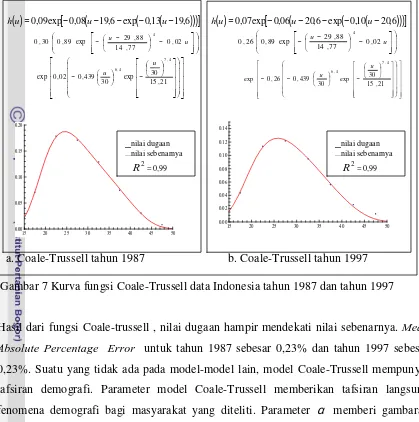
Gambar 7 Kurva fungsi Coale-Trussell data Indonesia tahun 1987 dan tahun 1997
Hasil dari fungsi Coale-trussell , nilai dugaan hampir mendekati nilai sebenarnya. Mean Absolute Percentage Error untuk tahun 1987 sebesar 0,23% dan tahun 1997 sebesar 0,23%. Suatu yang tidak ada pada model-model lain, model Coale-Trussell mempunyai
tafsiran demografi. Parameter model Coale-Trussell memberikan tafsiran langsung
fenomena demografi bagi masyarakat yang diteliti. Parameter
α
memberi gambaran perubahan umur perkawinan. Pada tahun1987 nilaiα
adalah 1,61 berarti rata-rata wanita mempunyai anak pada umur 16,6 tahun dan tahun 1997 nilaiα
adalah 2,14 berarti rata-rata wanita mempunyai anak pada umur 17,14 tahun. Hal ini menunjukkanadanya perubahan umur perkawinan.
Parameter M menggambarkan tingkat kelahiran alami. Dari hasil yang didapat, Indonesia pada tahun 1987 nilai parameter M sebesar 0,303 yang berarti kelahiran alami wanita Indonesia lebih tinggi jika dibandingkan tahun 1997 yaitu sebesar 0,264. Data ini
menunjukkan suatu penurunan dan dapat menggambarkan bahwa amalan perilaku
penjarangan di Indonesia telah mampu menurunkan tingkat kelahiran alami.
15 20 25 30 35 40 45 50 0.00
0.05 0.10 0.15 0.20
_nilai dugaan ...nilai sebenarnya R2= 0,99
15 20 25 30 35 40 45 50
0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14
_nilai dugaan ...nilai sebenarnya R2= 0,99
Parameter β menyatakan koefisien tingkat perilaku hentian kelahiran atau memberi gambaran tentang pencegahan kehamilan. Dari hasil yang didapat pada tahun 1987 nilai
parameter β adalah 0,024 dan tahun 1997 bernilai -0,262. Dilihat dari nilai Net Reproduction Rate ( NRR ) Indonesia tahun 1987 sebesar 2,8 dan tahun 1997 sebesar 2,1. Hal ini menunjukkan tahun 1997 rata-rata banyaknya anak yang dimiliki seorang ibu
yang akan tetap hidup hingga masa reproduksinya adalah dua orang. Penurunan nilai β di atas bukan karena amalan perilaku hentian di Indonesia menurun tetapi salah satunya,
disebabkan karena angka kelahiran sudah memasuki tingkatan yang cukup rendah
sehingga kemampuan intervensi program KB tidak begitu berpengaruh.
4.3 Perbandingan Model
4.3.1 Perbandingan Hasil TFR
Nilai dugaan TFR disajikan pada Tabel 1 berikut.
[image:49.612.89.526.406.486.2]
Tabel 1 Nilai dugaan TFR tahun 1987 dan 1997
Fungsi Hadwiger Gamma Beta Gompertz Coale-Trussell
∧
TFR tahun 1987 3,39 3,30 3,37 3,28 3,30
∧
TFR tahun 1997 2,31 2,31 2,37 2,29 2,30
Untuk tahun 1987 nilai TFR duga yang mempunyai perbedaan yang kecil dengan TFR
sebenarnya adalah fungsi Gamma dan Coale-Trussell. Sedangkan untuk tahun 1997 nilai
TFR duga yang mempunyai perbedaan yang kecil dengan TFR sebenarnya adalah Hadwiger, Gamma dan Gompertz.
4.3.2 Perbandingan Hasil R2 (koefisien determinasi) dan Mean Absolute Percentage Error.
Untuk mengetahui apakah benar model dapat menyesuaikan data dengan baik maka
dilakukan uji kelayakan model dengan R2 (koefisien determinasi), Mean Absolute Percentage Error (persentase rataan galat absolut). Nilai R2 terletak pada [0,1], makin dekat nilai R2 dengan 1, semakin kecil kesalahan akibat penggunaan nilai penduga. Semakin kecil nilai Mean Absolute Percentage Error (persentase rataan galat absolut) semakin baik model menyesuaikan dengan data. Tabel 2 dan Tabel 3 menyajikan nilai
2
[image:50.612.87.526.346.413.2]R dan Mean Absolute Percentage Error yang diperoleh lima fungsi di atas.
Tabel 2 Hasil 2
R dan MAPE tahun 1987
Fungsi Hadwiger Gamma Beta Gompertz Coale-Trussell
2
R 0,97 0,97 0,97 0,96 0,99 MAPE(%) 0,74 0,86 0,92 1,00 0,23
Tabel 3 Hasil R2 dan MAPE tahun 1997
Fungsi Hadwiger Gamma Beta Gompertz Coale-Trussell
R2 0,97 0,97 0,95 0,97 0,99
MAPE(%) 0,53 0,55 0,85 0,58 0,23
Berdasarkan nilai R2 (koefisien determinasi) dan Mean Absolute Percentage Error, fungsi Coale-Trussell pada tahun 1987 mempunyai nilai 2
[image:50.612.90.523.499.566.2]mempunyai nilai R2 paling tinggi dari lima fungsi tersebut dan Mean Absolute Percentage Error paling kecil dari lima fungsi tersebut. Akibatnya, fungsi Coale-Trussell merupakan fungsi terbaik untuk memodelkan angka kelahiran menurut umur.
Selain Coale-Trussell, jika diperlukan fungsi kedua untuk memodelkan angka kelahiran
menurut umur, model Hadwiger dapat digunakan sebagai model alternatif.
BAB V
SIMPULAN
Berdasarkan uraian di atas dapat disimpulkan sebagai berikut :
1. Metode Maximum Likelihood dapat digunakan untuk melakukan pendugaan parameter dengan baik terhadap fungsi kelahiran menurut umur.
2. Angka kelahiran total (TFR ) duga setiap fungsi mendekati angka kelahiran total sebenarnya.
3. Berdasarkan R2 (koefisien determinasi) dan Mean Absolute Percentage Error model yang terbaik untuk Indonesia adalah Coale-Trussell, sedangkan model
DAFTAR PUSTAKA
Abdul Aziz Jemain. 2001. Menjejak Fungsi Matematik Kadar Fertiliti Umur Tertentu untuk Kelahiran di Semenanjung Malaysia. Bulletin of the Malaysian Mathematical Sciences Society. Second Series 24: 137-148.
Agresti A, Barbara F. 1986. Statistical Methods for the Social Sciences. Ed. ke-2 California. D. Ellen Publishing Company.
Coale AJ. 1971. Age Pattern of Marriage. Population Studies 25:193-214.
Coale AJ, Trussell JT. 1974. Model Fertility Schedules Variations in the Age Structure of Childbearing in Human Populations. Population Index 40(2):185-258.
Cox DR, Oakes. 1984. Analysis of Survival Data. Cambrigde. University Press.
Gilije E. 1969. Fitting Curves to Age Specific Fertility Rates Some Examples. Statistical Review of the Swedish National Central Bureau of Statistics II 7: 118-134.
Grimmet GR, Stirzaker R. 1992. Probability and Random Process. Ed. ke-2. Oxford. Clarendom Press.
Hadi Sumarno, 2003. Bentuk Fungsional Tingkat Fertilitas Alami Dan Tingkat Perilaku Hentian. JMA. Vol.2, No.2: 23-26.
Hogg VR, Craig TA. 1995. Introduction to Mathematical Statistics. Ed. ke-5. New Jersey. Prentice-Hall Englewood Cliffs Publisher.
[Lembaga Demografi FE UI] Lembaga Demografi Fakultas Ekonomi Universitas Indonesia. 2000. Dasar-dasar Demografi. Jakarta: Lembaga Penerbit FEUI.
Matthews JH. 1992. Numerical Methods for Mathematics, Science, and Engineering. London. Prentice-Hall.
Paraskevi Peristera, Anastasia Kostaki. 2007. Modeling Fertility In Modern Population. Demographic Research 16:141-194.
Mitra S, Romaniuk A. 1973. Pearsonian Type I Curve and Its Fertility Potentials.
Demography10: 351-365.
Wei WWS. 1994. Time Series Analysis. California. Addison Wesley Publishing Company.
LAMPIRAN : 1
FUNGSI GOMPERTZ Nilai harapan = E(u)=M'
(
t=0)
− − − − − = α β α αβ m u m u u
h( ) exp exp
) ( ) ( tu e E t M =
= etuh(u)du
0
∫
∞= etu u m u m du
− − − − −
∫
∞ β α ααβ exp exp
0
=
∫
∞etu u m u m du − − − − −
0 exp α βexp α
αβ Misal − − = α
β u m
y exp dy y du ydu dy du m u dy α α α β α − = − = − − − = 1 exp 1
(
y)
m um u y m u y m u y = + − − − = − − + = − − = ln ln ln ln exp ln ln ln exp ln ln β α α β α β α β
Batas interval untuk y dipenuhi
∞ = → ∞ = = → = y u m y u α βexp 0
( )
( ) ( ) dyy e e e t M m y m m y tm y t
∫
∞ − + − − + − − − = α β α β α β α ααβ exp
( ) ( ) ( )
∫
∫
∞ − − − ∞ − − − − = − = α α β α β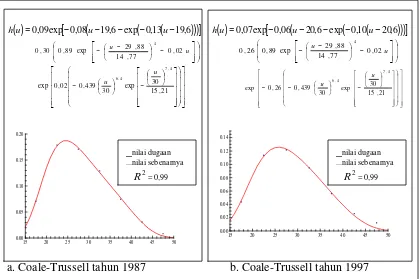


![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/59.612.86.405.62.704/table-h-u-u.webp)
![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/60.612.86.402.51.705/table-h-u-u.webp)
![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/61.612.83.412.82.651/table-h-u-u.webp)
![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/62.612.84.412.82.649/table-h-u-u.webp)
![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/65.612.84.411.87.627/table-h-u-u.webp)
![Table[h[u],{u,15,49}]](https://thumb-ap.123doks.com/thumbv2/123dok/659034.353784/66.612.84.409.88.626/table-h-u-u.webp)