Perencanaan Jaringan dengan Permintaan Acak Menggunakan Chance Constrained Programming

PROGRAMMING

SKRIPSI

SARDES MALAU 080803028

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERENCANAAN JARINGAN DENGAN PERMINTAAN ACAK MENGGUNAKAN CHANCE CONSTRAINED

PROGRAMMING

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana

Sains

SARDES MALAU 080803028

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

Judul : PERENCANAN JARINGAN DENGAN PER-MINTAAN ACAK MENGGUNAKAN CHANCE CONSTRAINED PROGRAMMING

Kategori : SKRIPSI

Nama : SARDES MALAU

Nomor Induk Mahasiswa : 080803028

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juli 2012

Komisi Pembimbing :

Pembimbing 1 Pembimbing 1

Prof. Drs. Tulus, Vordipl.Math, M.Si, Ph.D. Drs. Liling Peranginangin, M.Si.

NIP 196209011988031002 NIP 194707141984031001

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

ii

PERNYATAAN

PERENCANAAN JARINGAN DENGAN PERMINTAAN ACAK MENGGUNAKAN CHANCE CONSTRAINED

PROGRAMMING

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2012

PENGHARGAAN

Puji dan syukur penulis ucapkan kehadirat Tuhan Yesus Kristus karena Kasih dan penyertaan-Nya, sehingga penulis mampu menyelesaikan skripsi ini dengan baik dan sesuai waktu yang ditetapkan.

Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini, ucapan terima kasih saya sampaikan kepada :

1. Bapak Prof. Dr. Tulus. selaku pembimbing I dan Bapak Drs. Liling Perang-inangin, M.Si. selaku pembimbing II saya yang telah memberikan bimbingan dan pengarahan kepada saya sehingga skripsi ini dapat saya selesaikan.

2. Bapak Drs. Sawaluddin,M.IT. dan Bapak Drs. Open Darnius, M.Sc. selaku dosen penguji saya.

3. Bapak Prof. Drs. Tulus, Vordipl.Math, M.Si, Ph.D. dan Ibu Dra.Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika.

4. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

5. Semua Dosen pada Departemen Matematika FMIPA USU, pegawai di FMIPA USU.

6. Seluruh teman di jurusan Matematika khususnya stambuk 2008, serta kelompok PA saya dalam Kristus : Raja David Pasaribu, Anri Aruan, Lukas Panjaitan, Indra Sibuea, Charles Simamora, dan Binsar Nababan, serta kakak kelompok saya K’Tiur atas doa dan dukungannya yang telah memberi saya semangat.

7. Ayahanda Arlen Malau, Ibunda Korsinta br Sitio serta kakak-kakak dan abang saya saya Riana Malau, Rediana Malau, Simon Petrus Malau, dan Marissa Malau serta adik saya satu-satunya Janferi Malau yang selama ini selalu mem-berikan semangat, dorongan, inspirasi dan bantuan yang sangat berarti bagi penulis.

Dengan segala kerendahan hati penulis menyadari banyak kekurangan dan keti-dak sempurnaan pada skiripsi ini. Oleh karena itu Penulis sangat mengharapkan dan berterimakasih untuk semua bentuk saran dan kritikan yang membangun demi menambah wawasan dan pengetahuan Penulis.

Akhirnya Penulis mempersambahkan skiripsi ini kepada kedua orang tua saya tercinta Ayahanda Arlen Malau dan Ibunda Korsinta br Sitio, dengan ucapan terima kasih yang sedalam-dalamnya atas semua doa, dukungan, dan materi.

Medan, Juli 2012 Penulis

iv

ABSTRAK

Chance Constrained Programming(CCP) merupakan salah satu bagian daristochastik programming yang dikembangkan oleh Charnes dan Cooper. Chance Constrained Programming adalah salah satu teknik yang dapat dipakai untuk menyelesaikan per-masalahan yang mengandung kendala peluang. Dalam penelitian ini penulis mencoba memakaiChance Constrained Programming sebagai model dalam perencananaan su-atu jaringan yang mana permintaan (pemakaian bandwidth) seperti download dan

upload dalam jaringan ini bersifat tidak pasti atau dapat dikatakan acak, dalam hal inilah Chance Constrained Programming penulis gunakan yakni dalam menemukan suatu model pencarian lintasan-lintasan terbaik serta pengalokasianbandwidthsecara optimal dalam suatu jaringan, sehingga akan dicapai suatu jaringan yang baik ser-ta biaya minimal dalam pengalokasian bandwidth dalam jaringan tersebut . Chance Constrained Programming cocok digunakan dalam hal ini karena model ini dapat menggabungkan antara ketidakpastian permintaan pada jaringan dan tingkat jam-inan (level of guarantee) yang mau manajemen jaringan berikan kepada pengguna jaringan tersebut.

PERENCANAAN JARINGAN DENGAN PERMINTAAN ACAK MENGGUNAKAN CHANCE CONSTRAINED

PROGRAMMING

ABSTRACT

Chance constrained programming (CCP) is one part of stochastik programming which developed by Charnes and Cooper. Chance constrained programming technique is one which can be used to solve problems involving chance constraints, in this paper the writer try to use chance constrained programming as a model in network design under demand uncertainty (the using of bandwidth. e.g. random dowload and upload). in this case the writer use chance constrained programming to find a searching routes model and optimal bandwidth allocation in a network, so will be find a network with optimal bandwidth allocation in that network. Chance constrained programming is proper to use in this problem cause this model can united the uncertainty demand in the network and level of guarantee that network management want give to the users of the network.

vi

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR GAMBAR viii

DAFTAR TABEL ix

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 2

1.3. Batasan Masalah 3

1.4. Tujuan Penelitian 3

1.5. Tinjauan Pustaka 3

1.6. Kontribusi Penelitian 5

1.7. Metodologi Penelitian 5

2. DASAR TEORI 6

2.1. Jaringan Komunikasi 6

2.2. Distribusi Normal 10

2.3. Chance Constrained Programming 15

3. PEMBAHASAN 27

3.1. Model Umum CCP untuk Jaringan 27

3.2. Model Matematika Perencanaan Jaringan dengan CCP 28

4. KESIMPULAN 45

4.1. Kesimpulan 45

4.2. Saran 45

DAFTAR GAMBAR

Gambar Halaman

2.1 Wide Area Network dan Local Area Network 9

2.2 Grafik distribusi normal f(x) 11

2.3 Sifat grafik distribusi normal 12

2.4 Distribusi normal standar 13

2.5 Probabilitas x1 < X < x2 14

ix

DAFTAR TABEL

Tabel

2.1 Waktu operasi mesin dan parameter-parameter distribusi normal nya 21

ABSTRAK

Chance Constrained Programming(CCP) merupakan salah satu bagian daristochastik programming yang dikembangkan oleh Charnes dan Cooper. Chance Constrained Programming adalah salah satu teknik yang dapat dipakai untuk menyelesaikan per-masalahan yang mengandung kendala peluang. Dalam penelitian ini penulis mencoba memakaiChance Constrained Programming sebagai model dalam perencananaan su-atu jaringan yang mana permintaan (pemakaian bandwidth) seperti download dan

upload dalam jaringan ini bersifat tidak pasti atau dapat dikatakan acak, dalam hal inilah Chance Constrained Programming penulis gunakan yakni dalam menemukan suatu model pencarian lintasan-lintasan terbaik serta pengalokasianbandwidthsecara optimal dalam suatu jaringan, sehingga akan dicapai suatu jaringan yang baik ser-ta biaya minimal dalam pengalokasian bandwidth dalam jaringan tersebut . Chance Constrained Programming cocok digunakan dalam hal ini karena model ini dapat menggabungkan antara ketidakpastian permintaan pada jaringan dan tingkat jam-inan (level of guarantee) yang mau manajemen jaringan berikan kepada pengguna jaringan tersebut.

v

PERENCANAAN JARINGAN DENGAN PERMINTAAN ACAK MENGGUNAKAN CHANCE CONSTRAINED

PROGRAMMING

ABSTRACT

Chance constrained programming (CCP) is one part of stochastik programming which developed by Charnes and Cooper. Chance constrained programming technique is one which can be used to solve problems involving chance constraints, in this paper the writer try to use chance constrained programming as a model in network design under demand uncertainty (the using of bandwidth. e.g. random dowload and upload). in this case the writer use chance constrained programming to find a searching routes model and optimal bandwidth allocation in a network, so will be find a network with optimal bandwidth allocation in that network. Chance constrained programming is proper to use in this problem cause this model can united the uncertainty demand in the network and level of guarantee that network management want give to the users of the network.

PENDAHULUAN

1.1 Latar Belakang

Jaringan telekomunikasi dapat dipandang sebagai keterhubungan beberapa entitas

komunikasi yang saling berhubungan. Sebuah entitas komunikasi dapat diartikan

sebagai sebuah entitas yang dapat berdiri sendiri dan terlibat dalam suatu proses

komunikasi. Komputer, laptop dan telepon semuanya merupakan contoh dari

enti-tas komunikasi. Salah satu jaringan komunikasi saat ini yang sangat banyak dipakai

adalah jaringan nirkabel atau jaringan tanpa kabel (wireless) Contohnya adalah

in-ternet. Jaringan inilah yang akan dibahas dalam penelitian ini.

Karena pertumbuhan internet yang sangat cepat, berbagai masalah sering

dite-mui seperti loading yang lambat bahkan tidak dapat terhubung (lost connected).

Semua ini berhubungan dengan Routing dalam jaringan telekomunikasi yaitu proses dari penentuan sebuah lintasan yang dipakai untuk mengirim data ke tujuan tertentu.

dengan pengalokasian bandwidth atau dalam bahasa sehari-hari suatu penghitungan konsumsi data yang tersedia pada suatu telekomunikasi. Dihitung dalam satuan bits

per seconds (bps), karena itu diperlukan suatu perencanaanRoutingdan alokasi band-width pada arsitektur jaringan di masa yang akan datang dirancang sesuai dengan permintaan yang bergerak secara dinamis, ini berarti aturan Routing dapat dibu-at dalam jangka pendek (short-term). Maka dari itu, jumlah dari bandwidth yang dibutuhkan untuk melayani permintaan dapat berubah secara dinamis, dan sifat

in-ilah yang dalam penelitian ini penulis sebutkan dengan ketidakpastian permintaan

(permintaan acak).

Disebabkan oleh lingkungan yang dinamis, dibutuhkan perencanaan

jaringan jangka pendek untuk mengatasi ketidakpastian permintaan. Permasalan

ini berbeda dengan perencanaan jangka panjang yang berfokus pada peramalan

2

masa yang akan datang dan meminimalkan penalti sebagai sebuah hasil dari kesalahan

peramalan. Sebaliknya pokok permasalahan dalam penelitian ini adalah bagaimana

meminimalkan biaya dari routing dan alokasi bandwidth dengan kendala-kendala ja-ringan pada permintaan acak.

Kilpi dan Norros (2002), menjelaskan bahwa distribusi dari kumpulan trafik

per-mintaan (aggregation traffic demand) dapat dianggap berdistribusi Normal mempunyai rata-rata µ dan varian σ2_{. Pendekatan Chance Constrained} Program-ming (Rao, 1977) dapat menjadi alternatif terhadap pendekatan syarat pemesanan

bandwidth berdasarkan rata-rata dan berdasarkan nilai maksimum. Perencanaan berdasarkan permintaan rata-rata digunakan untuk menangani permintaan dengan

variasi yang rendah pada sekitar rata-rata. Sebaliknya, pendekatan berdasarkan

per-mintaan maksimun bertujuan untuk mengatasi variasi perper-mintaan yang jauh dari

rata-rata dengan menyediakanbandwidthsesuai dengan permintaan maksimum. Dalam penelitian ini, variasi permintaan diatas rata-rata dapat ditangani secara statistik

di-dasarkan pada tingkat jaminan (level of guaranteee) tertentu. Dalam penelitian ini penulis mencoba menerapkanChance Constrained Programming (CCP)dalam peren-canaan routing dan alokasi bandwidth pada jaringan telekomunikasi dengan kendala permintaan acak, keterbatasan bandwidth serta menggabungkannya dengan tingkat jaminan pelayanan.

1.2 Perumusan Masalah

Dalam penelitian ini yang menjadi permasalahan adalah bagaimana menentukan

1.3 Batasan Masalah

Untuk memudahkan pembahasan dan memberi hasil yang baik, maka penulis memberi

beberapa pembatasan permasalah, yaitu:

1. Kumpulan trafik permintaan antara node dianggap berdistribusi normal

2. Variabel utama dalam penentuan lintasan trafik optimal adalah kapasitas band-width

3. Permasalahan dalam penelitian ini terbatas pada penentuan lintasan optimal

dan alokasi bandwidth pada setiap link dalam suatu jaringan.

1.4 Tujuan Penelitian

Adapun yang menjadi tujuan penelitian ini adalah menentukan lintasan optimal dari

setiap trafik permintaan serta pengalokasianbandwidth optimal dengan demikian di-capai biaya minimum dari pengalokasian bandwidth pada jaringan.

1.5 Tinjauan Pustaka

Rao. (1977). Memberikan bentuk umum dari Chance Constrained Programming

(CCP)

min f(x) = n

X

j=1

cjxj (1.1)

Dengan kendala:

P[ n

X

j=1

aijxj ≤bi]≥pi, i= 1,2, ..., m (1.2)

xj ≥0, j = 1,2, ..., n (1.3)

dimanacj,aij, dan bi adalah variabel acak danpi merupakan peluang tertentu.

4

Misalkan G = (V, A) graph terhubung dari sebuah jaringan, n =| N | dan

m =| A |. Misalkan ca kapasitas dari link a ∈ A. Biaya routing dari satu unit trafik permintaan pada link a ∈ A. Misalkan I menunjukkan himpunan trafik per-mintaan, masing-masing i ∈I mempunyai asal si, dan sebuah tujuan di dan sebuah

bandwidth bi merupakan variabel acak. Misalkan n =| I | merupakan jumlah dari trafik permintaan. Variabel keputusan xia bernilai 1 jika lintasan untuk permintaan

i menggunakan linka, dan 0 untuk yang lain.

Untuk beberapa nodev ∈V,A+_{(v) menunjukkan himpunan link yang}

mening-galkan node v, sementara A−_{(v) merupakan link yang menuju node v. Misalkan X} himpunan routing:

X =

x_{∈ {}0,1_}N m

| ∀(i, a)_∈I_×A, X

a∈A+_(v)

xia−

X

a∈A−_(v)

xia =

                

1 if v =si

−1 if v =di

0 otherwise

Fungsi objektif dari penelitian ini yaitu meminimalkan peluang bahwa aliran

trafik melebihi kapasitas link yang ada. Hal ini menyebabkan masksimum jaringan

macet (Maximum Link Congestion Optimization Problem) (MLOP):

maxx∈X

mina∈AP(

X

i∈I

bixia ≤ca) (1.4)

Diasumsikan bahwa semua permintaan i ∈ I berdistribusi Normal:

bi ∼ N(µi, σi2), dengan µi > 0 dan σi > 0. maka didapat: P(P

i∈Ibixia ≤ca) =φ(

c_√a−P_i∈Iµixia

P i∈Iσ 2 ix 2 ia

), dimanaφ adalah distribusi kumulatif dari Nor-mal Standar N(0,1). Karenaφ meningkat, maka diperoleh untuk beberapa Routing

x : mina∈Aφ(

c_√a−Pi∈Iµixia

P i∈Iσ 2 ix 2 ia

) = mina∈A(

c_√a−Pi∈Iµixia

P i∈Iσ 2 ix 2 ia

). Ini berarti bahwa solusi optimal

untuk MLCOP dapat diperoleh dengan menyelesaikan formulasi dibawah ini:

maxx∈X{mina∈A

ca−P_i∈Iµixia

pP

i∈Iσ2ix2ia

}. (1.5)

keterbatasan sumber sepanjang lintasan karena dapat menggabungkannya dengan

masalah tingkat jaminan layanan(level of guarantee).

1.6 Kontribusi Penelitian

Melalui penelitian ini diharapkan akan memberikan kontribusi, yakni:

1. Menambah referensi bagi penelitian yang berhubungan dengan masalah

peren-canaan jaringan dengan permintaan tidak pasti.

2. Sebagai bahan masukan bagi para pengambil keputusan jaringan dalam

men-gatasi permasalahan routing.

1.7 Metodologi Penelitian

Karena penelitian ini bersifat studi literatur jadi penulis mencoba mencari sebanyak

mungkin bahan-bahan dari buku ataupun penelitian-penelitian sebelumnya yang

ber-hubungan dengan permasalahan dalam penelitian ini. Pada penulisan penelitian ini,

penulis mengembangkan metode dengan langkah-langkah sebagai berikut:

1. Menentukan variabel-variabel pokok permasalahan.

2. Mencari suatu model optimisasi dengan Chance Constrained Programming.

3. Menyelesaikan model yang diperoleh sehingga pada akhirnya diperoleh lintasan

BAB 2

DASAR TEORI

2.1 Jaringan Komunikasi

Jaringan komunikasi dapat dipandang sebagai sebuah keterhubungan dari

entitas-entitas komunikasi. Entitas komunikasi dapat diartikan sebagai sebuah entitas-entitas yang

berdiri sendiri dan terlibat dalam sebuah proses komunikasi. Komputer, laptop,

dan telepon merupakan contoh dari entitas komunikasi. Sebuah jaringan komunikasi

mungkin mengandung komputer, tetapi ini bukan berarti bahwa jaringan komunikasi

adalah sama dengan jaringan komputer.

Pada hakekatnya, sebuah jaringan komputer hanya salah satu bentuk dari

ja-ringan komunikasi, sebuah jaja-ringan komputer pada dasarnya berarti sebuah

keter-hubungan dari beberapa komputer. Sedangkan, istilah jaringan komunikasi

digu-nakan dalam arti yang lebih luas. Sekarang ini, dunia bergerak kepada jaringan yang

terintegrasi. Telepon, smartTV dan komputer bisa terhubung dengan jaringan yang

sama. Oleh karena itu, adalah lebih baik menyatakan jaringan saat ini sebagai sebuah

jaringan komunikasi, lebih dari sebuah jaringan komputer.

2.1.1 Topologi Jaringan.

Topologi dari sebuah jaringan diartikan sebagai keterhubungan fisik dari

elemen-elemen jaringan tersebut. Dengan kata lain, topologi dari sebuah jaringan menunjuk

kepada cara elemen-elemen jaringan terhubung. Topologi-topologi yang paling umum

adalah bus, ring, mesh, dan star (Wibi Hardani, 2004).

Bus

Topologi bus memiliki bentuk yang serupa dengan arsitektur bus di dalam komputer,

yang menghubungkan CPU ke memori utama, ke disk drive, dan berbagai

perangkat di dalam jaringan, sehingga hanya satu perangkat saja yang dapat

meng-gunakannya pada satu saat tertentu.

Ring

Secara logika, topologi Ring adalah konfigurasi di mana tiap-tiap terminal hanya

dapat mengirimkan data ke terminal tetangga yang berada di posisi sesudahnya, dan

menerima data dari terminal tetangga yang berada di posisi sebelumnya. Dengan

kata lain, apabila hendak menerima sebuah frame dari terminal tetangga di posisi

setelah anda, frame tersebut harus ”berjalan” mengelilingi seluruh cincin, melewati

semua terminal yang ada sampai akhirnya sampai kepada anda.

Mesh

Pada sebuah topology Mesh, Masing-masing node terhubung dengan dua atau lebih

node. Ada dua jenis topology Mesh yakni partially connected mesh dan full connect-ed mesh. Pada partially connected mesh, sebuah node mempunyai dua atau lebih tetangga. Untuk full connected mesh, terdapat sebuah link terhubung antara setiap dua node dalam jaringan.

Star

Dengan konfigurasi star, sebuah perangkat berperan sebagai pusat jaringan dan

ter-hubung ke semua perangkat lainnya, untuk melayani komunikasi di antara

perangkat-perangkat tersebut. Konfigurasi star atau Bintang seringkali disebut juga sebagai

konfigurasi hub and spoke karena bentuknya mirip roda pedalti.

2.1.2 Jenis Jaringan Berdasarkan Luas Daerah yang Diliputi.

Topology jaringan berhubungan erat dengan konsep luas jaringan dan

pengklasi-fikasian berdasarkan pada topoloy ini menghasilkan tipe berbeda dari area jaringan

(area networks). Alasan untuk hal ini adalah bahwa jaringan menjadi berbeda bentuk dan ukuran. lebih lanjut lagi, luas dari sebuah jaringan mempunyai pengaruh yang

signifikan dalam banyak aspek dalam sebuah jaringan. Seperti, faktor bandwidth

maksimum dan kecepatan (error rates ).

8

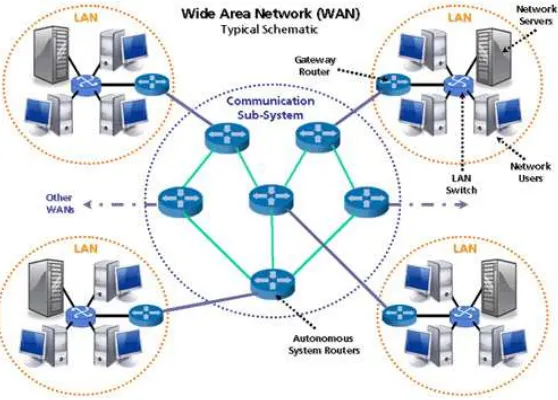
dan Wide Area Network(WAN). sebuah LAN adalah sebuah jaringan yang terbatas pada suatu wilayah kecil. Sebaliknya, WAN mencakup daerah yang sangat luas.

2.1.2.1 Local Area Network (LAN).

Sebuah jaringan LAN merupakan sebuah jaringan yang terbatas pada suatu

daer-ah kecil. LANs pada umumnya digunakan pada perusdaer-ahaan untuk menghubungkan

computer, server jaringan, printer dan entitas lainnya dalam jaringan. LAN dicirikan

oleh beberapa sifat di bawah ini:

• Mempunyai sebuah diameter (jangkauan) dalam beberapa kilometer.

• Biasanya milik pribadi dari sebuah perusahaan.

• Bandwidthnya dianggap gratis dan oleh karena itu biaya bandwidth bukanlah

sebuah pertimbangan penting. (perhatikan bahwa biaya hanya penting saat

jaringan tersebut dibangun. Setelah itu, terlepas dari penggunaan bandwidth,

tertentu dan variabel biaya kurang lebihnya akan sama. Oleh karena itu,

band-width dikatakan menjadi gratis).

• LANs dengan kecepatan rendah menyediakan bandwidth 416 Mbs. LANs yang

lebih cepat dapat menyediakan bandwidth sampai 100-1000 Mbps.

2.1.2.2 Wide Area Network (WAN).

Tidak seperti LAN, sebuah Wide Area Network (WAN) mencakup sebuah daerah

yang luas. WANs digunakan terutama untuk menghubungkan lokasi-lokasi yang

san-gat tersebar. WANs dicirikan oleh beberapa sifat di bawah ini:

• Mempunyai diameter (jangkauan) hingga ribuan kilometer.

• jarang dimiliki oleh sebuah perusahaan.

• Bandwidthnya sangat mahal. Oleh karena itu, biaya bandwidth memainkan

• Bandwidthnya berkisar 1-45 Mbps.

Untuk melihat perbedaan antara LANs dan WANs perhatikan gambar 2.1 berikut

ini

Gambar 2.1 : Wide Area Network dan Local Area Network

2.1.3 Routing.

Routing merupakan proses penyampaian paket data dari sumber ke tujuan

masing-masing menggunakan elemen dalam jaringan yang disebut Router. Router merupakan

perlengkapan yang digunakan memeriksa setiap paket yang datang

10

2.1.3.1 Parameter Jalur.

Terdapat beberapa parameter yang dapat menunjukkan bahwa suatu jalur adalah

optimal antara lain (Sumit, et.al. 2005.) :

• Jumlah Hop: Salah satu cara sederhana untuk mencari lintasan optimal adalah dengan mencari jumlah router yang diperlukan untuk mencapai tujuan.

Lintasan dengan jumlah router terkecil akan dipilih sebagai lintasan optimal.

Walaupun sederhana, jumlah hop bukanlah ukuran yang akurat untuk mencari

lintasan optimal. Sebuah lintasan dengan 3 router mungkin akan mentransfer

data lebih lama daripada lintasan dengan 4 router karena mempunyai kapasitas

link yang lebih baik.

• Bandwidth: Beberapa protokol routing menggunakan bandwidth dari link untuk mencari lintasan terbaik. Contohnya, pada Open Shortest Path First

(OSPF).

• Delay: Delay menunjuk kepada waktu yang diperlukan untuk menyampaikan paket data dari sumber sampai ke tujuan nya.

• Reliability: Ini menunjuk kepada tingkat kehilangan paket data dalam sebuah lintasan yang diberikan.

• Load: Load dalam hal ini menunjuk kepada tingkat pemakaian link. Suatu link yang terisi mungkin akan menyebabkan delay yang lebih besar, bahkan dalam

kasus yang ekstrim, menyebabkan kehilangan paket data.

2.2 Distribusi Normal

Boediono dan Wayan Koster. (2004). Distribusi normal merupakan distribusi

kon-tinu yang sangat penting dalam statistik dan banyak dipakai memecahkan persoalan.

Distribusi normal disebut juga distribusi Gauss. Distribusi ini sering digunakan untuk

menerangkan fenomena alam, industri, perdagangan, tingkat pendapatan masyarakat,

berdistribusi normal diberikan sebagai berikut:

n(x;µ, σ) = 1

σ√2πe

− 1 2σ2(x−µ)

2

(2.1)

dimanaµ=mean,σ =standar deviasi, π = 3,14159..., dane = 2,71828

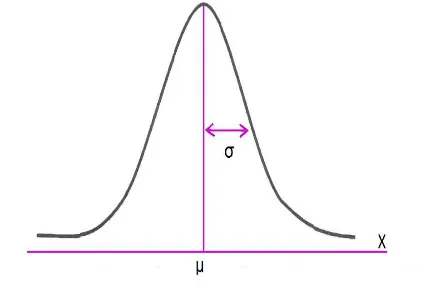
Grafik distribusi normal digambarkan sebagai berikut

Gambar 2.2 : Grafik distribusi normalf(x)

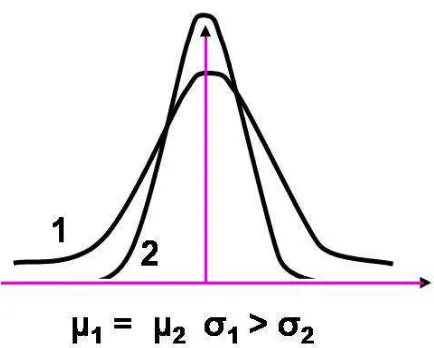
Distribusi normal f(x) didefinisikan pada interval terbuka −∞ < x < +∞. Distribusi normal dengan parameter µ dan σ2 biasanya ditulis N(0,1). Dengan memperhatikan persamaan umum dan grafik distribusi normal f(x), tampak bahwa bentuk kurva normal ditentukan oleh dua parameter, yaitu rata-rata dan simpangan

baku. Bila nilai simpangan baku mengecil, maka bentuk kurva akan lebih rapat dan

semakin runcing dan sebagian besar nilai x akan berkumpul atau mendekati nilai rata-rata. Sebaliknya semakin besar nilai simpangan baku, maka bentuk kurva akan

12

Gambar 2.3 : Sifat grafik distribusi normal

2.2.1 Sifat-sifat Distribusi Normal.

Ada beberapa sifat penting dari distribusi normal, yaitu sebagai berikut:

1. Grafik simetri terhadap garis tegak x=µ.

2. Nilai mean, Median dan modus adalah sama/berhimpit.

3. Grafik selalu di atas sumbu X atau f(x)<0.

4. Mempunyai satu nilai modus.

5. Kurva mempunyai titik belok pada x=µ_±σ, cekung dari bawah bilaµ₋σ < X < µ+σ dan cekung dari atas untuk x lainnya.

6. Grafiknya mendekati sumbuX, tetapi tidak akan pernah memotong sumbu X, sumbu X merupakan garis batas (asimtot).

7. Luas daerah di bawah kurva f(x) dan di atas sumbu X sama dengan 1.

2.2.2 Distribusi Normal Standar.

Sebuah distribusi normal dengan parameter µx = 0 dan σx = 1 disebut distribusi normal standar dan dinotasikanN(0,1). Dengan mentranformasikanZ = x−µx

σx maka

diperoleh fungsi densitas dari sebuah variabel Z normal standar sebagai berikut

fz(Z) = 1

√

2πe

Fungsi distribusi dan variabel Z normal standar sering disimbolkan denganφ(z). Grafik untuk fungsi densitas normal standar diberikan dalam gambar berikut

Gambar 2.4 : Distribusi normal standar

φ(z1) = pdan z1 =φ−1(p)

Dimana p adalah peluang kumulatif. Fungsi distribusi N(0,1). Tabel normal standar terlampir. Karena fungsi densitas dari fungsi densitas normal standar adalah

simetri di sekitar nilai rata-rata (z = 0), oleh karena itu (Rao. 1977.):

f(₋z) = f(z) (2.3)

φ(₋z) = 1₋φ(z) (2.4)

Dengan cara yang sama, nilai dariz yang bersesuaian denganp < 0.5 dapat diperoleh sebagai

14

2.2.3 Probabilitas.

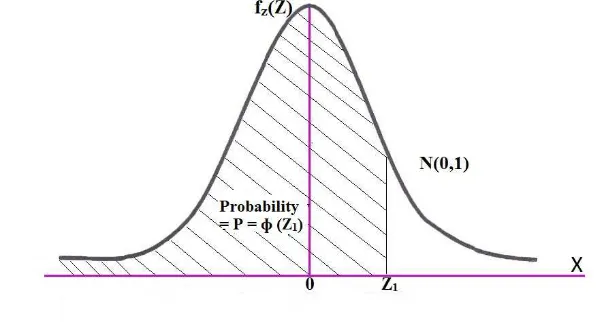
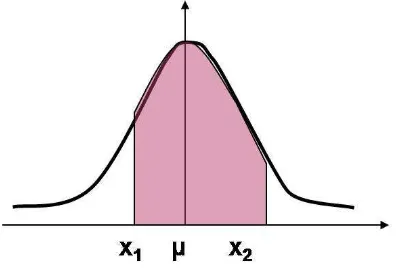
Rinaldi Munir. Probabilitas distribusi normalf(x) pada intervalx1 < X < x2

diten-tukan dengan memakai luas daerah di bawah kurva f(x) sebagaimana ditunjukkan pada gambar berikut ini.

Gambar 2.5 : Probabilitas x1 < X < x2

Pada gambar , probabilitas P(x1 < x < x2) ditunjukkan oleh luas daerah yang

diarsir, yang dibatasi oleh kurva f(x), sumbu X, garis tegak X = x1, dan X = x2.

Oleh karena f(x) merupakan fungsi kontinu, maka probabilitas P(x1 < X < x2)

dengan memakai integral dari fungsif(x) yang dibatasi olehx=x1 danx=x2 yaitu:

P(x1 < X < x2) = Rx2

x1 f(x)dx =

Rx2

x1

1

σ√2π

e−12

x−µ σ

dx

akan tetapi, secara matematis bentuk integral dari fungsi f(x) tersebut sulit dipec-ahkan secara langsung dengan teknik integral. Oleh karena itu, penyelesainnya

di-lakukan dengan memakai transformasi nilai-nilai X menjadi nilai-nilai baku Z. Se-hingga diperoleh fungsi distribusi normal Z, probabilitas nilai-nilai Z pada interval

z1 < Z < Z2 dapat dihitung dengan rumus berikut.

P(z1 < Z < z2) = Rz2

z1 f(z)dz =

Rz2

z1

1

√

2πe −1

2z 2

dz

Berdasarkan integral dari fungsi distribusi normal standar tersebut, probabilitasP(z1 < Z < z2) dihitung dengan memakai tabel distribusi normal standar.

Contoh 2.1

probabilitas untuk menemukan nilai X bernilai antara 45 dan 62?

Dari soal µ= 50 dan σ= 10, x1 = 45 dan x2 = 62

dengan mereduksi nilai x kez, diperoleh

z1 =

(x1−µ) σ

= 45−50

10 =−0.5

z2 =

(x2−µ) σ

= 62−50

10 = 1.2

sehingga

P(45< x < 62) = P(₋0.5< z <1.2)

P(₋0.5< z <1.2) = P(z <1.2)₋P(z <₋0.5)

= 0.8849−0.3085

= 0.5764

2.3 Chance Constrained Programming

Merupakan teknik kedua dari program stokastik yang dikembangkan oleh Charnes dan

Cooper, seperti yang dinyatakan dari namanya program chance constrained adalah satu teknik yang bisa dipakai untuk menyelesaikan persoalan yang mengandung

ken-dala peluang, kenken-dala tersebut mempunyai peluang terbatas tertentu untuk

dilang-gar. Program chance constrained ini memperbolehkan kendala untuk dilanggar oleh sebuah peluang tertentu (peluang kecil) dimana teknik lain tidak ada.

Rao. (1977). Bentuk umum progam chance constrained Programming dari persoalan program linier stokastik dapat dirumuskan sebagai berikut:

Minimize

f(x) = n

X

j=1

16

dengan kendala

P n

X

j=i

aijxj ≤bi

≥pi, i= 1,2, ..., m (2.7)

xj ≥0, j = 1,2, ..., n (2.8)

dimanacj,aij, danbiadalah variabel acak danpi adalah peluang tertentu. Perhatikan bahwa persamaan 2.7 menunjukkan bahwa kendala ke-i

n

X

j=i

aijxj ≤bi (2.9)

harus dipenuhi dengan sebuah peluang dari setidaknyapi dimana 0≤pi ≤1. Untuk penyederhanaan asumsikan bahwa variabel keputusan xj adalah deterministik. Akan dimisalkan kasus dimana hanyacj atauaij ataubi adalah variabel acak. Diasumsikan bahwa semua variabel acak adalah berdistribusi normal dengan mean dan standar

deviasi diketahui.

2.3.1 Untuk Hanya aij yang Variabel Acak.

Misalkan ¯aij dan Var (aij) = σa2ij merupakan rata-rata dan varians dari distribusi

normal variabel acak aij. Asumsikan bahwa distribusi multivariat dari aij, i = 1,2, ..., m;j = 1,2, ..., n, juga diketahui dengan covarian, Cov(aij, akl) antara vari-abel acak aij dan akl. Definisikan jumlah di sebagai

di = n

X

j=i

aijxj, i= 1,2, ..., m (2.10)

Karena ai1, ai2,...ain berdistribusi normal, dan x1, x2, ..., xn merupakan konstan, di juga akan berdistribusi normal dengan nilai rata-rata

¯

di = n

X

j=1

¯

aijxj, i= 1,2, ..., m (2.11)

dan sebuah varian dari

V ar(di) =σ_d2_i =XT_V

Dimana Vi adalah matriks covarian ke-i didefinisikan sebagai

Vi =

            

V ar(aij) Cov(ai1, a12) · · · Cov(ai1, ain)

Cov(ai2, ai1) V ar(ai2) · · · Cov(ai2, ain)

... ... . .. ...

Cov(ain, ai1) Cov(ain, ai2) · · · V ar(ain)              (2.13)

maka kendala dapat diperlihatkan sebagai

P[di ≤bi]≥pi (2.14)

P

di−d¯i

p

V ar(di) ≤

bi−d¯i

p

V ar(di)

≥pi, i= 1,2, ..., m (2.15)

dimana_{di−d¯i/

p

V ar(di)_}dapat dipandang sebagai sebuah variabel normal standar dengan sebuah rata-rata nol dan sebuah varian satu. Oleh karena itu peluangdi lebih kecil atau samadengan bi dapat dituliskan sebagai

P[di ≤bi] =φ

bi−d¯i

p

V ar(di)

(2.16)

Dimana φ(x) menunjukkan fungsi kumulatif distribusi dari distribusi normal standar terhadap x. Jika ei menunjukkan nilai dari variabel normal standar dimana

φ(ei) =pi (2.17)

maka kendala pada persamaan 2.15 dapat dinyatakan sebagai

φ

bi−d¯i

p

V ar(di)

≥φ(ei), i= 1,2, ..., m (2.18)

pertidaksamaan tersebut akan terpenuhi hanya jika

bi−d¯i

p

V ar(di)

≥ei (2.19)

atau,

¯

di+ei

p

V ar(di)−bi ≤0, i= 1,2, ..., m (2.20)

Dengan mensubsitusikan persamaan 2.11 dan 2.12 , diperoleh

n

X

j=1

¯

aijxj +ei

p XT_V

18

Oleh karena itu solusi dari persoalan program stokastik yang ditunjukkan pada

persamaan 2.6 dan 2.7 dapat diperoleh dengan menyelesaikan persoalan program

deterministik berikut

Minimize

f(X) = n

X

j=1

cjxj (2.22)

dengan kendala

n

X

j=i ¯

aijxj +ei

p XT_V

iX−bi ≤0, i= 1,2, ..., m (2.23)

xj ≥0, j = 1,2, ..., n (2.24)

Jika distribusi normal variabel acakaij adalah adalah saling bebas, maka covar-ian akan menjadi nol dan persamaan 2.13 bereduksi menjadi sebuah matriks diagonal

Vi =

            

V ar(aij) 0 · · · 0

0 V ar(ai2) · · · 0

... ... . .. ...

0 0 · · · V ar(ain)

            

Dalam kasus ini, kendala dari persamaan 2.21 diturunkan menjadi

n

X

j=i ¯

aijxj+e

v u u t n X

j=i

[V ar(aij)x2j]−bi ≤0, i= 1,2, ..., m (2.25)

2.3.2 Untuk Hanya bi yang Variabel Acak.

den-gan

P n

X

j=i

aijxj ≤bi

= P

Pn

j=1aijxj−bi

p

V ar(bi) ≤

bi−¯bi

p

V ar(bi)

= P

bi−¯bi

p

V ar(bi) ≥

Pn

j=1aijxj −¯bi p

V ar(bi)

≥pi

i = 1,2, ..., m

(2.26)

Dimana [bi−¯bi/

p

V ar(bi)] adalah sebuah variabel normal standar dengan rata-rata

nol dan varian satu. Pertidaksamaan 2.26 dapat dinyatakan sebagai

1−P

bi−¯bi

p

V ar(bi) ≤

Pn

j=1aijxj −¯bi

p

V ar(bi)

≥Pi, i= 1,2, ..., m (2.27)

atau,

P

bi−¯bi

p

V ar(bi) ≤

Pn

j=1aijxj−¯bi

p

V ar(bi)

≤1−pi, i= 1,2, ..., m (2.28)

Jika ei menunjukkan nilai dari variabel normal standar dimana

φ(ei) = 1−pi

kendala pada persamaan 2.28 dapat diperlihatkan sebagai

φ Pn

j=1aijxj −¯bi

p

V ar(bi)

≤φ(ei), i= 1,2, ..., m (2.29)

pertidaksamaan tersebut akan terpenuhi hanya jika

Pn

j=1aijxj −¯bi p

V ar(bi) ≤ei, i= 1,2, ..., m (2.30)

atau,

n

X

j=1

aijxj−¯bi−ei

p

V ar(bi)≤0, i= 1,2, ...m (2.31)

Oleh karena itu program stokastik linier pada persamaan 2.6 sampai 2.8 adalah sama

dengan persoalan linier program deterministik di bawah ini:

Minimize

f(X) = n

X

j=1

20

dengan kendala

n

X

j=1

aijxj−¯bi−ei

p

V ar(bi)≤0, i= 1,2, ...m (2.33)

dan

xj ≤0, j = 1,2, ..., n (2.34)

Contoh 2.2

Sebuah perusahaan memproduksi dua bagian mesin menggunakan mesin Lathes,

mesin milling dan dan mesin grinding. Waktu operasi mesin yang diperbolehkan

per minggu pada mesin yang berbeda dan keuntungan dari masing-masing bagian

mesin diberikan dibawah ini. Jika waktu operasi yang diperbolehkan pada tiap-tiap

mesin adalah berdistribusi normal dengan parameter yang diberikan pada tabel 2.1.

Tentukan jumlah dari bagian mesin I dan II yang akan diproduksi perminggu untuk

memaksimalkan keuntungan. fungsi kendala harus dipenuhi dengan seubah peluang

[image:33.612.107.544.148.306.2]

Tabel 2.1 : Waktu operasi mesin dan parameter-parameter distribusi normal nya

Tipe Mesin Waktu proses yang

diperlukan untuk satu bagian(menit)

Waktu operasi maksimum per minggu (menit)

Part I Part II Mean Standar Deviasi

Lathes a11 = 10 a12 = 5 ¯b1 = 2500 σb1 = 500

Milling a21 = 4 a22 = 10 ¯b2 = 2000 σb2 = 400

Grinding a31 = 1 a32 = 1.5 ¯b3 = 450 σb3 = 50

Profit per unit (Rs) c1 = 50 c2 = 100

Misalkan jumlah dari bagian mesin I dan II diproduksi per minggu sebagai x1

dan x2, nilai variabel normal standar (ei) pada (ei) = 1−pi = 1/100 tidak dapat didapat langsung dari tabel lampiran A secara langsung. tetapi, perhatikan bahwa

ei <0.0 karena 1−pi <0.5 dan oleh karena itu

φ(₋ei) = 1₋φ(ei) = 0.99.

sesuai denganpi = 0.99, dari tabel diperoleh bahwa ei =−2.33.

Oleh karena itu pertidaksamaan yang memenuhi dapat ditunjukkan dari persamaan

2.31 sebagai:

10x1+ 5x2−2500−(−2.33)(500) ≤0

4x1 + 10x2−2000−(−2.33)(400) ≤0 x1+ 1.5x2−450−(−2.33)(50)≤0

Persoalan persamaan deterministik program linier sekarang dapat ditetapkan,

meng-gunakan persamaan 2.31 sampai 2.33 sebagai:

Maksimum

f = 50x1+ 100x2

dengan kendala

22

4x1+ 10x2−1068≤0 x1+ 1.5x2−333.5≤0

x1 ≥0, x2 ≥0

Solusi dari program linier di atas dapat diperoleh dengan menggunakan metode grafik

atau metode simpleks

2.3.3 Untuk Hanya cj yang Variabel Acak.

Karenacj merupakan variabel acak berdistribusi normal, maka fungsi objektif f(X) juga akan menjadi variabel acak berdistribusi normal. Rata-rata dan varian dari f

diberikan sebagai berikut

¯ f = n X j=1 ¯

cjxj (2.35)

dan

V ar(f) = XTV X (2.36)

Dimana ¯cj adalah nilai rata-rata dan matriks V adalah matriks covarian dari cj didefinisikan sebagai V =             

V ar(c1) Cov(c1, c2) · · · Cov(c1, cn)

Cov(c2, c1) V ar(c2) · · · Cov(c2, cn)

... ... . .. ...

Cov(cn, c1) Cov(cn, c2) · · · V ar(cn)              (2.37)

Dengan V ar(cj) dan Cov(ci, cj) menunjukkan varian dari cj dan covarian antara ci dan cj.

Fungsi objektif deterministik baru untuk minimasi dapat diformulasikan sebagai

F(X) =k1f¯+k2 p

V ar(f) (2.38)

Dimana k1 dan k2 adalah konstanta positif yang nilai nya menunjukkan relative im-portancedari ¯f dan standar deviasi darif untuk meminimasi. Oleh karena ituk2 = 0

deviasi dari f. Sebaliknya,jika k1 = 0, itu menunjukkan bahwa perlu meminimalkan

variabilitas darif disekitar nilai rata-rata nya tanpa memperhatikan apa yang terjadi dengan nilai rata-rata f. Demikian pula, jika k1 = k2 = 1, ini menunjukkan bahwa

adanya kepentingan yang sama pada minimasi dari nilai rata-rata dan standar deviasi

dari f.

Oleh karena itu solusi dari persoalan program linier stokastik yang dinyatakan

pada persamaan 2.6 sampai 2.7 dapat diperoleh dengan menyelesaikan persamaan

program nonlinier deterministik :

Minimize

f(x) =k1

n

X

j=1

¯

cjxj +k2 √

XT_{V X (2.39)}

dengan kendala

n

X

j=1

aijxj −bi ≤0, i= 1,2, ..., m (2.40)

xj ≥0, j = 1,2, ..., n (2.41)

Jika semua varibel acakcj adalah saling bebas, maka fungsi objektif direduksi menjadi

f(x) =k1

n

X

j=1

¯

cjxj+k2 v u u t n X j=1

V ar(cj)x2j (2.42)

Setelah itu Liu mengembangkan CCP dalam permasalahan yang tidak hanya

kendala stokastik tetapi juga fungsi tujuan stokastik . misalkanxsebuah vektor kepu-tusan,ξsebuah vektor stokastik,f(x, ξ) adalah fungsi hasil, dangj(x, ξ) adalah fungsi kendala stokastik, j = 1,2..., p. karena kendala stokastik gj(x, ξ) ≤ 0, j = 1,2, ..., p

tidak menetapkan sebuah himpunan penyelesaian deterministik yang feasible, ma-ka perlu memberima-kan kendala stoma-kastik sebuah tingma-kat jaminan α. Oleh karena itu diperoleh sebuah kendala peluang seperti berikut (Liu B. 2009),

P r_{gj(x, ξ)≤0, j = 1, , ..., p} ≥α (2.43)

ini disebut dengan sebuah kendala peluang gabungan

Definisi 2.1: Titikxdisebutfeasiblejika dan hanya jika tingkat peluang dari kejadian

24

Dengan kata lain, kendala tersebut akan dilanggar paling banyak (1−α) kali. terkadang, kendala peluang gabungan dipisah sebagai

P r{gj(x, ξ)≤0} ≥α, j = 1, , ..., p (2.44)

2.3.4 Maximax Program Chance Constrained.

Dalam lingkungan stokastik, dalam tujuan untuk memaksimalkan hasil optimistik

dengan memberikan sebuah tingkat jaminan terhadap kendala peluang, Liu

mem-berikan CCP berikut ini:

max max ¯f (2.45)

dengan kendala

Pr{f(x, ξ)≥f¯} ≥β (2.46)

Pr{gj(x, ξ)≤0, j = 1,2, ..., p} ≥α (2.47)

Dimana α dan β adalah tingkat jaminan, dan maxf¯adalah β-optimistic return

2.3.5 Minimax Chance Constrained Programming.

Dalam lingkungan stokastik, untuk memaksimalkanpessimistic returndengan sebuah tingkat jaminan yang diberikan pada kendala peluang, Liu menyediakan model

max min ¯f (2.48)

dengan kendala:

Pr{f(x, ξ)≤f¯} ≥β (2.49)

Pr{gj(x, ξ)≤0, j = 1,2, ..., p} ≥α (2.50)

Dimana α dan β adalah tingkat jaminan, dan maxf¯adalah β-optimistic return

Persamaan Deterministik

Dalam mencari penyelesaian akhir dari CCP diperlukan mengubah kendala peluang

ke dalam masing-masing persamaan deterministiknya. Seperti yang diketahui, proses

ini biasanya sulit dan hanya berhasil untuk beberapa kasus saja. Misalkan dibawah

ini formula dari kendala peluang,

P r{g(x, ξ)≤0} ≥α. (2.51)

Theorema 1 Asumsikan bahwa vektor stokastik ξ degenerates menjadi sebuah vari-abel acakξdengan distribusi peluangφ, dan fungsig(x, ξ)mempunyai formulag(x, ξ) =

h(x)₋ξ. Maka P r_{g(x, ξ) _≤ 0_{} ≥} α jika dan hanya jika h(x) _≤ Kα, dimana Kα

adalah bilangan terbesar sehingga P r{Kα ≤ξ} ≥α.

Bukti: Asumsi tersebut secara tidak langsung menyatakan bahwaP r_{Kα ≤ξ} ≥α dapat dituliskan denggan formula di bawah ini,

P r{h(x)≤ξ} ≥α

Untuk setiap tingkat jaminan α(0< α <1), Misal Kα merupakan bilangan terbesar sehingga

P r{Kα ≤ξ} ≥α

26

Remark 1: Untuk varibel acak kontinuξ, persamaanP r{Kα ≤ξ}= 1−φ(Kα)selalu tetap, dan diperoleh,

Kα =φ−1(1−α)

Dimana φ−1 _{adalah fungsi invers dari φ}

Contoh 2.3

Asumsikan bahwa dibawah ini kendala peluang,

   

  

P r_{3x1+ 4x2 ≤ξ1} ≥0.8

P r{x2

1+x32 ≤ξ2} ≥0.9

Dimana ξ1 adalah variabel acak berdistribusi eksponensial Exp(2) dengan distribusi

peluang dinotasikan dengan φ1, dan ξ2 adalah variabel acak berdistribusi normal N(2,1) dengan peluang distribusi dinotasikan φ2. Memakai formula pada teorema 1

bahwa kendala peluang di atas samadengan

   

  

P r_{3x1+ 4x2 ≤φ1−1(1−0.8) = 0.446

P r{x2

PEMBAHASAN

Pada Bab ini penulis akan membahas model matematikachance constrained program-ming untuk perencanaan jaringan dengan permintaan acak. Untuk menguji model yang ada penulis akan mencoba memakai model tersebut dalam menyelesaikan

con-toh . Karena kesulitan dalam mengambil concon-toh kasus nyata, Maka dalam tulisan ini

penulis menggunakan contoh pemisalan saja.

3.1 Model Umum CCP untuk Jaringan

Misalkan N himpunan variabel acak, dinotasikan denganξi. Misalkan xi merupakan variabel keputusan yang dihubungkan dengan biaya ci. Dalam sebuah konteks jari-ngan, xi dapat menunjukkan kapasitas ataubandwidth yang dialokasikan pada link i dalam batas bi. Andaikan bahwa bandwidth tersebut dapat digunakan untuk mem-bawa beberapa permintaan acak dengan beberapa nilai peluang tertentu, sebuah

for-mulasi sederhana dari CCP yang diberikan oleh Koonlachat

Meesublak. 2008. Adalah sebagai berikut:

min

N

X

i=1

cixi (3.1)

Dengan kendala:

P(xi ≥ξi)≥αi,∀i = 1, ..., N (3.2)

xi ≤bi,∀i = 1, ..., N (3.3)

xi ≥0,∀i = 1, ..., N (3.4)

28

dimasukkan dalam model untuk memastikan permintaan acak dapat dibawa dengan

sebuah tingkat jaminan sebesar α.

Kendala dari persamaan 3.2, yakni

P(x≥ξ)≥α (3.5)

dapat diubah kedalam sebuah persamaan deterministik. Misalkan bahwa sebuah

variabel acak ξ mempunyai sebuah distribusi kumulatif φ(.) dan transformasi invers nya φ−1_{(.). Misalkan φ}−1_{(α) = K. Oleh karena itu, P(K ≥ ξ) = α. Adalah benar}

bahwaP(x_≥ξ)_≥αjika dan hanya jikax_≥K. Dalam tulisan ini, dimisalkan bahwa trafik permintaanξ adalah berdistribusi normal dengan rata-rata (µ) dan varian (σ2_).

Dengan standarisasi pertidaksamaan 3.5 menggunakan unit normal variabel acak z, diperoleh P(x−_σµ _≥ z)_≥ α jika dan hanya jika x−_σµ _≥ φ−1_{(α), atau dapat dituliskan}

sebagai

x_≥µ+φ−1_{(α)σ (3.6)}

Ini merupakan persamaan deterministik dari kendala peluang dari 3.5,

per-samaan ini dapat diartikan sebagai berikut. Untuk menjamin bahwa link dapat mendukung/menyangga permintaan acak setidaknya 100(α)%, perlu mengalokasikan bandwidth setidaknya sebanyak φ−1_{(α)σ diatas rata-rata (µ) dari permintaan. Jadi}

minimalbandwidthyang harus dialokasikan pada sebuah link dengan tingkat jaminan

α adalah

x=µ+φ−1(α)σ (3.7)

3.2 Model Matematika Perencanaan Jaringan dengan CCP

Akan dicoba mengembangkan sebuah model matematika programming didasarkan

pada CCP. Misalkan penulis ingin menentukan jumlah bandwidth yang harus di-alokasikan pada link j, asumsikan bahwa link tersebut membawa trafik permintaan

ξ1, ..., ξK, dengan masing-masing berdistribusi normal dengan rata-rata µk dan vari-an σ2

k, k = 1, ..., K, masing-masing permintaan mempunyai tingkat jaminan tertentu

lintasan dari sumber sampai ke tujuan. Didasarkan pada persamaan 3.7 yang telah

diperoleh, maka total bendwidthuntuk memenuhi semua trafik permintaan pada link tersebut dapat ditentukan sebagai berikut:

xj = K

X

k=1

µk+φ−1(αk)σk (3.8)

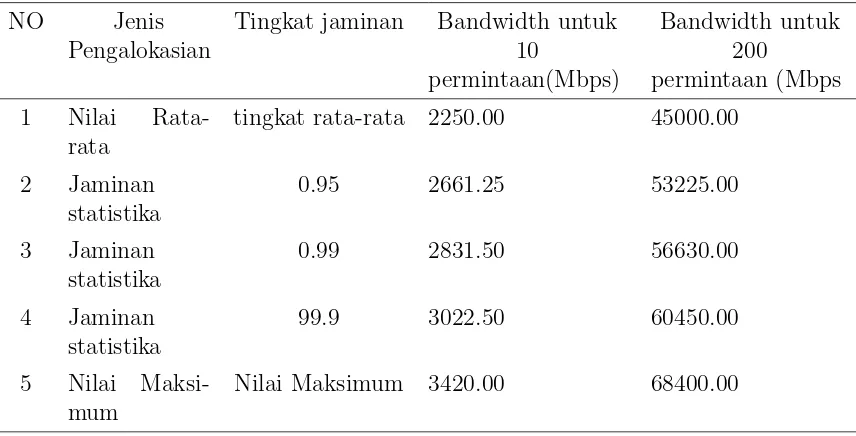
Berikut contoh jumlah bandwidth yang harus dialokasikan untuk sebuah link sepasang node, dicari meliputi tiga tipe pendekatan, yakni: berdasarkan rata-rata,

berdasarkan nilai maksimum, dan berdasarkan jaminan statistika yang dibahas dalam

tulisan ini. Misalkan dari beberapa permintaan diperoleh rata-rata permintaan adalah

225 Mbps, dan nilai maksimum adalah 342 Mbps, sedangkan standar deviasinya

adalah 25 Mbps. Misalkan tingkat jaminannya (α) = 0.95. Maka

α= 0.95, makaφ−1_{(0.95) = 1.645}

Misal banyak trafik permintaan : ξ1, ξ2, ..., ξ10 dengan distribusi dan parameter yang

sama

Xj = K

X

k=1

µ+φ−1_(αk)σ

k

= 10_∗225 +φ−1_(0.95)25 ∗10

= 2250 + 1.645∗25∗10

= 2250 + 411.25

= 2661.25

[image:42.612.110.538.146.364.2]

30

Tabel 3.1 : Perhitungan pengalokasian bandwidthuntuk sebuah link sepasang node

NO Jenis

Pengalokasian

Tingkat jaminan Bandwidth untuk 10

permintaan(Mbps)

Bandwidth untuk 200

permintaan (Mbps

1 Nilai

Rata-rata

tingkat rata-rata 2250.00 45000.00

2 Jaminan

statistika

0.95 2661.25 53225.00

3 Jaminan

statistika

0.99 2831.50 56630.00

4 Jaminan

statistika

99.9 3022.50 60450.00

5 Nilai

Maksi-mum

Nilai Maksimum 3420.00 68400.00

Koonlachat Meesublak. (2008). Memberikan suatu formulasi CCP untuk

peren-canaan jaringan dengan permintaan acak. Misalkan sebuah jaringan didefinisikan

sebagai sebuah graph (N,A), dimana N merupakan himpunan dari node, dan A

merupakan himpunan dari link. Notasi yang digunakan adalah sebagai berikut:

• Dmenunjukkan kumpulan trafik permintaan dari titik-ke-titik. Dengan

masing-masing rata-rata µdan varian σ2

k.

• Pk _{menunjukkan himpunan calon lintasan dari permintaan k ∈ D.}

• cj menunjukkan biaya per unitbandwidth pada linkj ∈ A.

• αk menunjukkan tingkat jaminan untuk permintaank ∈D.

• Wj menunjukkan batas bandwidth yang diperbolehkan pada link j ∈ A.

• fk,p _{menunjukkan variabel keputusan, dimana sama dengan 1 jika aliran dari}

permintaankmemilih lintasanpdari himpunan calon lintasanPk_{, dan 0 untuk} lainnya.

Tujuan dari model ini adalah untuk menentukan lintasan optimal atau dalam

model ini himpunan terbaik darifk,p _{sehingga total biaya jaringan berupa total} pen-galokasianbandwidthminimal. Masukan ke dalam model ini mengandung parameter-parameter : Topologi jaringan, sebuah himpunan dari trafik permintaan acak dengan

informasi probabilistik (rata-rata dan varian), parameter biaya, dan tingkat

jami-nan dari masing-masing permintaan. Sedangkan hasil keluaran dari model ini adalah

pemilihan lintasan optimal dengan batas yang tidak pasti,bandwidthyang dibutuhkan dalam setiap link, dan biaya optimal. Dengan notasi di atas, biaya minimum dari

perencanaan jaringan dengan permintaan acak dapat diformulasikan sebagai berikut.

Minimalkan

X

j∈A

X

k∈D

X

p∈Pk

cj(µk+φ−1(αk)σk)δjk,pf

k,p _(3.9)

dengan kendala

X

k∈D

X

p∈Pk

(µk+φ−1(αk)σk)δk,pj f k,p

≤Wj,∀j ∈ A (3.10)

X

p∈Pk

fk,p _{= 1,}

∀k ∈D (3.11)

fk,p_{∈ {}0,1_} (3.12)

32

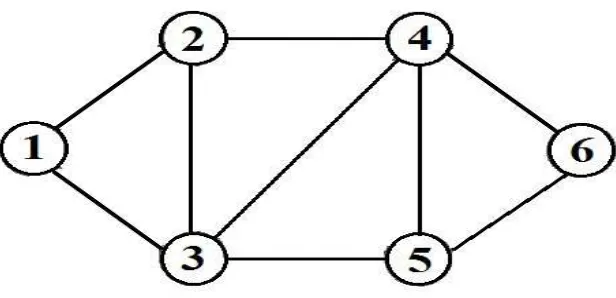
[image:44.612.171.479.165.314.2]

Contoh 3.1

Gambar 3.1 : Topologi Jaringan Dengan 6 Node dan 9 link

Diketahui sebuah jaringan dengan topologi seperti di atas mempunyai 6 node serta 9

link terhubung langsung. Dari jaringan di atas akan dicoba mencari lintasan-lintasan

terbaik untuk setiap permintaan yang diketahui di bawah ini sehingga diperoleh

pen-galokasianbandwidth optimal pada tiap link.

Himpunan trafik permintaan dari titik-ke-titik(D).

k1 : 1⇔6 dengan rata-rata (µ1) = 45 dan varian (σ12) = 36 k2 : 1⇔5 dengan rata-rata (µ2) = 40 dan varian (σ22) = 25 k3 : 1⇔4 dengan rata-rata (µ3) = 35 dan varian (σ32) = 16 k4 : 2⇔6 dengan rata-rata (µ4) = 30 dan varian (σ42) = 16 k5 : 2⇔5 dengan rata-rata (µ5) = 42 dan varian (σ52) = 36 k6 : 3⇔6 dengan rata-rata (µ6) = 50 dan varian (σ62) = 49

Setiap permintaan di atas menunjukkan trafik permintaan acak timbal-balik dari

sepasang node dalam hal ini penulis memisalkan bahwa sepasang node akan

meng-gunakan lintasan tunggal. Misalkan untuk setiap trafik permintaan titik-ke-titik

berlaku:

• Satuan biaya bandwidthRp. 1 /Mbps pada semua link

• Besar batas bandwidth (Wi) yang diperbolehkan untuk setiap link adalah 130 Mbps

Sehingga jumlahbandwidthyang harus disediakan pada setiap link yang dipakai untuk melewatkan sebuah trafik permintaan di atas adalah:

dari tabel distribusi normal standar diperolehφ−1_{(0.99) = 2.33}

xj = µk+φ−1(αk)σk

x1 = µ1+φ−1(αk)σ1

= 45 + 2.33(6)

= 58.98 = 59M bps

x2 = µ2+φ−1(αk)σ2

= 40 + 2.33(5)

= 51.65 = 52M bps

x3 = µ3+φ−1(αk)σ3

= 35 + 2.33(4)

= 44.32 = 44M bps

x4 = µ4+φ−1(αk)σ4

= 30 + 2.33(4)

= 39.32 = 39M bps

x5 = µ5+φ−1(αk)σ5

= 42 + 2.33(6)

= 55.98 = 56M bps

x6 = µ6+φ−1(αk)σ6

= 50 + 2.33(7)

34

Pk_{: Himpunan calon lintasan untuk trafik permintaank ∈ D, syarat pemilihan calon}

lintasan:

• Maksimum Hop/node = 4.

• Tidak terjadi loop. Ini berarti bahwa dalam lintasan tidak akan terjadi satu

paket data melewati sebuah node lebih dari satu kali.

Untuk k = 1 untuk k = 2

P1 :j2 →j6 →j9 P10:j2 →j6

P2 :j2 →j5 →j8 P11:j2 →j5 →j7

P3 :j2 →j6 →j7 →j8 P12:j2 →j4 →j3 →j7

P4 :j2 →j5 →j7 →j9 P13:j1 →j3 →j7

P5 :j2 →j4 →j3 →j8 P14:j1 →j4 →j6

P6 :j1 →j3 →j8 P15:j1 →j4 →j5 →j7

P7 :j1 →j3 →j7 →j9 P16:j1 →j3 →j5 →j6

P8 :j1 →j4 →j6 →j9

P9 :j1 →j4 →j5 →j8

Untuk k = 3 untuk k = 4

P17:j1 →j3 P23:j3 →j8

P18:j1 →j4 →j5 P24:j3 →j7 →j9

P19:j1 →j4 →j6 →j7 P25:j4 →j5 →j8

P20:j2 →j5 P26:j4 →j6 →j9

P21:j2 →j6 →j7 P27:j4 →j5 →j7 →j9

P22:j2 →j4 →j3 P28:j4 →j6 →j7 →j8

Untuk k = 5 untuk k = 6

P30:j3 →j7 P37:j6 →j9

P31:j3 →j8 →j9 P38:j5 →j8

P32:j3 →j5 →j6 P39:j5 →j7 →j9

P33:j4 →j6 P40:j6 →j7 →j8

P34:j4 →j5 →j7 P41:j4 →j3 →j8

P35:j1 →j2 →j6 P42:j4 →j3 →j7 →j9

36

Parameter binerδjk,P. Sama dengan 1 jika lintasanp∈ Pkuntuk permintaank meng-gunakan linkj, dan 0 untuk lainnya

Untuk j = 1

δ₁1,1 = 0 δ₁2,10= 0 δ₁3,17= 1 δ₁4,23= 0 δ₁5,30= 0 δ6₁,37= 0

δ₁1,2 = 0 δ₁2,11= 0 δ₁3,18= 1 δ₁4,24= 0 δ₁5,31= 0 δ6₁,38= 0

δ₁1,3 = 0 δ₁2,12= 0 δ₁3,19= 1 δ₁4,25= 0 δ₁5,32= 0 δ6₁,39= 0

δ₁1,4 = 0 δ₁2,13= 1 δ₁3,20= 0 δ₁4,26= 0 δ₁5,33= 0 δ6₁,40= 0

δ₁1,5 = 0 δ₁2,14= 1 δ₁3,21= 0 δ₁4,27= 0 δ₁5,34= 0 δ6₁,41= 0

δ₁1,6 = 1 δ₁2,15= 1 δ₁3,22= 0 δ₁4,28= 0 δ₁5,35= 1 δ6₁,42= 0

δ₁1,7 = 1 δ₁2,16= 1 δ₁4,29= 0 δ₁5,36= 1 δ6₁,43 = 1

δ₁1,8 = 1

Untukj = 2

δ₂1,1 = 1 δ₂2,10= 1 δ₂3,17= 0 δ₂4,23= 0 δ₂5,30= 0 δ6₂,37= 0

δ₂1,2 = 1 δ₂2,11= 1 δ₂3,18= 0 δ₂4,24= 0 δ₂5,31= 0 δ6₂,38= 0

δ₂1,3 = 1 δ₂2,12= 1 δ₂3,19= 0 δ₂4,25= 0 δ₂5,32= 0 δ6₂,39= 0

δ₂1,4 = 1 δ₂2,13= 0 δ₂3,20= 1 δ₂4,26= 0 δ₂5,33= 0 δ6₂,40= 0

δ21,5 = 1 δ2

,14

2 = 0 δ3

,21

2 = 1 δ4

,27

2 = 0 δ5

,34

2 = 0 δ6

,41 2 = 0

δ₂1,6 = 0 δ₂2,15= 0 δ₂3,22= 1 δ₂4,28= 0 δ₂5,35= 1 δ6₂,42= 0

δ₂1,7 = 0 δ₂2,16= 0 δ₂4,29= 0 δ₂5,36= 1 δ6₂,43 = 1

δ₂1,8 = 0

δ21,9 = 0

Untukj = 3

δ₃1,1 = 0 δ₃2,10= 0 δ₃3,17= 1 δ₃4,23= 1 δ₃5,30= 1 δ6₃,37 = 0

δ₃1,2 = 0 δ₃2,11= 0 δ₃3,18= 0 δ₃4,24= 1 δ₃5,31= 1 δ6₃,38 = 0

δ₃1,3 = 0 δ₃2,12= 1 δ₃3,19= 0 δ₃4,25= 0 δ₃5,32= 1 δ6₃,39 = 0

δ₃1,4 = 0 δ₃2,13= 1 δ₃3,20= 0 δ₃4,26= 0 δ₃5,33= 0 δ6₃,40 = 0

δ31,5 = 1 δ2

,14

3 = 0 δ3

,21

3 = 0 δ4

,27

3 = 0 δ5

,34

3 = 0 δ6

,41 3 = 1

δ₃1,6 = 1 δ₃2,15= 0 δ₃3,22= 1 δ₃4,28= 0 δ₃5,35= 0 δ6₃,42 = 1

δ₃1,7 = 1 δ₃2,16= 1 δ₃4,29= 1 δ₃5,36= 0 δ6₃,43 = 1

δ₃1,8 = 0

38

Untukj = 4

δ₄1,1 = 0 δ₄2,10= 0 δ₄3,17= 0 δ₄4,23= 0 δ₄5,30= 0 δ6₄,37= 0

δ₄1,2 = 0 δ₄2,11= 0 δ₄3,18= 1 δ₄4,24= 0 δ₄5,31= 0 δ6₄,38= 0

δ₄1,3 = 0 δ₄2,12= 1 δ₄3,19= 1 δ₄4,25= 1 δ₄5,32= 0 δ6₄,39= 0

δ₄1,4 = 0 δ₄2,13= 0 δ₄3,20= 0 δ₄4,26= 1 δ₄5,33= 1 δ6₄,40= 0

δ41,5 = 1 δ2

,14

4 = 1 δ3

,21

4 = 0 δ4

,27

4 = 1 δ5

,34

4 = 1 δ6

,41 4 = 1

δ₄1,6 = 0 δ₄2,15= 1 δ₄3,22= 1 δ₄4,28= 1 δ₄5,35= 0 δ6₄,42= 1

δ₄1,7 = 0 δ₄2,16= 0 δ₄4,29= 0 δ₄5,36= 0 δ6₄,43 = 0

δ₄1,8 = 1

δ41,9 = 1

Untukj = 5

δ₅1,1 = 0 δ₅2,10= 0 δ₅3,17= 0 δ₅4,23= 0 δ₅5,30= 0 δ6₅,37 = 0

δ₅1,2 = 1 δ₅2,11= 1 δ₅3,18= 1 δ₅4,24= 0 δ₅5,31= 0 δ6₅,38 = 1

δ51,3 = 0 δ2

,12

5 = 0 δ3

,19

5 = 0 δ4

,25

5 = 1 δ5

,32

5 = 1 δ6

,39 5 = 1

δ₅1,4 = 1 δ₅2,13= 0 δ₅3,20= 1 δ₅4,26= 0 δ₅5,33= 0 δ6₅,40 = 0

δ₅1,5 = 0 δ₅2,14= 0 δ₅3,21= 0 δ₅4,27= 1 δ₅5,34= 1 δ6₅,41 = 0

δ₅1,6 = 0 δ₅2,15= 1 δ₅3,22= 0 δ₅4,28= 0 δ₅5,35= 0 δ6₅,42 = 0

δ51,7 = 0 δ2

,16

5 = 1 δ4

,29

5 = 1 δ5

,36

5 = 1 δ6

,43 5 = 0

δ₅1,8 = 0

Untukj = 6

δ₆1,1 = 1 δ₆2,10= 1 δ₆3,17= 0 δ₆4,23= 0 δ₆5,30= 0 δ6₆,37= 1

δ₆1,2 = 0 δ₆2,11= 0 δ₆3,18= 0 δ₆4,24= 0 δ₆5,31= 0 δ6₆,38= 0

δ₆1,3 = 1 δ₆2,12= 0 δ₆3,19= 1 δ₆4,25= 0 δ₆5,32= 1 δ6₆,39= 0

δ₆1,4 = 0 δ₆2,13= 0 δ₆3,20= 0 δ₆4,26= 1 δ₆5,33= 1 δ6₆,40= 1

δ61,5 = 0 δ2

,14

6 = 1 δ3

,21

6 = 1 δ4

,27

6 = 0 δ5

,34

6 = 0 δ6

,41 6 = 0

δ₆1,6 = 0 δ₆2,15= 0 δ₆3,22= 0 δ₆4,28= 1 δ₆5,35= 1 δ6₆,42= 0

δ₆1,7 = 0 δ₆2,16= 1 δ₆4,29= 1 δ₆5,36= 0 δ6₆,43 = 0

δ₆1,8 = 1

δ61,9 = 0

Untukj = 7

δ₇1,1 = 0 δ₇2,10= 0 δ₇3,17= 0 δ₇4,23= 0 δ₇5,30= 1 δ6₇,37 = 0

δ₇1,2 = 0 δ₇2,11= 1 δ₇3,18= 0 δ₇4,24= 1 δ₇5,31= 0 δ6₇,38 = 0

δ71,3 = 1 δ2

,12

7 = 1 δ3

,19

7 = 1 δ4

,25

7 = 0 δ5

,32

7 = 0 δ6

,39 7 = 1

δ₇1,4 = 1 δ₇2,13= 1 δ₇3,20= 0 δ₇4,26= 0 δ₇5,33= 0 δ6₇,40 = 1

δ₇1,5 = 0 δ₇2,14= 0 δ₇3,21= 1 δ₇4,27= 1 δ₇5,34= 1 δ6₇,41 = 0

δ₇1,6 = 0 δ₇2,15= 1 δ₇3,22= 0 δ₇4,28= 1 δ₇5,35= 0 δ6₇,42 = 1

δ71,7 = 1 δ2

,16

7 = 0 δ4

,29

7 = 0 δ5

,36

7 = 1 δ6

,43 7 = 0

δ₇1,8 = 0

40

Untukj = 8

δ₈1,1 = 0 δ₈2,10= 0 δ₈3,17= 0 δ₈4,23= 1 δ₈5,30= 0 δ6₈,37= 0

δ₈1,2 = 1 δ₃2,11= 0 δ₈3,18= 0 δ₈4,24= 0 δ₈5,31= 1 δ6₈,38= 1

δ₈1,3 = 1 δ₈2,12= 0 δ₈3,19= 0 δ₈4,25= 1 δ₈5,32= 0 δ6₈,39= 0

δ₈1,4 = 0 δ₈2,13= 0 δ₈3,20= 0 δ₈4,26= 0 δ₈5,33= 0 δ6₈,40= 1

δ81,5 = 1 δ2

,14

8 = 0 δ3

,21

8 = 0 δ4

,27

8 = 0 δ5

,34

8 = 0 δ6

,41 8 = 1

δ₈1,6 = 1 δ₈2,15= 0 δ₈3,22= 0 δ₈4,28= 1 δ₈5,35= 0 δ6₈,42= 0

δ₈1,7 = 0 δ₈2,16= 0 δ₈4,29= 0 δ₈5,36= 0 δ6₈,43 = 1

δ₈1,8 = 0

δ81,9 = 1

Untukj = 9

δ₉1,1 = 1 δ₉2,10= 0 δ₉3,17= 0 δ₉4,23= 0 δ₉5,30= 0 δ6₉,37 = 1

δ₉1,2 = 0 δ₉2,11= 0 δ₉3,18= 0 δ₉4,24= 1 δ₉5,31= 1 δ6₉,38 = 0

δ91,3 = 0 δ2

,12

9 = 0 δ3

,19

9 = 0 δ4

,25

9 = 0 δ5

,32

9 = 0 δ6

,39 9 = 1

δ₉1,4 = 1 δ₉2,13= 0 δ₉3,20= 0 δ₉4,26= 1 δ₉5,33= 0 δ6₉,40 = 0

δ₉1,5 = 0 δ₉2,14= 0 δ₉3,21= 0 δ₉4,27= 1 δ₉5,34= 0 δ6₉,41 = 0

δ₉1,6 = 0 δ₉2,15= 0 δ₉3,22= 0 δ₉4,28= 0 δ₉5,35= 0 δ6₉,42 = 1

δ91,7 = 1 δ2

,16

9 = 0 δ4

,29

9 = 1 δ5

,36

9 = 0 δ6

,43 9 = 0

δ₉1,8 = 1

Dengan memasukkan semua parameter yang telah diperoleh kedalam persamaan 3.8

- 3.11 akan diperoleh:

Kendala

P

k∈D

P

p∈Pk(µk+φ−1(αk)σk)δjk,pfk,p ≤Wj,∀j ∈ A

59f1,6 _{+ 59f}1,7 _{+ 59f}1,8 _{+ 59f}1,9 _{+ 65f}2,13 _{+ 65f}2,14_{+ 65f}2,15 _{+ 65f}2,16 _{+ 44f}3,17₊

44f3,18_{+ 44f}3,19_{+ 56f}5,35_{+ 56f}5,36_{+ 66f}6,43 _≤130

59f1,1_+59f1,2_+59f1,3_+59f1,4_+59f1,5_+52f2,10_+52f2,11_+52f2,12_+44f3,20_+44f3,21₊

44f3,22_{+ 56f}5,35_{+ 56f}5,36_{+ 66f}6,43 _≤130

59f1,5 _{+ 59f}1,6 _{+ 59f}1,7_{+ 52f}2,12_{+ 52f}2,13_{+ 52f}2,16_{+ 44f}3,17_{+ 44f}3,22 _{+ 39f}4,23₊

39f4,24_{+ 39f}4,29_{+ 56f}5,30_{+ 56f}5,31_{+ 56f}5,32_{+ 66f}6,41_{+ 66f}6,42_{+ 66f}6,43_≤130

59f1,5 _{+ 59f}1,8 _{+ 59f}1,9_{+ 52f}2,12_{+ 52f}2,14_{+ 52f}2,15_{+ 44f}3,18_{+ 44f}3,19 _{+ 44f}3,22₊

39f4,25_{+ 39f}4,26_{+ 39f}4,27_{+ 39f}4,28_{+ 56f}5,33_{+ 56f}5,34_{+ 66f}6,41_{+ 66f}6,42_≤130

59f1,2 _{+ 59f}1,4 _{+ 59f}1,9_{+ 52f}2,11_{+ 52f}2,15_{+ 52f}2,16_{+ 44f}3,18_{+ 44f}3,20 _{+ 39f}4,25₊

39f4,27_{+ 39f}4,29_{+ 56f}5,32_{+ 56f}5,34_{+ 56f}5,36_{+ 66f}6,38_{+ 66f}6,39_≤130

59f1,1 _{+ 59f}1,3 _{+ 59f}1,8_{+ 52f}2,10_{+ 52f}2,14_{+ 52f}2,16_{+ 44f}3,19_{+ 44f}3,21 _{+ 39f}4,26₊

39f4,28_{+ 39f}4,29_{+ 56f}5,32_{+ 56f}5,33_{+ 56f}5,35_{+ 66f}6,37_{+ 66f}6,40_≤130

59f1,3 _{+ 59f}1,4 _{+ 59f}1,7_{+ 52f}2,11_{+ 52f}2,12_{+ 52f}2,13_{+ 52f}2,15_{+ 44f}3,19 _{+ 44f}3,21₊

39f4,24_+39f4,27_+39f4,28_+56f5,30_+56f5,34_+56f5,36_+66f6,39_+66f6,40_+66f6,42 _≤130

42

66f6,40_{+ 66f}6,41_{+ 66f}6,43 _≤130

59f1,1 _{+ 59f}1,4 _{+ 59f}1,7 _{+ 59f}1,8 _{+ 39f}4,24 _{+ 39f}4,26_{+ 39f}4,27 _{+ 39f}4,29 _{+ 56f}5,31₊

66f6,37_{+ 66f}6,39_{+ 66f}6,42 _≤130

P

p∈Pkfk,p= 1,∀k∈D

f1,1 _+f1,2_+f1,3_+f1,4_+f1,5_+f1,6_+f1,7 _+f1,8_+f1,9 _{= 1}

f2,10_+f2,11_+f2,12_+f2,13_+f2,14_+f2,15_+f2,16_{= 1}

f3,17_+f3,18_+f3,19_+f3,20_+f3,21_+f3,22_{= 1}

f4,23_+f4,24_+f4,25_+f4,26_+f4,27_+f4,28_+f4,29_{= 1}

f5,30_+f5,31_+f5,32_+f5,33_+f5,34_+f5,35_+f5,36_{= 1}

f6,37_+f6,38_+f6,39_+f6,40_+f6,41_+f6,42_+f6,43_{= 1}

Sedangkan fungsi tujuan

minP

j∈A

P

k∈D

P

p∈Pkcj(µk+φ−1(αk)σk)δ k,p j fk,p

MIN177f1,1_{+ 177f}1,2_{+ 236f}1,3_{+ 236f}1,4_{+ 236f}1,5_{+ 177f}1,6_{+ 236f}1,7_{+ 2366f}1,8₊

236f1,9_{+ 104f}2,10_{+ 156f}2,11_{+ 208f}2,12_{+ 156f}2,13_{+ 156f}2,14_{+ 208f}2,15_{+ 208f}2,16₊

88f3,17 _{+ 132f}3,18 _{+ 176f}3,19 _{+ 88f}3,20 _{+ 132f}3,21 _{+ 132f}3,22 _{+ 78f}4,23 _{+ 117f}4,24 ₊

117f4,25_{+ 117f}4,26_{+ 156f}4,27_{+ 156f}4,28_{+ 156f}4,29_{+ 112f}5,30_{+ 168f}5,31_{+ 168f}5,32₊

112f5,33_{+ 168f}5,34_{+ 168f}5,35_{+ 224f}5,36_{+ 132f}6,37_{+ 132f}5,38_{+ 198f}5,39_{+ 198f}5,40₊

198f5,41_{+ 264f}5,42_{+ 264f}5,43

Model matematika di atas penulis selesaikan dengan menggunakan program LINDO

Kumpulan lintasan terbaik/optimal yaitu:

• lintasan P2 :j2 →j5 →j8 untuk trafik permintaan k1.

• lintasan P10 :j2 →j6 untuk trafik permintaan k2.

• lintasan P17 :j1 →j3 untuk trafik permintaan k3.

• lintasan P25 :j4 →j5 →j8 untuk trafik permintaan k4.

• lintasan P30 :j3 →j7 untuk trafik permintaan k5.

• lintasan P37 :j6 →j9 untuk trafik permintaan k6.

Dari kumpulan lintasan optimal di atas dapat dilihat bahwa lintasan dengan jarak

terpendek (jumlah node paling sedikit) tidak secara langsung menjadi lintasan terbaik

untuk suatu trafik permintaan. Seperti pada k = 4 yang dirutekan dengan menggu-nakan lintasanP25:j4 →j5 →j8sementara terdapatP23 :j3 →j8yang lebih pendek.

Hal ini karena parameter utama yang menjadi ukuran dalam pemilihan lintasan pada

model ini adalah kapasitas bandwidth. Akan tetapi juga dapat dilihat bahwa model ini juga selalu berusaha mencari lintasan terbaik dengan kapasitas bandwidth yang memadai serta lintasan dengan jarak terpendek karena pada model yang menjadi

tujuan adalah meminimalkan pengalokasianbandwidth, karena lintasan dengan jarak terpendek secara otomatis menunjukkan alokasi bandwidth terkecil(lebih sedikit link yang menanggung trafik permintaan tersebut).

Dan besarbandwidthyang harus dialokasikan pada setiap link dapat dihitung dengan menjumlahkan semua trafik permintaan yang melewati link tersebut.

• Link 1: x3 = 44M bps

• Link 2: x1+x2 = 59 + 52 = 111M bps

• Link 3: x3+x5 = 44