SOAL SOAL KALKULUS LANJUTAN

(1)

TUGAS KALKULUS LANJUT

SIFAT-SIFAT INTEGRAL LIPAT

Oleh:

KAMELIANI

1211041016

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS NEGERI MAKASSAR

(2)

Universitas Negeri Makassar Page 2

SIFAT-SIFAT INTEGRAL LIPAT

A. SIFAT-SIFAT INTEGRAL LIPAT

Integral lipat dua dan integral lipat tiga mewarisi hampir semua sifat-sifat integral tunggal. Berikut adalah sifat-sifat integral lipat dua (yang juga dimiliki integral sifat tiga).

(1) Integral lipat dua bersifat linear, yaitu

∬[ , + , ] � = ∬ , � + ∬ , �

∬ , � = ∬ , �, ℎ

(2) . � , , , ,

∬ , � ∬ , �

. , , , ⊂

∬ , � ∬ , �,

. Integral lipat dua bersifat aditif (dapat dijumlahkan) pada daerah yang saling

berimpit pada hanya sebuah sisi atau ruas garis.

(3)

Sifat-sifat integral tersebut membawa beberapa akibat yang perlu dikemukakan di sini. Misalkan , � untuk semua , di maka

(luas R)

=

,

�

= �

(luas R)

Satu sifat lainnya yang perlu dikemukakan adalah akibat dari sifat

−| , | , | , |

Berdasarkan sifat integral nomor 2, maka berlaku

− ∬ | , | ∬ , ∬ | , |

Atau

∬ , ∬ | , |

Untuk fungsi yang kontinu, ternyata urutan pengintegralan tidak menjadi masalah. Hal ini dituliskan dalam teorema berikut.

Teorema urutan integral (Teorema Fubini)

∬ , = ∫ [∫ , ] = ∫ [∫ , ]

(4)

B. PENERAPAN SIFAF-SIFAT INTEGRAL DALAM

MENYELESAIKAN MASALAH

.

Soal dan Pembahasan

1. Hitunglah integral berikut berdasarkan daerah D yang diberikan!

∬ �

�

, � = { , | , }

Penyelesaian:

Dengan menerapkan sifat (1) dan (2), maka

∬ �

2. Hitunglah integral berikut berdasarkan daerah D yang diberikan!

∬ − �

�

,

D adalah segitiga dengan titik puncak (0,3) , (1,1), dan (5,3)

Penyelesaian:

Pertama-tama harus dibuat persamaan garis yang melalui titik-titik puncak tersebut, agar bisa diketahui batas-batas daerahnya.

Kita dapat membuat persamaan garis berdasarkan dua titik puncak yang diketahui.  Persamaan garis yang melalui titik (0,3) dan (1,1)

−

− ` =

−

(5)

 Persamaan garis yang melalui titik (0,3) dan (5,3)

−

 Persamaan garis yang melalui titik (1,1) dan (5,3)

−

(6)

Ada dua cara untuk mendeskripsikan daerah yang diarsir.

 Cara I

Jika kita menggunakan fungsi x, maka daerah D akan dibagi menjadi dua daerah karena fungsi yang berada di bawah berbeda bergantung pada nilai x. Pada kasus ini, daerah D diberikan sebagai � = � � , dimana

� = { , | , − + }

� = { , | , + }

Dengan menggunakan sifat (6), maka

∬ − �

(7)

 Cara II

Jika kita menggunakan fungsi y, maka daerah D tidak perlu dibagi menjadi dua bagian.

Batas-batas untuk x adalah

= − + → = − +

3. Hitunglah nilai integral berikut dengan membalikkan urutan dari integralnya. !

∫ ∫9

Penyelesaian:

(8)

Membalik urutan integral artinya kita akan melakukan integral terhadap terlebih dahulu kemudian terhadap . Ketika membalik urutan integral, maka batas-batsanya juga akan berubah.

Agar memudahkan mencari batas-batasnya, maka pertama-tama kita gambarkan daerah yang diberikan berdasarkan batas-batas yang telah diketahui. Berdasarkan integral di atas, batas-batas daerahnya adalah

Berdasarkan pertidaksamaan di atas, batas bawah pada sumbu y adalah = ^ dan batas atas pada sumbu y adalah = dengan batas pada sumbu yaitu antara

= dan = .

Berikut ini adalah gambar daerah yang dimaksud

Karena kita ingin mengintegralkan terhadap terlebih dahulu,maka kita perlu menentukan batas-batas untuk terlebih dahulu, kemudian batas-batas untuk . Batas pada sumbu adalah √

Batas pada sumbu adalah

Sehingga bentuk integralnya sekarang adalah sebagai berikut

(9)

Berikut adalah penyelesaian untuk bentuk integral yang baru

√

C.

Menerapkan Sifat-Sifat Integral untuk Menyelesaikan Soal Integral pada Daerah Persegi Panjang dan Bukan Persegi Panjang

Contoh Soal!

 Daerah Persegi Panjang

1. Tentukan Volume benda pejal di bawah bidang = + + pada =

(karena di integralkan terhadap , maka

dianggap konstanta, sehingga berlaku sifat linear

(10)

daerah = + + pada = { , : ,

2. Carilah Volume benda pejal yang berada di atas fungsi g(x,y) dan berada di bawah fungsi f(x,y) dengan batas-batas x dan y sebagai berikut.

(11)

 Daerah bukan Persegi Panjang

1. Carilah volume benda yang dibatasi oleh persamaan bola + + = dan Paraboloida = +

Penyelesaian:

Bentuk daerahnya adalah sebagai berikut

Gambar di atas adalah daerah yang dimaksud yakni irisan antara bola dan paraboloida.

Subsitusi = + ke persamaan + + =

(12)

+ + + =

+ + + − =

+ − + + =

Untuk + − = maka = ±√ −

untuk + + = tidak ada solusi

Batas-batas untuk y adalah −√ − √ − sedangkan untuk x adalah −√ √

Sehingga dengan menggunakan maple, volume benda yang diperoleh adalah diperoleh

∫ ∫√ − √ − −

−√ − − +

√

−√ = √ � − � = ,

Perhitungan dengan Maple

(13)

D.

Menerapkan Sifat-Sifat Integral untuk Menyelesaikan Soal Integral dalam

Koordinat Polar

Soal Dan Pembahasan

1. Hitunglah nilai integral berikut dengan mengubahnya ke dalam koordinat polar terlebih dahulu.

∬ �

�

D adalah daerah di antara lingkaran dnegan jari-jari 2 dan jari-jari 5 . lingkaran-lingkaran tersebut berpusat pada titik asal. Daerahnya berada pada kuadran I.

Penyelesaian:

(14)

= − ( ) cos � |�

=

2. Tentukan luas daerah yang dibatasi oleh = + sin � dan = Penyelesaian:

Daerah yang dimaksud adalah sebagai berikut.

Untuk mengetahui luas daerah di atas, maka terlebih dahulu perlu diketahui batas-batas untuk nilai � dimana kurva saling berpotongan.

Untuk mengetahui nilai � bisa dilakukan dengan cara sebagai berikut. Diketahui = + sin � dan =

Dapat dituliskan + sin � =

(15)

Berikut ini adalah gambar daerah �

Kita tahu bahwa −� adalah bentuk lain dari �

Jika kita gunakan � � � maka kita akan menghitung daerah yang tidak di arsir. Oleh karena itu batas yang digunakan adalah −� � �

Untuk menentukan nilai , fungsi yang terdekat dengan titik asal merupakan batas bawah, dan fungsi yang terjauh merupakan batas atas.

Sehingga luas daerah D adalah

(16)

Kita tahu bahwa rumus untuk menentukan volume adalah

� = ∬ , �

�

Ubah fungsi + + = ke bentuk = √ − + . Kita mengambil nilai yang positif karena kita akan menghitung di atas bidang =

Kini kita mempunyai dua fungsi yaitu = dan = √ − +

Kita ingin menghitung daerah yang berada di bawah bola tetapi berada pada silinder + = .

Untuk lebih jelasnya perhatikan gambar berikut.

(17)

Sebelumnya kita ubah terlebih dahulu batas-batasnya dalam koordinat polar.

� �

√ (jari-jari silinder)

Sehingga volume daerah yang dimaksud adalah

� = ∬ √ − −

� �

= ∫ ∫ √ − �� √ = +

= ∫ −� − |√ �

= − ∫ � − |√ �

= ∫ � �

= �

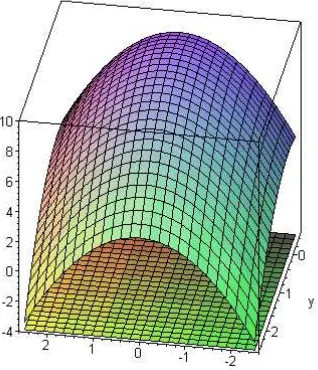
4. Hitunglah volume benda yang berada di antara fungsi = + dan bidang

= .

Penyelesaian:

(18)

Volume yang dicari adalah daerah selisih antara kedua kurva tersebut, yakni

� = ∬

� � − ∬� + � = ∬� − + �

Agar memudahkan dalam mencari nilai volume, fungsi di atas di ubah dalam koordinat polar. Demikian pula batas-batas daerahnya.

Berikut ini adalah batas-batas daerahnya

(19)

Universitas Negeri Makassar Page 19 DAFTAR PUSTAKA

Purcell,dkk.2011.Kalkulus Edisi Kesembilan Jilid 2. Jakarta: Erlangga

Budi Wono Setya.2001.Kalkulus Peubah Banyak dan Penggunannya.Bandung:ITB.

http://www.math24.net/definition-and-properties-of-double-integrals.html (di akses 24 Desember 2014)

http://tutorial.math.lamar.edu/Classes/CalcIII/DIGeneralRegion.aspx (di akses 24 Desember 2014)

http://ltcconline.net/greenl/courses/202/multipleintegration/Volume.htm (di akses 29 Desember 2014)

http://www2.seminolestate.edu/lvosbury/CalculusIII_Folder/ExamplesForExam4.ht m (di akses 5 Januari 2015)