PENURUNAN PERSAMAAN NAVIER STOKES DALAM BENTUK PERSAMAAN DIFERENSIAL UNTUK
GERAK FLUIDA LAMINER
SKRIPSI
RAHMAYANTI HARAHAP 070801001
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENEGTAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PENURUNAN PERSAMAAN NAVIER STOKES DALAM BENTUK PERSAMAAN DIFERENSIAL UNTUK
GERAK FLUIDA LAMINER
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
RAHMAYANTI HARAHAP 070801001
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENEGTAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul :PENURUNAN PERSAMAAN NAVIER STOKES DALAM BENTUK PERSAMAAN DIFERENSIAL UNTUK GERAK FLUIDA LAMINER
Kategori : SKRIPSI
Nama : RAHMAYANTI HARAHAP
Nomor Induk Mahasiswa : 070801001
Program Studi : SARJANA (S1) FISIKA
Departemen : FISIKA
Fakultas :MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, 09 Agustus 2011
Diketahui Pembimbing , Departemen Fisika FMIPA USU
Ketua,
PERNYATAAN
PENURUNAN PERSAMAAN NAVIER STOKES DALAM BENTUK PERSAMAAN DIFERENSIAL UNTUK GERAK FLUIDA LAMINER
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, 09 Agustus 2011
PENGHARGAAN
Puji dan syukur penulis panjatkan kehadirat Allah SWT yang Maha Pemurah dan Maha Penyayang, karena berkat limpah rahmat dan karunia-Nya, tugas akhir yang berjudul : “Penurunan Persamaan Navier Stokes Dalam Bentuk Persamaan Diferensial Untuk Gerak Fluida Laminer” dapat diselesaikan tepat pada waktunya. Sholawat serta salam semoga senantiasa tercurahkan pada nabi kita Muhammad SAW yang telah menuntun kita untuk senantiasa dapat memaknai hidup ini dengan penuh arti.
Ucapan terima kasih saya sampaikan kepada pihak-pihak yang telah banyak membantu serta mendukung saya dalam menyelesaikan skripsi ini, Untuk itulah patut kiranya apabila penulis mengucapkan terima kasih kepada:
1. Bapak Drs.Milangi Ginting.Ms, selaku dosen pembimbing yang bersedia meluangkan waktunya untuk membimbing penulis.
2. Bapak Prof. Drs. M. Syukur, Ms selaku dosen wali penulis.
3. Bapak Dr Marhaposan Situmorang selaku ketua departemen Fisika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara Medan. 4. Ibu Dra Yustinon Ms, Selaku sekretaris departemen Fisika Fakultas Matematika
dan Ilmu Pengetahuan Alam Universitas Sumatera Utara Medan.
5. Seluruh staf dosen departemen Fisika fakultas matematika dan Ilmu pengetahuan alam Universitas Sumatera Utara.
6. Dekan dan pembantu dekan Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara, seluruh pegawai dilingkungan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
7. Ibunda tercinta (Syahrina Siregar) yang telah melahirkan aku kedunia ini, yang merawat, memberikan kasih sayang, cinta yang tak terbatas, yang selalu menuntunku, mendoakanku agar menjadi orang yang berhasil dan berguna bagi semua orang.
9. Keluarga besarku terutama abangku (Erwin Harahap ) dan adikku (Irma, Rudi, Delima) engkau bagian dari hidupku, kebersamaan dan kasih sayang kita akan selalu ada sampai ajal memisahkan kita.
10. Sahabatku (Juli Harni, Eva Suraya, Rusdalena,Juriah,Ismatul Husna, Siska Futri Nst, Suci Rahmadani, Irhan Hanim, Fitri Susanti, Delovita Ginting, Julia Fadilla,Mila, Saima dan my Fatner.) yang selalu menemaniku, membantuku, memberi motivasi bagiku dan selalu menghiburku baik suka maupun duka. 11. Teman-temanku angkatan 07 yang selalu memberi semangat,dorongan, dan
dukungan untuk-ku sehingga tugas akhir ini dapat diselesaikan.
12. Someone who inside my heart ( K. Siregar ). Terimakasih telah memberiku makna sebuah kejujuran, kesabaran, serta kepercayaan.
13. Seluruh rekan-rekan mahasiswa fisika dan seluruh teman-teman di fakultas matematika dan ilmu pengetahuan alam Universitas Sumatera Utara. Semoga Allah SWT akan membalasnya.
ABSTRAK
DECREASE IN THE NAVIER STOKES EQUESTION IN THE FORM OF DIFFERENTIAL EQUATION FOR LAMINER FLUID MOTION
ABSTRACT
DAFTAR ISI
Persetujuan ... ii
Pernyataan ... iii
Abstrak ... vi
Abstract ... vii
Daftar Isi ... viii
Daftar Gambar ... x
Daftar Simbol... xi
BAB I Pendahuluan 1.1. Latar belakang masalah ... 1
1.2. Batasan Masalah... 2
1.3. Rumusan masalah... 2
1.4. Tujuan Penelitian... 3
1.5. Manfaat Penelitian... 3
1.6. Sistematika Penelitian ... 4
BAB II Tinjauan Pustaka 2.1. Dinamika fluida ... 5
2.2. Persamaan persamaan diferensial aliran fluida ... 6
2.2.1. Persamaan Navier Stokes... 7
2.2.1.1. Penyelesaian Persamaan Navier Stokes... 13
2.2.2. Persamaan Kontinuitas... 16
2.2.2.1. Bentuk diferensial persamaan kontinuitas... 19
2.2.3. Persamaan gerak ... 20
2.2.4. Persamaan gerak untuk fluida viskos... 22
BAB III Metode Penelitian
3.1. Rancangan penelitian ... 30 3.2. Teknik analisis data ... 30 3.3. Diagram alir penelitian ... 32 BAB IV Hasil dan Pembahasan
4.1. Persamaan navier stokes... 33 BAB V Kesimpulan dan Saran
5.1. Kesimpulan... 40 5.2. Saran ... 41
Daftar Pustaka
DAFTAR GAMBAR
Halaman Gambar
Gambar 2.1. Tegangan normal dan tegangan geser pada elemen fluida
berviskositas……… 8 Gambar 2.2. Fluida mengalir pada suatu bagian pipa dengan aliran
tunak……….………. 16 Gambar 2.3. Aliran Laminer…...………..……... 26 Gambar 2.4. Aliran Turbulen..……….………. 27
DAFTAR SIMBOL
•v kecepatan (rata-rata) fluida yang mengalir (m/s) •D adalah diameter dalam pipa (m)
•ρ adalah masa jenis fluida (kg/m3)
•μ adalah viskositas dinamik fluida (kg/m.s) atau (N. det/ m2) • adalah tegangan normal.
• adalah tegangan tangensial (tegangan geser). •
dt d
adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
•P adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
•Q = debit
• A = luas penampang
ABSTRAK
DECREASE IN THE NAVIER STOKES EQUESTION IN THE FORM OF DIFFERENTIAL EQUATION FOR LAMINER FLUID MOTION
ABSTRACT
BAB I
PENDAHULUAN
1.1.Latar Belakang
Persamaan Navier-Stokes adalah serangkaian persamaan yang menjelaskan pergerakan dari suatu fluida seperti cairan dan gas. Persamaan-persamaan ini menyatakan bahwa perubahan dalam momentum (percepatan) partikel-partikel fluida hanya bergantung kepada gaya viskos internal (mirip dengan gaya friksi) dan gaya viskos tekanan eksternal yang bekerja pada fluida. Oleh karena itu, persamaan Navier-Stokes menjelaskan keseimbangan gaya-gaya yang bekerja pada fluida.
Persamaan Navier-Stokes memiliki bentuk persamaan diferensial yang menerangkan pergerakan dari suatu fluida. Untuk mendapatkan hasil dari suatu permasalahan fisika menggunakan persamaan Navier-Stokes, perlu digunakan ilmu kalkulus. Secara praktis, hanya kasus-kasus aliran sederhana yang dapat dipecahkan dengan cara ini. Kasus-kasus ini biasanya melibatkan aliran non-turbulen dan tunak (aliran yang tidak berubah terhadap waktu) yang memiliki nilai bilangan Reynold kecil.
Dua konstribusi penting diberikan secara terpisah oleh Navier pada tahun 1823 dan Stokes pada tahun 1845 yang menurunkan persamaan diferensial parsial fluida viskos, persamaan ini membahas tentang persamaan gerak fluida viskos, persamaan ini dikenal dengan persamaan Navier-Stokes, dan persamaan inilah yang menjadi dasar kajian dinamika fluida saat ini. (Frank M. White. 1988).
1.2Batasan Masalah
Penelitian mengenai analisis persamaan Navier Stokes dalam persamaan difrensial untuk gerak fluida dibatasi pada:
1. Persamaan Navier Stokes sebagai persamaan dasar. 2. Aliran Laminer
3. Membahas tentang tegangan normal dan tegangan geser pada elemen fluida berviskositas.
4. Inkompresibel (Tak termampatkan).
1.3. Rumusan Masalah
Masalah yang timbul dalam melakukan penelitian adalah:
1. Bagaimana menentukan keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x, arah y dan arah z.
2. Bagaimana nenentukan tegangan normal dan tegangan geser yang bekerja pada elemen fluida berviskositas.
3. Bagaimana menentukan hubungan antara sistem tegangan dengan gerakan fluida.
1.4.Tujuan Penelitian
Tujuan Penelitian ini adalah:
1. Untuk mengetahui keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x, arah y, arah z pada elemen fluida.
2. Membuktikan persamaan momentum yang dikenal dengan persamaan Navier Stokes untuk fluida dengan viskositas tidak sama dengan nol.
1.5. Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah kita dapat mengetahui keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x, arah y dan arah z dan untuk membantu mendeskripsikan bagaimana fluida mengalir dengan tegangan permukaan pada elemen fluida yaitu teganagan normal (σ) dan tegangan geser (τ) dengan kondisi fluida
dalam keadaan bergerak. Untuk dapat mendeskripsikan aliran fluida Persamaan Navier Stokes
membutuhkan 2 hal informasi yaitu:
1. Kekentalan fluida, kita tahu bahwa madu dan air mempunyai kekentalan yang berbeda,dalam fisika kekentalan adalah gaya gesek internal pada fluida.
1.6. Sistematika Penulisan
Tugas akhir ini terdiri dari beberapa bab dan masing-masing bab dipecah beberapa sub-bab dengan memerinci pokok-pokok permasalahan sehingga penyajian tugas akhir ini dapat dilakukan secara sistematis.
1. BAB I : Pendahuluan
Berisi uraian mengenai hal-hal yang melatarbelakangi penulisan, permasalahan, batasan masalah, tujuan penelitian, manfaat penelitian, dan sistematika penulisan tugas akhir.
2. BAB II : Tinjauan pustaka
Bab ini berisi teori yang mendasari penelitian. 3. BAB III : Metodologi Penelitian
Bab ini membahas tentang metode yang digunakan dan diagram alir penelitian.
4. BAB IV : Hasil dan pembahasan
Bab ini membahas tentang hasil penelitian dan menganalisis data yang diperoleh dari penelitian.
5. BAB V : Kesimpulan dan Saran
BAB II
TINJAUAN PUSTAKA
2.1. Dinamika Fluida
Dinamika Fluida memberi gambaran tentang gerak fluida dalam batas ruang tertentu. Untuk dapat menjelaskan tentang gerak fluida maka gerak ini lebih dahulu harus dapat diketahui semua persamaan difrensial yang dapat diselesaikan secara analitik maupun numerik. Persamaan dasar yang dibutuhkan adalah persamaan kontinuitas dan persamaan gerak yang berkaitan dengan hukum Newton II.
Fluida didefinisikan sebagai substansi yang terus-menerus berdeformasi bila ada tegangan geser yang bekerja pada fluida tersebut. Fluida tidak mampu menahan tegangan geser pada saat fluida dalam keadaan diam. Hal ini menyatakan secara tidak langsung bahwa tegangan geser akan timbul hanya apabila fluida dalam keadaan bergerak. Juga tegangan geser akan ada apabila fluida memiliki viskositas dan viskositas merupakan karakteristik yang dimiliki oleh semua fluida nyata. Oleh karena itu fluida ideal dapat didefenisikan sebagai fluida yang tidak memiliki viskositas dan tegangan geser, tidak akan timbul pada fluida ideal, apabila fluida ideal dalam keadaan bergerak.
Beberapa fluida terutama zat cair mempunyai densitas yang hampir selalu mendekati konstan pada rentang tekanan dan temperatur yang lebar. Fluida-fluida yang menunjukkan kualitas seperti ini biasanya diperlukan sebagai zat yang inkompresibel (tak termampatkan).
Gaya-gaya yang bekerja pada suatu fluida dibagi menjadi 2 kelompok umum:
1. Gaya-gaya benda ( body forces)
Gaya-gaya benda adalah gaya-gaya yang bekerja tanpa kontak fisik, misalnya, gravitasi dan gaya elektrostatik.
Tekanan dan gaya-gaya gesekan membutuhkan kontak fisik agar dapat melakukan transmisi. Karena membutuhkan permukaan agar dapat bekerja gaya-gaya tersebut dinamakan gaya-gaya permukaan.
2.2 Persamaan-Persamaan Diferensial Aliran Fluida
Persamaan dasar aliran yang telah dinyatakan didalam bentuk matematis untuk suatu volume kontrol sembarang, juga dapat dinyatakan di dalam bentuk matematis untuk jenis volume kontrol yang istimewa, elemen difrensial. Persamaan-persamaan difrensial aliran fluida ini menyediakan cara untuk menentukan variasi titik-per-titik properti fluida.
Viskositas ( kekentalan) fluida besarnya dapat ditentukan melalui pengukurun terhadap tingkat hambatan yang ditimbulkan pada aliran fluida yang bersangkutan. Viskositas merupakan properti dari semua fluida nyata dan viskositas inilah yang membedakan fluida nyata dengan fluida ideal (fluida tak berviskositas). Hambatan geser terukur sebagai gaya geser total. Satuan tegangan geser adalah gaya geser persatu-satuan luas.
Viskositas dinamik µ ditunjukkan sebagai perbandingan antara tegangan geser dan gradien kecepatan. Oleh karena itu dimensinya adalah gaya dikalikan dengan waktu persatuan luas atau massa persatuan panjang dan waktu.
Dalam sistem SI tentang satuan, tegangan geser diberi satuan N/m2 dan gradient kecepatan dengan satuan (m/dt)/m. oleh karena itu satuan dari viskositas dinamik adalah sebagai berikut:
dt m
kg m
dt m dt kg m dt m
m N
. /
. . /
) / (
/
2 2 2
= =
= μ
v = ρ
μ (2.1)
2.2.1 Persamaan Navier-Stokes
Persamaan Navier Stokes adalah bentuk diferensial dari hukum kedua newton tentang gerakan. Persamaan gerak yang paling lengkap untuk elemen fluida berviskositas dalam medan gravitasi adalah persamaan Navier Stokes. Ditinjau elemen fluida dengan volume ΔxΔyΔz, seperrti gambar dibawah ini.
y y
zy zy Δ
∂ ∂ +( τ )
τ
z z
zz
zz Δ
∂ ∂ +( τ )
τ x
x zx
zx Δ
∂ ∂ +( τ )
τ
y
Δ
zy
τ
zz
τ
yx
τ
yy
τ
yz
τ
xz τ
xy
τ
xx
τ
x
Δ z Δ
z z
yz yz Δ
∂ ∂ +( τ )
τ
y y
yy
yy Δ
∂ ∂ +( τ )
τ
x x
yx
yx Δ
∂ ∂ +( τ ) τ
y y
xy
xy Δ
∂ ∂ +( τ )
τ
x x
xx
xx Δ
∂ ∂ +( τ ) τ
z z
xz xz ∂ Δ
∂ +( τ )
τ
zx
τ
Gambar 2.1 Tegangan normal dan tegangan geser pada elemen fluida berviskositas.
subskrib pertama menunjukkan bidang tempat bekerjanya tegangan geser dan subskrib kedua menunjukkan sumbu yang sesuai dengan arah kerja tegangan geser (notasi tensor).
Keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x , arah y dan arah z adalah:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y
Fx τXX τxx τxx τxy τxy τxy τxz τxz τxz
⎥⎦ ⎤ ⎢⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥⎦ ⎤ ⎢⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx xx y τ τ τ τ τ τ τ τ τ z y x g y x z z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx xx
z ⎥− ΔΔΔ
⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − = τ τ τ τ τ τ τ τ τ ρ ……...(2.2)
Persamaan diatas merupakan tegangan geser pada elemen fluida untuk aliran laminar satu dimensi. Dan untuk aliran 3 dimensi ( Hukum Viskositas Stokes):
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = x v y
vx y
xy μ
τ (2.4a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = y v z
vy z
yz μ
τ (2.4b)
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = x v z
vx z
xz μ
Dengan: zx xz yz zy xy yx τ τ τ τ τ τ = = =
Menurut Stokes, tegangan normal yang bekerja pada elemen untuk fluida Newtonian ( Newtonian Fluid) adalah:
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v x v
p x x y z
xx
x τ μ μ
σ
3 2
2 (2.5a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v y v
p y x y z
yy
y τ μ μ
σ
3 2
2 (2.5b)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v z v
p z x y z
zz
z τ μ μ
σ
3 2
2 (2.5c)
Dari persamaan (2.5a), (2.5b), (2.5c) untuk fluida yang berviskositas nilai rata-rata dari jumlah ketiga tegangan normal tersebut disebut tekanan.
Apabila vektor gaya F = m.a dan massa m = ρΔxΔyΔz serta koefisien viskositas kinematik v =
ρ
μ , dimasukkan ke persamaan dibawah ini:
F= ( −∇p+μ∇2v−ρg kˆ)ΔxΔyΔz (2.6)
Percepatan aliran fluida berubaah-ubah dalam ruang dan waktu. Hal ini dapat digambarkan dengan persamaan berikut.
ν = f(r,t) =
dt dx
(2.7)
ν = Vektor kecepatan fluida dengan komponen νx , νy, νz. r= x iˆ + y ˆ + z j kˆ
r= Vektor posisi dengan komponen x, y, z.
Vektor kecepatan ν dengan komponennya dapat ditulis dalam bentuk matriks kolom berikut ini.
ν = ⎪ ⎭ ⎪ ⎬ ⎫
⎪ ⎩ ⎪ ⎨ ⎧
z y x
v v v
(2.8)
Apabila νx ,νy dan νzmerupakan fungsi dari x, y, z, t maka fungsi komponen
kecepatan ini dapat ditulis dalam bentuk:
x
ν = ν x (x, y, z, t) (2.9a)
y
ν = ν y (x, y, z, t) (2.9b)
z
ν = ν z (x, y, z, t) (2.9c)
Difrensial total dari persamaan (2.9a), (2.9b), (2.9c) adalah:
dνx= dt
t v dz z v dy y v dx x
vx x x x
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂
∂ (2.10a)
dνy = dt
t v dz z v dy y v dx x
vy y y y
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
(2.10b)
dνz = dt
t v dz z v dy y v dx x
vz z z z
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂
∂ (2.10c)
t v dt dz z v dt dy y v dt dx x v
a x x x x
x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.11a)
t v dt dz z v dt dy y v dt dx x v
ay y y y y
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.11b)
t v dt dz z v dt dy y v dt dx x v
a z z z z
z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.11c)
,
x
a ay , dan az persamaan (2.11a), (2.11b), (2.11c) tidak lain adalah percepatan
dalam arah x, arah y dan arah z. Oleh karena itu vektor percepatan dapat ditulis menjadi: ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ = z y x a a a
a (2.12)
Dengan:
dt dv
a x
x= (2.13a)
dt dv
ay= y (2.13b)
dt dv
a z
Z= (2.13c)
Maka pada persamaan (2.11a), (2.11b) dan (2.11c) dapat ditulis kembali:
t v z v v y v v x v v
a x x
z x y x x x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.14a)
t v z v v y v v x v v
a z y y
y y y x y ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.14b)
t v z v v y v v x v v
a z z
z z y z x z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
Persamaan percepatan (2.14a), (2.14b), (2.14c) dikenal dengan sebutan percepatan total dengan:
x
ν =
dt dx
(2.15a)
y
ν =
dt dy
(2.15b)
z ν =
dt dz
(2.15c)
Dari persamaan (2.14a), (2.14b), (2.14c), pada ruas kanan,suku pertama, suku kedua, dan suku ketiga berkaitan dengan gerak partikel fluida dan disebut dengan percepatan konvektif, sedang suku keempat berkaitan dengan perubahan salah satu sifat fluida dalam hubungannya dengan waktu dan disebut dengan percepatan lokal, (Makrub,lalu,2001).
2.2.1.1 Penyelesaian Persamaan Navier Stokes.
Secara umum penyelesain untuk suatu masalah yang berkaitan dengan persamaan Navier Stokes dapat dilakukan dengan tiga cara:
1. Ujikasi.
2. Analitik atau Teori.
dapat diselesaikan karena kerumitan dalam mencari penyelesaian yang tepat. Bagi masalah yang sederhana, penyelesaian secara Analitik dapat dilakukan.
Indeks tegangan geser pertama adalah dalam arah tegak-lurus terhadap permukaan tempat komponen tegangan itu bekerja. Indeks kedua adalah dalam arah komponen tegangan yang bersangkutan.
Jika sistem koordinat tegak lurus arah x, arah y dan arah z dapat berorientasi (berarah) sembarang. Maka persamaan Navier Stokes dibatasi untuk fluida tak termampatkan, maka menjadi:
( )
xx
p
g
k
v
v
x
a
1
−
ˆ
+
∇
2∂
∂
=
ρ
(2.16a)( )
yy
p
g
k
v
v
y
a
1
−
ˆ
+
∇
2∂
∂
=
ρ
(2.16b)( )
zz
p
g
k
v
v
z
a
1
−
ˆ
+
∇
2∂
∂
=
ρ
(2.16c)Dengan ax, ay, dan az adalah percepatan pada arah x, arah y dan arah z.
Dan operator peubah-peubah turunan tertentu yang menentukan ciri atau sifat mekanika fluida adalah kekentalan, yang mengaitkan tegangan lokal dalam fluida yang bergerak dengan laju regangan dari unsur fluida tersebut.
Bila fluida mengalami geseran, maka fluida mulai bergerak dengan laju regangan yang berbanding terbalik dengan suatu besaran yang disebut koefisien kekentalan (µ), (Victor L.Steeter dan Benjamin wylie, 1992).
Persamaan momentum untuk massa, dm, dapat dicari dengan hukum kedua Newton dimana:
dF = dm
sistem
dt dv
⎟ ⎠
Dari persamaan sistem dt dv ⎟ ⎠ ⎞ = t v z v v y v v x v v dt
dv x x
z x y x x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (2.18)
Jadi
dF = dm ⎥
⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ + ∂ ∂ z v v y v v x v v z z y y x
x (2.19)
Dalam arah x, arah y dan arah z:
dFx =dm
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ t v z v v y v v x v
v x z
z x y x
x (2.20a)
dFy = dm
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ t v z v v y v v x v
vx y y y z y y (2.20b)
dFz = dm
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ t v z v v y v v x v
v z z
z z y z
x (2.20c)
Untuk aliran tak termampatkan dengan viskositas konstan, persamaan ini dapat disederhanakan ke bentuk:
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ 2 2 2 2 2 2 z v y v x v x p g dt
v x x x
x
x ρ μ
ρ (2.23a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2 z v y v x v y p g dt
dv y y y
y y
μ ρ
ρ (2.23b)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2 z v y v x v y p g dt
dv z z z
z
z ρ μ
ρ (2.23c)
Maka untuk aliran fluida tak termampatkan,
y p g dt dv
y y
∂ ∂ − =ρ
ρ (2.24b)
z p g dt dv
z z
∂ ∂ − =ρ
ρ (2.24c)
(Nawi, M.W.H, 2001)
2.2.2 Persamaan Kontinuitas
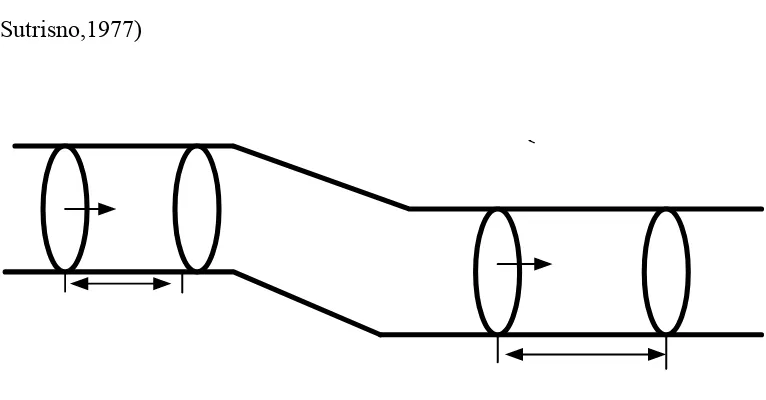
Gerak fluida didalam suatu tabung aliran haruslah sejajar dengan dingding tabung, meskipun besar kecepatan fluida dapat berbeda dari titik ke-titik lain didalam tabung.
Dalam selang waktu sebesar Δt suatu elemen fluida Δm yang melalui luas A1 adalah:
Δm1 = ρ1A1v1Δt (2.26)
(Sutrisno,1977)
Keterangan:
Fluida mengalir pada suatu bagian pipa dengan aliran tunak. A1 dan A2 adalah luas penampang pipa 1 dan 2.
v1 dan v2 adalah kecepatan partikel-partikel pada pipa 1 dan pipa 2.
1
ρ dan ρ2 adalah massa jenis fluida pada 1 dan 2
Dalam selang waktu Δt suatu elemen fluida Δm yang melalui luas A1 adalah:
Δm1 = ρ1A1v1Δt (2.27)
Dalam selang waktu Δt , fluida pada pipa 1 bergerak ke kanan menempuh jarak:
x1 = v1.Δt (2.28)
Volum v1 = A1 . x1 (2.29)
Massa fluida yang masuk:
m1 = ρ1.v1 (2.30)
m1 = ρ1 A1 ( v1 . Δt) (2.31) Fluida pada pipa 2 bergerak ke kanan menempuh jarak:
x2 = v2 .Δt (2.32)
Volum v2 = A2 . x2
Massa fluida yang keluar pada pipa 2:
Massa fluida yang masuk pada pipa satu sama dengan massa fluida yang keluar pada pipa 2.
m1 = m2 (2.34)
ρ1 A1 ( v1 . Δt) = ρ2A2 ( v2 . Δt) (2.35)
Persamaan kontinuitas menyatakan bahwa hasil kali antara luas penampang A dan kelajuan v pada titik sebarang selalu konstan. Secara matematis dapat ditulis:
A1v1 = A2v2= konstan (2.36)
1 2 2 1
A A v v
= (2.37)
Perbedaan tekanan antara dua titik mana pun pada ketinggian yang berbeda dalam suatu cairan diberikan :
p2 – p1 = ρg ( h2 – h1) (2.38)
Dengan ρg = satuan berat cairan ( N/m3)
h2 – h2 = perbedaan ketinggian (m) p2 – p1 = perbedaan tekanan (Pascal)
Jika titik 1 berada dipermukaan bebas cairan dan h positif kearah bawah, persamaan diatas menjadi:
Besaran yang menyatakan volume fluida yang mengalir persatuan waktu dinamakan
debit (Q).
Q =
t v
(2.40)
Karena (v) = luas penampang (A) x panjang lintasan ( l), maka:
Q = A.v (2.41)
Dengan: Q = debit
A = luas penampang
v = kecepatan fluida yang mengalir. (Ronald, H.S dan Desi,A, 2005)
2.2.2.1 Bentuk Diferensial Persamaan Kontinuitas
Persamaan kontitinuitas adalah salah satu persamaan dasar mekanika fluida. Persamaan kontinuitas dapat dituliskan:
( )
( )
( )
=0∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
z v y
v x
v t
z y
x ρ ρ
ρ
ρ (2.42)
Dalam notasi vektor persamaan (2.42) dapat ditulis sebagai berikut:
0 = • ∇ + ∂
∂ρ ρν
t (2.43)
Ada dua hal yang harus diperhatikan. Untuk aliran tunak dari fluida mampu-mampat:
0 = •
∇ ρv (2.44)
Hal ini disebabkan karena menurut definisi ρ bukanlah fungsi dari waktu dalam aliran tunak, namun bisa merupakan fungsi posisi, untuk fluida tak termampatkan kerapatan fluidanya.
2.2.3 Persamaan Gerak
Secara umum ada dua jenis gaya yang perlu diperhatikan: Gaya-gaya permukaan yang bekerja pada permukaan elemen difrensial, dan Gaya-gaya badan, yang terdistribusi diseluruh elemen.Satu-satunya gaya badan δFb , yang menjadi perhatian adalah massa dari elemen, yang dapat dinyatakan sebagai:
b F
δ = δm g (2.45)
Di mana g adalah pernyataan vektor dari percepatan gravitasi. Dalam bentuk komponen:
bx F
δ = δm gx (2.46a)
by F
δ = δm gy (2.46b)
bz F
Di mana gx, gy dan gz adalah komponen-komponen dari vektor percepatan gravitasi masing-masing dalam arah x, arah y, dan arah z.
Tegangan normal, σn, didefinisikan sebagai
A Fn
A n
δ δ σ δ
0 lim
→
= (2.47)
Dan Tegangan geser didefinisikan sebagai
A F
A δ
δ τ δ
0 lim
→
= (2.48)
σ untuk tegangan normal dan τ untuk tegangan geser. Dengan demikian intensitas dari gaya per satuan luas pada sebuah titik dapat disifatkan oleh sebuah tegangan normal dan tegangan geser, jika orientasi dari bidang ditentukan.
Dapat dinyatakan gaya-gaya permukaan yang bekerja pada sebuah elemen kubus dari sebuah fluida dalam bentuk tegangan-tegangan yang bekerja pada permukaan-permukaan elemen.
Gaya permukaan resultan dalam arah x, arah y dan arah z dapat dituliskan sebagai berikut:
z y x z y
x
F xx yx zx
x δ δ δ
τ τ
σ
δ ⎜⎜⎝⎛ ⎟⎟⎠⎞
∂ ∂ + ∂ ∂ + ∂ ∂
= (2.49a)
z y x z y
x
Fy τxy σ yy τzy δ δ δ
δ ⎜⎜⎝⎛ ⎟⎟⎠⎞
∂ ∂ + ∂ ∂ + ∂ ∂
= (2.49b)
z y x z y
x
F xz yz zz
z δ δ δ
σ τ
τ
δ ⎜⎜⎝⎛ ⎟⎟⎠⎞
∂ ∂ + ∂ ∂ + ∂ ∂
= (2.49c)
X
F
F δ
δ = î + δFy ˆ + j δFz kˆ (2.50)
(Munson, R.B, 2003).
Persamaan Navier Stokes adalah bentuk difrensial dari hukum kedua Newton tentang gerakan. Alat dasar yang akan digunakan di dalam mengembangkan persamaan Navier Stokes adalah hukum kedua Newton tentang gerakan untuk suatu volume kontrol sembarang.
Gaya-gaya yang bekerja pada volume kontrol adalah gaya-gaya yang disebabkan oleh tegangan normal dan tegangan geser dan gaya benda seperti ini disebabkan oleh gravitasi, (Welty, R. James, dkk, 2002)
2.2.4 Persamaan Gerak Uuntuk Fluida Viskos (Persamaan Navier Stokes)
Didalam suatu fluida yang viskos, gaya permukaan yang bekerja pada elemen fluida dengan lebih kompleks. Ada dua macam gaya permukaan.
1. Gaya normal atau tegangan normal yang serupa dengan tekanan, tetapi mungkin tidak sama besarnya dalam segala arah.
2. Gaya geser atau tegangan yang arahnya sejajar dengan permukaan, pada permukaan mana gaya tersebut bekerja.
Telah diperoleh secara eksperimentil bahwa dengan ketelitian yang besar tegangan dalam banyak fluida berhubungan secara linier dengan turunan dari kecepatan (
x v
∂ ∂ ,
y v ∂ ∂ ,
z v
∂ ∂ ).
Demikian pula kebanyakan fluida tidak memiliki arah yang terpilih, fluida yang demikian disebut isotropik. Tambahan pula tegangan ini tidak bergantung secara eksplisit pada koordinat kedudukan dan kecepatan dari fluida.
Maka suatu bentuk yang unik mengenai hubungan antara tegangan dan gradien kecepatan dapat diturunkan. Pada saat ini hanya akan diketengahkan hasil dari analisis matematik dan kemudian akan diselidiki karakteristik serta implikasi dari persamaan yang diperoleh. Hubungan antara tegangan dan turunan (gradien) kecepatan adalah:
p x vx
xx +
∂ ∂ + −
= λ μ θ μ
σ ) 2
3 2
( (2.51a)
p y vy
yy +
∂ ∂ + −
= λ μ θ μ
σ ) 2
3 2
( (2.51b)
p z vz
zz +
∂ ∂ + −
= λ μ θ μ
σ ) 2
3 2
( (2.51c)
Dengan
z v y v x
vx y z
∂ ∂ + ∂ ∂ + ∂ ∂ =
θ (dilasi)
Persamaan ini memiliki parameter µ, λ dan p. Berdasarkan pemisalan mengenai hubungan linier diantara tegangan dan gradien kecepatan, semua ketiga parameter harus tidak tergantung pada gradien kecepatan, tetap masih tergantung pada sifat fluida seperti temperatur dan massa jenis. Seperti akibat µ, λ dan p dapat juga bergantung pada waktu dan kedudukan.
semua tegangan geser sama dengan nol dan ketiga tegangan normal ( tegak lurus) sama dengan p.Sehingga:
p zz yy
xx =σ =σ =
σ (2.52)
Untuk aliran yang sederhana ini, p hanyalah merupakan harga negatif dari tekanan, dalam hal ini sama besarnya dalam segala arah. Disini fluida ada dalam keadaan seimbang dalam jenis yang dibicarakan dalam termodinamika dan tekanan p dapat dikenali sebagai tekanan termodinamik, (Djojodihardjo, harijono,1983).
Jadi Persamaan Navier Stokes merupakan model matematika untuk medeskripsikan bagaimana fluida mengalir, untuk bisa mendeskripsikan aliran fluida. Persamaan Navier Stokes membutuhkan 2 hal informasi yaitu:
2. Kekentalan fluida, kita tahu bahwa madu dan air mempunyai kekentalan yang berbeda, dalam fisika kekentalan adalah gaya gesek internal pada fluida
3. Kondisi awal yaitu kecepatan fluida disetiap titik pada saat t=0
Untuk fluida tak berviskositas ( µ = 0) diperoleh bahwa σx = σy = σz = -p. Sedang untuk fluida berviskositas nilai rata-rata untuk jumlah ketiga tegangan normal tersebut disebut tekanan.
Persamaan Navier-Stokes memiliki bentuk persamaan diferensial yang menerangkan pergerakan dari suatu fluida. Persaman seperti ini menggambarkan hubungan laju perubahan suatu variabel terhadap variabel lain. Sebagai contoh, persamaan Navier-Stokes untuk suatu fluida ideal dengan viskositas bernilai nol akan menghasilkan hubungan yang proporsional antara percepatan (laju perubahan kecepatan) dan derivatif dengan persamaan Navier Stokes tekanan internal.
Untuk mendapatkan hasil dari suatu permasalahan fisika menggunakan persamaan Navier-Stokes, perlu digunakan ilmu kalkulus. Secara praktis, hanya kasus-kasus aliran sederhana yang dapat dipecahkan dengan cara ini. Kasus-kasus ini biasanya melibatkan aliran non-turbulen dan tunak (aliran yang tidak berubah terhadap waktu) yang memiliki nilai bilangan Reynold kecil.
Bentuk umum persamaan Navier-Stokes untuk kekekalan momentum adalah :
( )
v gk vp dt
dv = 1∇ + ∇2 − ˆ
ρ (2.53)
dengan:
• ρ adalah densitas fluida,
dt dv
adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
• v adalah vektor kecepatan,
• P adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
P adalah tensor yang simetris. Secara umum, (dalam tiga dimensi). P memiliki bentuk persamaan:
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
zz zy zx
yz yy yx
xz xy xx
P
τ
τ
τ
τ
τ
τ
τ
τ
τ
(2.54)
Persamaan di atas sebenarnya merupakan sekumpulan tiga persamaan, yakni satu persamaan untuk tiap dimensi. Dengan persamaan ini saja, masih belum memadai untuk menghasilkan hasil penyelesaian masalah. Persamaan yang dapat diselesaikan diperoleh dengan menambahkan persamaan kekekalan massa dan syarat batas ke dalam persamaan di atas.
Dalam mekanika fluida, maka aliran fluida dapat dibagi menjadi 3 jenis: 1.Aliran Laminer
1. Aliran laminer
Aliran laminer terjadi apabila partikel-partikel zat cair bergerak teratur dengan membentuk garis lintasan kontiniu dan tidak saling berpotongan. Aliran laminer terjadi apabila kecepatan aliran rendah, ukuran saluran sangat kecil dan zat cair mempunyai kekentalan besar.
Aliran dengan fluida yang bergerak dalam lapisan-lapisan, atau lamina-lamina dengan satu lapisan meluncur secara lancar . Dalam aliran laminar ini viskositas berfungsi untuk meredam kecendrungan terjadinya gerakan relatif antara lapisan.
Gambar 2.3 Aliran Laminer
Aliran laminar berkembang penuh dalam saluran lingkaran dengan penampang konstan.
2. Aliran turbulen
Gambar 2.4 Aliran Turbulen
Aliran Turbulen tidak lepas dari hukum dasar yang berlaku yaitu: • Kekekalan massa
• Kekekalam momentum disebut juga ( Hukum kedua dari Newton) • Kekekalan energi ( Hukum pertama dari termodinamik).
4. Aliran transisi
Aliran transisi merupakan aliran peralihan dari aliran laminar ke aliran turbulen, (Kodoatie,R,J. 2002).
Bilangan Reynolds
Bilangan Reynolds merupakan bilangan tak berdimensi yang dapat membedakan suatu aliran itu dinamakan laminar, transisi atau turbulen.
μρ
vD =
Re (2.55)
Dengan : v kecepatan (rata-rata) fluida yang mengalir (m/s) D adalah diameter dalam pipa (m)
ρ adalah masa jenis fluida (kg/m3)
Klasifikasi aliran berdasarkan bilangan Reynolds dapat dibedakan menjadi tiga kategori sebagai berikut:
• Re < 2300 Aliran Laminer • 2300 < Re < 4000 Aliran Transisi • Re > 4000 Aliran Turbulen
Umumnya aliran pada saluran terbuka mempunyai Re > 4000 sehingga aliran tersebut termasuk dalam kategori aliran turbulen.
Berdasarkan bilangan Reynolds, aliran fluida dapat dibedakan menjadi dua yaitu aliran turbulen dan laminar, (Kodoatie,R,J 2002).
2.3Tekanan Fluida
Tekanan fluida dipancarkan dengan kekuatan yang sama ke semua arah dan bekerja tegak lurus pada suatu bidang. Dalam bidang datar yang sama kekuatan tekanan dalam suatu cairan sama. Pengukuran pengukuran satuan tekanan dikakukan dengan menggunakan dengan berbagai bentuk meteran. Kecuali ditetapkan lain, tekanan meteran atau tekanan relatif yang akan dipergunakan.Tekanan meteran menyatakan harga-harga diatas atau dibawah tekanan atmosfir.
p =
A F
(2.56)
Dengan: p = Tekanan (N/m2 atau pascal) F = Gaya (N)
Untuk suatu keadaan dengan gaya F terdistribusi merata diatas suatu permukaan akan diperoleh rumus sebagai berikut:
p (pascal) =
A F
dan p (bar) =
A F
BAB III
METODOLOGI PENELITIAN
3.1.Rancangan Penelitian.
Persamaan Navier Stokes didasarkan atas hukum gerakan Newton dan hukum gesekan viskos dari Newton yang telah diperluas. Sejauh ini tidak dibatasi dengan massa jenis yang konstan maupun viskositas yang konstan. Persamaan ini berlaku untuk fluida viskos dan kompresibel dengan viskositas yang bervariasi.
Didalam suatu fluida yang viskos, gaya permukaan yang bekerja pada elemen fluida dengan lebih kompleks. Ada dua macam gaya permukaan.
3. Gaya normal atau tegangan norman yang serupa dengan tekanan, tetapi mungkin tidak sama besarnya dalam segala arah.
3.2. Teknik Analisis Data
Langkah awal yang dilakukan terlebih dahulu dikaji sedikit tentang didalam suatu fluida yang viskos, gaya permukaan yang bekerja pada elemen fluida lebih kompleks.
Beberapa fluida, Terutama zat cair mempunyai densitas yang hampir selalu mendekati konstan pada rentang tekanan dan temperatur yang lebar. Fluida-fluida yang menunjukkan kualitas seperti ini biasanya diperlukan sebagai zat yang inkompresibel (tidak dapat dimampatkan). Namun demikian pengaruh-pengaruh konpresibilitas lebih merupakan properti dari situasi ketimbang dari fluida itu sendiri. Gaya-gaya yang bekerja pada suatu fluida dibagi menjadi 2 kelompok umum:
3.Gaya-gaya benda ( body forces)
Gaya-gaya benda adalah gaya-gaya yang bekerja tampa kontak fisik, misalnya, gravitasi dan gaya elektrostatik.
4.Gaya-gaya permukaan (surface forces)
BAB IV
HASIL DAN PEMBAHASAN
4.1 Persamaan Navier-Stokes
Persamaan Navier Stokes adalah bentuk difrensial dari hukum kedua Newton tentang gerakan. Persamaan gerak yang paling lengkap untuk elemen fluida berviskositas dalam medan gravitasi adalah persamaan Navier Stokes. Ditinjau elemen fluida dengan volume ΔxΔyΔz
Tegangan permukaan pada elemen fluida adalah tegangan normal (σ ) dan tegangan geser (τ ).
Subskrib tegangan geser (τ ) memberikan gambaran bahwa untuk subskrib pertama menunjukkan bidang tempat bekerjanya tegangan geser dan subskrib kedua menunjukkan sumbu yang sesuai dengan arah kerja tegangan geser (notasi tensor).
Ditinjau dari elemen fluida berbentuk kubus dengan sisi Δx, Δy, dan Δz .Massa dari elemen fluida: m = ρ Δx Δy Δz.
F = m. a
= (ρ Δx Δy Δz) . a (4.1)
Dengan v = vx iˆ + vy jˆ + vz kˆ (4.2)
v = Vektor kecepatan fluida dengan komponen vx, vy dan vz
r = x iˆ + y ˆ + zj kˆ
Vektor kecepatan v dengan komponennnya dapat ditulis dalam bentuk matriks kolom berikut ini.
v = ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ z y x v v v (4.3)
Apabila vx, vy dan vz merupakan fungsi dari x, y, z, t maka fungsi komponen
kecepatan ini dapat ditulis dalam bentuk:
vx = v(x, y, z, t) (4.4a) vy = v(x, y, z, t) (4.4b)
vz = v (x, y, z, t) (4.4c)
Difrensial total dari persamaan (4.4a), (4.4b) dan (4.4c) adalah:
dvx= dt
t v dz z v dy y v dx x
vx x x x
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂
∂ (4.5a)
dvy = dt
t v dz z v dy y v dx x
vy y y z
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ (4.5b)
dvz = dt
t v dz z v dy y v dx x
vz z z z
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂
∂ (4.5c)
Jika persamaan (4.5a), (4.5b) dan (4.5c) dibagi dengan dt maka akan diperoleh persamaan berikut: t v dt dz z v dt dy y v dt dx x v
a x x x x
x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (4.6a)
t v dt dz z v dt dy y v dt dx x v
ay y y y y
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
t v dt dz z v dt dy y v dt dx x v
a z z z z
z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (4.6c)
x
a , ay dan az persamaan (4.6a), (4.6b) dan (4.6c) tidak lain adalah percepatan dalam arah x, arah y dan arah z. Oleh karena itu vektor percepatan dapat ditulis menjadi: ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ = z y x a a a
a (4.7)
Dengan:
dt dv
a x
x= (4.8a)
dt dv
ay= y (4.8b)
dt dv
a z
Z= (4.8c)
Maka pada persamaan (4.6a), (4.6b), (4.6c) dapat ditulis kembali:
t v z v v y v v x v v
a z x x
x y x x x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (4.9.a)
t v z v v y v v x v v
ay x y y y z y y
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (4.9b)
t v z v v y v v x v v
a z z
z z y z x z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂
= (4.9c)
vx=
dt dx
(4.10a)
vy=
dt dy
(4.10b)
vz =
dt dz
(4.10c)
Keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x , arah y, dan arah z adalah:
⎥⎦ ⎤ ⎢⎣ ⎡ ΔΔ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥⎦ ⎤ ⎢⎣ ⎡ ΔΔ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx XX
X τ τ τ
τ τ τ τ τ τ ⎥⎦ ⎤ ⎢⎣ ⎡ ΔΔ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥⎦ ⎤ ⎢⎣ ⎡ ΔΔ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx XX y τ τ τ τ τ τ τ τ τ z y x g y x z z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx XX
z ⎥⎦− ΔΔΔ
⎤ ⎢⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥⎦ ⎤ ⎢⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − = τ τ τ τ τ τ τ τ τ ρ ………. (4.11) atau z y x z y x
F xx xy xz
x ⎟⎟⎠Δ Δ Δ
⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂
= τ τ τ (4.12a)
z y x z y x
Fy yx yy yz Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂
= τ τ τ (4.12b)
z y x g z y x
F zx zy zz
z Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − ∂ ∂ + ∂ ∂ + ∂ ∂
Maka tegangan geser pada elemen fluida ( Newtonian Fluid ): ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = x v y
vx y
xy μ τ (4.13a) ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = y v z
vy z
yz μ
τ (4.13b)
⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = x v z
vx z
xz μ τ (4.13c) Dengan: zx xz yz zy xy yx τ τ τ τ τ τ = = =
Sedangkan tegangan normal yang bekerja pada elemen untuk fluida Newtonian ( Newtonian Fluid) adalah:
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v x v
p x x y z
xx
x τ μ μ
σ
3 2
2 (4.14a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v y v
p y x y z
yy
y τ μ μ
σ
3 2
2 (4.14b)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v z v
p z x y z
zz
z τ μ μ
σ
3 2
2 (4.14c)
Dari persamaan (4.14a), (4.14b), dan (4.14c) untuk fluida yang berviskositas nilai rata-rata dari jumlah ketiga tegangan normal tersebut disebut tekanan.
z y x z v y v x v x p
F x x x
x Δ Δ Δ
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2
μ (4.15a)
z y x z v y v x v y p
Fy y y y Δ Δ Δ
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2
μ (4.15b )
z y x g z v y v x v z p
FZ z z z Δ Δ Δ
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ −
= μ 2 ρ
2 2 2 2 2 (4.15c)
Dalam notasi vektor persamaan (4.15a), (4.15b), (4.15c) adalah:
F=(−∇p+μ∇2v−ρgkˆ)ΔxΔyΔz (4.16)
Apabila vector gaya F = m.a dan massa m = ρΔxΔyΔz serta koefisien viskositas kinematik v =
ρ
μ dimasukkan ke persamaan (4.16) maka akan diperoleh persamaan :
+ ∇ − = p a ρ 1
v (∇2v)−gkˆ (4.17)
Gabungan persamaan (4.9a), (4.9b) dan (4.9c), dan persamaan (4.16) menghasilkan persamaan vektor berikut:
( )
v gk vp dt
dv 1 2 ˆ
− ∇ + ∇ − =
ρ (4.18)
Dalam koordinat kartesian persamaan (4.18) dapat ditulis dalam bentuk berikut:
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
v x x x x
z x y x x x
ρ (4.19a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
v y y y y
z y y y x y
g z v y v x v v x p z v v y v v x v v t
v z z z z
z z y z x z − ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1
ρ (4.19c)
Dalam koordinat kartesian persamaan (4.19a), (4.19b), dan (4.19c) dapat disusun kembali menjadi: ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
vx x x x y x z x x x
ρ (4.20a)
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
vy x y y y y z y y y
ρ (4.20b)
g z v y v x v v x p z v v y v v x v v t
vz x z y z z z z z z −
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1
ρ (4.20c)
BAB V
KESIMPULAN DAN SARAN
5.1 Kesimpulan
1.Keseimbangan gaya-gaya yang bekerja pada elemen fluida akibat tegangan normal dan tegangan geser dalam arah x , arah y, dan arah z adalah:
z y x z y x
F xx xy xz
x ⎟⎟⎠Δ Δ Δ
⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ = τ τ τ z y x z y x
Fy yx yy yz Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ = τ τ τ z y x g z y x
F zx zy zz
z Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ − ∂ ∂ + ∂ ∂ + ∂ ∂ = τ τ τ ρ
2.Persamaan kekekalan momentum yang dikenal dengan persamaan Navier Stokes sebagai berikut:
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
vx x x x y x z x x x
ρ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 z v y v x v v x p z v v y v v x v v t
vy x y y y y z y y y
ρ g z v y v x v v x p z v v y v v x v v t
vz x z y z z z z z z −
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ 2 2 2 2 2 2 1 ρ
5.2 Saran
UDAFTAR PUSTAKA
Djojodihardjo, Harijono, 1983, Mekanika Fluida, Jakarta: Erlangga. Kodoatie, R, J, Hidrolika Terapan, Aliran pada saluran terbuka dan Pipa,
Yogyakarta: Andi.
Makrup, Lalu, 2001, Dasar-Dasar Analisis Aliran di Sungai dan Muara, Jogjakarta: UI Press.
Munson, R.B, dkk, 2003, Mekanika Fluida, Edisi Keempat, Jilid 1, Jakarta: Erlangga. Nawi, M.W.H, 2001, Kajidaya Bendalir, Malaysia: Universiti Teknologi Malaysia
81310 Skudai, Johor Darul Ta’zim.
Streeter, L.V, dkk, 1988, Mekanika Fluida, Edisi Delapan, Jilid 1, Jakarta: Erlangga. Sitorus.H.R dan Anisya.D, 2008, Ringkasan Fisika, Bandung: Yrama Widya.
Sutrisno, 1977,Fisika Dasar,Mekanika, Jilid 1, Bandung: ITB
Victor, L. Steeter Dan E.Benjamin Wylie, 1988, Mekanika Fluida, Edisi Delapan, Jilid 1, Jakarta: Erlangga.
White, M. Frank, 1986, Mekanika Fluida, Edisi Kedua, Jilid 1, Jakarta: Erlangga. Welty, R. James, 2004, Dasar-Dasar Fenomena Transfort, Volume 1, Transfer
LAMPIRAN I
Pembuktian Persamaan : p v
( )
v gk dtdv = 1∇ + ∇2 − ˆ
ρ (5.3)
Dengan : F=( -∇p+μ∇2v−ρgkˆ)ΔxΔyΔz
m = ρΔxΔyΔz
v = ρ
μ → µ = ν.ρ
F = m.a
Maka: F = ( -∇p+μ∇2v−ρgkˆ)ΔxΔyΔz
m.a = ( − ∇p+ μ∇ v−gk ρΔxΔyΔz
ρ
ρ ˆ)
1
1 2
m.a = (− 1∇p+ ∇2v−gkˆ)m
ρ μ ρ
a = (− 1∇p+ ∇2v−gkˆ) ρ
μ ρ
p
( )
v gk dtdv =−1∇ + ∇2 − ˆ ρ
μ
LAMPIRAN II
Pembuktian Persamaan : x y z
z v y v x v x p
F x y z
x Δ Δ Δ
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2
μ (4.16a)
Dengan:
F = m. a
F = (ρΔxΔyΔz).a
F = (ρΔxΔyΔz ).
dt dv
Untuk Persamaan Pada sumbu-x:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y
Fx τxx τxx τxx τxy τxy τxy τxz τxz τxz
z y x z y x
F xx xy xz
x Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ = τ τ τ Dengan ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = = x v y
vx y
yx
xy τ μ
τ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = = x v z vx z zx
xz τ μ
τ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v x U
p x y z
xx
x τ μ μ
σ
3 2 2
z y x z x v z v y x v y v x z v y v x v x v p F z x y x z y x x
x Δ ΔΔ
⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ∂ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ + ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ + ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − ∂ = μ μ μ μ 3 2 2 ( − = x F 2 2 2 2 2 2 2 2 3 2 2 z v y v x v x v x
p x x x x
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ μ μ μ μ − = x F 2 2 2 2 2 2 3 8 z v y v x v x
p x x x
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂
LAMPIRAN III
Pembuktian persamaan: x y z
z v y v x v y p
Fy y y y Δ Δ Δ
⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − = 2 2 2 2 2 2
μ (4.16b )
Untuk Persamaan Pada sumbu-y:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ Δ Δ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ Δ ∂ ∂ + − Δ Δ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ΔΔ ⎠ ⎞ ⎜ ⎝ ⎛ Δ ∂ ∂ + − Δ Δ −
= z x y
z y x z x y y z x z y x x z y F xz xz xz xy xy xy xx xx XX y τ τ τ τ τ τ τ τ τ z y x z y x
Fy yx yy yz Δ Δ Δ
⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ = τ τ τ Dengan ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = = x v y
vx y
yx
xy τ μ
τ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ = y v z v z y zy yz τ μ
τ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − = = z v y v x v y v
p y x y z
yy
y τ μ μ
σ 3 2 2 Maka: z y x z x v z v y z v y v x v y v p x x v y v F z x z y x y y x
y Δ ΔΔ
⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ∂ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ + ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + − ∂ + ∂ ⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ = μ μ μ
− = y
F 2
2 2
2 2
2 2
2
3 2 2
z v
y v
y v
y p x
vy y y y
∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − ∂ ∂
μ μ
μ μ
− = y
F 2
2 2
2