Pendugaan Data Hilang pada Rancangan Bujur Sangkar Latin dengan Analisis Kovarian

(1)

LAMPIRAN

Lampiran 1. Proses Pendugaan Galat pada RBSL dengan Satu Data Hilang

(2)

�̂� =�

139

4 −34,3125� −1,17124688� 133

4 −33,1875�= 0,36429707

�̂�� =�_�� − ��_�� =�_�� − ��…− ��− �̂� − �̂�− �� − ��…�

�̂11� = 27−34,3125−(−0,50039746)−2,15710879−0,10742675 −1,17124688(24−33,1875) = 1,68419260

�̂12� = 25−34,3125−(−0,50039746)−(−1,59289121)−0,95679082 −1,17124688(26−33,1875) = 0,24233477

�̂13� = 40−34,3125−(−0,50039746)−0,03554395−(−1,42851465) −1,17124688(38−33,1875) = 1,94424256

�̂14� = 33−34,3125−(−0,50039746)−(−0,59976153)−0,36429707 −1,17124688(36−33,1875) =−3,87076993

�̂21� = 35−34,3125−0,53554395−2,15710879−0,95679082 −1,17124688(32−33,1875) =−1,57108789

�̂22� = 22−34,3125−0,53554395−(−1,59289121)−(−1,42851465) −1,17124688(26−33,1875) =−1,40830116

�̂23� = 34−34,3125−0,53554395−0,035543953−0,36429707 −1,17124688(31−33,1875) = 1,31421758

�̂24�= 44−34,3125−0,53554395−(−0,59976153)−0,10742675 −1,17124688(40−33,1875) = 1,66517147

�̂31� = 53−34,3125−(−0,84130139)−2,15710879−(−1,42851465) −1,17124688(50−33,1875) =−0,89138088

�̂32� = 42−34,3125−(−0,84130139)−(−1,59289121)−0,36429707 −1,17124688(40−33,1875) = 1,77827618

�̂33�= 33−34,3125−(−0,84130139)−0,03554395−0,10742675 −1,17124688(35−33,1875) =−2,73705428

�̂34� = 46−34,3125−(−0,84130139)−(−0,59976153)−0,95679082 −1,17124688(42−33,1875) = 1,85015898

(3)

�̂42�= 41−34,3125−0,80615489−(−1,59289121)−0,10742675 −1,17124688(40−33,1875) =−0,61230979

�̂43� = 26−34,3125−0,80615489−0,03554395−0,95679082 −1,17124688(25−33,1875) =−0,52140586

(4)

Lampiran 2. Langkah-langkah Analisis Kovarian pada RBSL dengan Satu Data

Menghitung Jumlah Kuadrat Total (JKT) dan Jumlah Hasil Kali Total (JHKT) untuk variabel X dan Y

�� = 18643−17622,5625 = 1020,4375 �� = 20203−18837,5625 = 1365,4375 �� = 19359−18219,9375 = 1139,0625

Menghitung Jumlah Kuadrat Baris (JKB) dan Jumlah Hasil Kali Baris (JHKB) untuk variabel X dan Y

�� =(124)

2_{+ (129)}2_{+ (167)}2_{+ (111)}2

4 −17622,5625 = 434,1875

�� =

(125)2_{+ (135)}2_{+ (174)}2_{+ (115)}2

4 −18837,5625 = 500,1875

�� =

(124)(125) + (129)(135) + (167)(174) + (111)(115) 4

−18219,9375 = 464,5625

Menghitung Jumlah Kuadrat Kolom (JKK) dan Jumlah Hasil Kali Kolom (JHKK) untuk variabel X dan Y

�� =

(132)2_{+ (132)}2_{+ (129)}2_{+ (138)}2

4 −17622,5625 = 10,6875

�� =(145)

2_{+ (130)}2_{+ (133)}2_{+ (141)}2

4 −18837,5625 = 36,1875

�� =

(132)(145) + (132)(130) + (129)(133) + (138)(141) 4

(5)

Menghitung Jumlah Kuadrat Perlakuan (JKP) dan Jumlah Hasil Kali Perlakuan (JHKP) untuk variabel X dan Y

�� =(139)

2_{+ (125)}2_{+ (134)}2_{+ (133)}2

4 −17622,5625 = 25,1875

�� =

(145)2_{+ (132)}2_{+ (133)}2_{+ (139)}2

4 −18837,5625 = 27,1875

�� =

(139)(145) + (125)(132) + (134)(133) + (133)(139) 4

−18219,9375 = 21,0625

Menghitung Jumlah Kuadrat Galat (JKG) dan Jumlah Hasil Kali Galat (JHKG) untuk variabel X dan Y

�� = 1020,4375−434,1875−10,6875−25,1875 = 550,375 �� = 1365,4375−500,1875−36,1875−27,1875 = 801,875 �� = 1139,0625−464,5625−8,8125−21,0625 = 644,625 Menghitung Jumlah Kuadrat Terkoreksi

�� terkoreksi = 801,875−(644,625)

2

550,375 = 46,85998183

��(�+�) terkoreksi = 1302,0625−(1109,1875)

2

984,5625 = 52,47508411

�� terkoreksi = 52,47508411−46,85998183 = 5,61510228 ��(�+�) terkoreksi = 838,0625−(653,4375)

2

561,0625 = 77,04110505

�� terkoreksi = 77,04110505−46,85998183 = 30,18112322

��(�+�) terkoreksi = 829,0625−(665,6875)

2

575,5625 = 59,13769139

�� terkoreksi = 59,13769139−46,85998183 = 12,27770956 Menghitung db terkoreksi untuk galat baris, kolom, dan perlakuan

db galat terkoreksi = (r – 1)(r – 2) -1= 5

db baris terkoreksi = r – 1 = 3

db kolom terkoreksi = r – 1 = 3

db perlakuan terkoreksi = r – 1 = 3

Menghitung Kuadrat Tengah (KT)

�� terkoreksi =46,85998183

5 = 9,37199637

�� terkoreksi =5,61510228

3 = 1,87170076

�� terkoreksi =30,18112322

3 = 10,06037441

�� terkoreksi =12,27770956

(6)

(7)

�̂�� =�� − �� =�� − ��…− ��− �̂� − �̂�− �� − ��…�

�̂11� = 27−34,25−(−0,49056041)−1,34009482−0,20754315 −1,14717238(24−33,1875) = 2,23256870

�̂12� = 25−34,25−(−0,49056041)−(−0,53490518)−(−0,27735351) −1,14717238(26−33,1875) = 0,29812060

�̂13� = 40−34,25−(−0,49056041)−(−0,29952589)−(−1,35849137) −1,14717238(38−33,1875) = 2,37781058

�̂14� = 33−34,25−(−0,49056041)−(−0,50566375)−1,42830173 −1,14717238(36−33,1875) =−4,90849989

�̂21� = 31,5−34,25−(−0,29952589)− −1,34009482−(−0,27735351) −1,14717238(32−33,1875) =−2,15094822

�̂22� = 22−34,25−(−0,29952589)−(−0,53490518)−(−1,35849137) −1,14717238(26−33,1875) =−1,81177606

�̂23� = 34−34,25−(−0,29952589)−(−0,29952589)−1,42830173 −1,14717238(31−33,1875) = 1,43018964

�̂24�= 44−34,25−(−0,29952589)−(−0,50566375)−0,20754315 −1,14717238(40−33,1875) = 2,53253464

�̂31� = 53−34,25−0,42733648− −1,34009482−(−1,35849137) −1,14717238(50−33,1875) =−0,94577561

�̂32� = 46−34,25−0,42733648−(−0,53490518)−1,42830173 −1,14717238(40−33,1875) = 2,61415512

�̂33�= 33−34,25−0,42733648−(−0,29952589)−0,20754315 −1,14717238(35−33,1875) =−3,66460368

�̂34� = 46−34,25−0,42733648−(−0,50566375)−(−0,27735351) −1,14717238(42−33,1875) = 1,99622417

�̂41� = 30−34,25−0,36274983− −1,34009482−1,42830173 −1,14717238(26−33,1875) = 0,86415512

(8)

�̂43�= 24,5−34,25−0,36274983−(−0,29952589)−(−0,27735351) −1,14717238(25−33,1875) =−0,14339655

(9)

Lampiran 4. Langkah-langkah Analisis Kovarian pada RBSL dengan Dua Data

Menghitung Jumlah Kuadrat Total (JKT) dan Jumlah Hasil Kali Total (JHKT) untuk variabel X dan Y

�� = 18643−17622,5625 = 1020,4375 �� = 20246,5−18769 = 1477,5

�� = 19369,5−18186,75 = 1182,75

Menghitung Jumlah Kuadrat Baris (JKB) dan Jumlah Hasil Kali Baris (JHKB) untuk variabel X dan Y

�� =(124)

2_{+ (129)}2_{+ (167)}2_{+ (111)}2

4 −17622,5625 = 434,1875

�� =

(125)2_{+ (131,5)}2_{+ (178)}2_{+ (113,5)}2

4 −18769 = 601,88

�� =

(124)(125) + (129)(131,5) + (167)(178) + (111)(113,5) 4

−18186,75 = 510,25

Menghitung Jumlah Kuadrat Kolom (JKK) dan Jumlah Hasil Kali Kolom (JHKK) untuk variabel X dan Y

�� =

(132)2_{+ (132)}2_{+ (129)}2_{+ (138)}2

4 −17622,5625 = 10,6875

�� =(141,5)

2_{+ (134)}2_{+ (131,5)}2_{+ (141)}2

4 −18769 = 18,88

�� =

(132)(141,5) + (132)(134) + (129)(131,5) + (138)(141) 4

(10)

Menghitung Jumlah Kuadrat Perlakuan (JKP) dan Jumlah Hasil Kali Perlakuan (JHKP) untuk variabel X dan Y

�� =(139)

2_{+ (125)}2_{+ (134)}2_{+ (133)}2

4 −17622,5625 = 25,1875

�� =

(145)2_{+ (127)}2_{+ (133)}2_{+ (143)}2

4 −18769 = 54,0

�� =

(139)(145) + (125)(127) + (134)(133) + (133)(143) 4

−18186,75 = 31,0

Menghitung Jumlah Kuadrat Galat (JKG) dan Jumlah Hasil Kali Galat (JHKG) untuk variabel X dan Y

�� = 1020,4375−434,1875−10,6875−25,1875 = 550,375 �� = 1477,5−601,88−18,88−54,0 = 802,75

�� = 1182,75−510,25−10,125−31,0 = 631,375 Menghitung Jumlah Kuadrat Terkoreksi

�� terkoreksi = 802,75−(631,375)

2

550,375 = 78,45403702

��(�+�) terkoreksi = 1404,63−(1141,625)

2

984,5625 = 80,88707802

�� terkoreksi = 80,88707802−78,45403702 = 2,428041 ��(�+�) terkoreksi = 821,63− (641,5)

2

561,0625= 88,16046675

�� terkoreksi = 88,16046675−78,45403702 = 9,70142973

��(�+�) terkoreksi = 856,75−(662,375)

2

575,5625 = 94,46850907

�� terkoreksi = 94,46850907−78,45403702 = 16,01447205 Menghitung db terkoreksi untuk galat baris, kolom, dan perlakuan

db galat terkoreksi = (r – 1)(r – 2) -2= 4

db baris terkoreksi = r – 1 = 3

db kolom terkoreksi = r – 1 = 3

db perlakuan terkoreksi = r – 1 = 3

�� terkoreksi =78,45403702

4 = 19,61350926

3 = 0,809347

3 = 3,23380991

�� terkoreksi =16,01447205

(11)

(12)

DAFTAR PUSTAKA

Fitri, V.R., Wuryandari, T., dan Safitri, D. 2014. Pendugaan Data Hilang pada Rancangan Acak Kelompok Lengkap dengan Analisis Kovarian. Jurnal Gaussian Vol. 3, No. 3, Tahun 2014. Semarang: Universitas Diponegoro.

Gaspersz, V. 1991. Metode Perancangan Percobaan. CV. Armico. Bandung.

Gomez, K.A. dan Gomez, A.A. 1995. Prosedur Statistik untuk Penelitian Pertanian. Penerbit Universitas Indonesia. Jakarta.

Hanafiah, K.A. 2011. Rancangan Percobaan: Teori dan Aplikasi. Rajawali Pers. Jakarta.

Kempthorne, Oscar. 1952. The Design and Analysis of Experiments. John Wiley & Sons. New York.

Little, R.J.A & Donald B. Rubin. 1987. Statistical Analysis with Missing Data. Jhon Wiley & Sons. New York.

Montgomery, D.C. 2009. Design and Analysis of Experiments: International Student Version. USA: Johm Wiley & Sons.

Schefler, William C. 1987. Statistika untuk Biologi, Farmasi, Kedokteran, dan Ilmu yang Bertautan. Bandung: Institut Teknologi Bandung.

Sudjana. 1994. Desain dan Analisis Eksperimen. Tarsito. Bandung.

Sugandi, E. dan Sugiarto. 1994. Rancangan Percobaan. Andi Offset. Yogyakarta.

(13)

BAB 3

PEMBAHASAN

3.1. Pendugaan Data Hilang pada Rancangan Bujur Sangkar Latin

Data yang hilang terjadi apabila pengamatan yang sah tidak dapat dilakukan untuk setiap satuan percobaan. Terjadinya data yang hilang menyebabkan dua kesulitan utama–hilangnya keterangan dan tidak dapat digunakannya sidik ragam baku. Meskipun pengumpulan data di lapangan percobaan biasanya dilakukan dengan sangat hati-hati, sejumlah faktor di bawah kemampuan peneliti dapat menyebabkan hilangnya data. Beberapa penyebab umum hilangnya data antara lain (Gomez & Gomez, 1995):

1. Perlakuan yang tidak tepat, 2. Kerusakan pada objek percobaan, 3. Data tidak logis.

Pendugaan data hilang pada rancangan percobaan dapat dilakukan dengan Metode Yates. Metode Yates merupakan metode pendugaan data hilang dengan meminimumkan ragam galat. Menurut Little dan Rubin (1987), Metode Yates pada dasarnya terdiri dari 3 tahap, yaitu:

1. Menduga data hilang,

2. Mengisi data hilang dengan nilai dugaan, 3. Menganalisis data yang lengkap.

(14)

Tabel 3.1. Hasil Pengamatan pada RBSL dengan Data Hilang Yuvw

Baris

Kolom

Yi..

1 2 3 ... v ... r

1 Y111 Y122 Y133 ... ... ... Y1rr Y1..

2 Y212 Y223 ... Y2..

3 Y313

...

Y3..

... ... ...

u ... Yuvw Yu..

... ... ...

r Yr1r Yr..

Y.j. Y.1. Y.2. Y.3. ... Y.v. ... Y.r. Y...

Perlakuan 1 2 3 ... w ... r

Y..k Y..1 Y..2 Y..3 ... Y..w ... Y..r

dalam hal ini

�� =ℎ (3.1)

�…= � � � �� ≠� � ≠� �≠�

+�_�� = �′ +ℎ (3.2)

��.. = � � �� ≠� � ≠�

+�_�� = �_�′ +ℎ (3.3)

�.�.= � � �� ≠� �≠�

+�_�� =�_�′ +ℎ (3.4)

�..� =� � �� ≠� �≠�

+�_�� = �_�′ +ℎ (3.5)

dengan

T’ = jumlah semua nilai pengamatan

(15)

K’v = jumlah nilai pengamatan kolom ke-v dengan data hilang P’w = jumlah nilai pengamatan perlakuan ke-w dengan data hilang

Dengan h adalah nilai dugaan data hilang yang dipilih sedemikian rupa sehingga meminimumkan jumlah kuadrat galat (JKG) percobaan.

�� =1

JKG = jumlah kuadrat galat

JKT = jumlah kuadrat total

JKB = jumlah kuadrat baris

JKK = jumlah kuadrat kolom

JKP = jumlah kuadrat perlakuan

(16)

�� =ℎ2+2(�

Untuk mendapatkan nilai h, JKG diturunkan terhadap h

�(��)

Nilai dugaan yang diperoleh dimasukkan ke dalam tabel pengamatan, dan untuk melakukan uji analisis, derajat bebas galat dan total dikurangi satu. Uji signifikansi dapat dilakukan, tetapi F akan terbias ke atas, sehingga jumlah kuadrat perlakuan perlu dikurangi dengan faktor koreksi bias dengan besar bias:

��= [� ′ _{− �}

�′ − ��′ −(� −1)��′]2

[(� −1)(� −2)]2 (3.13)

Jika terdapat lebih dari satu data yang hilang maka nilai pengamatan yang hilang diusahakan tinggal satu saja, yaitu dengan cara menentukan nilai awal data hilang yang lain berdasarkan rata-rata dari rataan marginalnya:

(17)

��′_{= rata-rata perlakuan yang mengandung data hilang d}

Masukkan semua nilai awal yang ditentukan tadi ke dalam tabel pengamatan dan duga satu data hilang sisanya dengan menggunakan persamaan (3.12). Masukkan semua nilai dugaan yang telah didapat ke dalam tabel pengamatan, kemudian dugalah semua data hilang tersebut dengan menggunakan persamaan (3.12). Duga kembali semua data hilang tersebut sampai nilai dugaannya konvergen ke satu nilai tertentu.

Masukkan semua nilai dugaan tersebut ke dalam tabel pengamatan, kemudian lakukan uji analisis dengan mengurangi derajat bebas galat dan total dengan banyaknya data yang hilang, dan jumlah kuadrat perlakuan dikurang faktor koreksi bias. Faktor koreksi bias untuk n data hilang adalah:

��= ∑ [� ′ _{− �}

�′ − ��′ −(� −1)��′ ]2 �

�=1

[(� −1)(� −2)]2 (3.15)

3.2. Analisis Kovarian pada Rancangan Bujur Sangkar Latin

Analisis kovarian secara serempak memeriksa varian (ragam utama) dan kovarian (peragam pengiring) di antara peubah terpilih, seperti pengaruh perlakuan pada sifat yang diamati disajikan lebih teliti daripada hanya dengan penggunaan analisis varian (Gomez & Gomez, 1995).

Prosedur analisis kovarian menggunakan kombinasi analisis varian dan regresi di mana model linier untuk sebarang rancangannya adalah model analisis varian ditambah suatu variabel tambahan untuk menggambarkan adanya variabel pengiring.

Berdasarkan model linier RBSL pada persamaan (2.9), maka model analisis kovarian dalam RBSL adalah sebagai berikut:

�� = �+�� +�� +�� +�� − ��…�+�� (3.16)

dengan:

i,j,k = 1, 2, …, r

Yijk = nilai pengamatan pada baris ke-i, kolom ke-j, dan perlakuan ke-k µ = rata-rata umum

αi = pengaruh baris ke-i

(18)

τk = pengaruh perlakuan ke-k

εijk = pengaruh galat pada baris ke-i, kolom ke-j, dan perlakuan ke-k

Xijk = nilai pengamatan ke-ijk pada variabel pengiring

��… = rata-rata semua nilai pengamatan pada variabel pengiring γ = koefisien regresi yang menunjukkan ketergantungan Xijk dan Yijk

3.3. Prosedur Analisis Kovarian pada Rancangan Bujur Sangkar Latin

Prosedur analisis kovarian yang dibahas di sini adalah analisis kovarian dalam RBSL dengan model tetap.

1. Pengujian asumsi analisis kovarian pada RBSL

Menurut Gaspersz (1991), asumsi yang diperlukan dalam analisis kovarian adalah:

a. Variabel pengiring tidak berkolerasi dengan perlakuan yang dicobakan.

Hipotesis untuk uji ini adalah:

H0: Variabel pengiring tidak berkorelasi dengan perlakuan yang dicobakan

H1: Variabel pengiring berkorelasi dengan perlakuan yang dicobakan

Taraf signifikansi: �

Statistik uji: � = ��⁄(�−1) ��⁄�(�−1)

dengan:

JKPx = jumlah kuadrat perlakuan untuk variabel X JKGx = jumlah kuadrat galat untuk variabel X r = banyaknya ulangan

t = banyaknya perlakuan

Kriteria keputusan: H0 ditolak jika Fhit > Fα(t-1), t(r-1)

(19)

titik-titik amatan mengikuti arah garis diagonal maka hal tersebut menunjukkan kecenderungan hubungan kedua variabel tersebut bersifat linier.

c. Galat berdistribusi normal. Bila penyimpangan dari kenormalan ternyata kecil maka tidak akan menimbulkan masalah, tetapi bila penyimpangannya besar maka perlu diperhatikan. Dengan menggunakan metode penduga kuadrat terkecil akan dilakukan pendugaan parameter pada persamaan (3.16) sebagai berikut:

�� =�� − � − �� − �� − ��− �� − ��…� (3.17)

Misalkan Q adalah jumlah kuadrat dari galat,

�= � �_��2 ��

�= � ��_�� − � − �_�− �_� − �_� − ��_�� − ��_…��2 ��

(3.18)

Estimasi parameter �

�� di atas menjadi

� ��

(20)

��

Estimasi parameter �_�

��

Estimasi parameter �_�

(21)

��

d. Koefisien regresi X mempengaruhi Y.

H0: γ = 0 (X tidak mempengaruhi Y)

H1: γ≠ 0 (X mempengaruhi Y) Taraf signifikansi: α

Statistik uji: � =_�� regresi terkoreksi

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db regresi, db galat terkoreksi)

Apabila asumsi-asumsi di atas telah dipenuhi maka dapat dilanjutkan ke pengujian hipotesis pengaruh baris, kolom, dan perlakuan.

2. Pengujian Hipotesis a. Menentukan hipotesis

Pengaruh baris

(22)

H1: minimal ada satu αi ≠ 0 (ada pengaruh baris terhadap respon yang diamati)

Pengaruh kolom

H0: β1 = β2 = ... = βj = 0 (tidak ada pengaruh kolom terhadap respon yang diamati)

H1: minimal ada satu βj ≠ 0 (ada pengaruh kolom terhadap respon yang diamati)

Pengaruh perlakuan

H0: τ1 = τ2 = ... = τk = 0 (tidak ada pengaruh perlakuan terhadap respon yang diamati)

H1: minimal ada satu τk ≠ 0 (ada pengaruh perlakuan terhadap respon yang diamati)

b. Taraf signifikansi: � c. Statistik uji

Pengaruh baris

� =�� terkoreksi

�� terkoreksi

dengan: KTB = Kuadrat Tengah Baris

KTG = Kuadrat Tengah Galat

Pengaruh kolom

� =�� terkoreksi

�� terkoreksi

dengan: KTK = Kuadrat Tengah Kolom

Pengaruh perlakuan

� = �� terkoreksi

�� terkoreksi

dengan: KTP = Kuadrat Tengah Perlakuan

(23)

Pengaruh baris

Menghitung Jumlah Kuadrat Total (JKT) dan Jumlah Hasil Kali Total (JHKT) untuk variabel X dan Y

�� = � ��2

Menghitung Jumlah Kuadrat Baris (JKB) dan Jumlah Hasil Kali Baris (JHKB) untuk variabel X dan Y

�� = ��..

Menghitung Jumlah Kuadrat Kolom (JKK) dan Jumlah Hasil Kali Kolom (JHKK) untuk variabel X dan Y

(24)

�� =��.�.

Menghitung Jumlah Kuadrat Perlakuan (JKP) dan Jumlah Hasil Kali Perlakuan (JHKP) untuk variabel X dan Y

�� =��..�

Menghitung Jumlah Kuadrat Galat (JKG) dan Jumlah Hasil Kali Galat (JHKG) untuk variabel X dan Y

�� =��− �� − �� − ��

�� =�� − �� − �� − ��

Menghitung Jumlah Kuadrat Terkoreksi

(25)

�� terkoreksi = ��(�+�) terkoreksi− �� terkoreksi

Menghitung derajat bebas (db) terkoreksi untuk galat baris, kolom, dan perlakuan

db galat terkoreksi = (r – 1)(r – 2) – 1

db baris terkoreksi = r – 1

db kolom terkoreksi = r – 1

db perlakuan terkoreksi = r – 1

�� terkoreksi = �� terkoreksi

�� galat terkoreksi

�� terkoreksi = ��

�� baris terkoreksi

�� kolom terkoreksi

�� perlakuan terkoreksi

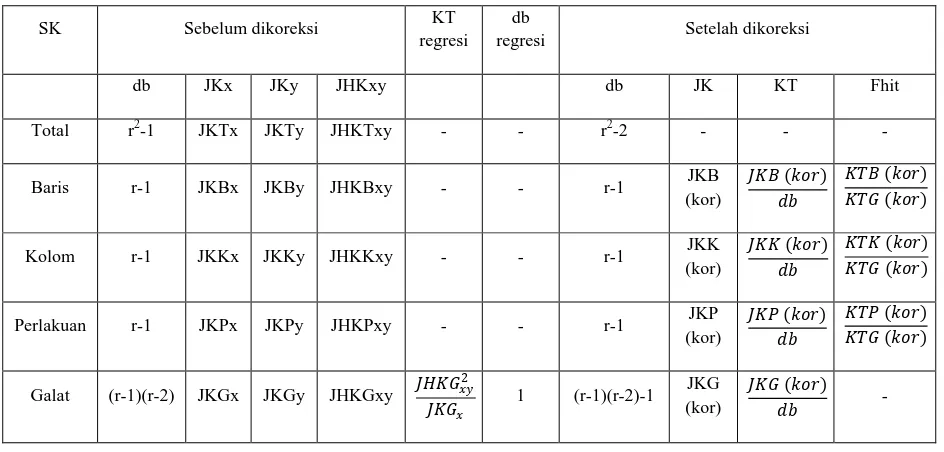
Tabel analisis kovarian pada RBSL adalah sebagai berikut:

Tabel 3.2. Analisis Kovarian pada Rancangan Bujur Sangkar Latin

SK Sebelum dikoreksi KT

regresi db

regresi Setelah dikoreksi

(26)

3.4. Penerapan Analisis Kovarian pada Rancangan Bujur Sangkar Latin

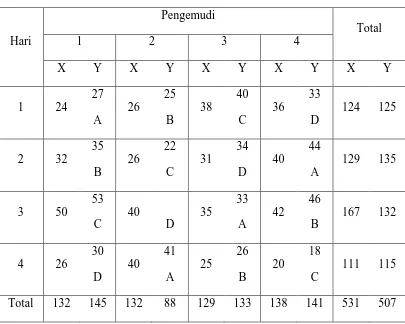
Data yang digunakan dalam penelitian ini berdasarkan dari buku Design and Analysis of Experiments karangan Douglas C. Montgomery (2009: 609) yang berupa rancangan acak kelompok (RAK), tetapi sudah dimodifikasi agar sesuai dengan RBSL.

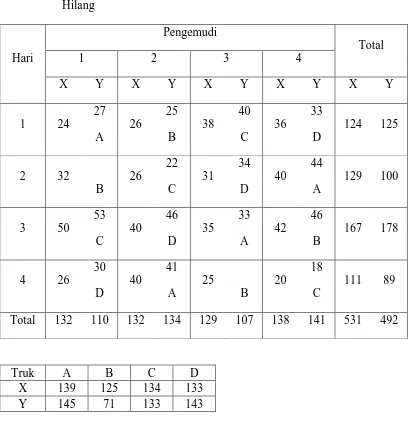
Seorang distributor minuman soda sedang mempelajari keefektifan metode pengantaran barang. Empat tipe truk dicobakan kepada empat orang pengemudi. Percobaan dilakukan selama empat hari, dengan lama pengantaran (dalam menit) sebagai variabel utama (Y) dan banyak barang yang diantar sebagai variabel pengiring (X). Untuk penerapan dengan satu data hilang, dianggap percobaan pada hari ke-3 truk D tidak dapat beroperasi. Dan untuk penerapan dengan dua data hilang, dianggap percobaan pada hari 2 pengemudi 1 sakit dan pada hari ke-4 truk B tidak dapat beroperasi.

3.4.1. Satu Data Hilang

(27)

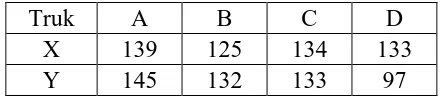
Truk A B C D X 139 125 134 133

Y 145 132 133 97

Sebelum dilakukan analisis kovarian, terlebih dahulu diduga data yang hilang:

Masukkan nilai dugaan ke dalam tabel pengamatan.

(28)

Asumsi-asumsi yang harus dipenuhi adalah sebagai berikut:

a. Variabel pengiring tidak berkorelasi dengan perlakuan yang dicobakan.

Hipotesis

H1: Variabel pengiring berkorelasi dengan perlakuan yang dicobakan

Taraf signifikansi: �= 0,05

Statistik uji: � =_��⁄(�−1) �⁄�(�−1)

Perhitungan:

� = 25,1875 (4⁄ −1)

550,375 4(4⁄ −1)= 0,18305701

�0,05(3, 12) = 3,49

H0 diterima karena Fhit ≤ Fα, artinya variabel pengiring tidak berkorelasi dengan perlakuan yang dicobakan.

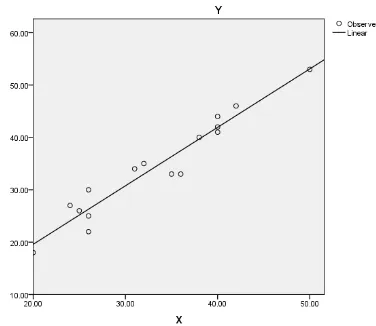
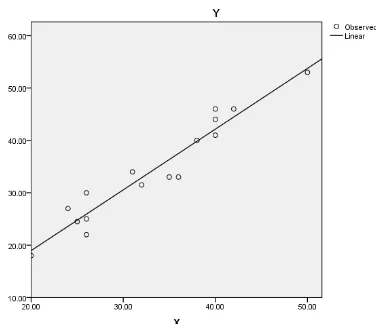
b. Hubungan antara variabel X dan Y bersifat linier

Terlihat bahwa variabel X dan Y bersifat linier karena gambar grafiknya mengikuti garis lurus.

Gambar 3.1. Grafik Hubungan Linier Variabel X dan Variabel Y

(29)

Prosedur pencarian komponen galat percobaan dapat dilihat pada Lampiran 1. Nilai dugaan galatnya adalah sebagai berikut:

Tabel 3.5. Data Dugaan Galat pada Percobaan dengan Satu Data Hilang

Baris

Kolom

Total

1 2 3 4

1 1,68419260 0,24233477 1,94424256 -3,87076993 0,00000000

2 -1,57108789 -1,40830116 1,31421758 1,66517147 0,00000000

3 -0,89138088 1,77827618 -2,73705428 1,85015898 0,00000000

4 0,77827618 -0,61230979 -0,52140586 0,35543947 0,00000000

Total 0,00000000 0,00000000 0,00000000 0,00000000 0,00000000

Komponen galat percobaan pada tabel diplotkan hasilnya seperti pada gambar berikut:

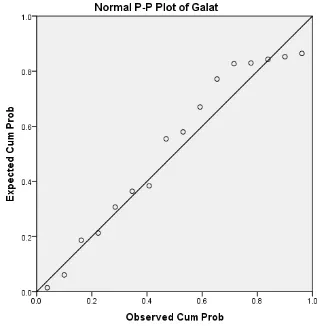
Gambar 3.2. Grafik Galat dengan Satu Data Hilang

Terlihat pada gambar grafik di atas bahwa titik-titik dugaan galat mengikuti garis diagonal yang berarti galat berdistribusi normal.

d. Pengaruh X terhadap Y

H0: γ = 0 (X tidak mempengaruhi Y)

(30)

Taraf signifikansi: α = 0,05

Statistik uji: � =_�� regresi terkoreksi

Perhitungan:

H0 ditolak karena Fhit≥ Fα, artinya X berpengaruh terhadap Y.

Setelah semua asumsi terpenuhi maka langkah selanjutnya dilakukan analisis kovarian. Adapun langkah-langkahnya dapat dilihat pada Lampiran 2. Tabel analisis kovariannya adalah sebagai berikut:

Tabel 3.6. Analisis Kovarian dengan Satu Data Hilang

regresi

db

db JKx JKy JHKxy db JK KT Fhit

Hipotesis yang diuji sebagai berikut:

a. Pengaruh baris

(31)

H0: α1 = α2 = ... = αi = 0 (tidak ada pengaruh baris terhadap respon yang diamati)

H1: minimal ada satu αi ≠ 0 (ada pengaruh baris terhadap respon yang diamati)

Statistik uji: � =�� terkoreksi �� terkoreksi

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db baris, db galat)

Perhitungan:

� =1,87170076

9,37199637= 0,19971207

�0,05(3, 5) = 5,41

H0 diterima karena Fhit ≤ Fα, artinya tidak ada pengaruh hari terhadap lama pengantaran.

b. Pengaruh kolom

Hipotesis untuk uji ini adalah

Statistik uji: � =�� terk oreksi �� terkoreksi

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db kolom, db galat)

Perhitungan:

� =10,06037441

9,37199637 = 1,07345052

�0,05(3, 5) = 5,41

(32)

c. Pengaruh perlakuan

H1: minimal ada satu τk≠ 0 (ada pengaruh perlakuan terhadap respon yang diamati)

Statistik uji: � =��_�� terkoreksi terkoreksi

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db perlakuan, db galat)

Perhitungan:

� =4,09256985

9,37199637= 0,43668069

�0,05(3, 5) = 5,41

H0 diterima karena Fhit ≤ Fα, artinya tidak ada pengaruh tipe truk terhadap lama pengantaran.

Akan dibandingkan ketepatan analisis antara analisis varian (sebelum dilakukan koreksi terhadap JK dan JHK) dengan analisis kovarian (sesudah dilakukan koreksi terhadap JK dan JHK) dengan menghitung koefisien keragaman sebagai berikut:

Koefisien keragaman untuk analisis varian

�� = ��

(� −1)(� −2) =

801,875

(4−1)(4−2) = 133,64583333

�� =√��

�� 100% =

�133,64583333

34,3125 100% = 33,69188812%

Koefisien keragaman untuk analisis kovarian

�� =√�� terkoreksi

�� 100% = √

9,37199637

34,3125 100% = 8,92203031%

(33)

menunjukkan bahwa analisis kovarian lebih tepat dibandingkan dengan analisis varian.

3.4.2. Dua Data Hilang

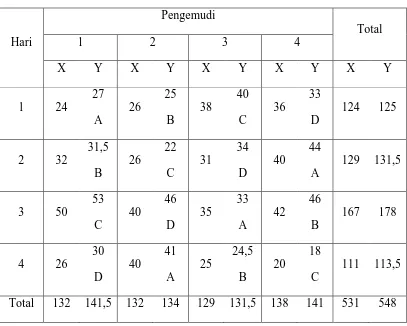
Tabel 3.7. Banyak Barang (X) dan Lama Pengantaran (Y) dengan Dua Data Hilang

(34)

Tabel 3.8. Iterasi Pendugaan Data Hilang

Iterasi Nilai Dugaan Y21B Y43B

Masukkan nilai dugaan ke dalam tabel pengamatan.

(35)

Truk A B C D X 139 125 134 133 Y 145 127 133 143

Asumsi-asumsi yang harus dipenuhi adalah sebagai berikut:

a. Variabel pengiring tidak berkorelasi dengan perlakuan yang dicobakan.

Hipotesis

H1: Variabel pengiring berkorelasi dengan perlakuan yang dicobakan Taraf signifikansi: �= 0,05

Statistik uji: � = ��⁄(�−1) ��⁄�(_�−1)

Perhitungan:

� = 25,1875 (4⁄ −1)

550,375 4(4⁄ −1)= 0,18305701

�0,05(3, 12) = 3,49

H0 diterima karena Fhit ≤ Fα, artinya variabel pengiring tidak berkorelasi dengan perlakuan yang dicobakan.

b. Hubungan antara variabel X dan Y bersifat linier

(36)

Gambar 3.3. Grafik Hubungan Linier Variabel X dan Variabel Y

c. Galat berdistribusi normal

Prosedur pencarian komponen galat percobaan dapat dilihat pada Lampiran 3. Nilai dugaan galatnya adalah sebagai berikut:

Tabel 3.10. Data Dugaan Galat pada Percobaan dengan Dua Data Hilang

Baris

Kolom

Total

1 2 3 4

1 2,23256870 0,29812060 2,37781058 -4,90849989 0,00000000

2 -2,15094822 -1,81177606 1,43018964 2,53253464 0,00000000

3 -0,94577561 2,61415512 -3,66460368 1,99622417 0,00000000

4 0,86415512 -1,10049966 -0,14339655 0,37974109 0,00000000

Total 0,00000000 0,00000000 0,00000000 0,00000000 0,00000000

(37)

Gambar 3.4. Grafik Galat dengan Dua Data Hilang

Terlihat pada gambar grafik di atas bahwa titik-titik dugaan galat mengikuti garis diagonal yang berarti galat berdistribusi normal.

d. Pengaruh X terhadap Y

H0: γ = 0 (X tidak mempengaruhi Y) H1: γ≠ 0 (X mempengaruhi Y) Taraf signifikansi: α = 0,05

Statistik uji: � = �� regresi �� terkoreksi

Perhitungan:

�� regresi =�� 2

�� =

(631,375)2

550,375 = 724,29596298

� = �� regresi

�� terkoreksi=

724,29596298

19,61350926 = 36,92842283

�0,05(1, 4) = 7,71

H0 ditolak karena Fhit≥ Fα, artinya X berpengaruh terhadap Y.

(38)

Tabel 3.11. Analisis Kovarian dengan Dua Data Hilang

regresi

db

db JKx JKy JHKxy db JK KT Fhit

Hipotesis yang diuji sebagai berikut:

a. Pengaruh baris

H0: α1 = α2 = ... = αi = 0 (tidak ada pengaruh baris terhadap respon yang

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db baris, db galat)

Perhitungan:

� = 0,809347

19,61350926= 0,04126477

�0,05(3, 4) = 6,59

(39)

b. Pengaruh kolom

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db kolom, db galat)

Perhitungan:

� = 3,23380991

19,61350926= 0,16487666

�0,05(3, 4) = 6,59

H0 diterima karena Fhit ≤ Fα, artinya tidak ada pengaruh pengemudi terhadap lama pengantaran.

c. Pengaruh perlakuan

H1: minimal ada satu τk≠ 0 (ada pengaruh perlakuan terhadap respon yang diamati)

Kriteria keputusan: H0 ditolak jika Fhit > Fα(db perlakuan, db galat) Perhitungan:

� = 5,33815735

19,61350926= 0,27216738

(40)

H0 diterima karena Fhit ≤ Fα, artinya tidak ada pengaruh tipe truk terhadap lama pengantaran.

Akan dibandingkan ketepatan analisis antara analisis varian (sebelum dilakukan koreksi terhadap JK dan JHK) dengan analisis kovarian (sesudah dilakukan koreksi terhadap JK dan JHK) dengan menghitung koefisien keragaman sebagai berikut:

Koefisien keragaman untuk analisis varian

�� = ��

(� −1)(� −2) =

802,75

(4−1)(4−2) = 133,79166667

�� =√��

�� 100% = √

133,79166667

34,25 100% = 33,77178036%

Koefisien keragaman untuk analisis kovarian

�� =√�� terkoreksi

�� 100% =

�19,61350926

34,25 100% = 12,93055234%

(41)

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Dari hasil analisis dan pembahasan yang telah dilakukan, dapat disimpulkan

bahwa:

1. Jika dalam suatu percobaan terdapat data hilang, maka sebelum dilakukan

analisis kovarian terlebih dahulu data hilang tersebut diduga dengan

persamaan pendugaan data hilang. Untuk satu data hilang, nilai data hilangnya

dapat langsung diduga. Dan untuk lebih dari satu data hilang, sisakan satu data

hilang dengan cara menduga nilai awal untuk data hilang lainnya berdasarkan

rata-rata dari rataan marginalnya, selanjutnya satu data hilang tadi diduga

dengan rumus pendugaan data hilang. Kemudian lakukan pendugaan data

hilang kembali terhadap semua data hilang, ulangi sampai nilai dugaannya

konvergen ke satu nilai tertentu. Untuk melakukan analisis kovarian, derajat

kebebasan galat dan total dikurangkan dengan banyaknya data yang hilang

dan jumlah kuadrat perlakuan dikurangkan dengan besar bias.

2. Berdasarkan penerapan kasus analisis kovarian pada rancangan bujur sangkar

latin, nilai koefisien keragaman untuk satu data hilang dan dua data hilang

menunjukkan bahwa analisis kovarian lebih tepat digunakan daripada analisis

varian.

4.2. Saran

Penelitian ini hanya menerapkan analisis kovarian pada RBSL dengan satu dan

dua data hilang, maka disarankan kepada peneliti berikutnya agar meneliti banyak

data hilang maksimal yang dapat diduga pada RBSL dengan melihat kesimpulan

(42)

BAB 2

LANDASAN TEORI

2.1. Rancangan Percobaan

Percobaan merupakan serangkaian kegiatan di mana setiap tahap dalam rangkaian benar-benar terdefinisikan; dilakukan untuk menemukan jawaban tentang permasalahan yang diteliti melalui suatu pengujian hipotesis (Hanafiah, 2011).

Rancangan percobaan bertujuan untuk memperoleh atau mengumpulkan informasi sebanyak-banyaknya yang diperlukan dan berguna dalam melakukan penelitian persoalan yang akan dibahas. Rancangan percobaan berusaha untuk memperoleh informasi yang maksimum dengan menggunakan biaya yang minimum (Sudjana, 1994).

Unsur-unsur dasar suatu percobaan adalah (Hanafiah, 2011):

1. Perlakuan (treatment), yaitu semua tindakan coba-coba (trial and error) yang dilakukan terhadap suatu objek, yang pengaruhnya akan diselidiki untuk menguji hipotesis.

2. Ulangan (replication), yaitu frekuensi suatu perlakuan yang diselidiki dalam suatu percobaan. Jumlah ulangan suatu perlakuan tergantung pada derajat ketelitian yang diinginkan oleh si peneliti terhadap kesimpulan hasil percobaannya. Ulangan ini berfungsi untuk menghasilkan suatu estimasi tentang galat dan menghasilkan ukuran pengaruh perlakuan-perlakuan yang lebih tepat terhadap hasil percobaan.

3. Pengendalian (local control), yaitu upaya pengendalian kondisi lapangan yang heterogen menjadi nisbi homogen, setidak-tidaknya pada lokal-lokal tertentu, yang ditujukan untuk menekan galat menjadi nisbi kecil, sehingga bisa menonjolkan satu atau beberapa perlakuan yang logisnya memang lebih menonjol dari perlakuan kontrol atau perlakuan-perlakuan lainnya.

2.2. Rancangan Bujur Sangkar Latin

(43)

diselesaikan dengan jaminan bahwa setiap perlakuan terjadi hanya sekali dalam setiap pengelompokan baik baris maupun kolom. Prosedur ini memungkinkan untuk menduga keragaman di antara pengelompokan baris dan juga pengelompokan kolom dan mengeluarkannya dari galat percobaan (Gomez & Gomez, 1995).

Penempatan perlakuan ke dalam unit-unit percobaan sedemikian rupa sehingga perlakuan tertentu harus terjadi satu kali dalam baris dan kolom. Hal ini hanya mungkin terjadi jika banyaknya perlakuan sama dengan banyaknya baris dan sama dengan banyaknya kolom. Oleh karena itu, diperlukan suatu pola tertentu agar syarat-syarat terpenuhi (Yitnosumarto, 1993)

Rancangan ini jarang digunakan karena memerlukan persyaratan (Hanafiah, 2011):

1. Jumlah baris = jumlah kolom = jumlah perlakuan, sehingga jika jumlah perlakuan terlalu sedikit derajat bebas yang berhubungan dengan galat percobaan menjadi terlalu kecil sebagai penduga yang layak; dan jika jumlah perlakuan terlalu besar akan menyebabkan ulangan perlakuan yang terlalu besar sehingga akan tidak ekonomis jika digunakan.

2. Tidak ada interaksi antara baris atau kolom dengan perlakuan. Jika ada interaksi, maka RBSL ini tidak dapat digunakan dan jika tetap digunakan, maka kesimpulan atau hasil-hasil percobaan tersebut menjadi samar.

3. Adanya dua sumber keragaman data di luar perlakuan yang diteliti. Dua sumber keragaman ini dapat berupa dua arah silang kemiringan lereng, dua arah silang kesuburan tanah, dua arah silang cara/tenaga/alat kerja, dua waktu pengamatan dan lain-lain, yang penting faktor-faktor ini bukanlah faktor yang diteliti.

Karena itu, RBSL digunakan hanya untuk percobaan dengan banyaknya perlakuan yang tidak kurang dari empat dan tidak lebih dari delapan. Karena keterbatasan tersebut, RBSL tidak digunakan secara luas dalam percobaan penelitian di samping potensinya yang besar dalam mengendalikan galat percobaan (Gomez & Gomez, 1995).

2.2.1. Pengacakan Perlakuan pada Rancangan Bujur Sangkar Latin

(44)

berikutnya) hingga pengacakan tak bebas (bukan pengacakan) untuk petak percobaan terakhir (Hanafiah, 2011).

Tabel 2.1. Pengacakan Perlakuan pada Rancangan Bujur Sangkar Latin

Baris

Kolom

Yi..

1 2 3 ... r

1 Y111 Y122 Y133 ... Y1rr Y1..

2 Y212 Y223 ... Y2..

3 Y313 ... Y3..

... ... ...

r Yr1r Yr..

Y.j. Y.1. Y.2. Y.3. ... Y.r. Y...

Perlakuan 1 2 3 ... r

Y..k Y..1 Y..2 Y..3 ... Y..r

dalam hal ini

�…= � ��

��

=� (2.1)

��.. =� ��

��

= �_� (2.2)

�.�.= � ��

��

=�_� (2.3)

�..� =� ��

��

=�_� (2.4)

dengan

(45)

Pk = jumlah nilai pengamatan perlakuan ke-k

2.2.2. Model Linier Rancangan Bujur Sangkar Latin

Misalkan (i,j,k) merupakan baris, kolom, dan perlakuan pada suatu petak percobaan. Sehingga ada sebanyak r3 nilai pengamatan yang memungkinkan, dalam hal ini tiap perlakuan masing-masing diterapkan ke tiap petak percobaan.

�� = �…+ (��..− �…) +��.�.− �…�+ (�..� − �…) + (��..− �…)��.�.− �…�

+(�_�_..− �_…)(�_.._� − �_…) +��_._�_.− �_…�(�_.._� − �_…) +

+(�_�_..− �_…)��_._�_.− �_…�(�_.._� − �_…) (2.5)

�,�,�= 1,2,3, … ,�

Karena pada RBSL tiap perlakuan hanya diterapkan sekali di masing-masing baris dan kolom, sekarang misalkan

�� = �� +�� (2.6)

di mana Xij merupakan nilai pengamatan di petak percobaan (ij), dan τk merupakan pengaruh pemberian perlakuan k terhadap nilai pengamatan. Persamaan (2.6) direduksi menjadi

�� = �..+ (��.+�..) +��.� +�..�+ (��.+�..)��.� +�..�+�.+ (�� +�.)

�� = (�..+�.) + (��.+�..) +��.� +�..�+ (�� +�.)

+��_�� − �_�.− �.� +�..� (2.7)

dapat ditulis menjadi

�� = �…+ (��..− �…) +��.�.− �…�+ (�..� − �…) +��.− ��..− �.�.+�…� (2.8)

atau

�� = �+�� +�� +�� +�� (2.9)

dengan

Yijk = hasil pengamatan pada baris ke-i, kolom ke-j, dan perlakuan ke-k µ = rata-rata umum

(46)

βj = pengaruh utama kolom ke-j

τk = pengaruh perlakuan ke-k

εijk = pengaruh acak (galat) pada baris ke-i, kolom ke-j, dan perlakuan ke-k

Apabila RBSL menggunakan model tetap, asumsinya:

� ��

Tabel analisis varian pada RBSL adalah sebagai berikut:

Tabel 2.2. Analisis Varian pada Rancangan Bujur Sangkar Latin

Sumber

Keragaman Derajat Bebas

Jumlah

Kadang-kadang ketika melakukan penelitian ataupun pengamatan terjadi satu atau mungkin lebih pengamatan yang hilang. Seekor binatang percobaan mati sebelum eksperimen berakhir, sebuah tabung percobaan pecah jatuh ke lantai, seorang pasien meninggal dunia ketika pengobatan masih sedang berlangsung, atau data hasil pengamatan hilang dan lain sebagainya (Sudjana, 1994).

Jika dalam percobaan dengan menggunakan RBSL �×� terdapat sebuah data hilang, maka nilai data yang hilang tersebut ditaksir oleh suatu nilai yang dihitung dengan rumus:

ℎ= �(�

′₊_�′₊_�′₎₋₂_�′

(47)

dengan

h = nilai data pengganti data yang hilang

B’ = jumlah nilai pengamatan dalam baris dengan data hilang K’ = jumlah nilai pengamatan dalam kolom dengan data hilang P’ = jumlah nilai pengamatan untuk perlakuan dengan data hilang T’ = jumlah semua nilai pengamatan yang ada

2.4. Analisis Kovarian

Analisis kovarian adalah alat uji statistik multivariat yang merupakan penggabungan antara analisis regresi dengan analisis varian (Schefler, 1987).

Prosedur dalam analisis kovarian menggunakan kombinasi analisis varian dan analisis regresi di mana model linier untuk sebarang rancangannya adalah model analisis varian ditambah suatu variabel tambahan untuk menggambarkan adanya variabel pengiring.

Model linier rancangan acak lengkap (RAL) dengan satu faktor adalah sebagai berikut:

�� =�+�� +�� (2.11)

dengan:

Yij = nilai pengamatan dari perlakuan ke-i dalam kelompok ke-j i = 1, 2, …, t (t menyatakan banyaknya perlakuan)

j = 1, 2, …, r (r menyatakan banyaknya ulangan) µ = rata-rata umum

τi = pengaruh dari perlakuan ke-i

εij = pengaruh galat yang muncul dari perlakuan ke-i dalam kelompok ke-j

Bentuk umum model linier aditif untuk analisis regresi adalah sebagai berikut:

(48)

Gabungan dari persamaan (2.11) dan (2.12) didapatkan model linier aditif dari analisis kovarian untuk RAL sebagai berikut:

�� =�+�� +�� − ��+�� (2.13)

Menurut Gaspersz (1991), asumsi yang diperlukan dalam analisis kovarian adalah:

1. Variabel pengiring tidak berkolerasi dengan perlakuan yang dicobakan.

2. Hubungan antara variabel pengiring (X) dengan variabel respon (Y) bersifat linier.

3. Galat berdistribusi normal.

4. Pengaruh X terhadap Y, yaitu X mempengaruhi Y.

Kemas Ali Hanafiah (2011) di dalam bukunya yang berjudul “Rancangan Percobaan: Teori dan Aplikasi” menuliskan bahwa analisis kovarian bermanfaat penting untuk:

1. Mengontrol galat dan memurnikan rata-rata pengaruh perlakuan, 2. Menaksir data hilang atau data rusak,

3. Meningkatkan keandalan interpretasi dari hasil-hasil percobaan.

2.5. Koefisien Keragaman

Koefisien keragaman merupakan suatu koefisien yang menunjukkan derajat ketepatan dari suatu kesimpulan atau hasil yang diperoleh dari suatu percobaan. Koefisien keragaman ini dinyatakan dalam bentuk persen (Hanafiah, 2011) yaitu:

�� =√��

�� × 100% (2.14)

dengan �� = rata-rata umum.

Dalam analisis kovarian, koefisien keragaman dinyatakan sebagai berikut:

�� =√��

�� × 100% (2.15)

(49)

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Percobaan adalah serangkaian kegiatan dalam upaya menemukan jawaban

mengenai permasalahan yang diteliti melalui suatu pengujian hipotesis. Sebelum

melakukan suatu percobaan sebaiknya dilakukan suatu rancangan percobaan

terlebih dahulu agar data yang semestinya diperlukan dapat diperoleh sehingga

akan membawa kepada analisis objektif dan kesimpulan yang berlaku untuk

persoalan yang sedang dibahas (Sudjana, 1994).

Rancangan percobaan bertujuan untuk memperoleh atau mengumpulkan

informasi sebanyak-banyaknya yang diperlukan dan berguna dalam melakukan

penelitian persoalan yang akan dibahas (Sudjana, 1994). Salah satu model

rancangan percobaan yang biasa dipakai adalah rancangan bujur sangkar latin.

Rancangan bujur sangkar latin pada umumnya digunakan bila dalam percobaan

yang ingin dilakukan terdapat dua sumber ragam lain selain ragam yang

diakibatkan oleh perlakuan. (Sugandi & Sugiarto, 1994)

Hal penting yang perlu diperhatikan terkait dengan data yang didapatkan

dari suatu percobaan yaitu sering terjadi satu atau lebih data hilang. Data yang

hilang terjadi akibat pengamatan yang sah tidak dapat dilakukan pada unit

percobaan. Meskipun pengumpulan data dilakukan dengan sangat hati-hati,

beberapa faktor di luar kemampuan peneliti dapat menyebabkan data hilang atau

tidak dapat digunakan. Misalnya dalam suatu percobaan dengan objek makhluk

hidup ada yang mati sebelum percobaan berakhir.

Analisis kovarian bermanfaat penting untuk (1) mengontrol galat dan

memurnikan rata-rata pengaruh perlakuan, (2) menaksir data hilang atau data

(50)

Analisis kovarian memerlukan hasil pengamatan terhadap ciri utama (variate)

objek dan juga hasil-hasil pengamatan terhadap satu atau lebih ciri peragam

pengiring (covariate). Selain itu analisis kovarian juga memerlukan adanya

hubungan fungsional tertentu (korelasi) antara ragam utama dan ragam pengiring

tersebut (Hanafiah, 2011).

Dari uraian singkat di atas, penulis merasa tertarik untuk mengangkat judul

“PENDUGAAN DATA HILANG PADA RANCANGAN BUJUR SANGKAR

LATIN DENGAN ANALISIS KOVARIAN”

1.2. Perumusan Masalah

Berdasarkan latar belakang masalah di atas, maka rumusan masalah yang akan

dibahas dalam penelitian ini adalah:

1. Bagaimana cara menduga data hilang pada rancangan bujur sangkar latin?

2. Bagaimana penerapan analisis kovarian pada rancangan bujur sangkar latin

yang mengandung data hilang?

1.3. Batasan Masalah

Permasalahan yang akan dibahas dalam penelitian ini adalah penerapan analisis

kovarian pada rancangan bujur sangkar latin model tetap dengan satu data hilang

dan dua data hilang.

1.4. Tujuan Penelitian

Penelitian ini bertujuan untuk:

1. Mengetahui bagaimana cara menduga data hilang pada rancangan bujur

(51)

2. Mengetahui bagaimana menerapkan analisis kovarian pada rancangan bujur

sangkar latin yang mengandung data hilang.

1.5. Kontribusi Penelitian

Tulisan ini diharapkan dapat bermanfaat sebagai:

1. Menambah wawasan penulis tentang penerapan analisis kovarian pada

rancangan percobaan, khususnya rancangan bujur sangkar latin yang

mengandung data hilang.

2. Sebagai tambahan informasi dan referensi untuk mahasiswa, khususnya

mahasiswa yang hendak melakukan penelitian serupa.

1.6. Metodologi Penelitian

Penelitian yang penulis lakukan adalah penelitian literatur yang disusun dengan

langkah-langkah sebagai berikut:

1. Menjelaskan definisi rancangan bujur sangkar latin, data hilang, dan analisis

kovarian.

2. Menjelaskan prosedur pendugaan data hilang dan analisis kovarian pada

rancangan bujur sangkar latin.

3. Menyelesaikan penerapan analisis kovarian pada rancangan bujur sangkar

latin dengan satu data hilang dan dua data hilang.

4. Menyimpulkan hasil dan informasi dari penyelesaian permasalahan yang

(52)

PENDUGAAN DATA HILANG PADA RANCANGAN BUJUR SANGKAR LATIN DENGAN ANALISIS KOVARIAN

ABSTRAK

Analisis kovarian adalah alat uji statistik multivariat yang menggabungkan antara analisis regresi dengan analisis varian. Prosedur dalam analisis kovarian menggunakan kombinasi analisis varian dan analisis regresi di mana model linier untuk sebarang rancangannya adalah model analisis varian ditambah suatu variabel tambahan untuk menggambarkan adanya variabel pengiring. Analisis kovarian pada Rancangan Bujur Sangkar Latin (RBSL) merupakan suatu analisis untuk percobaan yang berdasarkan pada pengelompokan baris dan pengelompokan kolom, di mana setiap perlakuan terjadi hanya sekali dalam setiap pengelompokan baris dan pengelompokan kolom, dengan banyak perlakuan sama dengan banyak baris dan banyak kolom, dan mengikutsertakan satu variabel pengiring dalam model. Apabila dalam percobaan tersebut terdapat data hilang maka data hilang tersebut diduga terlebih dahulu, kemudian derajat bebas galat dan total dikurangkan dengan banyaknya data yang hilang dan jumlah kuadrat perlakuan dikurangkan dengan besar bias. Berdasarkan contoh penerapan kasus analisis kovarian pada RBSL menunjukkan bahwa analisis kovarian lebih tepat digunakan dibandingkan analisis varian karena memiliki koefisien keragaman lebih kecil.

(53)

PENDUGAAN DATA HILANG PADA RANCANGAN BUJUR

SANGKAR LATIN DENGAN ANALISIS KOVARIAN

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat untuk mencapai gelar

Sarjana Sains

AWANG TERUNA SIDDIQ

110803052

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(54)

PERSETUJUAN

Judul : Pendugaan Data Hilang pada Rancangan Bujur Sangkar Latin dengan Analisis Kovarian

Kategori : Skripsi

Nama : Awang Teruna Siddiq

Nomor Induk Mahasiswa : 110803052

Program Studi : Sarjana (S1) Matematika Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara

Disetujui di

Medan, Februari 2016

Komisi Pembimbing:

Pembimbing 2, Pembimbing 1,

Drs. Gim Tarigan, M.Si Drs. Henry Rani Sitepu, M.Si NIP. 19550202 198601 1 001 NIP. 19530303 198303 1 002

Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

(55)

PERNYATAAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Februari 2016

(56)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT, Tuhan Yang Maha Esa dan Maha Penyayang, dengan limpahan karunia-Nya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul “Pendugaan Data Hilang pada Rancangan Bujur Sangkar Latin dengan Analisis Kovarian” guna memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan AlamUniversitas Sumatera Utara.

Terima kasih penulis sampaikan kepada Bapak Drs. Henry Rani Sitepu, M.Si dan Bapak Drs. Gim Tarigan, M.Si selaku pembimbing yang telah memberikan bimbingan dan telah meluangkan waktunya selama penulisan skripsi ini. Bapak Dr. Open Darnius, M.Sc dan Bapak Dr. Pasukat Sembiring, M.Si selaku penguji yang telah memberikan kritik dan saran yang membangun dalam penyempurnaan skripsi ini. Dekan dan Wakil Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara. Ketua dan Sekretaris Departemen Matematika Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dr. Mardiningsih, M.Si. Seluruh staf pengajar dan staf administrasi di lingkungan Departemen Matematika, serta seluruh sivitas akademika di lingkungan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Ucapan terima kasih juga ditujukan kepada kedua orang tua serta saudara-saudari penulis yang telah banyak memberikan semangat dan bantuan baik secara moril maupun materil kepada penulis selama masa pendidikan. Terima kasih kepada seluruh rekan mahasiswa, khususnya teman-teman angkatan 2011,dan kepada semua pihak yang tidak dapat penulis sebutkan satu persatu yang telah membantu dalam menyelesaikan skripsi ini.Semoga segala bentuk bantuan yang telah diberikan kepada penulis mendapatkan balasan yang lebih baik.

Medan, Februari 2016 Penulis

(57)

ABSTRAK

Analisis kovarian adalah alat uji statistik multivariat yang menggabungkan antara analisis regresi dengan analisis varian. Prosedur dalam analisis kovarian menggunakan kombinasi analisis varian dan analisis regresi di mana model linier untuk sebarang rancangannya adalah model analisis varian ditambah suatu variabel tambahan untuk menggambarkan adanya variabel pengiring. Analisis kovarian pada Rancangan Bujur Sangkar Latin (RBSL) merupakan suatu analisis untuk percobaan yang berdasarkan pada pengelompokan baris dan pengelompokan kolom, di mana setiap perlakuan terjadi hanya sekali dalam setiap pengelompokan baris dan pengelompokan kolom, dengan banyak perlakuan sama dengan banyak baris dan banyak kolom, dan mengikutsertakan satu variabel pengiring dalam model. Apabila dalam percobaan tersebut terdapat data hilang maka data hilang tersebut diduga terlebih dahulu, kemudian derajat bebas galat dan total dikurangkan dengan banyaknya data yang hilang dan jumlah kuadrat perlakuan dikurangkan dengan besar bias. Berdasarkan contoh penerapan kasus analisis kovarian pada RBSL menunjukkan bahwa analisis kovarian lebih tepat digunakan dibandingkan analisis varian karena memiliki koefisien keragaman lebih kecil.

(58)

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak iv

Daftar Isi v

Daftar Tabel vi

Daftar Gambar vii

Daftar Lampiran viii

Bab 1.Pendahuluan

1.1. Latar Belakang 1

1.2. Perumusan Masalah 2

1.3. Batasan Masalah 2

1.4. Tujuan Penelitian 2

1.5. Kontribusi Penelitian 3

1.6. Metodologi Penelitian 3

Bab 2. Landasan Teori

2.1. Rancangan Percobaan 4

2.2. Rancangan Bujur Sangkar Latin 4

2.2.1. Pengacakan Perlakuan pada Rancangan Bujur Sangkar Latin 5 2.2.2. Model Linier Rancangan Bujur Sangkar Latin 7

2.3.Data Hilang 8

2.4.Analisis Kovarian 9

2.5.Koefisien Keragaman 10

Bab 3. Pembahasan

3.1. Pendugaan Data Hilang pada Rancangan Bujur Sangkar Latin 11 3.2. Analisis Kovarian pada Rancangan Bujur Sangkar Latin 15 3.3. Prosedur Analisis Kovarian pada Rancangan Bujur Sangkar Latin 15 3.4. Penerapan Analisis Kovarian pada Rancangan Bujur Sangkar Latin 23

3.4.1. Satu Data Hilang 24

3.4.2. Dua Data Hilang 31

Bab 4. Kesimpulan dan Saran

4.1. Kesimpulan 39

4.2. Saran 39

Daftar Pustaka 40

(59)

DAFTAR TABEL

Tabel 2.1. Pengacakan Perlakuan pada Rancangan Bujur Sangkar Latin 6 Tabel 2.2. Tabel Analisis Varian pada Rancangan Bujur Sangkar Latin 8 Tabel 3.1. Hasil Pengamatan pada RBSL dengan Data Hilang Yuvw 12 Tabel 3.2. Analisis Kovarian pada Rancangan Bujur Sangkar Latin 23 Tabel 3.3. Banyak Barang (X) dan Lama Pengantaran (Y) dengan Satu

Data Hilang 24

Tabel 3.4. Banyak Barang (X) dan Lama Pengantaran (Y) dengan Satu

Data Hilang 25

Tabel 3.5. Data Dugaan Galat pada Percobaan dengan Satu Data Hilang 27 Tabel 3.6. Analisis Kovarian dengan Satu Data Hilang 28 Tabel 3.7. Banyak Barang (X) dan Lama Pengantaran (Y) dengan Dua

Data Hilang 31

Tabel 3.8. Iterasi Pendugaan Data Hilang 32 Tabel 3.9. Banyak Barang (X) dan Lama Pengantaran (Y) dengan Dua

Data Hilang 32

(60)

DAFTAR GAMBAR

Gambar 3.1. Grafik Hubungan Linier Variabel X dan Variabel Y 26

Gambar 3.2. Grafik Galat dengan Satu Data Hilang 27

Gambar 3.3. Grafik Hubungan Linier Variabel X dan Variabel Y 34

(61)

DAFTAR LAMPIRAN

Lampiran 1. Proses Pendugaan Galat pada RBSL dengan Satu Data Hilang 41 Lampiran 2. Langkah-langkah Analisis Kovarian pada RBSL dengan Satu

Data Hilang 44