DAFTAR PUSTAKA
Anaroga dan Pakarti. 2006. Pengantar Pasar Modal. PT. Rineka Cipta. Jakarta. Edward dkk. 2007. The Complete Ideal’s guide: Investing. Edisi Ketiga. Prenada.
Jakarta.
Engels. 2004. Portofolio Optimization: Beyond Markowitz. Universiteit Leiden. Leiden, Netherlands.
Fabozzi & Markowitz. 2011. The theory and practice of investment management. Edisi kedua. Willey & Sons, Inc. New Jersey.
Hartono, A. 2013. Penentuan Harga Saham Dengan Menggunakan Persamaan Diferensial Stokastik. [Skripsi]. Institut Teknologi Bandung. Bandung. Hull, John. 2003. Options, Futures & Other Derivative Securities. Fifth Edition.
Prentice-Hall. New Jersey.
Husnan, S. 1994. Dasar – Dasar Teori Portofolio. Edisi Kedua. UPP AMP YKPN. Yogyakarta.
Kartono. 1994. Penuntun Belajar Persamaan Diferensial. Edisi Pertama. Andi Offset. Yogyakarta.
Lin, X Sheldon. 2006. Introductory Stochastic Analysis for Finance and
Insurance. Willey & Sons, Inc. New Jersey.
Merton, Robert C. 1971. Optimum Consumption and Portofolio Rules in
Continuous-Time Model. Journal Of Economic Theory. 3: 373-413
Mulyono, Sri. 2004. Riset Operasi. Fakultas Ekonomi Universitas Indonesia. Jakarta
Oksendal, Bernt. 2003. Stochastic Differential Equations : An Introduction with
Applications. Sixth Edition. Springer-Verlag. Jerman.
Ruey, S. T. 2002. Analysis of Financial Time Series. JohnWiley and Sons. USA. Siagian, P. 1987. Penelitian Operasional Teori dan Praktek. Universitas Indonesia
PRESS. Jakarta.
Simatupang, E. 2011. Penentuan Portofolio Optimal Dengan Adanya Batasan
Value At Risk (VaR). [Tesis]. Universitas Sumatera Utara. Medan.
Soner, H. Mete. 2004. Stochastic Optimal Control in Finance. Koc University. Istanbul, Turkey.
Sudjana. 2005. Metoda Statistika. Edisi Keenam. Tarsito. Bandung.
Tandelilin, E. 2001. Analisis Investasi dan Manajemen Portofolio. Badan Penerbit Fakultas Ekonomi-Yogyakarta. Yogyakarta
Verbeg, Purcell dan Rigdon. 2010. Kalkulus. Edisi Kesembilan. Ahli Bahasa: Lemeda Simarmata. Erlangga. Jakarta
Yuliati dkk. 1996. Manajemen Portofolio dan analisis Investasi. Edisi Pertama. Andi Offset. Yogyakarta.
PORTOFOLIO OPTIMAL
Pada bab ini akan dibahas mengenai portofolio investasi yang optimal. Dalam menetukan portofolio investasi optimal ini akan ditentukan proporsi dari kekayaan investor pada investasi pada aset berisiko dan aset tidak berisiko dengan menggunakan teori-teori yang telah dijelaskan pada bab sebelumnya. Sebelumnya dimodelkan suatu portofolio investasi di mana model portofolio investasi yang dibentuk dengan persamaan diferensial stokastik diselesaikan dengan lemma Ito. Selanjutnya ditentukan proporsi optimal dari portofolio investasi dengan teori kontrol optimal. Dengan proporsi optimal ini diharapkan investor dapat memperoleh hasil yang maksimal saat berinvestasi.
Pada penentuan portofolio optimal ini, investor bersifat menghindari risiko atau risk averse sehingga digunakan fungsi utilitas yang telah dibahas pada bab sebelumnya. Pada tulisan ini solusi dari model portofolio optimal akan digunakan pada simulasi yang akan dibahas pada bab selanjutnya.
3.1 Model Optimisasi Portofolio Investasi
a. Model Investasi pada aset tidak berisiko
Investasi keuangan yang ditanamkan digolongkan ke dalam dua jenis yaitu investasi pada aset berisiko dan investasi pada aset tidak berisiko. Aset tidak berisiko adalah aset yang tingkat return di masa depan dapat diprediksikan saat ini. Aset tidak berisiko mempunyai return rendah tetapi bukan tetapi tidak memiliki risiko (Engels, 2004). Model investasi pada aset tidak beresiko adalah model eksponensial dengan waktu kontinu dimana tidak terdapat faktor acak (kepastian). Contoh investasi pada aset tidak berisiko adalah menabung uang di bank dengan memperoleh return dari bunga bank.
Misalkan sejumlah uang ditabung di bank dan mendapatkan bunga sebesar
ini disebut dengan istilah bunga berbunga (compound interest). Setiap bank memiliki aturan tentang bunga yang berbeda-beda yang dihitung bulanan, mingguan dan bahkan harian. Dalam selang waktu , besar tabungan S(t) menjadi S(t + ) yang dapat dituliskan sebagai berikut: S t( t) S t( )rS t( )t
sehingga besarnya bunga tetap adalah S t( t) S t( )rS t( )t. Jadi ( ) ( )
( ) S t t S t
rS t t
. Diasumsikan bahwa tabungan berbunga secara kontinu sehingga jika diambil limit untuk t 0, maka
0
( ) ( )
lim ( )
t
S t t S t
rS t t
berubah menjadi dS r S dt atau
dS r dt
S . Misalkan saat awal investasi dalan bentuk tabungan S(0)S0, maka solusi persamaan diferensial biasa diperoleh
0 ( ) rt
S t S e . Sehingga model persamaan investasi pada aset tidak beresiko dalam bentuk tabungan dapat ditulis dalam bentuk dSt0 aS dtt0 . . . (3.1) di mana
S
t0: jumlah uang yang ditabung pada saat waktu t.a: bunga bank.
b. Model Investasi pada aset berisiko
Aset beresiko adalah aset-aset yang tingkat return aktualnya di masa depan masih mengandung ketidakpastian. Model untuk investasi berisiko merupakan model investasi tidak berisiko ditambahkan faktor acak dalam hal ini fluktuasi harga saham yang berubah-ubah dan menjadikannya tidak pasti. Menurut Ruey (2002) mengenai hipotesis efisiensi pasar bahwa harga saham merupakan gerak random. Hipotesis efisiensi pasar ini dipengaruhi oleh dua faktor yaitu keadaan saham pada waktu lalu yang berpengaruh pada harga saham saat ini dan respon saham terhadap informasi baru tentang saham.
akan datang. Harga saham dilambangkan dengan S dan waktu dilambangkan oleh
t. Perubahan harga saham dinyatakan dS pada interval waktu dt. Model umum
return dari aset dinyatakan dengan dS
S yang terdiri atas dua bagian. Bagian pertama adalah bagian deterministik yang dilambangkan dengan dt . Ukuran
dari rata-rata pertumbuhan harga saham atau lebih dikenal sebagai drift ditunjukkan sebagai . Sedangkan bagian kedua merupakan model perubahan harga saham secara random yang disebabkan oleh faktor eksternal. Faktor eksternal dilambangkan dengan dWt . Nilai didefinisikan sebagai volatilitas dari saham yang digunakan untuk mengukur standar deviasi dari return dan dapat dinyatakan sebagai fungsi dari S dan t. Nilai dan dapat diestimasi menggunakan harga saham pada hari sebelumnya (H. Mete Soner, 2004).
Model harga saham yang dipengaruhi oleh nilai dan dengan masing-masing bergantung pada S dan t dirumuskan sebagai berikut
t dS
dt dW
S dengan
: return (nilai ekspektasi) tingkat suku bunga saham.
: volatilitas saham yang merupakan standar deviasi dari return.
dWt : gerak Brown atau proses Wiener.
Volatilitas harga saham dapat dikatakan sebagai ketidakpastian dan resiko kepemilikan suatu aset dari investasi berisiko atau sering diartikan sebagai standar deviasi dari perubahan harga aset dalam suatu saham. Jika volatilitasnya nol (0) dan konstan maka model menjadi
dS
dt
S
0
0
t
S
S
t dS
dt S
t S S e
ini serupa dengan model investasi tidak berisiko dalam bentuk tabungan. Sehingga dalam dibentuk portofolio gabungan antara investasi aset tidak berisiko dan berisiko di mana portofolio gabungan tersebut merupakan penjumlahan dari model tabungan dan harga saham.
c. Model portofolio Merton
Diawal tahun 1969, P. A. Samuelson telah terlebih dahulu mengembangkan sebuah model pemilihan portofolio tetapi didalam waktu diskrit dengan distribusi peluang. Kemudian Merton (1970) meneliti masalah penggabungan portofolio optimal dengan adanya konsumsi yang dikeluarkan oleh investor sebagai sebuah model dengan waktu kontinu. Di mana pendapatan/kekayaan investor bersumber dari return setiap aset yang diinvestasikan. Return atau percepatan pergerakan harga (growth rate) dari portofolio inilah merupakan parameter stokastik.
Portofolio optimal yang dimodelkan oleh Merton adalah portofolio dengan banyak aset (multi asset) dimana rata-rata rate of return dihasilkan dari sebuah proses Wiener. Dalam kasus biasa model waktu kontinu yang pasti (certain
continuous-time model), persamaaan kekayaan adalah sebuah persamaan
diferensial. Tetapi adanya faktor ketidakpastian yang direpresentasikan dengan variabel acak menyebabkan persamaan kekayaan tersebut menjadi persamaan diferensial stokastik.
optimal yang dibentuk.
Seorang investor memiliki sejumlah kekayaannya dan ingin membagi kekayaannya untuk dinvestasikan di kedua aset investasi dalam bentuk portofolio tanpa menghitung pemakaian konsumsi oleh investor. Dengan menggabungkan kedua model tersebut diharapkan akan diperoleh model jumlah keuntungan kekayaan investor.
Kembali dituliskan model persamaan investasi pada aset tidak beresiko dalam bentuk tabungan dapat ditulis dalam bentuk
0 0
t t
dS aS dt . . . (3.1)
di mana
S
t0: jumlah uang yang ditabung pada saat waktu t. a: bunga bank.Sementara model persamaan investasi berisiko pada saat waktu t dituliskan dalam bentuk
1 1 1
t t t t
dS bS dt
S dW . . . . (3.2) di mana b : return (nilai ekspektasi) tingkat suku bunga saham. : volatilitas harga saham.
1 t
S
: jumlah uang diperoleh dari berinvestasi di saham.Misalkan u merupakan proporsi kekayaan investor pada investasi berisiko sehingga 1-u merupakan proporsi kekayaan investor pada investasi tidak berisiko. Persamaan kekayaan investor tersebut dapat dituliskan menjadi
d S
t
(1
u dS
)
t0
u dS
1t . . . (3.3)atau
1
t t t t t
dX
u
a
X
d
t
u bX dt
X
dW
. . . (3.5) Persamaan (3.5) dapat disederhanakan menjadi
t t
dt
t tdX
a u b a X
u X dW
. . . (3.6) Persamaan (3.6) adalah model portofolio investasi pada dua aset investasi berbeda yang akan ditentukan besar proporsi kekayaan investor yang diinvestasikan. Keuntungan investasi berisiko berpotensi lebih besar dibanding dengan keuntungan investasi tidak berisiko maka dapat diasumsikan bahwa nilaib > a.
3.2 Proporsi Portofolio Optimal
Setelah kita mengetahui model persamaan dari kekayaan investor, selanjutnya akan ditemukan proporsi dari kekayaan investor yang digunakan untuk investasi berisiko yaitu u dengan tujuan untuk memperoleh kekayaan investor maksimal yang diperoleh dari keuntungan berinvestasi. Teori kontrol optimal pada persamaan diferensial stokastik yang telah dijelaskan pada Bab 2 bertujuan untuk memperoleh besarnya u sesuai yang diinginkan.
Model persamaan diferensial stokastik untuk portofolio optimal kembali dituliskan sebagai berikut
t t
dt
t tdX
a u b a X
u X dW
. . . (3.7) Akan dimaksimalkan ekspektasi fungsi keuntungan berupa suatu fungsi utilitas berbentuk fungsi pangkat (power function) yaitu( ) y
U x x . . . (3.8)
dengan x0 dan 0 y 1. y adalah risk premium. Risk premium merupakan
selisih antara rata-rata return dari saham dan return dari menabung di bank. Persamaan fungsi keuntungannya berbentuk
( , ) ( T)
J t x E U X . . . (3.9)
0
( , ) max (t, , ) ( , )
J t x E F x u dtK T x
. . . (3.10)
Nilai maksimum fungsi keuntungan tersebut dilambangkan dengan V t x( , )
berbentuk
V t x
( , ) max ( , )
J t x
. . . (3.11) di mana V t x( , ) harus memenuhi persamaan Hamilton-Jacobi-Bellman (HJB) yaitu
max LV t x( , ) 0 . . . (3.12) Dengan keadaan akhir yang diinginkan adalah
( , ) ( )
V t x U x . . . (3.13)
dengan L adalah operator linier yang mempunyai bentuk
22 2
,
,
1
2
, ,
L
p
u
q
u
t
t x
x
t x
x
. . . (3.14)Dari persamaan (3.7) diperoleh p t x( , )
a u
b a x
dan q t x( , )u
xsehingga persamaan (3.13) menjadi
22
2
1 2
a u b a
L x
t x u x x
. . . (3.15)atau
2 22 2 2
1
2
L
x
t
a
u b
a
x
u
x
x
. . . (3.16)Kedua ruas dikalikan dengan V t x( , ) sehingga persamaannya menjadi
22 2 2
2
1
( , )
2
V
V
V
LV t x
a
x
u
x
b
t
u
a
x
x
. . . (3.17)Untuk menyederhanakan persamaan (3.17), misalkan
t
V V
t
,Vx V
x
,Vxx V2
x
. . . (3.18)
2 2 2( , )
2
t a u b x xx
LV t x V a x V u x V
. . .(3.19) Persamaan (3.19) diturunkan terhadap u agar diperoleh keadaan maksimal pada
saat
LV t x( , )
0u
. . .
(3.20)
1
2 2 20
2
xxt x x
V
a
V
u b
a
xV
u
V
u
x
. . . (3.21)sehingga persamaan (3.21) menjadi
2 20
x xx
ba xV u
x V . . . (3.22)diperoleh
2x xx
b a
x
V
u
V
. . . (3.23)Subtitusikan persamaan (3.23) ke dalam persamaan (3.19)
2 2 2 2 2 2 2 2 2 2 21
( , )
0
2
1
( , )
0
2
x x xx x t xx xx x x t x xx xxb a
b a
a
V
b a
V
x
LV t x
V
x V
V
V
V
V
V
LV t x
V axV
V
x
x
b a
b a
x
V
2 22
( , )
0
2
x
t x
xx
V
LV t x
V
axV
V
b a
x
. . . (3.24)Bentuk akhir dari persamaan (3.24) tersebut harus memenuhi persamaan (3.13) oleh karena itu dimisalkan suatu fungsi V t x( , ) sebagai berikut
( , )
( )
y2 2 1 2 ( , ) ( ) ( , ) ( )
( , ) ( 1) ( )
y t y x y xx
V V t x f t x
t
V V t x y f t x
x
V V t x y y f t x
x '
. . . (3.26)
diperoleh
2 2 2 2 2 2 2 1 1 2 ( ) ( , ) ( ) ( )( 1) ( ) )
( ) ( ) ( ) 0
( 1)
( , ) ( ) ( ) 0
( 1 0 2 ( ( , 2 ) ) 2 y y y y
y y y
y y
y f t x LV t x f t x ax y f t x
y y f t x
f t x a y f t x y f t x
y y LV t b a x b a LV t x
b a
x f t x a y f t x
y ' ' '
. . . (3.27)
Misalkan
2 2 ( 2 1) y a y y b a
. . . (3.28) Sehingga persamaan (3.27) menjadi
( , )
( )
y( )
y0
LV t x
f t x
'
f t x
. . . (3.29)( )
y( )
y0
f t x
'
f t x
. . . (3.30) Persamaan (3.30) dapat diselesaikan sebagai berikut( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ln ( )
y y
f t x f t x
f t f t
df t f t dt df t dt f t df t dt f t
f t t
' '( ) t
( , )
t yV t x
e
x
. . . (3.32) Subtitusikan persamaan (3.32) ke persamaan (3.23) dengan1
( , ) t y
x
V V t x ye x
x dan 2 2 2 ( , ) ( 1) t y
xx
V V t x y y e x
x diperoleh
2 1 2 ( 1) t y t y ye xu b a
y y e x
x
. . . (3.33)
2 2 ( 1) (1 )b a y
b a y u y u y
. . . (3.34)
diperoleh proporsi u pada investasi berisiko yang memberikan keuntungan sebesar
2 (1 )
u a y
y b
. . . (3.35)
dimana0 u 1 dan ba.
3.3Solusi Model Portofolio Optimal
Persamaan (3.6) adalah model portofolio investasi yang berbentuk persamaan diferensial stokastik sehingga akan diselesaikan dengan menggunakan lemma Ito yang telah dijelaskan pada bab sebelumnya. Kembali dituliskan persamaan (3.6)
t t
dt
t tdX
a u b a X
u X dW
Selanjutnya untuk mempermudah perhitungan, misalkan
a u b a
dan
u
. . . (3.36) sehingga persamaan (3.6) menjadit tdt t t
dX X X dW . . . (3.37)
Misalkan f(t,Xt)lnXt sehingga
2
2 2
1 1
(t, t) 0, (t, t) , (t, t)
t t t t
f X f X f X
t X X X X
Dengan menggunakan Lemma 2.14.1 diperoleh
`
2 2
2 2
1 1 1 1
(ln ) 0 .
2
t t t t t
t t t
d X X X dt X dW
X X X
. . . (3.39)
Dengan mengintegralkan persamaan (3.38) diperoleh
2 2
2 2
0 0 0
1 1 1 1
(ln ) 0 .
2
t t t
t t t t t
t t t
d X X X dt X dW
X X X
. . . (3.40)
atau 2
0 0 0
1
(ln ) .
2
t t t
t t
d X
dt
dW
. . . (3.41)Dari persamaan (3.41) dapat diperoleh hasil sebagai berikut
2 2
0
1 1
ln ln .0 0
2 2
t t
X X t t W
. . . (3.42)
2 0 1 ln 2 t t X
t t W
X
. . . (3.43)
0
2
1 2
t t
t t W
X
e
X
. . . (3.44) Subtitusikan kembali nilai α dan ρ pada persamaan (3.36) sehingga diperoleh solusi persamaan diferensial stokastik model portofolio investasi optimal sebagai berikut:
0 1 2 2 t ua u b a t u W
t
X
X e
. . . . (3.45) dan proporsi untuk investasi dengan utilitas fungsi pangkat yang akan memberikan keuntungan maksimal (u) yaitu
2(1 )
u a y
y b
. . . (3.46)
0
2 2
1
2 1 1
1
t
b a y b a y
t Wt
b
y y
y
a y
a
X
X e
. . . (3.47)di mana
b = rate of return
a = bunga bank
BAB 4 SIMULASI
4.1 Hasil Simulasi
Untuk memperlihatkan bahwa u yang diperoleh memberikan hasil yang maksimal maka dilakukan simulasi dengan menggunakan Matlab dengan membangkitkan data acak (random numbers) yang berdistribusi N(0,1) yang akan dimasukkan ke dalam persamaan kekayaan investor sebagai Wt .
Dengan memasukkan data acak yang dibangkitkan dan nilai dari a = 0.001, b = 0.0015,
0.1,y0.1,X
0
100.000.000 ke dalam persamaan portofolio investasi optimal sebagai berikut
0
1 2
2
t
u t u W
a u b a t
X
X e
dengan
2
(1 )
u a y
y b
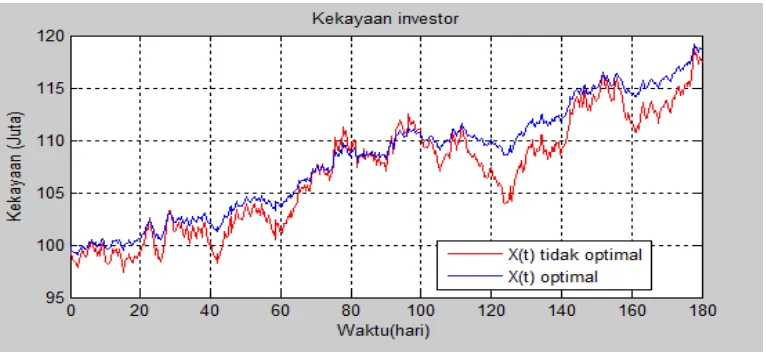
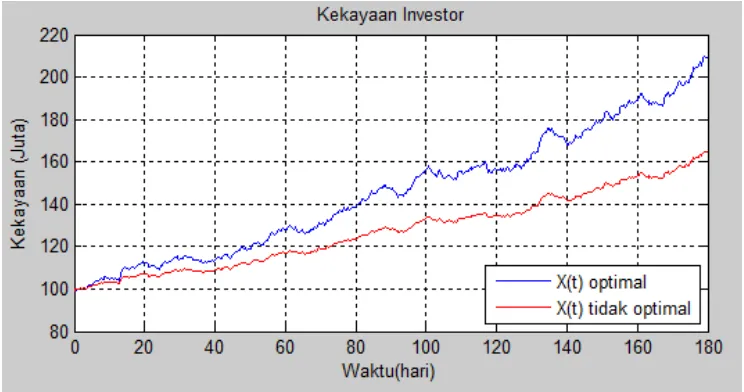
sehingga diperoleh grafik yang menggambarkan kekayaan
X
t dari portofolio investor selama 3 bulan (180 hari) sebagai berikut.Setelah dilakukan simulasi terlihat investasi optimal dengan u yang diperoleh memberikan hasil yang lebih stabil dan optimal dibandingkan dengan investasi tidak berisiko.
Selanjutnya akan dilakukan simulasi dan analisa terhadap nilai a b, ,
dengan aturan ba dan 0 u 1 untuk melihat perubahan apakah yang terjadi jika nilai- nilai tersebut diubah dan akan tetap memberikan hasil maksimal untuk kekayaan investor.
4.2 Suku Bunga Bank (a) Berubah-ubah
Akan dilakukan simulasi tehadap nilai suku bunga (a) yang berubah-ubah dengan aturan ba dan 0 u 1. Simulasi ini dilakukan pada X0100.000.000 dengan perubahan nilai a sebesar 0.001, 0.002 dan 0.003 sedangkan nilai b,, y tetap yaitu sebesar b = 0.004, 0.01, y0.01sehingga diperoleh grafik-grafik yang
menggambarkan kekayaan Xt dari portofolio investor di setiap saat sebagai berikut
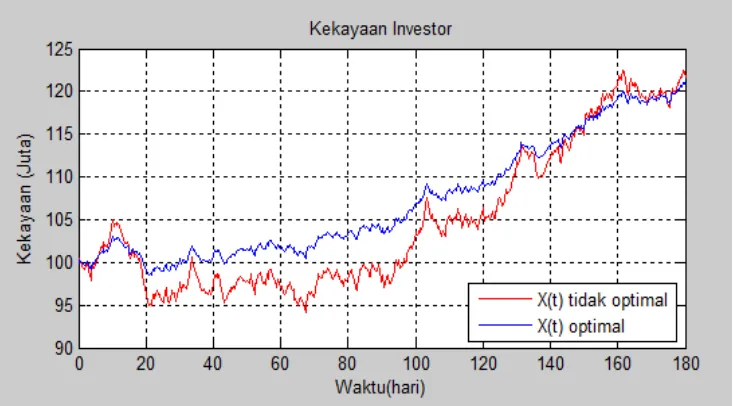
Gambar 4.3 Kekayaan investor dengan nilai a = 0.002 dan u = 0.049.
Gambar 4.4 Kekayaan investor dengan nilai a = 0.003 dan u = 0.049. Dari grafik-grafik tersebut terlihat bahwa:
Proporsi u tetap memberikan hasil maksimal dan membuktikan bahwa portofolio tetap optimal walaupun nilai dari a berubah-ubah.
[image:17.595.126.492.340.547.2]4.3 Rate of Return (RoR) Saham (b) Berubah-ubah
Akan dilakukan simulasi tehadap nilai rate of return (RoR) saham pada investasi aset berisiko (b) yang berubah-ubah dengan aturan ba dan 0 u 1. Simulasi ini dilakukan pada X0100.000.000 dengan perubahan nilai b sebesar 0.002, 0.003 dan 0.004 sedangkan nilai b, , y tetap yaitu sebesar a = 0.001, 0.01,
0.01
y sehingga diperoleh grafik-grafik yang menggambarkan kekayaan Xt
[image:18.595.129.491.272.479.2]dari portofolio investor di setiap saat sebagai berikut
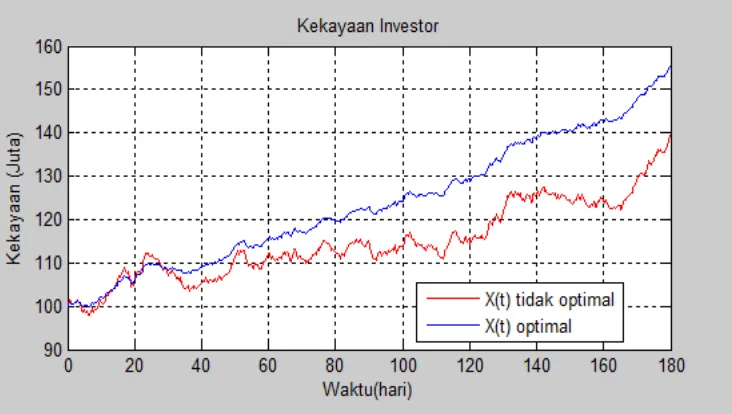
Gambar 4.5 Kekayaan investor dengan nilai b = 0.002 dan u = 0.049.
[image:18.595.123.496.529.726.2]Gambar 4.7 Kekayaan investor dengan nilai b = 0.004 dan u = 0.049. Dari grafik-grafik tersebut terlihat bahwa:
Proporsi u tetap memberikan hasil maksimal dan membuktikan bahwa u membuat portofolio tetap optimal walaupun nilai dari b berubah-ubah. Semakin besar nilai rate of return (RoR) saham pada investasi aset berisiko
(b) maka proporsi u untuk investasi berisiko semakin besar karena selisih dari b dengan a semakin besar.
Dari ketiga grafik diatas seorang investor disarankan lebih baik menginvestasikan kekayaannya pada investasi berisiko yaitu membeli saham dibandingkan dengan investasi tidak berisiko berisiko menabung di bank.
4.4 Volatilitas Harga Saham (
) Berubah-ubahAkan dilakukan simulasi tehadap nilai volatilitas harga saham pada investasi aset berisiko ( ) yang berubah-ubah dengan aturan ba dan 0 u 1. Simulasi ini dilakukan pada X0100.000.000 dengan perubahan nilai
sebesar 0.002, 0.003 dan 0.004 sedangkan nilai a b y, , tetap yaitu sebesar a0.001, b0.001,0.01
y sehingga diperoleh grafik-grafik yang menggambarkan kekayaan Xt
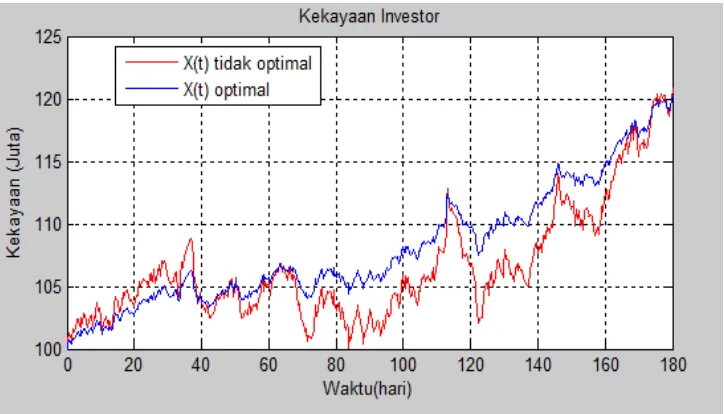
Gambar 4.8 Kekayaan investor dengan nilai = 0.002 dan u = 0.049.
Gambar 4.9 Kekayaan investor dengan nilai = 0.003 dan u = 0.049.
[image:20.595.129.498.545.724.2]Dari grafik-grafik tersebut terlihat bahwa:
Proporsi u tetap memberikan hasil maksimal dan membuktikan bahwa u membuat portofolio tetap optimal walaupun nilai dari berubah-ubah.
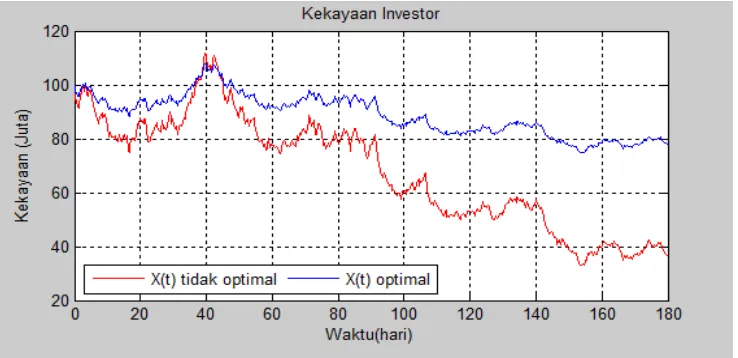
Semakin besar volatilitas harga saham ( ) maka proporsi untuk aset berisiko semakin kecil, ini berarti bahwa jika volatilitas harga saham ( ) besar maka investor sebaiknya menginvestasikan uangnya dengan menabung di bank. Apabila investor tetap menginvestasikan uangnya pada saham maka investor dapat menjadi bangkrut seperti ditunjukkan oleh grafik 4.10.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Berdasarkan pembahasan dan simulasi dapat disimpulkan bahwa:
1. Model
0
1 2
2
t
u t u W
a u b a t
X
X e
merupakan model optimaldiferensial stokastik untuk portofolio di kedua aset yaitu aset berisiko dan tidak berisiko serta adanya proporsi
2
(1 )
u a y
y b
memberikan keuntungan
yang optimal bagi kekayaan investor yang diinvetasikan.
2. Grafik kekayaan investor disertai dengan proporsi optimal selalu berada di atas grafik kekayaan investor tanpa adanya proporsi.Hal ini ditunjukkan pada gambar 4.1.
3. Semakin besar suku bunga maka proporsi untuk aset berisiko semakin kecil, ini berarti jika suku bunga besar maka investor sebaiknya menginvestasikan uangnya dengan menabung di bank.
4. Semakin besar Rate of Return maka proporsi untuk aset berisiko semakin besar, ini berarti jika rata-rata Rate of Return besar sebaiknya investor lebih memilih menginvestasikan uangnya pada saham.
5. Semakin besar volatilitas harga saham ( ) maka proporsi untuk aset berisiko semakin kecil, ini berarti jika volatilitas harga saham () besar sebaiknya investor menginvestasikan uangnya dengan menabung di bank. Apabila investor tetap menginvestasikan uangnya pada saham maka investor menjadi bangkrut seperti ditunjukkan oleh gambar 4.10.
5.2 Saran
LANDASAN TEORI
Pada bab ini akan dibahas mengenai teori-teori dasar yang berhubungan dengan investasi, persamaan diferensial stokastik dan simulasi yang menjadi landasan berpikir untuk mempermudah dalam pembahasan pada bab berikutnya.
2.1 Investasi
Investasi pada dasarnya adalah komitmen atas sejumlah dana atau sumber daya lainnya yang dilakukan pada saat ini, dengan tujuan memperoleh sejumlah keuntungan di masa yang akan datang (E. Tandelilin, 2001). Pihak-pihak yang melakukan investasi disebut investor. Hampir semua investasi mengandung unsur ketidakpastian dan mempunyai risiko mengalami kerugian pada waktu melakukan investasi. Tujuan investor dalam berinvestasi adalah memaksimalkan return dengan meminimalkan risiko investasi yang diterimanya.
2.2 Return dan Risiko
Suatu investasi yang mempunyai risiko yang tinggi seharusnya memberikan
return (tingkat pengembalian) yang diharapkan juga lebih tinggi. Return
merupakan suatu faktor yang membuat investor berinvestasi dan menerima nilai pengembalian/ imbal-hasil atas investasi yang dilakukan.
Menurut Fabozzi (1995), risiko merupakan kerugian yang dihadapi oleh para investor. Risiko dapat juga didefinisikan sebagai kemungkinan perbedaan antara return yang diterima dengan return yang diharapkan. Semakin besar kemungkinan perbedaannya, berarti semakin besar risiko investasi tersebut (E. Tandelilin, 2001).
dapat diukur seperti tingkat kepuasan terhadap suatu benda, jasa maupun pelayanan (Anaroga dan Pakarti, 2006).
2.3 Portofolio
Portofolio umumnya diartikan sebagai kumpulan sejumlah investasi yang dimiliki perseorangan atau perusahaan. Aspek pokok teori portofolio adalah konsep risiko yang terkait pada aset yang berada dalam suatu portofolio (E. Tandelilin, 2001).
Harry M. Markowitz (1952), seorang yang pertama kali mengembangkan teori pemilihan portofolio menyatakan bahwa sebagian besar investor termasuk dalam risk averter (menghindari risiko). Hal ini berarti investor akan selalu berusaha untuk menghindari risiko sehingga investor mencoba mengalokasikan kekayaannya ke berbagai portofolio untuk menghasilkan keuntungan yang optimal selama jangka waktu tertentu (holding period). Setelah itu investor akan menjual investasinya pada akhir masa tertentu.
Salah satu cara menurunkan risiko dalam investasi adalah dengan melakukan diversifikasi. Diversifikasi adalah kegiatan membentuk dan memasukkan semua kelas aset ke dalam portofolio sedemikian sehingga risiko dapat diminimalkan tanpa mengurangi return yang diharapkan. Umumnya aset-aset keuangan dibentuk menjadi satu portofolio yang dinamakan portofolio investasi. Portofolio investasi merupakan kumpulan investasi yang dibentuk untuk memenuhi suatu sasaran umum investasi dimana fokus utama untuk menentukan portofolio optimal (Zamli Zubir, 2011).
pembentukan portofolio optimal, yaitu:
1. Portofolio efisien dan portofolio optimal
Pada dasarnya manajemen portofolio terdiri dari 3 aktifitas utama, yaitu: pembuatan keputusan alokasi asset, penentuan proporsi dana yang akan diinvestasikan pada masing-masing kelas asset, dan pemilihan asset-asset dari setiap kelas yang telah dipilih. Dalam membentuk portofolio, investor selalu ingin memaksimalkan return yang diharapkan dengan tingkat risiko tertentu yang bersedia ditanggungnya atau mencari portofolio yang menawarkan risiko terendah dengan tingkat return tertentu.
Portofolio efisien adalah portofolio yang menyediakan return maksimal bagi investor dengan tingkat resiko tertentu atau portofolio yang menawarkan resiko terendah dengan tingkat return tertentu. Sedangkan portofolio optimal adalah portofolio yang dipilih investor dari sekian banyak pilihan yang ada pada portofolio efisien. Pemilihan portofolio optimal didasarkan pada preferensi investor terhadap return yang diharapkan dari resiko.
2. Aset berisiko dan aset tak berisiko
Investasi berdasarkan sifat aset yang ditanamkan digolongkan ke dalam dua jenis yaitu investasi pada aset berisiko dan investasi pada aset tidak berisiko. Aset berisiko adalah aset-aset yang tingkat return di masa depannya masih mengandung ketidakpastian sedangkan aset tidak berisiko adalah aset yang tingkat return di masa depannya umumnya sudah bisa dipastikan saat ini. Pada tulisan ini, investasi pada aset berisiko adalah menanamkan uang di saham dan investasi pada aset tidak berisiko adalah menabung uang di bank.
3. Fungsi utilitas
Secara umum, utilitas mengukur besarnya kepuasan yang dirasakan dari sebuah objek. Ukuran ini dinyatakan dalam indeks utilitas (utility index). Jadi dapat disimpulkan bahwa penentuan indeks utilitas dipengaruhi oleh karakteristik individu.
Pemilihan portofolio untuk model utilitas yang diharapkan dilakukan dengan menganalisis utilitas dari setiap hasil yang mungkin diperoleh investor. Objek yang dijadikan bahan pembahasan dari fungsi utilitas yang diharapkan adalah kekayaan (wealth) sehingga fungsi utilitas merupakan fungsi kekayaan yang dilambangkan dengan U(w).
Pilihan investasi pada aset berisiko didorong oleh adanya premium yang dinilai sebanding dengan risiko yang dihadapi. Investor hanya mempertimbangkan terhadap pilihan investasi di bebas risiko dan investasi yang memiliki risk premium positif. Risk premium adalah selisih antara rata-rata return investasi berisiko dengan rata-rata-rata-rata return investasi tidak berisiko sehingga fungsi utilitas merupakan fungsi keuntungan pada portofolio. Pada kasus investor yang selalu berusaha menghindari risiko terdapat berbagai macam fungsi utilitas yaitu:
(a) Utilitas Kuadratik (Quadratic Utility) (b) Utilitas Eksponensial (Eksponensial Utility) (c) Utilitas Pangkat (Power Utility)
2.4 Turunan
Definisi 2.4.1. Turunan fungsi f dari x atau f(x) adalah f'( )x f x h( ) f x( ) h
.
Selanjutnya jika U dan V adalah fungsi-fungsi dari x yang dapat didiferensialkan maka d (UV) UdV VdU
Misalkan y = f(u) dan u = g(x). Jika g terdiferensiasikan di u = g(x), maka fungsi komposit f g,yang didefinisikan oleh
(
f
g
)( )
x
f g x
( ( ))
, akan didiferensialkan di x sehingga
( ) ( ) ( ( )) ( ( )) ( ) x
'
f g x D f g x
' '
f g x g x
. . . (2.2)
Definisi 2.4.3. Turunan Parsial
( , )
Z f x y suatu fungsi dengan variabel x dan y dikatakan turunan pasial
1. Jika x berubah tetapi y tetap maka turunan parsial terhadap x adalah
0
( , ) ( , ) ( , ) lim
x
Z f x x y f x y f x y
x x x
. . . (2.3)
2. Jika y berubah tetapi x tetap maka turunan parsial terhadap y adalah
. . . (2.4)
AndaikanZ f x y( , ) fungsi kontinu pada variabel x dan y dengan turunan parsial
terhadap x adalah Z x
dan turunan parsial ke y adalah
Z y
(Kartono, 1994). Jika x,
y merupakan fungsi yang dapat didiferensialkan dengan x g t( ),yh t( )
pada suatu variabel t maka Z merupakan fungsi dari t dan Z t
disebut turunan total
dari Z dengan memperhatikan
Z Z x Z y
t x t y t
. . . . (2.5)
2.5 Integral
Integral merupakan kebalikan dari diferensial atau anti diferensial. Integral ada dua jenis yaitu
1. Integral tak tentu yaitu integral yang tidak memiliki batas-batas integral.
0
( , ) ( , ) ( , )
lim y
Z f x y y f x y f x y
y y y
dengan A(f) atau
F x dx( ) bilaF x
'
( )
f x
( )
. Lebih lengkap dituliskan sebagai berikut: Jika d F x c
( )
dF x( )F x'( ) maka
F x dx'( )
dF x( )F x c( ) , dimana
c
.
2. Integral tentu yang diambil pada suatu daerah atau interval tertentu.
Definisi 2.5.2. Suatu fungsi f(x) yang kontinu pada interval a x b maka
1
( ) lim ( )
n
k k n
k
b
a
f x dx f x x
. . . (2.6a)( ) ( ) | ( ) ( )
b
b a a
dF x dxF x F b F a
. . . (2.6b)Definisi 2.5.3. Jika F(x) = U(x).V(x) fungsi yang kontinu pada interval [a, b] maka b ( ) ( ) b ( ) b ( ) ( )
a a a
U x dV x dF x dx V x dU x
. . . (2.7a)atau b ( ) ( ) ( ) ( ) b ( ) ( )
a a
U x dV x F b F a V x dU x
. . . (2.7b)Selain dari kedua jenis integral tersebut terdapat juga integral parsial. Di dalam diferensial diketahui bahwa jika U dan V adalah fungsi-fungsi yang dapat didiferensialkan maka d UV( )UdvVdu apabila kedua ruas diintegralkan
diperoleh
UV
UdV
VdU . . . (2.8)UdV UV VdU
. . . (2.9)Integral parsial yang sering juga dikenal dengan integral by part memiliki sifat umum sebagai berikut
a. Peranan dalam memilih dVdiutamakan yang lebih mudah diintegralkan. b.
VdUsebaiknya tidak lebih sulit dari pada
UdV.2.6 Pendiferensialan Integral
Teorema 2.6.1 (Verbeg, Purcell dan Rigdon, 2010)
Jika f kontinu pada selang tertutup [a, b] dan jika x adalah variabel yang
merupakan sebuah titik dalam [a, b] maka x ( ) ( ) x
D f t dt f x
Bukti. Misalkan ( ) ( ) a
G x
f t dt akan dibuktikan G x'( ) f x( ).( ) ( ) ( ) ( ) ( )
x h x x h
a a a
G x h G x f t dt f t dt f t dt
dengan h > 0 dan m adalahnilai minimum serta M adalah nilai maksimum f pada selang [x, x+h] maka
( ) m f t M
( )
x h x h x h
a a a
m dt f t dt M dt
( ) x h am h f t dt M h
( ) ( ) m hG x h G x M h
( ) ( ) G x h G x
m M h 0 ( ) ( )
lim ( )
h
G x h G x
f x h ( ) ( ) '
G x f x ■
Bentuk pendiferensialan integral dapat dirumuskan sebagai berikut
0 0 0 ( , ) ( , ) ( , ) t t t t
d f s t
f s t ds f t t ds
dt t
. . . (2.10)
2.7 Persamaan Diferensial Linier
2.7.1 Permulaan Persamaan Diferensial
Persamaan diferensial adalah suatu persamaan yang didalamnya terdapat turunan-turunan yang merupakan hubungan antara variabel bebas dan variabel tak bebasnya serta variabel turunan terhadap variabel tak bebas dalam berbagai orde. Secara simbol ditulis:
F x y y
, , ,...,y
0n
'' '
. . . (2.11)
di mana
Suatu derivatif atau turunan tertinggi yang terdapat dalam suatu persamaan diferensial merupakan orde dari suatu persamaan diferensial sedangkan degree (derajat) suatu persamaan diferensial adalah pangkat tertinggi dari turunan tertinggi yang terdapat dalam suatu persamaan diferensial.
Penyelesaian umum dari suatu persamaan diferensial adalah suatu penyelesaian yang didalamnya terdapat konstanta sebarang, ditulis dengan
F x y c( , , )0 ; c adalah konstanta
Penyelesaian khusus (particulir solution) adalah suatu penyelesaian yang didalamnya sudah ditentukan konstanta sebarang menjadi konstanta absolut ditulis dengan F x y c( , , o)0. Jika terdapat variabel bebas yang tunggal, turunan merupakan turunan biasa maka persamaannya disebut persamaan diferensial biasa sedangkan jika terdapat dua atau lebih variabel bebas dan turunannya adalah turunan parsial maka persamannya disebut persamaan diferensial parsial (Kartono, 1994).
2.7.2 Persamaan Diferensial Linier Orde Satu
Persamaan diferensial linier orde satu ditulis dalam bentuk F x y y
, , '
0 atau( , )
y'F x y . Penyelesaian umumnya adalah y ( , )x c di mana penyelesaiannya
mengandung suatu konstanta c. Bila diberikan syarat awal xx0 dan yy0
maka konstanta c dapat dicari misalnya cc0. Penyelesaian atau jawaban untuk 0
cc dinamakan jawaban khusus dalam bentuk y ( ,x c0) (Kartono, 1994).
2.7.3 Persamaan Diferensial Linier Orde – n
Bentuk umum persamaan diferensial linier orde n adalah
1 1
0 1 2
...
n n n
n
0 0
P dan Q0
1, 2,..., n
P P P adalah konstanta.
Q adalah fungsi.
Untuk menyederhanakan dan memudahkan perhitungan persamaan diferensial tersebut dapat digunakan operator D dimana D d
dx
selanjutnya dapat ditulis
menjadi
(
P D
0 n
P D
1 n1
P D
2 n1
...
P y Q
n)
.Suatu persamaan differensial linier orde n dengan keofisien konstan disebut homogen apabila Q = 0 sehingga bentuknya menjadi
(
P D
0 n
P D
1 n1
P D
2 n1
...
P y
n)
0
. . . (2.13) dapat juga ditulis1 1
0 1 2
...
0
n n n
n
P D
P D
P D
P
. . . (2.14)dapat juga difaktorkan menjadi (D m 1)(D m 2)...(D m n1)(D m n)0dimana
1, 2... n1, n
m m m m merupakan akar karakteristik dari persamaan (2.13) (Kartono, 1994).
2.8 Probabilitas
Probabilitas atau peluang secara klasik dapat diartikan sebagai suatu ukuran tentang tingkat kemungkinan suatu peristiwa (event) akan terjadi di masa mendatang. Oleh karena itu diperlukan suatu pengamatan. Proses pengamatan tersebut dinamakan suatu percobaan. Hasil dari suatu percobaan dinamakan hasil (outcames) atau titik sampel. Himpunan yang berisi semua hasil yang mungkin dari suatu percobaan disebut dengan ruang sampel. Ruang sampel sering dinotasikan dengan S atau Ω. Sedangkan kejadian atau event adalah himpunan
Definisi 2.9.1 Misalkan Ω adalah ruang sampel dan A adalah suatu kejadian pada
ruang sampel Ω.
(1) Jika A = ∅ maka P(A) =0.
(2) Nilai probabilitas kejadian A, yaitu P(A) berkisar dari 0 sampai 1
0P A( ) 1 .
(3) Jumlah nilai probabilitas semua hasil dari suatu percobaan atau P(Ω)=1.2.10 Variabel Acak dan Distribusi Probabilitas 2.10.1 Variabel Acak
Untuk menggambarkan hasil-hasil percobaan sebagai nilai-nilai numerik secara lebih sederhana, maka digunakan variabel acak. Variabel acak biasanya menghubungkan nilai-nilai numerik dengan setiap kemungkinan hasil percobaan. Nilai numerik tersebut bersifat diskrit (hasil hitungan) dan bersifat kontinu (hasil pengukuran, oleh karenanya variabel acak dapat dikelompokkan menjadi:
1. Variabel Acak Diskrit
Variabel acak diskrit hanya dapat mengambil nilai-nilai tertentu yang terpisah, yang umumnya dihasilkan dari penghitungan suatu objek. Syarat yang harus dipenuhi untuk fungsi probabilitas diskrit:
(i) P x( ) 0 atau 0 P x( ) 1
(ii)
P x( i)1n i
Definisi 2.10.1 Nilai harapan (expected value) variabel acak diskrit adalah rata-rata tertimbang seluruh kemungkinan hasil di mana penimbangnya adalah nilai probabilitas yang dihubungkan dengan setiap hasil (outcome). Ekspektasi atau nilai harapan dapat dirumuskan dengan
( ) x i. ( )i
E X
x P xn
i =1
x = nilai ke-i dari variabel acak X i ( )i
P x = probabilitas terjadinya xi
Varians dari Variabel Acak diskrit X yang dinotasikan dengan x2 atau
Var[x] ditentukan dengan rumus:
2 2 2
[ ]
[ - ( )]
( ) -[ ( )]
Var x
E x E x
E x
E x
. . . (2.16)
2. Variabel Acak Kontinu
Jika mengukur sesuatu seperti lebar ruangan, tinggi badan, atau berat badan seseorang, maka variabel yang dihasilkan adalah variabel acak kontinu. Hasil pengukuran tersebut mungkin akan berbeda-beda tergantung pada siapa yang melakukan pengukuran dan tingkat ketelitian yang digunakan.
Oleh karena hasil pengukuran tidak bisa seakurat hasil perhitungan, maka nilai hasil pengukuran bisa bervariasi dalam suatu selang nilai tertentu. Misalnya jarak antara Medan dan Pematang Siantar dapat 127 km, 127,6 km, 128 km dan seterusnya tergantung pada ketelitian alat ukur atau si pengukur.
Berikut diberikan beberapa contoh variabel kontinu dari suatu percobaan.
Contoh 2.10.2. Variabel Kontinu
Percobaan Variabel Acak Kemungkinan Nilai-nilai Variabel Acak Membangun proyek
perkantoran baru setelah 12 bulan
Persentase proyek
yang diselesaikan 0 x 100 Isi botol minuman jadi
(maximum = 600 ml) Jumlah milliliter 0 x 600 Penimbangan 20 paket
kemasan (maximum = 2 kg)
Berat sebuah paket
Distribusi probabilitas variabel acak kontinu dinyatakan dengan fungsi f(x) dan sering disebut fungsi kepadatan (density function) atau fungsi kepadatan probabilitas. Nilai f(x) bisa lebih besar dari 1. Syarat yang harus dipenuhi oleh fungsi kepadatan probabilitas :
(i) f(x) 0 (ii) f x dx( ) 1
di mana f(x) dx = P[x X (x + dx)], yaitu probabilitas bahwa nilai X terletak pada interval x dan x + dx.
Definisi 2.10.3. Beberapa definisi mengenai variabel acak kontinu 1. Fungsi Probabilitas Kumulatif Variabel Acak Kontinu :
( ) ( ) ( )
F x P X x f x dx
. . . (2.17)Nilai-nilai x dalam rumus ini harus kontinu atau dalam suatu interval.
2. Ekspektasi atau mean untuk variabel acak kontinu X ditentukan dengan rumus : E x( ) x f x dx. ( )
. . . (2.18)Dan ekspektasi untuk x adalah sebuah fungsi (x = g(x)) ditentukan dengan rumus : E(g( ))x g x f( ). x( )x dx
. . .(2.19)
3. Varians dari Variabel Acak Kontinu X yang dinotasikan dengan 2x atau
Var[x] ditentukan dengan rumus:
2 2 2
[ ] [ - ( )] ( ) -[ ( )]
Var x E x E x E x E x . . . (2.20)
Distribusi normal merupakan distribusi kontinu yang paling penting dalam bidang statistik karena dapat mewakili kumpulan data observasi yang terjadi dalam alam semesta, industri, maupun penelitian. Distribusi normal sering dikenal sebagai distribusi Gauss.
Variabel acak x yang mempresentasikan distribusi normal disebut variabel acak normal, yang distribusinya bergantung pada dua parameter, yaitu mean () dan deviasi standar (). Fungsinya dinotasikan sebagai N(x ; ; ).
Definisi 2.11.1 Fungsi kepadatan (density function) dari variabel acak x dengan
mean dan varians 2 adalah :
2 1 2
1
( ; ; ) ( ) . ,
2
x
N x f x e x
. . . (2.21)
di mana
= 3,14159...
e = 2,71828...
= simpangan baku = 2
= rata-rata x
x = variabel kontinu
2.12 Model Stokastik 2.12.1 Proses Stokastik
Definisi 2.12.1 Proses Stokastik adalah suatu kumpulan variabel acak Xt, tT, dengan T adalah himpunan parameter waktu. Jadi dapat dikatakan bahwa proses stokastik merupakan keluarga fungsi waktu. Jika T terhitung maka dikatakan proses stokastik waktu diskrit dan jika T kontinu maka dikatakan proses stokastik waktu kontinu. Proses stokastik waktu kontinu {Xt; t T} dikatakan mempunyai
2 3 1
t t t tn
jika X(t s )Xt mempunyai distribusi yang sama untuk semua t.
Contoh 2.12.2 Xt p qt dengan p dan q adalah masing-masing variabel acak maka Xt yang merupakan jumlahan p dan q adalah kumpulan variabel acak sehingga Xt merupakan proses stokastik.
2.12.2 Data Deret Waktu
Data deret waktu merupakan sekumpulan observasi yang terurut dalam waktu dengan jarak interval sama (Box dan Jenkins, 1970). Data deret waktu disebut proses stokastik dikarenakan data saling berkaitan dalam rentang waktu yang sama (Wei, 2006). Saat ini data deret waktu keuangan (financial prices) dapat diperoleh dengan mudah, misalnya harga saham dan nilai kurs sehingga dapat dibangun model peluang terbaik yang dapat digunakan untuk memprediksi harga/nilai di masa yang akan datang. Data dari harga aset menghasilkan deret waktu. Deret waktu adalah proses stokastik yang menggunakan waktu integer didalam prosesnya.
Pemodelan portofolio dapat dimulai dengan mendefinisikan imbal hasil (return) dan volatilitas (volatility) sebagai statistik. Distribusi return dan volatilitas yang tepat dapat memberi gambaran perilaku data deret waktu. Pemodelan return pada dasarnya adalah pemodelan volatilitas. Proses atau model stokastik untuk harga tidak dapat dibangun dengan mudah.
a. Model Stokastik Return
1 t Rt V
. . . (2.22)
Di mana Vt dan Vt1 menotasikan nilai aset pada waktu ke-t dan t-1.
Proses stokastik adalah barisan return acak dengan distribusi probabilitas yang ditentukan oleh vektor parameter . Model stokastik untuk
return dapat dituliskan sebagai berikut:
t
t t
R
. . . (2.22b)
di mana t
: Volatilitas harga t
: Proses wiener berdistribusi normal
Sedangkan Rate of Return adalah tingkat pengembalian atau tingkat bunga yang diterima investor atas investasi tanpa amortisasi untuk menghitung tingkat pengembalian atas investasi.
Tinggi rendahnya tingkat keuntungan yang diterima portofolio dipengaruhi oleh tingkat keuntungan investasi tidak berisiko (risk free rate) dan risk premiun dari investasi berisiko dengan tujuan utuk mengurangi risiko pada aset portofolio yang dapat ditulis dalam persamaan sebagai berikut:
RpRf Risk Premium . . . (2.23) di mana
Rp: Rate of Return. Rf : Risk Free Rate.
(John Hull, 2003) b. Model Stokastik Volatilitas
volatilitas yang tinggi menunjukkan bahwa nilai aset berubah dengan sangat cepat. Salah satu metode untuk mengestimasi volatilitas adalah analisis yang berdasarkan nilai-nilai aset masa lalu kemudian diperoleh sejumlah return (tingkat keuntungan yang diperoleh dari akibat melakukan investasi) yang dimajemukkan secara kontinu dan diperoleh estimasi variansnya sebagai berikut:
1
1
ln 1
n t
Rt r n
. . . (2.24)Di mana Rtadalah return majemuk secara kontinu dan r menotasikan rata-rata
dari log return (John Hull, 2003).
2.12.3 Sifat Markov
Definisi 2.12.3 Sifat Markov adalah sifat nilai harapan suatu variabel random
ke-I dari suatu proses stokastik Xi dengan syarat semua nilai variabel random yang sebelumnya diketahui hanya bergantung pada nilai variabel random ke- i-1 atau
Xi 1 tetapi nilai harapan tersebut tidak harus sama dengan nilai variabel random ke- i-1. Sifat Markov dinotasikan dengan
E( Xi | X1, X 2,..., Xi 1) E( Xi | Xi 1) . . . . (2.25)
2.13 Proses Wiener (Gerak brown Baku)
2.13.1 Sejarah Gerak Brown
partikel tersebut, tetapi tidak mengerti penyebab partikel-partikel berkelakuan seperti itu. Oleh karenanya, gerakan partikel yang acak ini dinamai sebagai gerak Brown untuk menghargai kontribusi Brown.
Penjelasan gerak acak atau gerak Brown ini secara matematis pertama kali berhasil dirumuskan oleh Thorvald Thiele pada tahun 1880. Kemudian pada tahun 1900 matematikawan Prancis bernama Louis Bachelier menulis tesis doktornya
yang berjudul “Teori Spekulasi”, yang merupakan analisis matematis pertama terhadap pasar saham. Di sisi lain, Bachelier juga menyinggung persoalan gerak Brown yang dikaitkan dengan pemodelan pasar, yang sama-sama tampak acak. Sedangkan masalah pada saat itu adalah, para ilmuwan masih tidak bisa menemukan keterkaitan antara rumusan matematis dari konsep keteracakan dengan sumber penyebab gerak Brown, karena sumber gerak Brown itu sendiri masih tidak diketahui.
Permasalahan ini akhirnya dipecahkan oleh Albert Einstein pada 1905 di dalam 3 makalahnya. Hasil penelitian Einstein ini bersama dengan penelitian lainnya pada tahun 1906 oleh ilmuwan Polandia bernama Marian Smoluchowski menjadi solusi penjelasan terhadap gerak Brown yang dapat diterima hingga saat ini. Penelitian terhadap gerak Brown ini menjadi salah satu tonggak dimulainya pengembangan konsep matematis untuk keteracakan serta teori probabilitas.
2.13.2. Symmetric Random Walk
Sebuah koin dilempar atau di-toss berkali-kali dan hasilnya merupakan variabel acak X dengan j j1, 2,... untuk
j j
1 bila ω =H ( )
-1 bila ω =T
j j
X
. Hasil pelemparan antara
koin pertama dengan pelemparan koin selanjutnya adalah saling bebas sehingga dapat diasumsikan bahwa X X1, 2,...saling bebas dan ( ) ( ) 1
2
P M P B . Oleh definisi, variabel acak Xj memiliki sifat-sifat sebagai berikut:
1. [ ] 1. ( ) ( 1). (T) 1.1 ( 1).1 0
2 2
2. var[ ] 1 ( ) ( 1) (T) 1. 1. 1
2 2
Xj P H P
3. Fungsi Pembangkit Momen dari Xj adalah
( ) ( ) ( ) 1 1 . . . 2 2 j
Xj u
u u
u u
uX
E e
e P H e P T
e e
Definisikan Mk: X0 X1 X2 ... Xk atau
0 k k j j M X
dengan X00sehingga proses
0 k k
M
akan disebut sebagai symmetric random walk. Symmetric random walk
Mk k 0
memiliki beberapa sifat sebagai berikut:
1.
1 1
0
k k
k j j
j j
E M E X E X
. . . (2.26)
2.
1 0 k j j k
Var M Var X
. . . (2.27)
3. Inkremen dari M adalah saling bebas. k
2.13.3 Scaled Symmetric Random Walk
Misalkan n adalah bilangan bulat positif dengan t k n
atau ktn. Definisi scaled
symmetric random walk W( )n ( )t adalah 1 ( )
1
W t M
n M n (n) tn k
. . . (2.28) Teorema 2.13.4 Untuk t0 dan n, distribusi dari W( )n ( )t akan konvergen ke distribusi normal dengan mean 0 dan varians t.
Bukti. Fungsi pembangkit momen untuk ( ) 1
( ) n
tn
W t M
n
1 1 1 . ( ) ( ) . . . 1 1 ( ) 2 2 1 1
log ( ) log
2 2 tn tn j j n n u M n u X n
u u u
X X X
n n n
tn u u n n u u n n k uW t
k u E e
E e
E e
E e e e
k u e e
u tn e e
Andaikan x 1 n
maka diperoleh
2
1 1
log
2 2
lim log ( ) lim
ux ux k k x e e u t x
1 2 2 lim1 1 2
2 2
ux ux
x ux ux
u u e e t x e e
1 2 2
lim lim
1 1 2
2 2
ux ux
x ux ux x
u u e e t x e e 2 2 lim 2 ux ux x u u e e t x 2 2 2 2
lim log ( ) lim
2 ux ux k k x u u e e u t 2 log ( )
2 k
t
u u
Jadi akan diperoleh
2
1 2
( ) u t
k u e
dengan mean 0 dan varians t. ■ Untuk n, proses W