Pencarian Hasil Integral Multidimensi Menggunakan Metode Monte Carlo

SKRIPSI

Diajukan Untuk Menempuh Ujian Akhir Sarjana Program Strata Satu Jurusan Teknik Informatika

Fakultas Teknik Dan Ilmu Komputer Universitas Komputer Indonesia

ERRY HANDANI

10104202

JURUSAN TEKNIK INFORMATIKA

FAKULTAS TEKNIK DAN ILMU KOMPUTER

UNIVERSITAS KOMPUTER INDONESIA

BANDUNG

iii

Syukur Alhamdulillah penulis panjatkan kehadirat Allah SWT, yang tanpa

henti-hentinya senantiasa memberikan rahmat dan karuniaNya kepada kita semua.

Tidak lupa Shalawat serta salam penulis sampaikan kepada

Nabi Muhammad SAW

yang telah membawa cahaya penerang bagi seluruh alam.

Tugas akhir ini disusun untuk memenuhi salah satu syarat dalam menempuh

sidang program studi Strata Satu (S-1) pada jurusan Teknik Informatika, Universitas

Komputer Indonesia (UNIKOM) Bandung. Dalam tugas akhir ini penulis mengambil

judul ”

PENCARIAN HASIL INTEGRAL MULTIDIMENSI DENGAN

MENGGUNAKAN METODE MONTE CARLO

”.

Penulis menyadari bahwa dalam pembuatan laporan tugas akhir ini masih

jauh dari kesempurnaan, karena keterbatasan ilmu yang dikuasai penulis. Namun

demikian penulis berharap semoga laporan tugas akhir ini dapat bermanfaat

khususnya bagi penulis dan umumnya bagi pembaca semua.

Dalam penyelesaian tugas akhir ini banyak sekali kesulitan yang dihadapi

oleh penulis, namun berkat dorongan, bimbingan dan bantuan dari berbagai pihak

maka tugas akhir ini akhirnya dapat diselesaikan. Oleh karena itu dalam kesempatan

ini penulis mengucapkan banyak-banyak terima kasih kepada :

1. Ayahanda, ibunda yang tercinta yang senantiasa selalu mendoakan penulis dan

memberikan dorongan baik moril maupun materil.

2. Kakak-kakakku tersayang, yang telah memberikan dorongan baik moril maupun

iv

4. Bapak Irawan Afrianto S.T selaku dosen wali, yang telah memberikan bantuan

dan dorongan dalam penyelesaian skripsi ini.

5. Bapak Ir. Eddy Suryanto Soegoto, M.Sc selaku Rektor Universitas Komputer

Indonesia.

6. Bapak Prof.Dr.Ir.H.Ukun Sastraprawira, M.Sc, Selaku Dekan Fakultas Teknik

7. Ibu Mira Kania Sabariah S.T, M.T selaku Ketua Jurusan Teknik Informatika

Universitas Komputer Indonesia.

8. Seluruh staf dosen Jurusan Teknik Informatika, terima kasih atas ilmu yang telah

diberikan.

9. Erlangga, Andi, Agni, Ibrahim, Deden dan M. Sholeh Effendy terima kasih atas

semua bantuan dan dorongannya.

10. Teman- teman IF-5 angkatan 2004, terima kasih atas dorongan semangatnya.

11. Kepada semua pihak yang tidak dapat disebutkan satu persatu, yang telah

memberikan andil dalam menyelesaikan skripsi ini.

Semoga apa yang telah kita lakukan bukan merupakan satu kesia-siaan,

namun dapat memberikan manfaat dan meninggalkan sesuatu yang senantiasa selalu

dikenang sebagai kebajikan.

Bandung, Januari 2009

v LEMBAR PENGESAHAN

LEMBAR PERNYATAAN

ABSTRAK...i

ABSTRACT...ii

KATA PENGANTAR...iii

DAFTAR ISI...v

DAFTAR GAMBAR ...vi

DAFTAR TABEL...viii

DAFTAR SIMBOL ...ix

DAFTAR LAMPIRAN ...x

BAB I PENDAHULUAN...1

1.1 Latar Belakang...1

1.2 Rumusan Masalah ...2

1.3 Maksud dan Tujuan...3

1.4 Batasan Masalah ...3

1.5 Metodologi Penelitian ...4

1.6 Sistematika Penulisan...6

BAB II LANDASAN TEORI...8

2.1 Sejarah Kalkulus...8

2.2 Penerapan Kalkulus ...11

2.3 Diferensial ...12

2.4 Integral (Anti Turunan)...20

2.5 Integrasi Monte Carlo ...28

vi

3.3 Perancangan Menu Aplikasi ...62

3.4 Perancangan Antarmuka ...63

3.5 Jaringan Semantik ...66

3.6 Perancangan Prosedural...67

BAB IV IMPLEMENTASI DAN PENGUJIAN...74

4.1 Implementasi Sistem...74

4.2 Implementasi Antarmuka...75

4.3 Tampilan Implementasi Antar Muka...76

4.4 Pengujian Sistem ...80

4.5 Kesimpulan Hasil Pengujian Alpha...84

4.6 Pengujian Betha...84

4.7 Analisis Metode Perhitungan ...87

4.8 Kesimpulan Hasil Perbandingan Perhitungan...90

BAB V KESIMPULAN DAN SARAN...91

5.1 Kesimpulan ...91

5.2 Saran ...91

i

PENCARIAN HASIL INTEGRAL MULTIDIMENSI

MENGGUNAKAN

METODE MONTE CARLO

Oleh

ERRY HANDANI

10104202

Perancangan dan pembangunan aplikasi pencari hasil integral multidimensi ini dilakukan dengan metode pengembangan perangkat lunak Waterfall. Tugas akhir ini akan menjelaskan proses-proses yang dilakukan dalam pembangunan sistem ini. Data didapat dengan cara melakukan studi literatur dan studi lapangan dengan menganalisis kebutuhan dalam perancangan dan pembangunan sistem ini. Data yang didapat kemudian didisain mengunakan bahasa pemrograman Microsoft Visual Basic 6. Pengujian dilakukan dengan 2 langkah pengujian yaitu : pengujian alpha dan pengujian betha untuk melihat kelayakan dari aplikasi pencari hasil integral multidimensi ini.

Hasil akhir yang didapat dari perancangan dan pembangunan aplikasi pencarian hasil integral multi dimensi ini, didapatkan bahwa : Aplikasi ini cukup membantu dalam pencarian hasil integral terutama integral multidimensi.

ii

RESULT DETERMINATION OF

MULTIDIMENSIONAL INTEGRAL

USING MONTE CARLO METHOD

by

ERRY HANDANI

10104202

The designing and building of result determination of multidimensional integral application has been done with Waterfall method. This Final project will describe the processes that had been done in the system building. Data source were found by doing literature and field study like analyzing and designing the system. The data source being implemented in the system designing with Microsoft Visual Basic 6.0. The system testing was done in two steps, Alpha and betha testing.

The final result of the designing and building of this multidimensional integral application, can be concluded, this application is helping enough to find the result of multidimensional integral.

PENCARIAN HASIL INTEGRAL MULTIDIMENSI

MENGGUNAKAN

METODE MONTE CARLO

ERRY HANDANI

10104202

Pembimbing

Khusnul Novianingsih M.Si. NIP. 4127 70 06 013

Menyetujui,

Ketua Jurusan Teknik Informatika

PENCARIAN HASIL INTEGRAL MULTIDIMENSI

MENGGUNAKAN

METODE MONTE CARLO

ERRY HANDANI

10104202

Penguji I

Mira Kania Sabariah S.T., M.T. NIP. 4127 70 06 008

Penguji II

Khusnul Novianingsih, M.Si. NIP. 4127 70 06 013

Penguji III

DAFTAR PUSTAKA

1. Firrar Utdirartatmo, (2005), Teknik Kompilasi, Graha Ilmu, Yogyakarta.

2. http://www.wikipedia.com/Monte_carlo_integration (2 November 2008,

pukul 16.09 wib)

3. http://www.wikiversity.com/monte_carlo_method (2 November 2008, pukul

16.15 wib)

4. Kalos, Malvin H., Whitlock, Paula A., (1986),

Monte Carlo Methods

,

Wiley-VCH, New York.

5. Press, William H., Teukolsky, Saul A., Vetterling, William T., Flannery,

Brian P., (2007),

Numerical Recipes The Art of Scientific Computing Third

Edition

, Cambridge University Press, New York.

6. Pressman, Roger S., (2002),

Rekayasa Perangkat Lunak Pendekatan Praktisi,

1 1.1 Latar Belakang

Ilmu kalkulus memiliki aturan – aturan penyelesaian fungsi integral untuk memperoleh solusi analitik (dan eksak) dari fungsi integral tentu. Namun, dalam praktek rekayasa, terkadang fungsi yang diberikan terlalu rumit untuk diintegralkan dengan menggunakan ilmu kalkulus. Apalagi jika integral tersebut bersifat multidimensi yang tentunya akan membuat fungsi tersebut semaikn rumit untuk diselesaikan. Salah satu cara yang dapat digunakan adalah dengan menggunakan metodeMonte Carlo. Alasan pemilihan metodeMonte Carlo untuk menyelesaikan fungsi integral multidimensi tentu adalah karena kemampuannya untuk mencari nilai integral yang tak tentu sekalipun. Selain itu metode ini memiliki keakuratan dalam menghitung dan menghasilkan nilaierror yang sekecil mungkin.

kemungkinan distribusi fungsi atau berkonsentrasi pada daerah yang memberikan kontribusi terbesar pada integral.

Metode Monte Carlo merupakan metode yang dikenal mampu mencari nilai hampiran dari perhitungan yang sangat rumit seperti perhitungan persebaran molekul gas di bidang kimia dan prediksi keuangan suatu negara di bidang ekonomi. Selain dua hal di atas, metode ini juga dapat diterapkan untuk menghitung nilai hampiran dari integral multidimensi baik tentu maupun tak tentu. Hal ini terjadi karena kemampuanMonte Carlo yang mampu men-generate angka acak dalam perhitungannya.

Berdasarkan hasil pengamatan, perhitungan integral masih menjadi hal sulit dilakukan bagi sebagian orang. Oleh karena itu perlu dikembangkan suatu perangkat lunak yang mampu membantu perhitungan integral terutama dengan menggunakan metodeMonte Carlo.

1.2 Rumusan Masalah

1.3 Maksud dan Tujuan

1.3.1 Maksud

Maksud dari tugas akhir ini adalah menghasilkan suatu perangkat lunak yang dapat menyelesaikan fungsi integral multidimensi tentu dengan menggunakan metodeMonte Carlo.

1.3.2 Tujuan

Sedangkan tujuan dari latar belakang di atas adalah :

a) Membantu penyelesaian fungsi integral multidimensi tentu dengan menggunakan metodeMonte Carlo.

b) Perangkat lunak dapat digunakan sebagai fasilitas pendukung dalam proses belajar-mengajar.

1.4 Batasan Masalah

Karena keterbatasan waktu dan luasnya lingkup permasalahan, maka pembahasan akan dibatasi pada :

1. MetodeMonte Carlo mencakup plain Monte Carlo, MISERMonte Carlo dan VEGASMonte Carlo.

2. Input ekspresi aritmatika yang akan diturunkan maksimal terdiri dari dua jenis variabel.

3. Fungsi integral tentu, yakni batas atas dan batas bawah diketahui. 4. Fungsi integral yang dapat diselesaikan adalah adalah fungsi rasional. 5. Dimensi integral terbatas pada fungsi integral lipat 2.

7. Bahasa pemrograman yang dipakai adalah Microsoft Visual Basic 6.0 8. Analisis input ekspresi matematika menggunakan metode infix dengan

parsing left most derivation.

9. Tools yang digunakan untuk analisis sistem adalah dengan Data Flow Diagram (DFD).

1.5 Metodologi Penelitian

Adapun metode penelitian yang akan digunakan dalam penyusunan Tugas Akhir ini adalah :

1. Pengumpulan Data :

a. Pengamatan (Observasi)

Pengamatan akan difokuskan pada pembelajaran metodeMonte Carlo baik metode MISER Monte Carlo ataupun VEGAS Monte Carlo. Selain itu juga dilakukan pengamatan mengenai sampai sejauh mana kemampuan siswa untuk memahami dan menyelesaikan integral dengan metode analitik.

b. Studi Pustaka

2. Pengembangan Perangkat Lunak :

Metode yang digunakan dalam pengembangan perangkat lunak adalah metodewaterfall. Alur dari metodewaterfall dapat dilihat pada gambar 1.1.

Gambar 1.1. Alur Metode Waterfall

Adapun Penjelasan dari alur metodewaterfall ini adalah sebagai berikut : a. Rekayasa dan Pemodelan

Pada tahap ini, rekayasa informasi mencakup pengumpulan kebutuhan pada aplikasi yang akan dibangun;

b. Analisis

Kegiatan analisis perangkat lunak meliputi analisis spesifikasi perangkat lunak, analisis lingkungan pengembangan, dan analisis struktural;

c. Desain

d. Pembangkitan Kode

Dalam proses ini, hasil analisis dan desain sistem pada proses sebelumnya diterjemahkan kedalam bentuk mesin, jika desain dilakukan dengan cara yang lengkap, pembuatan kode dapat dilakukan secara mekanis;

e. Pengujian

Dalam tahap ini akan dilakukan pengujian untuk menguji apakah sistem yang telah dirancang dan diimplementasikan sudah sesuai dengan hasil analisis yang telah dilakukan;

f. Pemeliharaan

Pemeliharaan dilakukan terhadap kesalahan-kesalahan yang terjadi pada prototipe perangkat, dokumen teknis perangkat lunak, maupun laporan Tugas Akhir.

1.6 Sistematika Penulisan

Untuk lebih menjelaskan permasalahan dan pemecahannya, maka laporan Tugas Akhir dijabarkan dalam bab-bab sebagai berikut :

BAB I PENDAHULUAN

Bab ini berisi latar belakang, rumusan masalah, maksud dan tujuan, batasan masalah, metodologi penelitian dan sistematika penulisan.

BAB II DASAR TEORI

BAB III ANALISIS DAN PERANCANGAN

Bab ini berisi tentang analisis kebutuhan perangkat lunak dan perangkat keras yang dibutuhkan untuk membangun sistem. Selain itu, bab ini juga berisi perancangan antarmuka sistem yang akan dibangun.

BAB IV IMPLEMENTASI DAN PENGUJIAN

Bab ini berisi tentang implementasi dan pengujian sistem yang dibangun. BAB V KESIMPULAN DAN SARAN

8 2.1 Sejarah Kalkulus

Kalkulus integral terlahir lebih dari 2.000 tahun yang lalu pada waktu bangsa Yunani mencoba menentukan luas dengan suatu proses yang mereka sebut dengan metode pengeringan. Gagasan yang penting dari metode ini sangat sederhana dan dapat dilukiskan dengan singkat sebagai berikut:

“Diberikan suatu daerah yang luasnya akan ditentukan, kemudian kita buat di dalamnya suatu daerah poligonal yang mendekati daerah yang diberikan dan kita dapat menghitung luasnya dengan mudah. Kemudian dipilih

daerah poligonal yang lain yang memberikan suatu pendekatan yang lebih baik, dan kita lanjutkan proses tersebut dengan mengambil poligon-poligon dengan sisi-sisi yang semakin banyak, yang diistilahkan mencoba untuk mengeringkan daerah yang diberikan.”

Metode ini pernah sukses digunakan oleh Archimedes untuk mendapatkan rumus-rumus eksak untuk luas-luas lingkaran dan bangun-bangun khusus yang lain. Metode pengeringan untuk setengah lingkaran dapat dilihat pada gambar 2.1.

Perkembangan dari metode ini, di luar apa yang didapat oleh Archimedes, maka harus ditunggu sampai 18 abad baru digunakan simbol-simbol dan notasi-notasi aljabar sehingga menjadi salah satu bagian dari ilmu matematika. Aljabar elementer yang dikenal di sekolah lanjutan saat ini tidak dikenal sama sekali di zaman Archimedes.

Suatu percobaan yang perlahan-lahan tetapi revolusioner, dalam perkembangan notasi matematika di mulai pada abad ke 16 sesudah Masehi. Sistem bilangan dari bangsa Romawi yang sulit digantikan dengan huruf-huruf Hindu-Arabia yang digunakan sampai sekarang. Dan secara berangsur-angsur pula keuntungan pemakaian notasi dan simbol dalam matematika diakui lebih menguntungkan. Dalam periode yang sama ini, hasil-hasil yang gemilang dari ahli-ahli matematika Italia, seperti Tartag, Cardano, Ferrari dalam menentukan solusi persamaan kuadrat, persamaan pangkat tiga dan menstimulasikan banyak kegiatan dalam matematika memberikan dorongan pada pertumbuhan dan penerimaan dari suatu bahasa matematika yang baru dan lebih baik. Dengan pengenalan yang leibh luas, maka metode pengeringan diperhatikan kembali, dan sejumlah hasil-hasil baru dikemukakan pada abad ke 16 oleh perintis-perintis seperti: Cavalieri, Toricelli, Fermat, Pascal dan Waltes.

perkembangan yang terbesar pada abad ke 17 ketika Isaac Newton (1642-1727) dan Goltfried Leibniz (1646-1716) mendapat penemuan-penemuan baru dan perkembangannya berlangsung terus dengan baik sampai pada abad ke-19.

Gottfried Wilhelm Leibniz (1646-1716) adalah seorang jenius universal, seorang pakar dalam hukum agama, filsafat, kesusasteraan, politik, geologi, sejarah dan matematika. Lahir di Leipzig, Jerman, ia mendaftar di Universitas Leipzig dan menggondol doktor dari Universitas Altdrof. Seperti Decartes, yang karyanya ia pelajari, Leibniz mencari suatu metode universal dengan mana ia dapat memperoleh pengetahuan dan memahami kesatuan sifat-sifat dasarnya. Salah satu keinginan besarnya adalah mendamaikan keyakinan Katolik dan Protestan.

Bersamaan dengan Isaac Newton, ia membagi penghargaan untuk penemuan kalkulus. Masalah prioritas menyebabkan pertentangan yang tidak henti-hentinya antara pengikut dua orang besar ini, satu Inggris, yang lainnya Jerman. Sejarah menjadi hakim bahwa Newtonlah yang pertama mempunyai pemikiran utama (1665-1666), tetapi bahwa Leibniz menemukan mereka secara tersendiri selama tahun (1673-76). Dengan kebesaran itupun, Leibniz tidak menerima kehormatan seperti yang dicurahkan pada Newton. Ia meninggal sebagai orang kesepian, pemakamannya hanya dihadiri seorang pelayat yaitu sekretarisnya.

Mungkin Leibnizlah pencipta lambang-lambang matematis terbesar. Kepadanya kita berhutang nama-namakalkulus diferensial dankalkulus integral,

untuk integral. Istilah fungsi dan penggunaan secara konsisten dari simbol ‘=’ untuk kesamaan merupakan sumbangan-sumbangan lainnya. Kalkulus berkembang jauh lebih cepat di daratan Eropa daripada di Inggris, sebagian besar disebabkan oleh keunggulan perkembangannya.

2.2 Penerapan Kalkulus

Kemajuan ilmu pengetahuan dan teknologi (iptek) yang dicapai pada saat ini, terutama kemajuan pada abad-abad terakhir, pada dasarnya tidak terlepas dari akibat dari kemajuan matematika sebagai alat bantu yang sangat penting. Berbagai cabang matematika seperti Kalkulus Diferensial, ataupun Integral adalah merupakan senjata yang tepat dan sangat ampuh untuk menggarap berbagai problema yang timbul dalam fisika, kima, biologi dan berbagai cabang ilmu yang lain baik eksak maupun yang non-eksak.

Contoh-contoh yang dikemukakan di atas, yang diambil dari berbagai bidang disiplin ilmu, menggambarkan berbagai persoalan yang dapat dijawab dengan matematika, terutama kalkulus. Jadi kalkulus lebih dari suatu alat teknik, bahkan ia merupakan suatu sumber gagasan-gagasan yang memikat dan mengagumkan yang telah menarik perhatian dari berbagai ahli pikir selama berabad-abad. Para ahli pikir harus bekerja dengan gagasan-gagasan mengenai kecepatan, luas, isi kecepatan tumbuh kekontinuan, garis singgung serta konsep-konsep yang lain dari berbagai bidang. Kalkulus memaksa kita untuk berhenti dan berpikir dengan baik tentang arti dari konsep-konsep ini. Suatu aspek lain yang menarik perhatian dari subjek ini adalah kekuatan mempersatukannya. Gagasan-gagasan di atas dirumuskan dalam suatu bentuk perumusan yang khusus yang disertai dengan pemecahan masalahnya.

Kalkulus harus bekerja dengan perumusan yang tepat dan jawaban dari persoalan yang khusus dalam kalkulus. Untuk ini kita bisa bekerja denga ndua konsep, yakni Kalkulus Integral dan Kalkulus Diferensial.

Kalkulus Integral bekerja dengan persoalan luas dan volume sementara kalkulus diferensial banyak berbicara dengan garis singgung.

2.3 Diferensial (Turunan)

menggabungkan kalkulus integral dengan konsep kalkulus yang lain, yakni kalkulus diferensial.

Ide pokok dari kalkulus diferensial adalah pengertian turunan (derivative). Seperti halnya integral, turunan berasal dari suatu problema dalam geometri, yakni persoalan mencari garis singgung di suatu titik pada suatu kurva. Tetapi agak berbeda dengan integral, turunan berkembang sangat terlambat dalam sejarah matematika. Pada permulaan abad ke-17, ketika seorang ahli matematika Perancis bernama Pierre de Fermat mencoba menentukan maksimum dan minimum beberapa fungsi khusus, konsep turunan belumlah dirumuskan.

Fermat memberikan ide yang sangat sederhana, yakni berprinsip pada mencari garis singgung pada suatu kurva. Misalkan suatu kurva pada gambar 2.2, diandaikan bahwa setiap titik dari kurva mempunyai arah tertentu yang ditunjukkan oleh garis-garis singgung yang mempunyai arah tertentu.

Gambar 2.2 Jenis – Jenis Garis Singgung pada Kurva

harga ekstrim ini tergantung pada jawaban persoalan yang lain yakni mencari garis singgung yang horizontal.

Hal ini menimbulkan ide yang lebih luas, yakni menentukan arah dari garis singgung-garis singgung di suatu titik yang sembarang pada kurva. Ini adalah suatu usaha untuk memecahkan persoalan umum yang menjadi dasar dari pengertian turunan. Sepintas lalu tampaknya tidak ada hubungan sama sekali antara pesoalan mencari luas daerah yang berada di bawah suatu kurva dengan persoalan mencari garis singgung di suatu titik pada kurva. Orang pertama yang mengetahui hubungan kedua persoalan ini adalah Isaac Barrow (1630 – 1677), bekas guru dari Newton. Tapi bagaimanapun peranan Newton dan Leibniz-lah yang menentukan bagaimana pentingnya masalah tersebut, yang dapat membuka suatu era baru dalam perkembangan matematika.

Turunan mula-mula memang hanya ditujukan untuk mencari garis singgung suatu kurva, tetapi ternyata kemudian sangat berguna untuk menyelesaikan problema-problema yang ada hubungannya dengan kecepatan, atau secara lebih umum kecepatan perubahan suatu fungsi. Banyak persoalan-persoalan fisika maupun bidang lain yang akhirnya menggunakan konsep turunan untuk menyelesaikan masalahnya.

Bila kita melihat keadaan di sekeliling kita, maka akan banyak melihat adanya perubahan-perubahan misalnya,

Untuk mengetahui suatu sistem yang sedang berubah, di samping memperhatikan faktor-faktor yang ada (yang dianggap penting) dalam sistem tersebut perlu diperhatikan pula pengaruh dari suatu perubahan suatu faktor pada faktor yang lain. Selain itu, juga harus diperhatikan cepat dan lambatnya perubahan dari suatu faktor, sebagai akibat dari perubahan pada faktor lain. Dalam persoalan inilah konsep turunan memegang peranan yang sangat penting. Untuk lebih jelasnya ikuti contoh berikut ini,

a. Misalkan batang besi dipanaskan, maka akan bertambah panjang. Dalam contoh ini kita dapat mengatakan mengenai perubahan panjang dalam suatu selang suhu tertentu atau mungkin juga mengenai lajunya perubahan panjang pada suhu tersebut.

b. Mengenai hukum gravitasi Newton, kita mengetahui bahwa gaya tarik antara dua benda, berbanding terbalik dengan kuadrat jarak kedua benda tersebut. Dalam hal ini perubahan jarak mengakibatkan besarnya perubahan gaya tarik.

2.3.1 Diferensial dari Fungsi

Diferensial dari fungsi f sering dilambangkan dengan simbol f’ yang nilainya pada sembarang bilanganc dapat dicari dengan persamaan berikut,

f(c +h) –f(c) f’(c) = lim

Suatu fungsi dikatakan dapat dideferensialkan apabila fungsi itu dapat didiferensialkan di setiap titik pada wilayah domainnya. Diferensial dari beberapa fungsi dasar matematika dapat dilihat pada penjabaran berikut ini,

a. y =xn y’ =n .xn – 1

Cth: y =x3 y’ = 3x2

b. y =un, dimanau =f(x) y’ =n .un – 1 .u’ Cth: y =1/3 (x2 + 6)1.5

Misalkan:u = (x2 + 6), maka turunan dariy adalah: y’ =1/3 . 1.5 . (x2 + 6)0.5 . (2x)

y’ =1/3 . 1.5 . (x2 + 6)0.5 . (2x)

y’ = (x2 + 6)0.5 .x

c. y =u .v y’ =u’ .v +u .v’ Cth: y = (x3 + 5) . (x2 - 2)

Misalkan: u = (x3 + 5), makau’ = 3x2, v = (x2 - 2), makav’ = 2x y’ = (3x2) . (x2 - 2) + (x3 + 5) . (2x) y’ = 3x4 - 6x2 + 2x4 + 10x

y’ = 5x4 - 6x2 + 10x

d. y =u /v y’ = (u’.v –u .v’) /v2 Cth: y = (x3 + 5) / (x2 - 2)

Misalkan: u = (x3 + 5), makau’ = 3x2, v = (x2 - 2), makav’ = 2x y’ = ((3x2) . (x2 - 2) + (x3 + 5) . (2x)) / (x2 - 2)2 y’ = (3x4 - 6x2 + 2x4 + 10x) / (x4 - 4x2 + 4) y’ = (5x4 - 6x2 + 10x) / (x4 - 4x2 + 4)

f. y =ef(x) y’ =ef(x) .f’(x) Cth: y =e(x ^3 + 5)

Misalkan: f(x) = (x3 + 5), makaf(x)’ = 3x2 y’ =e(x ^3 + 5) . 3x2

g. y =ln x y’ = 1 /x

h. y =ln f(x) y’ = 1 /f(x) .f ’(x) Cth: y =ln(x3 + 5)

Misalkan: f(x) = (x3 + 5), makaf(x)’ = 3x2 y’ = (1 / (x3 + 5)) . 3x2

y’ = 3x2 / (x3 + 5)

2.3.2 Penerapan Diferensial

Diferensial dapat diterapkan untuk menyelesaikan beberapa persoalan yang sering dihadapi dalam kehidupan sehari-hari antara lain,

1. Masalah garis singgung pada kurva.

Garis singgung pada suatu titik pada kurva dapat dicari dengan terlebih dahulu mencari tanjakan (gradien) garis di titik tersebut. Gradien garis singgung pada kurva dapat dicari dengan terlebih dahulu mencari persamaan gradien dengan mendiferensialkan fungsi kurva tersebut, kemudian substitusikan nilai koordinat absis (sumbu x) pada titik tersebut ke dalam persamaangradien tersebut sehingga didapat nilaigradien garis. Secara matematis dapat dirumuskan sebagai berikut,

dy d f(x) m(x) =f ’(x) = =

dx dx

2. Masalah perubahan kecepatan.

Kegunaan turunan lainnya adalah untuk menerangkan kecepatan perubahan. Dalam hal ini ditinjau dari segi luas, perubahan yang dimaksud dapat menyangkut beberapa hal. Misalnya dalam mekanika, perubahan tersebut bisa menyangkut perpindahan, kecepatan ataupun percepatan. Misalkan ditinjau suatu partikel yang bergerak sepanjang kurva atau garis lurus. Untuk mendapat gambaran lengkap mengenai gerak partikel tersebut diciptakan besaran-besaran seperti kecepatan rata-rata, kecepatan sesaat, percepatan dan besaran lainnya.

Anggap suatu partikel bergerak sepanjang garis lurus. Gerak yang demikian disebut gerak lurus. Misalkan partikel tersebut bergerak dari kiri ke kanan. Misalkan s merupakan jarak dari titik tersebut dari titik semula pada saatt, makas sebagai fungsi darit dapat dituliskan sebagai,

s =f(t)

adalah menyatakan jarak titik 0 (titik asal mula partikel bergerak) ke titik setelah bergerak selama t. Persamaan s = f(t) dikatakan persamaan dari partikel. Untuk lebih jelasnya diambil contoh berikut,

s =t2 + 2t – 3,t = 0 Hal ini berarti,

t = 0 s = -3, partikel berada di 3 satuan panjang sebelah kiri dari titik 0. t = 1 s = 0, partikel tepat berada di titik 0.

[image:30.612.227.413.110.152.2]

Gambar 2.3 Grafik Lintasan

Pada intervalt = 1 dant = 2 perubahan jaraknya adalah 5 – 0 = 5, sehingga kecepatan rata-ratanya adalah 5/(2 – 1) = 5 satuan panjang / satuan waktu. Sedangkan kecepatan rata-rata dalam intervalt = 0 sampai t = 2 sebesar : (5 –(-3)) / (2 – 0) = 4 satuan panjang / satuan waktu. Ternyata kecepatan rata-rata akan selalu berubah untuk waktu yang berlainan. Kecepatan partikel yang bergerak dengan persamaan gerak s = f(t) dalam interval waktut1,t2 diberikan oleh rumus,

(

)

( ) ( )

1 2 1 2 2 1, t t t f t f t t v − − =

Dalam kenyataannya, kecepatan rata-rata tidak pernah tetap besarnya, sebagai contoh seseorang mengendarai sepeda motor sepanjang 70 km dalam waktu 2 jam, maka kecepatan rata-rata dalam interval ini adalah 70/2 = 35 km/jam. Dalam kenyataannya, orang tersebut akan mengendarainya dalam berbagai kecepatan yang berbeda setiap saat. Artinya setiap saat kecepatan berubah, dan kita dapat menerangkan gerak partikel apabila dapat mencari kecepatan yang berubah setiap saat itu. Untuk itu, diperkenalkan konsep kecepatan sesaat, yakni kecepatan

[t1,t2] sekecil mungkin atau untukt2 t1 atau (t2 –t1) 0. Maka didapat

persamaan matematika berikut,

f(t2) –f(t1)

v(t1) = lim

t2 t1 t2 –t1

Misalkan (t2 – t1) = t, maka untuk t2 t1 didapat t 0, sehingga

kecepatan sesaat dapat ditulis sebagai,

f(t1 + t) –f(t1)

v(t1) = lim

t 0 t

Kecepatan sesaat bisa positif, bisa negatif, tergantung pada arah gerak partikel. Arah ke kanan dianggap positif dan ke kiri negatif. Besarnya kecepatan sesaat, disebut besaran kecepatan atau laju partikel, adalah nilai mutlak kecepatan pada suatu saat.

2.4 Integral (Anti Turunan)

diberi nama integral. Secara garis besar, integral terdiri dari dua macam, yaitu integral tak tentu dan integral tentu.

2.4.1 Integral Tak Tentu

Misalkan kita harus menentukan suatu lengkungan yang garis singgungnya pada tiap titik (x,y) pada lengkungan tersebut, memiliki koefisien gradien 3x2. Maka untuk langkah pertama kita cari y = f(x) sedemikian rupa sehingga turunannya,

Dxy = 3x2

Kita tahu bahwa 3x2 adalah hasil penurunan dari x3, maka dapat disimpulkan bahwa

y =x3

merupakan persamaan lengkungan yang garis singgungnya di tiap titik pada lengkungan mempunyai gradien 3x2. Sehingga didapat bahwa anti turunan dari suatu fungsi f adalah suatu fungsi sembarang F yang turunannya F’ adalah sama denganf. Jadi,

F’ =f

1. Fungsi F(x) = x3 adalah anti turunan dari f(x) = 3x2, karena F’(x) = 3x2 = f(x).

2. Fungsi F(x) = x3 – 2 dan fungsi x3 + 6 juga merupakan anti turunan dari f(x) = 3x2.

Jadi, jelas bahwa suatu fungsi turunan, mungkin memiliki lebih dari satu fungsi primitif atau anti turunan. Sehingga muncul dua dalil berikut ini,

1. Jika H’(x) = 0 untuk semua x dalam selang buka (a,b), maka H(x) = C dalam selang tersebut, dimana C adalah konstanta sembarang.

2. Jika H’(x) = G’(x) untuk semua x dalam selang buka (a,b) maka berlaku, H(x) = G(x) + C

dimana, C adalah suatu konstanta sembarang.

Atau dengan perkataan lain dapat dinyatakan bahwa anti turunan dari f adalah F(x) + C dimana F adalah anti turunan dari f dan C adalah suatu konstanta sembarang dan semua anti turunan darif diperoleh dari F(x) + C dengan merubah nilai dari C.

Pembentukan anti turunan adalah proses menentukan anti turunan yang paling umum untuk suatu fungsi yang diberikan. Untuk operasi pembentukan anti turunan digunakan operasi yang diberi notasi : “ ”.

Integral tak tentu dari suatu fungsi f, ditunjukkan dengan, f(x) dx

adalah merupakan anti turunan f yang paling umum yakni,

Ternyata proses pembentukan anti turunan suatu fungsi adalah merupakan proses pembentukan integral tak tentu dari fungsi tersebut. Karenanya operasi pembentukan integral tak tentu sering disebut dengan pengintegralan tak tentu atau pengintegralan.

Jika diketahui suatu persamaan berikut,

d(F(x)) =F(x) + C Jika F(x) = x dalam persamaan di atas maka diperoleh,

dx =x + C Jika C suatu konstanta maka berlaku,

c.f(x)dx = c f(x)dx

yakni anti turunan perkalian konstanta C dengan suatu fungsi adalah sama dengan perkalian konstanta C dengan anti turunan fungsi tersebut.

Dari persamaan f(x)dx = F(x) + C maka dengan menurunkan ruas kiri dan ruas kanannya didapatkan,

Dx f(x)dx =F’(x)

Tetapi karenaF’(x) =f(x) maka diperoleh dalil berikut,

1. Turunan dari suatu anti turunan untuk suatu fungsi adalah fungsi itu sendiri.

Dx f(x)dx =f(x)

2. Jikar adalah suatu bilangan rasional danr -1 maka,

∫

+

+

= _x + _c

r dx

xy y 1

3. Anti turunan jumlah dua fungsi adalah jumlah anti turunan kedua fungsi tersebut.

[f(x) +g(x)]dx = f(x)dx + g(x)dx 4. Aturan rantai untuk anti turunan.

Jika suatu fungsi yang terdiferensialkan dan u = f(x) maka untuk n -1 berlaku, C n u du u n n ₊ + =

∫

+1₁

atau,

( )

[ ]

( )

[ ]

( )

C

n x f dx x f x f n n + + =

∫

' ₁+

1

Rumus-rumus integrasi untuk fungsi trigonometri dapat dinyatakan sebagai berikut,

1. sin x dx = -cos x +c 2. cos x dx =sin x + c

3. tg x dx = -ln cos x + c = ln sec x + c 4. ctg x dx = ln sin x + c = -ln cosec x + c 5. sec x dx = ln |sec x + tg x| + c

6. cosec x dx = -ln |cosec x + ctg x| + c

Untuk fungsi f(x)dx dengan bentuk akar dapat diselesaikan dengan menerapkan rumus-rumus berikut ini,

a. Bilaf(x) =√a2 –x2, maka misalkanx =a cosθ ataux = a sinθ

b. Bilaf(x) = √a2 +x2, maka misalkanx = a tgθ ataux = a ctgθ

2.4.2 Integral Tentu

Konsep integral tentu merupakan inti hitung integral yang sangat luas sekali pemakaiannya. Berbagai bidang ilmu pengetahuan menggunakan konsep ini. Perhitungan luas suatu daerah, isi benda putar, penentuan titik berat suatu benda, menghitung momen inersia atau pengukuran luas permukaan bola (speric) menggunakan konsep integral tentu.

Suatu fungsif dikatakan dapat diintegralkan dalam suatu selang tutup [a,b] jika integral tentu f dari a ke b ada (terdefinisi). Ungkapan dapat diintegralkan sering juga diartikan sama dengan memiliki integral atau terintegralkan atau integrabel. Berikut ini akan diberikan beberapa dalil dasar yang merupakan sifat dari integral tentu,

1. Jikaf dang adalah fungsi yang memiliki integral (integrabel) dalam selang tutup [a,b] maka,

b b b

[f(x) +g(x)]dx = f(x)dx + g(x)dx

a a a

2. Jika f fungsi yang integrabel pada selang tutup [a,b] dan k sebuah konstanta maka,

b b

k f(x)dx =k f(x)dx

a a

3. Jika f integrabel dalam selang tutup [a,b] dan f(x) 0 untuk a x b, maka,

b

4. Jika f dan g adalah dua fungsi yang memiliki integral (integrabel) pada selang tutup [a,b] dan 0 f(x) g(x) untuka x b, maka,

b b

f(x)dx g(x)dx

a a

[image:37.612.245.396.384.524.2]

Jika suatu fungsi tidak negatif dalam suatu selang tutup, maka integral tentu fungsi itu untuk selang yang sama adalah tak negatif juga. Sifat perbandingan ini menunjukkan bahwa jika untuk suatu selang tutup, fungsi f lebih kecil atau sama dengan g (dengan f dan g keduanya fungsi tak negatif), maka pada selang tutup yang sama, integral tentu f akan lebih kecil atau sama dengan integral tentug. Secara geometri dapat dilihat pada gambar 2.4, sebagai interpretasi dari poin 4,

Gambar 2.4 Interpretasi Poin 4

5. Jikaf kontinu dalam selang tutup [a,b] [b,c] dan [a,c] maka,

b c c

f(x)dx + f(x)dx = f(x)dx

a b a

6. Jika f fungsi kontinu dalam sebuah selang tutup yang mengandung tiga bilangana,b danc maka,

b c b

f(x)dx = f(x)dx + f(x)dx

Secara geometris, maka didapat grafik pada gambar 2.5.

Gambar 2.5 Interpretasi Poin 6 c

f(x)dx = LI

a b

f(x)dx = LII

c

b L= LI + LII = f(x)dx

a 7. Jika k suatu konstanta maka berlaku,

b

k dx =k (b –a) a

8. Misalkan f fungsi kontinu dalam selang tutup [a,b]. Jika m adalah nilai minimum mutlak dari f di dalam [a,b] dan M nilai maksimum mutlak di dalam selang tutup [a,b] sehingga,

m f(x) M untuka x b maka,

b

9. Jikaf adalah fungsi kontinu dalam selang tertutup [a,b] dan jikaf(a) f(b) maka untuk tiap bilangan k antara f(a) dan f(b) ada sebuah bilangan c antaraa danb sehingga berlaku,

f(c) =k

10. Jikaf fungsi kontinu dalam selang tutup [a,b] maka ada bilanganµ antara

a danb sehingga,

b

f(x) dx =f(µ) (b –a) a

atau dapat juga dinyatakan sebagai,

( )

( )

a b dx x f f b a − =

∫

µ

2.5 Integrasi Monte Carlo

Nama Monte Carlo pertama kali diberikan pada metode matematika yang dikerjakan oleh para peneliti di pengembangan senjata nuklir di Los Alamos tahun 1940an. Inti dari metode ini adalah penemuan permainan peluang yang sifat dan hasilnya dapat digunakan untuk mempelajari beberapa fenomena menarik. Karena belum ada keterhubungan berarti dengan komputer, keefektifan peluang simulasi atau numerik menjadi terangkat berkat ketersediaan komputer digital modern.

Prinsip dasar dari metode Monte Carlo adalah bahwa harga pendekatan integral suatu fungsi berbading lurus dengan harga rata-rata fungsi tersebut untuk sejumlah besar sampel yang dipilih secara acak atau dengan distribusi tertentu dalam interval integrasi.

2.5.1 Plain Monte Carlo

Plain Monte Carlo adalah metode dasar dari integrasi Monte Carlo. Metode ini melakukan pengambilan titik sampel secara acak untuk memperkirakan distribusi probabilitas. Integral diselesaikan dengan mengambil sejumlah titik acak di atas interval yang ditentukan dan menjumlahkan hasil evaluasi fungsi pada titik-titik ini. Daerah interval yang telah ditentukan tersebut lalu dikalikan dengan nilai fungsi rata-rata dari titik-titik yang dipilih.

( )

(

)

( )

∫

∑

= − ≈ b a N i N xi f a b x f 1 *

N adalah banyaknya titik sampel yang digunakan untuk mencari nilai hampiran dari integral.

2.5.2 MISER Monte Carlo

membuat potongan yang lebih penting untuk memberikan kontribusi yang lebih akurat bagi nilai akhir integral.

Prinsip dari metode ini adalah mengurangi nilai error integral secara keseluruhan dengan mengkonsentrasikan titik integrasi pada daerah dengan varians tertinggi. Idenya diawali dengan mengamati dua bagian terpisah a dan b dengan Monte Carlo. Algoritma MISER berlanjut dengan membagi dua daerah dalam satu koordinat axis yang menghasilkan dua sub-daerah per langkah. Arah ini dipilih dengan menguji semua kemungkinan pembagian dua dan memilih salah satu yang akan memperkecil kombinasi varians dari tiap sub-daerah. Varians tiap subdaerah dihitung dengan sampling sebuah fraksi dari seluruh titik yang tersedia sampai langkah ini. Prosedur yang sama lalu diulangi secara rekursif untuk tiap dua bagian sisa dari pembagian. Titik sampel yang tersisa dialokasikan ke subdaerah. Alokasi titik integrasi berlanjut kepada kedalaman yang ditentukan user dimana tiap subdaerah diintegrasikan menggunakan plain Monte Carlo. Nilai-nilai tunggal dan perkiraan error-nya ini lalu dijumlahkan untuk menghasilkan nilai dan perkiraan error keseluruhanya.

( )

( )

∫

∑

∑

= = ≈ b a m i N j j i N x f Panjang x f i 1 1 *

2.5.3 VEGAS Monte Carlo

Teknik sebelumnya menunjukkan bahwa penggunaan distribusi non-uniform titik acak akan menghasilkan sampling yang lebih baik dan hampiran yang lebih akurat dari sebuah integral.Importance sampling adalah perluasan dari teknik tersebut, tapi daripada menggunakan batasan untuk membagi interval, sebuah fungsi distribusi digunakan untuk memilih titik acak.

Importance sampling adalah memilih distribusi yang bagus dari fungsi untuk mensimulasikan variable acaknya. Hal ini termasuk mengkalikan integran dengan 1 (biasanya terselubung dengan suatu fungsi “palsu”) untuk menghasilkan nilai ekspektasi dari kuantitas yang sedikit berbeda dari integran asli di atas area integrasi. Sebagai contoh, p(x) adalah densitas untuk variable acak X yang hanya

mengambil nilai dalam A sehingga

∫

( )

∈A =

x p xdx 1. Maka

( )

( )

=1

x p x p dan

( )

( ) ( )

( )

( )

( ) ( )

( )

( )

_      Ε = = =

∫

∫

∫

∈ ∈ ∈ _{p X}

X f dx x p x p x f dx x p x p x f dx x f _h A x A x A x

Selama p(x) 0 untuk semua x∈A untuk g(x) 0, dan dimana Εhmenyatakan

ekspektasi terhadap densitas h. Ini menjadikan estimator Monte Carlo menjadi :

( )

∑

( )

( )

= = n i h n Xi p Xi f n X g 1 ~ ₁

dimana Xi~ p

( )

x .

( )

(

)

( )

( )

∫

∑

= − ≈ b a N i n n N x p x f a b x f 1 *

Adapun fungsi p(x) yang baik mempunyai beberapa syarat sebagai berikut: 1. p(x) > 0 dan f(x) 0

2. p(x) harus mendekati proporsi |f(x)| 3. simulasi nilai p(x) harus mudah

4. perhitungan densitas p(x) harus mudah untuk nilai x apapun.

2.6 Visual Basic 6.0

Visual Basic adalah sebuah sarana pembuatan program yang lengkap namun mudah. Basic pada Visual Basic diambil dari kata BASIC yang merupakan bahasa pemrograman juga. Memang Visual Basic merupakan sebuah pengembagan terakhir dari bahasa BASIC.

2.6.1 Keistimewaan Visual Basic 6.0

Sejak dikembangkan pada tahun 80-an, Visual Basic kini telah mencapai versi yang ke-6. Beberapa keistimewaan utama dari Visual Basic 6 ini antaranya seperti :

1. Menggunakan platform pembuatan program yang diberi nama Developer Studio, yang memiliki tampilan dan sarana yang sama dengan Visual C++ dan Visual J++. Dengan begitu dapat bermigrasi atau belajar bahasa pemrograman lainnya dengan mudah dan cepat, tanpa harus belajar dari nol.

2. Memiliki compile andal yang dapat menghasilkan file executable yang lebih cepat dan lebih efisien dari sebelumnya. 3. Memiliki beberapa tambahan sarana Wizard yang baru.

Wizard adalah sarana yang mempermudah di dalam pembuatan aplikasi dengan mengotomatisasi tugas-tugas tertentu.

4. Tambahan kontrol-kontrol baru yang lebih canggih serta peningkatan kaidah struktur bahasa Visual Basic.

5. Kemampuan membuat ActiveX dan fasilitas Internet yang lebih banyak.

6. Sarana akses data yang lebih cepat dan andal untuk membuat aplikasi database yang berkemampuan tinggi.

2.6.2 Lingkungan atau Layar Visual Basic 6.0

Layar Visual Basic hampir sama dengan layar program-program aplikasi Windows pada umumnya, terutama jika pernah menggunakan bahasa pemrograman visual lainnya, misalnya seperti Microsoft Visual FoxPro, Microsoft Access, Visual C++, dan sebagainnya.

Layar Visual Basic adalah suatu lingkungan besar yang terdiri dari beberapa bagian-bagian kecil yang kesemuannya memiliki sifat :

a) Floating : dapat digeser-geser ke posisi mana saja. Untuk menggeserkan elemen layar Visual Basic, klik dan tahan tombol mouse pada judul (Title Bar) elemen tersebut, lalu geserlah ke tempat yang diinginkan.

b) Sizable : dapat diubah-ubah ukurannya, seperti mengubah ukuran jendela windows. Untuk mengubah ukuran suatu elemen atau jendela, klik dan tahan tombol mouse pada sisi (border) jendela tersebut, lalu geserlah hingga ke ukuran yang diinginkan.

2.6.3 Control Menu

Control Menu adalah menu yang digunakan terutama untuk memanipulasi jendela Visual Basic. Dari menu ini bisa mengubah ukuran, memindahkan, atau menutup jendela Visual Basic atau jendela Windows lainnya.

Untuk mengaktifkan Control Menu ini, klik tombol mouse pada pojok kiri atas jendela. Berikutnya akan muncul menu Control Menu, dimana bisa memilih salah satu dari perintah ini :

§ Restore :mengubah ukuran jendela ke ukuran sebelumnya. § Move : untuk memindahkan letak jendela.

§ Size :untuk mengubah ukran jendela.

§ Minimize :untuk meminimalkan ukuran jendela. § Maximize :untuk memaksimalkan ukuran jendela. § Close :untuk menutup jendela.

2.6.3.1 Menu

2.6.3.2 Toolbar

Toolbar adalah tombol-tombol yang mewakili suatu perintah tertentu dari Visual Basic. Setiap tombol tersebut dapat langsung diklik untuk melakukan perintah tertentu. Biasanya tombol-tombol ini merupakan perintah-perintah yang sering digunakan dan terdapat pula pada menu Visual Basic. Toolbar yang umum adalah toolbar Standar.

2.6.3.3 Form Window

37 3.1 Analisis Sistem

Dalam analisis sistem dilakukan penguraian dari suatu sistem yang utuh ke dalam bagian-bagian komponennya dengan maksud untuk mengidentifikasikan dan mengevaluasi permasalahan-permasalahan sehingga ditemukan kelemahan-kelemahannya, kesempatan-kesempatan, hambatan-hambatan yang terjadi dan kebutuhan-kebutuhan yang diharapkan sehingga dapat diusulkan perbaikannya.

3.1.1 Analisis Masalah

Berdasarkan pengamatan, pembelajaran integral masih menjadi hal yang cukup sulit untuk dipahami. Apalagi jika pencarian hasil integral menggunakan metode analitik yang cukup panjang dan rumit. Oleh karena itu, perlu dibangun suatu sistem yang dapat mempermudah pembelajaran dan pencarian hasil integral dengan menggunakan metode lain (non-analitik) yang lebih mudah dipahami.

3.1.2 Gambaran Umum Sistem

Ketika pertama kali masuk ke dalam sistem, maka akan ditampilkan menu pilihan untuk user. Di bagian ini user harus meng-input-kan fungsi, batasan fungsi (batas atas dan batas bawah), memilih banyaknya dimensi integral (integral lipat satu atau lipat dua), dan memilih jenis metodeMonte Carlo yang akan digunakan. Sistem akan menampilkan langkah-langkah perhitungan fungsi integral yang diinputkan oleh user. User dapat memilih untuk menyimpan hasil latihannya ke dalam bentuk file. User juga dapat menambahkan fungsi yang akan disimpan di dalammemory yang kapasitas penyimpanannya terbatas.

3.1.3 Analisis Kebutuhan Sistem Non Fungsional

Analisis non-fungsional merupakan analisis yang dibutuhkan untuk menentukan spesifikasi kebutuhan sistem. Spesifikasi ini juga meliputi elemen atau komponen-komponen apa saja yang dibutuhkan untuk sistem yang akan dibangun sampai dengan sistem tersebut diimplementasikan. Analisis kebutuhan ini juga menentukan spesifikasi masukan yang diperlukan sistem, keluaran yang akan dihasilkan sistem dan proses yang dibutuhkan untuk mengolah masukan sehingga menghasilkan suatu keluaran yang diinginkan.

3.1.3.1 Analisis Input

Sebuah sistem harus memiliki masukkan agar menghasilkan sesuatu. Masukkan (input) dari user bagi aplikasi ini adalah fungsi aljabar rasional dalam bentuk ekspresi matematika, titik sampel, batasan fungsi, pilihan dimensi integral, nilai pembagian interval untuk metode MISERMonte Carlo, dan fungsi hampiran p(x) untuk metode VEGASMonte Carlo.

Bentuk input memiliki aturan tertentu agar fungsi yang akan dimasukkan nanti dapat diterima oleh sistem. Aturan bentuk input adalah sebagai berikut :

1. Fungsi integral yang dimasukkan adalah fungsi aljabar rasional yang didalamnya hanya mengandung operator ^, *, /, +, -.

2. Fungsi aljabar yang dimasukkan maksimal mengandung dua variabel. 3. Batas maksimal input fungsi aljabar adalah 15 digit.

4. Batas atas dan batas bawah fungsi bertipe data integer, dengan batas atas harus selalu lebih besar dari batas bawah dan inputan berupa bilangan bulat positif dari 0-99.

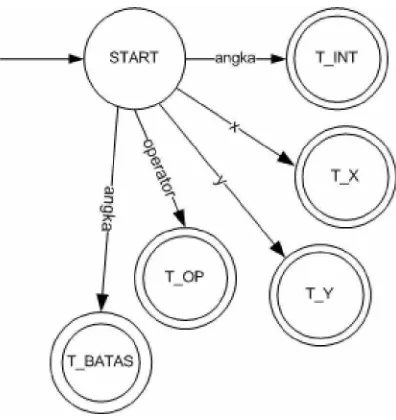
3.1.3.1.1 Analisis Leksikal

[image:51.612.220.418.103.313.2]

Gambar 3.1 State Diagram

3.1.3.1.2 Analisis Sintaksis

Analisis sintaksis merupakan kelanjutan dari analisis leksikal yang mengubah prosedur scan ke dalam bentuk token beserta parsing-nya. Di bagian ini akan dibahas contoh bentuk masukan dan mencari bentuk BNF (Backus Naur Form) dan diagram sintaksnya.

3.1.3.1.2.1 Token

Contoh bentuk input : (2*x*y)+( x^2) -(x^(1/2)). Dari contoh diatas dapat dianalisa sintaks :

V = { <exp>, <operand>, <operator>, <delimeter>, <batas> }

T = {t_INT, t_X, t_Y, t_BATAS, t_PLUS, t_MIN, t_MUL, t_DIV, t_SQR, t_LPARENT, t_RPARENT}

P =

<exp> ::= <operand> <operator> <operand> | <operand> <operator> <operand> <operator> <operand> | <operand> <operator> <delimeter> <operand> <operator> <operand> <delimeter> | <delimeter> <operand> <operator> <operand> <delimeter> <operator> <operand> | <operand> <operator> <delimeter> <operand> <operator> <delimeter> <operand> <operator> <operand> <delimeter> <delimeter>

<delimeter> ::= t_LPARENT | t_RPARENT

<operator> ::= t_PLUS | t_MIN | t_MUL | t_DIV | t_SQR <operand> ::= t_INT | t_X | t_Y

<batas> ::= t_BATAS t_INT ::= 0..9

t_BATAS ::= 0..99 t_X ::= x

t_Y ::= y

Dari bentuk BNF diatas maka dapat dibentuk diagram sintaksnya sebagai berikut :

Gambar 3.2 Diagram Sintaks Exp Lipat1

[image:53.612.237.405.103.275.2]

Gambar 3.4 Diagram Sintaks Operand

[image:53.612.236.404.317.640.2]

[image:54.612.235.405.105.225.2]

Gambar 3.6 Diagram Sintaks Delimeter 3.1.3.1.2.2 Parsing

Ekspresi aritmatika yang digunakan di dalam perangkat lunak adalah ekspresi aritmatika dalam bentuk notasi infix. Notasi infix merupakan cara penulisan ekspresi aritmatika, dimana operator diletakkan di tengah-tengah atau di antara operand-operand. Operator merupakan fungsi pangkat, kali, bagi, tambah dan kurang, sedangkan operand adalah angka atau variabel. Contoh notasiinfix: (a + b) / 2.

Misalkan, fungsix yang akan diintegralkan adalah sebagai berikut:

3 / 2

3 / 1

1

x

x

+

Maka, ekspresi aritmatika dari fungsix di atas dapat ditulis dalam bentuk notasi infixsebagai berikut:

((1 +

x

^(1/3)) ^ (1/2)) / (

x

^(2/3))

sebelah kiri ke sebelah kanan. Ekspresi aritmatika yang di-input oleh user harus dipecah menjadi sub-sub ekspresi aritmatika yang paling sederhana (terdiri atas 1 operator dan 2 operand), supaya perangkat lunak dapat menyelesaikan ekspresi aritmatika tersebut. Pemecahan ekspresi aritmatika ke bentuk sub-sub ekspresi aritmatika harus mengikuti urutan atau prioritas operasi. Operasi dengan prioritas yang lebih tinggi harus dikerjakan terlebih dahulu. Berikut adalah prioritas pengerjaan operasi dari yang tertinggi sampai prioritas yang paling rendah:

1. Operasi perpangkatan.

Operasi perpangkatan adalah operasi yang memiliki prioritas tertinggi dan akan dikerjakan terlebih dahulu. Operasi pangkat dilambangkan dengan tanda ^.

2. Operasi perkalian dan pembagian.

Kedua operasi ini memiliki prioritas tertinggi setelah operasi perpangkatan. Operasi perkalian dilambangkan dengan tanda *, sedangkan operasi pembagian dilambangkan dengan tanda/.

3. Operasi penambahan dan pengurangan.

Kedua operasi ini merupakan operasi yang paling akhir dikerjakan. Operasi penambahan dilambangkan dengan tanda +, sedangkan operasi pengurangan dilambangkan dengan tanda-.

aritmatika akan disimpan dalam bentuk E[n] = <operand> <operator> <operand>.

Secara umum, cara kerja algoritma untuk memeriksa validasi struktur ekspresi aritmatika (apakah benar atau tidak) dan sekaligus memecah ekspresi aritmatika menjadi sub-sub ekspresi adalah sebagai berikut:

1. Periksa apakah fungsi integral masih kosong. Bila ya, maka munculkan pesan kesalahan dan keluar dari algoritma.

2. Periksa apakah jumlah tanda kurung buka ‘(‘ sama dengan tanda kurung tutup ‘)’. Bila tidak sama, maka munculkan pesan kesalahan dan keluar dari algoritma.

3. Carilah tanda kurung tutup yang pertama ‘)’, dimulai dari ekspresi aritmatika yang paling kiri. Kemudian, cari tanda kurung buka ‘(’ yang ada di depan tanda kurung tutup tersebut. Sub ekspresi yang berada di antara kedua tanda kurung tersebut di-passing ke langkah ke-4. Bila tidak terdapat tanda kurung, makapassing semua ekspresi aritmatika ke langkah ke-4.

4. Bentuklah sub ekspresi baru (dalam bentuk E[n]) dari sub ekspresi yang dihasilkan pada langkah-3, dengan mengikuti prosedur berikut:

b. Cari operator kali (‘*’) atau operator bagi (‘/’) di dalam ekspresi aritmatika. Apabila ditemukan operasi tersebut, maka konversi sub ekspresi aritmatika ke bentukE[n] =a * b atau E[n] = a / b. Apabila tidak ditemukan operasi kali atau operasi bagi, maka lanjutkan ke poin 4c. Periksa juga bahwa operasi harus diapit oleh 2 operand atau 2 angka. Bila tidak, maka munculkan pesan kesalahan dan keluar dari algoritma.

c. Cari operator tambah (‘+’) atau operator kurang (‘-’) di dalam ekspresi aritmatika. Apabila ditemukan operasi tersebut, maka konversi sub ekspresi aritmatika ke bentukE[n] =a +b atau E[n] =a –b. Periksa juga bahwa operasi harus diapit oleh 2 operand atau 2 angka. Bila tidak, maka munculkan pesan kesalahan dan keluar dari algoritma. 5. Ulangi proses di atas hingga ekspresi aritmatika selesai dikonversi ke dalam

bentukE[n].

Agar lebih jelas, coba perhatikan contoh berikut ini. Misalkan ekspresi aritmatika yang akan dipecah adalah ((1 + x^(1/3)) ^ (1/2)) / (x^(2/3)), maka langkah-langkah pemecahan ekspresi aritmatika ke bentuk sub ekspresi adalah sebagai berikut:

Langkah-1:

Langkah-2:

Bentuk sub ekspresi baru, E[2] = x ^ E[1].

Langkah-3:

Bentuk sub ekspresi baru, E[3] = 1 + E[2].

Langkah-4:

Bentuk sub ekspresi baru, E[4] = 1 / 2.

Langkah-5:

Langkah-6:

Bentuk sub ekspresi baru, E[6] = 2 / 3.

Langkah-7:

Bentuk sub ekspresi baru, E[7] = x ^ E[6].

Langkah-8:

Pada langkah ke-8, ekspresi aritmatika sudah selesai dipecah menjadi sub-sub ekspresi dalam bentukE[n]. Secara umum, proses pemecahan ekspresi aritmatika di atas dapat juga digambarkan sekaligus sebagai berikut:

Dengan demikian, hasil pemecahan ekspresi aritmatika ((1 + x^(1/3)) ^ (1/2)) / (x^(2/3))ke bentuk sub ekspresi aritmatika adalah sebagai berikut:

Misalkan, nilai x = 1, maka hasil perhitungan dari ekspresi aritmatika ((1 + x^(1/3)) ^ (1/2)) / (x^(2/3)), dengan menggunakan sub ekspresi aritmatika adalah sebagai berikut:

1. E[1] = 1 / 3 = 0.33333

2. E[2] = x ^ E[1] = 1 ^ 0.33333 = 1 3. E[3] = 1 + E[2] = 1 + 1 = 2 4. E[4] = 1 / 2 = 0.5

5. E[5] = E[3] ^ E[4] = 2 ^ 0.5 = 1.4142 6. E[6] = 2 / 3 = 0.66667

7. E[7] = x ^ E[6] = 1 ^ 0.66667 = 1 8. E[8] = E[5] / E[7] = 1.4142 / 1 = 1.4142

Ini berarti, fungsi ((1 + x^(1/3)) ^ (1/2)) / (x^(2/3)) akan menghasilkan nilai 1.4142, untukx = 1.

3.1.3.1.2 Analisis Semantik

Analisis semantik bertugas untuk mengubah hasil parsing ke dalam kode antara atau intermediate code agar masukan yang dimasukkan user dapat dibaca oleh mesin. Terdapat dua macam kode antara, yaitu Notasi Postfix dan N-Tuple. Sistem ini akan menggunakan notasiQuadruple dengan format

<operator> <operand> <operand> <hasil>

Hasil adalahtemporary variable yang bisa ditempatkan pada memory atau register. Contoh instruksi :

Bentuk kode antaranya adalah : 1. /, 1, 3, E[1]

2. ^, x, E[1], E[2] 3. +, 1, E[2], E[3] 4. /, 1, 2, E[4] 5. ^, E[3], E[4], E[5] 6. /, 2, 3, E[6] 7. ^, x, E[6], E[7] 8. /, E[5], E[7], E[8]

Pada kode antara di atas dapat dijelaskan, kode antara nomor satu adalah membagi 1 dengan tiga dan menyimpannya di E[1]. Kode antara nomor dua adalah memangkatkan variabel x dengan hasil dari kode antara nomor satu yang tersimpan di E[1], dan seterusnya.

Selanjutnya adalah melakukan pembangkitan kode (code generation) dengan mengubah kode antara di atas ke dalam bahasa mesin.

Contoh : Kita akan mengubah kode antara 1 dan 2 ke dalam bahasa mesin. LDA 1

DIV 3 STO E[1] LDA x SQR E[1] STO E[2]

3.1.3.2 Analisis Output

3.1.3.3 Analisis Kebutuhan Perangkat Keras

Agar aplikasi dapat berjalan dengan baik, maka dibutuhkan perangkat keras yang sesuai dengan kebutuhan aplikasi. Adapun perangkat keras yang dibutuhkan oleh pengguna (user) agar dapat menjalankan aplikasi ini adalah sebagai berikut :

Tabel 3.1 Spesifikasi Perangkat Keras

Spesifikasi

Prosesor 1.7 MHz Monitor SVGA 14“ Memori 256 MB Harddisk 40 GB Papan ketik (keyboard) Tetikus (Mouse)

3.1.3.4 Analisis Kebutuhan Perangkat Lunak

Sistem dibangun pada Sistem Operasi Windows XP Service Pack 2. Sedangkan tools yang dipakai untuk membangun aplikasi adalah Microsoft Visual Basic 6.0.

3.1.3.5 Analisis Pengguna (User)

secara sederhana, menarik dan interaktif agar pengguna dapat mengoperasikannya dengan mudah (user friendly).

3.2 Analisis Kebutuhan Fungsional

Perancangan sistem merupakan suatu proses yang mengaplikasikan berbagai teknik dan prinsip yang bertujuan mendefinisikan kebutuhan suatu sistem sedemikian detail sehingga mendekati keadaan fisik yang sebenarnya dan untuk menghasilkan sesuatu yang baru atau memperbaharui sistem yang ada untuk meningkatkan efektifitas kerja yang sesuai dengan teknologi dan fasilitas yang tersedia. Dimana suatu perancangan sistem informasi merupakan suatu langkah awal dalam pembuatan suatu sistem sehingga perlu diperhatikan kebutuhan dari sistem atausoftware yang diharapkan.

3.2.2 Diagram Konteks Sistem

Berikut adalah context diagram atau diagram konteks dari sistem yang akan dibangun.

3.2.3 Data Flow Diagram (DFD)

Data flow diagram merupakan model dari sistem untuk menggambarkan pembagian sistem ke model yang lebih kecil. Berikut ini adalah gambar data flow diagram untuk aplikasi pencarian hasil integral multidimensi menggunakan metodeMonte Carlo.

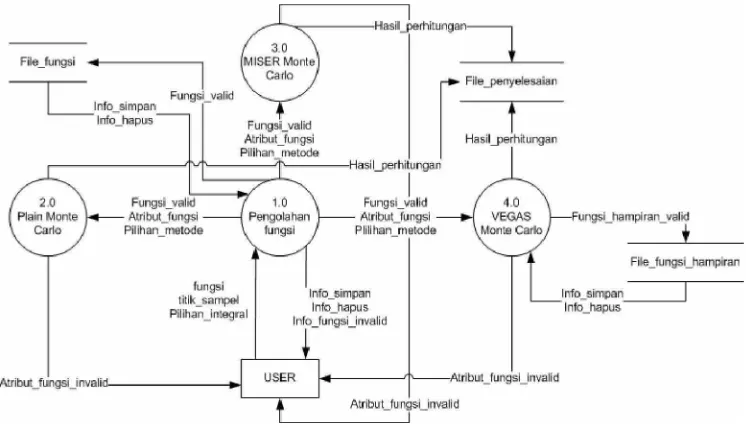
3.2.3.1 DFD Level 0

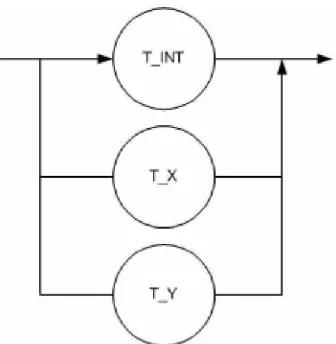
[image:65.612.133.506.338.552.2]

Berikut adalah DFD level 1 dari diagram konteks di atas. DFD level 1 ini menggambarkan proses yang lebih lengkap dari diagram konteks yang telah ada.

3.2.3.2 DFD Level 1

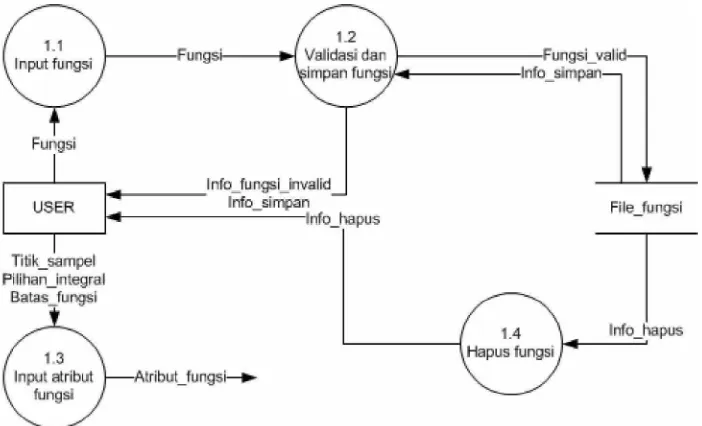
Berikut adalah DFD level 2 dari DFD level 1. DFD level 2 ini menggambarkan proses yang lebih lengkap yang terjadi pada DFD level 1 proses 1 (pengolahan fungsi).

Gambar 3.9 DFD Level 1 Proses 1

[image:66.612.144.495.234.447.2]

DFD level 2 ini menggambarkan proses yang lebih lengkap yang terjadi pada DFD level 1 proses 2 (plain monte carlo).

DFD level 2 ini menggambarkan proses yang lebih lengkap yang terjadi pada DFD level 1 proses 2 (miser monte carlo).

Gambar 3.11 DFD Level 1 Proses 3

DFD level 2 ini menggambarkan proses yang lebih lengkap yang terjadi pada DFD level 1 proses 2 (vegas monte carlo).

3.2.4 Spesifikasi Proses

Spesifikasi proses digunakan untuk menggambarkan proses model aliran yang terdapat pada DFD. Spesifikasi tersebut meliput :

Tabel 3.2 Spesifikasi Proses

No Proses Keterangan

No Proses 1.2

Nama Proses Validasi dan Simpan Fungsi

Input fungsi

Output fungsi_valid

1 Logika Proses Begin

If input_fungsi valid and simpan_fungsi Then fungsi_valid and fungsi_tersimpan Else

Notifikasi (fungsi salah) End

No Proses Keterangan

No Proses 1.4

Nama Proses Hapus fungsi

Input fungsi_valid

Output Info_hapus

2

Logika Proses Begin

If Hapus_fungsi Then fungsi terhapus End

No Proses Keterangan

No Proses 2.1

Nama Proses Hitung Plain MC

Input fungsi_valid

Output Hasil_perhitungan

3

Logika Proses Sum = 0

For (i = 0 ; i <= n ; i = i+1) do Presum = f(xi)

Sum = presum + sum Mean = sum / n End

Delta = b-a

Approx = Mean*Delta

No Proses Keterangan

No Proses 3.2

Nama Proses Hitung MISER MC 4

pembagian_interval_valid

Output Hasil_perhitungan

Logika Proses Begin

If input_pembagian_interval valid Then pembagian_interval_valid Sum = 0

Delta = b-a

Disjoint = delta / 2 Disjoint1 = disjoint - a Disjoint2 = b - disjoint For (i = 0 ; i <= n ; i = i+1) do Presum = f(xi)

Sum = presum + sum Mean = sum / n End

Approx1 = Mean*Disjoint1 Approx2 = Mean*Disjoint2 Approx = Approx1+Approx2 Else

Notifikasi (pembagian_interval salah) End

No Proses Keterangan

No Proses 4.2

Nama Proses Validasi dan simpan fungsi hampiran

Input fungsi_hampiran

Output Fungsi_hampiran_valid

5

Logika Proses Begin

If input_fungsi_hampiran valid and simpan_fungsi

Then fungsi_hampiran_valid and fungsi_tersimpan

Else

Notifikasi (fungsi salah) End

No Proses Keterangan

No Proses 4.4

Nama Proses Perhitungan VEGAS MC

Input fungsi_valid

Output Hasil_perhitungan

6 Logika Proses Sum = 0

For (i = 0 ; i <= n ; i = i+1) do Presum = f(xi) / p(xi)

Delta = b-a

Approx = Mean*Delta

3.2.5 Kamus Data

Kamus data atau data dictionary adalah katalog fakta tentang data dan kebutuhan-kebutuhan informasi dari suatu sistem informasi. Dengan menggunakan kamus data, dapat menggambarkan data yang mengalir di sistem dengan lengkap.

Kamus data dibuat berdasarkan arus data yang ada di diagram alir data (DFD). Arus data di diagram alir data sifatnya adalah global, hanya menunjukan nama arus data-datanya saja.

Kamus data dari aplikasi pencarian hasil integral adalah sebagai berikut :

Tabel 3.3 Kamus Data

Nama fungsi

Where used / how used

Proses 1.1 – Input fungsi (input)

Proses 1.2 – Validasi dan simpan fungsi (input) Deskripsi Berisi data fungsi yang diinput oleh user Struktur data Fungsi

Fungsi [ x – y | 0 – 9 | + | - | * | / | ^ ]

Nama Fungsi_valid

Where used / how used

Proses 1.2 – Validasi dan simpan fungsi (output)

Deskripsi Berisi data fungsi yang diinput oleh user Struktur data Fungsi

Fungsi [ x – y | 0 – 9 | + | - | * | / | ^ ]

Nama titik_sampel

Where used / how used

Proses 1.0 – Pengolahan fungsi (input) Deskripsi Berisi data titik sampel yang diinput oleh user Struktur data n

Nama batasan_fungsi Where used /

how used

Proses 1.0 – Pengolahan fungsi (input) Deskripsi Berisi batasan fungsi yang diinput oleh user Struktur data x1+x2+y1+y2

x1 x2 y1 y2

[ 0-9 ] [ 0-9 ] [ 0-9 ] [ 0-9 ]

Nama pembagian_interval Where used /

how used

Proses 3.1 – Input pembagian interval (input)

Proses 3.2 – Validasi pembagian interval dan Hitung MISER MC (input)

Deskripsi Berisi pembagian interval yang diinput oleh user Struktur data M

m [ 0-9 ]

Nama Pembagian_interval_valid Where used /

how used

Proses 3.2 – Validasi pembagian interval dan Hitung MISER MC (output)

Deskripsi Berisi pembagian interval yang diinput oleh user Struktur data M

m [ 0-9 ]

Nama fungsi_hampiran

Where used / how used

Proses 4.1 – Input fungsi (input)

Proses 4.2 – Validasi dan simpan fungsi (input) Deskripsi Berisi data fungsi hampiran yang diinput oleh user Struktur data Fungsi

Fungsi [ x – y | 0 – 9 | + | - | * | / | ^ ]

Nama Fungsi_hampiran_valid Where used /

how used

Proses 4.2 – Validasi dan simpan fungsi (output) Proses 4.4 – Hitung Vegas MC (input)

Deskripsi Berisi data fungsi hampiran yang diinput oleh user Struktur data Fungsi

Fungsi [ x – y | 0 – 9 | + | - | * | / | ^ ]

Nama Info_simpan

Where used / how used

Proses 1.2 – Validasi dan Simpan fungsi (output)

Proses 4.2 – Validasi dan Simpan fungsi hampiran (output) Deskripsi Berisi notifikasi simpan

Nama Info_hapus Where used /

how used

Proses 1.4 – Hapus fungsi (output) Proses 4.3 – Hapus fungsi (output) Deskripsi Berisi notifikasi hapus

Struktur data

Nama Hasil_perhitungan

Where used / how used

Proses 2.2 – Simpan Penyelesaian (input) Proses 3.3 – Simpan Penyelesaian (input) Proses 4.5 – Simpan Penyelesaian (input) Deskripsi Berisi nilai hampiran hasil perhitungan Struktur data Nilai_hampiran

Nilai_hampiran [ 0-9 ]

Nama Pilihan integral Where used /

how used

Proses 1.0 – Pengolahan fungsi (input)

Deskripsi Berisi pilihan dimensi integral Struktur data

Nama Info_fungsi_invalid Where used /

how used

Proses 1.2 – Analisis semantik (output)

Deskripsi Berisi info data fungsi yang diinput oleh user salah Struktur data

Nama Info_fungsi__hampiran_invalid Where used /

how used

Proses 4.2 – Analisis semantik (output)

Deskripsi Berisi info data fungsi hampiran yang diinput oleh user salah Struktur data

Nama Info_pembagian_interval_invalid Where used /

how used

Proses 3.2 – Pemeriksaan pembagian interval (output)

Deskripsi Berisi info data pembagian interval yang diinput oleh user salah

Struktur data

Nama Atribut_fungsi_invalid Where used /

how used

Proses 2.0 – Plain MC (output) Proses 3.0 – Plain MC (output) Proses 4.0 – Plain MC (output)

3.3 Perancangan Menu Aplikasi

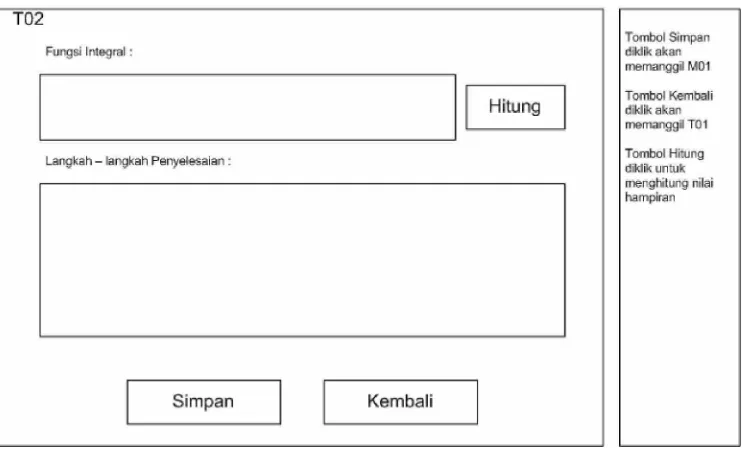
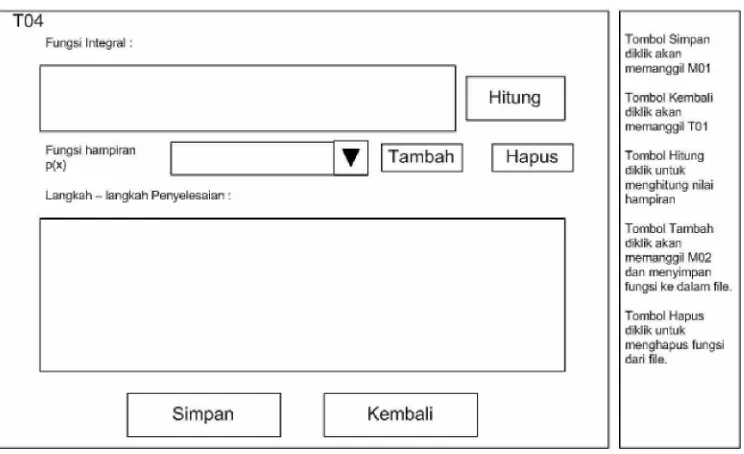
Perancangan menu aplikasi digunakan untuk menjelaskan menu, submenu yang terdapat di dalam sistem, agar pengguna dapat lebih mudah dalam menggunakanya.

Gambar 3.13 Bagan Menu

Menu ini dapat diakses oleh user / pengguna. Menu ini berguna untuk mengelola data sistem. Masukkan dilakukan di dalam menu, namun ada beberapa masukan tambahan bagi tiap metode karena berbeda metode berbeda pula masukannya. Menu ini memiliki fasilitas :

1. Plain MC

Di dalam submenu ini user tidak perlu memasukkan masukan tambahan,

karena semua input yang diperlukan sudah diinputkan di bagian menu. 2. MISER MC

3. VEGAS MC

Di dalam submenu ini user perlu memasukkan masukan tambahan berupa fungsi hampiran, karena metode VegasMonte Carlo memerlukan masuka