UJIAN TENGAH SEMESTER
METODE STATISTIKA (STK211)
Perhatikan:
a. Waktu yang disediakan untuk mengerjakan soal selama 120 menit
b. Ujian diselenggarakan dengan catatan tertutup, mahasiswa hanya diijinkan membawa alat tulis, penghapus, penggaris dan kalkulator
c. Kerjakan soal sendiri, dilarang mendiskusikan soal dengan sesama peserta. Bila ada soal yang tidak jelas tanyakan langsung pada pengawas ujian. d. Jawablah soal pada lembar jawaban yang telah disediakan panitia ujian e. Tuliskan nama, nrp, program studi dan tipe soal pada tempat yang telah
disediakan
I. Silanglah huruf B bila menurut Anda pernyataannya benar dan S bila pernyataannya salah. Untuk jawaban benar diberi nilai 2, jawaban salah diberi nilai -1 dan jika tidak menjawab diberi nilai 0.
N o
Pernyataan Jawaban
1 Median adalah ukuran pemusatan yang sensitive terhadap data ekstrim, sedangkan nilai tengah (mean) adalah ukuran pemusatan data yang kekar (robust) terhadap nilai ekstrem. diagram kotak garis (box-plot) dan plot titik (dot plot)
B S
kontinu yang berbentuk lonceng, simetri terhadap ragam 25, maka peluang pada saat X bernilai 100 adalah 0.5.
B S
12 Sebaran peluang populasi dari peubah acak diskrit
antara lain Bernoulli, Binomial dan Normal B S 13 Nilai harapan dari peubah acak kontinu
merupakan jumlah hasil kali antara nilai peubah acak tersebut dengan peluang kejadiannya.
B S
14 Seorang pengembang menawarkan 4 jenis disain rumah, yaitu mawar (lb 36/ lt 70), melati (lb 45/lt 90), soka (lb 52/lt 110) dan kenari (lb 70/ lb 120). Rumah tersebut dapat dibangun di pusat kota, di pantai atau di perbukitan. Jumlah kemungkinan
II. Silanglah huruf A, B, C atau D yang menurut Anda paling tepat untuk pernyataan-pernyataan dibawah ini. Untuk jawaban benar diberi nilai 2, jawaban salah diberi nilai -1 dan jika tidak menjawab diberi nilai 0
1. Dari contoh acak berukuran 5 diperoleh X={50, 60, 70, 80, 90}. Rata-rata dan ragam dari data tersebut adalah:
A. 68 dan 15.8 B. 70 dan 250 C. 70 dan 15.8 D. 80 dan 250
2. Empat dari 5 pengamatan diketahui sebagai berikut: X={…, 20, 20, 30, 40}. Dari catatan yang tertingggal diperoleh rata-rata kelima pengamatan sebesar 30. Pengamatan yang hilang adalah sebesar:
A. 5 B. 0 C. 10 D. Semua jawaban salah
dikalikan 10 dan pengamatan terbesarnya dikalikan 100 maka median setiap ibu yang akan melahirkan dipastikan hanya melahirkan seorang bayi)
A. 0.125 B. 0.250 C. 0.500 D. 0.875
5. Jika x1, x2, …,x10 memiliki rata-rata 10 maka rata-rata dari x1/2+1, x2/2+2, …., x10/2+10 adalah:
A. 10.5 B. 60 C. 55 D. 10 6. Peubah acak X memiliki nilai harapan sebesar 10 dan ragam 4. Jika
diketahui Y = 2X – 5 maka besarnya ragam peubah acak Y adalah:
A. 3 B. 8 C. 11 D. 16
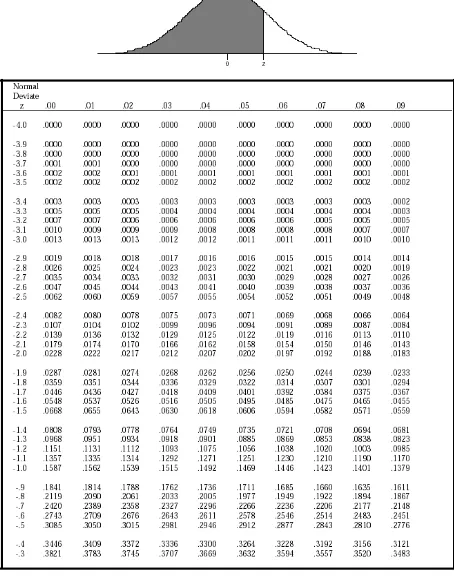
7. Berat badan mahasiswi IPB menyebar normal dengan nilai tengah (mean) sebesar 50 Kg dan simpangan baku (standard deviation) sebesar 5 Kg. Seorang mahasiswi IPB menimbang berat badannya, berapakah peluang berat badan mahasiswi tesebut sebesar 60 Kg.
A. 0.02275 B. 0 C. 0.95 C. 0.97725
8. Kiriman uang per bulan dari orang tua yang diterima mahasiswa menyebar normal dengan nilai tengah (mean) sebesar 500 ribu rupiah dan simpangan baku sebesar 100 ribu rupiah. Jika diketahui terdapat 5% mahasiswa mendapat kiriman uang terendah, tentukanlah batas kiriman uang tertinggi dari kelompok mahasiswa tersebut: (dalam satuan ribu rupiah)
A. 394.0 B 335.5 C. 664.5 D. 695.0
9. Distribusi peluang dari peubah acak X diperoleh sebagai berikut adalah:
0. Dalam suatu percobaan, salah satu respon yang diukur adalah jumlahtanaman yang terserang penyakit (Y). Jika kejadian penyakit antar tanaman diasumsikan saling bebas maka sebaran peluang peubah respon Y adalah:
A. Bernoulli B. Binomial C. Normal D. Weibull 1
1. Peluang seorang mahasiswa lulus kuliah Matematika adalah 2/3, sedangkan peluang lulusnya kuliah Metode Statistika adalah 4/9. Jika kelulusan matematika dan statistika saling bebas, berapakah peluang lulus sedikitnya satu dari kedua matakuliah tersebut:
A. -0.31 B. 0.81 C. 0.80 D. 0.31 1
2.
Dari suatu data pengamatan diketahui mediannya sebesar 5 dan rata-ratanya sebesar 20. Berdasarkan informasi tersebut maka sebaran data pengamatan yang paling sesuai adalah:
C. Menjulur ke kiri D. Tidak ada jawaban yang sesuai
1 3.
Hasil pengukuran yang diperoleh dengan skala pengukuran interval tidak dapat digunakan untuk:
A. Mengklasifikasikan B. Mengurutkan C. Membedakan D. Memperbandingkan 1
4. Peluang suatu penerbangan yang telah terjadwal teratur berangkattepat waktu P(B) = 0,83; peluang sampai tepat waktu P(S)=0,82 dan peluang berangkat dan sampai tepat waktu P(B∩S) = 0,78. Peluang bahwa pesawat sampai tepat waktu bila diketahui berangkat tepat waktu adalah:
III.
Jawablah soal-soal berikut dengan singkat dan jelas
Jawablah soal-soal berikut dengan singkat dan jelas
3.1.
a. Hitunglah nilai tengah (Hitunglah nilai tengah (mean) dan ragam dari data tersebut. mean) dan ragam dari data tersebut.
b. diketahui menyebar normal dengan nilai tengah 5 mg dengan ragam 0.0625 diketahui menyebar normal dengan nilai tengah 5 mg dengan ragam 0.0625 mg2. Hitunglah:
mg2. Hitunglah: a.
a. Peluang kandungan vitamin B12 dalam suatu minuman energy kurangPeluang kandungan vitamin B12 dalam suatu minuman energy kurang dari 5 mg
dari 5 mg
b.
d.
d. Jika ingin dibuat kategori kandungan vitamin B12 dalam berbagaiJika ingin dibuat kategori kandungan vitamin B12 dalam berbagai minuman energy yang beredar di pasaran, dengan ketentuan 10% minuman energy yang beredar di pasaran, dengan ketentuan 10% berkadar sangat tinggi, 30% berkadar tinggi, 50% berkadar sedang berkadar sangat tinggi, 30% berkadar tinggi, 50% berkadar sedang dan sisanya berkadar rendah. Tentukanlah batasan kandungan dan sisanya berkadar rendah. Tentukanlah batasan kandungan vitamin B12 untuk setiap kategori.
vitamin B12 untuk setiap kategori.
(