DIMENSI PARTISI GRAF AMALGAMASI BINTANG nS_(m,k)

(1)

PARTITION DIMENSION OF AMALGAMATION OF STARS GRAPH Abstract

by Ana Istiani

Given graph G = (V,E), and . The distance between v and

S is d(v,S) = { }, where is the distance from v to x. Let = { } as the partition of V(G). The representation of v with respect

to is the k-vectors r(v| Π) = (d(v, S1), d(v, S2),..., d(v, Sk)).The partition is called as a resolving partition of if ∣ ∣ for every two different vertices of V(G). The partition dimension of G, written as pd(G) is the minimum k

for which there is a resolving k-partition. The amalgamation of star graphs obtained from n copies of amalgamation stars by connecting a leaf from each

through a path. The result of the research is ( ) {

for k ≥ m.

(2)

DIMENSI PARTISI GRAF AMALGAMASI BINTANG

Abstrak

Oleh Ana Istiani

Misalkan G = (V,E) suatu graf, dan . Jarak dari titik v ke himpunan S, dinotasikan dengan d(v,S) adalah { } dengan adalah jarak dari titik v ke x. Misalkan { } adalah partisi dari V(G). Representasi v terhadap dinotasikan dengan ∣ adalah

k - pasang terurut ( ). Selanjutnya disebut partisi pembeda dari V(G) jika ∣ ∣ untuk setiap dua titik berbeda u, . Dimensi partisi dari G, dinotasikan dengan pd (G), adalah nilai k terkecil sehingga G mempunyai partisi pembeda dengan k kelas. Graf amalgamasi bintang

diperoleh dari n buah graf amalgamasi bintang dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan. Hasil dari

penelitian ini adalah ( ) {

untuk k ≥ m.

(3)

DIMENSI PARTISI GRAF AMALGAMASI BINTANG

Oleh

Ana Istiani

Tesis

Sebagai Salah Satu Syarat Untuk Memperoleh Gelar

Magister Sains

Pada

Jurusan Matematika Program Studi Magister Matematika

Fakultas Matematika Dan Ilmu Pengetahuan Alam

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(4)

DIMENSI PARTISI GRAF AMALGAMASI BINTANG

TESIS

Oleh

Ana Istiani

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(5)

DAFTAR GAMBAR

Gambar Halaman

1. Jembatan Konigsberg ... 1

2. Graf ... 4

3. Contoh graf dengan 5 titik dan 7 sisi ... 6

4. Contoh graf lengkap ... 8

5. Contoh graf tak lengkap ... 8

6. Contoh Lintasan ... 8

7. Graf Terhubung ... 9

8. Graf Tak Terhubung ... 9

9. Contoh pohon G dengan enam titik ... 10

10. Contoh Hutan ... 10

11. Graf Bintang ... 12

12. Graf Bintang Ganda ... 13

13. Contoh graf Ulat ... 13

14. Dimensi Partisi Graf G ... 14

15. Dimensi Partisi Graf Bintang ... 17

16. Dimensi Partisi Graf Ulat , ... 18

17. Dimensi Partisi Graf Ulat ... 19

(6)

19. Partisi Pembeda pada Graf untuk n ≤ 4 ... 26

20. Partisi Pembeda pada Graf untuk n lainnya ... 27

21. Partisi Pembeda pada Graf ... 28

22. Partisi Pembeda pada Graf untuk n = 1 ... 29

23. Partisi Pembeda pada Graf ... 30

25. Partisi Pembeda pada Graf untuk n ≥ 1 ... 32

27. Partisi Pembeda pada Graf untuk n ≥ 2 ... 34

28. Partisi Pembeda pada Graf untuk n ≤ 4 ... 35

29. Partisi Pembeda pada Graf untuk n lainnya ... 36

30. Partisi Pembeda pada graf nS2,2 ... 38

31. Partisi Pembeda pada graf S2,3 untuk n = 1 ... 39

32. Partisi Pembeda pada graf nS2,3 untuk n ≥ 2 ... 40

33. Partisi Pembeda pada graf nS2,4 untuk n = 1 ... 41

35. Partisi Pembeda pada graf nS2,k untuk n =1 ... 43

36. Partisi Pembeda pada graf nS2,k untuk n lainnya ... 44

(7)

43. Partisi Pembeda pada graf nS3,kuntuk n ≥ ... 52

51. Partisi Pembeda pada graf nS5,kuntuk 1≤ n ≤ ... 63

52. Partisi Pembeda pada graf nS5,kuntuk n ≥ ... 64

53. Partisi Pembeda pada graf nS5,8untuk 1≤ n ≤ ... 65

54. Partisi Pembeda pada graf nSm,kuntuk kasus 1≤ n ≤ - ... 68

55. Partisi Pembeda pada graf nSm,k untuk kasus n lainnya ... 70

56. Kontruksi graf ... 70

(8)

DAFTAR ISI

Halaman

DAFTAR ISIi

DAFTAR GAMBAR

BAB I PENDAHULUAN

1.1 Latar Belakang Masalah ... 1

1.2 Batasan Masalah ... 4

1.3 Tujuan Penelitian ... 5

1.4 Manfaat Penelitian ... 5

BAB II TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf ... 6

2.2 Graf Pohon dan Beberapa Sifatnya ... 10

2.3 Dimensi Partisi Graf ... 13

BAB III METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 24

(9)

BAB IV HASIL DAN PEMBAHASAN

4.1 Dimensi Partisi Graf ( ) ... 26

(10)

4.22 Dimensi Partisi Graf ( ) ... 61 4.23 Dimensi Partisi Graf ( ) ... 63 4.24 Dimensi Partisi Graf ( ) ... 68

BAB V KESIMPULAN DAN SARAN

5.1 Kesimpulan ... 72

5.2 Saran ... 73

(11)

(12)

(13)

MOTO

Jika kita meringankan beban kesulitan hidup orang lain

InsyaAlloh Alloh akan meringankan beban kita di dunia dan

(14)

(15)

PERSEMBAHAN

Karya tulis ini kupersembahkan untuk suamiku Eko Kusmiran

Buah hatiku

(16)

RIWAYAT HIDUP

Penulis di lahirkan di desa Pandansari pada tanggal 24 Desember 1983 merupakan

anak kedua dari lima bersaudara pasangan bapak Suyut dan ibu Sugini. Pada tanggal

22 September 2005 penulis menikah dengan Eko Kusmiran dan diberi karunia tiga

orang anak, Naswa Larissa Baiduri (8 tahun), Apta Ghani Yudhistira (5 tahun),

Danendra Labib Bayusuta (2 tahun).

Pendidikan formal yang pernah ditempuh :

1. Sekolah Dasar Negeri 1 Pandansari pada tahun 1990-1996

2. Sekolah Menengah Pertama Negeri 2 Sukoharjo pada tahun 1996-1999

3. Sekolah Menengah Atas Negeri 1 Pringsewu pada tahun 1999-2002

4. S1 Pendidikan Matematika di STKIP Muhammadiyah Pringsewu Lampung

pada tahun 2002-2006

Pada tahun 2008 sampai dengan 2014 penulis bekerja sebagai guru di SD

Muhammadiyah Pringsewu dan sebagai tenaga pengajar di STKIP Muhammadiyah

(17)

SANWACANA

Rasa syukur terucap kepada Alloh SWT, sehingga penulis dapat menyelesaikan

pendidikan S2 dengan gelar Magister Sains di Universitas Lampung.

Penulis menyadari bahwa penulisan tesis ini tidak terlepas dari bantuan semua pihak.

Terimakasih penulis ucapkan kepada :

1. Ibu Dr. Asmiati, M.Si. selaku pembimbing 1 yang telah sabar dan telaten dalam

memberikan arahan dan sumbangan pemikiran dalam penulisan tesis ini.

2. Ibu Dra. Wamiliana,M.A, Ph.D. selaku pembimbing 2 yang begitu teliti dalam

memeriksa penulisan tesis ini.

3. Bapak Drs. Suharsono, M.S.,M.Sc., Ph.D. selaku pembahas yang telah

memberikan saran yang terbaik untuk penulisan tesis ini.

4. Bapak Drs. Mustofa Usman, M.A., Ph.D., selaku ketua program studi yang telah

memberikan motivasi.

5. Seluruh staf pengajar Universitas Lampung yang telah membantu penyelesaian

proses studi.

6. Ibu Dr. Triyuni Hendrowati, M.Pd yang selalu memberikan semangat dan

motivasi untuk melanjutkan studi.

7. Teman-teman STKIP Muhammadiyah Pringsewu yang memberikan dukungan

(18)

8. Kepada Orang tuaku terimakasih atas doa yang tak henti-hentinya, mbak dan

Adek-adekku yang telah mendukung studi ini.

9. Suamiku, anak-anakku Naswa, Apta, Suta yang selalu menjadi motivasi dan

penyemangat hidup terimakasih atas pengertiannya selama ini.

10. Teman-teman seperjuangan OR Club‟s (Suly, Mbak Ayu, Mbak Ike, Agus Mbak Uty, Mbak Fita, Pak Edy, Kak Permata) dan teman-teman Statistik

(Mbak Herly, Mbak Ade, Mbak Dwi, Ayu, Viviana, Rini, Pak War, Kris, Ibnu,

Rahman, Nurman, Pak Anton) yang selalu menjalin kerjasama dan kebersamaan

dalam sedih maupun senang, pengalaman kuliah yang tak terlupakan.

Penulis menyadari tesis ini masih jauh dari sempurna sehingga saran maupun kritik

yang membangun sangat diharapkan . Semoga tulisan ini dapat memberikan manfaat

dan semoga Alloh SWT memberikan keberkahan kepada semua pihak yang telah

membantu terselesainya studi ini. Aamiin Yaa Robal „Alamin.

(19)

I. PENDAHULUAN

1.1 Latar Belakang

Teori graf merupakan salah satu bagian ilmu dari matematika dan merupakan

pokok bahasan yang relatif muda jika dibandingkan dengan cabang ilmu

matematika yang lain seperti aljabar dan geometri. Teori graf pertama kali

dikenalkan pada tahun 1736 oleh seorang matematikawan Swiss yang bernama

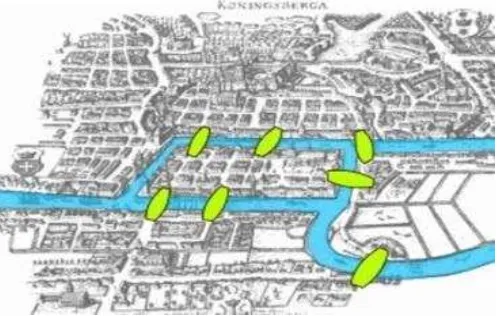
Leonard Euler untuk menyelesaikan permasalahan jembatan Konigsberg

(sekarang bernama Kaliningrad). Konigsberg merupakan suatu kota yang terletak

di bagian utara Jerman dan memberikan pengaruh besar tehadap sejarah

perkembangan teori graf. Sungai Pregel yang melalui Konigsberg membagi

wilayah daratan menjadi empat bagian. Di atas sungai Pregel dibangun tujuh

jembatan yang menghubungkan keempat wilayah tersebut. Berikut gambar dari

jembatan Konigsberg.

(20)

2

Graf merupakan kumpulan dari titik (vertex) dan sisi (edge) didefinisikan sebagai

G = (V,E). V menyatakan himpunan titik yang tak kosong dan E menyatakan

himpunan sisi yang merupakan pasangan sisi tak terurut dari titik-titik V. Setiap

sisi menghubungkan satu titik ke titik yang lain, dan setiap titik dapat

mempunyai banyak sisi yang menghubungkannya ke titikyang lain.

Banyak penelitian telah dilakukan pada graf, diantaranya pelabelan sisi,

pelabelan titik,pewarnaan graf, teori Ramsey pada graf, dimensi partisi pada graf,

dan lain-lain. Pada teori graf, terdapat cabang kajian yang disebut dimensi

metrik. Dimensi metrik pertama kali dikenalkan oleh Harary dan Melter pada

tahun 1976, kemudian dikembangkan menjadi dimensi partisi pertama kali oleh

Chartrand dkk. pada tahun 1998. Konsep dimensi partisi juga merupakan salah

satu konsep yang melatar belakangi munculnya konsep bilangan kromatik lokasi.

Misalkan G = (V,E) suatu graf, dan . Jarak dari titik v ke himpunan S, dinotasikan dengan d(v,S) adalah { } dengan

adalah jarak dari titik v ke x. Misalkan { } adalah partisi dari V(G) dengan adalah kelas-kelas partisi dari . Representasi v

terhadap dinotasikan dengan | adalah k pasang terurut

( ). Selanjutnya disebut partisi pembeda dari

V(G) jika ∣ ∣ untuk setiap dua titik berbeda u, .

Dimensi partisi dari G, dinotasikan dengan pd (G), adalah nilai k terkecil sehingga

(21)

3

Penentuan dimensi partisi dari graf terhubung sebelumnya telah dilakukan oleh

Chartrand dkk.(1998), khusus untuk kelas pohon diperoleh dimensi partisi dari

graf lintasan Pn, n ≥ 2, yaitu pd(Pn) = 2 dan graf bintang K 1,n, yaitu pd(K1,n) = n.

Dimensi Partsisi Graf bintang ganda T berorde n ≥ 6, dengan x dan y dua titik yang bukan daun, maka pd(T) = { } . Selain itu mereka mendapatkan batas atas dan batas bawah dimensi partisi dari graf ulat. Graf ulat

adalah graf pohon yang mempunyai sifat jika semua daunnya dihapus maka akan

menghasilkan lintasan (Asmiati,2012b). Penelitian terus dilakukan untuk

mendapatkan dimensi partisi graf terhubung lainnya. Kelas graf tertentu dapat

ditentukan dimensi partisinya secara tepat, tetapi pada kelas graf yang lain baru

dapat ditentukan batas atas atau batas bawahnya.

Chartrand dkk. (2000) telah mengkaji dimensi partisi pada graf bipartit Km,n dan

Tomescu dkk. (2007) untuk graf roda Wn untuk n tertentu, dimensi partisi graf

roda Wntelah dapat dilakukan secara tepat. Misalnya, pd(Wn) = 3 untuk 4 ≤ n ≤ 7 dan pd(Wn) = 4 untuk 8 ≤ n ≤ 19. Pada tahun 2011 dan 2012, Asmiati dkk. telah berhasil menentukan bilangan kromatik lokasi graf amalgamasi bintang . Selanjutnya Asmiati (2012) telah mendapatkan dimensi partisi pada graf

Amalgamasi Bintang.

Ketertarikan penulis pada penelitian ini adalah terkait masalah penentuan dimensi

(22)

4

1.2 Batasan Masalah

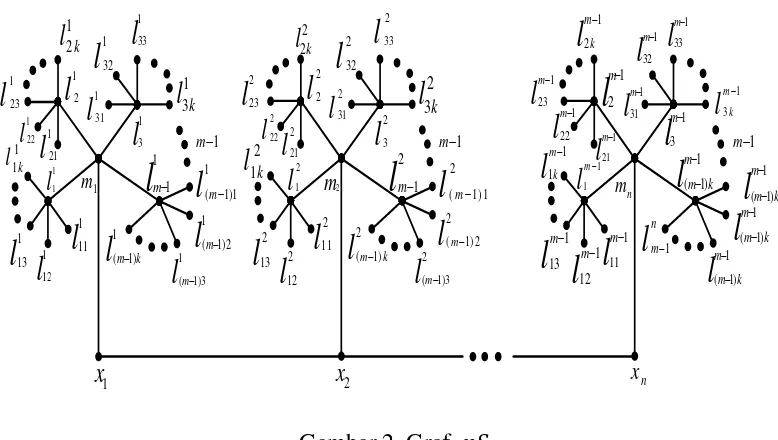
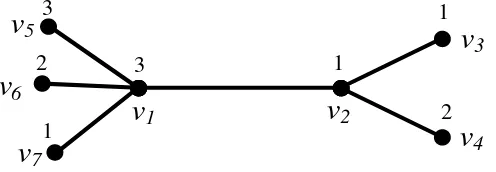
Graf amalgamasi bintang adalah graf yang diperoleh dengan mengidentifikasi sebuah daun dari setiap bintang. Titik hasil identifikasi disebut

pusat amalgamasi, dinotasikan dengan . Titik yang berjarak satu dari pusat

amalgamasi disebut titik tengah, dinotasikan dengan , dan titik daun ke- dari titik tengah adalah , . Jika dengan

untuk semua , graf bintang amalgamasi dinotasikan sebagai .

Diberikan graf sebagai berikut

1

x

1

m

l

11

l

111

l

112

l

113

1 1k

l m1

l

12

l

121

l

122

l

123

1 2k

l

13

1 3k

l

133

l

132

l

131

l

m

1 1



l

1₍_m_₁₎₁

l

m 1 2 ) 1 (

l

m 1 3 ) 1 ( 

l

m k

1 ) 1 (

l

12

l

112

l

122

l

132

2 1k

l

m1

l

22

l

221

l

222

l

223

l

32

2 3k

l

332

l

232

l

312

l

m

2 1



l

2₍_m_₁₎₁

l

m 2 2 ) 1 ( 

l

m 2 3 ) 1 ( 

l

m k

2 ) 1 (  2

x

m2 2 2k

l

1  m n x n m

l

1m1



l

11m1



l

12m1



l

13m1



l

mk

1 1



l

m21



l

m211 

l

m221



l

m231 

l

mk

1 2



l

m31



l

31m1 

l

32m1



l

m₃₃1

l

mk

1 3



l

mm k

1 ) 1 (

 

l

m

k m 1 ) 1 (  

l

mm k

1 ) 1 (  

l

mm k

1 ) 1 (  

l

nm1

Gambar 2. Graf

Pada penelitian ini akan ditentukan dimensi partisi graf nSm,k , untuk setiap n,m,k

(23)

5

1.3 Tujuan Penelitian

Tujuan dari penelitian tugas akhir ini adalah menentukan dimensi partisi dari graf

amalgamasi bintang nSm,k untuk n,m,k sebarang bilangan asli.

1.4 Manfaat Penelitian

Manfaat yang didapat dari penelitian ini adalah sebagai berikut:

1. Mengembangkan wawasan tentang teori graf terutama tentang dimensi partisi

dari graf amalgamasi bintang .

2. Memberikan sumbangan pemikiran untuk memperluas dan memperdalam

ilmu matematika dalam bidang teori graf terutama tentang dimensi partisi dari

graf amalgamasi bintang .

3. Sebagai bahan kajian untuk referensi penelitian lanjutan mengenai dimensi

(24)

II. TINJAUAN PUSTAKA

Pada bagian ini akan dijabarkan tentang dasar teori graf dan dimensi partisi pada

suatu graf sebagai landasan teori pada penelitian ini.

2.1 Konsep Dasar Graf

Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari

Deo, (1998).

Graf G adalah himpunan terurut , dengan menyatakan himpunan titik (vertex) { } yang tak kosong dari , dan menyatakan himpunan sisi (edge) { } yakni pasangan tak terurut dari

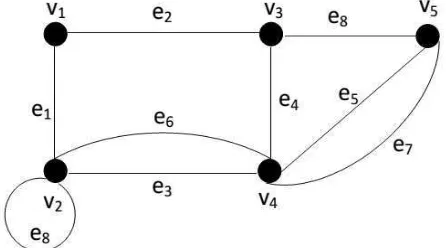
. Berikut contoh graf dengan 5 titik dan 7 sisi.

(25)

7

Banyaknya himpunan titik disebut orde dari graf , jika dan dihubungkan oleh sisi maka dan dikatakan bertetangga (adjacent),

sedangkan titik dan dikatakan menempel (incident) dengan sisi , demikian

juga sisi dikatakan menempel dengan titik dan . Himpunan tetangga dari v,

dinotasikan dengan N(v) adalah himpunan titik-titik yang bertetangga dengan v.

Pada Gambar 3 titik v1 bertetangga dengan v2 dan v3. Sisi e3 menempel pada titik

v2dan v4. Derajat (degree) dari adalah banyaknya sisi yang menempel pada titik

. Derajat dari titik dinotasikan . Daun (pendant vertex) adalah titik digraf yang berderajat satu. Pada Gambar 3 d(v1) = 2, d(v2) = 3, d(v3) = 3,

d(v4) = 5, d(v5) = 3 dan graf tersebut tidak mempunyai daun karena setiap titiknya

memiliki derajat lebih dari satu.

Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Pada

Gambar 3 terdapat loop pada titik v2yaitu e8. Sedangkan e3,e5,e6 dan e7

merupakan sisi paralel. Sisi paralel adalah sisi yang memiliki dua titik ujung yang

sama. Graf sederhana adalah graf yang tidak memiliki dua atau lebih sisi yang

menghubungkan dua titik yang sama (multiple edge) dan loop. Graf pada Gambar

3 bukan merupakan graf sederhana karena terdapat loop (e8) dan sisi ganda (e7).

Suatu graf G disebut graf lengkap (complete graph) jika graf tersebut

merupakan graf sederhana dan setiap titik terhubung ke setiap titik yang lain.

Sedangkan pada graf tak lengkap terdapat pasangan titik yang tidak

dihubungkan oleh sisi. Banyaknya sisi pada graf lengkap dengan n titik

(26)

8

b

c d

Graf T a

a b

c _d

Graf U

Gambar 4. Contoh graf lengkap Gambar 5. Contoh graf tak lengkap

Jalan (walk) adalah barisan berhingga dari titik dan sisi dimulai dan diakhiri

dengan titik sedemikian sehingga setiap sisi menempel dengan titik sebelum dan

sesudahnya. Lintasan (path) adalah jalan yang melewati titik yang berbeda-beda Contoh lintasan yang ditunjukkan pada Gambar 6 adalah .

a

b

c

e

3

d

e

2

e

4

e

₅

e

1

Gambar 6. Contoh lintasan

Siklus (cycle) adalah lintasan tertutup (closed path), yaitu lintasan yang memiliki

titik awal dan titik akhir yang sama. Contoh siklus pada Gambar 3 adalah

.

Suatu graf G dikatakan terhubung jika terdapat sekurang-kurangnya satu lintasan

antara sembarang dua titik berbeda, jika tidak demikian G disebut tak terhubung.

(27)

9

s

p _q

r

Gambar 7. Graf terhubung Gambar 8. Graf tidak terhubung

Graf G Graf H

a _b

c _d

e

f g

h

Pada Gambar 8 tidak terdapat lintasan dari titik a,b,c,d ke titik e,f,g,h sehingga

graf tersebut tak terhubung.

Lemma 2.1 (Deo dkk. 1989) Jumlah derajat semua titik pada graf G adalah genap, yaitu dua kali jumlah sisi pada graf tersebut. Dengan kata lain jika

G(V,E), maka :

∑

Jumlah derajat seluruh titik graf pada Gambar 3 adalah +

= = 14 = dua kali jumlah sisi .

Teorema 2.1 (Deo dkk. 1989) Untuk sembarang graf G, banyaknya titik yang berderajat ganjil, selalu genap.

Bukti : Misalkan Vgenap dan Vganjil masing – masing adalah himpunan himpunan titik yang berderajat genap dan berderajat ganjil pada G(V,E). Persamaan (2.1.1)

dapat ditulis sebagi berikut :

∑

∑ ( )

∑

(28)

10

Karena ( ) untuk setiap , maka suku pertama dari ruas kanan persamaan harus bernilai genap. Ruas kiri persamaan (2.1.2) juga harus bernilai

genap. Nilai genap pada ruas kiri hanya benar bila suku kedua dari ruas kanan

juga harus genap. Karena untuk setiap , maka banyaknya titik di dalam harus genap agar jumlah seluruh derajatnya bernilai genap. Jadi banyaknya titik yang berderajat ganjil selalu genap.

2.2 Graf Pohon dan Beberapa Sifatnya

Graf pohon (Tree) adalah suatu graf terhubung yang tidak memuat siklus.

Sedangkan hutan (forest) merupakan gabungan dari beberapa pohon.

v1

v2

v3 v4

v5

v6

Gambar 9. Contoh pohon G dengan enam titik

(29)

11

Selanjutnya akan diberikan teorema mengenai graf pohon.

Teorema 2.1 (Harsfield dan Ringel, 1994) Jika adalah pohon dengan titik dan sisi , maka .

Bukti: Jika adalah pohon dengan satu sisi maka teorema benar untuk . Asumsikan teorema benar untuk semua pohon dengan sisi kurang dari , artinya

untuk maka . Misal pohon dengan sisi. Pilih satu lintasan terpanjang di G dari a ke b. Titik harus berderajat . Karena kalau tidak

lintasan akan menjadi lebih panjang atau terbentuk siklus di . Selanjutnya buang titik , akibatnya sisi terhubung titik terbuang. Sehingga, pohon

terbentuk dengan (p – 1) dan (n – 1) sisi dengan asumsi diperoleh atau

Teorema 2.2 (Harsfield dan Ringel, 1994) Graf adalah pohon jika dan hanya jika ada terdapat tepat satu lintasan diantara kedua titik tersebut.

Bukti:

Akan ditunjukkan graf adalah pohon maka ada terdapat tepat satu

lintasan diantara kedua titik . Asumsikan adalah pohon. Misal

(30)

12

lihat pada . Untuk beberapa , , karena ada dua lintasan sebagai asumsi. Selanjutnya dari sampai ditemukan suatu titik yang terkandung dalam dan , selanjutnya ambil kembali ke

, dan didapatkan siklus lagi. Tetapi adalah pohon, sehingga tidak ada siklus. Jadi asumsi bahwa ada dua lintasan salah.

Akan ditunjukkan ada terdapat tepat satu lintasan diantara kedua titik

maka graf adalah pohon . Asumsikan adalah graf dengan tepat satu

lintasan diantara dua titik. Pertama perhatikan terhubung. Anggaplah

bahwa mengandung siklus. . Jelas bahwa ada dua lintasan dari ke . Ini kontradiksi , karena mempunyai tepat satu lintasan diantara dua titik. Jadi graf tidak mengandung siklus dan adalah pohon.

Kelas graf pohon yang berkaitan dengan penelitian ini adalah sebagai berikut:

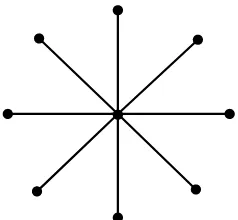
1. Graf bintang (Star)

Graf bintang adalah suatu graf tehubung yang mempunyai satu titik berderajat yang disebut pusat atau titik lainnya berderajat satu (Chartrand

[image:30.595.252.371.595.705.2]

dkk.,1998).

(31)

13

2. Graf Bintang Ganda

Suatu graf pohon disebut graf bintang ganda (double star) jika graf pohon

tersebut mempunyai tepat dua titik dan berderajat lebih dari satu. Jika

[image:31.595.210.424.232.323.2]

dan berturut-turut berderajat dan , dinotasikan dengan (Chartrand dkk.,1998).

Gambar 12. Graf Bintang Ganda

3. Graf Ulat (Caterpillar Graf)

Graf ulat adalah graf pohon yang memiliki sifat apabila dihapus semua

daunnya akan menghasilkan lintasan (Chartrand dkk.,1998).

Gambar 13. Contoh Graf ulat

2.3. Dimensi Partisi Graf

Pada bagian ini akan diberikan definisi dan sifat-sifat dari dimensi partisi pada

suatu graf yang diambil dari Chartrand dkk. (1998).

[image:31.595.138.488.466.537.2]

(32)

14

adalah jarak dari titik v ke x. Misalkan { } adalah partisi dari V(G). Representasi v terhadap dinotasikan dengan ∣ adalah k

pasang terurut ( ). Selanjutnya disebut partisi pembeda dari V(G) jika ∣ ∣ untuk setiap dua titik berbeda

u, . Dimensi partisi dari G, dinotasikan dengan pd (G), adalah nilai k

terkecil sehingga G mempunyai partisi pembeda dengan k kelas.

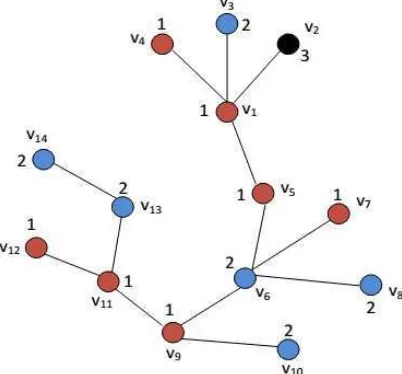
[image:32.595.202.403.310.497.2]

Berikut ini akan diberikan graf G dan akan ditentukan dimensi partisinya.

Gambar 14. Dimensi Partisi graf G

Graf G dipartisi, sehingga diperoleh = { }, dengan S1 = {

}, S2 ={ }, S3 ={ }. Selanjutnya perhatikan bahwa

| = (0,1,1); | = (1,2,0); | = (1,0,2); | = (0,2,2);

| = (0,1,2); ( ) = (1,0,3); | = (1,0,4); | = (2,0,4);

| = (0,1,4); | = (1,0,5); | = (0,1,5); | = (0,1,6);

| = (1,0,6); | = (0,1,7). Karena representasi dari semua titik

(33)

15

Untuk menunjukkan pd (G) ≥ 3, andaikan terdapat partisi pembeda = { } dari G . Perhatikan titik , titik mempunyai 3 daun yaitu . Jika hanya terdapat dua kelas partisi pembeda, maka dua dari tiga daun tersebut akan

memiliki partisi pembeda yang sama. Akibatnya representasi kedua daun itu

akan sama, karena memiliki jarak yang sama terhadap titik-titik lainnya pada

graf G, maka hal ini kontradiksi dengan pengandaian. Jadi pd (G) ≥ 3. (2.3.2)

Berdasarkan persamaan (2.3.1) dan (2.3.2) diperoleh pd (G) = 3. Berikut ini akan diberikan lemma dan teorema penting dari dimensi partisi

yang telah dibuktikan Chartrand dkk. (1998).

Lemma 2.2.1

Diberikan G graf terhubung dengan partisi pembeda dari V(G), untuk u,v V(G), jika d(u,w) = d(v,w) untuk setiap w V(G) – { }, maka u dan v

merupakan elemen yang berbeda dari

Berikut ini akan diberikan teorema untuk menentukan dimensi partisi pada

graf bintang ganda.

Teorema 2.2.2

Jika T adalah graf bintang ganda berorde n ≥ 6 dengan x dan y dua titik yang

(34)

16

Bukti :

Misalkan r = deg(x) – 1 dan s = deg (y) -1, dengan r ≥ s. Misalkan adalah daun dari T yang bertetangga dengan x dan adalah daun yang bertetangga dengan y . Untuk membuktikannya dibagi menjadi dua khusus.

Kasus 1. Jika r = s.

Diberikan = { }, dengan { } { }

{ } untuk 3 ≤ i ≤ r. Perhatikan bahwa | = (0,2,2,2,…,2);

| = (1,0,2,2,…,2); | = (0,1,2,2,…,2); | = (2,0,2,2,…,2);

| = (0,1,1,…,1); | = (1,0,1,1,…,1); untuk 3 ≤ i≤ r,

| = (1,2,…,0,…); | = (2,1,…,0,…), komponen ke – i bernilai 0. Akibatnya semua titik mempunyai representasi yang berbeda . Jadi, pd (T) ≤ r

Kasus 2. Jika r > s. Pada kasus 2 ini, dapat dipecah lagi menjadi sub kasus.

Bagian 2.1. Jika s = 1. Maka r ≥ 3.

Diberikan = { } dengan { }, { } { }

{ }untuk 2 ≤ i≤ r. Karena | ;

| ; | |

(35)

17

Bagian 2.2 Jika s ≥ 2.

Diberikan = { } dengan { }; { }

{ }untuk 3 ≤ i≤ s, dan { }untuk s + 1 ≤ i≤ r. Pernyataan sama

yang digunakan pada bagian 2.1 menunjukkan bahwa adalah partisi pembeda

dari V(T) dan pd(T ) ≤ r. Jadi terbukti bahwa pd (T) = m { } .

Contoh penentuan dimensi partisi graf bintang ganda. Diberikan graf bintang

ganda S3,2 , akan ditentukan bahwa pd(S3,2) = 3.

v

1

v

2

v

3

v

4

v

5

v

6

v

7

1

2 1 3

3 2

[image:35.595.187.435.312.398.2]

1

Gambar 15. Dimensi partisi graf bintang (S3,2)

Graf bintang ganda (S3,2) dipartisi sedemikian sehingga diperoleh = { } dengan { } { } , { } . Representasi dari graf bintang ganda (S3,2) adalah sebagai berikut : | = (1,1,0);

| = (0,1,1); | = (0,2,2); | = (1,0,2); | = (2,2,0);

| = (2,0,1); | = (0,2,1). Karena representasi dari setiap titik berbeda, maka adalah partisi pembeda dari graf S3,2dan pd(G) ≤ 3.

Untuk menunjukkan pd(G) ≥ 3, andaikan terdapat partisi pembeda = { } dari G dengan { } { }, maka titik akan memiliki representasi yang sama yaitu (2,0), hal ini kontradiksi dengan pengandaian. Jadi

(36)

18

Teorema 2.2.3

Misalkan K1,n graf bintang berorde n ≥ 1 maka pd(K1,n) = n

[image:36.595.220.406.164.344.2]

Bukti :

n

1

2

3

4

5

6

7

8

9

10

11

1  n

v

2

v

3

v

4

v

5

v

6

v

7

v

8

v

9

v

10

v

11

v

12

v

1

v

1

Gambar 16. Dimensi Partisi graf bintang K1,n

Graf K1,n dipartisi sedemikian sehingga = { }, dengan

{ }, { } { }, { } { }, { }, . . ., dan { }. Perhatikan bahwa representasi dari Graf K1,n adalah sebagai berikut

| = (0,1,1,1,1,1,1,...,1); | = (0,2,2,2,2,...,2); | = (1,0,2,2,2,2,...,2); | = (1,2,0,2,2,2,...,2); | = (1,2,2,0,2,2,...,2); | = (1,2,2,2,0,2,...,2); | = (1,2,2,2,2,2,...,0). Karena representasi dari semua titik berbeda, maka adalah partisi pembeda dari

graf K1,n dan pd (K1,n) ≤ n.

Untuk menunjukkan pd (K1,n) ≥ n,andaikan terdapat partisi pembeda

(37)

19

graf K1,n, hal ini kontradiksi dengan pengandaian. Jadi pd (K1,n) ≥ n . Akibatnya

pd (K1,n) = n

Teorema 2.2.4

Jika T adalah graf ulat dengan

. Untuk membuktikan Teorema 2.2.4, perhatikan partisi pembeda pada graf ulat berikut :

v1 v2 v3

v4 v5 v6 v8 1 1 1 2 2 2 3

v1 v2

v3 v4

v5 v6 2 2 1 1 3 3

Gambar 16. Dimensi partisi graf ulat T1,T2

v

1

v

2

v

3

v

4

v

5

v

6

v

7

v

8

1 2 ₂

1

3 2

[image:37.595.124.489.293.629.2]

1 3

(38)

20

v

1

v

₂

v

3

v

4

v

5

v

6

v

7

v

8

v

9

v

10

v

11

v

12

v

13

v

14

v

15

v

16

1 1

1

1 1

2 2

2

2 2

3 3

3

[image:38.595.191.440.91.242.2]

4

Gambar 18. Dimensi partisi graf ulat T4

Graf ulat T1 pada Gambar 16 memiliki dengan minimal partisi pembeda = { } dengan { } { } dan { }.

Graf ulat T2 pada Gambar 16 memiliki dengan minimal partisi pembeda = { } dengan { } { } dan

{ }.

Graf ulat T3 pada Gambar 17 adalah graf bintang ganda dan berdasarkan Teorema

2.2.2 maka .

Graf ulat T4 pada Gambar 18 memiliki dengan partisi pembedanya

{ } { }

{ } dan { }; { }. Untuk menunjukkan pd (T4) = 4 cukup dengan menunjukkan bahwa tidak ada partisi pembeda dengan

tiga kelas partisi dari V(T4). Misalkan = { } sebagai partisi pembeda dari

(39)

21

mengakibatkan representasinya akan sama juga. Sehingga = { } bukanlah partisi pembeda yang tepat untuk T4, hal ini kontradiksi dengan

pengandaian. Akibatnya

Selanjutnya akan diberikan beberapa Lemma hasil penelitian Asmiati dkk. tentang

dimensi partisi dari graf amalgamasi bintang.

Lemma 2.2.2 Misal adalah partisi pembeda dari graf

dan| | . Partisi pembeda adalah hasil partisi dari graf jika dan hanya jika dan dalam kelas yang sama pada kelas kombinasi pada { } dan jika { } adalah pembeda.

Bukti :

Misal adalah hasil partisi dari graf dengan | | dan

adalah kelas yang sama dari . Jika kombinasi kelas dari

dan jika adalah sama. Karena

untuk setiap {{ | } { | }}

maka representasi dari dan adalah sama. Jadi bukan hasil dari partisi.

Maka kontradiksi dengan pengandaian.

(40)

22

dimana dan . Akan ditunjukkan bahwa representasi dari setiap adalah unik.

1. Jelas, | | karena representasinya berbeda dalam m-ordinat dan n-ordinat.

2. Jika dan adalah kelas yang sama pada dengan akan ditunjukkan bahwa ( | ) | . Bagi dalam 2 kasus.

(1) Kasus 1, jika dan adalah kelas yang sama pada maka diperoleh alasan pada teorema ini, yaitu A = B. Jadi ( | ) | .

(2) Kasus 2, misal dan maka ( | ) | adalah berbeda dalam x-ordinat dan y-ordinat.

Jadi ( | ) | .

3. Jika dan dalam kelas yang sama pada maka representasi

| mempunyai setidaknya satu komponen yang bernilai 1. Sedangkan

( | ) mempunyai tepat satu komponen yang bernilai 1. Maka | ( | ).

4. Jika dan dalam kelas yang sama pada maka representasi | mempunyai setidaknya satu komponen yang bernilai 1. Sedangkan ( | ) mempunyai tepat satu komponen yang bernilai 1. Maka | ( | ). 5. Jika dan dalam kelas yang sama pada . Bagi dalam 2 kasus.

(1) Kasus . Representasi | mempunyai komponen yang bernilai 1. Sedangkan | mempunyai kurang dari

komponen yang bernilai 1. Maka | | .

(41)

23

Lemma 2.2.3. Misal adalah partisi , maka .

Bukti :

Misal adalah partisi pada , tetap untuk , misal , maka jumlah kombinasi partisi dapat digunakan oleh { | } adalah . Karena partisi dari , untuk setiap Berdasarkan Lemma 2.2.1 kita peroleh jumlah dari adalah . Akan tetapi, jika dalam kelas partisi yang sama dan maka kita harus menghilangkan , untuk memastikan bahwa semua titik akan mempunyai

representasi yang berbeda. Maka jumlah maksimum dari adalah -1

(42)

III. METODE PENELITIAN

3.1. Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester genap Tahun Akademik 2014-2015, di

Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Lampung.

3.2. Metode Penelitian

Metode yang dilakukan untuk menentukan dimensi partisi dari graf adalah dengan langkah-langkah sebagai berikut :

1. Mengkonstruksi graf tertentu

2. Memilih titik tertentu dalam graf amalgamasi bintang yaitu titik pusat graf sebagai titik awal dalam graf

3. Memberi label pada kelas-kelas partisi dengan partisi seminimal mungkin

4. Menentukan batas bawah dari pd . Berdasarkan lemma 2.2.1 dapat ditentukan batas bawah dari dimensi partisi . Hal ini dapat dilakukan karena terdapat titik pada ( ) yang mempunyai k daun, akibatnya

(43)

25

5. Menentukan batas atas dari pd . Batas atas dari pd diperoleh dengan cara mengkonstruksi graf . Himpunan titik-titik pada graf

dikelompokkan berdasarkan diameternya kedalam kelas partisi pembeda. Minimum banyaknya partisi pembeda itulah yang merupakan

(44)

BAB V. KESIMPULAN DAN SARAN

5.1 Kesimpulan

Dari hasil-hasil penelitian dimensi partisi pada graf amalgamasi bintang untuk bilangan asli dapat disimpulkan bahwa bentuk umum dari dimensi partisi graf ( )untuk k ≥ m adalah :

( ) { ⌊ ⌋

Berikut ini diberikan konstruksi graf untuk kasus 1≤ n ≤

-1

x

1

m l11

l

111

l

112

l

113 1 1k

l m1

l

12

l

121

l122

l

123

1 2k

l

13

1 3k

l

133

l

132

l

131

l

m

1 1



l

1₍_m_₁₎₁

l

m 1 2 ) 1 (

l

m 1 3 ) 1 ( 

l

m k

1 ) 1 (

l

12

l

112

l

122

l

132 2 1k

l

m1

l

22

l

221

l222

l

223

l

23

2 3k

l

332

l

232

l

231

l

m

2 1



l

2₍_m_₁₎₁

l

m 2 2 ) 1 ( 

l

m 2 3 ) 1 (

l

m k

2 ) 1 (  2 x m2 2 2k l 1  m n x n m

l

m1 1



l

11m1



l

12m1



l

13m1



l

mk

1 1



l

m21



l

m211



l

m221 

l

m231



l

mk

1 2



l

m31 

l

m311



l

m321



l

m₃₃1

l

mk

1 3



l

mm k

1 ) 1 (

 

l

m

k m 1 ) 1 (  

l

mm k

1 ) 1 (  

l

mm k

1 ) 1 (  

[image:44.612.124.519.508.690.2]

l

nm1

(45)

73

Sedangkan konstruksi dari graf untuk kasus n lainnya adalah sebagai berikut :

1

x x₂

1  m k x

l

m k k m11)( 1) ( 

1

x

1

m

l

11

l

111

l

112

l

113

1 ) 1 ( 1k

l

12

l

121

l

122

l

123

1 ) 1 ( 2k

l

13

l

131

l

232

l

133

1 ) 1 ( 3k

l

m 1 1 

l

m 1 2 ) 1 ( 

l

m 1 3 ) 1 ( 

l

m k

2 )1 )( 1 (  2 m

l

12

l

112

l

122

l

132

2 ) 1 ( 1k

l

22

l

221

l

222

l

223

2 )1 ( 2k

l

23

l

312

l

232

l

233

2 ) 1 ( 3k

l

m 2 1 

l

m 2 3 ) 1 ( 

l

m k

2 )1 )( 1 (  2 x

l

m 1 1 ) 1 ( 

l

m 2 2 ) 1 (

l

m 2 1 ) 1 ( n x 1  m m

l

m k 1 1 1 11  m k l

l

m k 1 12

l

m k 1 13

l

m k k11) ( 1  

l

m k 1 2

l

m k 1 21

l

m k 1 22

l

m k 1 23

l

m k

k11) ( 2

l

m k 1 3

l

m k k m11)(1) ( 

l

m k k m11)(1) ( 

l

m k

k m11)( 1) ( 

l

nm1

l

m k k11) ( 3 [image:45.612.116.516.117.329.2]

l

m k 1 33

l

m k 1 32

l

m k 1 31

Gambar 57. Partisi Pembeda pada graf nSm,k untuk kasus n lainnya

5.2 Saran

Penelitian ini memberikan masalah terbuka untuk penelitian selanjutnya, yaitu

(46)

DAFTAR PUSTAKA

Asmiati, Assiatun, H, Baskoro, E.T, Locating-Chromatic Number of Almagamation of Starts, ITB J.Sci., 43A, 1-8, 2011.

Asmiati. 2012. Partition Dimension of Amalgamation of Stars. Bulletin of Mathematics. Vol 04, No. 02, 161-167.

Chartrand, G, Erwin, D, Henning, M.A, Slater, P.J, dan Zhang, P.2002. The locating-chromatic number of a graph, Bull.inst. combin. Apll., 36, 89-101.

Chartrand, G., E. Salehi, dan P. Zhang. 1998. On The Partition Dimension of Graph, Congr. Numer,.130, 157-168.

Chartrand, G., E. Salehi, dan P. Zhang. 2000. The Partition Dimension of a Graph,

Aequationes Math.59, 45-54.

Deo, Narsigh. 1989. Graph Theory With Applications to Engineering And Computer Science. Prentice Hall Inc. New York.

Harsfield,N, dan G. Ringel.1994. Pearl In Graph Theory. A Comprehensive Introduction. Revised And Augmented. Academic Press Inc. USA

Harary dan Melter. (1976). ― On the Metric Dimension of Graph.

Combinatoria. Volume 2 Pages 1991-1995, Wesley Publishing, Inc.

Ristanti, Dinda. 2015. Dimensi Partisi pada Graf nS4,k . Skripsi ; Fakultas MIPA, Universitas Lampung.