DIMENSI PARTISI PADA GRAF nS4,k

ABSTRAK

DIMENSI PARTISI PADA GRAF nS_4,k

Oleh

Dinda Ristanti

Dimensi partisi pertama kali dikaji oleh Chartrand dkk. pada tahun 1998 yang merupakan pengembangan dari dimensi metrik. Misalkan ∏ = {S1,S2,...,Sk} adalah partisi dari V(G). Representasi v terhadap dinotasikan dengan r(v| )= ) ) )). Jika untuk setiap u,v  V(G), r(u| ) ≠ r(v| ) maka disebut partisi pembeda. _{Banyaknya minimum partisi pembeda} disebut dimensi partisi dari G, dan dinotasikan dengan pd(G). Graf diperoleh dari graf dan setiap titik nya dihubungkan oleh suatu lintasan. Pada penelitian dimensi partisi pada graf nS4,k untuk n,k sebarang bilangan asli

telah diperoleh hasilnya.

RIWAYAT HIDUP

Penulis dilahirkan di Panjang pada tanggal 20 Mei 1993. Penulis merupakan anak kedua dari pasangan Bapak M. Aripin dan Ibu Endang Tri Astuti, adik dari Dyni Areta Ningrum serta kakak dari Nadia Ayu Rifani dan Shepia Putri Anggraini.

Penulis menyelesaikan pendidikan dari Taman Kanak-kanak Setia Kawan di Panjang, Bandar Lampung pada tahun 1998. Pendidikan sekolah dasar di SD Negeri 1 Purwodadi Simpang, Lampung Selatan pada tahun 2004. Pendidikan sekolah menengah pertama di SMP Negeri 23 Bandar Lampung pada tahun 2007. Pendidikan sekolah menengah atas di SMA Al-Azhar 3, Bandar Lampung pada tahun 2010.

Pada tahun 2010, Penulis melanjutkan pendidikan di perguruan tinggi dan terdaftar sebagai mahasiswa Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung melalui jalur SNMPTN. Pada periode tahun 2010/2011 penulis terdaftar sebagai anggota GEMATIKA (Generasi Muda HIMATIKA) Himpunan Mahasiswa Matematika FMIPA Unila. Penulis pernah menjadi anggota biro Kesekretariatan Organisasi Himpunan Mahasiswa Matematika FMIPA Unila pada periode tahun 2011/2012 - 2012/2013.

MOTO

“Man Jadda Wa Jada - Siapa yang bersungguh-sungguh akan

berhasil”

“Man Shobaro Zafiro – Siapa yang bersabar akan beruntung”

“Man Saaro „Alaa Darbi Washola – Siapa yang berjalan di

jalur Nya akan sampai”

“Selalu berusaha memberikan yang terbaik untuk orang

di sekitar kita”

PERSEMBAHAN

Dengan penuh rasa syukur kepada Allah SWT atas nikmat

yang luar biasa yang selalu diberikan kepadaku sehingga

aku dapat menyelesaikan hasil karyaku ini

Kupersembahkan hasil karyaku ini untuk Bapak dan Ibuku

tersayang sebagai salah satu wujud cintaku.

terima kasih untuk setiap doa, semangat, dan kasih sayang

yang selalu menemani disetiap hariku

Untuk kakakku Dyni Areta Ningrum, kedua adikku Nadia

Ayu Rifani dan Shepia Putri anggraini, sepupuku Siti

Nurmala, Kakak angkatku Mas Prapto, Richi Arif Pratama

Saputra, terima kasih untuk dukungan serta doa yang selalu

diberikan untukku

Sahabat-sahabat terbaikku, terima kasih untuk semua kisah

SANWACANA

Alhamdulillahi robbil ‘alamin, puji dan syukur penulis kepada Allah SWT atas izin serta ridho-Nya dalam menyelesaikan skripsi ini. Shalawat serta salam kepada junjungan nabi besar Muhammad SAW yang telah menjadi suri tauladan yang baik bagi kita.

Pada proses penyusunan skripsi ini, penulis memperoleh banyak bimbingan, kritik, dan saran yang membangun sehingga skripsi ini mampu penulis selesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada :

1. Ibu Dr. Asmiati, S.Si., M.Si., selaku pembimbing I yang senantiasa membimbing, memberikan arahan, saran, dan dukungan kepada penulis dalam menyelesaikan skripsi ini.

2. Ibu Fitriani, S.Si., M.Si., selaku dosen pembimbing II yang telah banyak membantu dan memberikan pembelajaran serta bimbingan kepada penulis. 3. Ibu Dra. Wamilliana, M .A., Ph.D., selaku penguji yang telah memberikan

penulis kritik dan saran pada penelitian ini.

4. Ibu Dra. Dorrah Aziz, S.Si., M.Si., selaku pembimbing akademik.

4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.

Lampung.

7. Untuk kedua orang tuaku, mbak Dyni, adikku Ayu, dan PSutri serta Mala dan Mas Prapto yang luar biasa yang tak pernah letih memberikan saran, perhatian, doa serta semangat kepada penulis.

8. Untuk Richi Arif Pratama Saputra atas nasehat, kesabaran, kebersamaan serta waktu luang yang sangat bermanfaat selama ini.

9. Sahabat-sahabat penulis, Agustia Indriani, Agustina Ambar Wulan, Christy Engine Nita, Dian Ekawati, Tri Handayani, Hasby Alkarim, Miftah Farid Artama, Muhammad Ridho, Rohandi, serta Sofyan Saputra yang selalu ada dan memberi semangat melalui keceriaan serta nasihatnya.

10. Sahabat seperjuangan sebimbingan, Erwin Hendrianto, Epy lestari, Suryadi serta untuk teman-teman Matematika 2010 dan keluarga besar HIMATIKA. 11. Seluruh pihak yang telah membantu dalam penyusunan skripsi ini yang tidak

dapat disebutkan satu persatu.

Akhir kata, penulis menyadari skripsi ini jauh dari kesempurnaan, akan tetapi semoga dapat berguna dan bermanfaat bagi kita semua.

Bandar Lampung, Agustus 2014 Penulis,

DAFTAR ISI

Halaman

DAFTAR ISI ... i

DAFTAR GAMBAR ... ii

BAB I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Perumusan Masalah... 2

1.3 Tujuan Penelitian... 3

1.4 Manfaat Penelitian... 4

BAB II TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf ... 5

2.2 Beberapa Kelas Pohon ... 8

2.3 Dimensi Partisi Graf ... 10

BAB III METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 18

IV. HASIL DAN PEMBAHASAN

4.1 Dimensi Partisi Graf nS4,2 ... 20

4.1 Dimensi Partisi Graf nS4,3 ... 22 4.1 Dimensi Partisi Graf nS4,k untuk k≥ 4 ... 23

V. SIMPULAN DAN SARAN

DAFTAR PUSTAKA

DAFTAR GAMBAR

Halaman

Gambar 1. Graf S4,k ... 3

Gambar 2. Contoh graf dengan lima titik dan delapan sisi ... 5

Gambar 3. TG ... 7

Gambar 4. T adalah pohon dan H adalah hutan ... 8

Gambar 5. Graf S4,k ... 8

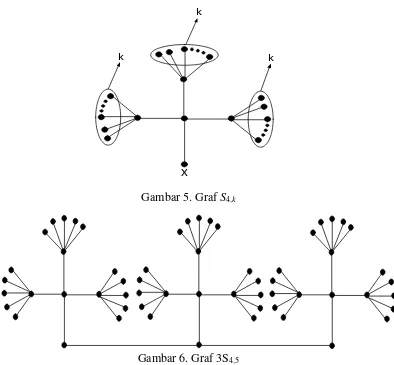
Gambar 6. Graf 3S4,5 ... 9

Gambar 7. Graf bintang K1,6... 10

Gambar 8. Graf bintang ganda S3,2 ... 10

Gambar 9. Contoh graf ulat ... 10

Gambar 10. Dimensi Partisi graf G ... 11

Gambar 11. Dimensi partisi graf bintang ganda S3,2 ... 13

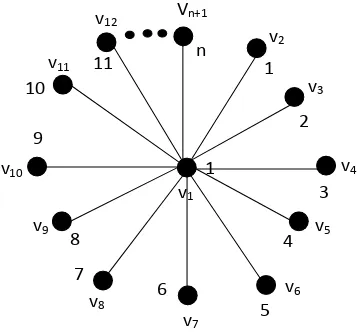
Gambar 12. Dimensi partisi graf bintang K1,n ... 14

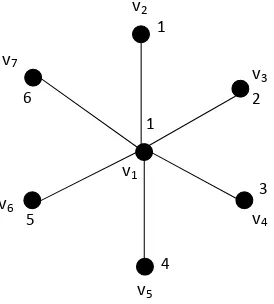
Gambar 13. Dimensi partisi graf K1,6 ... 15

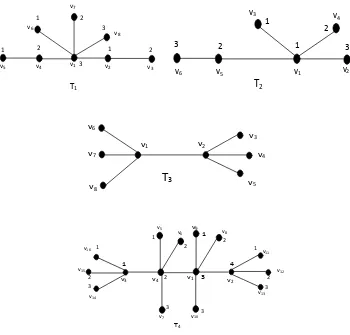
Gambar 14. Dimensi partisi graf ulat T1, T2, T3 dan T4 ... 16

Gambar 16. Partisi pembeda pada graf S4,2 untuk n = 1 ... 20

Gambar 17. Partisi pembeda pada graf nS4,2 untuk n≥ 2... 21

Gambar 18. Partisi pembeda pada graf nS4,3 untuk n≥ 1... 22

Gambar 19. Partisi pembeda pada graf nS4,k untuk n  ... 24

1

I. PENDAHULUAN

1.1. Latar belakang Masalah

Teori graf merupakan salah satu bagian ilmu dari matematika. Banyak permasalahan yang dapat dinyatakan dan diselesaikan dengan menggunakan teori graf. Graf merupakan kumpulan titik dan sisi, dinotasikan dengan G=(V,E), dimana V menyatakan himpunan titik yang tak kosong dan E

menyatakan himpunan sisi yang merupakan pasangan sisi tak terurut dari titik-titik V.

Seiring kemajuan ilmu pengetahuan dan teknologi, banyak terdapat penelitian tentang graf, diantaranya pewarnaan graf dan dimensi partisi graf. Konsep dimensi partisi dari suatu graf pertama kali diperkenalkan oleh Chartrand dkk. pada tahun 1998. Konsep ini merupakan pengembangan dari konsep dimensi metrik yang sebelumnya sudah diperkenalkan oleh Slater dan Melter dkk. pada tahun 1975 dan 1976. Konsep dimensi partisi juga merupakan salah satu konsep yang menjadi latar belakang munculnya konsep bilangan kromatik lokasi.

2

adalah jarak dari titik ke . Misalkan { } adalah partisi

dari dengan kelas-kelas dari . Representasi terhadap , dinotasikan dengan , adalah -tupel terurut

. Selanjutnya, disebut partisi pembeda dari

jika untuk setiap dua titik berbeda

Dimensi partisi dari , dinotasikan adalah nilai terkecil

sehingga mempunyai partisi pembeda dengan kelas (Chartrand dkk., 1998).

Penentuan dimensi partisi dari graf terhubung telah dilakukan oleh Chartrand dkk. (1998), khususnya untuk kelas pohon telah mendapatkan dimensi partisi dari graf lintasan Pn, n ≥ 2, yaitu pd( Pn) = 2 dan graf bintang K1,n, yaitu

pd(K1,n) = n. Graf bintang ganda T berorde n ≥ 6, pd(T)=max{deg(x),deg(y)}

– 1, dengan x dan y dua titik yang bukan daun. Selain itu, mereka mendapatkan batas atas dan batas bawah dimensi partisi dari graf ulat. Penelitian terus dilakukan untuk mendapatkan dimensi partisi graf terhubung lainnya. Kelas graf tertentu dapat ditentukan dimensi partisinya secara tepat, tetapi pada kelas graf lain baru dapat ditentukan batas atas atau batas bawahnya.

Chartrand dkk. (2000) telah mengkaji dimensi partisi pada graf bipartit Km,n

dan Tomescu dkk. pada tahun 2007 untuk graf roda Wn. Untuk n tertentu,

dimensi partisi graf roda Wn telah dapat ditentukan secara tepat. Misalnya,

3

Asmiati (2012) telah mendapatkan dimensi partisi pada graf amalgamasi bintang.

Ketertarikan penulis pada penelitian ini adalah terkait masalah penentuan dimensi partisi graf untuk n,k sebarang bilangan asli.

1.2.Perumusan Masalah

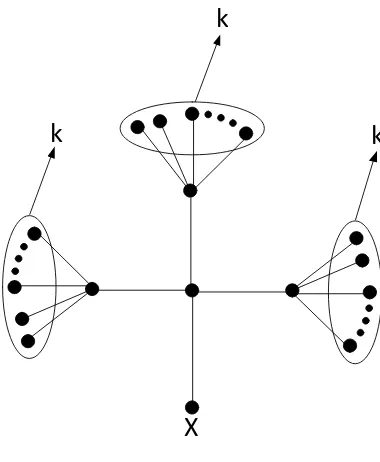
Diberikan graf sebagai berikut :

X

k

k

k

Gambar 1. Graf

Graf diperoleh dari graf dan setiap titik nya dihubungkan oleh suatu lintasan. Pada penelitian ini akan ditentukan dimensi partisi graf nS4,k

untuk n,k sebarang bilangan asli.

1.3.Tujuan Penelitian

4

1.4.Manfaat Penelitian

Adapun manfaat dari penelitian ini adalah :

1. Memberikan pemahaman dan wawasan mengenai dimensi partisi dari graf khususnya graf .

5

II. TINJAUAN PUSTAKA

Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini.

2.1. Konsep Dasar Graf

terurut dari titik-titik di V.

v

5

6

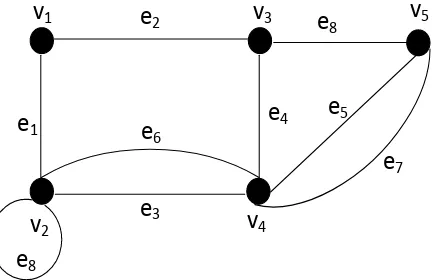
Dua titik pada graf G dikatakan bertetangga (adjacent) bila keduanya terhubung dengan suatu sisi. Suatu sisi dikatakan menempel (incident) dengan suatu titik u, jika titik u merupakan salah satu titik ujung dari sisi tersebut. Pada Gambar 2, titik v3 bertetangga dengan titik v1 dan v5. Sisi e3

menempel pada titik v2 dan v4.

Derajat suatu titik v pada graf G adalah banyaknya sisi yang menempel pada titik v , dinotasikan dengan d(v). Daun (pendant vertex) adalah titik yang berderajat satu. Pada Gambar 2, d(v1) = 2, d(v2) = 3, d(v3) = 3, d(v4) = 5 dan

d(v5) = 3 dan graf tersebut tidak memiliki daun karena setiap titiknya

memiliki derajat lebih dari satu.

Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Sisi paralel adalah sisi yang memiliki dua titik ujung yang sama. Graf yang tidak mempunyai sisi ganda dan atau loop disebut graf sederhana. Pada Gambar 2, terdapat loop pada titik v2 yaitu e8, sedangkan e3, e6, e5dan e7 disebut sisi

paralel. Graf pada Gambar 2 bukan graf sederhana karena terdapat loop (e8)

dan sisi ganda (e7).

7

2.2. Beberapa Kelas Graf Pohon

Berikut ini akan diberikan beberapa kelas graf pohon yang berkaitan dengan penelitian ini.

Misalkan G adalah graf terhubung, G disebut pohon jika dan hanya jika G

8

T H

Gambar 4. Contoh pohon dan hutan

Pada Gambar 4, T adalah pohon dan H adalah hutan.

Graf adalah graf yang diperoleh dari graf dan setiap titik nya dihubungkan oleh suatu lintasan.

X k

k k

Gambar 5. Graf S4,k

9

Graf bintang K1,n (star) adalah suatu graf terhubung yang mempunyai satu

titik berderajat n yang disebut pusat dan titik lainya berderajat satu (Chartrand dkk., 1998).

Gambar 7. Graf bintang K1,6

Suatu graf pohon disebut graf bintang ganda (double star) jika graf pohon tersebut mempunyai tepat dua titik x dan y berderajat lebih dari satu. jika x

dan y berturut-turut berderajat a + 1 dan b + 1, dinotasikan dengan Sa,b

(Chartrand dkk., 1998).

Gambar 8. Graf bintang ganda S3,2

Graf ulat (caterpillar graf) adalah graf pohon yang memiliki sifat apabila dihapus semua daunnya akan menghasilkan lintasan (Chartrand dkk., 1998).

10

2.3. Dimensi Partisi Graf

Pada bagian ini akan diberikan definisi dan sifat-sifat dari dimensi partisi pada suatu graf yang diambil dari Chartrand dkk (1998).

Misalkan suatu graf, dan . Jarak dari titik ke

sehingga mempunyai partisi pembeda dengan kelas.

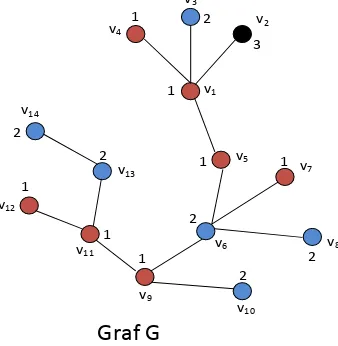
Berikut ini akan diberikan graf G dan akan ditentukan dimensi partisinya.

v1

11

Graf G dipartisi sedemikian sehingga diperoleh = {S1,S2,S3}, dengan S1 = {v1,v4,v5,v7,v9,v11,v12}, S2 = {v3,v6,v8,v10,v13,v14} dan S3 = {v2}. Perhatikan

bahwa r(v1|) = (0,1,1); r(v2|) = (1,2,0); r(v3|) = (1,0,2); r(v4|) = (0,2,2);

r(v5|) = (0,1,2); r(v6|) = (1,0,3); r(v7|) = (1,0,4); r(v8|) = (2,0,4); r(v9|) =

(0,1,4); r(v10|) = (1,0,5); r(v11|) = (0,1,5); r(v12|) = (0,1,6); r(v13|) =

(1,0,6); r(v14|) = (0,1,7). Karena representasi dari setiap titik berbeda, maka adalah partisi pembeda dari graf G dan pd(G) ≤ 3.

Untuk menunjukkan pd(G) ≥ 3, andaikan terdapat partisi pembeda  = {S1,S2} dari G. Perhatikan titik v1, v1 memiliki 3 daun yaitu v2, v3 dan v4. Jika

hanya terdapat dua kelas partisi pembeda, maka dua dari tiga daun tersebut akan memiliki partisi pembeda yang sama. Akibatnya representasi kedua daun itu akan sama, karena memiliki jarak yang sama terhadap titik-titik lainnya pada graf G, kontradiksi. Jadi pd(G) ≥ 3. Akibatnya, pd(G) = 3.

Berikut ini akan diberikan lemma dan teorema penting dari dimensi partisi yang telah dibuktikan Chartrand dkk. (1998).

Lemma 2.2.1

Diberikan G graf terhubung dengan partisi pembeda dari V(G), untuk u,v



V(G), jika d(u,w) = d(v,w) untuk setiap w



V(G) – {u,v}, maka u dan v

12

Berikut ini akan diberikan teorema untuk menentukan dimensi partisi pada graf bintang ganda.

Teorema 2.2.2

Jika T adalah graf bintang ganda berorde n≥ 6, dengan x dan y dua titik yang bukan daun, maka pd(T) = max{deg(x),deg(y)} – 1.

Contoh penentuan dimensi partisi graf dari graf bintang ganda.

Diberikan graf bintang ganda S3,2, akan tentukan bahwa pd(S3,2) = 3.

Gambar 11. Dimensi partisi graf bintang ganda S3,2

Graf bintang ganda S3,2 dipartisi sedemikian sehingga diperoleh  = {S1,S2,S3}, dengan S1 = {v2,v3,v7}, S2 = {v4,v6}, dan S3 = {v1,v5}.

Perhatikan bahwa r(v1|) = (1,1,0); r(v2|) = (0,1,1); r(v3|) = (0,2,2); r(v4|)

= (1,0,2); r(v5|) = (2,2,0); r(v6|) = (2,0,1); r(v7|) = (0,2,1). Karena

representasi dari setiap titik berbeda, makaadalah partisi pembeda dari graf S3,2 dan pd(G) ≤ 3.

13

Gambar 12. Dimensi partisi graf bintang K1,n

14

Untuk menunjukkan pd(K1,n) ≥n, andaikan bahwa terdapat partisi pembeda 

= {S1,S2,S3,S4,S5,…,Sn-1} dari K1,n maka akan ada representasi yang sama

yaitu pada titik vn dan vn+1. Maka  bukan merupakan partisi pembeda dari

graf K1,n, kontradiksi. Jadi pd(K1,n) ≥ n. Akibatnya, pd(K1,n) = n.

Berikut ini akan diberikan contoh penentuan dimensi partisi dari graf bintang

K1,6.

Gambar 13. Dimensi partisi graf K1,6

Graf K1,6 dipartisi sedemikian sehingga diperoleh  = {S1,S2,S3,S4,S5,S6}

15

Sehingga,  bukan merupakan partisi pembeda dari graf K1,6, kontradiksi.. Jadi pd(K1,6) ≥ 6. Akibatnya, pd(K1,6) = 6.

Teorema 2.2.4

Jika T adalah graf ulat dengan t(T) ≥ 3, makat(T) –2 ≤ pd(T) ≤ t(T) + 1.

16

Graf ulat T1 pada Gambar 14 memiliki pd(T1) = 3 = t(T1) – 2 dengan

minimal partisi pembeda = {S1,S2,S3} dengan S1 = {v2,v5,v6}; S2 = {v3,v4,v7}

dan S3 = {v1,v8}.

Graf ulat T2 pada Gambar 14 memiliki pd(T2) = 3 = t(T2) – 1 dengan

minimal partisi pembeda = {S1,S2,S3} dengan S1 = {v1,v4}; S2 = {v3,v5} dan

S3 = {v2,v6}.

Graf ulat T3 pada Gambar 14, adalah graf bintang ganda dan berdasarkan teorema 2.2.2 maka t(T3) = pd(T3) = 3.

Graf ulat T4 pada Gambar 14 memiliki t(T4) = 3 dengan partisi pembedanya

 = {S1,S2,S3,S4} dari V(T4), dengan S1 = {v3,v5,v9,v11,v16}; S2 =

{v4,v6,v8,v12,v15}; S3 = {v1,v7,v10,v13,v14} dan S4 = {v2}. Untuk menunjukkan

pd(T4) = 4 cukup dengan menunjukkan bahwa tidak ada partisi pembeda dengan tiga kelas partisi dari V(T4). Misalkan  = {S1,S2,S3} sebagai partisi pembeda dari V(T4) maka akan ada kesamaan partisi pembeda dari titik v1 dan

v2 sehingga mengakibatkan representasinya akan sama juga. Sehingga  =

18

III. METODE PENELITIAN

3.1 Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester genap tahun ajaran 2013/2014 bertempat di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

3.2 Metode Penelitian

Metode yang dilakukan untuk menentukan dimensi partisi dari graf yaitu sebagai berikut :

1. Menentukan batas bawah dari ( )

Berdasarkan Lemma 2.2.1, dapat ditentukan batas bawah trivial dari dimensi partisi . Hal ini dapat dilakukan karena terdapat titik pada

yang mempunyai daun, akibatnya, ( 2. Menentukan batas atas dari ( )

Batas atas dari diperoleh dengan cara mengkonstruksi graf

V. SIMPULAN DAN SARAN

Pada bagian ini akan diberikan simpulan dan saran dari hasil yang sudah diperoleh untuk penelitian ini.

5.1. Simpulan

Adapun kesimpulan dalam penelitian ini secara umum adalah sebagai berikut : 1. Pd(nS4,2) = {

2. Pd(nS4,3) = 4 ; n ≥ 1

3. Untuk k ≥ 4, Pd(nS4,k) = {

5.2. Saran

DAFTAR PUSTAKA

Asmiati. 2012. Partition Dimension of Amalgamation of Stars. Bulletin of Mathematics. Vol 04, No. 02, 161-167.

Chartrand, G., E. Salehi, dan P. Zhang. 1998. On The Partition Dimension of Graph, Congr. Numer,.130, 157-168.

Chartrand, G., E. Salehi, dan P. Zhang. 2000. The Partition Dimension of a Graph, Aequationes Math.59, 45-54.

Deo, N. 1998. Graph Theory with Applications to Engineering and computer Science. Prentice Hall Inc, New York.

Johnson, M., 1993. Structure-activity Maps For Visualizing The Graph variables Arising In Drug Design, J. Biopharm., 3, 203-236.