ANALYSIS
Alleviating soil erosion
/
pollution stock externalities: alternative
roles for government
Edna T. Loehman *, Timothy O. Randhir
Department of Agricultural Economics,Purdue Uni6ersity,West Lafayette,IN47907,USA Received 1 March 1994; received in revised form 15 June 1998; accepted 18 June 1998
Abstract
This paper addresses two temporal externalities due to agriculture: soil erosion and related pollution. The possibility of decentralization of decisions, the appropriate role of a resource manager, and the efficiency of alternative policies are examined using traditional welfare economics concepts for a two-sector model of rural – urban linkage. Three alternative types of policies can be socially efficient, but imply different involvement by government, and have different knowledge requirements. A Pigouvian policy requires full information. A bargaining solution involves government only in setting an entitlement, but it may require too much knowledge by rural households in terms of understanding dynamic environmental relationships. A third way is that government and rural households be co-producers of environmental goods. This concept assigns government the responsibility for maintaining knowledge about environmental relationships, and government is a participant in a market system that determines prices for environmental-related goods. © 1999 Elsevier Science B.V. All rights reserved.
Keywords: Soil erosion; Pollution; Stock externalities; Policies; Incentives; Tax; Subsidy; Bargaining entitlements; Decentralization
1. Introduction
Soil degradation is a common occurrence in Third World countries as growing populations try to satisfy subsistence requirements with limited resources. If current trends continue, agricultural
output will not be sustainable in the long run in many areas. For example, from an interview with a scientist at the Chinese Academy of Sciences in 1988: ‘Unless urgent measures are undertaken, desertification will erode an additional 29000 square miles by the year 2000, more than twice the area of Taiwan’ (Postel, 1991). This is an example of the ‘tragedy of the commons,’ consid-ering soil quality to be a common property resource.
* Corresponding author. Fax: +1 765 4949176; e-mail: [email protected]
For problems of the commons, a solution often put forth has been privatization or assignment of ownership rights (see, for example, Anderson, 1991). With privatization, an individual will sup-posedly act in his/her own best interests to pre-serve the resource. The argument is that an individual who owns land for the purpose of food production should be interested in sustainable production, unless the personal discount rate is so high that the future is ignored.
However, in spite of the best intentions, as pointed out by Larson and Bromley (1990), soil depletion can still occur under privatization. Lar-son and Bromley developed a dynamic household model of agricultural production that included the relation between soil quality on food production, the effects of food production on soil, and activi-ties that improve soil quality such as allowing land. They showed that degradation can come about — even when property rights to land have been assigned — as a response to economic incen-tives. Furthermore, Perrings (1989) showed that the struggle to meet food consumption needs un-der conditions of poverty or other limited re-sources can result in degradation. Therefore, the assignment of property rights may be no panacea. That soil erosion is a stock externality is an-other reason why privatization is not a sufficient social solution. Soil erosion is also associated with another type of stock externality: persistent water pollution related to fertilizers and pesticides car-ried by soil particles to water bodies. A stock externality is a case in which decisions made at one time period have cumulative effects over time (Nordhaus, 1982; Brito and Intriligator, 1987; Ko et al., 1992). In such situations, as in the static externality case, private decisions may not be socially efficient.
Many dynamic resource studies have focussed on existence and stability of steady-state solutions assuming that production would be carried out by profit-maximizing institutions (see, for example, Fisher, 1981; Conrad and Clarke, 1987). In con-trast, here we are concerned with identifying the types of policies and social organization that could satisfy social efficiency for the soil erosion/
pollution stock externality.
To examine alternative policies, we first define social efficiency in a society with urban and rural sectors that engage in manufacturing and agricul-tural production. The urban sector is assumed to be more wealthy than the rural. The types of tax/subsidy policies examined range from central-ization (with government determining taxes/ subsi-dies) to complete decentralization (with government determination of an initial entitle-ment followed by market decisions about pollu-tion reducpollu-tion). To tradipollu-tional Pigouvian and bargaining solutions extended to a dynamic set-ting, a third alternative is government as a co-pro-ducer of environmental goods.
2. Policy alternatives
2.1. Prices and standards
Tax, subsidy, and standard policies are alterna-tives that have been considered to be equivalent in terms of efficiency for the static externality case (Baumol and Oates, 1990). Taxes and subsidies decentralize production decisions. That is, given a tax, a producer can choose based on relative costs whether to pay the tax or to clean up emissions, thus minimizing costs to achieve a desired level of environmental quality. However, although a tax policy decentralizes production decisions, full pri-vatization cannot occur because monitoring and enforcement are required. While some advocate the ‘polluter pays’ principle, subsidies may be more appropriate than taxes when there are bind-ing income and food consumption constraints, as in the case of soil erosion in a poverty setting.
For a Pigouvian solution, a central authority must first determine the efficient level for the tax or subsidy — that level which leads to an efficient pollution level for the given distribution of in-come. At an efficient level, the marginal return to pollution equals its marginal social costs (Kula, 1992). Full information is needed to determine the efficient level; such a policy is practically infeasi-ble in terms of information needed.
ineffi-cient if regulators have incorrect information. An advantage of a tax over a standard is that the tax provides incentives for technology change, since a reduction in tax cost may be obtained with an improved technology; a standard would not provide such an incentive. (See Stevenson, 1991, for a discussion of economic instruments in envi-ronmental contexts.)
2.2. Bargaining
For the static externality case, the Coase theo-rem has been the support for a bargaining solu-tion between polluters and sufferers, with government intervention limited to determining rights. Coase suggested that an assignment of property rights can lead to a socially efficient solution through bargaining or market transac-tions among parties concerned. An idea that has been associated with the Coase theorem is that the nature of assignment of property rights does not matter when there are no transaction costs. That is, the same quantity outcome may be achieved whether polluters or sufferers are initially advan-taged by rights. (Of course, the distribution of income may differ with the assignment of rights.) However Eggertsson (1990) pointed out that the assignment of rights does matter to the outcome if preferences are not linear in money. (The case of firms maximizing profits does satisfy linearity.) In many cases, preferences do not satisfy linearity, e.g. when a smoker inflicts an externality on a person with smoke allergies. As Eggertsson demonstrates with an Edgeworth box, different property right endowments then can lead to dif-ferent social outcomes that are still efficient but differ in the level of environmental quality achieved.
An entitlement is a statement of property rights (Bromley, 1991). An entitlement defines the envi-ronmental quality level to which all citizens are minimally entitled. In our context, it indicates the starting position, or initial endowment, from which bargaining can occur. Then, a better qual-ity could be achieved through bargaining about cost-sharing arrangements for pollution reduction among polluters and sufferers (see Loehman and Dinar, 1994, for an example). A cost-sharing type
of solution is actually being utilized by the Con-servation Reserve Program executed by the USDA (Osborn, 1994).
2.3. Dynamic extensions
Taxes and subsidies are not equivalent policy instruments in a poverty context, as in Larson and Bromley: a pure tax can lead to accelerated deterioration because of the need to satisfy house-hold consumption constraints. Therefore, in the dynamic production situation studied here, a combination of tax and subsidy policies is needed to achieve social efficiency. The appropriate tax/
subsidy combination would generally vary across time with resource use. If a steady state with constant resource utilization were reached, the associated policy parameters could then be con-stant as well.
Besides the type of policy instrument, an addi-tional requirement for the dynamic context is to assign management responsibilities in terms of maintaining knowledge about dynamic produc-tion relaproduc-tionships for environmental resources. Such knowledge does not necessarily imply own-ership of a resources. In the static production case, the profit-maximizing firm controls produc-tion. But, management of the biological growth relationship need not be assigned to direct re-source users.
efficiency could be achieved by either assignment of management responsibilities and knowledge.
For dynamic resource problems, government involvement in management may be necessary at least as a repository of knowledge about the resource (see Hurwicz and Weinberger, 1990, for discussion about the transversality condition as a reason for government involvement in dynamic problems). Therefore, full privatization may not be possible. Below we develop this argument for the soil erosion/pollution framework.
3. Social efficiency in the dynamic system
The basis for policy design is the First Funda-mental Theorem of welfare economics extended to a dynamic setting with externalities. The First Theorem of welfare economics in the static case states the correspondence of a decentralized equi-librium (with private decision-making) to social efficiency, given certain conditions about prefer-ences and production sets. For an externality, a policy — such as a tax or subsidy — is added to the equilibrium system to bring about the correspon-dence. (See Negishi (1960) and Laffont (1989) for the static correspondence. See Kemp and Long (1982) for discussion of the dynamic extension without externalities. Eichhorn and Spremann (1982) is also relevant for discussion of pricing when there are intertemporal externalities.)
Two types of mathematical models for our two-sector dynamic externality setting are given in Appendix A: (Section A.1) social efficiency; (Sec-tion A.2) decentralized equilibrium under alterna-tive policies (Sections A.2.1, A.2.2 and A.2.3) to achieve efficiency. For each of Sections A.2.1, A.2.2 and A.2.3, first-order conditions for social efficiency are satisfied by a decentralized equi-librium corresponding to private decisions modified by a given policy. Each alternative type of decentralization has different implications about the role of government. Below, we describe these policy alternatives.
3.1. Basic relationships
Our extension of Larson and Bromley’s model
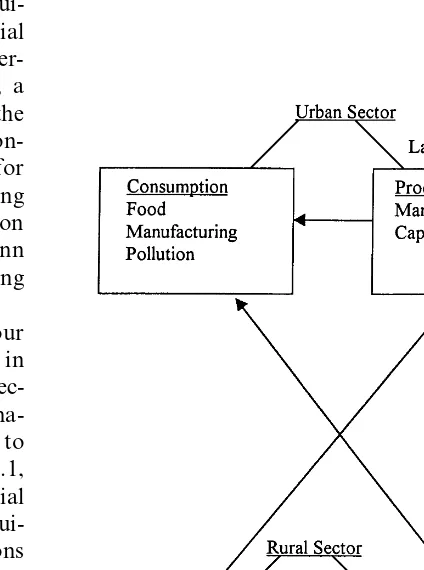
embeds the rural (agricultural) household that performs agricultural production in a two-sector economy that also includes urban (manufactur-ing) households. This simplified economic system is the basis for defining social efficiency and iden-tifying policies that could lead to social efficiency. Fig. 1 describes the basic flows of labor and capital inputs, and food, manufacturing and pol-lution outputs among rural and urban sectors in the economy. Both rural and urban households consume manufactured goods (M) and food (F), and supply labor (L) for production. Utility or satisfaction levels for urban households are deter-mined by pollution, consumption of food and manufactured items, and labor supplied. Simi-larly, rural household preferences are in terms of consumption of food and manufactured items and labor supplied; pollution is not assumed to affect
rural households directly. Declining marginal util-ity of consumption and declining marginal product of inputs are assumed. A constraint on resource allocation is providing a minimum food consumption for each type of household to avoid starvation in any time period.
On the production side, agricultural households use labor and purchase capital to produce food for both themselves and urban households; agri-cultural labor can also be used for soil resource improvement/pollution reduction. Urban house-holds supply labor to produce capital that is used for manufactured goods and for agricultural production.
Intensive capital used for food production by rural households is assumed to cause soil erosion. Soil erosion is a stock externality because it re-duces food production over time. At the same time soil erosion causes pollution, with soil parti-cles carrying pollutants such as fertilizer and pes-ticides to water bodies. Pollutants accumulate in streams in sedimentary layers over time; thus as-sociated pollution is also a stock externality. These pollutants can affect the welfare of urban households, e.g. urban drinking water quality. Rural residents may get their drinking water from wells that are less affected by pollutants. Rural labor can simultaneously reduce soil erosion and pollution through improved practices. For exam-ple, labor for terracing and buffer strips can im-prove soil loss and reduce pollution.
Production is described not only by the familiar production functions of classical economics but also by dynamic relationships. In this simplified economy, there are three dynamic production re-lationships for capital, pollution, and soil quality. The dynamic relationship describing capital is similar to that used in macroeconomic models: capital is a stock which grows in proportion to labor input and declines with depreciation. Both pollution and soil quality are described by stock relationships similar to the capital relation. In the dynamic relationship describing soil, its quality is reduced by use of intensive capital, and it can be improved either through the reduction of inten-sive capital or through increased labor used for pollution reduction.
3.2. Social efficiency
Following the paradigm of welfare economics, the conditions for socially efficient (Pareto opti-mal) resource allocation for this dynamic context are described. Social efficiency (see Appendix A, Section A.1), as in the static case, concerns the allocation of capital and labor inputs among food and manufacturing and the allocation of final goods between the two sectors, considering the impacts of pollution and soil erosion.
The social objective function used to describe the social efficiency problem (Section A.1) is the weighted sum of discounted utility for all persons in the society, here represented by the two sectors (C and A). An allocation of a consumption good (x) in limited supply satisfies — from the slope of the social objective function — the following rela-tion between the marginal utilities for each sector:
(uC
That is, given weights ai on sectors, each
con-sumption good produced (x) is allocated so that marginal utility of consumption for each sector is inversely proportional to its social weight. Then, because of declining marginal utility, relatively more is given to a sector with a larger weight.
Extending the static case (Negishi, 1960), we do not assume there is a social planner who defines these weights, but rather that any efficient solu-tion can be associated with some weights. By varying the weights over the set of possible weightings, all possible socially efficient solutions can be generated. We assume that society would rather be at an efficient solution than otherwise; that is, our arguments do not require determining which of the efficient outcomes should be selected. The first-order conditions necessary for social effi-ciency apply for any set of weights.
today’s generation. A discount rate of zero would imply equal weights over time. The same form for efficiency conditions holds for any dis-count rate: by varying the rate, alternative effi-cient solutions can be generated. Below, we assume that the discount rate used by each sec-tor in equilibrium formulations is the same as in the social efficiency problem.
In determining policy implications below, we focus particularly on the dynamic first-order conditions for soil quality and pollution and on the marginal value conditions for labor and cap-ital. (See Kamien and Schwartz, 1982, for the general method of dynamic optimization.) The first-order conditions given in the appendix are necessary conditions formulated in terms of shadow prices for pollution, soil, and capital. The shadow price for capital reflects the long-term social opportunity cost of current capital use decisions. Similarly, the opportunity cost of soil quality reflects the marginal long-term benefits of maintaining soil quality. The shadow price for pollution indicates the long-term mar-ginal social damage from pollution; it is nega-tive. First-order conditions given in Appendix A show that the opportunity cost for pollution at the optimal level should reflect the long-term ef-fects of pollution on the welfare of urban house-holds. Similarly, the opportunity cost for soil quality relates to its long-term productivity.
The optimal time path that solves the set of first-order conditions and constraints depends on the initial conditions in an economy: societies with different initial conditions (here including pollution and soil quality) will have different op-timal time paths. Regardless, from the supply – demand constraints for labor and capital, the marginal value for each input should be the same in each of its uses.
3.3. Decentralized equilibrium and pri6ate
decision-making
Decentralized equilibrium models (see Ap-pendix A, Sections A.2.1, A.2.2 and A.2.3) rep-resent different organizations of consumption
and production through private decision-making by actors in the economic system. Generally, manufacturing decisions are made in the urban area, with urban households determining the labor supplied for manufacturing. Ownership and production of capital are assigned to the urban sector. The rural households make deci-sions about food production and allocate labor for food and pollution reduction production. Consumption decisions are made separately by urban and rural sectors. Manufacturing is as-sumed to operate in a ‘spot’ market, so that production decisions and demand for labor are made period by period given relative prices.
By dynamic equilibrium we mean a simulta-neous set of decisions across time for each actor in the dynamic system, such that no actor would change her decisions given the equilibrium deci-sions by the other actors. Necessary conditions that determine equilibrium are the first-order conditions for each sector’s decentralized prob-lem, the constraints for each sector’s decentral-ized decision problem, and supply – demand equilibrium conditions. The dynamic equilibrium includes prices for each period; equilibrium prices are a time vector for each commodity. Given the equilibrium vector of prices over time, households make decisions about consumption and labor supply for the whole time period.
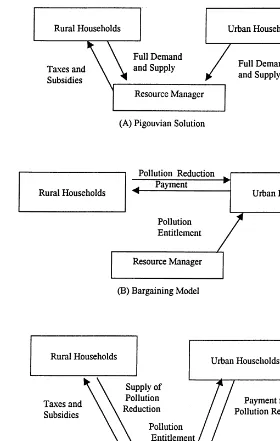
Fig. 2. Alternative decentralized policy models to alleviate soil erosion. 3.4. Alternati6e policy designs
Alternative policy designs below differ in terms of who is assigned the responsibility for managing dynamic production relationships for soil and pol-lution. Each policy brings about the correspon-dence of private decisions with social efficiency. Policies could involve different price and income
effects in the economy as a whole. (See Fig. 2 for a comparison of policy types.)
3.4.1. Pigou6ian solution(Section A.2.1)
role that can be carried out by government) to know all demand and supply relationships in the economy (including the dynamic relationships), to solve the social optimality problem, and to deter-mine and apply the appropriate tax and subsidy package accordingly. Urban and rural household private decisions are affected only through price levels. The rural household would not have to know the dynamic environmental relationships in order for the efficiency conditions to be satisfied.
3.4.2.Bargaining solution (Section A.2.2)
In this case, an entitlement level Pefor pollution
is first defined such that pollution should never be greater than this level. The urban household may then pay the rural household to obtain pollution below the entitlement level. In this model, it is assumed that rural producers know the dynamic production relationships for soil and pollution and manage them in response to payment levels from urban households. Rural producers then choose intensive capital and labor for pollution reduction to satisfy both the urban demand for pollution reduction and for food.
While the first-order efficiency conditions are satisfied at any equilibrium, the nature of the equilibrium would generally depend on the enti-tlement level. The role of government in this case would be to set the entitlement level, e.g. based on equity considerations.
3.4.3.Go6ernment as co-producer of
en6ironmental goods (Section A.2.3)
This model differs from the Pigouvian model in that the government is required to know only the dynamic environmental relationships. It also dif-fers from the bargaining model in that the govern-ment resource manager becomes a part of the equilibrium system as a co-producer of environ-mental goods. The resource manager purchases the labor input for pollution reduction from agri-cultural labor to meet the urban demand for pollution reduction; urban payment pp per unit
pollution reduced is paid to the resource manager. At the same time, the government resource man-ager receives a tax (t) on intensive capital from rural producers, pays a subsidy (s) per unit labor for pollution reduction, and also pays rural
pro-ducers ps per unit soil improvement. The tax,
subsidy, and the prices for soil improvement and pollution reduction are then determined through operation of the equilibrium system. The combi-nation of these four price instruments is required to satisfy social efficiency conditions. Prior to any market exchange, the pollution entitlement is set at Pe. The initial soil level is So. Equilibrium prices
and outcomes would generally be affected by the entitlement and initial soil levels.
Knowledge is required about the dynamic envi-ronmental relations for soil and pollution for the resource manager’s decision problem. Rural pro-ducers operate in a spot market without require-ments for knowledge of dynamic environmental relations.
4. Conclusions
Decentralization of production decisions should not be confounded with privatization. Privatiza-tion of land ownership may not provide an appro-priate solution for the stock externality associated with soil erosion. But, other ‘economist’ policy solutions are available! Traditional welfare eco-nomics concepts were applied here in a dynamic setting to identify three policy combinations for a soil erosion stock externality that could satisfy social efficiency, each with different roles for a government resource manager and with different knowledge requirements.
The other extreme applies if rural households do not have the appropriate knowledge about production relationships and hence cannot suc-cessfully manage resources in the long term. The Pigouvian solution would require the resource manager to have full knowledge of preference and production relations to determine the appropriate tax and subsidy combination. Rural production decisions could then be made in a myopic fashion, taking prices, taxes, and subsidies as given.
A third alternative can achieve social efficiency with less knowledge required for rural producers than in a bargaining solution and with much less government information collection than for a Pigouvian policy. The resource manager’s role is
to be a co-producer — with rural labor — of envi-ronmental goods, given knowledge of dynamic environmental relationships. The resource man-ager purchases agricultural labor for pollution reduction. Equilibrium price levels for soil im-provement and pollution reduction are found by matching urban demand with rural supply, as in any other production situation. The setting of an entitlement for environmental quality by govern-ment is an important part of this solution.
The choice before us is what type of manage-ment and information responsibilities and knowl-edge should reasonably be assigned to which actors in the social system, including government as one of the actors.
Appendix A. Mathematical models
A.1.Social efficiency problem
Max
Mi,Li,Fi,Ki
&
[a1u C(MC
,LC
,FC
,P)+a2uA(M A
,LA
,FA
)]e−rtdt
s.t.
Multipliers (current values) Constraints
Supply and demand:
(pˆM)
MC+MA5M
KF+KM5K (rˆ)
(pˆF)
FA+FC5F
(wˆC)
LCM+LCK5LC
LAF+LAP5LA (wˆA)
Production:
(g.1)
M5g(LCM
,KM
) (mfg.)
(g.2)
F5h(KF
,LAF
,S) (food) K: =o1L
CK
−d1K (capital) (m.1)
S: =b2L AP
−o2K F
(soil) (m.3)
(m.3)
P: = −b3L AP
+o3K
F (pollution)
Fi
]Foi (no starvation) (x. i)
Initial conditions: Po,Ko, So. [Note: m.2\0 and m.3B0]
Conditions Goods
pˆM=g.1
M Total manufacturing Mfg.:
MA Manufacturing consumed by rural pˆ
M=a2uAM
MCManufacturing consumed by urban pˆ
M=a1uCM
Labor: LCM Labor for manufacturing (urban) wˆC=g. 1gL
LCK Labor for capital (urban) wˆC=m. 1o1
LC Total urban labor supply wˆC= −a 1uCL
LA Total rural labor supply wˆA= −a 2uAL
wˆA
=g.2hL
LAF
Rural labor for food production LAP
Rural labor for soil conservation wˆA
=m.2b2−m.3b3
Food: F Total food supply pˆF=g.2
pˆF
=a2u A F+x.
A
FA
Rural food demand
FC Urban food demand pˆ F=a1u
C F+x.
C
Capital: KFCapital for producing food rˆ
−o3m.3+o2m.2=g.2hk
KM Capital in manufacturing rˆ
=g.1gK
K Capital stock Shadow prices:
mˆ;
1−rmˆ1= −
(H.
(K= −rˆ+d1mˆ1
S Soil quality
mˆ;2−rmˆ2= −(H.
(S= −gˆ2hS
P Pollutant stock
m:.3−rm.3= −
(H.
(P= −a1u
C P
Hamiltonian:
H. =[a1uC+a2uA]+pˆM[M−MC−MA]+rˆ[K−KF−KM]+pˆF[F−FA−FC]
+wˆC[LC−LCM−LCK]+wˆA[LA−LAF−LAP]+g.
1[g(LCM,KM)−M]+g.2[h(LAF,KF,S)−F]
+m.1[d1LCK−d1K]+m.2[b2LAP−o2KF]+m.3[−b3LAP+o3KF]+x. A[FA−FAo]+x. C[FC−FCo]
A.2.Decentralized Equilibrium with Alternati6e Policies
A.2.1. Pigou6ian solution with a tax on polluting capital (t) and subsidy of labor (s) to reduce pollution
(1) Rural households make choices each time period separately, choosing labor and capital inputs; food and manufacturing consumption are also chosen, taking soil quality (S) as given:
Max
MA,LA,FA,KF,LAF,LAPu
A(MA,LA,FA)
s.t.
Multipliers Constraints
(XF)
FA
]F0A
(g2)
F5h(KF,LA,S)
(wA)
LAF
+LAP
5LA
Budget constraint:
(lA)
(2) Resource Manager sets tax (t) and subsidy (s) by solving (A.1).
t=(o2m.2−o3m.3)a2
s=(b2m.2−b3m.3)a2
(3) Urban households choose labor inputs and consumption for the entire time period:
Max
MC,LC,FC,LCK,LCM
&
uC(MC,LC,FC,P)e−rtdt
s.t.
Multipliers Constraint
(xC
) FC
]Fo C
K: =o1L CK
−d1K (m1)
LCM
+LCK
5LC
(wC
) Budget constraint:
(lC)
pMM C
+pFF C
5IC+rK+wLCM
(4) Mfg. Firm operates in a spot market
Max
M,KM,LCM[pMM−rK M
−wLCM]
s.t.
M5g(KM
,LCM
) (g1)
Equilibrium Conditions (d=demand; s=supply): (i) Labor supply and demand for manufacturing:
wC[LCM
d −LCMs ]=0
(ii) Labor by urban household balance:
wC[LC−LCM
s −LCKs ]=0
(iii) Captital supply and demand balance:
r[K−KM d −K
F d]=0
(iv) Food supply and demand balance:
pF[F−F A d−F
C d]=0
(v) Manufacturing supply and demand balance:
pM[M−MAd−MCd]=0
Urban Households: Md
C p
M=uM C
/lC
pF=uF
C/lC+xC/lC
Fd C
wC=wlC
LsCM
LsCK wC=e1m1
LC wC= −u
L C/lC
m:1−rm1= −rlC+d1m1
K
Mfg Firm:
M pM=g1
KM
r=g1gK
wC
=g1gL
Ls CM
Rural Households: MA
pM=uM A
/lA
pF=uF A
/lA
+xA
/lA
FA
pF=g2/l A
F LA
−uL A
=wA g2hK=(r+t)l
A
KF
wA=g 2hL
LsAF
LsAP wA=slA
Correspondence between (A.1) and (A.2.1):
I IIA
pM
pˆM
pF
pˆF
rlC
rˆ
xC
/lA x.C
wA/lA
wˆA
g2/lA g.2
g.1 g1
m1 m1
1/lC a1
a2 1/lA
A.2.2. Bargaining solution with a price for pollution reduction(pp) and entitlement (Pe)
(1) Rural Households receive a price pp for pollution reduction beyond Peand make choices for the
entire time period:
Max
MA,LA,FA,F,LAP,LAF,KF
&
uA(MA,LA,FA)e−rtdt
Constraints Multipliers
FA]F o
A (xF)
(g2)
F5h(KF,LAF,S)
(m2)
S: =b2LAP−o2KF
P: = −b3LAP+o3KF (m3)
LAP+LAF5LA (wA)
Budget constraint:
pFFA+pMMA+rKF5IA+pFF+pp(Pe−P) (lA)
(2) Urban Households demand reduction in P at a price ppgiven entitlement Pe; choices are made for
the entire time period:
Max
MC,LC,FC,LCK,LCM,KF
&
u C(MC,
LC,
FC,
P)e−rtd
t
s.t.
Constraints: Multiplier
(xC)
FC]F o C
(m1)
K: =o1LCK−d1K
LCM
+LCK
5LC
(wC
) Budget constraint:
(lC
) pMM
C
+pFF C
+pp(Pe−P)5I C
+rK+wLCM
(3) Mfg. Firm: Max
M,KM,LCM[pMM−rK M
−wLCM]
s.t.
M5g(KM,LCM) (g 1)
Equilibrium Conditions:
(i) Labor supply and demand for manufacturing: wC
[LCM d −L
CM s ]=0
(ii) Labor by urban household balance: wC
[LC
−LCM s −L
CK s ]=0
(iii) Captital supply and demand balance: r[K−KM
d −K F d]=0
(iv) Food supply and demand balance: pF[Fs−FAd−FCd]=0
pM[Ms−M A d−M
C d]=0
(vi) Pollution supply and demand balance: pp[Pd−Ps]=0
First-order Conditions:
Urban Households:
Correspondence between (A.1) and (A.2.2):
A.2.3. Go6ernment is a co-producer of en6ironmental goods, with four price parameters and an
entitlement Pe
(1) Rural households make choices each time period separately, given tax (t) on polluting capital, subsidy (s) on labor to reduce pollution, and price Ps on soil quality improvement
Max
MA,LA,F,FA,LAF,LAP,KFu
A(MA,LA,FA)
s.t.
Constraints Multipliers
FA
]F0A (xF)
(g2)
F5h(KF,LAF,S)
(wA)
LAF+LAP5LA
Budget constraint:
pFFA+pMMA+(r+t)KF5IA+pFF+sLAP+pS(S−So) (lA)
(2) Resource Manager supplies P at price pp, demands S at price ps, pays s per input L
APand receives tax
t on KF, given entitlement P
eand So
Max
S,P,KF,LAP
&
[pp(Pe−P)−ps(S−So)+tKF−sLAP]e−rtdt
s.t.
S: =b2L AP−o
2K
F (m
2)
P: = −b3LAP+o3KF (m3)
(3) Urban households choose labor and consumption for the entire time period and pay for pollution reduction given the entitlement Pe.
Max
MC,LC,FC,LCK,LCM
&
uC(MC,LC,FC,P)e−ptdt
s.t.
Constraints Multipliers
(xC)
FC
]FoC
K: =o1L CK
−d1K (m1)
(wC)
LCM
+LCK
5LC
Budget constraint:
(lC)
(4) Mfg. Firm: Max
M,KM,LCM[pMM−rK M
−wLCM]
s.t.
M5g(KM,LCM) (g 1)
Equilibrium Conditions:
(i) Labor supply and demand for manufacturing: wC[LCM
d −LCMs ]=0
(ii) Labor by urban household balance: wC
[LC
−LCM s −L
CK s ]=0
(iii) Capital supply and demand balance: r[K−KM
d −K F d]=0
(iv) Food supply and demand balance: pF[F−F
A d−F
C d]=0
(v) Manufacturing supply and demand balance: pM[M−MAd−MCd]=0
(vi) Agricultural labor for pollution reduction balance: s[LAP
s −L AP d ]=0
(vii) Pollution supply and demand balance: pp[Ps−Pd]=0
(viii) Soil supply and demand balance: pS[Ss−Sd]=0
First-order Conditions
Urban Households:
MdC pM=uMC/lC
pF=uFC/lC+xC/lC
FdC
wC=wlC
LsCM
wC
=o1m1
Ls CK
wC
= −uL C
/lC
LC
m:1−rm1= −rl C
+d1m1
K
Pd uP
C
/lC
=pp
Mfg Firm:
M pM=g1
KM r
=g1gK
wC=g 1gL
Ls CM
Rural Households:
MA p
M=uMA/lA
pF=uFA/lA+xA/lA
pF=g2/l
Correspondence between A.1 and A.2.3:
A.1 A.2.3
Anderson, T.L., 1991. Free Market Environmentalism. West-view Press, Boulder, CO.
Baumol, W.J., Oates, W.E., 1990. The Theory of Environmen-tal Policy. Cambridge.
Brito, D.L., Intriligator, M.D., 1987. Stock externalities, pigouvian taxation, and dynamic stability. J. Public Econ. 33, 59 – 72.
Bromley, D.W., 1991. Environment and Economy: Property Rights and Public Policy. Cambridge University press, Cambridge.
Conrad, J.M. Clarke, C.W., 1987. Natural Resource Econom-ics. Cambridge University Press, Cambridge.
Eggertsson, T. 1990. Economic Behavioural Institutions, Cam-bridge University Press, CamCam-bridge.
Eichhorn, W., Spremann, K., 1982. Efficient pricing of natural resources and intertemporal externalties, in: Eichhorn, W.,
Neumann, K., Shephard, R.W. (Eds.), Economic Theory of Natural Resources. Physica Verlag, Springer Verlag, Berlin, Germany.
Fisher, A., 1981. Resource and Environmental Economics. Cambridge University Press, Cambridge.
Hurwicz, L., Weinberger, H.F., 1990. in: Majumdar, M. (Ed.), A Necessary Conditon for Decentralization and an Appli-cation to Intertemporal AlloAppli-cation in Decentralization in Infinite Horizon Economics, Westview Press, Boulder, CO, pp. 119 – 151.
Kamien, M.I., Schwartz, N.L., 1982. The role of common property resources in optimal planning models, in: Smith, V.K., Krutilla, J.V. (Eds.), Explorations in Natural Re-source Economics. John Hopkins Press, Baltimore, MD. Kemp, M.C., Long, N.V., 1982. The efficiency of competitive
Ko, L.D., Lapam, E., Sandler, T., 1992. Controlling stock externalities: flexible versus inflexible pigouvian correc-tions. Eur. Econ. Rev. 36, 1263 – 1276.
Kula, E., 1992. Economics of Natural Resources, the Environ-ment and Policies. Chapman and Hall, London.
Laffont, J.J., 1989. Fundamentals of Public Economics, MIT Press, Cambridge, MA.
Larson, B.A., Bromley, D.W., 1990. Property rights, externali-ties, and resource degradation. J. Dev. Econ. 33, 235 – 262. Loehman, E., Dinar, A., 1994. Cooperative solutions of local externality problems: a case of mechanism design applied to irrigation. J. Env. Econ. Manage. 26, 235 – 256. Negishi, T., 1960. Welfare economics and the existence of an
equilibrium for a competitive economy. Metroeconomica 12, 92 – 97.
Nordhaus, W., 1982. How fast should we graze the global commons? Am. Econ. Rev. Papers Proc. 72, 242 – 246. Osborn, T., 1994. RTD Updates: the Conservation Reserve
Program. US Department of Agriculture, Economic Re-search Service. January, 1994.
Perrings, C.P., 1989. Optimal path to extinction? Poverty and resource degradation in the open agrarian economy. J. Dev. Econ. 30, 1 – 24.
Postel, S., 1991. Restoring degraded land in the World Watch Reader on Global Environment Issues. Lester R. Brown (Ed.) W.W. Nortan, Cambridge.
Stevenson, G.G., 1991. Common Property Economics, World Watch, The World Watch Reader on Global Environmen-tal Issues. W.W. Norton, Cambridge.