PENYELESAIAN MASALAH PL DENGAN METODE SIMPLEKS

(1)

PENYELESAIAN MASALAH PL DENGAN METODE

SIMPLEKS

Metode simpleks merupakan suatu teknik standar yang digunakan untuk memecahkan masalah Program Linear sejak tahun 1940. Pada prinsipnya, metode simpleks mencari penyelesaian optimal dengan menentukan titik-titik sudut dari daerah feasible, proses dilakukan berulang-ulang dari suatu titik sudut ke titik sudut berikutnya yang meningkatkan nilai fungsi tujuan sampai diperoleh nilai optimal atau sampai terlihat bahwa tidak ada nilai optimal.

Masalah PL dua variabel dapat diselesaikan dengan metode grafik. Secara umum, masalah PL n variabel dapat diselesaikan dengan metode aljabar yang disebut dengan metode simpleks. Metode grafik dan metode simpleks pada dasarnya adalah mencari PO yang merupakan titik-titik batas daerah layak.

Pertama-tama akan dibahas dicari PO masalah PL bentuk baku. Bentuk baku masalah PL :

1. maksimum baku 2. minimum baku

Kendala sistem pertidaksamaan linear pada masalah PL baku diubah menjadi SPL dengan menambahkan variabel baru yang mengetatkan atau melonggarkan, yaitu :

- Variabel Slack, yaitu variabel yang mengetatkan kendala bertanda menjadi bertanda =

Ruas kiri kendala ke-k

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

b

_k ditambah variabel slack

s

_k

0

sehingga menjadi

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

s

_k

b

_k. Variabel

s

_k menjadi variabel basis.

- Variabel surplus, yaitu variabel yang melonggarkan kendala bertanda menjadi bertanda =.

Ruas kanan kendala ke-k

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

b

_k ditambah variabel surplus

t

_k

0

sehingga menjadi

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

b

_k

t

_k atau

(2)

k k n kn k k

x

a

x

a

x

t

b

a

₁ ₁ ₂ ₂

...

. Variabel

t

_k

0

bukan variabel basis (koefisiennya bukan +1)

- variabel artifisial, yaitu variabel yang membawa kendala PL yang belum memuat variabel basis

Pada

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

t

_k

b

_k perlu ditambah variabel artifisial

0

k

q

sehingga menjadi

a

_k₁

x

₁

a

_k₂

x

₂

...

a

_kn

x

_n

t

_k

q

_k

b

_k,

0

k

q

merupakan variabel basis.

1. PENYELESAIAN PL MAKSIMUM BAKU

Diberikan masalah PL maksimum baku :

Memaksimumkan n j j j j

c

x

f

1

)

(

(1) Dengan kendala _i n j ij j

b

x

a

1 ,

i

,

i

1 ,

2 ,...,

m

(2)

x

_j

0 ,

j

,

j

1 ,

2 ,...,

n

(3)

Kendala (2) diubah menjadi SPL dengan menambahkan variabel slack sehingga diperoleh

m m n mn m m n n n n

b

s

x

a

x

a

x

a

b

s

x

a

x

a

x

a

b

s

x

a

x

a

x

a

...

2 2 1 1 2 2 2 2 22 1 21 1 1 1 2 12 1 11

Agar nilai fungsi tujuan tidak berubah, maka koefisien biaya

c

_i untuk

s

_i adalah nol,

m

i

,

1 ,

2 ,...,

. Sehingga fungsi tujuan menjadi memaksimumkan m n n m n

s

c

x

c

x

s

x

f

(

₁

,...,

,

₁

,...,

)

₁ ₁

...

0

₁

...

0

Variabel slack

s

_i

0 ,

i

,

i

1 ,

2 ,...,

m

merupakan variabel basis yang nilainya tak nol, sedangkan

x

_j

0 ,

j

,

j

1 ,

2 ,...,

n

menjadi variabel non basis yang nilainya dinolkan atau

x

_j

0 ,

j

,

j

1 ,

2 ,...,

n

.

(3)

Akibatnya nilai awal fungsi tujuan adalah

0 )

,...,

,

0 ,...

0 (

)

,...,

,

,...,

(

x

₁

x

_n

s

₁

s

_m

f

s

₁

s

_m

f

dengan penyelesaian optimal awal/plb

(

x

₁

,...,

x

_n

,

s

₁

,...,

s

_m

)

(

0 ,...

0 ,

b

₁

,...,

b

_m

)

.

Masalah PL yang kendalanya berbentuk SPL dan memuat variabel basis tersebut dinamakan berbentuk kanonik. Masalah PL bentuk kanonik dalam tabel simpleks dituliskan sebagai berikut.

j

c

₁

c

₂ ... n

c

0 0 ... 0 i

b

R

_i i

c

x

j i

x

1

x

₂ ... n

x

s

₁

s

₂ ... m

s

0 1

s

a

₁₁

a

₁₂ ... n

a

₁ 1 0 ... 0 1

b

R

₁ 0 2

s

a

₂₁

a

₂₂ ... n

a

₂ 0 1 ... 0 2

b

R

₂ ... ... ... ... .... ... ... ... ... ... ... ... 0 m

s

a

_m₁

a

_m₂ .... mn

a

0 0 ... 1 m

b

R

_m j

z

₁

z

₂ .... n

z

c

₁

c

₂ ... n

c

Z j

z

-

c

_j

z

₁-

c

₁

z

₂-

c

₂

z

_n-

c

_n 0 0 ... 0 Z

Keterangan tambahan tabel :

i

x

variabel basis pada bentuk kanonik i

c

koefisien unit ongkos dari

x

_i

ij m i i j

c

a

z

1 i m i i

b

c

Z

1

nilai fungsi tujuan

i

(4)

Algoritma Simpleks PL maksimum baku 1. Masalah PL dibawa ke bentuk kanonik 2. Susun tabel awal simpleks

3. Uji keoptimuman

Tabel simpleks dikatakan optimum jika

z

_j

c

_j

0 ,

j

Nilai fungsi tujuan ada pada baris ke m+1 kolom

b

_i dan POnya adalah susunan nilai

b

_i untuk variabel basis dan nol untuk variabel non basis.

Jika masih ada

z

_j

c

_j

0

, maka dilanjutkan langkah 4. 4. Memperbaiki tabel simpleks

Memperbaiki tabel simpleks dilakukan dengan mengganti variabel basisnya dengan variabel basis yang baru dengan harapan variabel basis baru tersebut mengoptimalkan fungsi tujuan.

Langkah memperbaiki tabel:

- menentukan variabel masuk yang akan menjadi variabel basis baru, yaitu

variabel dengan

z

_j-

c

_j

0

terkecil. Misal

z

_k

c

_k terkecil, maka

x

_k menjadi variabel masuk

- menentukan variabel keluar yang akan digantikan oleh variebel basis baru.

Pada kolom koefisien

x

_k, yaitu

a

_ikdihitung rasio

_,

₀

ik ik i i

a

b

R

,

kemudian pilih

R

_i terkecil. Misal

R

_l terkecil, maka

q

_l menjadi variabel keluar.

- menyusun tabel baru.

Variabel basis baru dalam tabel baru adalah

q

₁

,...,

q

_l ₁

,

x

_k

,

q

_l ₁

,...,

q

_m. Koefisien

a

_lk menjadi elemen pivot. Pada kolom ke-k,

a

_lk harus diubah menjadi 1 dan

a

_ik

0 ,

i

l

. Perubahan ini dilakukan dengan OBE dan berlaku untuk semua elemen pada baris yang sesuai sehingga diperoleh tabel baru.

(5)

CONTOH 1

Selesaikan masalah PL berikut berikut dengan metode simpleks.

Memaksimumkan

f

(

x

₁

,

x

₂

,

x

₃

,

x

₄

)

5 x

₁

3 x

₂

2 x

₃ Dengan kendala

0 ,

,

30

4

3

20

2

5

4

4 3 2 1 4 3 2 1 4 3 2 1

x

Penyelesaian : Langkah 1

Masalah PL ini diubah menjadi bentuk kanonik dengan menambahkan variabel slack

0

1

s

pada kendala 1 dan

s

₂

0

pada kendala 2 sehingga kendala menjadi

0 ,

,

30

4

3

20

2

5

4

2 1 4 3 2 1 2 4 3 2 1 1 4 3 2 1

s

x

s

x

s

x

Kendala ini sudah memuat variabel basis, yaitu

s

₁ dan

s

₂. Fungsi tujuan dapat ditulis secara lengkap menjadi

2 1 4 3 2 1 2 1 4 3 2 1

,

)

5

3

2

0

0 (

x

s

x

s

f

Langkah 2

Tabel simpleks awalnya adalah

j

c

5 3 2 0 0 0 i

b

R

_i i

c

x

_j i

x

1

x

2

x

₃ 4

x

1

s

2

s

0 1

s

4 5 2 1 1 0 20 5 0 2

s

3 4 -1 1 0 1 30 10 j

z

0 0 0 0 0 0 0 j

z

-

c

_j -5 -3 -2 0 0 0 0

(6)

Langkah 3

Karena masih terdapat

z

_j-

c

_j

0

, maka tabel belum optimal. Langkah 4

- variabel masuk

Nilai

z

_j-

c

_j

0

terkecil ada pada kolom variabel 1

x

sehingga 1

x

merupakan variabel baru yang masuk

- variabel keluar

Nilai

R

_i terkecil adalah 5, yaitu pada variabel

s

₁, sehingga

s

₁ keluar digantikan 1

x

- memperbaiki tabel

Elemen pivotnya adalah 4 yang terletak pada perpotongan kolom

x

₁ dan baris

s

₁. Untuk mengubah 4 menjadi 1, dilakukan OBE yaitu mengalikan baris 1 dengan

4 1

. Elemen pada kolom

x

₁ lainnya, yaitu 3 diubah menjadi 0 dengan melakukan OBE menambah baris ke-2 dengan -3 kali baris ke-1 baru. Diperoleh tabel simpleks baru sebagai berikut.

j

c

5 3 2 0 0 0 i

b

R

_i i

c

x

_j i

x

1

x

2

x

₃ 4

x

1

s

2

s

5 1

x

1 5/4 2/4 1/4 1/4 0 5 0 2

s

0 1/4 -5/2 1/4 -3/4 1 15 j

z

5 25/4 5/2 5/4 5/4 0 25 j

z

-

c

_j 0 13/4 1/2 5/4 5/4 0 25

5. Menguji keoptimuman tabel

Dari tabel lanjutan diperoleh bahwa

z

j

c

j

0

sehingga tabel sudah optimum

dengan PO

(

x

₁

,

x

₂

,

x

₃

,

x

₄

,

s

₁

,

s

₂

)

(

5 ,

0 ,

15 )

dan nilai maksimum

25

15 .

0

0 .

0

0 .

0

0 .

2

0 .

3

5 .

5 )

15 ,

0 ,

5 (

f

(7)

SOAL LATIHAN

Tentukan PO dan nilai optimal masalah PL berikut dengan metode simpleks.

1. Memaksimumkan fungsi

z

3 x

2 y

dengan kendala

0 , 55 8 10 65 10 6 70 6 5 y x y x y x y x

f

(

x

₁

,

x

₂

,

x

₃

)

2 x

₁

8 x

₂

x

₃ dengan kendala

0 , , 5 3 3 2 4 2 3 2 1 3 2 3 2 1 3 2 1 x x x x x x x x x x x

z

5 x

₁

7 x

₂

12 x

₃

x

₄ dengan kendala

0 ,

,

55

4

2

3

38

2

3

2

4 3 2 1 4 3 2 1 4 3 2 1

x

f

(

x

₁

,

x

₂

,

x

₃

)

2 x

₁

2 x

₂

x

₃, dengan kendala

0 ,

,

40

45

2

30

2

3 2 1 3 2 3 1 2 1

x

5. Meminimumkan

z

2 x

y

, dengan kendala

0 ,

7

2

4

3 y

x

y

x

y

x

(Petunjuk: meminimumkan z = memaksimumkan – z)

(8)

Diberikan masalah PL minimum baku sebagai berikut. Meminimumkan n j j j j

c

x

f

1

)

(

dengan kendala i n j j ij

x

b

a

1 , i,i 1,2,...,m,

x

_j

0 ,

j

,

j

1 ,

2 ,...,

n

Dalam proses penyelesaian PL minimum, nilai fungsi tujuan akan makin diperkecil menuju ke nilai minimumnya, berkebalikan dengan pola maksimumn. Oleh karena itu, walaupun langkah-langkahnya sama dengan PL berpola maksimum, ada beberapa petunjuk yang berbeda.

Algoritma Simpleks PL minimum baku 1. Masalah PL dibawa ke bentuk kanonik

Kendala pertidaksamaan diubah menjadi persamaan dengan menambahkan

variabel surplus _t_i ₀ ke ruas kanan pertidaksamaan. Koefisien

t

_i pada fungsi tujuan adalah 0.

Karena kendala persamaan belum memuat basis, maka ditambahkan variabel

artifisial

q

_i

0

ke ruas kiri pertidaksamaan yang akan menjadi basis dalam tabel awal. Koefisien q pada fungsi tujuan adalah M (M adalah bilangan positif cukup _i

besar).

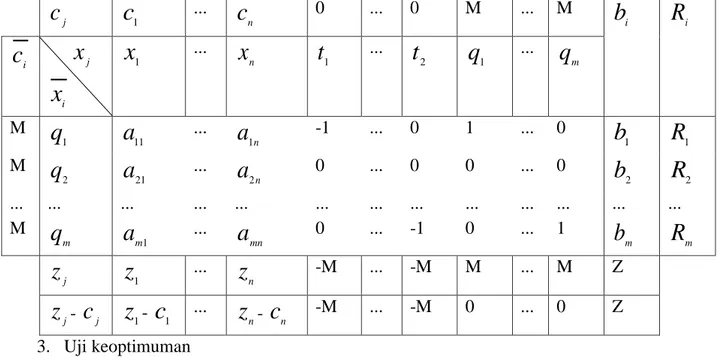
2. Susun tabel awal simpleks

j

c

₁ ... n

c

0 ... 0 M ... M i

b

R

_i i

c

x

j i

x

1

x

... n

x

t

₁ ... 2

t

q

₁ ... m

q

M 1

q

a

₁₁ ... n

a

₁ -1 ... 0 1 ... 0 1

b

R

₁ M 2

q

a

₂₁ ... n

a

₂ 0 ... 0 0 ... 0 2

b

R

₂ ... ... ... ... ... ... ... ... ... ... ... ... ... M m

q

a

_m₁ ... mn

a

0 ... -1 0 ... 1 m

b

R

_m j

z

₁ ... n

z

-M ... -M M ... M Z j

z

-

c

_j

z

₁-

c

₁ ...

z

_n-

c

_n -M ... -M 0 ... 0 Z 3. Uji keoptimuman

(9)

Nilai fungsi tujuan ada pada baris ke m+1 kolom

b

_i dan POnya adalah susunan nilai

b

_i untuk variabel basis dan nol untuk variabel non basis.

Jika masih ada

z

_j-

c

_j

0

, maka dilanjutkan langkah 4. 4. Memperbaiki tabel simpleks

Memperbaiki tabel simpleks dilakukan dengan mengganti variabel basisnya dengan variabel basis yang baru dengan harapan variabel basis baru tersebut mengoptimalkan fungsi tujuan.

Langkah memperbaiki tabel:

- menentukan variabel masuk yang akan menjadi variabel basis baru, yaitu

variabel dengan

z

_j-

c

_j

0

terbesar. Misal

z

_k

c

_k terbesar, maka

x

_k menjadi variabel masuk

- menentukan variabel keluar yang akan digantikan oleh variebel basis baru.

Pada kolom koefisien

x

_k, yaitu

a

_ikdihitung rasio

_,

₀

ik ik i i

a

b

R

, kemudian pilih i

R

terkecil. Misal l

R terkecil, maka

s

l menjadi variabel keluar. - menyusun tabel baru.

Variabel basis baru dalam tabel baru adalah

s

₁

,...,

s

_l ₁

,

x

_k

,

s

_l ₁

,...,

s

_m. Koefisien lk

a

menjadi elemen pivot. Pada kolom ke-k,

a

_lk harus diubah menjadi 1 dan

l

i

a

_ik

0 ,

. Perubahan ini dilakukan dengan OBE dan berlaku untuk semua elemen pada baris yang sesuai sehingga diperoleh tabel baru.

5. Lakukan kembali langkah 3 dan 4 sehingga optimum tercapai.

SOAL LATIHAN

1. Hitunglah nilai minimum dari

f

3000

x

2000

y

dengan kendala

, ,

60 x

60 y

3600

,

0 , y

x

.

2. Tentukan nilai x, y yang meminimumkan

z

3 x

2 y

dan memenuhi

70

6

5 x

y

,

6 x

10 y

65

,

10 x

8 y

55

,

x

, y

0

. 3. Selesaikan masalah PL : 2000 20 100x y 40x 80y 3200

(10)

Meminimumkan

f

4 x

5 y

z

Dengan kendala 0 , , 4 2 3 z y x y x z y x

3. METODE SIMPLEKS UNTUK KENDALA UMUM

Masalah PL maksimum baku mempunyai kendala yang semua tandanya ,

sedangkan PL minimum baku semua kendalanya bertanda . Jika kendala-kendalanya

bertanda , , atau =, maka dikatakan PL berkendala umum. Secara umum, langkah penyelesaiannya sama dengan PL maksimum baku atau minimum baku. Hanya saja ketika mengubah menjadi bentuk kanonik agak berbeda sedikit.

Jika kendala bertanda , maka ditambah variabel slack yang sekaligus menjadi

variabel basis. Jika kendala bertanda , maka ditambah variabel surplus di ruas kanan pertidaksamaan dan variabel artifisial (variabel artifisial akan menjadi variabel basis). Jika kendala bertanda = maka ditambah variabel artifisial yang akan berperan sebagai variabel basis.

Jika PL berpola memaksimumkan maka koefisien variabel artifisial pada fungsi tujuan adalah –M, sedangkan jika berpola minimum maka koefisien variabel artifisial adalah M dengan M bilangan positif yang cukup besar.

CONTOH 2

Akan dicari pasangan nilai x, y, z tak negatif yang

memaksimumkan

f

3 x

5 y

2 z

yang memenuhi

2

2 y

z

5

2

4 y

z

x

.

Kendala 1,

2 y

z

2

memuat sumber daya/suku tetap yang bernilai negatif sehingga harus dikalikan -1 menjadi

2 y

z

2

. Pada kendala 1 perlu ditambahkan

(11)

variabel surplus t dan variabel artifisial q. Kendala 2 sudah bertanda = sehingga tidak perlu ditambahklan variabel slack atau variabel surplus. Kendala 2 juga sudah memuat variabel basis, yaitu x.

Dengan demikian, PL siap simpleks (berbentuk kanonik) berbentuk:

Memaksimumkan

f

3 x

5 y

2 z

0 t

Mq

Dengan kendala

2 y

z

t

q

2

x

4 y

2 z

5 x

,

y

,

z

,

t

,

q

0

.

Selanjutnya, tabel simpleks masalah PL ini sebagai berikut.

j

c

3 5 2 0 -M i

c

x

_j i

x

x y z t q i

b

R

_i -M 3 q x 0 -2 1 -1 1 1 4 2 0 0 2 5 2 5/2 zj 3 12+2M 6-M M -M 15-2M zj-cj 0 7+2M 4-M M 0 15-2M 2 3 z x 0 -2 1 -1 1 1 8 0 2 -2 2 1 zj 3 20 2 4 -4 7 zj-cj 0 15 0 4 M-4 7 PO (x, y, z, t, q) = (1, 0, 2, 0, 0).

PO soal asli (x, y, z) = (1, 0, 2) dengan nilai maksimum f = 7.

SOAL LATIHAN

Tentukan PO dan nilai optimum masalah PL berikut dengan metode simpleks

1. Memaksimumkan

f

x

y

dengan kendala

0 , 11 3 9 2 2 2 y x y x y x y x

2. Maksimumkan

z

3 x

₁

2 x

₂

4 x

₃ dengan kendala

x

₁

x

₂

x

₃

10

,

5

3

(12)

3. Minimumkan

z

4 x

y

dengan kendala

3 x

y

3

,

4 x

3 y

6

,

4 2 y

x

,

x

, y

0

.

4. Minimumkan

z

3 x

₁

2 x

₂

4 x

₃ dengan kendala

4 x

₁

5 x

₂

2 x

₃

22

,

30

2

₂ ₃

1