Matrik perspektif dan sifat garis dalam gambar perspektif.

(1)

ABSTRAK

Pilipus Neri Agustima, 2015. Matrik Perspektif dan Sifat Garis Dalam Gambar

Perspektif. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan

Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.

Dalam kehidupan sehari-hari, terutama di kalangan arsitek dan seniman, dikenal teknik menggambar perspektif. Teknik menggambar perspektif merupakan suatu teknik menggambar sehingga diperoleh gambar yang lebih realistik, sesuai apa yang terlihat oleh mata. Gambar yang dihasilkan menggunakan teknik ini disebut gambar perspektif. Dalam dunia matematika, dikenal transformasi untuk menghasilkan gambar perspektif. Transformasi tersebut adalah proyeksi perspektif. Hasil dari proyeksi perspektif dapat dipandang sebagai titik tembus antara garis yang menghubungkan titik proyeksi dan titik yang terletak pada objek gambar dengan bidang proyeksi. Penelitian ini membahas matrik perspektif dan sifat garis dalam gambar perspektif.

Penelitian ini menggunakan metode studi pustaka. Buku acuan yang digunakan

adalah “Math and Art: An Introduction to Visual Geometry” karangan Sasho

Kaldjevski. Penelitian ini juga menggunakan konsep koordinat homogen dan transformasi sistem koordinat sehingga diperoleh matrik perspektif secara umum. Sedangkan sifat garis dalam gambar perspektif ditulis lengkap dengan pembuktian sifatnya.

(2)

ABSTRACT

Pilipus Neri Agustima, 2015. Perspective Matrix and Property of Line in Perspective

Drawing. Thesis. Mathematic Education Study Program, Mathematic and Science

Education Departement, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

In our life, especially for architect and artist, was known a term about perspective drawing. Perspective drawing is a technique to produce a realistic painting which appropriate to what was seen by eye. A painting which was produce from this techique is called perspective painting. But in mathematic, perspective drawing is known as perspective projection. Perspective projection is an intersect point between projective plane and a line segment which connected point of projection and any point in the object. This research is discussed about perspective matrik and property of line in perspective drawing.

This research use study method with “Math and Art: An Introduction to Visual Geometry” of Sasho Kaldjevski as a main book. This research use homogenous

coordinate and transformation of coordinate system concept to get the general perspective matrix. Beside that, property of line in perspective projection is written

with it’s verification.

The result of this research is a perspective matrix if coordinate point of projection and equation of plane projectian was given. Line has three property in perspective drawing, there are perspective painting of a line is a line, perspective painting a class of paralel lines which paralel to projection plane is a class of paralel lines in projection plane, perspective painting a class of paralel lines which not paralel to projection plane is a class of line which intersect in one point in projection plane. That point also known as vanishing point. And coordinate of vanishing point if coordinate of point of projection and equation of projection plane was given.

(3)

i

MATRIK PERSPEKTIF DAN SIFAT GARIS DALAM GAMBAR PERSPEKTIF

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Oleh:

PILIPUS NERI AGUSTIMA NIM :111414042

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(4)

(5)

(6)

iv

I have always studied,

no matter what the

result is...

HALAMAN PERSEMBAHAN

(7)

(8)

(9)

vii ABSTRAK

Pilipus Neri Agustima, 2015. Matrik Perspektif dan Sifat Garis Dalam Gambar

Perspektif. Skripsi. Program Studi Pendidikan Matematika, Jurusan

Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma.

Dalam kehidupan sehari-hari, terutama di kalangan arsitek dan seniman, dikenal teknik menggambar perspektif. Teknik menggambar perspektif merupakan suatu teknik menggambar sehingga diperoleh gambar yang lebih realistik, sesuai apa yang terlihat oleh mata. Gambar yang dihasilkan menggunakan teknik ini disebut gambar perspektif. Dalam dunia matematika, dikenal transformasi untuk menghasilkan gambar perspektif. Transformasi tersebut adalah proyeksi perspektif. Hasil dari proyeksi perspektif dapat dipandang sebagai titik tembus antara garis yang menghubungkan titik proyeksi dan titik yang terletak pada objek gambar dengan bidang proyeksi. Penelitian ini membahas matrik perspektif dan sifat garis dalam gambar perspektif.

Penelitian ini menggunakan metode studi pustaka. Buku acuan yang digunakan adalah “Math and Art: An Introduction to Visual Geometry” karangan Sasho Kaldjevski. Penelitian ini juga menggunakan konsep koordinat homogen dan transformasi sistem koordinat sehingga diperoleh matrik perspektif secara umum. Sedangkan sifat garis dalam gambar perspektif ditulis lengkap dengan pembuktian sifatnya.

Hasil dari penelitian ini adalah matrik perspektif yang dapat ditentukan jika koordinat titik proyeksi dan persamaan bidang gambar diketahui. Sifat-sifat garis dalam gambar perspektif meliputi gambar perspektif dari suatu garis lurus merupakan garis lurus, gambar perspektif dari garis-garis lurus yang saling sejajar dan sejajar dengan bidang proyeksi merupakan garis-garis lurus yang sejajar pula pada bidang proyeksi, gambar perspektif dari garis-garis lurus yang sejajar namun tidak sejajar dengan bidang proyeksi merupakan garis-garis lurus yang berpotongan di satu titik, yang disebut dengan titik lenyap. Penelitian ini juga menghasilkan koordinat titik lenyap jika koordinat titik proyeksi dan persamaan bidang proyeksinya diketahui..

(10)

viii ABSTRACT

Pilipus Neri Agustima, 2015. Perspective Matrix and Property of Line in

Perspective Drawing. Thesis. Mathematic Education Study Program,

Mathematic and Science Education Departement, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

In our life, especially for architect and artist, was known a term about perspective drawing. Perspective drawing is a technique to produce a realistic painting which appropriate to what was seen by eye. A painting which was produce from this techique is called perspective painting. But in mathematic, perspective drawing is known as perspective projection. Perspective projection is an intersect point between projective plane and a line segment which connected point of projection and any point in the object. This research is discussed about perspective matrik and property of line in perspective drawing.

This research use study method with “Math and Art: An Introduction to

Visual Geometry” of Sasho Kaldjevski as a main book. This research use homogenous coordinate and transformation of coordinate system concept to get the general perspective matrix. Beside that, property of line in perspective projection is

written with it’s verification.

(11)

ix

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa karena atas berkat dan rahmat-Nya lah saya dapat menyelesaikan skripsi dengan judul

“Matrik Perspektif dan Sifat Garis Dalam Gambar Perspektif”. Skripsi ini disusun dalam rangka melengkapi salah satu syarat untuk memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.

Banyak hambatan dan rintangan yang dialami oleh penulis selama penyusunan skripsi ini. Namun atas bantuan dan dukungan dari berbagai pihak, maka penulis dapat mengatasi segala hambatan dan rintangan yang dialami. Oleh karena itu, pada kesempatan kali ini penulis ingin mengucapkan terima kasih kepada:

1. Keluargaku, Bapak Agustinus Sarman dan Ibu Anastasia Sutinem, serta adikku Veronika Kania Anindita, yang selalu memberikan doa, dukungan dan semangat kepada penulis.

2. Bapak Dominikus Arif Budi Prasetyo, S.Si., M.Si. sebagai dosen pembimbing skripsi yang dengan sabar telah membimbing serta memberikan kritik dan saran selama penulis menyelesaikan skripsi ini. 3. Bapak Dr. M. Andy Rudhito selaku Kaprodi Pendidikan Matematika

Universitas Sanata Dharma serta dosen penguji skripsi, terima kasih atas bimbingannya selama ini.

4. Bapak Rohandi, Ph.D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan.

5. Ibu Veronika Fitri Rianasari, S.Pd., M.Sc., sebagai dosen pembimbing akademis yang telah memberikan bimbingan akademis selama penulis melaksanakan perkuliahan di Universitas Sanata Dharma.

6. Bapak Antonius Yudhi Anggoro selaku dosen penguji skripsi, terima kasih atas bimbingan dan sarannya selama ini.

(12)

x

menuntut ilmu di Program Studi Pendidikan Matematika Universitas Sanata Dharma sehingga penulis memperoleh ilmu yang berguna untuk menyelesaikan tugas akhir ini.

8. Bapak dan ibu karyawan Universitas Sanata Dharma, khususnya sekretariat JPMIPA dan perpustakaan Universitas Sanata Dharma atas segala jenis bantuan dan fasilitas yang telah diberikan.

9. Putu Diah Pramita Dewi yang dengan setia selalu menemani dan memberiku semangat selama penulisan tugas akhir ini.

10.Teman seperjuanganku, Singgih Satriyo Wicaksono, yang telah menemani dan membantuku mengatasi hambatan yang dialami selama penulisan tugas akhir ini.

11.Sahabat-sahabatku, Leonardus Igor Sidha Malelang, Chatarina Anjar Putri L.D., Emilia Jevina Lintang Puspita, Thevea Yurike Redianawati, Veronika Dyah Febriana, Yuliana Pebri Heriawati, Ana Karisma A.P., Regina Wahyudyah Sonata Ayu,Theresia Veni Dwi Lestari, Margaretha Nobilio Pasia Janu, Gregorius Andy Krismanto, dan Patricia Merdekawati yang telah menemaniku selama proses pembelajaran di Universitas Sanata Dharma.

12.Semua pihak yang telah membantu penulis menyelesaikan tugas akhir ini, baik secara langsung maupun tidak langsung yang tidak dapat disebutkan satu persatu.

Penulis menyadari bahwa masih banyak kekurangan dalam penulisan tugas akhir ini. Oleh karena itu, dengan rendah hati, penulis mengucapkan terima kasih atas kritik dan saran yang dapat membangun tugas akhir ini. Semoga tulisan ini dapat memberikan manfaat dan wawasan yang lebih kepada setiap pembacanya.

Yogyakarta, 21 April 2015

(13)

xi DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH .. vi

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xi

DAFTAR SIMBOL ... xiii

DAFTAR GAMBAR ... xiv

BAB I PENDAHULUAN ... 1

A. Latar Belakang ... 1

B. Batasan Masalah ... 2

C. Rumusan Masalah ... 3

D. Tujuan Penelitian ... 3

E. Manfaat Penelitian ... 3

F. Metode Penulisan ... 4

G. Sistematika Penulisan ... 5

BAB II LANDASAN TEORI ... 7

A. Titik, Garis dan Bidang dalam ℝ ... 7

B. Sistem Koordinat ... 17

C. Persamaan Garis dan Bidang Datar Dalam ℝ ... 19

D. Transformasi Sistem Koordinat ... 30

E. Proyeksi ... 37

(14)

xii

BAB III MATRIK PERSPEKTIF DAN SIFAT GARIS DALAM GAMBAR

PERSPEKTIF ... 45

A. Koordinat Gambar Perspektif ... 45

B. Matrik Translasi Salib Sumbu ... 57

C. Matrik Rotasi Salib Sumbu ... 60

D. Matrik Perspektif ... 64

E. Sifat Garis Dalam Gambar Perspektif ... 100

BAB IV PENUTUP ... 110

A. Kesimpulan ... 110

B. Saran ... 113

(15)

xiii

DAFTAR SIMBOL

′ : Koordinat hasil proyeksi perspektif dari titik A ℎ : Koordinat homogen dari titik A

: Koordinat titik proyeksi ℝ : Ruang Dimensi Dua ℝ : Ruang Dimensi Tiga

− − : Keantaraan, diantara dan

̅̅̅̅ : Segmen garis yang titik ujungnya berada di titik A dan titik B ⃗⃗⃗⃗⃗⃗ : Sinar garis yang titik pangkalnya adalah titik A dan melalui titik B ⃡⃗⃗⃗⃗ : Garis yang melalui titik A dan titik B

∥ : Sejajar

ℎ~ ℎ : koordinat homogen titik A dan koordinat homogen titik B merepresantisakan titik yang sama

: Matrik Perspektif

: Matrik Translasi Salib Sumbu : Matrik Rotasi Terhadap Sumbu Y : Matrik Rotasi Terhadap Sumbu Z

: Matrik Rotasi Total

(16)

xiv

DAFTAR GAMBAR

Gambar 2.1: Pembuktian Teorema 2.1 Gambar 2.2: Pembuktian Teorema 2.2 Gambar 2.3: Pembuktian Teorema 2.3 Gambar 2.4: Pembuktian Teorema 2.4 Gambar 2.5: Pembuktian Teorema 2.5 Gambar 2.6: Koordinat Kartesius Gambar 2.7: Sudut Arah Suatu Garis Gambar 2.8: Sudut Arah Garis Sebarang Gambar 2.9: Cosinus Arah Suatu Garis Gambar 2.10: Translasi salib sumbu pada ℝ Gambar 2.11: Translasi salib sumbu pada ℝ Gambar 2.12: Rotasi salib sumbu pada ℝ

Gambar 2.13: Rotasi salib sumbu pada ℝ dengan sumbu X sebagai poros Gambar 2.14: Rotasi salib sumbu pada ℝ dengan sumbu Y sebagai poros Gambar 2.15: Rotasi salib sumbu pada ℝ dengan sumbu Z sebagai poros Gambar 2.16: Proyeksi Paralel

Gambar 2.17: Proyeksi Perspektif

Gambar 2.18: Contoh Lukisan Tanpa Menggunakan Prinsip Proyeksi Perspektif Gambar 2.19: Contoh Lukisan Menggunakan Prinsip Proyeksi Perspektif Gambar 3.1 Bidang proyeksi = dan titik proyeksi , ,

Gambar 3.2 Gambar Perspektif salib-salib sumbu di bidang proyeksi x=k Gambar 3.3 Bidang proyeksi = dan titik proyeksi , ,

Gambar 3.4 Gambar Perspektif salib-salib sumbu di bidang proyeksi y=k Gambar 3.5 Bidang Proyeksi z = k dan Titik Proyeksi P , , p

(17)

xv

Gambar 3.10 Translasi Salib Sumbu Jika Bidang Proyeksi =

Gambar 3.11 Gambar Perspektif Dari Segiempat di bidang proyeksi = Gambar 3.12 Translasi Salib Sumbu Jika Bidang Proyeksi =

Gambar 3.13 Gambar Perspektif Dari Piramida . di bidang proyeksi = Gambar 3.14 Translasi Salib Sumbu Jika Bidang Proyeksi =

Gambar 3.15 Gambar Perspektif Dari Prisma . di bidang proyeksi = Gambar 3.16 Bilangan Arah dan Sudut Arah dari Bidang Proyeksi

Gambar 3.17 Rotasi Terhadap Sumbu Z Gambar 3.18 Rotasi Terhadap Sumbu Y’

Gambar 3.19 Ilustrasi Titik Proyeksi Berada di Sumbu Z’ Gambar 3.20 Ilustrasi Titik Proyeksi Tidak Berada di Sumbu Z’ Gambar 3.21 Sifat Garis Pada Gambar Perspektif 1

Gambar 3.22 Ilustrasi Titik V

(18)

1 BAB I PENDAHULUAN

A. Latar Belakang

Kata “geometri” berasal dari bahasa Yunani yaitu “geometrein” (“geo” artinya bumi dan “metrein” artinya pengukuran). Jadi secara harafiah, geometri berarti ilmu pengukuran bumi. Ahli sejarah Yunani bernama Herodotus dan Proculus (5 SM) mengatakan bahwa orang-orang yang memakai ilmu geometri pertama kali adalah orang-orang Mesir. Mereka menggunakan geometri untuk mengukur lahan mereka setelah banjir tahunan sungai Nil melanda daerah Mesir. Aristoteles menyetujui bahwa bangsa Mesir lah yang pertama kali menggunakan subjek geometri, tetapi dengan alasannya sendiri. Dalam bukunya yang berjudul

Metaphysics, Aristoteles berpendapat bahwa geometri di Mesir muncul

dikarenakan para pemuka agama di Mesir memiliki waktu yang sangat luang. (Owen Byer, 2010)

(19)

gambar yang dihasilkan tidak sesuai dengan apa yang mereka lihat. Kemudian muncullah keinginan dari para seniman untuk menghasilkan gambar pada bidang gambar sesuai dengan apa yang mereka lihat. Kemudian, pada tahun 1435, seorang seniman dari Florence, Italia bernama Leon Battista Alberti mengemukakan idenya mengenai salah satu metode menggambar yaitu costruzione legittima untuk menghasilkan gambar agar terlihat lebih nyata pada bidang gambar (David A. Thomas, 1998). Kemudian sekitar awal abad ke-19, berkembang sistem geometri yang lebih umum dari Geometri Euclides, yaitu geometri proyeksi. Proyeksi terbagi menjadi dua bagian yaitu proyeksi paralel dan proyeksi perspektif.

Selama perkuliahan di Universitas Sanata Dharma penulis memperoleh perkuliahan mengenai geometri ruang, geometri analitik ruang, geometri analitik bidang, dan aljabar linear elementer. Berdasarkan ide mengenai proyeksi perspektif dan apa yang telah diperoleh penulis pelajari pada perkuliahan-perkuliahan tersebut, penulis mencoba mengkaji proyeksi perspektif tersebut menggunakan pengetahuan-pengetahuan yang diperoleh pada saat perkuliahan geometri ruang, geometri analitik ruang, geometri analitik bidang dan aljabar linear elementer sehingga menghasilkan matrik perspektif dari suatu titik dan sifat-sifat garis dalam gambar perspektif.

B. Batasan Masalah

Pembahasan mengenai Proyeksi Perspektif dan Sifat-Sifat Garis Dalam Gambar Perspektif ini dibatasi pada:

(20)

2. Objek gambar berupa bangun datar dan bangun ruang sisi datar dalam ℝ .

C. Rumusan Masalah

Rumusan masalah dalam penelitian ini yaitu:

1. Bagaimana bentuk matrik perspektif jika koordinat titik proyeksi dan persamaan bidang proyeksinya diketahui?

2. Bagaimana sifat - sifat garis dalam gambar perspektif?

D. Tujuan Penelitian

Tujuan dalam penelitian ini adalah:

1. Untuk mengetahui bentuk matrik perspektif jika titik proyeksi dan persamaan bidang proyeksinya diketahui.

2. Untuk mengetahui sifat-sifat garis dalam gambar perspektif.

3. Untuk menentukan koordinat titik lenyap dari kumpulan garis-garis yang sejajar.

E. Manfaat Penelitian

Manfaat yang dapat diambil dari penelitian ini adalah: 1. Bagi Pembaca

(21)

2. Bagi Penulis

Penulis dapat menambah pengetahuan mengenai matrik perspektif dari suatu titik dan dapat menerapkan apa yang telah dipelajari selama perkuliahan sehingga dapat mengkaji kembali matrik perspektif dan sifat-sifat garis dalam gambar perspektif.

3. Bagi Universitas

Universitas dapat menambah koleksi skripsi dalam bidang geometri, khususnya mengenai geometri proyeksi dengan spesialisasi proyeksi perspektif.

F. Metode Penulisan

Metode yang digunakan oleh peneliti untuk menyusun skripsi ini adalah metode studi pustaka, yaitu dengan membaca referensi-referensi yang berkaitan dengan geometri ruang, geometri analitik ruang, geometri analitik bidang, aljabar linear elementer, dan gambar perspektif. Lalu peneliti mencoba mengkaji ulang gambar perspektif menggunakan apa yang telah dipelajari pada geometri ruang, geometri analitik ruang, geometri analitik bidang dan aljabar linear elementer. Pembahasan dalam skripsi ini mengacu pada buku “Math and Art: An Introduction to Visual Mathematics” karangan Sasho Kalajdzievski (2008).

Langkah-Langkah yang dilakukan dalam penelitian ini adalah:

(22)

2. Menyajikan ilustrasi atau gambaran mengenai gambar perspektif.

3. Menyajikan kembali beberapa teori pada geometri ruang, geometri analitik ruang, geometri analitik bidang, dan aljabar linear elementer.

4. Memberikan penjelasan yang diperlukan dan contoh-contoh dari teori yang digunakan.

5. Mencari hubungan antara geometri ruang, geometri analitik ruang, geometri analitik bidang, aljabar linear elementer dengan gambar perspektif.

6. Menyusun seluruh materi yang telah dikumpulkan secara runtut agar memudahkan pembaca dalam memahaminya.

G. Sistematika Penulisan

Tujuan akhir penulisan skripsi ini yaitu untuk mengetahui matrik perspektif dari suatu titik dan sifat-sifat garis dalam gambar perspektif. Untuk itu pada bab pertama disampaikan terlebih dahulu latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan dan sistematika penulisan dalam skripsi ini.

(23)

bab kedua akan dibahas pula mengenai matrik yang nantinya akan digunakan untuk pemahasan matrik perspektif dan sifat-sifat garis dalam gambar perspektif.

Bab ketiga yang merupakan inti dari penulisan ini berisi tentang Koordinat titik perspektif, matrik translasi salib sumbu, matrik rotasi salib sumbu, matrik perspektif, prinsip – prinsip dalam gambar perspektif, dan koordinat titik lenyap dari kumpulan garis sejajar yang tidak sejajar dengan bidang proyeksi. Pada bab tiga juga diberikan contoh-contoh yang terkait dengan proyeksi perspektif dan sifat-sifat garis dalam gambar perspektif.

(24)

7 BAB II

LANDASAN TEORI

Pada bab II, terlebih dahulu kita akan mempelajari titik, garis dan bidang melalui teorema-teorema. Setelah itu, akan dibahas pula sistem koordinat kartesius dan koordinat homogen. Kemudian setelah kita mempelajari garis dan bidang melalui teorema-teorema, kita akan mempelajari pula garis dan bidang datar secara analitik sehingga diperoleh persamaan garis dan persamaan bidang. Selanjutnya akan dipelajari transformasi salib sumbu dalam ℝ dan akan diperumum untuk ℝ . Karena skripsi ini membahas proyeksi perspektif, maka di subbab selanjutnya akan disajikan definisi umum tentang proyeksi dan macam-macam proyeksi yang salah satunya adalah proyeksi perspektif. Kemudian di bagian akhir dari bab ini, akan dibahas pula mengenai matrik.

Berikut ini adalah pembahasan titik, garis dan bidang dalam ℝ melalui teorema-teorema.

A. Titik, Garis dan Bidang dalam ℝ�

(25)

Postulat 2.1 (Zakaria T., -:5):

Melalui sebuah garis, dapat dibuat tak hingga banyak bidang yang melalui garis tersebut.

Diketahui bahwa � merupakan himpunan titik. Himpunan � memiliki anggota lebih dari satu titik. Definisi 2.1 berikut ini menjelaskan bahwa jika � merupakan himpunan titik-titik, maka � dikatakan kolinear jika semua titik pada himpunan � terletak pada satu garis yang sama.

Definisi 2.1 (Millman & Parker, 1991:22):

Misalkan � adalah himpunan titik-titik dalam ℝ dan memiliki lebih dari satu anggota. Himpunan � dikatakan kolinear jika ada sebuah garis sehingga � ⊆ .

Dengan kata lain, jika untuk semua garis ∈ ℝ , � ⊈ maka � dikatakan tidak kolinear. Postulat 2.2 berikut menyatakan sebuah bidang memiliki paling sedikit tiga titik yang tidak kolinear.

Postulat 2.2 (Owen & Felix, 2010:18)

Bidang memiliki sedikitnya tiga buah titik yang tidak kolinear.

(26)

bahwa tiga buah titik yang berbeda dan tidak kolinear terletak pada tepat satu bidang datar.

Teorema 2.1 (Zakaria, -:5):

Melalui tiga buah titik yang tidak kolinear dapat dilukiskan tepat satu bidang datar. Bukti: (lihat di buku Ilmu Ukur Ruang karangan Zakaria T. halaman 5)

Gambar 2.1

Melalui sebuah garis dan sebuah titik di luar garis tersebut dapat dilukis tepat satu bidang datar.

Bukti:

Titik A terletak di luar garis l. Ambil dua buah titik yang berbeda yang terletak pada garis l. Misalkan titik P dan Q. Berdasarkan Postulat 2.3, maka titik A,

P, dan Q terletak pada tepat satu bidang datar. ∎

(27)

Dalam ℝ terdapat tiga jenis kedudukan antara dua buah garis yang berbeda yaitu berpotongan, sejajar dan bersilangan. Definisi 2.2 berikut ini menjelaskan kedudukan antara dua buah garis.

Definisi 2.2:

Diberikan garis l dan garis m dalam ℝ . Kedudukan garis l terhadap garis m memenuhi salah satu kondisi berikut ini:

a. Berpotongan jika garis l memiliki satu titik persekutuan dengan garis m. b. Sejajar jika garis l dan garis m terletak pada satu bidang dan garis-garis tersebut

tidak memiliki satu titik persekutuan.

c. Bersilangan jika garis l dan garis m tidak terletak pada satu bidang dan garis tersebut tidak memiliki titik persekutuan.

Melalui dua buah garis yang saling berpotongan dapat dilukiskan tepat satu bidang datar.

Bukti:

(28)

Melalui dua buah garis yang sejajar hanya dapat dilukis sebuah bidang datar.

Gambar 2.4

Bukti:

Garis l dan garis g sejajar. Ambil sebarang titik yang terletak pada garis l . Misalkan titik A. Jelas bahwa titik A tidak dilalui oleh garis g. Hal ini dikarenakan � ∥ . Berdasarkan Teorema 2.1, maka dapat dibentuk sebuah bidang datar. ∎

Teorema 2.5 (Zakaria, -:5)

Melalui dua buah garis yang tidak berpotongan maupun tidak sejajar maka kita tidak dapat melukis sebuah bidang datar yang melalui garis-garis tersebut.

Bukti:

Andaikan dapat dilukiskan sebuah bidang melalui garis-garis tersebut. Berdasarkan teorema-teorema sebelumnya, maka kedua garis tersebut memiliki dua kemungkinan yaitu sejajar atau berpotongan. Kontradiksi dengan pernyataan kedua garis tidak sejajar maupun tidak berpotongan. ∎

(29)

Postulat 2.3 (Wallace and West, 1992:376):

Melalui satu titik di luar garis, hanya dapat dilukiskan sebuah garis yang sejajar dengan garis tersebut.

Postulat 2.3, menjelaskan bahwa dari satu titik di luar suatu garis, dapat dibentuk satu garis yang sejajar dengan garis pertama. Dengan kata lain jika satu titik terletak pada satu garis, maka kita tidak dapat melukiskan garis yang sejajar dengan garis pertama.

Definisi 2.3 (Prenowitz & Jordan, 1965:186)

Notasi untuk keantaraan adalah − − dan dibaca B di antara A dan C. Relasi keantaraan memenuhi sistem postulat berikut:

A.1 Jika − − maka − − . (Sifat Simetri)

A.2 Jika − − maka bukan − − . (Sifat Antisiklik)

A.3 , , adalah titik-titik yang berbeda dan kolinear jika dan hanya jika − − atau − − atau − − . (Koherensi Linear)

A.4 Misalkan titik kolinear dan berbeda dengan titik , , . Maka, − − mengakibatkan − − atau − − tetapi tidak keduanya. (Sifat Memisahkan)

(30)

Definisi 2.3 menjelaskan konsep keantaraan dari tiga buah titik. Postulat A.1 mengatakan jika titik B di antara titik A dan C, maka titik B juga diantara titik C dan

A. Postulat A.2 mengatakan bahwa jika titik B berada di antara titik A dan C tidak

sama dengan titik C di antara titik A dan B. Postulat A.3 merupakan biimplikasi sehingga dapat diartikan menjadi dua implikasi yaitu:

A.3(a) Jika titik A, B, C adalah titik-titik yang berbeda dan kolinear, maka (A-B-C) atau (B-C-A) atau (C-B-A).

A.3(b) Jika (A-B-C) atau (B-C-A) atau (C-B-A), maka titik A, B, C adalah titik-titik yang berbeda dan kolinear.

Postulat A.4 mengatakan jika titik P memisahkan titik A dan titik B, maka titik P juga memisahkan titik A atau B dari titik C tetapi tidak keduanya. Postulat A.5 mengatakan jika titik A tidak sama dengan titik B maka

A.5(a) ada sebuah titik yang dipisahkan oleh titik A dari titik B, dengan kata lain titik A berada di antara titik B dan suatu titik.

A.5(b) ada sebuah titik yang memisahkan titik A dari titik B.

A.5(c) ada sebuah titik yang dipisahkan oleh titik B dari titik A, dengan kata lain titik B berada di antara titik A dan suatu titik.

Setelah membahas konsep keantaraan, sekarang kita akan membahas konsep segmen garis dan sinar garis. Definisi 2.3 berikut menjelaskan segmen garis. Definisi 2.3 (Millman & Parker, 1991:52)

Jika dan adalah merupakan dua buah titik yang berbeda, maka segmen garis dari A ke B didefinisikan sebagai

(31)

Definisi 2.3 merupakan definisi dari segmen garis. Definisi 2.3 mengatakan bahwa segmen garis adalah himpunan titik-titik yang terletak di antara dua buah titik tertentu dan kolinear dengan dua buah titik tersebut. Selanjutnya akan dibahas mengenai jarak dua buah titik. Postulat berikut ini akan menjelaskan tentang jarak antara dua buah titik yang berbeda.

Postulat 2.4 (Owen & Felix, 2010:18):

Titik-titik pada suatu garis berkorespondensi dengan bilangan real sedemikian sehingga, 1) setiap titik yang ada pada garis berkorespondensi dengan tepat satu bilangan real. 2) setiap bilangan real berkorespondensi dengan tepat satu titik yang ada pada garis. 3) jarak antara dua buah titik merupakan nilai mutlak dari selisih bilangan real yang berkorespondensi dengan titik tersebut.

Postulat 2.4 memberikan definisi mengenai jarak antara dua buah titik. dalam postulat tersebut, jarak didefinisikan sebagai bilangan positif yang berkorespondensi dengan sepasang titik yang berbeda. Jarak bisa disebut sebagai panjang segmen garis. Setelah kita memahami konsep segmen garis, dan jarak antara dua buah titik, selanjutnya kita akan mempelajari konsep sinar garis. Definisi 2.4 berbicara mengenai sinar garis.

Definisi 2.4 (Millman & Parker, 1991:54)

Jika A dan B adalah dua titik yang berbeda, maka sinar garis dari A melewati B didefinisikan sebagai:

(32)

Sinar garis ⃗⃗⃗⃗⃗ merupakan himpunan bagian dari garis ⃡⃗⃗⃗⃗ . Sinar garis ⃗⃗⃗⃗⃗ merupakan himpunan titik-titik yang kolinear sedemikian sehingga titik berada di antara titik dan suatu titik. Titik dinamakan titik pangkal atau titik asal sinar garis ⃗⃗⃗⃗⃗ . Berikutnya akan dikenalkan konsep sudut. Dua buah garis berbeda yang berpotongan di satu titik membagi sebuah bidang datar menjadi beberapa daerah. Daerah yang dibatasi sinar-sinar garis tersebut dinamakan sudut seperti dijelaskan pada definisi 2.5 berikut ini.

Definisi 2.5:

Sudut adalah gabungan antara dua buah sinar garis berbeda yang memiliki satu titik pangkal.

Postulat 2.5 (Wallace & West, 1996:377):

Setiap sudut berkorespondensi dengan sebuah bilangan real diantara sampai .

Setelah memahami konsep sudut, selanjutnya akan dibahas mengenai kedudukan garis dan bidang. Dalam ℝ terdapat dua jenis kedudukan garis dan bidang yaitu garis menembus bidang, garis terletak pada bidang dan garis sejajar bidang. Definisi 2.6 berikut ini menjelaskan kedudukan antara garis dan bidang.

Definisi 2.6 (Zakaria, -:5):

(33)

Definisi 2.6 berbicara mengenai salah satu kedudukan garis dan bidang. Dengan kata lain, jika sebuah garis dan sebuah bidang tidak memiliki satu titik persekutuan, maka garis tersebut dikatakan sejajar dengan bidang. Setelah membahas hubungan antara sebuah garis dan sebuah bidang, kita akan mempelajari hubungan antara dua buah bidang. Secara umum tiga jenis kedudukan bidang yaitu sejajar, berpotongan dan berimpit. Definisi 2.7 berikut ini menjelaskan kedudukan antara dua buah bidang.

Definisi 2.7 (Zakaria, -:5):

Dua buah bidang dikatakan berpotongan jika dua buah bidang tersebut memiliki garis persekutuan.

Jika dua buah bidang datar mempunyai satu titik persekutuan, maka kedua bidang tersebut juga mempunyai sebuah garis persekutuan yang melalui titik tersebut.

Gambar 2.5

Bukti: (lihat di buku Ilmu Ukur Ruang karangan Zakaria T. halaman 6)

Definisi 2.8:

(34)

Setelah kita memahami tentang titik, garis dan bidang, kita akan mempelajari sistem koordinat Cartesius dalam ℝ dan koordinat homogen. Sistem koordinat kartesius akan sangat berguna untuk menentukan letak atau posisi suatu titik dalam ℝ dan akan sangat berguna untuk pembahasan selanjutnya tentang persamaan garis dan persamaan bidang. Sedangkan koordinat homogen akan sangat berguna untuk pembentukan matrik perspektif yang akan dibahas di bab III. Berikut ini pembahasan mengenai sistem koordinat.

B. Sistem Koordinat

Letak suatu titik yang terletak dalam ℝ dapat ditentukan dengan bantuan sistem koordinat ruang. Ada beberapa jenis sistem koordinat, tetapi dalam skripsi ini akan dibahas sistem koordinat Cartesius saja.

(35)

Gambar 2.6 Koordinat Cartesius

Dalam skripsi ini akan dikenalkan konsep baru yaitu koordinat homogen. Koordinat homogen akan sangat berguna untuk membentuk matrik perspektif yang merupakan topik dari skripsi ini. Berikut ini akan disajikan definisi dari koordinat homogen.

Definisi 2.9:

Jika suatu titik dalam ℝ memiliki koordinat , , maka dipilih ∈ ℝ sehingga koordinat homogen dari titik tersebut adalah , , , dengan = , = , =

dan ≠ , serta , , , merepresentasikan titik yang sama yaitu . . untuk ∈ ℝ dan ≠ .

(36)

Contoh 2.1:

Jika diketahui titik dengan koordinat , , − maka koordinat homogen dari titik , , − adalah _ℎ , , − , atau _ℎ , , − , . Kedua koordinat A_ℎ dan A_ℎ merepresentasikan satu titik yang sama yaitu titik , , − .

Setelah mempelajari garis dan bidang secara aksiomatik, maka pada subab ini akan membahas garis dan bidang secara analitik sehingga menghasilkan persamaan garis dan persamaan bidang. Berikut ini adalah pembahasan tentang persamaan garis dan persamaan bidang datar dalam ℝ .

C. Persamaan Garis dan Bidang Datar Dalam ℝ�

Sebelum kita mempelajari persamaan garis dan persamaan bidang, kita akan mempelajari terlebih dahulu sudut arah dan cosinus arah dari suatu garis dalam ℝ .

Definisi 2.10 (Charles & Irving, 1980:148):

Sudut Arah dari suatu sinar garis yang berpangkal di titik asal adalah sudut-sudut , , dan yang dibentuk oleh sinar garis tersebut terhadap sumbu positif, sumbu positif dan sumbu positif, sedemikian sehingga ° ≤ ≤ °, ° ≤ ≤

°, dan ° ≤ ≤ °.

(37)

Gambar 2.7 Sudut Arah

Sudut arah dari sebarang garis di ℝ adalah sudut arah dari sinar garis yang berpangkal di titik asal dan sejajar dengan garis tersebut. Gambar 2.7 merupakan ilustrasi dari sudut arah sebarang sinar garis yang pangkalnya tidak terletak di titik asal. merupakan sebarang sinar garis yang titik pangkalnya tidak terletak pada titik asal, sedangkan merupakan sinar garis yang sejajar dengan . Sudut-sudut , , dan merupakan sudut-sudut arah dari yang juga merupakan sudut-sudut arah dari sinar garis .

Gambar 2.8 Sudut Arah Garis Sebarang Definisi 2.11 (Charles & Irving, 1980:148):

Cosinus arah dari suatu garis adalah nilai cosinus dari masing-masing sudut arahnya.



l

 

  

(38)

Setelah memahami sudut arah dan cosinus arah, selanjutnya akan dipelajari teorema mengenai jarak antara dua buah titik dalam ℝ .

Teorema 2.7 (F. Riddle, 1996:318):

Jarak antara dua buah titik berbeda , , dan , , adalah

= √ − + − + −

(Bukti lihat di buku Analytic Geometry karangan Douglas F Riddle halaman 318)

Teorema 2.8 (Charles & Irving, 1980:149):

Jika d adalah jarak antara titik , , dan , , , maka cosinus arah dari garis yang melalui titik dan adalah

cos = − , cos = − , cos = −

Teorema 2.8 merupakan teorema mengenai cosinus-cosinus arah dari suatu garis yang melalui dua titik tertentu. Gambar 2.9 merupakan ilustrasi dari sudut-sudut arah suatu garis yang melalui titik , , dan titik , , .

Gambar 2.9 Cosinus Arah Suatu Garis yang melalui dua buah titik

 

2 2, 2, 2

A x y z

 

1 1, 1, 1 A x y z 





(39)

Untuk membantu memahami sudut arah dan cosinus arah suatu garis, maka perhatikan contoh berikut ini.

Contoh 2.2:

Jika suatu garis yang melalui titik , , dan , , , maka cosinus-cosinus arahnya adalah

= √ − + − + −

= √ + +

= √

cos = − = −

√ = √

cos = − = −

√ = −√

cos = − = −

√ = −√

Setelah pembahasan sudut arah dan cosinus arah dari suatu garis, sekarang akan dibahas mengenai bilangan arah dari suatu garis serta hubungan antara cosinus arah dan bilangan arah suatu garis.

Definisi 2.12 (Charles & Irving, 1980:150):

Bilangan arah [ , , ] dari suatu garis adalah tiga bilangan berurutan dari hasil kali antara cosinus arah garis tersebut dengan sebarang konstanta yang tidak sama dengan nol.

(40)

dengan sebarang konstanta k di mana ∈ ℝ dan ≠ . Untuk lebih memahami bilangan-bilangan arah suatu garis jika cosinus-cosinus arahnya diketahui, maka perhatikanlah contoh berikut ini.

Contoh 2.3:

Jika cosinus arah dari suatu garis adalah

cos = , cos = − , cos = ,

Di mana untuk sebarang k0, maka

[ , − , ]

Juga merupakan bilangan arah garis tersebut. Untuk k = − , bilangan arahnya adalah [− , , − ]; untuk = − , bilangan arahnya adalah [− , , − ].

Jika suatu garis melalui titik , , dan , , , maka untuk setiap bilangan arah [ , , ], ada sebarang bilangan real ≠ sedemikian sehingga

= − , = − , = −

Bukti:

Berdasarkan teorema 2.8 diperoleh:

cos = − , cos = − , cos = −

Berdasarkan definisi 2.12, diperoleh:

= . cos , = . cos , = . cos

(41)

= . − , = . − , = . − atau

= − , = − , = −

Dengan memisalkan = , maka diperoleh

= − , = − , = − ∎

Teorema 2.9 menjelaskan bahwa bilangan arah dari suatu garis yang melalui titik , , dan , , adalah [ − , − , − ]. Jika kita ambil nilai k 1, maka bilangan arah dari suatu garis yang melalui titik , , dan , , adalah [ − , − , − ]. Bilangan arah

[ − , − , − ] merupakan bilangan arah paling sederhana dari suatu

garis yang melalui dua titik yang diketahui. Untuk lebih memahami bilangan-bilangan arah dari suatu garis yang melalui dua buah titik yang diketahui, maka perhatikanlah contoh berikut ini.

Contoh 2.4:

Jika suatu garis melalui titik , , dan − , , , maka bilangan arah dari suatu garis yang melalui titik dan adalah

[ − − , − , − ]

atau bisa ditulis sebagai berikut

[− , , − ]

(42)

Untuk nilai = − , maka bilangan arah A A⃡⃗⃗⃗⃗⃗⃗⃗⃗ adalah [ , − , ].

Teorema 2.10 (Charles & Irving 1980:151):

Jika [ , , ] adalah himpunan dari bilangan arah suatu garis, maka cosinus arahnya adalah

cos =_{√ + +} , cos =

√ + + ,

cos =

√ + +

Setelah dibahas sudut arah, cosinus arah dan bilangan arah dari suatu garis, maka selanjutnya akan dibahas persamaan garis. Ada berbagai macam bentuk untuk menyatakan persamaan garis dalam ℝ , tetapi dalam skripsi ini akan digunakan persamaan parametrik dari suatu garis.

Teorema 2.11 (Charles & Irving, 1980:158): Jika suatu garis melalui titik , , dan

a) Jika bilangan arah garis tersebut [ , , ] dan tidak ada bilangan arah yang nol, maka persamaan garisnya adalah:

−

= − = −

b) Jika bilangan arah garis tersebut [ , , ] dan salah satu bilangan arahnya nol, maka persamaan garisnya adalah

(43)

iii. Jika = , maka = dan − = −

c) Jika bilangan arah garis tersebut [ , , ] dan dua dari bilangan arahnya nol, maka persamaan garisnya adalah

i. Jika = = , maka = dan = ii. Jika = = , maka = dan = iii. Jika = = , maka = dan =

(Bukti: buku Analytic Geometry karangan Charles C. Carico dan Irving Drooyan halaman158)

Teorema 2.10 a) merupakan persamaan kanonik atau persamaan umum dari suatu garis dalam ℝ di mana garis teresebut memiliki bilangan arah [ , , ]. Selain dalam bentuk persamaan kanonik, suatu garis juga dapat ditulis dalam bentuk parameter:

−

= − = − =

Persamaan di atas dikenal dengan persamaan parameter garis lurus dengan ∈ ℝ. Telah kita ketahui bahwa kedudukan dua garis dalam ℝ adalah sejajar, berpotongan dan bersilangan. Kedua garis yang sejajar, berpotongan dan bersilangan memiliki sudut yang dibentuk oleh kedua garis tersebut.. Berikut ini adalah pembahasan sudut antara dua garis pada ℝ .

Definisi 2.13 (Douglas F. Riddle, 1996:323):

(44)

Definisi 2.13 menjelaskan bahwa walaupun kedua garis dalam ℝ tidak berpotongan maupun tidak sejajar, kedua garis tersebut tetap memiliki sudut antara dua garis tersebut. Sudut antara dua garis tersebut merupakan sudut yang dibentuk oleh dua buah sinar garis yang sejajar dengan garis-garis tersebut dan berpotongan di satu titik

Dua buah garis yang memiliki bilangan arah [ , , ] dan [ , , ] akan: a) Sejajar jika dan hanya jika untuk sebarang ∈ ℝ dan ≠ berlaku

= , = , dan = b) Tegak lurus jika dan hanya jika

+ + =

Teorema 2.11 a) mengatakan bahwa dua buah garis yang memiliki bilangan arah [ , , ] dan [ , , ] dikatakan sejajar jika dan hanya jika bilangan arah dari salah satu garis merupakan perkalian bilangan arah garis yang lain dengan suatu konstanta yang tidak sama dengan nol. Sedangkan Teorema 2.11 b) mengatakan bahwa dua buah garis yang memiliki bilangan arah [ , , ] dan [ , , ] dikatakan tegak lurus jika dan hanya jika jumlah dari perkalian bilangan-bilangan arah yang seletak sama dengan nol.

Teorema 2.13 (F. Riddle, 1996:358):

(45)

Setelah kita mempelajari sudut antara dua garis dalam ℝ , maka kita akan mempelajari persamaan bidang datar dalam ℝ . Andaikan suatu garis yang melalui titik asal memiliki bilangan arah [ , , ]. Maka persamaan suatu bidang datar yang melalui titik , , dan tegak lurus dengan garis tersebut adalah:

+ + = + +

atau dapat dinyatakan juga dalam bentuk

+ + − − − =

atau

+ + + = di mana = − − −

Persamaan ini disebut dengan persamaan umum bidang datar dengan bilangan arah

[ , , ]dan melalui titik , , .

Selanjutnya akan dibahas sudut arah, cosinus arah dan bilangan arah dari suatu bidang datar. Sebelum membahas ketiga hal tersebut, perhatikanlah definisi berikut ini.

Definisi 2.14 (Charles & Irving, 1980):

Suatu garis yang tegak lurus dengan bidang datar disebut normal dari bidang datar tersebut (garis normal bidang).

(46)

+ + + =

Maka [ , , ] adalah bilangan-bilangan arah dari garis normal bidang atau bilangan-bilangan arah bidang tersebut dan

cos =_{√ + +}

adalah cosinus-cosinus arah bidang tersebut. Sedangkan , dan adalah sudut-sudut arah bidang tersebut.

Ada beberapa cara untuk menyatakan suatu persamaan bidang datar, salah satunya dengan persamaan bidang datar bentuk normal dari Hesse. Persamaan dari suatu bidang datar dapat dinyatakan dalam bentuk

cos + cos + cos + = dengan =

√ + +

Persamaan di atas dapat disebut dengan persamaan bidang datar bentuk normal dari Hesse di mana , dan adalah sudut-sudut arah dari bidang datar dan

n merupakan jarak bidang datar tersebut dari titik pangkal O. Untuk lebih

memahami persamaan bidang, maka perhatikan contoh berikut.

Contoh 2.6

Jika ⃡ memiliki bilangan arah [ , , − ]. Maka persamaan bidang datar yang tegak lurus dengan garis ⃡ dan melalui titik , , adalah

+ − − . − . + . =

(47)

Cosinus-cosinus arah bidang tersebut adalah

cos =_{√ + + −} = _√ = √

cos =_{√ + + −}− = −_√ = √

Persamaan normal Hesse bidang tersebut adalah

√ + √ + √ − √ =

Setelah kita memahami persamaan garis dan persamaan bidang, maka selanjutnya kita akan mempelajari transformasi sistem koordinat. Transformasi sistem koordinat yang dibahas adalah transformasi di ℝ , namun selanjutnya diperumum menjadi transformasi sistem koordinat dalam ℝ . Berikut adalah pembahasan transformasi sistem koordinat.

D. Transformasi Sistem Koordinat

Menurut Fuller & Tarwater (1986:90) transformasi sistem koordinat adalah proses perubahan sistem koordinat yang lama ke sistem koordinat yang baru. Dalam skripsi ini akan dibahas transformasi sistem koordinat berupa translasi salib sumbu dan rotasi salib sumbu.

1. Translasi (Pergeseran) Salib Sumbu

(48)

dibahas teorema yang berkaitan dengan translasi salib sumbu yang akan digunakan untuk pembahasan dalam skripsi ini.

Teorema 2.14 (Charles & Irving, 1980:75)

Jika titik asal ′ dari sumbu-sumbu ′ ′ memiliki koordinat , pada

Gambar 2.10 Translasi Salib Sumbu pada ℝ

Gambar 2.10 merupakan ilustrasi dari translasi salib sumbu pada ℝ . Dari gambar tersebut, titik , ditranslasikan ke sebuah titik yang memiliki koordinat , sehingga terbentuklah sumbu-sumbu baru yaitu

′ dan ′ yang sejajar dengan sumbu dan .

(49)

relasi antara koordinat titik , , pada sumbu-sumbu dengan koordinat titik ′ ′, ′, ′ pada sumbu-sumbu ′ ′ ′ dinyatakan dalam persamaan

= ′₊ ′_{= −}

= ′₊ _atau ′_{= −}

= ′₊ ′_{= −}

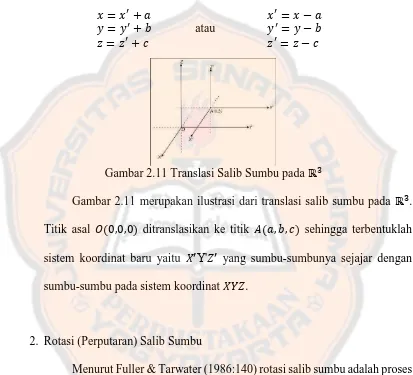
Gambar 2.11 Translasi Salib Sumbu pada ℝ

Gambar 2.11 merupakan ilustrasi dari translasi salib sumbu pada ℝ . Titik asal , , ditranslasikan ke titik , , sehingga terbentuklah sistem koordinat baru yaitu ′Y' ′ yang sumbu-sumbunya sejajar dengan sumbu-sumbu pada sistem koordinat .

2. Rotasi (Perputaran) Salib Sumbu

(50)

Teorema 2.15 (Charles & Irving, 1980:87)

Jika sumbu-sumbu dan dirotasikan terhadap titik asal , dengan sudut rotasi � terhadap sumbu + sehingga menghasilkan sumbu-sumbu baru yaitu sumbu-sumbu ℝ , maka relasi antara koordinat titik , pada sumbu-sumbu dengan koordinat titik ′ ′, ′ pada sumbu-sumbu ℝ dinyatakan dalam persamaan

= ′ _{� − ′} _�

= ′ _{� + ′} _�

atau

′₌ _{� +} _�

′ _{= −} _{� +} _�

Gambar 2.12 Rotasi ℝ

Berdasarkan teorema 2.15 maka persamaan rotasi salib sumbu akan diperumum untuk ℝ , sehingga dalam ℝ terdapat tiga macam rotasi salib sumbu yaitu rotasi salib sumbu terhadap sumbu , rotasi salib sumbu terhadap sumbu , dan rotasi salib sumbu terhadap sumbu .

a. Rotasi Salib Sumbu Terhadap Sumbu

(51)

pada sebarang titik di ℝ tetap sedangkan komponen dan komponen nya berubah dan dapat dinyatakan dalam persamaan

′_{= cos � + sin �}

′ _{= − sin � + cos �}

Gambar 2.13 Rotasi ℝ terhadap sumbu X

Jika suatu titik memiliki koordinat , , dan salib-salib sumbunya dirotasikan terhadap sumbu sejauh dengan sudut rotasi � terhadap sumbu , maka koordinat titik tersebut terhadap salib sumbu yang baru dapat dicari dengan persamaan

′ ₌

′_{= cos � + sin �}

′ _{= − sin � + cos �}

Jadi koordinat titik tersebut adalah , cos � + sin � , − sin � + cos � terhadap salib sumbu yang baru.

b. Rotasi Salib Sumbu Terhadap Sumbu

(52)

′ _{= −} _{� +} _�

′ ₌ _{� +} _�

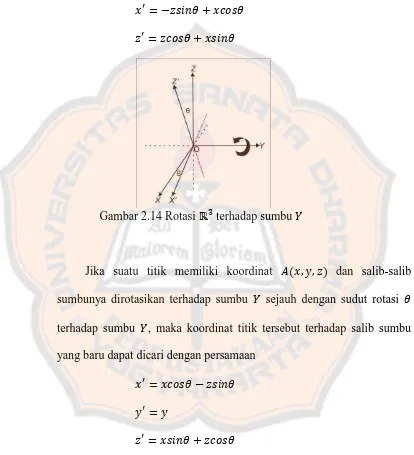
Gambar 2.14 Rotasi ℝ terhadap sumbu

Jika suatu titik memiliki koordinat , , dan salib-salib sumbunya dirotasikan terhadap sumbu sejauh dengan sudut rotasi � terhadap sumbu , maka koordinat titik tersebut terhadap salib sumbu yang baru dapat dicari dengan persamaan

′ ₌ _{� −} _�

′₌

′ ₌ _{� +} _�

Jadi koordinat titik tersebut adalah � − �, , � + � terhadap salib sumbu yang baru.

c. Rotasi Salib Sumbu Terhadap Sumbu

(53)

′ ₌ _{� +} _�

′_{= −} _{� +} _�

Gambar 2.15 Rotasi ℝ terhadap sumbu

Jika suatu titik memiliki koordinat ( , , )x y z dan salib-salib sumbunya dirotasikan terhadap sumbu sejauh dengan sudut rotasi � terhadap sumbu +, maka koordinat titik tersebut terhadap salib sumbu yang baru dapat dicari dengan persamaan

′ ₌ _{� +} _�

′_{= −} _{� +} _�

′ ₌

Jadi koordinat titik tersebut adalah � + �, − � + �, terhadap salib sumbu yang baru.

(54)

mengenai proyeksi. Pada bagian awal akan disajikan definisi umum dari proyeksi, namun selanjutnya akan dibahas proyeksi perspektif yang merupakan topik utama dari skripsi ini.

E. Proyeksi

Ada berbagai macam jenis proyeksi. Namun terlebih dahulu kita akan melihat definisi proyeksi secara umum.

Definisi 2.15 (Foley & Dam, 1983):

Proyeksi merupakan transformasi dari suatu titik dalam sistem koordinat ℝ menjadi titik dalam sistem koordinat yang lebih kecil dari dimensi asalnya.

Dalam pembahasan kali ini proyeksi yang digunakan adalah proyeksi dari ℝ ke ℝ . Proyeksi dari suatu benda yang ada di ℝ dapat dihasilkan dari sinar-sinar garis yang berasal dari suatu titik tertentu dan melalui setiap titik pada benda tersebut serta memotong suatu bidang datar. Sinar-sinar garis disebut proyektor, titik tertentu disebut titik proyeksi, dan bidang datar disebut bidang proyeksi. Berdasarkan letak titik proyeksi terhadap bidang proyeksi, proyeksi dibagi menjadi dua yaitu proyeksi paralel dan proyeksi perspektif.

1. Proyeksi Paralel

(55)

paralel secara umum, sedangkan Gambar 2.16 b mengilustrasikan proyeksi orthogonal.

a b

Gambar 2.16 Proyeksi Paralel 2. Proyeksi Perspektif

Proyeksi Perspektif adalah proyeksi di mana titik proyeksinya terletak di suatu tempat yang berhingga. Gambar 2.15 mengilustrasikan proyeksi perspektif.

A b

c

Gambar 2.17 Proyeksi Perspektif

(56)

Teknik menggambar perspektif merupakan suatu teknik menggambar yang bertujuan untuk menghasilkan gambar dari beberapa objek dalam ℝ sesuai dengan apa yang terlihat ke ℝ dalam bidang gambar sehingga ketika kita melihat gambar tersebut, kita dapat membayangkan objek-objek tersebut secara nyata (Sasho Kalajdzievski, 2008:169). Pada teknik menggambar perspektif ini, titik proyeksi dengan benda dipisahkan oleh bidang proyeksi.

Gambar 2.16 Gambar 2.17

Gambar 2.16 merupakan suatu lukisan yang dihasilkan tanpa menggunakan teknik menggamar perspektif sedangkan gambar 2.17 merupakan suatu gambar yang dihasilkan dengan menggunakan teknik menggambar perspektif.

F. Matrik

(57)

sehingga susunan bilangan-bilangan tersebut membentuk suatu segi empat beraturan. Definisi 2.16 di bawah ini menjelaskan pengertian matrik.

Definisi 2.16 (Howard Anton, 2010:26):

Matrik adalah susunan bilangan-bilangan yang teratur sedemikian sehingga membentuk segi empat beraturan. Bilangan-bilangan yang terdapat di dalam susunan tersebut dinamakan elemen dari matrik

Contoh 2.7:

[ ], [ ], [ ], [ ]

Di dalam matrik, susunan bilangan-bilangan tersebut ditentukan oleh baris dan kolom. Baris merupakan susunan yang horisontal, sedangkan kolom merupakan susunan yang vertikal. Ukuran dari suatu matrik ditentukan oleh banyaknya baris dan kolom dari matrik tersebut dan dituangkan ke dalam definisi 2.17 berikut ini.

(58)

Contoh 2.8:

Matrik pertama pada contoh 2.7 memiliki 4 baris dan 3 kolom, maka ukuran matrik tersebut dapat ditulis × .

Dalam menuliskan nama matrik akan digunakan huruf kapital, sedangkan untuk menuliskan elemen matrik akan digunakan huruf kecil. Matrik A yang berukuran × dapat dituliskan dengan A _×

Contoh 2.9: diagonal utama dari A.

11 12 1

Definisi 2.18 (Howard Anton, 2010:27)

(59)

Definisi 2.19 (Howard Anton, 2010:27)

Jika A dan B adalah dua buah matrik yang memiliki ukuran yang sama, maka jumlah dari matrik A dan B (A+B) adalah suatu matrik yang elemen-elemennya merupakan jumlahan dari elemen matrik A yang berkorespondensi dengan elemen matrik B. Selisih dari matrik A dan B (A-B) adalah suatu matrik yang elemen-elemennya merupakan selisih dari elemen-elemen dari matrik A yang berkorespondensi dengan elemen matrik B.

Definisi 2.19 menjelaskan operasi penjumlahan dan operasi pengurangan antara dua buah matrik A dan matrik B. Selain operasi penjumlahan dan operasi pengurangan, operasi perkalian juga berlaku dalam matrik. Operasi perkalian dalam matrik terbagi menjadi dua yaitu perkalian matrik dengan skalar dan perkalian matrik dengan matrik. Definisi 2.20 dan definisi 2.21 berikut ini menjelaskan operasi perkalian di dalam matrik.

Jika A adalah suatu matrik dan ∈ ℝ, maka hasil dari A adalah suatu matrik yang diperoleh dengan cara mengalikan setiap elemen pada matrik A dengan . Matrik

A disebut hasil kali skalar dari matrik A.

(60)

Contoh 2.10:

Jika matrik 2 1 0 2

A   _

 , maka

6 3

3

0 6

A   _

 

Jika A _× dan B _× , maka hasil perkalian matrik A dengan matrik B adalah suatu matrik yang berukuran × yang elemen-elemennya didefinisikan sebagai berikut:

= ∑ .

=

di mana ≤ ≤ dan ≤ ≤ .

Untuk lebih memahami perkalian antara matrik dengan matrik, maka perhatikan contoh 2.11 berikut ini.

Contoh 2.11:

(61)

[ ] . [ ] = [ ]

   

1.2  1.1 3

Perhitungan untuk elemen yang tersisa sebagai berikut: . + . =

. + . =

. + . = A. B = [ ]

. + . =

(62)

45 BAB III

MATRIK PERSPEKTIF DAN SIFAT GARIS DALAM GAMBAR PERSPEKTIF

Setelah mempelajari teori-teori pada bab II, maka pada bab III kita akan mempelajari matrik perspektif dan sifat garis dalam gambar perspektif. Perspektif merupakan suatu konsep yang setiap hari kita alami, contohnya adalah ketika kita melihat, pembentukan bayangan ketika proses pengelihatan kita menggunakan konsep perspektif. Hal yang sama terjadi ketika kita menggambil gambar dari kamera. Teknik menggambar construzione legittima juga menggunakan konsep perspektif.

A. Koordinat Gambar Perspektif

Sebelum kita mencari matrik perspektif dari suatu titik, mari kita terlebih dahulu mencari koordinat hasil proyeksi perspektif dari suatu titik. Koordinat hasil proyeksi perspektif merupakan koordinat titik tembus dari garis yang menghubungkan titik proyeksi dengan objek.

1. Koordinat titik proyeksi P( , , ) dan bidang proyeksi =

(63)

titik yang terletak pada objek yang akan digambar sedangkan A′ ′, ′, ′ merupakan koordinat hasil proyeksi perspektif titik A , , . Pada gambar 3.1 terlihat bahwa A′ terletak pada bidang proyeksi yang memiliki persamaan =

, sehingga komponen pertama dari koordinat titik A′ sama dengan . Dengan kata lain koordinat dari titik A′ berbentuk A′ , ′, ′ .

Gambar 3.1 Bidang proyeksi = dan titik proyeksi ( , , )

Perhatikan segmen garis yang melalui titik P dan A PA̅̅̅̅ . Persamaan garis yang melalui titik P( , , ) dan titik A , , adalah:

− � =

− �− =

−

�− =

⟹ − �

� = �= � =

atau dapat ditulis menjadi persamaan parametrik yaitu:

{ = . ( − ) += .

= .

titik tembus PA⃡⃗⃗⃗ dengan bidang x = k adalah:

( − ) + =

(64)

= − � koordinat titik proyeksi adalah P( , , ), maka hasil proyeksi perspektif titik A , , adalah titik A′ dengan koordinat ( , ( �− )

�− ,

( �− ) �− ).

Untuk lebih memahami koordinat hasil proyeksi perspektif jika koordinat titik proyeksi adalah P( , , ) dan bidang proyeksi memiliki persamaan =

, maka perhatikanlah contoh berikut ini.

Contoh 3.1 :

(65)

Dari rumus yang telah diperoleh, maka koordinat hasil proyeksi perspektif titik

A − , , − adalah:

, _{− −}− ,−_{− −}−

= , . ,− .

= , , −

Pada contoh 3.2 berikut ini kita akan mencari hasil proyeksi perspektif sumbu Y. Hasil yang diperoleh pada contoh 3.2 akan digunakan untuk mengambil kesimpulan hasil proyeksi perspektif sumbu Z.

Contoh 3.2:

Akan ditentukan hasil proyeksi perspektif sumbu Y jika koordinat titik proyeksi berada di P , , , serta bidang proyeksi adalah bidang = dan x ≠ k. Titik yang melalui sumbu Y memiliki koordinat , , , akibatnya berdasarkan rumus yang telah diperoleh, hasil proyeksi perspektif untuk titik tersebut adalah ( , ( �− )

�− ,

( �− )

�− ) = ( , ( − �) , ). Karena ∈ ℝ, ∈

ℝ dan ∈ ℝ, maka ( −

�) ∈ ℝ . Akibatnya himpunan titik ( , ( −

�) , ) juga merupakan sumbu Y pada bidang proyeksi yang sejajar dengan sumbu Y dalam ruang dan berjarak k satuan dari sumbu Y di ruang.

(66)

sumbu Y′ yang merupakan hasil proyeksi perspektif sumbu Y dalam ℝ . Gambar 3.2 mengilustrasikan gambar proyeksi dari salib sumbu Y dan Z.

Gambar 3.2 Hasil Proyeksi Perspektif salib-salib sumbu di bidang proyeksi x=k

2. Koordinat titik proyeksi P( , , ) dan bidang proyeksi = .

Gambar 3.3 yang merupakan ilustrasi untuk mencari koordinat hasil proyeksi perspektif dari titik A , , dengan titik proyeksi P( , , ) dan persamaan bidang proyeksinya = . Pada gambar 3.4, A , , merupakan titik yang terletak pada objek yang akan digambar sedangkan A′ ′, ′, ′ merupakan koordinat hasil proyeksi dari titik , , . Pada gambar terlihat bahwa A′ terletak pada bidang proyeksi yang memiliki persamaan = , sehingga komponen kedua dari koordinat titik A′ sama dengan . Dengan kata lain koordinat dari titik A′ berbentuk A′ ′, , ′ .

(67)

Perhatikan segmen garis yang melalui titik P dan A

(68)

= �− �− �. = �( �− )

�− �

Jadi jika bidang proyeksinya berjarak k satuan dari bidang XOZ dan koordinat titik proyeksi adalah P( , , ), maka hasil proyeksi perspektif titik A , , adalah titik A′ dengan koordinat ( ( �− )

�− , ,

( �− ) �− ).

Untuk lebih memahami koordinat hasil proyeksi perspektif jika koordinat titik proyeksi adalah P( , y , ) dan bidang proyeksi memiliki persamaan = maka perhatikanlah contoh berikut ini.

Contoh 3.3 :

Akan dicari koordinat hasil proyeksi perspektif titik A , − , jika koordinat titik proyeksi adalah , , dan bidang proyeksinya adalah = . Dari rumus yang telah diperoleh, maka koordinat hasil proyeksi perspektif titik

(69)

Contoh 3.4:

Akan ditentukan hasil proyeksi perspektif sumbu X jika koordinat titik proyeksi berada di P( , , ) serta bidang proyeksi adalah bidang = . Ingat bahwa sumbu X berada di sisi lain dari bidang proyeksi yang tidak memuat koordinat titik proyeksi. Titik yang melalui sumbu X memiliki koordinat , , , akibatnya berdasarkan rumus yang telah diperoleh, hasil proyeksi

perspektif untuk titik tersebut adalah ( ( �− ) �− , ,

( �− )

�− ) = ( ( − �) , , ).

Karena ∈ ℝ, ∈ ℝ dan ∈ ℝ, maka ( −

�) ∈ ℝ Akibatnya himpunan titik ( ( −

�) , , ) juga merupakan sumbu x pada bidang proyeksi yang sejajar dengan sumbu X dalam ruang dan berjarak satuan dari sumbu X di ruang.

(70)

Gambar 3.4 Hasil Proyeksi Perspektif Salib-Salib Sumbu di Bidang Proyeksi y=k

3. Koordinat titik proyeksi P( , , ) dan bidang proyeksi = .

Gambar 3.6 yang merupakan ilustrasi untuk mencari koordinat hasil proyeksi perspektif titik A , , dengan persamaan bidang proyeksinya =

. Pada gambar 3.5, A , , merupakan titik yang terletak pada objek yang akan digambar sedangkan A′ ′, ′, ′ merupakan koordinat hasil proyeksi perspektif dari titik A , , . Pada gambar terlihat bahwa A′ terletak pada bidang proyeksi yang memiliki persamaan = , sehingga komponen kedua dari koordinat titik A′ sama dengan k. Dengan kata lain ′ = Akibatnya koordinat dari titik A′ berbentuk A′ ′, ′, ′ .

(71)

−

(72)

Jadi jika bidang proyeksinya berjarak satuan dari bidang XOY dan koordinat titik proyeksi adalah P( , , ), maka hasil proyeksi perspektif titik A x, y, z adalah titik A′ dengan koordinat ( ( �− )

�− ,

( �− ) �− , ).

Untuk lebih memahami mengenai koordinat gambar perspektif jika koordinat titik proyeksi adalah P( , , z ) dan bidang proyeksi memiliki persamaan = , maka perhatikanlah contoh berikut ini.

Contoh 3.5 :

Akan dicari koordinat hasil proyeksi perspektif titik A , , − jika koordinat titik proyeksi adalah P , , dan bidang proyeksinya adalah = . Dari rumus yang telah diperoleh, maka koordinat hasil proyeksi perspektif titik

A , , − adalah:

− − − ,

= ( . , . , )

= ( , , )

(73)

Contoh 3.6:

Akan ditentukan hasil proyeksi perspektif sumbu X jika koordinat titik proyeksi berada di P( , , ), serta bidang proyeksi adalah bidang = . Titik yang melalui sumbu X memiliki koordinat , , , akibatnya berdasarkan rumus yang telah diperoleh, hasil proyeksi perspektif untuk titik tersebut adalah ( ( �− )

�− ,

( �− )

�− , ) = ( ( − �) , , ).Karena ∈ ℝ, ∈ ℝ, dan ∈ ℝ , maka ( −

�) ∈ ℝ. Akibatnya himpunan titik ( ( −z�) , ) juga merupakan sumbu pada bidang proyeksi yang sejajar dengan sumbu X dalam ruang dan berjarak satuan dari sumbu X di ruang.

Begitu pula dengan sumbu pada bidang proyeksi akan berjarak satuan dengan sumbu Y pada ruang. Akibatnya pada bidang proyeksi akan digunakan koordinat kartesius dengan sumbu Y′ yang merupakan hasil proyeksi perspektif sumbu Y dalam ℝ dan sumbu X′ yang merupakan hasil proyeksi perspektif sumbu Y dalam ℝ . Dalam kasus seperti ini, X′ akan menjadi sumbu X di bidang gambar. Sedangkan Y′ akan menjadi sumbu Y pada bidang gambar. Gambar 3.6 mengilustrasikan gambar proyeksi dari salib sumbu X dan Y.

(74)

Setelah kita memperoleh koordinat-koordinat titik proyeksi, maka selanjutnya kita akan mencari matrik translasi salib-salib sumbu dan matrik rotasi salib-salib sumbu dalam ℝ . Pertama-tama akan kita pelajari terlebih dahulu matrik translasi salib sumbu.

B. Matrik Translasi Salib Sumbu

Matrik translasi salib sumbu adalah suatu matrik yang berguna untuk mendapatkan hasil translasi salib sumbu jika salib sumbu digeser ke titik , , . Hasil translasi salib sumbu diperoleh dengan cara mengalikan matrik translasi dengan titik A , , . Pada bab II subbab D telah dibahas mengenai translasi salib sumbu serta diperoleh rumus translasi sebagai berikut:

′, ′, ′ = − , − , −

dapat ditulis dalam bentuk:

′ _{= −}

′_{= −}

Jika ditulis dalam bentuk persamaan matrik menjadi:

[ ′′

′] = [ ] . [ ]

...(1)

(75)

sehingga koordinat homogen dari titik A , , adalah A_h , , , dan koordinat homogen dari titik hasil proyeksi prspekifnya adalah A′_h − , − , − , . Kita pilih matrik translasi salib sumbu berupa suatu matrik yang berukuran × .

Misalkan matrik perspektifnya adalah = [ ], maka

[

Jadi matrik translasi salib sumbu ke titik , , adalah

= [

− − − ]

(76)

Contoh 3.7:

Akan dicari koordinat titik ′ jika koordinat titik A , , dan titik asal ditranslasikan ke titik B , − , . koordinat homogen dari titik A , , adalah Ah , , , . Karena titik asal ditranslasikan ke titik B , − , , maka matrik translasi dari salib-salib sumbunya adalah

= [

−

− ]

Maka koordinat thomogen dari titik _ℎ′ adalah

[ ′ ′ ′] = [

−

− ] [ ]

= [− ]

Dari perhitungan di atas diperoleh koordinat titik A′_h adalah A′_h , − , , dan merupakan koordinat homogen dari titik A′ , − , .

(77)

C. Matrik Rotasi Salib Sumbu

Matrik rotasi salib sumbu adalah suatu matrik yang berguna untuk mendapatkan hasil rotasi salib sumbu jika salib sumbu dirotasikan dengan sudut rotasi �. Pada tulisan ini akan digunakan rotasi salib sumbu terhadap sumbu Y dan rotasi salib sumbu terhadap sumbu Z untuk memperoleh matrik perspektif. Hasil rotasi salib sumbu diperoleh dengan cara mengalikan matrik rotasi dengan titik

A , , .

1. Matrik Rotasi Salib Sumbu Terhadap Sumbu Y Pada bab II subbab D diperoleh persamaan

′ _{= cos � − sin�}

′₌

′_{= sin � + cos�}

Jika persamaan diatas ditulis dalam bentuk operasi matrik maka diperoleh

[ ′′ ′] = [

cos� −sin�

sin� cos� ] . [ ]

Maka matrik rotasi salib sumbu terhadap sumbu adalah

= [cos� −sin�

sin� cos� ]